1. INTRODUCCIÓN
En este artículo presentaremos los resultados de nuestro trabajo de investigación6 en torno a la incorporación de la computadora, en el marco de la enseñanza de las funciones en los primeros años de la Educación Secundaria (ES) (alumnos de 12 a 14 años).
La investigación se desarrolló en el seno de un Grupo Colaborativo (GC) integrado por profesores de Matemática de ES y docentes-investigadores de la Universidad Pedagógica Nacional (UNIPE). Nos propusimos, en forma colaborativa, diseñar, implementar y estudiar en su funcionamiento una propuesta para el aula que integre la computadora al trabajo matemático de los estudiantes entorno a la modelización con funciones. A partir de la decisión de incorporar en el diseño el software libre GeoGebra, analizamos los desafíos que debe afrontar la enseñanza cuando asume la posición de preservar el rol de productor de conocimientos matemáticos de los estudiantes. En ese sentido, el diseño con-templa la gestión docente de espacios de intercambio y producción colectiva de conocimientos en los cuales intervienen procedimientos de resolución realizados con la computadora. Frente a este escenario, donde se despliegan nuevos tipos de tareas, nuevos asuntos a discutir y nuevas formas de organizar la dinámica de la clase, consideramos que los resultados de nuestro estudio aportan elementos para comprender la riqueza potencial de un tipo de trabajo que resulta impensable sin la utilización de recursos tecnológicos.
En el marco del trabajo colaborativo, se diseñó7 una secuencia de actividades que fue implementada en las aulas donde enseñan algunos integrantes del grupo, se observó y analizó lo sucedido en esas clases, se ajustó la propuesta y se volvió a implementar. En este proceso iterativo -que distingue todas las investigaciones llevadas adelante por el grupo- identificamos tres planos8 de trabajo:
— La reflexión sobre el propio dispositivo de trabajo grupal, que se va modificando en la búsqueda de la conformación genuina de un grupo colaborativo.
— La producción colaborativa de una secuencia de enseñanza para un determinado tema del currículo con la incorporación de la computadora a las actividades diseñadas, y su implementación en algunas de nuestras aulas.
— El estudio de fenómenos relativos al trabajo matemático con computadora en el aula, a partir de los materiales recogidos durante la implementación.
En relación con el primer plano identificado, en la sección 3 abordaremos aspectos generales de la organización de la investigación colaborativa y algunas reflexiones acerca de la construcción de la colaboración.
En cuanto al segundo plano, en la sección 4 presentamos aspectos generales de la secuencia diseñada, resaltamos las diversas representaciones puestas en juego y mencionamos diferentes tareas que deberán realizar los estudiantes.
Respecto al tercer plano, que es el foco de interés en este artículo, en la sección 5 presentamos tres episodios de aula. El análisis que realizamos sobre los mismos nos permitió identificar diferentes fenómenos inherentes al uso de la computadora, que trascienden el trabajo con esta propuesta en particular.
A continuación, en la sección 2, daremos cuenta de las referencias teóricas que dan un marco tanto a las tareas de diseño como a la etapa de análisis. En particular, nos detendremos en algunos autores que abordan el papel de las representaciones cuando está involucrada la pantalla de una computadora.
2. ALGUNOS ELEMENTOS TEÓRICOS Y REFERENCIAS A OTRAS INVESTIGACIONES
2.1 Teoría de Situaciones Didácticas
La Teoría de Situaciones Didácticas (Brousseau, 1998) es un marco de referencia que ha acompañado el trabajo del GC y del equipo de investigación desde sus inicios, fundamentalmente en el proceso de diseño y planificación de las secuencias de enseñanza/aprendizaje. En esta teoría el alumno es modelizado como un sujeto que produce conocimiento matemático al interactuar con situaciones que son propuestas por el docente. La situación didáctica engloba el conjunto de interacciones que ocurren entre un sujeto que aprende y un medio (milieu). Es, por lo tanto, un concepto que sobrepasa la idea de problema incluyendo el conjunto de decisiones que el docente toma para hacer evolucionar el conocimiento matemático de sus alumnos. Las interacciones entre el docente y los alumnos, a propósito de la interacción del estudiante con el medio, se modelizan a través de la noción de contrato didáctico.
2.2 Investigaciones sobre la incorporación de TIC en el aula de matemática
En el campo de la investigación en educación matemática se sostiene que el trabajo con TIC trae aparejado un cambio en el tipo de conocimiento que se produce. Al respecto en Sessa, Duarte, Cicala, Borsani y Di Rico (2018) se sostiene:
La inclusión del trabajo con software educativo en los procesos de enseñanza y de aprendizaje plantea la necesidad de tomar en cuenta modificaciones en relación con el trabajo matemático de los alumnos y el trabajo matemático-didáctico de los profesores. En referencia a la actividad de los alumnos, los cambios se presentan tanto en los problemas y tareas que se pueden abordar, como en las formas de abordarlos y en las posibles técnicas que se constituyen. Al respecto diríamos que se incorporan actividades que no serían factibles para la enseñanza sin computadora. (p. 16)
Las nociones del Enfoque Instrumental (Trouche, 2004; Drijvers, Kieran y Mariotti, 2010), que asume la complejidad de la enseñanza de la matemática mediada por la tecnología, nos aportan elementos teóricos para pensar nuestra investigación.
De acuerdo con este enfoque el uso de una herramienta tecnológica implica un proceso de génesis instrumental, en el cual el objeto o artefacto se convierte en un instrumento. Este instrumento es un constructo psicológico, que combina el artefacto y los esquemas (en el sentido de Vergnaud, 1996) que el usuario desarrolla para usarlos frente a tipos específicos de tareas. (Drijvers, Doorman, Boon, Reed y Gravemeijer, 2010, p. 214) (La traducción es nuestra)
Para Trouche (2004), la construcción del instrumento implica un movimiento en dos direcciones, un “ida y vuelta” dialéctico entre el sujeto y la computadora -o el programa-: mediante el uso del programa el sujeto desarrolla y se apropia de esquemas de acción que se transforman en técnicas para resolver nuevas tareas (instrumentación) al mismo tiempo que el programa, desde el punto de vista del sujeto, se irá dotando de nuevas funciones y potencialidades (instrumentalización) (p. 184).
Arcavi y Hadas (2000), estudian el aporte del entorno tecnológico cuando los estudiantes abordan situaciones geométricas a través de modelos funcionales vía entornos dinámicos (como es el caso de la secuencia que diseñamos). Estos autores señalan algunos aspectos de la actividad matemática que se ven enriquecidos por el uso de la tecnología:
— La exploración empírica potenciada por el acceso a muchas representaciones de casos particulares y a las transiciones dinámicas entre ellos. Estas exploraciones posibilitarían un inter-juego entre exploraciones, conjeturas/anticipaciones y retroalimentaciones.
— La coordinación entre los cambios en los estados de la situación geométrica y el movimiento de un punto en el gráfico de una función que expresa la relación entre dos magnitudes de las figuras involucradas en el modelo geométrico. Esto daría lugar a observar y estudiar nuevos aspectos de la situación y de la función que podrían quedar ocultos al estudiar los cambios en forma separada.
Estos autores señalan que, en líneas generales, este tipo de propuestas promueve un ambiente experimental en la clase de matemática que probablemente cambie la naturaleza del aprendizaje.
2.3 El papel de las representaciones
Diferentes investigadores en didáctica de la matemática buscaron formas de caracterizar el conocimiento en matemática. Autores como Vergnaud (1990) y Janvier (1987) han señalado el papel central de las representaciones en la actividad matemática. Por su parte, Douady (1986) y Duval (1995), en trabajos ya clásicos en la disciplina, plantean, como condición para la evolución de las concepciones y nociones, la interacción del estudiante con situaciones que permitan desplegar un “juego de marcos” y cambios de “registros de representación”. En particular Duval (2006), sostiene que “la comprensión conceptual surge de la coordinación de los diversos sistemas semióticos usados” (p.167).
En el mismo texto, Duval señala:
La única forma de acceder y trabajar con ellos [los objetos matemáticos] es a través de signos y representaciones semióticas. Sin embargo, la necesidad de signos no se limita a esto, pues su principal papel no es representar objetos matemáticos sino trabajar en ellos y con ellos, sustituyendo unos signos por otros (p. 157).
La actividad matemática requiere una coordinación interna, que ha de ser construida, entre los diversos sistemas de representación que pueden ser elegidos y usados; sin esta coordinación, dos representaciones diferentes significarían dos objetos diferentes, sin ninguna relación entre ambos. (p. 145)
En relación con las funciones y los gráficos cartesianos, tema central en nuestra investigación, la incorporación de un software da entrada a nuevas formas de representación y modifica las condiciones en las cuales se realiza el cambio de un registro de representación a otro, cambio que Duval (1995) considera indisolublemente asociado al proceso de conceptualización. En un entorno informático como el GeoGebra, las reglas de uso en torno a las representaciones en la pantalla hacen que la conversión entre registros de representación -esto es, producir una representación a partir de otra en otro registro- sea automática y se realice sin mucho costo para los alumnos9. Esto nos lleva a preguntarnos cómo se ve afectada la valencia epistémica10 del trabajo de conversión. Se podría pensar que necesariamente hay que proponer a los estudiantes tareas de transformación para ser realizadas en “lápiz y papel” o, asumir el desafío de diseñar tareas en un entorno informático que generen condiciones potentes para la coordinación entre registros de representación. Esta es nuestra posición y uno de los objetivos de la actividad que presentaremos en este artículo.
El trabajo con funciones utilizando el programa GeoGebra trae la novedad de poder disponer de representaciones múltiples -es decir, en varios registros de representación- y ligadas en la pantalla. La riqueza potencial de esto último para el aprendizaje es destacada por Morgan et al. (2009) mencionando también a otros autores:
El beneficio pedagógico parece residir en la modificación de las posibilidades funcionales [affordances] que ofrecen estas nuevas contrapartes computacionales de la representación estándar y en la posibilidad de enlaces automáticos entre diferentes representaciones. [véanse, por ejemplo, los micromundos Function Probe (Confrey y Smith 1994), Function Explorer (Olsen 1995), SimCalc (Kaput y Schorr 2008) y, para una discusión general sobre la potencialidad de múltiples representaciones para desarrollar el concepto de función, véase Yerushalmy y Schwartz (1993)]. (p. 247) (La traducción es nuestra)
En el diseño de nuestra secuencia, hemos aprovechado esta posibilidad de representaciones múltiples y ligadas de una función. En el apartado 3 de la sección 5 analizaremos un episodio en el aula que permite entender -en ese particular- la riqueza que posibilita este tipo de representación en el proceso de aprendizaje de los estudiantes.
Morgan et al. (2009), refiriéndose a un trabajo realizado en un equipo multinacional, con diversidad de marcos teóricos, relatan: “A basic formulation of the notion of representation was thus agreed: ‘something which stands for something else from someone’s point of view’’’11 (p. 242). A partir de esta definición, las autoras realizan un estudio en el cual examinan la distancia entre las representaciones usuales en “lápiz y papel” y aquellas producidas en las pantallas de la computadora, trabajando con algún programa de geometría dinámica. Las diferencias que aparecen entre los procesos de conversión de registro en ambos medios y la existencia de representaciones múltiples y ligadas en la pantalla -sin correlato en las representaciones sobre una hoja de papel- son ejemplos de estas distancias. Las autoras señalan que el hecho de que haya evidentes similitudes visuales entre las representaciones en ambos medios puede hacer que la distancia entre ellas sea opaca para un estudiante. Más aún, un estudiante podría considerar la imagen producida en la pantalla como una representación de imágenes similares en “lápiz y papel”, más que como representación de un objeto matemático. Esta última consideración nos va a permitir hacer una interpretación del episodio que analizaremos en el apartado 2 de la sección 5.
3. ACERCA DE NUESTRO TRABAJO COLABORATIVO
Los profesores que integran el GC trabajan en forma conjunta desde el año 2008.12 Desde entonces se reúnen quincenalmente el primer día de la semana por lo que adoptó internamente el nombre de “Grupo Lunes”. A lo largo de estos años se encararon distintos proyectos con el propósito de pensar de manera compartida la enseñanza de la matemática, diseñando propuestas para diferentes contenidos curriculares cuyo funcionamiento se analiza a partir de la implementación en sus propias aulas. Con esta dinámica se elaboraron diversos documentos destinados a los docentes del sistema con el propósito de que este material -rico en ideas, experiencias y análisis- resulte un insumo para pensar la enseñanza.13
Desde el año 2012, a partir del vínculo institucional de algunos integrantes, el trabajo del GC se encuadra en proyectos de investigación de la UNIPE. El equipo de docentes-investigadores de la Universidad cuyos integrantes son parte del GC, a las reuniones quincenales que realiza la totalidad del grupo, suma reuniones semanales en las cuales trabaja a partir y, frecuentemente, en función de las reuniones del GC.14 En el año 2017, dos profesoras que integran el GC desde el inicio, logran disponer del tiempo y comienzan a participar de las reuniones semanales en la Universidad. Se nos presenta entonces la disposición de tiempo como una variable relevante en relación con la decisión de participar en las distintas instancias de trabajo del GC. El tiempo y las condiciones laborales de los docentes universitarios, diferentes de aquellas de los profesores de ES, juegan un rol decisivo.
Por otro lado, los profesores que conforman el GC construyen -o reconstruyen- una posición investigativa, de indagación frente a los hechos del aula. El proceso grupal de diseño de una propuesta alberga preguntas que son tenidas en cuenta tanto en la implementación como en el análisis. En ese sentido, el aula es un espacio de indagación donde los docentes (tanto el que está a cargo del curso como los que observan15 la clase) despliegan cada propuesta teniendo en cuenta las preguntas elaboradas en la instancia de planificación y atentos al surgimiento de nuevas cuestiones para estudiar con el GC. Estas consideraciones nos llevan a hacer más difusa la frontera que distinguiría el trabajo que realiza el equipo universitario de aquel que lleva adelante el grupo colaborativo completo.
La relación entre las dos instancias de trabajo -los encuentros del GC y las reuniones intermedias del equipo de docentes-investigadores- es objeto de discusión y revisión permanente y un asunto de constante reelaboración por parte de todos. Al respecto, Sadovsky, Quaranta, Itzcovich, Becerril y García (2015) señalan que realizar un trabajo compartido entre investigadores y docentes obliga a considerar la colaboración misma como objeto de reflexión:
Construir un espacio colaborativo supone, como hemos señalado, un trabajo a largo plazo que implica rupturas tanto para los docentes como para los investigadores. Se trata de tejer un tipo de vínculo cuyas características no se conocen a priori. En este sentido las cuestiones metodológicas son constitutivas de la colaboración. (p. 224)
En particular, en las reuniones del equipo de docentes-investigadores, al retomar las problemáticas surgidas en los encuentros del GC, se nos plantea la necesidad de estar alertas para no perder de vista los intereses y preguntas originales. Por ejemplo, persisten interrogantes acerca del modo de devolver a todo el GC de manera genuina lo elaborado por el equipo de docentes-investigadores y cómo hacer accesible a los docentes, en el tiempo acotado de una reunión, los resultados de las investigaciones en el campo. En un plano más general, esta última cuestión interpela la relación entre las producciones teóricas en Didáctica de la Matemática y los docentes.
4. ACERCA DE LA SECUENCIA DISEÑADA
En esta sección presentamos aspectos generales de la secuencia diseñada, con el objetivo de ofrecer elementos para situar el análisis de los episodios que desarrollaremos en la próxima sección16.
La secuencia requiere la presencia de computadoras en el aula y el trabajo de los estudiantes con un archivo GeoGebra, diseñado por nuestro grupo.17 Está ubicada curricularmente al comienzo del tema funciones en la ES y en particular, a continuación de algunas actividades de lectura e interpretación de gráficos realizadas en “lápiz y papel”. Se asume que la noción de función con la que abordarán los estudiantes estos problemas es muy incipiente. Esta secuencia tiene como intención enriquecer este concepto, entendiéndolo ahora como modelo para estudiar la variación de magnitudes geométricas.
El trabajo funcional que se les propone se apoyará en el registro numérico y en el de gráficos cartesianos. En particular, estos últimos -que serán accesibles en una vista gráfica (VG) del archivo- estarán ligados a una figura dinámica representada en un registro geométrico en otra VG, sin poner en juego las fórmulas de las funciones involucradas.
Más específicamente se trata de estudiar una situación geométrica que contiene un triángulo dinámico, construido adentro de un rectángulo18 (ver figura 1).
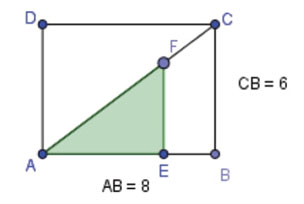
Figura 1: Imagen de la figura geométrica dinámica que se presenta al inicio de la secuencia en la VG1 del archivo GeoGebra.
La tarea de los estudiantes, inicialmente, se centra en la manipulación de un archivo GeoGebra -provisto por nosotros- con este modelo dinámico en la VG1. En esta primera etapa se pregunta qué cambia y qué no cambia de la figura dinámica al desplazar el punto F sobre el segmento AC. Nos interesa desplegar en el aula distintas posibilidades de magnitudes variables, para destacar el hecho de que la función que se elegirá es una entre varias posibles y no está determinada por la situación.
Luego se elige una primera función (la variación del área del triángulo AEF en función de la medida de AF) y se habilita la VG2 donde se representará su gráfico. Al principio se ubican puntos aislados de la función y luego se introduce un punto P móvil. Este punto está ligado a la figura geométrica dinámica por su definición ya que, para cada posición del punto F, la coordenada “x” del punto P es la medida de AF y la coordenada “y” es el área del triángulo que se obtiene en esa posición. De esta manera, al mover el punto F en la VG1, el punto P actualizará sus coordenadas y se “desplazará” -ligado al movimiento de F- por el plano cartesiano de la VG2 (ver figura 2).
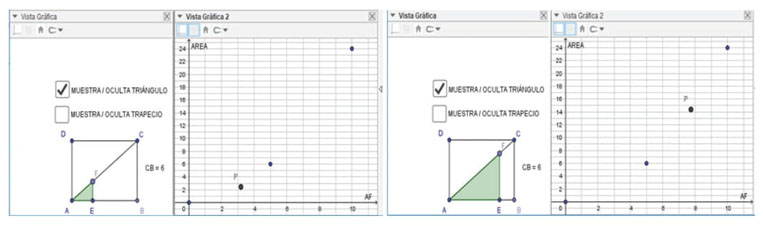
Figura 2: Dos imágenes de la pantalla con diferente ubicación del punto P en la VG2 para dos posiciones distintas del punto F de la VG1.
Luego se incorpora la gráfica completa de la función que, junto con los primeros puntos ubicados, el punto P móvil y la figura geométrica dinámica, conforman una representación que compromete, de manera ligada, el registro geométrico y el registro de gráficos cartesianos en el marco funcional (ver figura 3).
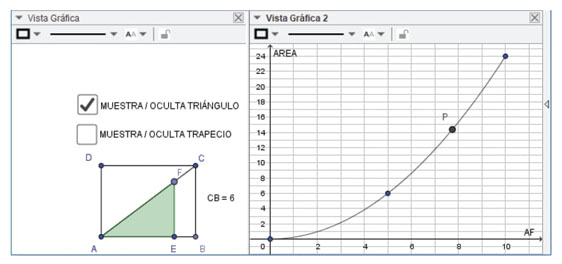
Figura 3: Imagen de la pantalla con la representación gráfica de la función en la VG2, y un estado de la situación geométrica dinámica en la VG1. El punto P sobre el gráfico está ligado al punto F en la diagonal del rectángulo.
Consideramos que este complejo sistema de representación resulta potente para trabajar una noción central para el concepto de función como es la variabilidad entre las magnitudes.
En la siguiente etapa, se define y estudia una nueva función: la relación entre el área del trapecio ADGF y la medida de AF (ver figura 4). De manera análoga a lo realizado con el estudio del triángulo AEF, se graficará esta nueva función mediante el punto móvil Q. El trabajo propuesto con esta función es una nueva oportunidad para que los estudiantes manipulen este sistema de registros y reinviertan las formas de trabajo desplegadas en la primera etapa.
Por último, se les propone estudiar las dos funciones simultáneamente. Es así como, en las últimas actividades de la secuencia, deberán trabajar con la representación de las dos gráficas y sus respectivos puntos móviles ligados a la figura geométrica dinámica (ver figura 4).

Figura 4: Imagen de la pantalla con las representaciones gráficas de las dos funciones en la VG2, y un estado de la situación geométrica dinámica en la VG1. Los puntos P y Q están ligados ambos al punto F en la diagonal del rectángulo.
Nos interesa poner de relieve que, a medida que se avanza con las actividades19 en la secuencia, se produce un incremento en la complejidad de las representaciones con las que los estudiantes deben interactuar: se comienza con una figura geométrica dinámica en una sola vista gráfica (uno de cuyos estados se muestra en la figura 1) y en las últimas actividades los estudiantes deben interactuar con una sofisticada pantalla como la que se observa en la figura 4.
El hecho de que la posición de los puntos móviles P y Q dependa del estado de la figura dinámica permite proponer tareas que, como se verá en la siguiente sección, requieran de los estudiantes una cierta coordinación entre un trabajo centrado en el marco geométrico y otro centrado en el marco funcional.
5. FENÓMENOS IDENTIFICADOS EN TORNO AL TRABAJO DE LOS ESTUDIANTES CON COMPUTADORA
En esta sección presentaremos tres episodios -identificados a partir de observaciones realizadas en las aulas de dos profesoras de nuestro grupo, en distintos momentos de trabajo con la secuencia- que nos van a permitir estudiar ciertos fenómenos relativos al trabajo de los estudiantes mediado por computadora. En todos ellos juegan un papel central las representaciones en la pantalla que van produciendo los estudiantes. Como dijimos en la sección 4, a medida que se avanza en las actividades de la secuencia las representaciones con las que interactúan van incorporando nuevos elementos. Los tres episodios serán presentados según la complejidad creciente de la representación que están considerando los estudiantes:
Episodio 1. Los invariantes en la situación geométrica: de la visualización a la incorporación de propiedades en la argumentación.
Episodio 2. Posibles interpretaciones de los estudiantes sobre el efecto que produce la herramienta “zoom”.
Episodio 3. El papel de las representaciones múltiples y dinámicas en los diálogos que mantienen dos estudiantes a propósito de un conocimiento en construcción.
5.1. Los invariantes en la situación geométrica: de la visualización a la incorporación de propiedades en la argumentación
En este episodio pudimos identificar los siguientes asuntos relativos al papel de las representaciones en la pantalla:
— Estudiantes que están trabajando en computadoras distintas, y visualizando imágenes diferentes mientras dialogan en torno a propiedades de una figura dinámica, formulan enunciados contrapuestos.
— Durante el trabajo colectivo de pruebas y refutaciones de una propiedad aparecen tensiones entre los argumentos matemáticos y las visualizaciones en la pantalla.
Como dijimos, la secuencia comienza por una situación geométrica dinámica en la VG1 de un archivo GeoGebra en la cual se propone a los estudiantes identificar magnitudes que varían y otras que no, como instancia previa a la selección de una función particular. La primera tarea para los estudiantes es:
| Actividad 1. Exploren el modelo dinámico moviendo el punto F que está sobre la diagonal AC |
| ¿Qué cambia y qué no cambia al mover el punto F? Respondan por escrito. |
Al diseñar la secuencia de trabajo pensamos que el momento de discusión colectiva generaría buenas condiciones para que surjan argumentos que permitan justificar las afirmaciones. Los argumentos, necesariamente, deberían apoyarse en relaciones matemáticas y permitirían ir más allá de la certeza dada por la visualización en la pantalla.
Nos detendremos en algunos intercambios que se produjeron entre los estudiantes en esa instancia de discusión colectiva, posterior a la resolución autónoma de la tarea 1 en pequeños grupos. Como se verá en el fragmento que vamos a analizar, la docente cumplirá funciones importantes en el sostenimiento de la discusión: por ejemplo, cuida que el trabajo más privado de algunos alumnos encuentre un lugar en el espacio colectivo y, en otro momento, plantea preguntas para que las expresiones de algunos estudiantes puedan ser comprensible para la mayoría.
1 M: nosotros dijimos que lo que no cambia es la jerarquía de los lados
2 Docente (D): ¿qué quieren decir?
3 M: Como que el lado AF es siempre el más largo, AE poco más largo, y FE es siempre el más corto.
4 D: (en referencia a uno de los grupos): acá las chicas están moviendo porque les parece que no, pero están viendo.
5 V (una chica de ese grupo): Creemos que el triángulo AFE puede ser isósceles.
6 T (una chica de otro grupo): No, eso no puede ser. Los ángulos son siempre iguales, en ningún caso puede ser isósceles.
7 D: ¿Qué ángulos?
8 T: Del triángulo. Cuando movés F los ángulos siguen siendo de la misma amplitud y A no puede llegar a ser de 45°
(Se escucha que V habla bajito)
9 D: A ver… las chicas acá dicen (refiriéndose al grupo de V), que A es de 45° y acá ella (refiriéndose a T) dice que no, ¿qué opinan los demás?
(Se oyen varios “no”, hablan todos juntos.)
10 D: A ver… Analicemos esto. Si yo tengo un rectángulo con la diagonal…
11 V: La diagonal es bisectriz del ángulo… (hace un pequeño silencio) …
¡¡¡Ah!!!… ya entendimos…
12 D: Lo que ustedes dicen pasa si es un cuadrado.
13 V: Claro
Nos interesa detenernos en la oposición que expresa V, en la intervención 5, a la afirmación de M, en la intervención 3. Interpretamos que las afirmaciones de los estudiantes se sustentan en lo visual y que los alumnos “están viendo” cosas contrapuestas. De hecho, estos dos estudiantes están trabajando en computadoras diferentes y manipulan el archivo de manera autónoma. En particular, el grupo de V, al mover el punto F hacia el vértice A, llegaba a triángulos pequeños en los cuales era difícil visualizar la diferencia entre las longitudes de los catetos, tal como afirmaba M. Es probable que ambos estudiantes estuvieran apoyando sus afirmaciones en la visualización de triángulos de diferentes tamaños generados por el movimiento del punto F.
Estas impresiones, contrarias desde lo visual, dan origen a una discusión donde se comienza a incorporar relaciones matemáticas. Es así como, en la intervención 6, T se centra en los ángulos, afirmando que sus medidas no cambian al mover el punto F; probablemente apela a la propiedad de la congruencia de los ángulos correspondientes considerando como paralelas dos posiciones del segmento EF. Con esta afirmación de T quedaría descartada la posibilidad de que los triángulos que visualizan M y V tengan ángulos de diferente medida. T concluye su intervención afirmando que no habrá triángulos isósceles. Gracias a un pedido de la docente, T explicita sus argumentos centrando su atención en el ángulo A del cual afirma que no mide 45°. En este caso estaría poniendo en juego otra relación: como todos los triángulos son rectángulos, si fueran isósceles, los dos ángulos iguales de cada triángulo deberían medir 45°.
Nuevamente no hay acuerdo en el aula, esta vez en torno a la afirmación de T sobre la medida del ángulo A. De esta manera el contenido de la discusión avanza desde la conservación de “la jerarquía de los lados” -observada en la pantalla por M- hacia la pregunta sobre si los ángulos de alguno de los triángulos pueden ser de 45°. El grupo de la estudiante V -que inicialmente sostenía que había algún triángulo isósceles en la familia- afirma ahora que el ángulo A mide 45°, y posteriormente lo justifica recurriendo a la siguiente propiedad: la diagonal de un rectángulo divide a los ángulos en partes iguales, que solo es válida para los cuadrados.
En estos intercambios los argumentos matemáticos, correctos e incorrectos, que ponen en juego algunos estudiantes se hacen necesarios para dirimir entre dos asuntos opuestos que diferentes actores “ven” en sus pantallas.
En la intervención 4 podemos observar, a partir del comentario de la docente, que los alumnos están utilizando la computadora como medio de constatación o refutación de lo que afirma un compañero. Tener la computadora disponible habilita un diálogo entre las interacciones que están sucediendo en la clase y las respuestas del programa. De esta manera, los estudiantes tienen una herramienta potente tanto para comunicar sus ideas como para indagar e interpretar las de otros a partir de la visualización en la pantalla y la exploración de la figura dinámica de la situación a la que se está haciendo referencia.
Si bien los alumnos que están en posiciones contrapuestas utilizan la misma figura dinámica, posiblemente estén moviendo el punto F de manera diferente y, como consecuencia, estén viendo triángulos diferentes. Considerando una representación como “algo que representa alguna otra cosa para alguien” (Morgan et al., 2009), una misma imagen podría representar algo distinto para distintos sujetos. En el caso de las representaciones dinámicas, además, lo que “ve” cada sujeto depende del movimiento que realiza (en nuestro ejemplo pueden enfocarse en zonas distintas de la figura dinámica) y entonces, distintos sujetos podrían estar viendo imágenes diferentes
En la intervención 8, T hace referencia al movimiento como vía de acceso a los invariantes de la situación dinámica, las medidas de los ángulos que se mueven y el ángulo A, que es fijo. En relación con esto, Arcavi y Hadas (2000) sostienen que el dinamismo de los programas permite, a partir de una figura particular, estudiar las variaciones, tener indicios visuales de invariantes, y dar una base intuitiva para las justificaciones formales de conjeturas (p. 25). Consideramos que la intervención de T expresa de manera clara un tipo de mirada sobre la figura dinámica: lo que no cambia en el movimiento. Esto le permite el acceso a ciertas relaciones y propiedades de la situación que aportan nuevos elementos a la discusión y a la producción de argumentos, aún desde su lugar de conjeturas sostenidas en la evidencia empírica.
Si bien en este episodio los estudiantes avanzan autónomamente hacia la producción de argumentos matemáticos y la docente se enfoca en la gestión de la circulación de la palabra, en otras ocasiones podría ser necesaria una participación más activa del docente para que el trabajo en el aula no se agote en la formulación de una propiedad a partir de lo que “se ve en la pantalla” y que la elaboración de argumentos basados en propiedades matemáticas tenga lugar y sentido en la clase.
5.2. Posibles interpretaciones de los estudiantes sobre el efecto que produce la herramienta “zoom”
Para estudiar el episodio que será presentado a continuación nos vimos ante la necesidad de precisar las siguientes cuestiones, que devienen del hecho de que el trabajo matemático que realizan los alumnos está mediado por la computadora:
— El trabajo con la computadora implica acciones del usuario que producen una respuesta del programa. Estas respuestas necesitan ser interpretadas por el alumno para decidir la siguiente acción -en pos de un objetivo a lograr- configuran-do una cadena de acciones y respuestas. En este proceso, las decisiones que van tomando los estudiantes también se apoyan en la anticipación que hacen acerca del funcionamiento de la herramienta del programa que están utilizando. Ambas, interpretaciones y anticipaciones, se encuentran muy condicionadas por sus experiencias anteriores en “lápiz y papel” y por el proceso de instrumentación (Trouche, 2004) que cada estudiante está transitando.
— Coincidimos con Lagrange (2000) en destacar que, en contraste con el trabajo en “lápiz y papel”, la principal característica de un sistema informático es su inmediatez: si el sistema da un resultado, el usuario lo obtiene inmediatamente después de la emisión del comando (p. 4). Agregamos nosotros que, producto de esta inmediatez, los estudiantes se ven enfrentados a una sucesión de imágenes, durante su trabajo, que requieren una interpretación en conjunto de todas ellas.
— Algunas herramientas del programa como, por ejemplo, “intersección de objetos”, posibilitan acciones que tienen un correlato en el trabajo de “lápiz y papel”, mientras que otras, como el “zoom”, no lo tienen. Asimismo, ciertos objetos, como por ejemplo un punto móvil cuyas coordenadas dependen de las magnitudes de una figura dinámica, existen solamente en entornos informáticos como el GeoGebra.
Analicemos ahora los hechos. Como ya detallamos en la sección 4, en cierto momento de la secuencia, los estudiantes definen un punto dinámico P. Este punto se mueve en la VG2 como resultado del arrastre del punto F sobre la diagonal de un rectángulo en la VG1.
La tarea que tienen que resolver a continuación pone en juego el reconocimiento del punto móvil P, en sus distintas posiciones, como punto del gráfico de la función en estudio. Más precisamente, estábamos interesados en un uso del gráfico cartesiano como “ábaco”20. El enunciado de la actividad es el siguiente:
Los estudiantes deben decidir si determinada posición del punto P en la VG2, a la que llegan por arrastre del punto F en la VG1, cumple con el valor de la coordenada que se da como dato en cada ítem y luego deben determinar el valor de la otra coordenada (lo que conlleva un trabajo en el registro numérico). Para cada una de estas acciones podrán apelar a diferentes herramientas del programa con el objetivo de lograr una respuesta con la mayor precisión posible.
En el transcurso de nuestra investigación, registramos con diferentes medios el proceso de producción de los alumnos, lo que nos permitió analizar este trabajo en otros tiempos y con otros insumos. El análisis colectivo en el seno del GC nos dio la posibilidad de reconstruir los hechos del aula y construir explicaciones acerca de ciertos comportamientos de los estudiantes que nos habían sorprendido en el tiempo de la clase.
Más precisamente, nos detuvimos a analizar el trabajo de un grupo de estudiantes al resolver el ítem b) de la actividad 5. Pudimos observar21 que, en cierto momento, las estudiantes mueven el punto F hasta que logran ver, en la VG2, que el punto móvil P se ubica sobre la recta horizontal “y=17”, que es par-te de la cuadrícula. De este modo garantizan -visualmente- el cumplimiento de la condición que se daba como dato (ver figura 5).

Figura 5: Imagen de la pantalla donde se “visualiza” el punto móvil P sobre la recta horizontal “y=17”
Luego, al utilizar el “zoom de acercamiento”, las estudiantes observan en la pan-talla que el punto móvil P “se va alejando” de la recta horizontal (ver figura 6).
La siguiente acción de las estudiantes es utilizar el “zoom de alejamiento” hasta volver a la situación anterior donde “se ve” que el punto queda nuevamente sobre la recta.
En la etapa de planificación de la secuencia esperábamos que el uso de la herramienta “zoom” mostrara a los estudiantes, en un caso así, que el punto P no está sobre la recta horizontal “y=17”. Por eso nos sorprendió -al analizar los videos de la pantalla de la computadora en la que trabajaron estas alumnas- que, aparentemente, despreciaran esa información y volvieran para atrás con el “zoom de alejamiento”. El proceso de discusión en el GC nos llevó a conjeturar que las estudiantes podían creer que al hacer zoom realmente modificaban la posición del punto, por lo que era mejor volver atrás y, de ese modo, lograr nuevamente que quede ubicado sobre la recta “y=17”.
Las ideas de Morgan et al. (2009), acerca de la distancia entre los objetos en la pantalla -y las manipulaciones posibles de hacer con ellos- y los objetos y manipulaciones propias del trabajo en “lápiz y papel”, nos permiten avanzar en la interpretación de este episodio. Conjeturamos que cuando las estudiantes hacen zoom, podrían estar considerando cada imagen en la pantalla- en distintos momentos del uso de la herramienta- como representando a gráficos diferentes en “lápiz y papel”. En la medida en que no tengan en cuenta las diferencias de escala entre los distintos gráficos producidos, podrían estar asociando cada imagen en la pantalla con un objeto matemático diferente. De este modo leen en la pantalla, en cada momento, informaciones matemáticas que pueden ser incompatibles unas de otras. Las estudiantes de nuestro episodio, al volver para atrás haciendo zoom, estarían buscando una imagen particular que represente a aquel objeto que dé mejor respuesta al problema.
Confirmamos nuestra conjetura analizando la continuación del trabajo de estas estudiantes. Una vez que ellas llegaron a una posición del punto P que las conformara, quisieron determinar el valor de su abscisa. Para ello, trazaron una recta vertical por ese punto buscando leer el valor de la abscisa de P a partir de las marcas de la graduación del “eje x”, cuyos valores numéricos eran visibles. Para lograr mayor precisión utilizaron el “zoom de acercamiento” en la intersección de esa recta vertical con el “eje x” y, a medida que lo hacían, el programa mostraba nuevas marcas y valores con más decimales en algunas de ellas. En determinado momento de este trabajo las estudiantes “ven” que la recta vertical coincide con una de las marcas de la escala (ver figura 7).

Figura 7: Imagen de la pantalla en el momento en que se visualiza la recta vertical sobre la marca correspondiente al valor 8,425.
Frente a esta situación una de las estudiantes exclama “lo logramos”, ya que de ese modo podrían leer el valor de la abscisa de P de manera “exacta”. Pero su compañera continúa haciendo zoom de acercamiento provocando que la vertical se separe visualmente de la marca (ver figura 8), lo cual es valorado negativamente por la primera estudiante quien manifiesta “¡antes lo teníamos!” e intenta volver al estado anterior mediante el “zoom de alejamiento”.
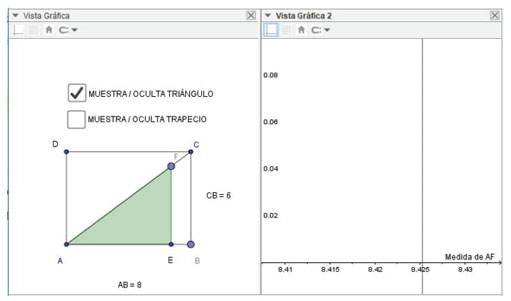
Figura 8: Imagen de la pantalla donde puede verse que la recta vertical no pasa por la marca en x= 8,425, valor numérico que ahora aparece en la pantalla y antes no.
Interpretamos que, para estas estudiantes, el uso del “zoom de acercamiento” habría cambiado la posición de la recta, cuando en realidad lo que se produjo fue un cambio de escala sobre el eje x que hizo visible que la intersección con la recta no estaba donde parecía. Este es un ejemplo de una característica de la herramienta “zoom”: su aplicación no modifica los objetos matemáticos representados, sino que cambia la representación de esos objetos en la pantalla.
El hecho de que las diferentes imágenes que aparecen en la pantalla -al hacer uso de la herramienta “zoom”- son representaciones del mismo objeto matemático, es un asunto por construir para algunos estudiantes. En nuestro ejemplo, la coordinación entre los registros diferentes que aparecen en las dos vistas gráficas podría funcionar de control: si no cambio el triángulo en la VG1, el punto P de la VG2 no cambia. Pero el episodio revela la necesidad de un docente que, siendo consciente de esta distancia entre las representaciones en la pantalla y en “lápiz y papel”, proponga una tarea para hacerlo explícito en el aula.
5.3. El papel de las representaciones múltiples y dinámicas en los diálogos que mantienen dos estudiantes a propósito de un conocimiento en construcción
Como ya dijimos, en una etapa posterior de la secuencia se define y estudia una nueva función: la relación entre el área del trapecio ADGF y la medida de AF. Nos ubicamos en el momento en que los estudiantes deben considerar en conjunto los gráficos de las dos funciones que están estudiando. Son las últimas actividades de la secuencia y la representación en la pantalla se ha complejizado (ver figura 9).

Figura 9: Imagen de una pantalla con el gráfico de las dos funciones y los respectivos puntos dinámicos en la vista VG2.
La presencia de representaciones múltiples (en una vista gráfica figuras geométricas dinámicas y en la otra los gráficos cartesianos de dos funciones) habilita que en el aula diferentes alumnos desplieguen miradas -y recortes- muy distantes entre sí y, en algunos casos, lejanos de aquello que se pretendió poner en juego desde la enseñanza. Recordemos también que las representaciones en ambas vistas son dinámicas y están ligadas, lo cual potencia la exploración que los estudiantes pueden realizar ampliando aún más el espectro de interpretaciones posibles.
En el episodio que estudiaremos a continuación, dos estudiantes -que trabajan juntos con una sola computadora- parten de interpretaciones muy diferentes de lo que ven y, en un diálogo en el cual la pantalla con sus múltiples representaciones juega un papel protagónico, convergen hacia formulaciones y explicaciones compartidas, ricas en contenido matemático. Más precisamente, están resolviendo la siguiente tarea:
| Actividad 8. Observen que, cuando mueven el punto F de la VG1, los puntos P y Q también se mueven en la VG2. |
| Escriban al menos 3 afirmaciones referidas a la relación entre P y Q. |
Después de que la profesora da la consigna, uno de los integrantes de nuestro equipo a quien llamaremos D -ya que cumple funciones de docente en el aula- se acerca a una pareja (V y E) que están trabajando juntos. Uno de ellos (V) comienza afirmando que ve “el ala de un avión” en la figura que encierran las dos gráficas de la VG2. Y empieza a caracterizar la forma de esta figura que está visualizando, mencionando también su interés por la aerodinámica. Describe la forma indicando partes rectas y otras curvas, “como un círculo”. Estas son ideas muy distantes de las que habíamos anticipado para el trabajo con este problema, ya que esperábamos una comparación entre los gráficos y no la consideración de la figura que encierran. Su compañero (E), por el contrario, se centra en las dos figuras geométricas de la VG1. Apoyado en estas figuras, intenta explicar cómo va cambiando la forma de las curvas.
Tomando la definición de representación de Morgan et al. (2009) que citamos en el inciso 2.3., diríamos que la imagen en la pantalla constituye una representación diferente para cada estudiante: mientras que para uno de ellos (E) se trata de una representación de las funciones que estuvieron estudiando, para el otro (V), las dos curvas de los gráficos cartesianos representan en conjunto el perfil de un objeto físico. Partiendo de posiciones tan distantes, la interacción entre ambos continúa, sostenida por el docente, y veremos cómo los argumentos de los dos se van enlazando para explicar, con otras palabras, las observaciones iniciales de cada uno.
En cierto momento la profesora comparte con toda la clase el hecho de que los puntos P y Q están siempre en la misma recta vertical, uno arriba del otro y pide a los estudiantes que busquen una explicación de eso que se ve.
En el grupo que estamos estudiando se da el siguiente diálogo:
D: ¿Está siempre el punto Q arriba del punto P?
V: No, acá debajo de todo, en el 0, cambia.
D: ¿Qué le pasa ahí?
V: Pasa que queda P arriba del Q [con esto se refiere a que están superpuestos].
E: Lo que pasa … al principio, son iguales. Después va tomando mayor, mayor área el trapecio.
D: ¿Siempre mayor área? ¿Por qué?
E: Sí… Lo que pasa es que él va comiendo de a mucho y él de a poco.
D: ¿Quiénes son él y él? ¿Quién es el que va comiendo de a mucho?
E: El trapecio
D: ¿Qué quiere decir que va comiendo de a mucho?
E: (Superponiéndose con la docente): Pero también tienen un límite…
D: Esperá… no avances. Yo no entendí bien “él va comiendo de a mucho”. ¿Vos entendiste? (dirigiéndose a V)
V: No
E (señalando el trapecio en la VG1): Porque esto al principio va comiendo de a mucho.
V: (hablando en voz baja): ¿Cómo “comiendo”?
D: Él te pregunta cómo “comiendo”. E (dudando): ¿Cómo? Porque…
D: ¿Qué querés decir con “comiendo”?
V: Porque crece.
E: Crece de área.
V: Aumenta el área.
E: De manera exagerada.
En estos intercambios los estudiantes se separan de la pregunta inicial de la profesora para ir hilvanando una explicación referida a la manera en que crece el área de cada figura. Comienza E, usando expresiones muy personales que V no comprende. Notablemente, a un pedido de mayor explicación, es V mismo el que va aportando términos que permiten precisar la idea de E. Los últimos cuatro intercambios, que se producen rápidamente muestran una sintonía entre ellos que se van completando en sus decires.
A continuación, E comienza a mover el punto F por la diagonal hasta el extremo C y se produce el siguiente diálogo:
E: Hay un punto en que el triángulo empieza a exagerarse, vuelve a “comer” la parte que le queda (señalando con el cursor la región EFCB de la VG1 (ver figura 9)) y vuelve a exagerarse de manera tan rápida que… lo hace tanto que hay un punto en que se van juntando.
D (dirigiéndose a V y señalando en la pantalla la imagen de las dos curvas en la VG2): ¿Eso tiene que ver con lo que vos decías al principio, que acá va recto, acá curvo?
V: Sí. En uno como que se acelera y en el otro…
E: Es verdad, tiene razón él… ¡también! Los dos apuntamos igual.
La docente haciendo una síntesis, recupera las palabras de E cuando decía que el trapecio iba “comiendo” área dando lugar a las siguientes intervenciones de los estudiantes:
V: Como que el trapecio aumentaba más rápido de área. Como que este (señalando el trapecio) va creciendo tanto que este (señalando el triángulo) se tiene que apurar.
E: Y este (señalando el triángulo con el punto F cerca del extremo C) con lo pequeño que le quedaba, empieza a subir de manera exagerada acá (señalando en la otra vista gráfica).
En los dos intercambios que acabamos de presentar, cuando la docente restituye las primeras ideas de cada estudiante, estas son aceptadas rápidamente y se despliegan entre ambos diálogos fluidos que permiten profundizarlas y precisarlas.
Después de estos intercambios, V vuelve a sus primeras afirmaciones sobre la forma de “ala de avión” que ve en la figura que encierran las dos curvas y comenta que suele hablar con su papá de aerodinámica. Los dichos de V nos muestran hasta qué punto la representación -entendida como la relación que establece un sujeto entre una imagen y un objeto que esa imagen le evoca- queda permeada no solo por los conocimientos sino también por los intereses y experiencias del sujeto que construye la representación. Por otro lado, el clima de trabajo en esta clase permite que la referencia a experiencias e intereses más personales de los estudiantes tengan un lugar en la escena del aula.
En todos los intercambios de este episodio aparecen argumentos matemáticos y no matemáticos, algunos centrados en la situación geométrica y otros en el gráfico de las funciones que modelizan el crecimiento de las dos áreas. Los estudiantes se mueven rápidamente entre las dos ventanas gráficas apoyando sus argumentos en la visualización de estas representaciones múltiples, dinámicas y ligadas. La trama de relaciones que van construyendo, partiendo de recortes y formas de expresarse muy diferentes, les permite llegar a elaborar un discurso común que explica tanto el comportamiento de las áreas de las figuras de la situación dinámica como el tipo de crecimiento, en diferentes tramos de las dos funciones que se estaban estudiando. El dinamismo del modelo geométrico en la VG1 y el hecho de que las representaciones gráficas de las funciones estuvieran ligadas a la situación geométrica vía los puntos móviles P y Q, son dos características propias de las representaciones en la pantalla que jugaron un papel fundamental en el trayecto de aprendizaje de estos dos estudiantes.
6. REFLEXIONES FINALES
A modo de síntesis, queremos recuperar aquí algunas ideas que estuvieron presentes en distintos tramos de este artículo.
En los tres episodios que hemos presentado hay alumnos interactuando entre ellos mientras trabajan en sus computadoras. Las acciones que van realizando son a menudo provocadas por los intercambios orales con los compañeros (para constatar, precisar o aún refutar lo que se está afirmando); y a la vez, los resultados de las acciones que realizan, visibles en sus pantallas, enriquecen el contenido de la discusión que se está dando. En relación a esto último, Noss y Hoyles (1996) citado por Arcavi y Hadas (2000) señalan que el medio elegido para resolver un problema media también en la gama de significados y conexiones que probablemente estructurarán la interacción y, a su vez, estas interacciones harían surgir nuevas relaciones y significados (p. 245). Algunos particulares de este fenómeno se nos hicieron visibles en cada episodio analizado en el artículo:
— En el primer episodio, el trabajo con la figura dinámica permite a varios alumnos “atrapar” algunos invariantes en la familia de figuras determinada por el movimiento. La identificación de estos invariantes invita a una tarea de formulación de relaciones y propiedades valiosa para la formación matemática de los estudiantes, aun cuando se trate de conjeturas sostenidas en la evidencia empírica. Ahora bien, al estar trabajando cada estudiante con computadoras diferentes, cada uno puede hacer su propia exploración y la visualización de distintos estadios de la situación geométrica da lugar a la formulación de conjeturas contrapuestas. En el espacio colectivo, esas contradicciones necesitan y habilitan el surgimiento de argumentos matemáticos para tratarlas. Estos argumentos se van construyendo en diálogo con nuevas exploraciones en la pantalla que eventualmente modifican el contenido de la afirmación sobre la que se está argumentando. En ese sentido, el ambiente dinámico contribuyó a cerrar el ciclo de experimentación-retroalimentación-reflexión suministrando “las semillas” para la argumentación (Arcavi y Hadas, 2000, p. 27).
— En el segundo episodio, el trabajo colaborativo de un grupo de estudiantes se ve alterado ante el uso de una herramienta del programa cuyo funcionamiento no conocen en profundidad. No pueden anticipar el efecto que provoca ni tampoco interpretar -en relación con los objetos matemáticos en juego- el resultado que se visualiza después de utilizarla. El uso del “zoom”, que no tiene correlato en el trabajo con “lápiz y papel”, deja un margen grande de interpretación por parte de los estudiantes, pudiendo alojar concepciones en las cuales se asocia cada imagen en la pantalla -antes y después de su aplicación- con un objeto matemático diferente. Las reflexiones que realizamos respecto al uso del “zoom”, nos permitieron identificar la necesidad de una intervención docente, por ejemplo, proponiendo una discusión matemática sobre la coordinación entre las representaciones de las dos vistas gráficas. De este modo, se pondría en relieve la invarianza del objeto matemático ante la aplicación de la herramienta.
— El tercer episodio trae a dos estudiantes -trabajando en una misma computadora- ante una pantalla en la que se muestran representaciones múltiples y ligadas de la situación que se está estudiando. La tarea que los convoca es abierta y favorece tanto la exploración como la coordinación entre el marco geométrico y el funcional. Uno de los estudiantes parte de una interpretación estática, enfoca la atención en la figura determinada por las curvas en la VG2 y encuentra similitudes con objetos físicos que pertenecen a una zona de la realidad que él valora. El otro estudiante ofrece una lectura dinámica de la variación de las áreas en la representación geométrica en la VG1 para explicar la forma de las curvas. Esta distancia entre las interpretaciones de uno y otro estudiante deja en evidencia la componente personal de la construcción de una representación, tal como es señalada en la definición dada en Morgan et al. (2009).
Con la intervención del docente, los estudiantes interactúan incorporando palabras e ideas del otro, y logran establecer una coordinación entre los registros de representación en los cuales se enfocó cada uno en su interpretación. El hecho de que estén trabajando en la misma pantalla, favorece que construyan una explicación compartida sobre el comportamiento de la función. En ese sentido, Arcavi y Hadas (2000) afirman que jugar primero con una situación geométrica y luego interpretar sus representaciones parece mejorar tanto la comprensión de la situación como de las representaciones (p. 42).
En concordancia con nuestro enfoque didáctico, la incorporación de la computadora al trabajo matemático de los estudiantes debe preservar espacios importantes de producción autónoma -individual y colectiva- y permitir que ellos adquieran una posición crítica respecto de las respuestas que el software genera. Consideramos que los asuntos estudiados en este artículo son un aporte para pensar la enseñanza en esa perspectiva.











 nueva página del texto (beta)
nueva página del texto (beta)




