1. INTRODUCCIÓN
A lo largo de la enseñanza escolar, los estudiantes trabajan desde el sistema de los números naturales hasta el de los números complejos, ambos sistemas numéricos infinitos. Sin embargo, es poco probable concluir que la formación esperada para un estudiante permita alcanzar una noción coherente sobre el infinito. La comprensión profunda del infinito actual es difícil porque toma el estatus de obstáculo epistemológico y genera cierta resistencia en los aprendices (Mena-Lorca et al., 2015). Esta noción es fundamental en el conocimiento matemático y transversal para alcanzar la comprensión de otros conceptos vinculados al dominio del análisis, el álgebra, de la teoría de conjuntos, entre otros.
Es por ello que es interés de esta investigación indagar, desde el enfoque cognitivo de la teoría APOE, cómo realizan estudiantes de secundaria la compa-ración entre conjuntos numerables, en particular, el conjunto de los números naturales y el de los enteros. Esto provee aspectos a considerar en el diseño de una enseñanza que permita que los aprendices puedan alcanzar nociones del infinito actual.
2. ANTECEDENTES
Existen diversos estudios sobre el concepto de infinito, esta investigación considera aquellos que se enfocan en la epistemología, así como también, aquellos relacionadas a las concepciones que tienen los estudiantes y profesores de matemática. En general, los estudios suelen tener un mismo punto de encuentro: la complejidad que tiene alcanzar la comprensión del objeto infinito actual. Es así, como Mena-Lorca et al. (2015) afirman que “el transito del infinito potencial al actual es difícil de lograr y parece claro que, si se desea conseguir que los estudiantes secundarios y otros logren tener un concepto apropiado del infinito, se necesita modificar las estrategias utilizadas” (p. 353).
El concepto de infinito ha estado concebido desde la percepción y basado en la experiencia con el mundo físico, lo que conlleva a paradojas, pues se abordan desde un mundo finito, generando una serie de confusiones en su comprensión (Ortiz, 1994). Por otra parte, D’Amore et al. (2006), proponen varias situaciones que permiten confrontar el infinito actual y el infinito potencial en estudiantes de Europa y América Central, cuyos resultados muestran que cierto sentido de infinito puede existir, y que casos extremadamente específicos pueden comprenderlo a cabalidad.
Igualmente, la formalización matemática del concepto de infinito actual data de una larga historia y complejidad, y además siempre estará ligado a un problema educativo, en el sentido que se suele vincular únicamente a un proceso ilimitado (Fedriani y Tenorio, 2010).
Por su parte, Montoro et al. (2016), analizan las concepciones sobre la cardinalidad infinita de conjuntos numéricos en estudiantes con formación matemática secundaria y universitaria. Dentro de sus hallazgos, se encuentra que los estudiantes tienen visiones finitas muy arraigadas. Las justificaciones que ellos realizan al comparar el conjunto de los naturales, enteros y racionales, hacen referencia a que un conjunto está incluido en el otro o que abarca más tipos de números que el otro, lo cual es válido desde un punto de vista finitista que contiene el principio: el todo es mayor que las partes. Además, emanan fuertes argumentos del tipo ambos son infinitos, haciendo alusión a la unicidad de infinito al momento de comparar un infinito numerable con uno continuo. También, el infinito cardinal está muy lejos de ser una noción que los estudiantes adquieren por el solo hecho de estar trabajando con conjuntos numéricos infinitos (Montoro et al., 2016).
Además, desde una mirada cognitiva, Garbin y Azcárate (2002) plantean una categorización en relación al grado de construcción que presentan los estudiantes del infinito actual: individuo coherente y consistente, individuo coherente pero inconsistente e individuo incoherente. Por añadidura, destacan que la tarea de conexión debe ser una práctica constante cuando el docente trabaja con el infinito actual.
Respecto a los estudios desde la teoría APOE, Dubinsky et al. (2005) plantea que el infinito actual es el objeto mental que se obtiene de un determinado proceso. Este objeto mental se denomina como objeto trascendente y se obtiene de un proceso iterativo infinito (Brown et al., 2010). Además, Brown et al. (2010) mencionan que una concepción dinámica del infinito será definida como un proceso iterativo infinito (entre el conjunto de los números naturales y otro conjunto cualquiera) y, los objetos trascendentes serán aquellos objetos que se abstraen de dicho proceso. Si el individuo tiene una construcción de objeto del infinito actual, entonces lo concibe desde una concepción estática.
Asimismo, hay evidencias sólidas de la importancia del conjunto de los números naturales en la construcción del infinito matemático, en el sentido de que la concepción dinámica o estática que un individuo pueda lograr de este conjunto influye en su capacidad para alcanzar un estado de construcción mental de objeto, trascendiendo un proceso iterativo infinito (Villabona y Roa-Fuentes, 2016), por lo cual la comprensión es compleja pues el objeto pue-de ser resultado de la abstracción de dicho proceso.
3. EL PROBLEMA DIDÁCTICO
Las bases curriculares en Chile (MINEDUC, 2018, 2016) consideran propiedades algebraicas de los diferentes sistemas numéricos, y luego su trabajo operativo.
No obstante, existen otras nociones de los sistemas numéricos que aportan al razonamiento matemático, cuyos tratamientos son débiles, escasos o simple-mente obviados en la enseñanza escolar. Tales como, la teoría de conjuntos y de la topología, que conjugan elementos constitutivos de los sistemas numéricos, tales como el concepto de cardinalidad de conjuntos, los cuantificadores, con-juntos numerables, densidad, y otros.
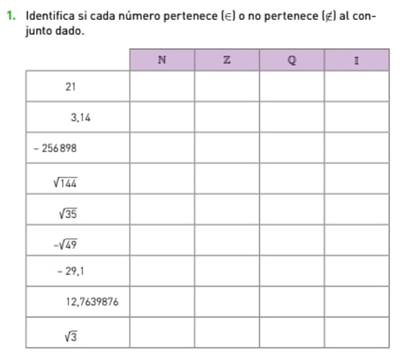
Del mismo modo, se evidencia la escasa e inconsistente existencia del concepto de infinito en el currículo chileno. Si bien la enseñanza de los sistemas numéricos comienza desde los primeros años preescolares, en que se enfoca en el “emplear cuantificadores (más/menos, mucho/poco), en situaciones cotidianas” (MINEDUC, 2019, p. 99), es en primero y segundo año de educación media donde el currículo establece que los estudiantes deben identificar el tipo de número, racional, entero y natural, y las operaciones involucradas, para luego reconocer números cuyo desarrollo decimal es infinito y no tiene periodo (MINEDUC, 2016). Más aún, estos objetivos de aprendizaje buscan que los estudiantes conozcan y utilicen las propiedades de los sistemas numéricos, presentando un enfoque basado solo en la clasificación e identificación de los sistemas numéricos, como se ejemplifica en la figura 1:
Casi en su totalidad, las actividades del Texto de Matemática del estudiante de I° Medio (Editorial Santillana, 2018) y II° Medio (Ediciones SM, 2019), se abordan contenidos relacionados con los sistemas numéricos de los racionales y de los reales, invisibilizado un tratamiento explícito o implícito de los conceptos de cardinalidad, continuidad e infinito.
Este enfoque, también está en los textos del docente que entrega el MINE-DUC. Ejemplo de ello es el tomo I de la guía didáctica para el docente para segundo año medio, donde existen consideraciones del concepto infinito:
Cuando se les pregunta a los y las estudiantes sobre cuáles son los números reales, generalmente ellos contestan los números enteros o los números naturales. A pesar de estar en parte en lo correcto, detrás de esa respuesta está la noción de lo con-mensurable. Por lo tanto, es la misión del docente durante esta lección lograr ampliar esta noción a la inconmensurabilidad y a la idea de infinito (MINEDUC, 2019, p. 27).
La orientación anterior, es para iniciar la lección de los números reales, la cual supone que los docentes manejan conceptos claros del infinito o la noción de inconmensurabilidad, lo cual, repercutiría directamente en la enseñanza si no fuese así.
En la medida que se progresa en el currículo escolar en educación media, se empieza a abordar la función matemática y sus variantes, la cual es importante para vincular la igualdad de la cardinalidad entre conjuntos, y el concepto de conjuntos infinitos.
Esta investigación es de carácter exploratorio y se enmarca en el estudio de los estados de construcción y mecanismos mentales. Para esto, se analiza el trabajo matemático de estudiantes (17 a 18 años de edad) a partir de algunas tareas que promueven la comparación de las cardinalidades de los sistemas numéricos ℕ y ℤ. En relación a lo anterior, el objetivo de investigación es: Conocer las estruc-turas y mecanismos mentales que presentan los estudiantes de III° y IV° años medio al momento de comparar los cardinales de los conjuntos ℕ y ℤ.
4. APROXIMACIÓN EPISTEMOLÓGICA DEL INFINITO
Uno de los principales indicios de la noción de infinito data del siglo IV-III a. C en Grecia, con las paradojas de Zenón. Posteriormente, Aristóteles, marcó un avance importante en la clasificación del infinito, al asegurar la existencia del infinito potencial y en cambio negar la existencia del infinito actual (Aristóteles, trad. 1985). Con la característica potencial se apunta a un proceso ilimitado, que se repite sin fin. Agustín de Hipona (426/1965) se opuso a los pensamientos de Aristóteles, y le atribuye solo a Dios el conocimiento del infinito actual. Sin embargo, las ideas de Aristóteles generaron tanta influencia que aun después de mil años luego de su muerte, todavía se consideraban verdaderas.
Es recién en el Renacimiento que, Galileo (1638/2010) da un primer paso para tratar cardinales de conjuntos infinitos al mostrar que se puede establecer lo que hoy llamamos una función biyectiva, entre los números naturales y sus cuadrados, cuestionando el axioma el todo es mayor que la parte de Euclides. Pese a esto, una de sus conclusiones es la imposibilidad de comparar si es que de infinitos se trata.
Más adelante, con Newton y Leibniz emana la rama del cálculo infinitesimal, la cual retoma la discusión del infinito, fundamentada en la idea de cantidades infinitamente pequeñas no nulas, germinando la idea del concepto de límite (Kline, 1980) que permite determinar el valor exacto de una magnitud, en un proceso para lo cual se obtiene un valor aproximado, se sigue con aproximaciones más precisas, para dar con una cadena de aproximaciones, cada una más precisa que la anterior para concluir que converge a un valor determinado.
Un estudio formal y crucial del infinito matemático lo realiza Bernhard Bolzano, el primero en aceptar y fundamentar la noción de infinito actual, en su obra póstuma Paradojas del infinito, publicada en el año 1851. Además, enfatizo que el concepto de equivalencia entre dos conjuntos era aplicable tanto a conjuntos finitos como infinitos, y acepto que los conjuntos infinitos tuvieran el mismo cardinal que una parte de ellos mismos. Los trabajos de Bolzano cimentan la base para la teoría de conjuntos.
Recién a finales del siglo XIX se termina un trabajo de formalización de los sistemas numéricos y el fundamento de sus cualidades que posteriormente da paso a la teoría de conjuntos. En este contexto, Cantor (1932) se dedica a trabajar de manera rigurosa con el infinito actual; reconoce que hay distintos infinitos, menciona que tanto el conjunto de los enteros, como el de los racionales son conjuntos numerables, esto es, tienen el mismo cardinal que el con-junto de los números naturales. Para denominar el cardinal de los conjuntos numerables Cantor utiliza la primera letra del alfabeto hebreo ℵ0 (Aleph cero).
5. EL MARCO TEÓRICO
5.1 Teoría APOE
La Teoría APOE permite examinar cómo un individuo eventualmente construye un concepto matemático determinado en sus diversos estados y mecanismos de construcción mental (Dubinsky, 1996), inspirado en la abstracción reflexiva de Piaget (1970).
En efecto, la teoría APOE del acrónimo de acción, proceso, objeto, esquema, que rotulan los estados de construcción mental de un concepto de la matemática es un constructo que permite describir cognitivamente las construcciones mentales y los mecanismos por los cuales un concepto matemático es aprendido por un sujeto.
Un estado de construcción mental es cualquier estructura relativamente estable capaz de desarrollarse en un individuo para dar sentido y respuesta por adaptación a una situación matemática, mientras que, un mecanismo mental es el medio por el cual este estado puede desarrollarse en la mente de uno o más individuos para pasar de un estado a otro (Stenger et al., 2008, p. 98).
Es así como la construcción mental del conocimiento matemático puede ser comprendida en relación a los estados de: acción, proceso, objeto y esquema, las cuales no necesariamente son secuenciales. El estado de construcción mental del tipo acción consiste en una transformación de un objeto que es percibida por el individuo como externa y se realiza como una reacción a sugerencias que proporcionan detalles de los pasos a seguir. Si el sujeto solo es capaz de trabajar sobre un objeto con base en estímulos externos, decimos que está operando la concepción acción. “Las acciones son más limitadas que otras construcciones mentales, pero son el principio crucial en la construcción del cono-cimiento” (Dubinsky, 1996, p. 34). Cuando una acción se repite y el individuo reflexiona sobre ella, puede interiorizarse en un proceso. Es decir, se realiza una construcción interna, en donde se ejecuta la misma acción, pero en la mente del individuo, y no necesariamente dirigida por un estímulo externo.
Un individuo que tiene una concepción proceso, puede realizar una transformación, reflexionar sobre esta, describirla, o incluso invertir los pasos. Se habla de una concepción objeto cuando un individuo reflexiona sobre las operaciones aplicadas a un proceso en particular, toma conciencia del proceso como un todo, realiza aquellas transformaciones (ya sean acciones o procesos) que pueden actuar sobre él, y puede construir de hecho esas transformaciones. En este caso, decimos que el proceso ha sido encapsulado en un objeto. “Un individuo tiene una concepción objeto de un concepto si él puede desencapsular el concepto de vuelta al proceso subyacente y construir transformaciones que pueden ser aplicadas al objeto” (Dubinsky et al., 2005, p. 5).
Es así como las estructuras y mecanismos se organizan en esquemas, que son “un nivel de mayor elaboración en la comprensión de un concepto mate-mático y está relacionado de manera coherente en la mente del estudiante” (Asiala et al., 1996, p. 12). Es decir, los esquemas son las construcciones más amplias que se pueden determinar de un concepto matemático, ya que forman una colección coherente de acciones, procesos, objetos y otros esquemas. La coherencia alude a la capacidad del individuo para establecer si un esquema le permite solucionar un problema particular. Del mismo modo, Dubinsky (1994) señala que un esquema puede ocuparse para resolver una situación matemática y ser tematizado en un objeto para realizarle nuevas transformaciones (acciones y procesos), o para que sea asimilado por otro esquema.
Ya se mencionaron los mecanismos de interiorización y encapsulación, sumados a ellos están los mecanismos de coordinación, generalización y reversión. Para profundizar, la interiorización se resume como la transferencia de una actividad específica del mundo externo al mundo interno. Así, mediante este mecanismo es posible que una acción sea transformada en un proceso. La coordinación fue descrita por Piaget como la organización general de acciones, para construir nuevos objetos o acciones, o dos o más procesos pueden coordinarse para generar nuevos procesos.
La encapsulación consiste básicamente en la conversión de un proceso (una estructura dinámica) en un objeto (una construcción estática). Finalmente, el mecanismo de reversión consiste básicamente en pensar un proceso a la inversa.
Es así que la coordinación toma gran importancia en el estudio del infinito, ya que se requiere coordinar dos procesos. En algunos casos inclusive es necesario coordinar dos procesos de diferente naturaleza: uno divergente y uno convergente (Villabona y Roa-Fuentes, 2016).
En Arnon et al. (2014) se presenta un esquema que muestra las estructuras y mecanismos mentales presentes en la Teoría APOE (ver figura 2):
Por otro lado, la teoría también aborda el término coherencia, el cual está relacionado con la capacidad del individuo para aplicar un determinado esquema en un contexto distinto.
5.2 Descomposición genética genérica del infinito
En la Teoría APOE, la Descomposición Genética (DG) es un modelo de construcción de un concepto o noción matemática. La DG muestra las estructuras y los mecanismos mentales mediante los cuales un individuo puede construir un concepto de manera exitosa. Es decir, la DG es un modelo cognitivo (hipotético) que se entiende, metafóricamente, como una ruta topográfica que se levanta con base en las estructuras y mecanismos mentales que están inmersos en la comprensión de un concepto matemático.
Dubinsky et al. (2008), en relación con el trabajo de iteraciones infinitas, mencionan que se debe dar la coordinación de uno o más procesos de iteración infinita, y que el éxito se dará cuando al menos uno de los procesos se visualice como un objeto. Por ende, lo que permitiría a un individuo pensar en un proceso iterativo infinito como un todo es aceptar la idea de que el proceso ha alcanzado a todos los números naturales, es decir, el proceso de iteración ter-mina. Evidentemente esta no es una tarea fácil.
Asimismo, cuando hablamos de infinito debemos considerar que “las estructuras y mecanismos tradicionales no han sido suficientes para explicar la manera como los individuos intentan comprender situaciones matemáticas que involucran el infinito” (Roa-Fuentes y Oktaç, 2014, p. 74). Es así como el estudio infinito matemático en la Teoría APOE es de suma importancia, ya que han emanado nuevas estructuras y mecanismos mentales para poder explicar el proceso constructivo que implica este concepto. Específicamente, Dubinsky et al. (2013) plantearon una nueva estructura independiente, la cual se encuentra entre las estructuras de proceso y objeto; esta estructura permite que el estudiante pueda ver el proceso iterativo infinito como un todo terminado; a esta nueva estructura la denominaron Totality, que aquí se llamará totalidad.
Además, Villabona y Roa-Fuentes (2016), mencionan que el mecanismo para alcanzar la estructura de totalidad tiene una particularidad, la de descentralizar la mirada de los elementos del proceso y enfocarla en ver el proceso como un todo terminado; es decir, este mecanismo tiene una característica distintiva, de abstracción del proceso para poder visualizarlo como una estructura estática. Es por esto que no denominan a este mecanismo como encapsulación, sino que recibe un nuevo nombre: completez. El mecanismo completez está asociado con la construcción por parte de un individuo de “elementos fundamentales relacionados con la teoría de conjuntos de Cantor; por ejemplo, la relación entre un conjunto infinito y sus partes, los conceptos de cardinal y ordinal y, la construcción de conjuntos infinitos con diferentes cardinalidades” (Villabona y Roa-Fuentes, 2016, p. 132). La siguiente figura ilustra lo anteriormente expuesto (ver figura 3):

Figura 3. Estructuras y mecanismos mentales en la construcción del infinito actual. Basado en Villabona y Roa-Fuentes (2016)
5.3 Descomposición genética preliminar particular: comparando ℕ y ℤ
Para poder concluir que el cardinal del conjunto de los números naturales es equivalente al cardinal del conjunto de los números enteros, el estudiante debería identificar alguna transformación que itere los elementos del conjunto de los números naturales con el de los números enteros. En este sentido, debe pensar en trasformaciones𝑓𝑖, para 𝑖 = 1,2,3,..., n , las cuales transformen a cada elemento de los números naturales en un único elemento del conjunto de los números enteros y, a su vez, a cada elemento del conjunto de los números enteros relacionado con un único elemento de los números naturales.
En la comparación de los cardinales ℕ y ℤ las iteraciones que podrían estar en juego son las siguientes:
Tabla 1 I Procesos iterativos infinitos entre ℕ y ℤ
| Número de la iteración (II) | Número natural (I N ) | Número entero (I Z ) |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 1 | -1 |
| 3 | 2 | 1 |
| n | n - 1: parn - 1: impar |
|
Tabla 2 II Procesos iterativos infinitos entre ℕ y ℤ
| Número de la iteración (II) | Número natural (I N ) | Número entero (I Z ) |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 1 | 1 |
| 3 | 2 | -1 |
| n | n - 1: parn - 1: impar |
|
Destacar que se espera que los estudiantes aludan a esta idea y no que necesariamente planteen de manera explícita la generalidad de las iteraciones.
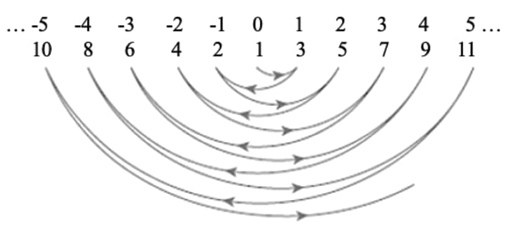
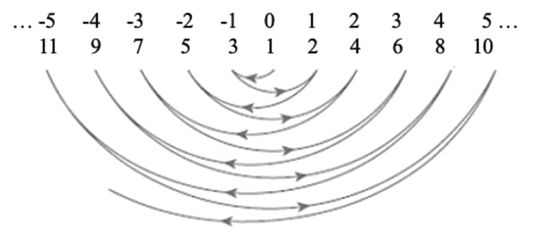
Las iteraciones presentadas muestran que el conjunto de los números enteros es un conjunto numerable, es decir, que los números enteros son contables por medio de los números naturales. A continuación, se muestra cómo es el conteo de la primera iteración y luego el de la segunda (ver figuras 4 y 5):
En relación a las estructuras y mecanismos mentales, el estudiante se encontrará en una estructura acción si es capaz de establecer una iteración para una cantidad pequeña de elementos, asociando a cada número natural un único número entero. Si se toman como base las acciones, y se coordinan, entonces el individuo ha interiorizado las acciones en un único proceso iterativo infinito I, desde una concepción dinámica. La coordinación será posible mediante una relación biyectiva. Cabe mencionar que cada uno de los procesos iterativos infinitos II, IN, IZ, son a su vez iteraciones. El mecanismo que permitirá al individuo ver al proceso como un todo terminado, es decir, como una estructura totalidad, será el mecanismo completez. Alcanzar la estructura totalidad dependerá de ver al menos a uno de los procesos iterativos infinitos II, IN, IZ, como un todo terminado. Posteriormente, mediante el mecanismo de encapsulación, los estudiantes podrían alcanzar el objeto trascendente ℵ0 (Aleph cero), correspondiente al cardinal de los conjuntos numerables.
A continuación, se muestra parte de la DG preliminar particular de nuestro cuestionario (ver figura 6):
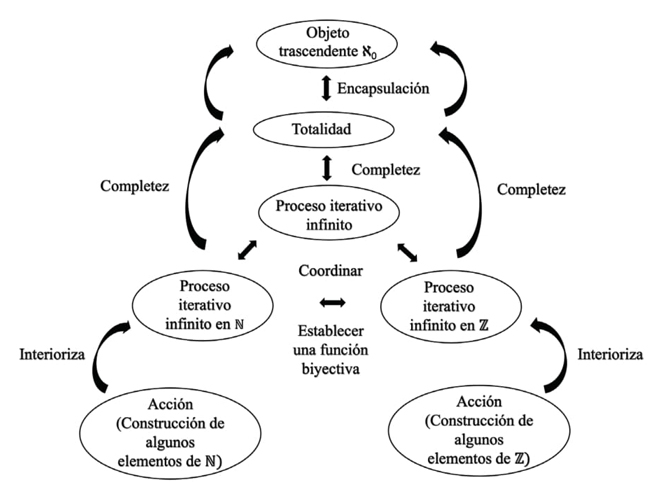
Figura 6 Parte de la descomposición genética preliminar y teórica particular para la comparación del cardinal del conjunto de los números naturales y enteros. Elaboración propia.
Se espera que los estudiantes puedan coordinar los procesos iterativos infinitos entre ℕ y ℤ mediante una relación biyectiva que no necesariamente se traduzca en una expresión matemática, sino que expresen la idea de relacionar a cada elemento de los naturales con un único elemento de los números enteros y viceversa. Luego, que la relación se pueda, mediante el mecanismo completez, visualizar como una totalidad. Esperamos, gracias a la estructura de totalidad, que los estudiantes puedan concluir que los conjuntos en cuestión tienen la misma cantidad de elementos.
6. Método de investigación
6.1 Enfoque, paradigma y tipo de investigación
Esta investigación tiene un enfoque cualitativo y se sitúa en el paradigma interpretativo. Además, esta investigación utiliza el estudio de casos para abarcar “la particularidad y complejidad de un caso singular” (Stake, 2010).
El método utilizado es una adaptación del ciclo de investigación propuesto por la Teoría APOE, donde se busca describir e interpretar cómo un estudiante logra ciertos estados de construcción mental sobre el concepto de infinito actual. Este ciclo propone el desarrollo de tres componentes, (I) un análisis teórico, del cual se desprende una descomposición genética preliminar; (II) un diseño e implementación de un modelo de enseñanza; (III) observación, análisis y verificación de datos a partir de los cuales se reestructura y valida el análisis teórico inicial (Asiala et al., 1996). La aplicación de este ciclo permite obtener una descripción detallada y cercana a la construcción cognitiva de los conceptos mate-máticos. Cada vez que es aplicado con base en la descomposición genética de un concepto, esta se refina como resultado del análisis sobre los datos empíricos que se obtuvieron en el desarrollo de la tercera componente.
El análisis teórico, como ya se mencionó, es la primera componente del método de investigación. Aquí realizamos un estudio profundo sobre el infinito potencial y actual, en las bases curriculares en Chile, su evolución histórica-epistemológica y cómo ha sido abordado en estudios previos (estado del arte), que contribuyeron a levantar una descomposición genética preliminar para el problema planteado en la comparación de los dos conjuntos numéricos ℕ y ℤ. Uno de los análisis teóricos más importantes fue la descomposición genética genérica que se plantea en Roa-Fuentes y Oktaç (2014), esta DG nos permitió retomar ciertas características para nuestro contexto particular.
Luego, a partir de la descomposición genética preliminar, se diseñó el instrumento, el cual fue enfocado en la coordinación del proceso iterativo infinito en el conjunto de los números naturales y del proceso iterativo infinito en el conjunto de los números enteros. Finalmente, con base en los análisis anteriores y teniendo en cuenta la población que nos interesa, se realizó la recolección, observación y análisis de los datos obtenidos en la implementación del instrumento (la población se describe a continuación). El análisis de los datos obtenidos nos ha permitido plantear una nueva descomposición genética, acorde a los diferentes acercamientos que los estudiantes manifestaron. Cabe destacar que no se implementó un modelo de enseñanza o ciclo de enseñanza. A continuación, se presenta el ciclo de investigación para nuestra investigación (ver figura 7).
6.2 Participantes
Para la implementación y aplicación del instrumento diseñado, nos centramos en dos establecimientos educacionales secundarios chilenos de la región metropolitana con el objetivo de evidenciar las concepciones presentes en estudiantes de tercero y cuarto año medio, al momento de comparar la cardinalidad de los sistemas numéricos y así precisar las concepciones que poseen los estudiantes en torno al infinito. A continuación se detallan los dos casos para esta etapa, que temporalmente corresponde al primer semestre del año 2019 (ver tabla 3).
Caso A: Compuesto por 72 estudiantes de tercero y cuarto año medio de un colegio de dependencia particular subvencionado de la región metropolitana, ubicado en la comuna de La Granja. Es un grupo mixto entre mujeres y hombres, cuyas edades fluctúan entre 15 y 18 años.
Caso B: Compuesto por 92 estudiantes de tercero año medio de un colegio de dependencia particular subvencionado de la región metropolitana, ubicado en la comuna de Maipú. Es un grupo mixto entre mujeres y hombres, cuyas edades fluctúan entre los 15 y 16 años.
Se escogen estos niveles puesto que los estudiantes deben tener ciertos conocimientos previos para la comparación entre las cardinalidades de sistemas numéricos y noción de infinito, descritos a continuación:
Noción e identificación de los sistemas numéricos y sus respectivas propiedades.
Noción del concepto de función y función biyectiva.
Tabla 3 Caracterización de la muestra
| Tipo de establecimiento | Cantidad de estudiantes | Nivel |
|---|---|---|
| Establecimiento particular subvencionado con financiamiento compartido | 36 | III° Medio |
| Establecimiento particular subvencionado con financiamiento compartido | 36 | IV° Medio |
| Establecimiento particular subvencionado con financiamiento compartido | 92 | III° Medio |
| TOTAL | 164 |
Los establecimientos cuentan con estudiantes de similares características eco-nómicas y sociales.
Para fines prácticos, los estudiantes serán identificados por la letra del Caso y un subíndice de un número, así por ejemplo, el quinto estudiante del Caso A, será identificado con A5.
6.3 Instrumento
Hemos escogido un cuestionario con respuestas abiertas. El diseño está conformado por un cuestionario de una pregunta (ver tabla 4), la cual busca determinar y constatar las estructuras y mecanismos mentales en la que se encuentran los estudiantes a través de la comparación de la cardinalidad de los conjuntos de los números naturales y números enteros. El cuestionario fue implementado al finalizar el primer semestre del año 2019. Además se realizó un análisis a priori y uno a posteriori del cuestionario.
Se optó por una definición por extensión de los conjuntos naturales y enteros ya que al aplicar un instrumento de recogida inicial pudimos notar que los estudiantes no se familiarizan con las notaciones ℕ y ℤ. Los estudiantes solían confundir ℕ y ℤ con el conjunto de los números racionales o reales.
Por otro lado, las respuestas al instrumento, dadas por los participantes, serán analizadas considerando la DG preliminar particular teórica presentada en el apartado 5.3. Reconoceremos en las respuestas las estructuras mentales presentes al momento de responder.
7. RESULTADOS
En este análisis se presentan las evidencias más relevantes del Caso A y Caso B. Entre las diversas respuestas al cuestionario, 80 de los estudiantes respondieron, a las preguntas: ¿Alguno de ellos tiene más elementos que el otro? ¿Podrías establecer una relación biyectiva? ¿Qué piensas ahora?, respuestas como las que proporciona el estudiante B 45 (ver figura 8), en la cual se percibe una noción de que el conjunto de los números enteros tiene mayor cardinal que el conjunto de los números naturales haciendo alusión a argumentos que conllevan a la idea de que los naturales están contenidos en los enteros, por contención. Es decir, los estudiantes dan respuestas a esta situación sin llegar a utilizar un razonamiento matemático sino más bien a través de argumentos respaldados por su intuición.
Los estudiantes utilizan el argumento todo es mayor que las partes, el cual es válido en conjuntos finitos, pero que no es válido necesariamente en los conjuntos infinitos. Estos estudiantes coordinan procesos iterativos infinitos mediante una transformación inyectiva, con esto desprenden que el cardinal del conjunto de los números naturales es menor que el del conjunto de los números enteros.
Asimismo, 38 de los estudiantes, aluden a la unicidad de infinito. En este sentido, el estudiante podría estar en la estructura proceso, entendiendo el proceso iterado para generar el conjunto de los números naturales y el proceso para generar los números enteros, o inclusive, podría estar en la estructura de totalidad, entendiendo la existencia del conjunto de los números naturales o de los números enteros como un todo, pero no existe una coordinación que le permita dar argumentos válidos para mostrar que los cardinales de los conjuntos son iguales, es decir, no se establecen las iteraciones respectivas para realizar la coordinación.
En este aspecto, es posible analizar en la figura 9, que el estudiante intenta razonar los procesos iterativos por separado, lo que impide comprender la naturaleza del proceso único que da cuenta de la igual de cardinalidad de los conjuntos. Además se aprecia una concepción acción y proceso iterativo infinito.
Una tercera mayoría, 35 estudiantes responden que el conjunto de los números enteros equivale al doble del conjunto de los números naturales (ver figura 10). Esta conclusión la obtienen al realizar acciones, los estudiantes iteran en un intervalo finito. Por ejemplo, un estudiante realiza la transformación del primer millón de números naturales, concluyendo que siempre quedarán elementos sin preimagen, en este caso exactamente 1 millón de elementos quedará sin preimagen, esta idea impide dar el paso al mecanismo de interiorización, y por tanto tampoco a alcanzar el proceso iterativo infinito.
También, 11 respuestas de los estudiantes se conectan históricamente con los griegos ya que ellos niegan la utilidad del infinito matemático e inclusive de su existencia, esto puede interpretarse como con el infinito no se puede; con infinitos no comparo o no puedo comparar. Es decir, realizan la estructura de acción, pero se queda en el proceso iterativo infinito, de cada uno de los conjuntos y no logra verlo como un proceso terminado, para luego coordinar esos procesos y realizar la comparación (ver figura 11).
Solo dos estudiantes logran coordinar procesos iterativos infinitos entre el con-junto de los naturales y en el conjunto de los números enteros, esto, mediante una transformación biunívoca declarada de manera explícita. Además, pueden concluir que tienen la misma cantidad de elementos gracias a la estructura de totalidad.
La figura 12 es un ejemplo de respuesta que alcanza la estructura mental totalidad. El estudiante asume que el conjunto ℕ está contenido en el conjunto ℤ y suma a esto, sin generar una contradicción, que ambos tienen igual cardinal, es decir, es capaz de superar el axioma de Euclides que el todo es mayor que las partes y se acerca a idea de infinito como objeto. Dado que el estudian-te realiza la biyección podemos concluir que está presente la coordinación entre dos procesos iterativos, para dar con un único proceso iterativo infinito. Este caso deja ver las concepciones dinámicas y estáticas de los conjuntos ℕ y ℤ ya que hace referencia a los conjuntos como entidades terminadas con el mismo número de elementos y también hace referencia al proceso que debe seguir para relacionar cada elemento de ℕ con un único elemento de ℤ y viceversa. Por lo tanto, se observa la estructura proceso iterativo infinito y la estructura totalidad.
Los resultados refuerzan la problemática evidenciada en los antecedentes respecto a la complejidad de comprender el infinito actual. Se corrobora la idea de D'Amore et al. (2006) de que el objeto trascendental puede ser comprendido a cabalidad solo en casos extremadamente específicos, así como también la idea de Montoro (2016), que plantea que la manipulación de conjuntos infinitos a lo largo de la enseñanza escolar no es suficiente para que los estudiantes puedan construir concepciones correctas acerca de las cardinalidades de con-juntos infinitos.
8. CONCLUSIONES Y REFLEXIONES FINALES
Aunque la construcción del infinito matemático se ve supeditada al contexto, la determinación de un modelo genérico de construcción de esta noción es de vital importancia para su estudio (Villabona y Roa-Fuentes, 2016). Nuestro estudio, basado en un modelo provisorio, evidencia que las dificultades de los estudiantes para comprender que el conjunto de los números naturales y el de los números enteros tienen el mismo cardinal están determinadas por el mecanismo de coordinación y la capacidad de ver el proceso iterativo infinito como un todo terminado. Esto se refleja en sus argumentos ya que están supeditados a una coordinación basada en una función inyectiva. Es por esto que, al considerar una planificación de un ciclo de enseñanza, esta debería estar basada en el trabajo de funciones biyectivas entre diversos conjuntos numerables, para establecer luego una coordinación y, además, el desarrollo de la capacidad para ver el proceso como un todo terminado. Todo esto, podrá dar pie a la estructura mental de objeto trascendente.
Igualmente, el lector podrá encontrar en este artículo la construcción mental que debe llevar a cabo un estudiante para poder concluir que el cardinal de los números naturales es equivalente al cardinal de los números enteros, es decir, se evidencia parte de la descomposición genética preliminar y teórica particular para la comparación del cardinal del conjunto de los números naturales y enteros. Asimismo, el análisis de los datos presentados concuerda con los aspectos tomados en cuenta en ella.
Además, dado que nuestro instrumento no buscaba visualizar la estructura objeto trascendente, no fue posible visualizarla. Nos parece importante trabajar en contextos que permitan encontrar evidencias de esta estructura. Para esto, será necesario, una vez que emerjan, realizar acciones sobre ellas. En nuestro caso, analizar el cardinal de la unión de conjuntos numerables, por ejemplo.
Puesto que profundizamos solamente los mecanismos y estructuras menta-les de los estudiantes al momento de hacer una comparación de cardinales entre el conjuntos de los números naturales y enteros, el estudio queda limitado únicamente a conjuntos numerables, sería interesante profundizar esta investigación en las estructuras y mecanismos que tienen los estudiantes respecto a los cardinales de conjuntos no numerables, por ejemplo en la comparativa del cardinal del conjunto de los números irracionales con el de los números reales. Indagar en comparativas de otros conjuntos infinitos podría ampliar la mirada del estudio.
En efecto, los estudiantes suelen trabajar a lo largo de toda la enseñanza escolar con sistemas numéricos, nuestro trabajo intenta ser una guía para el docente, en el sentido que puede dar luces de las estructuras mentales y mecanismos presentes en los estudiantes para luego, desde ese punto de inicio, guiarlos en la construcción del objeto trascendente. Además, en la escolaridad chilena, el Ministerio de Educación plantea la incorporación de nuevos tópicos para el área de matemáticas, como límites y derivadas, por ejemplo. Los cuales se deben incorporar a cabalidad para el año 2020. Es por esto que el desafío para el docente de matemática es impregnarse de conocimiento que le permita llevar a cabo una enseñanza que fomente la construcción del objeto infinito, pues es un objeto indispensable para comprender los nuevos tópicos. Por esto, se requiere profesionales de la educación que profundicen en su estudio. Tanto para la generación de propuestas innovadoras, como también, para poder capacitar a los docentes que tendrán que asumir estos nuevos desafíos de la educación chilena.
A modo de proyección, se propone diseñar un ciclo de enseñanza que aborde el cardinal de conjuntos numerables, basado en las estructuras mentales y los mecanismos presentes en la descomposición genética presentada y trabajar, desde este lugar, la estructura de objeto del infinito. Para esto será necesario “analizar situaciones relacionadas con el infinito a partir de la construcción de procesos iterativos infinitos y sus objetos trascendentes, pues esto puede darle a un estudiante una herramienta formal que le permita confrontar sus propias creencias sobre el infinito” (Roa-Fuentes y Oktaç, 2014, p. 147), lo cual es bastante complejo pues, según Roa-Fuentes y Oktaç (2014) es poco lo que se ha podido indagar sobre cómo se lleva a cabo la coordinación de procesos, sobre todo si son de naturaleza diferente.
Las conclusiones expuestas clarifican las complejidades inmersas en el objeto mismo de infinito actual y en la enseñanza de este. Por esto, los docentes debemos asumir el desafío de indagar en marcos teóricos explícitos que permitan profundizar en la manera en que un estudiante aprende las nociones matemáticas ligadas al infinito. Con este estudio se propone a la comunidad de profesores e investigadores en didáctica de la matemática una respuesta a la pregunta de investigación planteada, acerca de las estructuras y mecanismos mentales presentes al momento de comparar los cardinales del conjunto de los números naturales y enteros, así como también la descomposición genética involucrada que se puede extrapolar a cualquier comparación de cardinales entre conjuntos numerables. Esto representa una herramienta para el diseño de la enseñanza del cardinal de conjuntos numerables.











 nueva página del texto (beta)
nueva página del texto (beta)