INTRODUCCIÓN
Dos ranas avanzan cada una cierta distancia en cierto número de saltos. ¿Cuál da los saltos más grandes? En torno a esta sencilla trama, se diseñó una secuencia de situaciones con dos tipos de problemas de proporcionalidad -de comparación de razones y de cuarta proporcional-,2 mediante los cuales se buscó propiciar que los alumnos de quinto grado de primaria adquirieran conocimientos específicos sobre:
Procedimientos de resolución de dichos problemas, y las propiedades de la proporcionalidad que lo sustentan;
La inadecuación de las estrategias aditivas;
El comportamiento de una magnitud cociente (tamaño de un salto), la cual varía de manera directamente proporcional a la distancia avanzada y de manera inversamente proporcional al número de saltos.
Algunas propiedades de la operación de división.
A través de los aspectos específicos señalados, se buscó propiciar el desarrollo de una capacidad más general, conocida en la literatura sobre el tema como pensamiento proporcional, esto es, la capacidad de establecer relaciones entre cantidades en un contexto “que implica a la vez co variación de las cantidades e invariancia de razones o productos” (Lamon, 2007, p. 638).
Por otra parte, el uso de las razones de números naturales permite incursionar en el territorio de los números racionales, sin tener que expresarlos todavía de manera explícita, lo cual crea un antecedente para su estudio (Block, 2008).
Razones, fracciones, proporcionalidad, multiplicación y división, constituyen nociones del campo conceptual de las estructuras multiplicativas, que se aprenden de manera integrada mediante situaciones que las implican a todas (Vergnaud, 1983). Con el presente estudio queremos contribuir al conocimiento de situaciones fértiles para la enseñanza escolar que respondan a esta hipótesis y, recíprocamente, al fortalecimiento de esta.
En lo que sigue, precisaremos el estatuto de las cantidades y de las razones en juego. Después haremos un análisis de las tareas y de los procedimientos a priori posibles, el cual servirá como guía para ver los resultados de una aplicación de la secuencia en un grupo de quinto grado. Al final, elaboramos algunas conclusiones.
En el análisis de la aplicación de las situaciones, nos centramos únicamente en las situaciones de comparación.
¿Razones, cocientes o fracciones?
¿Qué se puede hacer con una división como 3 entre 4 cuando aún no se conocen las
fracciones, ni los decimales, y por lo tanto no se puede expresar el resultado
como
El presente estudio se inscribe en una línea de investigación3 en la que exploramos la hipótesis siguiente: un trabajo con razones, previo a su expresión con fracciones, puede contribuir al conocimiento de la proporcionalidad, y a sentar bases para el estudio posterior de las fracciones.
Coincidimos con la apreciación de Freundenthal (2002) con respecto a que las fracciones son maneras de simplificar la operatoria con razones, pero a costa de su lucidez:
El significado de la razón aparece cuando se habla de la igualdad (y la desigualdad) de razones, sin conocer su tamaño, cuando se dice, con sentido, “a es a b como c es a d” sin anticipar que “a es a b” puede reducirse a un número o a un valor de magnitud a/b (...) La razón es una relación de equivalencia en el conjunto de parejas ordenadas (o de valores de magnitud) ... Los cocientes y las fracciones constituyen formas de reducir esta complejidad, de bajar su estatuto lógico, a costa de la lucidez (p. 180 y 181).
En el Anexo 1 se presenta el conjunto de trabajos publicados en el marco de la línea de investigación sobre la temática de las razones y las fracciones, y se ubica el presente texto en ese conjunto.
2. LA SECUENCIA “LOS SALTOS DE LAS RANAS”, LOS TIPOS DE TAREAS
El contexto es el de unas ranas que dan, cada una, saltos del mismo tamaño en una recta numérica.4 Los problemas de comparación de razones consisten en comparar el tamaño de los saltos de dos ranas, conociendo -de cada una- dos datos: el número de saltos que dan y la distancia total que avanzan. También se incluyen problemas de cuarta proporcional, en los que se desconoce uno de los cuatro datos de dos ranas que dan saltos del mismo tamaño. Las magnitudes (número de saltos, distancia recorrida, tamaño del salto) son muy accesibles.
La situación ofrece la posibilidad de verificar empíricamente las respuestas mediante un programa de computadora diseñado exprofeso:5 una vez introducidos los dos datos de cada rana, el programa las muestra saltando sobre rectas numéricas, lo que permite comparar los saltos visualmente (Block y Martínez, 1999).
Las razones en juego en esta experiencia son heterogéneas, esto es, se establecen entre magnitudes de distinta naturaleza (número de saltos y metros).
Revisaremos aquí los principales procedimientos para la comparación del tamaño de los saltos. Veremos primero los procedimientos que se basan en relaciones cualitativas entre las cantidades y en cálculos aproximados. En la tabla 1 enlistamos los procedimientos organizados en función de los términos que se relacionan, ya sea homogéneos: dos cantidades de saltos (s y s’) por un lado, y dos cantidades de metros por otro (m y m’), o bien heterogéneos: una cantidad de saltos y la correspondiente cantidad de metros (m y s) de una rana, y otra similar de otra rana (m’ y s’).
En la tabla 1 se indican los principales casos de comparaciones cualitativas entre los tamaños de los saltos de dos ranas:6
Tabla 1 Procedimientos cualitativos en problemas de comparación de razones
| Relaciones entre términos homogéneos. |
Es decir, si la rana A da más saltos que la B, y avanza la misma distancia, los saltos de la rana A son más pequeños. Es decir, si la rana A da el doble o más saltos que la rana B, pero avanza menos del doble de distancia, entonces sus saltos son más chicos. |
| Relaciones entre términos heterogéneos |
Es decir, si en la Rana A la cantidad de saltos es más del doble que la de metros, y en la B es menos del doble, los saltos de A son más chicos.
|
Poner en juego las relaciones anteriores lleva a una primera exploración de la noción de razón. Se espera que, en cierto momento, se institucionalice la existencia de razones equivalentes -que en este contexto significa razones a las que les corresponde el mismo tamaño de salto- y la manera de obtenerlas: multiplicando o dividiendo ambos términos por un mismo número.7
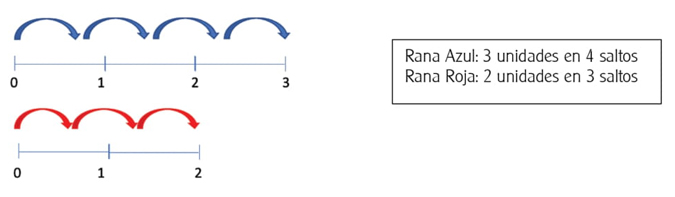
Para comparar las razones en los casos en que no proceden los métodos cualitativos,
se prevén dos procedimientos: el cálculo del valor unitario (cuántos metros avanzan
por salto) o la obtención de otras razones equivalentes con un término común, por
ejemplo, para comparar 3 metros en 4 saltos contra 2 metros
en 3 saltos se pueden obtener las razones equivalentes 6 metros
en 8 saltos vs 6 metros en 9 saltos. Este segundo
procedimiento es el que ofrece una alternativa que evita el uso de números no
enteros (en este caso,
Finalmente, entre los procedimientos erróneos que se pueden esperar, interesan especialmente dos: el centramiento en una variable dejando de lado la otra (“Son más grandes los saltos de la rana x, porque avanzó más metros”); y los que ponen en juego comparaciones aditivas, en lugar de multiplicativas, por ejemplo, la rana x dio un salto más y avanzó 1 metro más que la rana y, entonces sus saltos son del mismo tamaño. Se espera que la retroalimentación empírica (se explica más adelante) y los debates ayuden a visibilizar y cuestionar estos errores.
Las situaciones de la secuencia “Los saltos de las ranas”, se diseñaron bus-cando satisfacer las características de una situación adidáctica de la noción de razón (Brousseau, 1998). Las principales características de este tipo de situaciones son: 1) el concepto en cuestión -en este caso, la noción de razón- subyace a la estrategia óptima de resolución; 2) el problema que plantea la situación debe poder ser abordado -más no necesariamente resuelto, o no resuelto de manera óptima- a partir de los conocimientos previos del sujeto; 3) la situación debe permitir generar, mediante el manejo de ciertas variables, dificultades que favorezcan la evolución de los conocimientos; y finalmente, 4) la situación debe permitir a los alumnos validar por sí mismos el éxito o fracaso de sus acciones. Respecto de esta última característica, se previeron dos modalidades: la verificación empírica de respuestas utilizando una recta numérica en la computadora, mediante un programa hecho ex profeso y, por otra parte, la organización de puestas en común en las que se comparan resultados y procedimientos, y eventualmente se organizan debates y más pruebas, si se consideran necesarias.
3. APORTES AL ESTUDIO DE LA NOCIÓN DE RAZÓN DESDE OTRAS PERSPECTIVAS
Los procedimientos para resolver problemas de cuarta proporcional y de comparación, como los anteriores, han sido estudiados en investigaciones sobre el desarrollo de la noción de proporcionalidad. Se han caracterizado las estrategias más importantes, por ejemplo, las estrategias que implican el uso del operador escalar o el uso del operador función (Vergnaud, 1983), las estrategias inter e intra (within, between) (Noelthing, 1980 a y b).8 Se han destacado variables que complejizan los problemas o que propician un tipo de estrategia en lugar de otro (Hart, 1988; Karplus et al., 1983; Lamon, 2007; Noelthing, 1980 a y b; Vergnaud, 1983; entre otros).
Noelthing (1980 a y b), mediante su estudio ya clásico de la naranjada -en el que niños y adolecentes de distintas edades y escolaridad comparan la intensidad de sabor a naranja de dos mezclas preparadas con distintas cantidades de vasos de agua y de jugo-, estableció niveles de desarrollo relativos a esta noción y los vinculó a las etapas piagetanas de desarrollo del pensamiento lógico.
La situación de la naranjada que utilizó Noelthing, resultó muy adecuada para la exploración del desarrollo de ciertos aspectos del razonamiento proporcional de los niños y jóvenes, pero, no lo fue en cambio, para el aprendizaje, en la medida en que la situación no retroalimentaba a los alumnos, ellos no tenían manera de saber si su respuesta fue incorrecta y, por lo tanto, no tenían ocasión de cuestionar y regresar. Una pregunta que queremos contribuir a contestar entonces es si, en una situación como la de los saltos de las ranas que sí ofrece retroalimentación -en la que intervienen magnitudes más accesibles que las de una mezcla, y que permite hacer visible el carácter erróneo de las estrategias aditivas- puede propiciarse cierta evolución de los procedimientos de los alum-nos del último ciclo de la primaria.
Finalmente, cabe destacar el estudio de Brousseau (1981) sobre los decima-les, el cual constituye el primero, y casi el único, en el que se explora de manera sistemática el uso de razones en una génesis artificial de las fracciones. La secuencia construida es muy amplia, compleja y distinta de lo usual, por lo que puede ser difícil de implementar, pero sin duda abre un camino para explorar opciones, como la que estudiamos aquí.
4. HIPÓTESIS DE TRABAJO Y METODOLOGÍA
a) Hipótesis
En las líneas anteriores hemos ido precisando las hipótesis que nos ha interesado estudiar. Sintetizamos aquí una hipótesis de investigación que orienta este estudio:
Las situaciones de la secuencia “Los saltos de las ranas” funcionan como situaciones adidácticas de la noción de razón en un grupo escolar de quinto grado de primaria.
Y, las hipótesis más específicas son:
Las situaciones favorecen que los alumnos pongan en juego procedimientos de resolución relacionados con la noción de razón;
La retroalimentación que se ofrece a los alumnos a través del programa de cómputo, les permite reconocer sus errores.
Lo anterior favorecerá una evolución de los procedimientos en cada tipo de tarea;
Además, los alumnos lograrán manipular las medidas no enteras de los saltos a través de razones de números naturales, apoyándose en propiedades de la proporcionalidad.
b) Tipo de estudio y condiciones de la experimentación
Se trata de una experiencia de ingeniería didáctica (Artigue, 1995). A partir de un estudio preliminar sobre las nociones de fracción y razón en la escuela primaria (Block, 2006), en un proyecto de largo plazo se han ido diseñando secuencias didácticas para el aprendizaje de estas nociones en la primaria. En el presente artículo se expone una de estas secuencias.
La secuencia fue aplicada en un grupo de quinto grado de primaria de una escuela de la Ciudad de México. La conducción estuvo a cargo de la maestra titular del grupo, con experiencia en la gestión de situaciones bajo el mismo enfoque didáctico que la presente.
Los datos recabados fueron de dos tipos: las notas, con apoyo de audio, de seis observadores (lo que permitió que fueran observados entre cuatro y cinco equipos de alumnos) y las hojas de trabajo de los alumnos.
c) Distribución de actividades
A lo largo de seis sesiones, se alternaron situaciones de comparación de razones (comparar razones, redactar y evaluar reglas) y situaciones de cuarta proporcional (hallar uno o varios valores faltantes). Casi siempre, en una sesión de una hora, o un poco más, se propusieron dos o más actividades. La distribución se muestra en el Anexo 2.
5. RESULTADOS
5.1 Comparar de manera cualitativa
En la sesión 1 se planteó a los alumnos la siguiente actividad:
La rana verde y la rana morada hicieron cuatro competencias. En cada competencia cambiaron el tamaño de sus saltos. Escribe el color de la rana a la que le apuestas en cada competencia y explica por qué. Recuerda: NO gana la que dé más saltos, ni la que recorra más distancia, sino la que dé saltos más grandes.
En la figura 2 se muestra la parte de la ficha que corresponde a la primera competencia y en la tabla 2 los datos de las cuatro competencias. En todos los casos la comparación se puede hacer sin transformar los pares (y por lo tanto sin hacer cálculos).
Tabla 2 Datos que involucraron las cuatro competencias
| Competencia | 1ª | 2ª | 3ª | 4ª |
|---|---|---|---|---|
| Verde | 12, 12* | 28, 5 | 30, 8 | 24, 5 |
| Morada | 7, 5 | 36, 5 | 30, 11 | 15, 8 |
*El primer número de cada par indica el recorrido y, el segundo, el número de saltos
Los alumnos resolvieron en parejas. La mayor parte del grupo logró poner en juego procedimientos pertinentes para realizar las comparaciones, lo que supuso identificar las tres variables (número de saltos, distancia recorrida, tamaño de cada salto), y algunas relaciones entre ellas. En la tabla 3 puede observarse que no hay un procedimiento dominante para todas las competencias, los procedimientos son sensibles a las características de los datos numéricos de las razones. Al día siguiente se les pidió que compararan sus respuestas con las de otra pareja y que acordaran una respuesta de equipo. A continuación, se muestran algunos procedimientos.
Tabla 3 Frecuencias de procedimientos en Ficha 1 (sesión 1)9
| Procedimiento | Primera Competencia 12, 12 7, 5 | Segunda Competencia 28, 5 36, 5 | Tercera Competencia 30, 30, 8 30, 11 | Cuarta Competencia 24, 5 15, 8 |
|---|---|---|---|---|
| A. Número de saltos constante y mayor recorrido implica mayor tamaño del salto | 8 + 2 s/j* | |||
| B. Recorrido constante y mayor número de saltos implica menor tamaño del salto | 4 + 7 s/ | |||
| C. Mayor recorrido y menos saltos, implica mayor tamaño de salto | 10 + 1 s/ | |||
| D. Estimación o cálculo de uno o los dos valores unitarios | 7 | 2 | 3 | 3 |
| E. Respuesta correcta, pero justificación errónea | 9 | 3 | 1 | |
| F. Respuesta errónea | 2 |
* s/j = falta la justificación del resultado, o está incompleta.
a. Los procedimientos más frecuentes: cualitativos
Los argumentos que los alumnos dieron para justificar su respuesta, por escrito o verbalmente, dejan ver que la mayoría identificó las relaciones que permiten comparar con pocos cálculos numéricos, o sin cálculos.
En la primera competencia (12m, 12s, vs 7m, 5s) si bien se registraron más dificultades que en las demás, probablemente por ser la primera, identificaron que el tamaño de un salto de una de las ranas es de una unidad, mientras que el de la otra es de más, por ejemplo:
Julio: Porque con 12 metros y 12 saltos da un metro por salto, en cambio aquí (rana morada) 5 saltos en 7 metros da un metro y un poco más.
En la segunda competencia (28m, 5s vs 36m, 5s) la mayoría comparó los dos recorridos aprovechando que los números de saltos son iguales:
Carlos y Juan Eduardo: (Gana la morada porque) salta más metros en iguales saltos.
Itzel e Ingrid: 36 metros recorre más que 28 metros y los saltos son iguales.
En la tercera competencia (30m, 8s vs 30m, 11s), consideran que siendo los recorridos iguales, a mayor número de saltos, menor tamaño de cada salto:
Arih: (Gana la verde porque) el recorrido de los dos es igual pero los saltos de la verde son menos.
Julio y Andrés: 30 entre ocho es mas grande la cantidad que 30 entre once.
En la cuarta competencia (24m, 5s vs 15m, 8s) algunos observan que una rana avanza más distancia en menos saltos que la otra:
Arith: (verde) …Es más grande su recorrido y sus saltos son menos.
Itzel: ¡Ah! Entonces la verde, porque la morada tiene el espacio más chico, pero da 8 saltos y la verde tiene el espacio más grande y da menos saltos.
b. Otros procedimientos: el valor unitario, estimado o exacto
Algunos alumnos estimaron uno o los dos valores unitarios en lugar de utilizar las relaciones disponibles para comparar de manera cualitativa. En la mayoría de los casos la parte entera del cociente permitía comparar.
Tania y Lidia (para 28, 5 vs 36, 5): La rana verde le toca más de 4 y a la rana morada más de 7.
Tania y Lidia (para 30, 8 vs 30, 11): (La rana verde) porque la rana morada sus saltos son más de 2 m. Pero la rana verde da más de 3.
Pocos alumnos calcularon, en este momento, de manera exacta los valores unitarios.
Eduardo y Ricardo (para 12, 12, vs 7, 5): (…) La rana morada salta 7 metros y los dividimos entre 5 que de a 1 y sobran 2 metros pero lo convertimos en decimales y queda 1.4 y en la rana verde cada metro es un salto y queda de que la rana verde salta nada más un metro.
Arturo y Gabriel (para 28, 5 vs 36, 5): (La morada salta más porque) la verde da saltos de 5.6 y la morada de 7.2.
En esta experiencia, a diferencia de otras, no apareció el recurso a la igualación de dos términos homólogos: para poder comparar 2 metros en 3 saltos contra 3 metros en 4 saltos, se puede ver cuánto avanzan las dos ranas en 12 saltos. Esto se debió probablemente a que los números en juego, por su tamaño, no facilitaron dicho procedimiento (por ejemplo, no es fácil para los niños hallar un número de saltos múltiplo de 8 y 11).
c. Las dificultades: explicitar, representar, argumentar
La explicitación clara de una idea, con palabras, implica también una construcción. Este es otro proceso que los alumnos viven durante la experiencia, propi-ciado por la demanda de comunicar -oralmente sobre todo pero también por escrito- lo que tuvieron en cuenta para hacer la comparación. En el proceso, ocurre con cierta frecuencia que dejan alguna condición implícita, como en los siguientes ejemplos.
En la segunda competencia (28, 5 vs 36, 5), dejan implícito que los números de saltos son iguales:
Arith: Porque la verde su recorrido es más chico que el de la morada, por eso gana.
En la tercera competencia (30, 8 vs 30, 11), varios tuvieron dificultad para explicitar claramente la relación en juego y a veces dejaron implícita una condición:
Eduardo y Ricardo: (Gana la verde porque) entre menos sean los saltos más brincan.
Hubo varias manifestaciones de la dificultad para explicitar las relaciones en juego, y varias alternativas para superarla, por ejemplo, en un caso, unos alumnos trasladaron el problema al contexto de reparto de pasteles en el que la relación “entre más niños, les toca menos pastel” es más clara.
No se identificaron respuestas erróneas pero si algunas cuya argumentación era incorrecta. Esto ocurrió más en la situación 1 (12, 12 vs 7, 5) en la que varios siguieron aplicando el criterio que resultó exitoso en la situación anterior, según el cual, entre menos saltos, mayor es el tamaño de salto, por ejemplo:
Efrén: Porque entre menor sean los saltos serán más grandes.
Arith: Porque la rana morada recorre 7 metros y el número de saltos es más chico.
En la puesta en común del día siguiente, los argumentos fueron leídos y comentados. Después, los alumnos pudieron comprobar en la computadora qué saltos resultaban más grandes.
5.2 Formular y evaluar reglas generales
Las situaciones que se analizan a continuación van un poco más allá de la comparación de dos razones del tipo “número de metros, número de saltos”. Se trata de explicitar las condiciones que deben cumplir esas razones para que el tamaño de salto que se desprende de una sea mayor que el que se desprende de la otra. La situación se planteó a los alumnos en dos ocasiones: una en la última parte de la sesión 2, y otra en la última parte de la sesión 3. Entre las dos, se plantearon situaciones de cuarta proporcional.
a) Primera experiencia de formulación de reglas
En la segunda sesión, se planteó un primer ejercicio de formulación de criterios generales: se les pidió que expresaran la condición que debían cumplir los datos de las ranas verde y morada para que los saltos de la morada resultaran más grandes que los de la verde. La consigna que se dio no fue muy clara de entrada, pero fue reexplicada y, aparentemente, terminó siendo comprendida por todos.
(Expliquen) la condición que deben cumplir los números para que a fuerza gane la morada. No sólo damos el ejemplo de que con estos números gana la morada, sino (explicamos) cómo le hice, cómo escogí los números, qué condición cumplieron los números para asegurarme que ganará la morada.
Hubo dos propuestas y opiniones divididas, pero todavía pocos argumentos.
Ehecatl: Es que cuando pones menos saltos y más recorrido en la morada, gana la morada.
La maestra los invitó a encontrar un caso con el que no se cumpliera la regla, para “echarla abajo”. Pese a que no todos estaban convencidos, nadie intentó un contraejemplo y entre varios propusieron el siguiente ejemplo.
Después, Miguel propuso:
No importa el número de metros que recorra la rana sino los saltos que va a dar.
Nuevamente las opiniones se dividieron. Pocas voces, mostraron escepticismo, por ejemplo, Julio dijo: “Es que habría veces que gana y otra que perdería”. Otras, más numerosas, o más audibles, apoyaron la regla. Los argumentos fueron escasos. La primera prueba empírica que se planteó, con datos propuestos por el autor de la regla, permitió validarla: ganó la morada, con menos saltos.
La maestra, naturalmente, propuso hacer una segunda prueba, extremando los datos, pero respetando la condición de que la morada tenga menos saltos.
Con la participación de varios alumnos se llegó a los siguientes datos:
Nuevamente la maestra invitó a los alumnos a que anticiparan cuál creían que iba a ganar. Las preferencias se dividieron, pero la mayoría siguió siendo a favor de la morada. Entre el murmullo se escuchó a un alumno decir “es menos de un entero” (el salto). Enseguida, el autor de la propuesta dijo, no muy convencido:
Miguel: Tiene que ser mayor el recorrido que el salto.
Con ello, Miguel mostró que establece dos relaciones correctas: 1) cuando el número de metros es menor que el de saltos, el salto es menor que una unidad, y, 2) con esos datos, no va a ganar la morada aunque tenga menos saltos. Él intentó perfeccionar su regla10 pero sus intervenciones ya no fueron retomadas y se metieron los datos a la computadora. Varios niños muestran sorpresa.
Cuando la maestra pidió explicaciones de por qué perdió la morada, Miguel, con más convicción, agregó una condición a su regla: “Porque en la morada (el salto) fue menor que un entero”. Se probó nuevamente, haciendo que el salto de la morada sea mayor a un metro:
Las opiniones se dividieron, pero siguieron siendo más los que le van a la morada. La maestra volvió a pedir argumentos. Únicamente el autor de la regla habló, limitándose a estimar el tamaño del salto de la morada:
Miguel: (…) Como son 3 metros, va a dar un metro, la morada por un tercio de metro.
La verificación empírica mostró que los saltos de la verde eran considerablemente más grandes.
Desde esta primera sesión, una buena parte del grupo pudo poner en juego las relaciones entre los datos “distancia recorrida, número de saltos”, para anticipar el orden de los tamaños de los saltos, esto es, el orden de los cocientes no enteros, sin calcularlos. Con más dificultad, empezaron a formular los criterios utilizados. No obstante, en la segunda parte que acabamos de ver, al proponer y evaluar reglas “para que gane la morada”, fue notorio que los criterios todavía no están bien establecidos para los alumnos. Pueden usarlos implícitamente, y están aprendiendo a evaluarlos explícitamente en tanto criterios generales. Al final de la sesión 3, que veremos a continuación, se propuso nuevamente una actividad con las reglas, frente a la cual el grupo manifiesta avances.
b) Segunda experiencia de formulación de reglas
Al final de la tercera sesión, después de abordar la tarea de calcular valores faltantes, cuando los alumnos tenían ya mayor familiaridad con las relaciones involucradas (número de saltos, tamaño del salto y distancia recorrida),11 se les plantearon nuevamente problemas de comparación (ver la figura 3). En un primer momento, se les pidió que generaran “reglas para que gane la rana morada” (o sea, para que sus saltos sean más grandes que los de la verde), y también para que empaten.12 Al día siguiente, se les dieron dos de las reglas elaboradas por ellos, para que las evaluaran -una correcta y la otra no- y, finalmente, sus opiniones se discutieron en una puesta en común.
La actividad duró 20 min. Se formaron 17 parejas de trabajo. Se dio una consigna similar a la de la primera sesión y se entregó la siguiente ficha.
En la tabla 4 se presenta una síntesis cuantitativa de los recursos a los que acudieron los alumnos para producir las reglas. Puede apreciarse que, en con-junto, en el grupo se movilizaron varias propiedades. Enseguida se muestran algunos ejemplos.
Tabla 4 “Que gane la morada”. Frecuencia de procedimientos
| Para que gane la rana morada se necesita: | Frecuencia |
|---|---|
| A. Más recorrido y mismo nº de saltos que la verde | 3 |
| B. Mismo recorrido y menos saltos que la verde | 10 |
| C. Más recorrido y menos saltos que la verde | 12 |
| D. Más metros que saltos en la morada (tamaño >1), y menos en la verde (tamaño < 1) | 1? |
| E. Otros (erróneos) | 5 |
Mantener fija una de las dos variables, y mover la otra (A y B). Trece alumnos usan este recurso. Fue más frecuente que mantuvieran fijo el recorrido y variaran el número de saltos, que a la inversa.
Alan y Jesica: Poner el número igual de recorrido y el número de saltos menor.
Más recorrido y menos número de saltos (C). Este tipo de mensaje también fue frecuente.
Tania y Lidia: Debe de ser el recorrido más grande y sus saltos sean menos; Verde (25, 8) vs Morada (35, 3)
Otro ejemplo, con dificultad para explicitar:
Paulina y Mercedes: Entre más chicos sean los saltos más largos son y entre más largos sean los saltos más cortos son. (27, 5 de la verde vs 27, 4 de la morada).
Se observa cierta confusión entre tamaño del salto y número de saltos. Cuando dicen “entre más chicos sean los saltos más largos son” el “más chicos” se refiere al número de saltos. Luego Paulina agrega:
(…) Se debe poner menos saltos, para que sean más grandes.
La omisión del recorrido parece no ser accidental pues un poco más adelante dijeron explícitamente que el recorrido no importa.
Más metros que saltos (tamaño >1) en la morada, y menos en la verde (tamaño < 1) (D)
Ehecatl: Que el número de recorrido sea mayor al número de saltos -de la rana mora-da- y la rana verde tiene que ser menor el recorrido y mayor el número de saltos.
Este tipo de regla se identificó una sola vez. Puede estar influido por las experiencias previas en las que calcularon el valor unitario.
Errores: no importa el recorrido (E). Varios alumnos escribieron reglas ambiguas, o poco claras. Algunos generaron reglas erróneas. Nuevamente, como en la primera sesión de la experiencia, aparece la idea de que el recorrido no importa.
Mercedes y Paulina: No importa el recorrido sino los saltos de la rana aunque sea más grandes o chicos.
No obstante, en general, la mayoría demostró una mejoría -en comparación con lo que hicieron en la segunda sesión- en su manera de expresar reglas que aseguran un tamaño mayor de salto, a partir de manipular las dos variables que lo determinan: recorrido y número de saltos. En el siguiente apartado veremos un segundo encuentro de los alumnos con las reglas, ya no como productores de estas, sino como evaluadores de las reglas producidas por otros. Al final, analizaremos la dificultad que se manifestó para argumentar si una implicación lógica del tipo “si a entonces b”, es verdadera o no.
5.3 Evaluar reglas, desarrollar la argumentación
Al día siguiente (sesión 4) de las resoluciones anteriores, se entregó a los alumnos la ficha 5 (ver la figura 4) con dos de las reglas que ellos escribieron en la sesión pasada -una correcta y otra no-, y se les pidió que las evaluaran en parejas.
Se les dio la siguiente consigna:
M: Analicen las reglas y vean si es verdad lo que dicen, y si no comprueben que no sirven, ¿listos? A trabajar.
Veamos los resultados.
a. Dificultad para interpretar la expresión de “No importa el recorrido de la morada…”
Muy pocos alumnos se dieron cuenta de que la regla 1: “No importa el recorrido de la rana morada, lo que importa es que su número de saltos sea menor”, es incorrecta y pudieron dar un contra ejemplo. Iván propuso V 8m, 4s vs M 20m, 3s, pero no logró explicar su sospecha: “Es que no sé por qué, pero estoy seguro [de] que esta sí está mal”.
Ehécatl, por su parte, propuso ejemplos V 60m, 9s vs M 3m, 1s y luego V 60m, 9s vs M 1m, 1s, con los que claramente cuestionó la regla, pues la morada, a pesar de dar menos saltos, no tiene un salto mayor, y concluyó que: “Está mal porque si fuera mayor el recorrido de la rana contraria, sería mayor el salto”. Suponemos que lo que quiere decir es que aún con menos saltos en la morada, esta podría perder si la verde tiene un recorrido mayor. Su argumentación es todavía incompleta pues no con cualquier recorrido “mayor” de la rana verde, el salto de esta quedaría mayor que el de la morada, pero se puede decir que representa un avance importante.
Algunos alumnos encontraron un caso que sí “cumple” con la condición de la regla: la morada tiene menos saltos que la verde y a la vez arroja un salto mayor, con lo cual dan por buena la regla, por ejemplo, Julio y Paris proponen el caso V 1m, 50s y M 50m, 1s, y exclaman: “Mira, sí se cumple, aquí sólo da un salto y es mayor, ¿ya ves? Las dos reglas están bien… ¡Ya terminamos, ya terminamos!" Como ellos, varios alumnos interpretaron la expresión: “no importa el recorrido de la morada” como si se tratara de encontrar un caso en el que se cumpliera la condición (en lugar de valorar si se cumplía para cualquier caso), por ejemplo, Eduardo y Ricardo, proponen V 40m, 8s vs M 40m, 4s.
Algunos alumnos encontraron ejemplos y también contra ejemplos y no supieron qué concluir, o bien concluyeron algo como: “a veces es correcta y a veces es incorrecta”. Es el caso de Beatriz y Patricia.
Beatriz: Puede ser 50, por ejemplo, la rana verde puede dar 50 metros y menor salto y da 5 ¡no! 6 saltos, y la rana morada da, por ejemplo, recorre 5 metros en 2 saltos y entonces ahí no se cumpliría. (Queda: verde 50m, 6s y morada 5m, 2s).
Pero más adelante ellas mismas encuentran un ejemplo que satisface las condiciones de la regla 1 (menos saltos a la morada) y con el que sí se logra que los saltos salgan mayores, entonces concluyen: “Sí, pero en algunas veces No”, y proponen dos ejemplos, uno para cuando sí, uno para cuando no.
Frente a respuestas como esta, la docente y los observadores intentaron explicitar uno de los principios (implícitos) de la argumentación matemática, a saber, que una regla no puede ser a la vez cierta y falsa. Este análisis se retomará más adelante, en la confrontación.
b. Papel de la búsqueda de ejemplos en el análisis de una regla
La segunda regla (poner la misma cantidad de saltos, pero más recorrido en la morada) fue hallada correcta por la mayoría de los alumnos, quienes proporcionaron ejemplos sin dificultad. Fue interesante observar a algunos alumnos que al principio pensaron que la regla era incorrecta, y no fue sino después de intentar en vano poner ejemplos que lo probaran, que sospecharon que era correcta. Así, Juan Carlos y Pablo dijeron que la regla 2 era incorrecta, pero después de elaborar un ejemplo -V 9m, 2s, M 12m, 2s- concluyeron que era correcta. Jessica y Arlen intentaron encontrar un ejemplo con el que se incumpliera la regla y parece que se dan cuenta de que eso no es posible. Concluyen que la regla es correcta.
c. Papel de la retroalimentación mediante el programa informático
Los alumnos acudieron con frecuencia a la computadora para verificar si sus datos correspondían a saltos de la morada mayores que los de la verde. La validación que recibían los ayudó a desechar una comparación equivocada o a afirmar una correcta, como en el siguiente ejemplo ocurrido en la evaluación de la regla “Poner la misma cantidad de saltos, pero más recorrido en la Morada”.
Pablo: (Hace las dos tablas y pone primero la misma cantidad de saltos) Por ejemplo, pones dos aquí ...(en la rana verde)... y dos aquí ...(en la rana morada)... Luego podemos poner por ejemplo aquí 9 ...(en la verde)... y aquí mmm, a ver, 12.
Observadora: ¿Cuál va a dar saltos más grandes?
Aos: Esta (la morada, no logran explicar por qué decían antes que estaba mal la regla. Ahora dicen que está bien; regresan contentos porque sí funcionó lo que ellos dijeron).
En cambio, la verificación en computadora no los ayudó -no podía hacerlo- a identificar un razonamiento incorrecto, cuando la usaron para buscar un ejemplo en lugar de un contraejemplo.
d. La confrontación grupal: malentendidos sobre el sentido de una implicación
En la confrontación grupal emergió la problemática que subyace a la regla: No importa el recorrido de la rana morada, lo que importa es que su número de saltos sea menor. Esta regla se puede formular como una implicación, con un antecedente: “Si el número de saltos de una rana es menor que el de otra”, y un consecuente: “Entonces sus saltos son mayores”, quedando fuera la distancia recorrida.
Miguel, quien en una sesión anterior había propuesto una regla muy parecida, cuestionó con un buen contra ejemplo: V 14m, 7s y M 2m, 3s. Los datos que propone cumplen en efecto con el antecedente de la implicación -que la morada dé menos saltos que la verde-, y, sin embargo, no cumplen con el consecuente -que los saltos de la morada sean mayores que los de la verde-. Es decir, la regla no se cumple. Algunos alumnos se sorprenden con el contra ejemplo, pues al parecer ellos pensaban que la regla era buena. “Hace brujerías” comenta uno, con lo que podría pensarse que cuestiona la lógica subyacente.
Un poco más adelante, otro alumno, Paris, da un ejemplo en el que los datos también cumplen con el antecedente de la regla (morada con menos saltos), pero sí dan lugar a saltos de la morada mayores que los de la verde: V 42m, 8s, M 42m, 3s. En este punto, la maestra interviene para cuestionar el ejemplo, el cual vino a complicar las cosas. Se armó entonces una discusión que analizamos a continuación.
M: Ahí (en la regla) no dice que el recorrido sea igual, ahí dice que no importa el recorrido y aquí (RM) pusimos, puede ser aquí 2 y 1413 y se cumple la regla. Tenemos que revisar si se cumple la regla con todo.
Paris: Pero sí se cumple la regla.
El primer cuestionamiento que hace la docente al calor de la discusión (“ahí no dice el recorrido igual”), es incorrecto pues si bien la regla no dice que los recorridos deban ser iguales, tampoco dice que no puedan serlo, de hecho, lo hace posible puesto que los recorridos “no importan”.
El segundo cuestionamiento realizado por la maestra, “tenemos que revisar si cumple con todo” es probablemente una expresión de la necesidad de que la regla sea válida para todos los casos que cumplen el antecedente de la implicación (“si el número de saltos es menor…”), y no solo para algunos. Se trata de una característica de la implicación lógica sobre la cual los alumnos segura-mente no han reflexionado. Las distintas interpretaciones de “cumplir con la regla” que se entrecruzaron, y la dificultad para sacar a la superficie con claridad lo que está detrás, causó que la discusión se alargara todavía unos minutos más.
Maestra: (escribe en el pizarrón a lado de la propuesta de Miguel)
Oreal: Las dos reglas son casi iguales. Puedes poner el mismo recorrido.
Miguel: Pero no cumple la regla.
M: En esta (la de Miguel) sí se cumple, pero en esta (señala la propuesta de Paris) ¿sí se cumple?, ¿qué es lo importante?
Pablo: No lo sé.
Por sugerencia de uno de los observadores, la docente propuso a los alumnos verificar en la computadora, pero esta acción no era lo que se precisaba en este momento para desenredar el nudo. Se verificó que la rana morada de Paris (42m, 3s) en efecto da saltos mayores que los de la verde (42m, 8s) y que la de Miguel no. Ciertamente, algunos alumnos se sorprendieron. Pero el problema no era solamente ese, sino la necesidad de que todos los pares cumplieran la regla, sin excepción, para poder afirmar que la regla era cierta.
Al final, la maestra logró identificar el problema.
M: (...) Con un ejemplo (señala el ejemplo de Miguel) que encontremos que la regla no funciona, entonces está mal, aunque haya ejemplos donde sí nos funcione, pero de todos modos está mal si con un ejemplo no sale cierta. ¿Sí Julio?
Al final, algunos alumnos dejaron ver que no quedaron conformes con la conclusión. Cuando se presenta la segunda regla (“poner la misma cantidad de saltos, pero más recorrido en la morada”), el tiempo está encima y casi no hay discusión: varios se pronuncian a favor de que “se cumple la regla”, y se revisan dos ejemplos en la computadora. En este caso, tampoco se hace explícito que la razón por la cual se considera que la regla funciona no es porque funcionó con dos ejemplos sino porque, analizándola, puede inferirse que no se encontrarán contra ejemplos. Estos son pendientes para otras ocasiones.
6. CONCLUSIONES
Las situaciones de comparación de razones del contexto de “Saltos de las ranas” -en este caso son también cocientes indicados-, pudieron ser abordadas por alumnos que, aun sin saber de antemano cómo hacer las comparaciones solicitadas, comprendieron la trama de relaciones en juego; propusieron y argumentaron respuestas; pudieron reconocer propuestas erróneas gracias a la retroalimentación ofrecida por la situación. Gracias a la socialización de procedimientos, cada vez más alumnos pusieron en juego razonamientos correctos para comparar razones, lo cual confirma que la situación implica al conocimiento que interesa. Puede decirse entonces que las situaciones, con una gestión adecuada, funcionaron bien como situaciones adidácticas de la noción de razón para alumnos de quinto grado de primara.
La explicitación de los criterios para hacer las comparaciones fue otro aspecto que mejoró notablemente en los alumnos. La formulación de reglas “para que gane la rana morada”, permitió, poner en evidencia hipótesis falsas, y también, dio lugar para discutir interpretaciones incorrectas de la noción misma de “regla válida”.
La verificación mediante el programa de computadora cumplió bien su papel de medio que retroalimenta las respuestas de los alumnos, y a la vez, mostró sus límites: se puede constatar que algo está mal (incluso, qué tan mal, qué tan alejado), pero no por qué está mal; se pueden verificar casos particulares, pero un caso particular “no hace a una regla” (excepto si es un contraejemplo).
En las situaciones de comparación, los números que corresponden a las medidas de los diferentes saltos no son enteros. Se confirma el hecho, ya reportado en otros trabajos, de que los alumnos pueden desarrollar razonamientos que involucran a dichas medidas sin hacerlas explícitas, mediante las razones entre números naturales -o cocientes indicados- “tantos metros en tantos saltos”.
En lo que respecta a la situación final de valoración de una regla producida en el grupo (“no importa el recorrido…”), pese a las dificultades debidas a cierta confusión momentánea de parte de la docente, las discusiones dejaron ver que, cuando se presentan situaciones que favorecen la elaboración de conjeturas y la posibilidad de verificarlas, y cuando se dan condiciones para que los alumnos expresen sus opiniones, es posible seguir propiciando el desarrollo del razona-miento lógico matemático. Se abona así a la tesis de que no hace falta separar el trabajo para favorecer el pensamiento lógico del estudio de los contenidos específicos de matemáticas, como se pensó en la reforma llamada “de las matemáticas modernas” de los años 60-70 del siglo pasado.
En esta experiencia, como en otras que hicimos entre 1990 y 2010, pusimos poco énfasis en los momentos de institucionalización, en los que correspondía al docente destacar procedimientos y errores, así como nombrar y definir algunas nociones. Los análisis que hemos ido realizando dejan ver la necesidad de estos momentos.
Por lo anterior, consideramos que, pese a los tropiezos ya identificados, los alumnos tuvieron condiciones favorables para avanzar en su capacidad de establecer relaciones entre cantidades en un contexto “que implica a la vez co variación de las cantidades e invariancia de razones o productos” (Lamon, op.cit).
¿Qué sigue? En el estudio del largo recorrido que inicia con la comparación intuitiva de razones usando únicamente números naturales, y que culmina con el uso bien fundamentado de fracciones y decimales en su papel de expresar razones, si bien hay ya avances importantes -como lo hemos esbozado en la introducción-, queda todavía mucho por hacer, incluyendo un trabajo de diseño y experimentación de situaciones, y de articulación entre ellas en proyectos de largo plazo. Por supuesto, otros ámbitos como el del desarrollo curricular y el de la formación docente, requieren también lo suyo en el tratamiento de este tema.











 nueva página del texto (beta)
nueva página del texto (beta)