INTRODUCCIÓN
Una de las funciones de la institución escolar -en particular de la escuela obligatoria- en la sociedad es conseguir que las nuevas generaciones de ciudadanos aprendan los conocimientos que forman parte de su legado cultural. En general, la enseñanza de esos conocimientos tiene como objetivo que los miembros de dicha sociedad puedan llegar a desenvolverse de modo eficaz en la vida cotidiana.
Habitualmente una de las disciplinas que forma parte del legado cultural incluido en el currículo son las matemáticas. De hecho, los conocimientos mate-máticos son considerados como una parte importante de la enseñanza escolar, lo que lleva a pensar que debe haber una especial articulación entre lo que se propone para ser enseñado. Sin embargo, no es así ya que, por ejemplo, en la estructura del currículo español de matemáticas (Ministerio de Educación, Cultura y Deporte [MECD], 2015) para la Educación Secundaria Obligatoria (ESO) (alumnos de 12 a 16 años) aparece un listado de contenidos separados por bloques, cuyas temáticas se presentan de forma aislada. Ello se traduce en que en la enseñanza de las matemáticas existe una cierta desarticulación que sugiere, por ejemplo, que estudiar geometría y estudiar funciones son asuntos completamente separados, pues aparecen en bloques aislados.
De este modo, a pesar de que en el currículo diseñado se suele indicar que los contenidos propuestos para ser enseñados deben presentarse de manera integrada y articulada, finalmente esta responsabilidad termina dejándose, implícitamente, solo en manos de los profesores. Esto, por supuesto, constituye un encargo complejo que los profesores por sí solos difícilmente pueden abordar, ya que se trata de un problema de investigación didáctica que desborda su práctica profesional.
En la Teoría Antropológica de lo Didáctico (TAD) se postula que para llevar a cabo la enseñanza de un saber es importante considerar cuáles son algunas de las cuestiones a las que responde dicho saber; es decir, cuáles son sus posibles razones de ser, en una institución determinada. La búsqueda de las razones a las que debería responder la enseñanza de la geometría en la enseñanza secundaria, en particular la geometría bidimensional (2D) y la geometría tridimensional (3D), nos llevó a diseñar e implementar un dispositivo didáctico, que, dentro de la TAD, se denomina recorrido de estudio e investigación (REI), en torno al diseño y construcción de envases. Pretendimos que dichas razones de ser de la enseñanza de la geometría ayudaran no solo a dar sentido a varios de los saberes propuestos en el currículo de la ESO, sino también a encontrar la conexión y la articulación, tanto entre las geometrías 2D y 3D, como con otros saberes matemáticos que propone este currículo.
En este artículo, analizamos la actividad matemática desarrollada por 14 estudiantes de secundaria al abordar uno de los tipos de tareas que formaron parte del REI propuesto. Con lo cual, pretendemos establecer si efectivamente las cuestiones que aparecen en dicho REI pueden constituirse en una posible razón de ser de algunos de los saberes geométricos propuestos para la ESO y qué conocimientos de la geometría 2D y 3D se ponen en juego durante su abordaje. Para ello, usamos los indicadores del grado de completitud de una organización matemática local (Bosch et al., 2004), que nos permiten caracterizar la organización matemática (OM) realmente construida por los alum-nos y dar cuenta de algunas de las restricciones que han dificultado la búsque-da de respuestas a cuestiones sobre el diseño y elaboración de un envase en cartulina, con capacidad para un litro.
El contraste entre estos indicadores y la actividad matemática desarrollada por los estudiantes nos va a permitir determinar hasta qué punto, en qué medi-da, las praxeologías matemáticas puestas en juego se han mostrado como relativamente completas y, en consecuencia, si ha sido posible llevar a cabo una actividad de modelización.
En lo que sigue, mostramos algunos antecedentes de la investigación de la que forma parte este trabajo. Explicamos el marco teórico que fundamenta nuestra investigación. Describimos el REI que hemos implementado, centrándonos en la actividad matemática desarrollada que queremos analizar. Presentamos algunos resultados obtenidos al aplicar el instrumento de análisis y algunas de las restricciones y limitaciones encontradas, y terminamos con nuestras conclusiones.
ALGUNOS ANTECEDENTES
Santaló (1985), trató la problemática en torno a la enseñanza de la geometría en el ciclo secundario en España (alumnos de 12 a 16 años), mostrando que tanto en el ciclo primario (alumnos hasta los 12 años) como al terminar la secundaria había dos tendencias claramente diferenciadas, la geometría experimental e intuitiva y, la geometría axiomática. El problema se encontraba pues en el ciclo de la enseñanza secundaria, específicamente en el ciclo básico de tres años (alumnos de 12 a 14 años) que correspondía a la etapa obligatoria, porque para ese momento primaban las presentaciones rigurosas y sistemáticas que habían abandonado el carácter práctico de la geometría, elevándola al mundo de las ideas. Así, Santaló afirmaba:
La máxima preocupación debe ser para el ciclo básico. Si el Estado impone su obligatoriedad debe procurar que su enseñanza sea verdaderamente útil a los alumnos, tanto en su aspecto formativo, cosa no fácil de evaluar, como en su aspecto informativo, más fácil de decidir a través de los contenidos. Estos contenidos, que deben ser adaptados a las necesidades de la sociedad ambiente, deben revisarse periódicamente y son rápidamente cambiantes, de manera que un primer obstáculo a vencer es la inercia usual de los enseñantes, que quisieran enseñar siempre lo que ellos aprendieron, y de los responsables de la enseñanza, casi siempre misoneístas y temerosos de introducir cambios con demasiada frecuencia, sin tener en cuenta que la escuela no debe distanciarse demasiado del mundo exterior a ella. Cuando lo que se enseña en el aula es muy distinto de lo que se aprende en la calle, el sistema educativo se desequilibra. (Santaló, 1985, p. 14)
Dentro de las propuestas planteadas por Santaló (1985) para que la enseñanza de la geometría resulte útil a los estudiantes, destacan; primero, no pensar que se deba partir de cero en el aula, pues los estudiantes traen consigo varios conocimientos provenientes de la escuela, y de la vida familiar y social; segundo, “lo que sea intuitivamente evidente para el alumno debe aceptarse como tal, para poder seguir adelante en la adquisición de conocimientos menos evidentes” (p. 20); y tercero, mostrar cada vez que sea posible, la conexión entre las diferentes partes de las matemáticas.
Esta problemática sobre la diferenciación que existe entre la enseñanza de la geometría experimental y la geometría axiomática, que ha advertido Santaló, guarda relación con el trabajo de tesis doctoral llevado a cabo por René Berthelot y Marie-Hélène Salin (1992); quienes resaltan la importancia de un tipo de conocimiento que sirve para operar directamente sobre el espacio sensible - conocimiento espacial-, y de cómo los conocimientos geométricos aparecen diluyendo este conocimiento en la medida en que se avanza en la vida escolar; y porque proponen la necesidad de vincular estos dos tipos de conocimiento.
En un estudio exploratorio llevado a cabo por Pérez y Guillén (2007), en el que se indagó sobre las creencias y las concepciones en torno a la enseñanza de la geometría de un grupo de 19 profesores de secundaria, se encontró, entre otras cosas, que los bloques que se privilegian en la enseñanza de las matemáticas en la ESO son los de aritmética y de álgebra y también, aunque algo menos, el de análisis. Así, en el caso de que no hubiese tiempo suficiente para abordar todo el currículo, la geometría no se abordaría. Estos autores señalaron también que en el estudio que realizan los alumnos de la ESO, sobre la geometría, se presta mucha atención a los problemas de operar o calcular áreas y volúmenes, y se dedica mucho menos tiempo a los procesos de reproducción, descripción, clasificación, representación, construcción, etcétera.
En lo referente a los poliedros, en Pérez y Guillén (2008), se encontró que su estudio se limita a los prismas, pirámides, poliedros regulares, cilindros, conos y esferas. Y, en Guillén, González y García (2009), donde se analizó la propuesta que hacen los textos escolares sobre los cuerpos de revolución se afirma que:
“El cálculo de áreas y volúmenes en secundaria se basa fundamentalmente en la aplicación de las fórmulas a partir de sus elementos” (p. 255). Por ejemplo, el cálculo del área de una superficie rectangular dada la medida de sus lados, o el del volumen de un paralelepípedo dada la medida de sus aristas. Esto des-vela el fenómeno didáctico de reducir la enseñanza de las figuras geométricas a su estudio aritmético y algorítmico, dejando de lado el análisis de su determinación y construcción. Lo que conlleva también un uso exclusivamente aritmético de las fórmulas en geometría. Dicho fenómeno forma parte de un problema más general de la situación actual de las matemáticas en la educación primaria y secundaria, tal como se señala en las conclusiones del Libro Blanco de las Matemáticas: “[…] es frecuente que la enseñanza de las matemáticas se reduzca a procedimientos y rutinas” (RSME, 2020, p. 544).
También en la Educación Secundaria, pero en el contexto costarricense, se ha estudiado la problemática que presenta la enseñanza de la geometría, porque los contenidos en la educación formal son mostrados como productos acabados (Gamboa y Ballestero, 2010). Es decir, como aquellos que no son susceptibles de cambios y que aparecen como cristalizados, de modo que su enseñanza no considera ninguna reflexión en torno a su construcción. Esta forma de concebir y presentar los contenidos de una disciplina se sitúa dentro de lo que Chevallard (2013, 2017) llama el paradigma de la visita de las obras.
Como alternativa al paradigma de la visita de las obras, Chevallard propone el paradigma de cuestionamiento del mundo, en el que la lógica lineal dominante del currículo se rompe mediante el estudio funcional de las matemáticas, donde los conocimientos matemáticos surgen a partir de las cuestiones a las que responden, proponiendo tipos de tareas o problemas en los que dichos conocimientos sean una buena herramienta para resolverlos. De este modo, los contenidos que son propuestos en el currículo aparecerán como necesarios para el abordaje de dicho problema, y no como un listado a priori de contenidos que apenas aparecen justificados.
Los estudios sobre la enseñanza-aprendizaje de la geometría realizados dentro de la teoría de las situaciones didácticas (TSD) (Berthelot y Salin, 1992, 2001), permiten postular que una vía para recuperar algunas de las razones de ser de algunos de los saberes geométricos propuestos en el currículo de la ESO, se encuentra en torno a la resolución de un tipo de problemas que dichos autores llaman problemas espaciales. Estos tratan sobre situaciones que tienen lugar en el espacio sensible. Así, en el tipo de problema de diseño, que consideramos en este trabajo, los conocimientos geométricos sirven como herramienta eficaz para su solución.
En Perrin-Glorian et al., (2013), se afirma también que la problemática de modelización o espacio-geométrica que proponen Berthelot y Salin, consistente en partir de un problema del espacio sensible o problema espacial, pasar a representarlo mediante un modelo geométrico, utilizar las propiedades geométricas correspondientes y terminar validándolo en el espacio sensible, resulta de gran interés para llevarla a cabo en la enseñanza. Lo que ha de permitir considerar la relación entre el espacio sensible y el espacio geométrico, y en particular realizar una enseñanza coherente de la geometría a lo largo de la escolaridad obligatoria, que necesita tener en cuenta ambos espacios y ligarlos con el desarrollo del alumno.
A continuación, describimos brevemente el marco teórico en el que nos situamos, que dispone a su vez de un modelo metodológico, y esbozamos en qué consisten los problemas espaciales y su relación con los conocimientos espaciales y geométricos, ya que estos se encuentran estrechamente ligados con nuestro postulado.
MARCO TEÓRICO
Para hacer frente al fenómeno didáctico general de la pérdida de las razones de ser de la enseñanza de la geometría, utilizamos las herramientas que pro-pone la TAD y nos apoyamos en diferentes estudios realizados dentro de la TSD que han mostrado la interrelación entre algunos problemas espaciales y los conocimientos geométricos.
La Teoría Antropológica de lo Didáctico y los recorridos de estudio e investigación
La TAD puede entenderse como una evolución de la TSD, propuesta por Guy Brousseau. Según Gascón (2013), la TSD constituye el germen del programa epistemológico que surge frente a la “insuficiencia manifiesta de los modelos epistemológicos dominantes en las instituciones escolares para formular y abordar los problemas didáctico-matemáticos” (p. 79). Dicha insuficiencia proviene de cómo conciben la enseñanza-aprendizaje de las matemáticas, y las matemáticas mismas, tales modelos. La diferencia con dichos modelos es que:
En el caso particular de la TSD se postula que un conocimiento matemático está definido por las situaciones que lo determinan, esto es, por un conjunto de situaciones para las que dicho conocimiento es idóneo porque proporciona la solución óptima en el contexto de una institución determinada. Las situaciones contienen la “razón de ser” del conocimiento que definen, esto es, las cuestiones que le dan sentido, así como las restricciones que limitan su uso en una institución determina-da y las aplicaciones potenciales del mismo. (Gascón 2013, p. 79)
Yves Chevallard propone, a principios de los ochenta, estudiar los fenómenos de trasposición didáctica siguiendo, al igual que la TSD, los principios del programa epistemológico. Es decir, cuestiona los diferentes modelos epistemológicos del saber matemático que viven en cada una de las instituciones que intervienen en la transposición didáctica y propone nuevos modelos alternativos que posibilitan; de una parte, poner de relieve los fenómenos didácticos que se presentan en dichas instituciones; y de otra, formular y abordar los problemas didácticos relacionados con esos fenómenos (Gascón, 2014). A partir de allí, surge la TAD, que, a diferencia de los otros enfoques en didáctica de las matemáticas, basados en modelos cognitivos, precisa de “un modelo de las matemáticas institucionales que incluya la matemática escolar como un caso particular y de un modelo de las actividades matemáticas institucionales que incluya la enseñanza-aprendizaje escolar de las matemáticas, como una actividad matemática institucional particular” (Gascón, 1998, p. 20). Con lo cual, la TAD propone concebir el cono-cimiento matemático en estructuras cuya unidad mínima es la organización o praxeología matemática (OM). Estas estructuras se componen de:
[…]un bloque práctico o “saber-hacer” formado por los tipos de tareas y las técnicas [Τ/τ] y por un bloque teórico o “saber” formado por el discurso tecnológico-teórico [θ/Θ] que describe, explica y justifica la práctica. […] Las OM surgen como producto de un proceso de estudio estructurado en seis dimensiones o momentos didácticos. La forma concreta de llevar a cabo un proceso de estudio en una institución determinada se describe a su vez en términos de organizaciones o praxeologías didácticas [OD]. (Bosch et al., 2004, p. 7)
La TAD propone un modelo ideal de proceso de estudio para el aprendizaje de las matemáticas a través de la modelización, los REI (Barquero, 2009; Fonseca, Pereira, y Casas, 2011), caracterizado porque parte de una cuestión importante viva y rica, con fuerte poder generador. En ellos el objetivo del estudio no viene definido como un conjunto de saberes designados de antemano, sino como un conjunto de cuestiones cruciales -derivadas de dicha cuestión inicial- a las que la comunidad de estudio se propone aportar una respuesta. Se recupera así la relación natural entre cuestiones y respuestas de cualquier actividad de formación.
Los REI pueden describirse mediante una estructura arborescente de cuestiones y respuestas, que surgen con la movilización de los medios, saberes y respuestas disponibles. Son, por tanto, una herramienta muy apropiada tanto para describir los procesos de estudio existentes o posibles como para imple-mentar en el aula secuencias de enseñanza basadas en la actividad matemática de modelización (Rodríquez-Quintana, 2005).
En suma, los REI son un dispositivo didáctico concreto que permite el estudio de las OM en la escuela e implican un cambio en la lógica tradicional que rige las formas de hacer en la enseñanza de las matemáticas. Primero, porque los conocimientos aparecen como necesarios para dar respuesta a las cuestiones que se abordan; y segundo, porque las respuestas a dichas cuestiones y las propias cuestiones no son responsabilidad exclusiva del profesor, sino también de los estudiantes, quienes las construyen como fruto del trabajo grupal.
LOS PROBLEMAS ESPACIALES Y LOS CONOCIMIENTOS GEOMÉTRICOS
En estudios que parten de la tesis de René Berthelot y Marie-Hélène Salin (Berthelot y Salin, 2001; Bloch y Salin, 2005), y en otros previos donde se cuestiona la geometría y su enseñanza (Brousseau, 2000), se afirma que existe una interrelación entre problemas espaciales y conocimientos geométricos. Dicha interrelación pone de relieve que, durante la resolución de un problema espacial pueden emerger -como necesarios- ciertos conocimientos geométricos. Esta resolución del problema implica una relación de modelización espacio-geométrica (Bloch y Salin, 2005), que viene caracterizada por “una relación con el espacio, [que aparece] inscrito en situaciones donde las nociones geométricas intervienen como medios de decisión, de acción o de previsión razonada sobre un espacio sensible"3 (p. 130). Berthelot y Salin consideran que una problemática de modelización espacio-geométrica es aquella donde se trabaja con objetos físicos, la validación se lleva a cabo en el espacio sensible, y en el proceso de resolución se utilizan las propiedades geométricas.
En nuestra investigación tomamos la definición de problemas espaciales que ha presentado Salin (2004), debido al amplio espectro de situaciones que abarca. Estos, se caracterizan a nivel general porque:
Su finalidad concierne al espacio sensible [y] pueden tratar sobre la realización de: acciones [como] fabricar, desplazarse, desplazar, dibujar, etc., [y sobre] comunicaciones a propósito de acciones o de constataciones […] [Además, porque] el éxito o el fracaso viene determinado para el individuo por la comparación entre el resultado esperado y el resultado obtenido. (p. 39)
Esta definición de problema espacial nos lleva de manera implícita a la caracterización de los conocimientos espaciales. Según Berthelot y Salin (1992), dichos conocimientos; de una parte, pueden ser descritos mediante la geometría; y de otra, “permiten a cada uno controlar la anticipación de los efectos de sus acciones sobre el espacio […], así como la comunicación de información espacial"4 (p. 9).
Según Salin (2004), los conocimientos espaciales surgen de forma natural y no es necesario ir a la escuela para su utilización. Sin embargo, los conocimientos geométricos deben ser enseñados de manera explícita. Además, la geometría constituye una buena herramienta para actuar de manera efectiva sobre el espacio sensible, es decir, el espacio físico en el que todos nos encontramos. Ahora bien, ¿por qué esto es importante en la enseñanza de la geometría? Para responder a esta pregunta pensemos en un carpintero que debe construir un marco para una ventana. Si un día le pidiesen construir un marco para una ventana con forma de elipse, ¿qué estrategia debería de tomar? Una solución práctica podría ser copiar la forma de la ventana con un trozo de papel lo suficientemente grande. Otra, implicaría conocer qué elementos definen una forma elíptica y ello requeriría el estudio de la elipse. Así, en este ejemplo, algunos de los conocimientos espaciales necesarios para construir el marco de la ventana, copiando su forma, estarían vinculados con la orientación, con la estimación tanto del tamaño del trozo de papel necesario para copiar su forma como de la cantidad de madera suficiente para construirla, con la manipulación de herramientas de carpintería, etc. Sin embrago, si el carpintero quisiera resolver cual-quiera de las situaciones en las que tuviese que construir muchos marcos elípticos, le resultará más eficaz conocer las propiedades geométricas de la elipse y utilizar dicho modelo para resolverlas.
A continuación, presentamos el problema de investigación que estamos abordando y las hipótesis planteadas. Luego, explicamos la metodología empleada en la experimentación del dispositivo didáctico con el que hemos sometido a prueba dichas hipótesis.
PROBLEMA DE INVESTIGACIÓN
Tras el análisis de algunos de los libros de texto propuestos para la ESO (Rojas y Sierra, 2017), encontramos que, en la enseñanza de la geometría se suelen proponer tipos de tareas asociadas con un listado de temas poco relacionados entre sí. Además, cuando se propone una tarea, por lo general se sugiere una única vía de solución para esta, bien sea a través de un ejemplo o de una secuencia de instrucciones. Dicho análisis nos condujo a concluir principalmente que: (a) los manuales escolares son una extensión del currículo de matemáticas porque reproducen las visiones segmentadas y segregadas que este refleja del conocimiento, y (b) los tipos de tareas y técnicas propuestos en los manuales escolares presentan una relación cíclica, es decir, que las tareas pro-mueven la aplicación de las técnicas y estas se proponen para justificar la presencia de las tareas. Esto ratificó la existencia del fenómeno didáctico, que hemos explicitado así:
Actualmente, en el currículo de matemáticas para la ESO y en los manuales escolares correspondientes, se proponen una serie de saberes geométricos a enseñar, sin que aparezcan de modo explícito las cuestiones a las que responden, es decir, no se explicitan las razones de ser de dichos saberes.
En correspondencia con este fenómeno, sumado al hecho de que tanto en el currículo de la ESO como en los manuales escolares se presenta una separación entre la geometría 2D y 3D, y permeados por los presupuestos epistemológicos de la TAD, la pregunta general de nuestra investigación puede formularse brevemente como sigue:
¿Qué tipo de organizaciones matemático-didácticas (OMD) permitirían sacar a la luz y situar en el centro del proceso de estudio las razones de ser de algunos de los contenidos geométricos de la ESO, permitiendo articular su relación dentro de la geometría en 2D y 3D?
Ahora bien, en este trabajo nos hemos centrado en la siguiente cuestión derivada de este problema didáctico general:
| Los problemas espaciales tal como fueron caracterizados en (Salin, 2004), ¿pueden constituirse en una posible razón de ser de un ámbito significativo de los conocimientos de la geometría elemental de la ESO? Más concretamente, ¿qué conocimientos de la geometría 2D y 3D requieren las cuestiones y las tareas que se plantean cuando se pretende diseñar y construir un envase de un litro? ¿Qué restricciones y limitaciones es previsible que surjan a lo largo del desarrollo de un REI generado por el problema espacial asociado a dicha construcción? |
METODOLOGÍA
La implementación de un REI supone tener en cuenta diferentes restricciones (Rodríquez-Quintana, 2005), tales como la limitación de los tiempos para abordar un problema en profundidad y poder indagar y discutir las posibles soluciones con todo el grupo de estudio. Para disponer de más tiempo del que brindan las clases de matemáticas, decidimos hacer una convocatoria abierta a estudiantes de cuarto de la ESO y de primero de bachillerato5 de un instituto de Educación Secundaria de Getafe, para conformar un grupo de estudio al que llamamos Semillero matemático, que funcionaría una vez a la semana durante una hora y media, en horario extraescolar. Catorce estudiantes acudieron tras la convocatoria, 10 de cuarto de la ESO y cuatro de primero de bachillerato. En el grupo de alumnos, había 12 que obtenían buenos resultados en las evaluaciones de las asignaturas de Matemáticas y 2 que no, según nos informó la profesora titular del área de matemáticas. Estos dos alumnos mostraron una especial motivación por el problema planteado a lo largo del estudio realizado.
En el REI, sobre el análisis, diseño y construcción de un envase, planteamos cuestiones en torno a tres tipos de tareas que fueron abordadas en grupos de 3 o 4 estudiantes. En el primer tipo de tareas, instamos a los estudiantes a realizar un primer análisis de la forma, dimensiones y capacidad, de algunos de los recipientes que actualmente se usan para envasar leche, zumo, vino y caldo de pollo. En el segundo, les pedimos que construyeran un envase en cartulina con capacidad para un litro. Y en el tercero, les propusimos diseñar el mejor envase para un perfume. Al final, los estudiantes debieron entregar un informe argumentando por qué el envase diseñado es el mejor. En el desarrollo del REI, se pretendió que la responsabilidad del planteamiento de las cuestiones fuera compartida por los alumnos y el profesor. El profesor asumió el papel de director del estudio más que el de un enseñante tradicional que muestra a los alumnos las respuestas a las cuestiones planteadas.
La estructura de trabajo seguida comportó tres fases: presentación de la cuestión inicial por el profesor, trabajo grupal y puesta en común. La segunda estuvo a cargo de los estudiantes y la tercera compartida por los estudiantes y el profesor. El profesor, que hizo la función de investigador, pasaba por cada grupo preguntando por las ideas, decisiones, procedimientos, etc., que emergían durante el abordaje de cada tarea. En la puesta en común, el profesor intervino planteando preguntas con el objetivo de intentar desvelar la mayor cantidad de elementos que pudieran emerger durante la búsqueda de res-puestas a cada tarea. Como los alumnos necesitaron más de una sesión para responder a cada tarea, al inicio de cada sesión se hacía un breve recuerdo de lo realizado en la anterior.
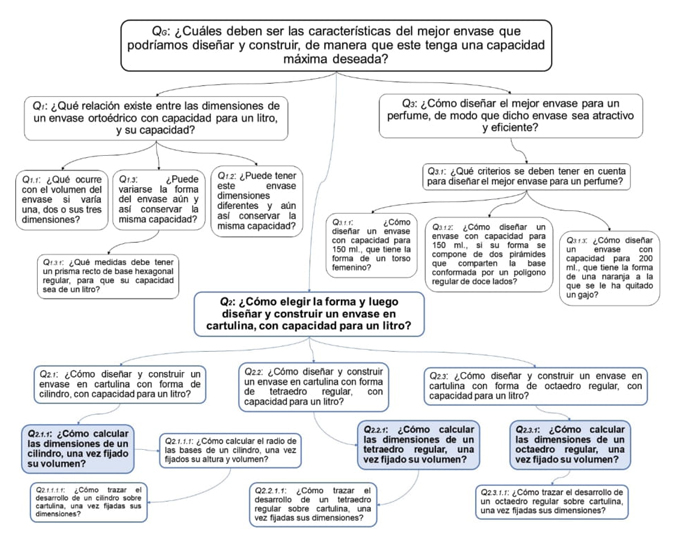
Los datos empíricos recogidos del desarrollo del estudio provienen de la información proporcionada por tres fuentes: (a) registros audiovisuales, (b) el diario de campo del investigador, y (c) el cuaderno que usan los estudiantes para escribir los procedimientos empleados. En el trabajo que presentamos, los datos provienen de algunas de las trascripciones de los diálogos entre los estudiantes y el profesor de las sesiones tercera, cuarta y quinta de la experimentación del REI en las que se propuso Q 2 (Figura 1. Mapa de cuestiones que han aparecido durante la implementación del REI.). Las trascripciones se obtuvieron del registro audiovisual de dichas sesiones, donde hemos extraído y analizado las respuestas que dieron los estudiantes, utilizando para ello, lo indicadores del grado de completitud de una OM.
DESARROLLO DE LA EXPERIMENTACIÓN
Durante la implementación del REI emergieron varias cuestiones derivadas de la cuestión generatriz (Q G). Dichas cuestiones, que hemos estructurado en un mapa (Figura 1. Mapa de cuestiones que han aparecido durante la implementación del REI.), se corresponden con los tres tipos de tareas mencionados en la sección de metodología.
En este artículo nos limitamos solo a los datos que hacen referencia al modo en que los alumnos intentaron buscar una respuesta a la cuestión Q 2 = ¿Cómo elegir la forma y luego diseñar y construir un envase en cartulina, con capacidad para un litro? Específicamente, consideramos los que contienen información sobre la manera en que los estudiantes calcularon las dimensiones del envase que diseñaron.
Una vez propuesta Q 2, los estudiantes desarrollaron su trabajo en tres grupos:
- El grupo 1 (G 1), formado por los estudiantes E1, E2, E3 y E4, buscó responder a Q 2.1 = ¿Cómo diseñar y construir un envase en cartulina con forma de cilindro, con capacidad para un litro? Y después a Q 2.1.1 = ¿Cómo calcular las dimensiones de un cilindro, una vez fijado su volumen? (Figura 2. Cilindro construido por los integrantes del G 1.)
- El grupo 2 (G 2) (constituido por E5, E6, E7, y E8), trató de encontrar la respuesta a Q 2.2 = ¿Cómo diseñar y construir un envase en cartulina con forma de tetraedro regular, con capacidad para un litro? Y después a Q 2.2.1 = ¿Cómo calcular las dimensiones de un tetraedro regular, una vez fijado su volumen? (Figura 3. Tetraedro regular construido por los integrantes del G 2.)
- El grupo 3 (G 3) (integrado por E9, E10 y E11), se propuso responder a Q 2.3 = ¿Cómo diseñar y construir un envase en cartulina con forma de octaedro regular, con capacidad para un litro? Y después a Q 2.3.1 = ¿Cómo calcular las dimensiones de un octaedro regular, una vez fijado su volumen? (Figura 4. Octaedro regular construido por los integrantes del G 2.)
El tiempo dedicado a responder a Q 2 fue de tres semanas, a partir de la tercera sesión del semillero, con una sesión de hora y media por semana.
Durante la puesta en común, los estudiantes arguyeron en relación con el envase construido: (a) sobre la forma elegida, (b) sobre el porqué de dicha elección, y (c) sobre la manera en que calcularon las dimensiones del envase. Por tanto, hemos transcrito los diálogos en los que los estudiantes presentaron dichos argumentos al profesor (P) y a los demás compañeros, y los hemos toma-do como objeto de análisis y de discusión para rastrear el tipo de conocimientos geométricos que han emergido en repuesta a Q 2.
Puesta en común de G 1
| E1: | […] hemos optado por el cilindro (Figura 2. Cilindro construido por los integrantes del G 1), porque tiene una forma cómoda y porque nos supone menos trabajo realizar uno […] la altura treinta centímetros, porque, más o menos, hemos semejado -creo- a una lata de Pringles… |
| E2: | […] también hemos optado por un cilindro… por la comodidad a la hora de cogerlo. |
Cuando les preguntamos qué debieron tener en cuenta para hacer los trazos del desarrollo del cilindro sobre la cartulina, respondieron:
| E3: | Las medidas del cilindro. La altura, el diámetro de las bases, y el ancho que va a tener el cilindro. |
| P: | […] el desarrollo de ese cilindro en particular, ¿qué figuras implicó trazar [sobre la cartulina]? |
| E3: | Un círculo y un rectángulo. ¡Dos círculos! |
| E2: | Dos círculos que eran las dos bases, y el rectángulo, que sería el cuerpo del cilindro. |
| P: | ¿Qué medidas debieron tener esas figuras? |
| E2: | Bueno, pues realmente la altura la hicimos un poco así a ojo. Treinta, pues por hacer una altura medianamente decente. Y luego, por la fórmula para hallar el área… averiguamos el radio […]. |
| E4: | Pensamos que el volumen [del cilindro] que es la altura, por pi [π], por el radio al cuadrado, tenía que ser mil centímetros cúbicos. Entonces, sustituimos la altura por treinta, el pi por […] la tecla de la calculadora, y luego tuvimos que calcular el radio, que nos salió 3,25. Y de ahí […] el diámetro. |
| P: | ¿Por qué es necesario calcular el diámetro de la circunferencia? |
| E4: | Pues calculamos el diámetro, para poder calcular el perímetro [de la circunferencia], […] esto es una medida del rectángulo. |
Minutos después, preguntamos:
| P: | […] para poder hacer los trazos […] y poder construir ese recipiente, las medidas que tu-vieron en cuenta sobre la cartulina, ¿fueron exactamente aquellas que calcularon […] o tuvieron algunas tolerancias? |
| E2: | […] la verdad es que hubo muchos decimales, entonces, fuimos redondeándolo lo más posible […]. |
Cuando sometieron a prueba la fórmula usada por ellos (i.e., V = hπr², siendo el radio, la altura del cilindro, y el volumen buscado), encontraron que el cilindro diseñado tenía un volumen de 995,492 cm 3.
| E2: | […] da así… porque hemos cogido aproximaciones. En realidad, no son 3,25 el radio, es 3,257… Si no, al coger más decimales, sí que nos da… no nos da el mil, pero nos da 999,9. Entonces… aquí … lo hemos redondeado, lo hemos aproximado, pero realmente es por un milímetro […]. |
Puesta en común de G 2
| E5: | […] nosotros lo primero que hicimos fue decidir qué forma iba a tener nuestra figura, para poder después hacer todas las fórmulas […] Hemos decidido hacer un tetraedro regular (Figura 3. Tetraedro regular construido por los integrantes del G 2), […] y lo primero que hicimos fue la fórmula de volumen. Y a partir de allí, pues hicimos la fórmula de equis elevado a tres por raíz de dos… |
| E6: | Bueno, al principio intentamos averiguar la medida de un lado,… |
| E5: | ¡Exacto! Lo hicimos por estándar, o sea por tanteo de… a base de prueba y error de… Hicimos 21, vimos que nos pasamos mucho, luego hicimos 20,1, 20,2, hasta llegar más o menos. Y luego nos dimos cuenta de que obviamente se podría hacer con la equis, y lo hicimos ya por exactitud. Y cuando ya tuvimos el lado, pues decidimos […] planificar en el papel cómo haríamos la forma para después empezar a doblarla […] cuando quisimos plasmarlo en el papel, pues… nos costaba mucho, entonces decidimos […] romper en triángulos rectángulos, cada uno de los triángulos que no eran rectángulos. Pues necesitábamos hallar la hipotenusa, y para eso hicimos el teorema de Pitágoras… |
| E6: | Necesitábamos saber la altura […] de un triángulo equilátero. |
| P: | ¿Por qué surgió la necesidad de hallar esa altura? |
| E5: | ¡Porque no teníamos compás! |
| P: | ¿Para qué necesitaban el compás? |
| E5: | Para poder hallar a partir de esta base [señalando la base de uno de los triángulos equiláteros que constituyen el desarrollo del tetraedro], directamente pincha aquí y hacer así, pinchar aquí y hacer así [haciendo un gesto con sus manos sobre la pizarra, para simular el trazado e intersección de dos arcos], y ya nos daba el punto exacto. Como no lo teníamos, pues… |
Luego preguntamos por el proceso que siguieron para calcular el valor de x que aparece en la fórmula usada (i.e., V = [(x 3√2)/12], donde x es la longitud de la arista del tetraedro regular y V el volumen buscado).
| P: | […] Han dicho al principio, que comenzaron a probar con varios números […], pero después dijeron: entonces tomamos la decisión de trabajarlo con equis, porque es más preciso. Y, ¿cómo fue ese trabajo con equis? |
| E6: | Pues, al tener la fórmula general de un tetraedro […] la hemos igualado a mil. […] Y nos da básicamente, […] 23,9, y muchísimos decimales, por lo que optamos por el redondeo. Porque precisar tantos decimales en una regla, pues, no podemos. |
Con relación a la elección de la forma tetraédrica, los estudiantes indicaron:
| E5: | No tuvimos en cuenta, ni la comodidad, ni la capacidad de… vacío de él [refiriéndose al orificio de entrada y salida del contenido]. |
| E6: | Por lo que hemos hecho esta figura, no es más para… un motivo comercial, sino para demostrar que hay muchísima variedad de figuras… |
Puesta en común de G 3
| E9: | […] Nosotros para este proyecto, quisimos innovar un poco, y pues pensamos en hacer un octaedro regular (Figura 4. Octaedro regular construido por los integrantes del G 3). Al principio pensamos en hacer… un cono o una pirámide, pero… quisimos probar otro. Es cierto que… nos ha costado bastante […]. Como podéis ver aquí en esta fórmula [V = [(l³√2)/3], donde l es la longitud de la arista del octaedro regular y V el volumen buscado] da exactamente… un litro, pero se pasa, a lo mejor unas centésimas o un poco más. |
| P: | Si se trata de innovar […], ¿por qué esa forma en particular? |
| E10: | […] porque es la que nos salían los cálculos mejor. |
| E9: | […] Justo los cálculos los hicimos así: primero pensamos en números enteros y cuando vimos que se nos aproximaba un poco, empezamos con decimales, y exactamente cada lado equilátero mide 12,85 centímetros […]. |
Cuando preguntamos por la manera como calcularon la medida del lado de los triángulos que constituyen el desarrollo del octaedro, los estudiantes respondieron:
| E9: | […] Primero, para aproximarnos… a un litro, lo que pensamos en hacer es por tanteo, y primero pusimos 13 y vimos que se acercaba un poco, y luego bajamos a 12,5, y ya veíamos que se bajaba un poco. Entonces, ahí fuimos aproximando hasta que nos dio eso. |
| P: | Y les dio en este caso 1000,23 centímetros cúbicos. Ciertamente un poco más que el litro… |
| E10: | ¡Claro, un poquito! ¡Hombre, no se va a notar!, digo yo. |
Sobre el proceso seguido para trazar el desarrollo del octaedro regular, los estudiantes indicaron:
PRESENTACIÓN DEL INSTRUMENTO DE ANÁLISIS DE LA OM ELABORADA Y DE SUS RESULTADOS
Dentro de la TAD “toda actividad matemática puede ser interpretada como una actividad de modelización” (Fonseca, Gascón, y Lucas, 2014, p. 294). Queremos analizar hasta qué punto ha sido posible llevar a cabo una actividad de modelización espacio-geométrica en el REI experimentado. Uno de los instrumentos que nos proporciona la TAD para analizar las OMD, que tomaremos aquí como herramienta de análisis, lo constituye los indicadores del grado de completitud de una OM local relativamente completa. A propósito de ello:
Parece evidente que una OM local que permita abordar -y, por tanto, integre en cierta medida- este tipo de cuestiones [de modelización matemática] también cumplirá los indicadores anteriores relativos a la flexibilidad de las técnicas, el desarrollo de los tipos de tareas y la existencia de un cuestionamiento tecnológico funcional. (Bosch, Fonseca y Gascón, 2004, p. 219)
En Bosch et al., (2004), se definen siete indicadores del “grado de completitud” de una OM, que nos van a servir para analizar la OM elaborada durante el REI implementado. A continuación, mostramos y analizamos hasta qué punto se cumplen cada uno de los indicadores, porque ello nos servirá; de una parte, para identificar las limitaciones y restricciones encontradas durante el desarrollo de la tarea propuesta; y de otra, para desvelar los conocimientos geométricos que se pusieron en juego durante la búsqueda de respuestas a Q 2.
- El primer indicador pretende analizar en qué medida se ha producido una integración de los tipos de tareas.
Todos los tipos de tareas tienen un nexo común que es responder a Q 2. Cada grupo de estudiantes debió llevar a cabo una tarea del tipo T 2: Diseñar y construir un envase en cartulina, con capacidad para un litro, que dentro de cada grupo se tradujo en una tarea:
- En G 1, t 21: Diseñar y construir un envase con forma de cilindro con capacidad para un litro; y una vez elegida la forma del envase resolvieron: t 211 = Calcular las dimensiones de un cilindro, sabiendo que su volumen es de un litro. Esta tarea requiere una técnica compleja de resolución que consiste en bus-car la solución de una ecuación con dos incógnitas, por lo que la ecuación tiene infinitas soluciones. Los alumnos de este grupo simplificaron la tarea dando un valor concreto (30 cm) a la altura y la técnica utilizada se redujo a resolver una ecuación con una incógnita. Después construyeron un círculo con el radio obtenido y un rectángulo de lados la longitud del círculo y la altura del cilindro.
- En G 2, t 22: Diseñar y construir un envase con forma de tetraedro, con capacidad para un litro; y una vez elegida la forma del envase resolvieron: t 221: Calcular las dimensiones de un tetraedro regular, con un volumen de un litro. Aquí la técnica se reduce a “resolver una ecuación con una incógnita”, que es la utilizada por los alumnos del grupo. Después construyeron cuatro triángulos equiláteros iguales con la longitud de lado obtenida.
- En G 3: t 23: Diseñar y construir un envase con forma de octaedro, con capacidad para un litro; y una vez elegida la forma del envase resolvieron: t 231: Calcular las dimensiones de un tetraedro regular, con un volumen de un litro. Aquí la técnica también consiste en resolver una ecuación con una incógnita. Sin embargo, aquí los alumnos utilizaron la técnica de ir probando valores en la fórmula hasta acercarse al valor del volumen. Luego construyeron 8 triángulos equiláteros iguales con la longitud del lado obtenida.
Para elegir las formas de los envases, buscaron en su libro de texto y eligieron la forma de dos poliedros regulares y del cilindro, porque allí tenían disponible la fórmula de su volumen. Tomaron dichas fórmulas sin ningún cuestionamiento sobre su validez. Así, podemos concluir que los tipos de tareas propuestos anteriormente aparecen integradas, porque todas pretenden responder a Q 2, pero apenas existe un cuestionamiento tecnológico de las técnicas utilizadas. Para existir dicho cuestionamiento debería haberlo provocado el profesor, pues los propios alumnos no tienen por costumbre hacerlo por propia iniciativa.
- Con el segundo indicador se pretende estudiar si existen diferentes técnicas y criterios para elegir entre ellas.
En el desarrollo de T 2, las técnicas empleadas en cada grupo para calcular las medidas del envase fueron:
- En G 1, han utilizado primero τ21: elegir una forma cómoda y fácil de manejar y que suponga poco trabajo realizarla. Así han elegido el cilindro. Para resol-ver t 211, han utilizado:
τ211: Usar la fórmula V = hπr² (donde V representa el volumen del cilindro, h, la altura del cilindro y r el radio de las circunferencias de las bases) y asignar valores a h parecidos a algún objeto real conocido y después obtener r en la ecuación V = hπr² utilizando las propiedades de simplificación.
Han decidido asignar a la altura h el valor de 30, porque han encontrado que en el mercado hay un envase de parecida altura y han obtenido que r es 3,2576…, donde viene dado en cm3 y h y r en cm. Aquí se observa que los alumnos han hecho un uso de la fórmula del volumen del cilindro, primero aritmético y después algebraico, pero no han sido capaces de utilizarla como una función, donde h y r jueguen el papel intercambiable de variables dependiente e independiente.
- En G 2, han utilizado primero τ22: elegir una forma genérica cualquiera de la que dispongamos de la fórmula de su volumen. Y han elegido un tetraedro. Para resolver t 221, han empleado las dos técnicas siguientes:
τ2211: Utilizar la fórmula V = [(x³√2)/12] (donde V representa el volumen del tetraedro regular y x representa la arista del tetraedro) y hallar el valor de x, por tanteo, dando valores hasta acercarse lo más posible a V = 1000.
τ2212: Utilizar la fórmula V = [(x³√2)/12] (donde representa el volumen del tetraedro regular y representa la arista del tetraedro) y hallar el valor de x utilizando las propiedades de simplificación en la ecuación que proporciona la fórmula.
En ambos casos, V viene dado en cm3 y en cm.
Posteriormente para la elaboración del desarrollo del envase utilizaron diversas técnicas para construir el triángulo equilátero que ya han sido explicadas y analizadas en Rojas y Sierra (2018).
- En G 3, han utilizado primero τ23: elegir una forma innovadora de la que se disponga de la fórmula de su volumen y para la que sea posible realizar los cálculos de forma más ajustada. Y han elegido un octaedro. Luego, para resolver t 231, han usado la técnica:
τ23: Emplear la fórmula V = [(l³√2)/3] (donde V representa el volumen del octaedro regular y l, la arista del octaedro) y hallar el valor de ??, probando y dando valores hasta acercarse lo más posible a V = 1000. Donde V viene dado en cm3 y l en cm.
Por tanto, en la búsqueda de respuestas a T 2 se han utilizado diferentes técnicas. Los criterios empleados se basan principalmente en que exista un fácil acceso a una fórmula para calcular el volumen del sólido elegido y en que resulte fácil y cómodo tanto calcular las dimensiones del sólido como elaborar su desarrollo plano en cartulina. También se propusieron otros criterios menos claros como el de innovar y el de escoger un sólido cualquiera, para dar la idea de que hay muchos posibles. Las técnicas utilizadas muestran que los alumnos manejan las fórmulas, en primer lugar, como programas de cálculo aritmético y solo algunos, en segundo lugar, son capaces de usarlas como ecuaciones. En ningún caso, los alumnos son capaces de considerar las fórmulas como modelos funcionales. En general, los criterios tienden a intentar simplificar y cerrar la tarea a resolver.
- El tercer indicador, analizar si existe independencia de los ostensivos que integran las técnicas.
Hemos visto, en el indicador anterior, que los estudiantes han utilizado la notación que aparecía en el libro de texto o en el documento resumen donde venían las diferentes fórmulas del volumen de sólidos. Así, las fórmulas del volumen del tetraedro y del octaedro que venían en dichos textos eran V = [(l³√2)/12] y V = [(l³√2)/3] respectivamente. Pero en el caso del tetraedro, como los alumnos decidieron considerar la fórmula como una ecuación donde la incógnita era el valor del lado, cambiaron la l por la x, ya que para ellos la incógnita de una ecuación siempre debe venir representada por la letra x.
Por tanto, se observa que existe rigidez en el uso de ostensivos en la actividad matemática desarrollada por los alumnos.
El tipo de tareas T 2 propuesto hace referencia a un tipo de tareas inversas de las que se suelen proponer en las clases de Secundaria que son del tipo T 2 inv: “Elegir la forma de un envase y, conocidas sus dimensiones, calcular su volumen”. Además, T 2 resulta de una mayor dificultad, pues tiene un carácter abierto; los estudiantes primero, deben elegir la forma del envase que pretenden diseñar; y luego, decidir la manera en que calcularán sus medidas. Los alumnos de G 1 y G 3 al principio intentan resolver las tareas del tipo T 2, utilizando la técnica directa que consiste en asignar valores a las dimensiones del envase probando hasta conseguir que el volumen sea aproximadamente un litro. Sin embargo, G 1 y G 2 acaban usando la técnica inversa que consiste en considerar la fórmula como un modelo algebraico. En general, los alumnos tienden a forzar y modificar la tarea para evitar usar una técnica no habitual y así poder aplicar una técnica escolar estándar.
Los estudiantes no se cuestionaron sobre la validez de las fórmulas utilizadas y las aceptaron sin que anteriormente hubieran sido justificadas en clase o en el libro de texto.
Ninguno de los estudiantes se cuestionó sobre la relación existente entre la capacidad de un objeto y su volumen. Asimismo, ninguno consideró que el envase a elaborar debería tener un determinado grosor.
En general, no hubo interpretación del funcionamiento de las técnicas.
- Con el sexto indicador se analiza si ha habido necesidad de construir técnicas nuevas capaces de ampliar los tipos de tareas inicialmente considerados.
En este caso, hemos visto que la elección del tipo de tareas T 2 estuvo fuertemente condicionada por las ventajas que ofrecen las técnicas empleadas para calcular las medidas del envase. Esto se puede evidenciar en los argumentos presentados por los estudiantes, cuando indagamos por los motivos que les condujeron a la elección de la forma del envase diseñado y construido. Así, en G 1, fue la comodidad a la hora de manipularlo y la presunción de menos trabajo en la construcción. En G 2, dicen que hay muchísimas figuras con capacidad de un litro, pero eligen el tetraedro porque disponen de una fórmula sencilla para calcular el volumen. En G 3, primero pretenden innovar, pero después optan por el octaedro porque es el sólido para el que les resulta más fácil realizar los cálculos.
En la actividad matemática llevada a cabo, creemos que sí se construyó, por algunos alumnos, la técnica que consiste en utilizar la fórmula del volumen como un modelo algebraico. Además, pensamos que se puede crear la necesidad de construir otra técnica nueva donde se considere la fórmula del volumen del envase elegido como un modelo funcional. Así, en una etapa posterior del desarrollo del REI hemos propuesto el uso de GeoGebra para facilitar la elaboración de dicha técnica.
Este indicador contiene en cierta forma los otros seis indicadores, en la medida que estos caracterizan al tipo de tareas abiertas y, en particular, las tareas de modelización matemática. Para que estas existan con normalidad en una institución escolar se requiere que las OM con las que se trabaja sean relativamente completas, esto es, OM que cumplan en una medida apreciable los indicadores en cuestión. Dado que las OM escolares no cumplen en general estas condiciones, era previsible que, ante una tarea abierta como la propuesta, los estudiantes encontraran muchas dificultades. En efecto, las tareas propuestas son abiertas porque no se conoce de antemano qué técnica o técnicas permitirán resolverlas. Así, para llevar a cabo T 2, los alumnos necesitaron elegir la técnica de resolución, y esto les llevó a elegir de entre las disponibles, que aparecían en su libro de texto o en sus apuntes de clase, aquellas más fáciles de aplicar. Al final, hemos visto que los alumnos tienen tendencia a cerrar las tareas propuestas y apenas optan por crear técnicas nuevas.
RESTRICCIONES Y LIMITACIONES ENCONTRADAS
En la escuela secundaria existen ciertas restricciones, es decir, condiciones inmodificables por el profesor y, limitaciones, que se derivan de sus propias normas y estructura, para poder implementar nuevos dispositivos didácticos. De este modo,
[…]para la TAD, no es posible modificar las praxeologías matemáticas y didácticas que viven en una institución determinada como consecuencia exclusiva de la voluntad de los agentes de las instituciones en cuestión, sean estos profesores, autores de cualquier tipo de materiales escolares o autoridades educativas. (Fonseca et al., 2014, p. 314).
Así, los profesores y estudiantes están sujetos a un currículo -sobre el que no pueden intervenir- que supone la segmentación de la enseñanza en un con-junto de temas separados, que se deben tratar en un horario de clases de 50 a 55 minutos. Esto, aunque ha generado las condiciones necesarias para que el modelo de enseñanza actual se lleve a cabo, también genera importantes restricciones para abordar, en profundidad, cuestiones que podrían dar sentido a varios de los saberes propuestos en el currículo actual.
En nuestro caso, algunas de las restricciones y limitaciones encontradas, durante el desarrollo del tipo de tareas propuesto (i.e., T 2), están íntimamente relacionadas con los indicadores del grado de completitud discutidos anterior-mente. Los cuales, recíprocamente, son condiciones necesarias para llevar a cabo una actividad abierta de modelización. Con lo cual, dichas restricciones y limitaciones se reflejaron, por ejemplo, en:
- la ausencia de una interpretación algebraico-funcional de T 2, ya que los estudiantes buscaron una solución particular para el cálculo de las medidas del envase, sin detenerse a cuestionarse sobre el hecho de que dicha solución forma parte de un conjunto infinito de soluciones que, está asociado a la posible variación del conjunto de dimensiones de dicho envase que, hacen que su volumen pudiera ser de 1000 cm3;
- el uso casi excluido de las fórmulas empleadas como programas de cálculo aritmético, porque la tendencia fue a introducir valores en las fórmulas a fin de que el volumen de los envases se aproximase al solicitado;
- la dependencia de ostensivos empleados habitualmente en el cálculo de volúmenes, vinculada con el uso de un listado-resumen de fórmulas que habitualmente usan los estudiantes en la clase de geometría, y con la necesidad de incluir la letra x en el planteamiento y solución de ecuaciones, como fue el caso del grupo que diseñó el envase con forma de tetraedro regular;
- la falta de planteamiento de tareas inversas en el currículo habitual genera en los estudiantes la necesidad de transformar T2, de naturaleza inversa, en un tipo de tarea directa. Muestra de ello es que los estudiantes tendieron al diseño de un envase cuyo volumen pudiese calcularse, preferiblemente, con una fórmula que incluyese una sola variable, incluso, reduciendo T2 al cálculo del volumen de un sólido a partir de la medida de uno de sus elementos;
- la ausencia del cuestionamiento de la validez de las fórmulas empleadas y de la construcción de nuevas técnicas. Principalmente, porque los estudiantes están habituados a usar las fórmulas sin que previamente se discuta su significado y su validez, y porque no se acostumbra a proponer que sean ellos quienes construyan dichas fórmulas.
Esto significa que, tanto en el currículo como en la actividad matemática escolar que siguen habitualmente los estudiantes, las tareas abiertas de modelización no suelen estar presentes.
CONCLUSIONES
El análisis de los resultados obtenidos y las hipótesis que pretendíamos validar nos permiten concluir que, durante la resolución del problema espacial sobre el diseño y construcción de un envase con capacidad para un litro, pueden emerger algunos de los saberes geométricos propuestos en el currículo escolar para ser enseñados. Por ejemplo, los contenidos de geometría tridimensional en 3o ESO (alumnos de 14/15 años), y de conocimientos geométricos para la resolución de problemas del mundo físico: medida de longitudes, áreas y volúmenes en 4o ESO (alumnos de 15/16 años), tanto en enseñanzas académicas como en aplicadas (MECD, 2015). Al construir el desarrollo de los envases aparece la necesidad de representar y estudiar las características y propiedades de las figuras planas, por ejemplo, en nuestro caso, triángulos equiláteros, triángulos rectángulos, rectángulos, círculos. Aquí ha surgido la necesidad de relacionar las geometrías 2D y 3D, lo que ha ayudado a articular ambos tipos de conocimientos geométricos. Los tipos de conocimientos geométricos van a estar muy relacionados con el tipo de envase que deseen diseñar y construir cada grupo de alumnos. Por ello, será muy útil que el profesor haga una buena gestión de las sesiones de clase, con el objetivo de que sea necesario elaborar una variedad de tipos de envase, que permita abordar la mayor parte de los conocimientos geométricos que propone el currículo.
Las cuestiones que han surgido en el desarrollo del REI al resolver los problemas espaciales de diseño y construcción de un envase, se han constituido en algunas de las razones de ser de los saberes geométricos mencionados en el apartado anterior, que forman parte del currículo de la ESO. Por tanto, consideramos relevante incluir dichos problemas en las OMD para enseñar geometría. Llevar a cabo procesos de estudio parecidos al experimentado, implicaría cambios importantes en la lógica de enseñanza habitual, porque les otorgaría mayor responsabilidad a los estudiantes en su formación académica y obligaría a hacer frente a ciertas limitaciones y restricciones que el sistema escolar impone, superando la obligación de un horario escolar compartimentado en clases de 50 minutos. Se necesita al menos un tiempo de 90 minutos para poder realizar una actividad matemática que permita reflexionar, cuestionar y contrastar en equipo las posibles respuestas al tipo de tareas planteado.
Consideramos necesario proponer procesos de estudio en secundaria como el implementado, para que los estudiantes se vean abocados a elaborar técnicas para resolver las tareas propuestas. Es importante crear la necesidad de que describan, expliquen y justifiquen dichas técnicas. Se deben plantear tareas donde las técnicas, ya conocidas, fracasen y los alumnos sientan la necesidad de construir técnicas nuevas que permitan su resolución.
En la actividad matemática efectivamente desarrollada hemos podido constatar que los estudiantes intentan afrontar el tipo de problemas planteado con técnicas que proporciona el libro de texto o los apuntes y documentos aportados por los profesores. La tendencia de los alumnos es resolver las tareas propuestas con técnicas ya construidas o proporcionadas por otros sin cuestionarse si dichas técnicas son válidas o no. En general, renuncian a construir técnicas nuevas. Hemos constatado que durante el desarrollo del REI los propios estudiantes construyeron alguna de las técnicas necesarias para la resolución del tipo de tareas propuesto, como se documenta en (Rojas y Sierra, 2018).
En la búsqueda de respuestas al tipo de problema planteado, los alumnos han utilizado las propiedades geométricas de las figuras planas como el triángulo equilátero y rectángulo, el círculo y el rectángulo para construir los diferentes envases. Así, han utilizado la modelización espacio-geométrica (aunque no de manera explícita), y algunos han sido capaces de utilizar las fórmulas del volumen como modelos algebraicos, pero ninguno ha considerado las fórmulas como posibles modelos funcionales. Por todo ello, hemos pensado continuar este trabajo diseñando y experimentando, con la ayuda de GeoGebra, un proceso de estudio donde la necesidad de considerar las fórmulas geométricas como modelos algebraico-funcionales surja como respuesta a un problema espacial.
Finalmente, consideramos que el REI implementado se ha llevado a cabo de una forma abierta y libre, dejando que los estudiantes tomasen decisiones sin apenas influencia y dirección por parte del profesor. Sin embargo, pensamos que si nuestro objetivo es conseguir que los estudiantes construyan nuevas técnicas geométricas, sean capaces de cuestionar su validez, interpreten las fórmulas geométricas como modelos algebraico-funcionales y, en definitiva, lleven a cabo una genuina actividad de modelización, se necesita una gestión del REI donde el profesor oriente el estudio favoreciendo cuestiones fructíferas en la dirección de potenciar, provocar y posibilitar dichos resultados. Dicha estrategia didáctica vendrá justificada y fundamentada por la construcción de un modelo epistemológico de referencia de los conocimientos en juego al querer resolver el tipo de tareas de elaboración de un envase, que estamos desarrollando en estos momentos.











 nueva página del texto (beta)
nueva página del texto (beta)