INTRODUCCIÓN
En los últimos años la introducción del álgebra en educación básica ha sido objeto de estudio por parte de varios investigadores (Godino y Font, 2003; Butto, 2005; Cai, Ng y Moyer, 2011; Godino, Castro y Rivas, 2011; Vergel, 2014; Kieran et al., 2016; Gaita y Wilhelmi, 2019). Quienes han mostrado un gran interés en desarrollar el razonamiento algebraico desde los primeros años de escolaridad, donde se promueva su estudio a través de situaciones de variación y cambio, que involucren la generalización de patrones, secuencias y leyes que vinculen la visualización, exploración y manipulación de números y figuras, con el pensamiento matemático de quien aprende (National Council of Teachers of Mathematics [NCTM], 2000; Murray, 2010; Cantoral, 2013; Aké, Godino y Gonzato, 2013). Pues no cabe duda que el estudio de dichas situaciones es de gran importancia en la formación de los estudiantes, ya que constituye un eje fundamental para estructurar y desarrollar el razonamiento algebraico como una manera matemática de pensar, que facilite el acceso al cálculo (Ministerio de Educación Nacional, 2006; Dolores, 2013; Kieran et al., 2016). Así mismo, este tipo de situaciones son fundamentales para el acceso al cálculo (Hitt, 2003) y para el desarrollo de habilidades y destrezas que según Farfán (2012), los estudiantes podrán utilizar en cualquier contexto de las matemáticas y de la vida diaria.
Sin embargo, un curso de álgebra no es usual que se ofrezca de manera explícita en los currículos escolares, hasta el tradicional curso ofrecido en la escuela secundaria (NCTM 2000, Radford, 2014), y es habitual que los estudiantes experimenten dificultades en la transición de la aritmética al álgebra porque tienen poca o ninguna experiencia previa con el tema, (Silver y Kenney 2001; Kaput, Carraher y Blanton, 2008). Unido a lo anterior, en el momento que se aborda dicho curso, se hace abruptamente, sin dar continuidad a los temas de aritmética, medida y geometría tratados en primaria (Godino et al., 2014). Hay consenso entre varios autores (Butto, 2005; Cai y Knuth, 2011; Radford, 2014) que, la transición de la aritmética al álgebra no se debe realizar de manera abrupta, sino que sea un proceso progresivo y que se vaya adquiriendo grado tras grado, sin saltos ni rupturas.
Estos conflictos curriculares podrían resultar problemáticos, considerando que, si se dejan de lado elementos que ayudan en la enseñanza y aprendizaje del pensamiento variacional, los procesos de generalización propios del álgebra carecerán de significado y sentido para quien aprende en el trabajo que se realiza en grados superiores (Carraher y Schliemann, 2007), y porque un desarrollo temprano del pensamiento algebraico puede facilitar que los estudiantes tengan un acercamiento gradual al simbolismo algebraico (Cai y Knuth, 2011). Además, porque el álgebra es una pieza clave del éxito en el aprendizaje de las matemáticas, debido a su papel fundamental en todas las ramas de esta, ya que provee herramientas para representar y analizar relaciones cuantitativas, modelar situaciones y resolver problemas en cada dominio matemático (NCTM, 2000; Blanton M. et al.,2018).
En este trabajo se tuvo como objetivo analizar el desarrollo del razona-miento algebraico elemental, a través del uso de patrones y secuencias numéricas o geométricas en estudiantes de quinto grado de educación básica. Se enfatizó en categorizar las prácticas que realiza un estudiante de primaria para resolver tareas matemáticas que involucran patrones, y a partir de ello, ir haciendo un seguimiento a la evolución de sus progresos en la adquisición de razonamiento algebraico.
RAZONAMIENTO ALGEBRAICO ELEMENTAL
Según el NCTM (2000), el álgebra comprende las relaciones entre cantidades, el uso de símbolos, el modelado de fenómenos, y el estudio matemático de la variación y el cambio. Y para Kieran (2004) el razonamiento algebraico elemental se refiere a la forma en que una persona piensa al relacionar cantidades, identificar estructuras, estudiando el cambio y la variación, la generalización, la modelación, la predicción y la argumentación de los procesos realizados al resolver una tarea matemática en educación primaria. Similarmente, Godino y Font (2003) lo relacionan con el estudio de patrones y regularidades en diferentes contextos de las matemáticas y la manera cómo se llega a la generalización de las secuencias. Es decir, constituye el sistema de prácticas utilizadas en educación primaria en la resolución de tareas, en las cuales intervienen objetos y procesos algebraicos, tales como simbolización, relación, variables, incógnitas, ecuaciones, patrones, generalización y modelación, etc. (Godino et al., 2011). Esta manera analítica de pensar en los números desconocidos y tratarlos a la par con números conocidos, es una de las características que distingue la aritmética del álgebra (Radford, 2014). Para Radford, esta naturaleza analítica del álgebra, permite deducir fórmulas y encontrar soluciones al resolver ecuaciones. Así mismo, la generalización de un patrón consiste en la identificación de una característica común a todos los elementos de una secuencia, la cual se puede usar para encontrar una expresión que permita encontrar cualquier elemento de esta (Radford, 2006).
De esta manera, el razonamiento algebraico elemental refiere a prácticas matemáticas en las cuales se pueden establecer diferentes niveles de algebrización, que emergen en la solución de una tarea matemática en la escuela primaria (Godino et al., 2014; Gaita y Wilhelmi, 2019), por lo que tener criterios para su análisis puede proporcionar información que permita promover un óptimo desarrollo del razonamiento algebraico en los estudiantes. Para analizar la actividad algebraica que desarrolla un estudiante al resolver una tarea matemática cotidiana en la escuela primaria, y hacer un seguimiento a su evolución, se han propuesto varios modelos: (a) por niveles de algebrización (Godino et al., 2011; 2014), (b) por nociones clave (Radford, 2014). El nivel se asigna, no a la tarea como tal, sino a la solución, que dé la actividad matemática comunicada, así que dependiendo de la solución que se dé a la tarea, esta puede ser clasificada en uno u otro nivel de algebrización (Godino et al., 2014).
MODELO POR NIVELES DE ALGEBRIZACIÓN
Este modelo (Godino et al., 2011; 2014), está constituido por cuatro categorías:
(1) Nivel cero o de ausencia de razonamiento algebraico: se identifica una regla recursiva, la cual se expresa en lenguaje natural, numérico, icónico, verbal o gestual, y los procedimientos utilizados son aritméticos.
(2) Nivel uno: se reconoce explícitamente una regla recursiva y se generaliza usan-do lenguajes natural, numérico, icónico o gestual. Se puede usar lenguaje simbólico-literal, pero sin ejecutar las operaciones indicadas con dichos símbolos.
(3) Nivel dos: se determina un patrón por análisis de términos específicos de una secuencia, el lenguaje utilizado es natural, numérico, icónico o gestual, y, se formaliza expresando una regla general. Se establecen conexiones entre los elementos de las representaciones producidas y se dan o usan propiedades del patrón, sin hacer transformaciones tipo tratamiento en lenguaje simbólico-literal.
(4) Nivel tres: se determina una regla general y se expresa formalmente. La información se reporta, partiendo de un lenguaje simbólico literal formalizado median-te símbolos, variables o parámetros, que refieren objetos generales que representan el caso general. Puede utilizarse inductivamente un lenguaje natural, numérico, icónico o gestual en la descripción del método de construcción del patrón. Además, se manipula la escritura formal para obtener expresiones más simples, sin necesariamente analizar su relación con el método de construcción, centrándose el trabajo en la manipulación simbólico-literal. Se establecen relaciones entre las representaciones producidas, y de los elementos de estas con los del contexto sociocultural donde se les asignan significado y sentido (Castaño et al., 2008; Amaya, Pino-Fan y Medina, 2016).
MODELO POR NOCIONES CLAVE
Este modelo (Radford, 2014), establece tres condiciones para el análisis de la actividad algebraica que desarrolla un estudiante:
(1) Indeterminación: el problema a resolver involucra términos desconocidos (incógnitas, variables, parámetros, etc.). (2) Denotación: los términos indeterminados involucrados en el problema deben ser simbolizados y esta simbolización se puede lograr de varias maneras: usando lenguaje natural, números, letras, gestos, signos no convencionales, o una mezcla de estos. (3) Analiticidad: las cantidades indeterminadas se tratan como si se conocieran, por lo que, se opera con ellas de forma analítica. Y para encontrar un término desconocido no se adivina o se llega por tanteo, se deduce de forma analítica.
Además de los criterios descritos para el análisis de la actividad algebraica, son importantes los registros y las representaciones que se usen para comunicar la actividad matemática desarrollada, ya que, a través de ellos se hacen construcciones con las que las personas externalizan sus representaciones mentales, las cuales deben ser configuradas en un registro (Duval, 2017). El registro de partida que se escoja para proponer una situación, es fundamental para que el estudiante, en su solución logre transformar dicha representación. Una representación admite dos tipos de transformaciones: 1) tipo conversión cuando se cambia el registro, es decir, se decodifican los elementos de la representación y se recodifican en otro registro; o 2) tipo tratamiento, cuando se decodifican los elementos de una representación y se recodifican en el mismo registro. Un aspecto fundamental en el uso de las representaciones con fines de enseñanza es poder producirlas, hacer el mayor número de transformaciones posibles del objeto en estudio, y establecer conexiones entre ellas. Cuando dos representaciones coinciden en el orden de sus elementos, y su orden de aprehensión también es el mismo, se dice que son congruentes, si no, se dice que son incongruentes (Duval, 2017). El análisis de congruencias e incongruencias es el que permite el estable-cimiento de las conexiones entre las representaciones del objeto estudiado.
En este contexto, las situaciones de variación y cambio son el fundamento principal de los procesos de generalización, por lo que, con su estudio desde los niveles iniciales de escolaridad, se puede lograr que el estudiante vaya progresan-do en el uso del lenguaje y de símbolos, para apoyar el desarrollo de habilidades en el aprendizaje posterior del álgebra (Godino y Font, 2003; Dolores, 2013; Radford, 2014). Esto también incluye representar, o modelar situaciones concretas con expresiones, establecer ecuaciones y encontrar una incógnita como solución de un problema, de tal modo, que los símbolos algebraicos se vayan introduciendo gradualmente (Carraher y Schliemann, 2007). Esto según Butto (2005) y Butto y Rojano (2004), porque los niños son capaces de razonar sobre las variables con-tenidas en una situación, de operar con regularidades implícitas y, de entender que las relaciones funcionales que las involucran, permanecen invariables para todos los valores posibles que una entidad puede tomar. Es decir, implica producir representaciones, generalizar y formalizar patrones y regularidades en el estudio de un objeto matemático. Así mismo, con el progreso de este razonamiento, se avanza en el uso del lenguaje y el simbolismo necesario para apoyar y comunicar el pensamiento algebraico y algunos elementos con rasgos funcionales.
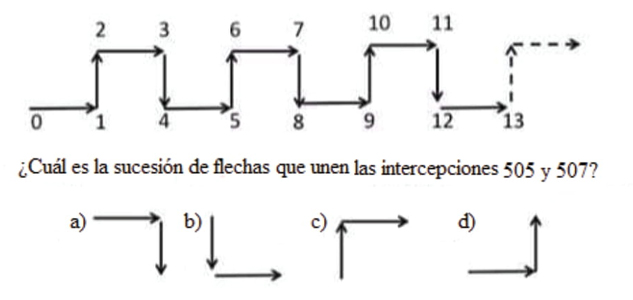
A continuación, se muestran tres tipos de respuestas dadas por profesores en ejercicio, en el desarrollo de un taller con esta temática, al problema mostrado en la figura 1. Si la configuración de flechas sigue el mismo patrón que se indica:
Solución tipo 1:
La ubicación del 0 se repite en las intersecciones 4, 8, 12…, la del 1 en 5, 9, 13, …, la del 2 en 6, 10, 14, ... y la del 3 en la sucesión 7, 11, 15, ... y si dividimos 505 entre 4, da 126 y sobra 1, por lo que la posición del 505 es similar a la del 1, y como 507 dividido 4 da 126 y sobran 3, su posición es similar a la del 3, por lo que la respuesta es c).
Solución tipo 2:
Los términos pedidos terminan en cinco y siete respectivamente, y la secuencia va de uno en uno, así que cada diez términos se repite el último dígito, por lo tanto, la solución es c).
Solución tipo 3:
Las flechas agrupadas por sentido de dirección forman una secuencia de diferencia 4. Como 504 es múltiplo de 4, cae en la secuencia de flechas de abajo: 0, 4, 8, 12, …, 504, se cumple que an = 4×n y si 504 = 4×n, entonces n = 126, es decir, 504 = 4×126, lo cual significa que 504 está ubicado en el lugar donde la flecha vertical llega bajando, el 505 estaría ubicado a la derecha, al final de la flecha siguiente, el 506 estaría arriba, en la punta de la flecha vertical, y desplazándose a la derecha se llegaría al 507, así que la solución es c).
La solución tipo 1, parece ser netamente aritmética, pues, identifica una regla recursiva para cada secuencia, divide el término n-ésimo de la secuencia por la diferencia 4 y ubica los términos solicitados. Sin embargo, en ella subyacen conceptos algebraicos que se salen del foco de dicha solución. Tiene mucha similitud con 505 4 == 1 y 507 4 == 3, que es de las entrañas del álgebra.
La solución tipo 2, analiza una sola secuencia, determinando dos reglas recursivas: la diferencia que va de 1 en 1, y que el dígito final se repite cada 10 términos. Sin embargo, este razonamiento no siempre lleva a una solución correcta, ya que como cada secuencia está formada por 4 números sucesivos, en 4 posiciones diferentes, y la diferencia entre los números que ocupan la misma posición en dos secuencias sucesivas es 4, el último dígito no siempre se repite en la misma posición. En soluciones de este tipo, donde para comunicar la respuesta se usa solo lenguaje natural, cabe preguntar ¿es aritmética o es algebraica esta solución? La solución tipo 3, parece ajustarse mejor a una solución algebraica, pues identifica una regla recursiva, usa letras y verifica su resultado.
ASPECTOS METODOLÓGICOS
Se hizo una investigación cualitativa, desarrollada en tres fases: diagnóstica, interventiva y de contraste, cuya secuenciación y continuidad, permitió una mejor comprensión del fenómeno estudiado. En la primera fase se diagnosticó el problema, y a partir de los resultados se diseñó una propuesta de intervención, la cual se implementó, con el fin de generar cambios y transformaciones en la práctica educativa y social, con la participación activa de los estudiantes en la solución de tareas asociadas al razonamiento algebraico. En la fase interventiva, luego de la aplicación de cada actividad se evaluaban los niveles de algebrización en que lograran ubicarse los estudiantes, y se daban orientaciones buscando minimizar las dificultades encontradas, y afianzar fortalezas. La fase de contraste consistió en la aplicación del cuestionario final, y el procesamiento y análisis de la información. Se analizó el desarrollo progresivo del nivel de razonamiento algebraico elemental de los estudiantes, y, al comparar los resultados de sus respuestas, con los niveles de algebrización (Godino et al., 2014), ir haciendo un acompañamiento guiado, en su proceso evolutivo, hacia niveles más avanzados.
MUESTRA DE INFORMANTES
Estuvo constituida por 38 estudiantes de quinto grado de una institución educativa pública colombiana, con edades entre 10 y 12 años. Se hizo un muestreo intencional, teniendo como criterios de inclusión, que el estudiante quisiera participar voluntariamente, que presentara baja tasa de inasistencia y que mostrara interés por el aprendizaje de las matemáticas. En Colombia el Ministerio de Educación Nacional (2006), en los Estándares Básicos de Competencias en Matemáticas, sugiere que los estudiantes, al finalizar el quinto grado, deben dominar las operaciones básicas con números enteros, resolver problemas que las involucren, encontrar secuencias, patrones, regularidades, variaciones y cambios, y equivalencias entre expresiones numéricas.
INSTRUMENTOS Y TÉCNICAS PARA RECOGER LA INFORMACIÓN
Se utilizaron cuestionarios abiertos y entrevistas semiestructuradas basadas en las soluciones dadas por los estudiantes a las tareas (Goldin, 2000). En los cuestionarios se plantearon secuencias numéricas o geométricas, con elementos del contexto sociocultural, que involucran patrones de variación y cambio. Para que los cuestionarios fueran comparables, todos se diseñaron con la misma estructura, atendiendo los descriptores de los niveles de algebrización (Godino et al., 2014), buscando poder categorizar la actividad matemática individual de cada estudiante, y ubicarlo en el nivel correspondiente, de acuerdo a la solución por él comunicada, luego de verificar las condiciones o nociones clave propuestas por Radford (2014).
Las entrevistas fueron vídeo grabadas, y en ellas se hicieron preguntas de sondeo durante, o inmediatamente después de resolver cada tarea, con lo que se buscaba evidenciar los conocimientos, y razonamientos utilizados por los estudiantes, en sus soluciones (Koichu y Harel, 2007). Las entrevistas basadas en tareas son apropiadas para recoger información cualitativa en matemáticas, pues, permiten identificar las ideas y procedimientos matemáticos que utilizan los estudiantes al resolverlas (Rivera, Salgado y Dolores, 2019).
La información se recogió en el segundo semestre de 2018, en siete sesiones de trabajo de dos horas cada una. La primera sesión fue la aplicación de la prueba diagnóstica, donde se caracterizó el nivel de algebrización inicial de los estudiantes y se identificaron fortalezas y debilidades. En las cinco sesiones siguientes se hizo un proceso de afianzamiento, donde se iban aplicando pruebas para analizar el progreso parcial alcanzado durante el proceso y tomando decisiones para mejorarlo. En la séptima sesión, se aplicó la prueba final validatoria. Cada sesión de la fase interventiva se dividió en cuatro momentos: I) presentación de la actividad; II) trabajo individual en la solución de las situaciones planteadas y entrevista; III) discusión en grupos de dos o tres estudiantes para socializar las respuestas de cada uno y generar un espacio de discusión para intercambiar ideas, asistidos por los miembros del equipo investigador. Finalmente, IV) se hacía una discusión general con el grupo completo para la socialización de la actividad, donde los estudiantes exponían y defendían las estrategias utilizadas para dar sus respuestas y daban sus opiniones sobre las respuestas de sus compañeros. Al final del momento IV), se llevó a cabo un proceso de enseñanza explícita, donde los investigadores mostraban formas alternativas de solución, y a partir del análisis de términos cercanos, se reconocían reglas implícitas en las secuencias, se explicaban y establecían patrones. Se introdujo un poco de lenguaje técnico de las matemáticas, todo con el fin de facilitar a los estudiantes hallar términos alejados, hacer generalizaciones y usar lenguaje simbólico. En la tabla 1, se presenta una muestra del tipo de actividades desarrolladas en cada fase del trabajo.
Tabla 1 Muestra del tipo de actividades desarrolladas.
PROCESAMIENTO DE LA INFORMACIÓN
La información, tanto oral como escrita, se procesó utilizando la técnica análisis de contenido, agrupándose las ideas básicas por criterios temáticos (Bernárdez, 1995), y comparando similitudes y diferencias para hacer el análisis. Toda la información se pasó a una matriz de valoración, donde se establecieron los descriptores que permitieron valorar los conocimientos y competencias alcanza-dos por los estudiantes. Para minimizar la posibilidad de hacer análisis errados, se hicieron entrevistas basadas en las soluciones dadas por los estudiantes a las tareas, pues según Howe (2005) y Radford (2014), las generalizaciones también pueden hacerse adivinando o por tanteo, basados solo en conceptos y razonamientos aritméticos. Luego de la revisión frente a los descriptores, los resultados se compararon con los niveles de algebrización, y a partir de esta comparación, se hizo la descripción, que luego se analizó frente a los referentes teóricos que fundamentan la investigación. Para dar algunos detalles del pro-ceso, se muestran ejemplos de las soluciones de tres niños (Gio, Memo y Ana: nombres ficticios utilizados con el fin de proteger su identidad), desde donde se pueden apreciar algunas generalidades del grupo.
RESULTADOS Y ANÁLISIS DE LA INFORMACIÓN
En la fase diagnóstica, las soluciones dadas por los estudiantes se pueden clasificar en dos subgrupos: la mayoría (89.5%) recurrió al conteo o a la construcción término a término, de los elementos de la secuencia, hasta llegar al elemento solicitado. En particular, en las situaciones que involucran secuencias geométricas, iniciaron contando el número de figuras que se mostraban en la situación y luego dibujaban las siguientes figuras, hasta llegar a la de la posición que se les pedía; y en las que involucran secuencias numéricas, hacían el conteo paso a paso, hasta llegar al elemento solicitado. Después de algunos intentos fallidos en la consecución de soluciones adecuadas, tratando de encontrar un elemento en una posición distante, estos estudiantes, comenzaron a identificar el patrón de crecimiento, reconociendo una regla recursiva, que les permitió continuar la secuencia y expresarla en lenguaje natural, icónico o numérico. Las soluciones dadas por este subgrupo, se pueden ubicar en un nivel cero de algebrización. No obstante, otro pequeño subgrupo (10.5%), hizo generalizaciones aritméticas, estableciendo relaciones de variación entre los términos que conforman la secuencia. En concordancia con lo reportado por Butto (2005), las estrategias utilizadas fueron aditivas/multiplicativas o aritméticas/prealgebraicas, con procesos de generalización dados en lenguaje natural, por lo que las soluciones de este otro subgrupo pueden ubicarse en el nivel uno de algebrización. Pero como en Godino et al. (2003), ninguno de los dos subgrupos hacía emerger objetos algebraicos.
A continuación, se presenta un fragmento de la entrevista realizada a Gio, al resolver la situación que trata sobre el número de galletas repartidas por Camila.
| Entrevistador: | Hazme el favor de decirme ¿cómo cambia el número de galletas a medida que cambia el número de cajas? |
| Gio: | El número de cajas va de uno en uno, y el de galletas de doce en doce. |
| Entrevistador: | ¿Cómo hiciste para generar los términos de la secuencia que escribiste en la tabla? |
| Gio: | En la secuencia se ve que los números de galletas van de doce en doce. |
| Entrevistador: | ¿Qué expresión nos puede ayudar a determinar el número de galletas para cualquier número de cajas? |
| Gio: | La expresión es que las galletas van de doce en doce. |
Respecto a la solución de Gio, se puede apreciar que completa los términos de la secuencia, expresa numéricamente el siguiente, reconoce una regla recursiva y la escribe en lenguaje natural, es decir, se da cuenta que los términos de la secuencia van de doce en doce, y lo usa para completar la tabla, al hallar los términos siguientes, sin expresar una regla general. Asimismo, no logra establecer una relación explícita entre el número de cajas y el de galletas, pero deja implícita la generalización, al expresar “la expresión es que las galletas van de doce en doce”, como puede apreciarse en su manuscrito, mostrado en la figura 2. De acuerdo a los descriptores por niveles, podemos decir que la actividad matemática desarrollada por Gio en la solución de esta tarea, puede ubicarse en un nivel cero de algebrización.
En el proceso interventivo, en las entrevistas, los estudiantes argumentaban sobre los procesos realizados y, similar a lo reportado por Butto (2005), daban explicaciones adecuadas de cómo los realizaban, con ciertas limitaciones al justificar el porqué de sus acciones, para hacer generalizaciones y encontrar valores de las secuencias para posiciones alejadas. Las soluciones dadas en las primeras cuatro sesiones, tenían como marco referencial el aritmético, puesto que, utilizaban nociones de sus conocimientos aritméticos previos, para dar cuenta de sus progresos en el aprendizaje inicial del álgebra (Gascón, Bosch y Ruiz-Munzón, 2017). En estas sesiones, en las soluciones los procedimientos utilizados eran meramente aritméticos, donde primaba el conteo, algunos llegaron a determinar y utilizar un patrón y, a usar lenguaje simbólico literal, sin realizar las operaciones indicadas, que los llevaran a simplificar las expresiones producidas, llegando a hacer generalizaciones en lenguaje natural. Por lo que atendiendo los niveles de algebrización (Godino et al., 2014), las soluciones dadas por los estudiantes, en las primeras cuatro sesiones, se ubicaron entre los niveles, del cero al dos.
A continuación, se muestra un fragmento de la entrevista realizada a Memo, en la cuarta sesión, al resolver la situación donde se le pedía trabajar con la secuencia 5, 9, 13, 17, 21,..
| Entrevistador: | ¿Cómo encontraste los números que colocaste en la tarjeta 6 y en la tarjeta 7? |
| Memo: | Para llegar al término 6 le sumé 4 más al 21 y para llegar al término 7, le sumé 4 más al 25. |
| Entrevistador: | Encontraste una regla que te permitió continuar la secuencia y hallar, ¿Qué número debe colocarse en la tarjeta 12 y en la 33? |
| Memo: | Sí profe. |
| Entrevistador: | Hazme el favor de describirla. |
| Memo: | Es ir sumando de 4 en 4 hasta llegar a la tarjeta 12 y seguir sumando 4 hasta llegar a la tarjeta 33, como lo hice aquí -y muestra su manuscrito- entonces, el número que va en la tarjeta 12 es 29 y en la tarjeta 33 es 133. |
| Entrevistador: | ¿Encontraste alguna expresión que te permita encontrar un número cualesquiera de la secuencia? |
| Memo: | Sí profe, sumándole cuatro al anterior, se consigue el siguiente. |
Memo, en su solución, encuentra una regla recursiva, que le permite encontrar los términos siguientes de la secuencia, y los expresa en un lenguaje numérico, pero para encontrar términos alejados, utiliza la misma regla recursiva, escribiendo todos los términos hasta llegar al solicitado. En su solución no emergen objetos algebraicos y de acuerdo a los niveles de algebrización esta actividad matemática de Memo se encuentra en un nivel cero, ya que encuentra un patrón, pero no lo usa para generalizar.
Fue a partir de la quinta sesión, en el desarrollo de actividades donde se pedía determinar los elementos desconocidos de una secuencia geométrica, cuando los estudiantes comenzaron a hacer generalizaciones, con reglas simples, en su gran mayoría ligadas al lenguaje natural o al numérico, y algunos al algebraico. A partir de entonces, empezaron a utilizar la letra como variable, y a hacer algunas transformaciones sobre las expresiones halladas, y como en Vergel (2014), utilizaron acciones de conteo, y operaciones básicas para comprobar y validar las soluciones dadas. Entonces, ante la necesidad de representar y manipular términos desconocidos, empezaron a emerger algunas expresiones algebraicas (Bolea, 2002), y a hacerles pequeñas transformaciones.
A continuación, se muestra un fragmento de la entrevista realizada a Gio, en la quinta sesión de trabajo, al resolver la situación donde se le pedía encontrar el número de círculos para hacer una decoración:
| Entrevistador: | ¿Cómo hiciste para hallar el número de círculos de cada decoración? |
| Gio: | Partí de observar el comportamiento de los términos dados en la secuencia, como lo escribí aquí -y señala con el dedo su propio escrito- para hallar los círculos de la decoración 12 se multiplica (12×2=24) y para la decoración 35 se multiplica (35×2=70). |
| Entrevistador: | ¿Por qué multiplicas por 2? |
| Gio: | Lo multipliqué por 2 porque 2 es el patrón. |
| Entrevistador: | ¿Cómo supiste que 2 es el patrón? |
| Gio: | Porque cada figura tiene 2 círculos más que la anterior. |
| Entrevistador: | ¿Pudiste determinar una expresión, para encontrar el número de círculos para cualquier número de la decoración? |
| Gio: | Sí, la expresión es multiplicar por 2 cada número de la decoración. |
| Entrevistador: | Podrías explicarme cómo lo hiciste |
| Gio: | Como ya le dije profe, multipliqué por 2 el 1, 2, 3, 4, 5, y así sucesivamente hasta el 12 y después hasta el 35. |
En la solución dada por Gio, comienza reconociendo una regla recursiva: sumar dos círculos a la decoración anterior, que le permite generar la siguiente figura para cualquier posición de esta, y lo describe combinando lenguaje natural con números, gestos, signos de operación y de agrupación. Las respuestas de Gio muestran, que identifica el 2 como la diferencia entre dos términos consecutivos, en las representaciones producidas para la secuencia y lo utiliza para encontrar un elemento cualquiera de esta. Aunque los rasgos de la generalización realizada en esta fase, son similares a los de la fase diagnóstica, en esta solución, explicita la generalidad, cuando dice “y así sucesivamente”, además, logra explicar cómo lo hizo, da razones del por qué lo hace, lo que muestra claros rasgos de razonamiento algebraico en su solución (Howe, 2005; Radford, 2006, 2014, Vergel, 2014). Asimismo, Gio hace una conversión al registro analítico-aritmético y luego de algunas transformaciones tipo tratamiento, en que parece encontrar el patrón de regularidad y crecimiento, el cual utiliza para dar sus respuestas. La variedad de transformaciones tipo conversión realizada por Gio en el desarrollo de esta actividad (ver figura 4), deja ver significativos avances en su pen-samiento variacional (Cantoral, 2013; Dolores, 2013), pues, además de producir varias representaciones de la secuencia: figural, analítico-aritmética, y del lenguaje coloquial; logra relacionar algunos elementos de estas (Rico, 2009; Amaya et al., 2016; Duval, 2017), estableciendo una relación de correspondencia entre el número de círculos y la posición de la decoración.

Figura 4 Manuscrito de Gio al comunicar su repuesta a una de las actividades del proceso interventivo.
En la solución dada por Gio a esta actividad, no emerge ningún objeto algebraico, mostrando una forma aritmética de pensar, en uno de sus primeros intentos por acceder al álgebra (Radford, 2014; Kieran et al., 2016), donde el uso del conteo y la determinación de un patrón de regularidad, fueron la base para encontrar el número de círculos que se necesitarían para cada decoración. De acuerdo a los descriptores por niveles (Godino et al., 2014), esta forma de resolución de Gio, permite ubicarlo en el nivel uno de algebrización, pues se adaptó a la tarea con bastante flexibilidad (Gaita y Wilhelmi, 2019), estableció relaciones entre los elementos de la secuencia, y encontró un patrón, que expresó en lenguaje natural, el cual le permitió hallar el número de círculos para las posiciones de la decoración que le fueron solicitadas.
En la solución dada a las actividades del cuestionario final, los estudiantes mostraron un poco más de pericia en los procesos de transición de la aritmética al álgebra: 31.5% encontraron un patrón y lo utilizaron para hallar una expresión algebraica en lenguaje simbólico literal. En particular, Gio en sus soluciones, utilizó técnicas similares a las empleadas en actividades anteriores, esto es, reconocer una regla recursiva y expresarla combinando lenguaje natural con símbolos numéricos, gestos, signos de agrupación y de operación, para determinar los términos de la secuencia. Seguidamente, a partir del análisis de unos pocos casos, encontraba una regla general (un objeto intensivo) que le permitió descubrir un término alejado de la secuencia, como se muestra en la figura 5. Aunque en su proceso de solución cometió algunos errores de escritura (Carrión, 2007), luego generalizó, usando lenguaje simbólico, utilizando la expresión × + ,2la que seguidamente transformó en ² + 2, donde se aprecian características propias del nivel tres de algebrización (Godino et al. 2014; Gaita y Wilhelmi, 2019), evidenciándose en él un crecimiento progresivo durante todas las actividades.
Asimismo, en su solución a las actividades del cuestionario final, Ana empieza reconociendo una regla recursiva, la cual expresa en lenguaje natural, combi-nado con números, utilizando conteo y operaciones aritméticas para determinar términos alejados en la secuencia. En particular, en su solución a la situación del crecimiento de la planta, construye una tabla donde establece la correspondencia entre el número de semanas y la altura en centímetros de esta, partiendo de casos particulares conocidos, hasta encontrar una regla general que expresa en un lenguaje simbólico-literal, que le permite hallar términos alejados, como se muestra en la figura 6. Seguidamente, se muestra parte de la entrevista realizada a Ana al resolver la situación del crecimiento de una planta.
| Entrevistador: | ¿Qué observas a medida que se va avanzando en la posición de las figuras? |
| Ana: | Que la figura uno tiene 3 centímetros, la figura dos tiene 6 centímetros, y la figura tres tiene 11 centímetros y así... |
| Entrevistador: | ¿Crees que puedes predecir la altura de la planta de la figura 10? |
| Ana: | Sí. |
| Entrevistador: | Entonces, ¿Cuántos centímetros debe tener la planta de la figura 10? |
| Ana: | Tiene 102 centímetros profe. |
| Entrevistador: | Ahora, dime la regla que utilizaste para hallar la cantidad de centímetros que tiene la planta a los 12 y 26 semanas respectivamente. |
| Ana: | Multipliqué el patrón: la semana por la semana y sumé un dos. |
| Entrevistador: | ¿Podrías escribir una expresión para determinar la cantidad de centímetros que tendría la planta en una semana cualquiera? |
| Ana: | Creo que sí -piensa un rato y escribe en la hoja- n × n + 2 |
| Entrevistador: | ¿Por qué crees que sería así? |
| Ana: | Porque n es el número de la semana. |
Como puede apreciarse en la solución dada por Ana, inicia mostrando objetos extensivos, considerando casos particulares para cierto número de semanas, pero logra configurar objetos intensivos, haciendo generalizaciones, expresa-das en lenguaje simbólico-literal, sin hacer ningún tipo de transformaciones en esta, por lo que su actividad podría ubicarse un nivel dos de algebrización (Aké et al., 2013).
En la solución a las actividades de la prueba final, Memo al igual que el resto de sus compañeros, utiliza estrategias muy similares a las usadas en las soluciones dadas en las fases previas, además, comete varios errores de escritura. En particular, en la situación donde se pedía analizar el crecimiento de una planta (figura 7), Memo intenta encontrar inicialmente una regla recursiva restando un término con el anterior, pero verifica que solo le funciona con el primer término y prueba otra opción que le resultó adecuada para conseguir el patrón, y lo utiliza para encontrar términos alejados en la secuencia. El patrón lo encuentra por inspección inductiva, usando casos particulares, con procedimientos aritméticos expresados en lenguaje natural, combinados con números enteros y signos de operación, sin utilizar lenguaje simbólico-literal. Este análisis, lo lleva a determinar la correspondencia entre el número de semanas, la altura, y el crecimiento por semanas de la planta, así, la actividad matemática desarrollada por Memo al resolver esta situación, podríamos ubicarla en el nivel uno de algebrización (Godino et al., 2014).
La forma en que los estudiantes que lo lograron, obtuvieron la regla que determina el patrón al resolver la prueba final, parece no ser un rasgo que por sí solo sea suficiente para caracterizar la generalización algebraica, pues para que lo sea, además de ver lo general en lo particular, se debe ser capaz de expresarlo alge-braicamente (Howe, 2005; Radford, 2006; Kieran, 2004). Según Radford (2006), la generalización de los patrones como una ruta al álgebra se basa en la idea de una correspondencia natural entre el pensamiento algebraico y la forma de generalizarlo, así, pensar algebraicamente es más que pensar en lo general (Kieran, 2004), es pensar sobre lo general, de tal forma que el razonamiento algebraico sea un componente necesario para la generalización, es el uso del simbolismo algebraico para razonar y expresar algo de manera general (Radford, 2006). Por lo que esta forma de solución reportada por este grupo de estudiantes, puede ubicarse entre los niveles cero al dos de algebrización.
De acuerdo con los análisis realizados a las soluciones reportadas por este grupo de estudiantes, se puede decir que la mayoría de los estudiantes se encuentran entre los niveles cero y dos de algebrización. Sin embargo, la actividad matemática predomínate en los estudiantes fue de nivel uno, ya que logra-ron generalizar patrones en un lenguaje diferente al simbólico-literal, y (excepto Gio), los que utilizaron lenguaje simbólico no hicieron transformaciones tipo tratamiento en la representación algebraica producida.
REFLEXIONES FINALES
En el desarrollo del trabajo vemos que los registros de partida en que se presentan las situaciones, no producen reales diferencias en cómo emerge el razonamiento algebraico en quien aprende. Sin embargo, la posibilidad de establecer conexiones entre diferentes representaciones permite que el simbolismo algebraico emerja al representar los objetos y hacerles transformaciones, pudiéndose evidenciar razonamiento algebraico sin, necesariamente, usar lenguaje simbólico-literal. Por lo que, como dice Radford (2014), el uso de la letra no es condición necesaria ni suficiente para pensar algebraicamente. No obstante, se pueden diseñar y aplicar actividades globales que lleven al estudiante a generalizar patrones, y así, darles la oportunidad de evidenciar su pensamiento algebraico (Radford, 2006), en representaciones diferentes a la analítico-algebraica.
Además, las dificultades presentadas por estudiantes al resolver tareas que impliquen el paso de una forma de razonamiento aritmético a otro algebraico, parecen estimular a investigadores y profesores de matemática educativa, a estan-darizar las características del razonamiento aritmético y del algebraico, para dife-renciarlos, y así poder establecer si la solución a una tarea matemática, moviliza alguno de los dos modos de pensamiento. Pues la revisión bibliográfica muestra que ha sido ampliamente estudiada la conveniencia de superar la oposición aritmético-algebraico, y se ha generado la necesidad de estructurar los currículos de las instituciones como un continuo epistemológico, más que como el paso de actividades meramente aritméticas a otras donde el álgebra se presenta como un producto acabado (Radford, 2006, 2014; Kieran et al., 2016; Gaita y Wilhelmi, 2019). En este sentido, interesa trabajar la forma de armonizar planes de estudio que faciliten una formación algebraica integral, donde la transición del pensamiento algebraico informal al formal sea lo más simple posible (Cai et al., 2011).
Atendiendo lo anterior, coincidimos con Kieran et al. (2016) y Blanton et al. (2018) en que el inicio temprano del estudio del álgebra en el currículo de matemáticas, podría ser favorable para los estudiantes, ya que los ayudaría a hacer una transición suave a un estudio más formal del álgebra en grados posteriores. Es decir, no es preciso algebrizar ciertos contenidos matemáticos para enseñar álgebra (Gaita y Wilhelmi, 2019), ya que, con el uso de relaciones funcionales de variación y cambio presentadas en diferentes registros, desde los que se hagan transformaciones semióticas y conexiones entre todos los registros que sea posible, podría facilitarse un acceso moderado a la actividad algebraica. Esto podría llevar-nos a sopesar las matemáticas como algo que adquirimos, con las matemáticas con las que convivimos (Castaño et al., 2008; Cantoral, 2013; Dolores, 2013), faci-litar su integración en todos los grados y temas (Kaput et al., 2008), y proveer herramientas que permitan enfrentar los desafíos asociados con el desarrollo del pensamiento algebraico de los estudiantes desde los primeros grados de ense-ñanza básica (Cai et al., 2011).
Consideramos que, un proceso de inclusión temprana del álgebra elemental en la educación primaria, sugiere el fortalecimiento de algunos aspectos: la forma de abordarla desde los primeros grados, considerar el tipo de tareas que faciliten su desarrollo, y el apoyo a profesores en esta área, en el diseño y apli-cación de tareas globales, que ayuden a potenciar en los niños su razonamien-to algebraico elemental desde los primeros grados.
CONCLUSIONES
A partir del análisis de la información se puede concluir que el estudio de patrones, a través de secuencias numéricas y geométricas, aportó elementos importantes para el desarrollo del razonamiento algebraico en los estudiantes; llevándolos a analizar los elementos de las secuencias y, al establecer una regla recursiva, encontrar términos faltantes o generalizar un patrón, y en algunos casos, usar la letra como variables mediante notaciones simbólico-literales. Y como se preveía teóricamente, una misma situación fue abordada según diferentes niveles de algebrización (Gaita y Wilhelmi, 2019), utilizando distintas alternativas de solución para llegar a resultados comparables. Así, cada actividad favoreció el uso de diversos lenguajes y en algunos casos, procesos argumentativos bien fundamentados.
Respecto a la pertinencia del marco teórico, observamos que los elementos teóricos fueron importantes, pues los niveles de algebrización (Godino et al., 2014) se convirtieron en parte del proceso interventivo, y las nociones clave (Radford, 2014) ayudaron a clarificar los procesos realizados, ambos, posibilitaron categorizar la actividad matemática de los estudiantes, y dieron direccionamiento a la propuesta. La implementación de la propuesta, permitió un aumento progresivo del poder heurístico en la resolución de problemas en este grupo de estudiantes, quienes dieron variadas y ricas soluciones a las actividades que se les plantearon. Las interacciones discursivas obligaban a los estudiantes a construir argumentos bien fundamentados, pues, buscando defender una postura, o refutar algo con lo que hubiera un desacuerdo, terminaban produciendo y articulando diferentes tipos de representaciones: destacándose el uso de lenguaje icónico, natural, numérico o simbólico-literal. La actividad matemática de la mayo-ría de los estudiantes se puede ubicar entre los niveles cero a dos de algebrización, destacándose, los niveles uno y el proto-algebraicos de nivel dos, solucionando problemas de valores faltantes (Godino et al., 2014).











 nueva página del texto (beta)
nueva página del texto (beta)