1. INTRODUCCIÓN
El concepto de números negativos es introducido en séptimo año de Enseñanza Básica según las bases curriculares del Ministerio de Educación de Chile (MINEDUC, 2018), después de tratar con operaciones con números naturales N, las fracciones y los decimales positivos Q+. El marco curricular deja para la Educación Media el contenido de los números racionales -que incluyen las fracciones positivas y negativas- y los números reales que contienen a los números decimales positivos y negativos.
En diversas investigaciones entre las cuales consideramos las de: Gallardo (2002); Gallardo y Basurto (2009), (2010); Gallardo y Mejía (2015) y Cid (2015) explican las dificultades que la mayoría de los estudiantes tienen, para representar las diversas situaciones por medio de número con signo y que para ello recurren generalmente al dominio de los números naturales, conceptos adquiridos durante los años previos de escolarización, reconociendo que estas dificultades son un problema complejo de resolver.
Generalmente la introducción de los números negativos, en la escuela actual fomenta la concepción de que el número puede entenderse como resultado de una medida, ya sea por modelos concretos o la aritmetización contextualizada no evidenciada de manera creíble para los estudiantes, como lo indican los textos escolares. Esto según Cid (2015), induce a lo que parece ser un obstáculo epistemológico similar al que tuvo que salvar la comunidad de matemáticos a través de la historia.
A pesar de las dificultades detectadas en estudiantes de diferentes edades al tratar con problemas con números negativos, es decisiva la necesidad de un buen desempeño en el uso de los números enteros en su conjunto, para la comprensión futura del álgebra, la resolución de problemas en otras áreas del conocimiento como son las ciencias, y para dar paso al aprendizaje de conocimientos más complejos.
Si bien los niños reconocen cantidades negativas como números, mucho antes de ser enseñado en séptimo año de Enseñanza Básica, a diferencia de los matemáticos de antaño, los cuales no reconocían estos números por no tener una representación física en el mundo real, nuestros estudiantes de hoy en día, se encuentran en un mundo en el que los números negativos aparecen no solo en las matemáticas escolares, sino también en diversos contexto como son las temperaturas, los ascensores, medidas de profundidad, deber-haber, pérdidas y ganancias. Los estudiantes de hoy en día también tienen acceso a modelos no solo concretos sino virtuales que con herramientas tecnológicas como son los programas computacionales, tales como Scratch, entorno y presentaciones que utilizan dichos números, sin embargo, reconoce su existencia, pero no su operatividad.
La inserción de las Tecnologías de la Información y Comunicación (TIC) ha permitido que los ambientes mediados por ellas ayuden a establecer relaciones mucho más enriquecedoras, recursos que están siendo insertados en el Curriculum Escolar de forma transversal como lo ha propuesto el MINEDUC, en Mi Taller Digital, (2019).
En numerosas investigaciones como las de: Bishop et al., (2014); Bofferding (2014); Bofferding et al., (2017); Cid (2015); Gallardo (2002) y Gallardo y Mejía (2015), han intentado abordar el problema al que se enfrentan los profesores al enseñar los números enteros. Pese a sus esfuerzos, los estudiantes tienen grandes dificultades para dar sentido a las operaciones entre números enteros, cometiendo frecuentes errores en los cálculos que los involucran y olvidando su existencia en los razonamientos matemáticos.
Teniendo en cuenta las dificultades cognitivas que tienen los estudiantes cuando se enfrentan a las operaciones entre números enteros, en esta investigación se pretende analizar las concepciones que van adquiriendo los estudiantes de cuarto año de Enseñanza Básica sobre los números negativos, cuando son enfrentados a situaciones-problemas a través de modelos concretos mediante un medio didáctico tecnológico, situaciones como las creadas mediante la programación en Scratch, invitando al estudiante a la reflexión en el aprendizaje de la matemática.
En esta investigación nos basamos en las situaciones adidácticas creadas a través del medio tecnológico, con el propósito de analizar los procesos cognitivos informales que se dan en la adquisición conceptual y operativa de los números negativos en los estudiantes, cuando se les pide resolver tareas elementales, sin haber tenido instrucción formal, así como los posibles obstáculos epistemológicos que tienen y que es posible evidenciar en el proceso de resolución de la tarea.
Por lo tanto, las preguntas que nos planteamos para el desarrollo de esta investigación son:
¿Cuáles son las concepciones de números que ponen en acción los estudiantes cuando tratan con situaciones adidáctica concretas?
¿Las actividades en el entorno de programación en Scratch, favorecen la conceptualización numérica planteada a través de situaciones adidácticas?
¿Existen diferencias entre el camino histórico seguido por los matemáticos para aceptar cantidades negativas como números negativos y el camino que toman los estudiantes para aceptar números negativos en la actualidad?
2. FUNDAMENTACIÓN TEÓRICA
En varias investigaciones en que tratan la conceptualización de números negativos, siendo las más importantes las de Gallardo (2002) y Cid (2015), se pone de manifiesto los conflictos que tienen los estudiantes para extender el dominio numérico de los naturales a los enteros. En ellas se identifican cuatro niveles conceptuales de negatividad que adquieren los estudiantes: Número sustractivo, Número signado, Número relativo y Número aislado. Los que ahora e históricamente han representado una dificultad para el entendimiento.
El trasfondo histórico de esto se da, porque los números enteros reflejan que los negativos son de naturaleza abstracta, y porque no se desarrollaron como una percepción intuitiva que surge de las experiencias personales. Así entonces, no es de sorprender que sea difícil desarrollar las concepciones de enteros negativos en los estudiantes como menciona Wessman-Enzinger (2015), sin embargo, hoy en día, la percepción intuitiva de este tipo de enteros está mucho más cercana a los estudiantes a través del uso de ascensores, escalas de temperaturas, deudas entre otras, pero no así la operatividad con estos números. (Wessman-Enzinge y Mooney, 2019).
Por otra parte, aunque los adultos pueden usar convencionalmente números negativos con deudas de dinero, o con temperaturas sobre y bajo 0, esto no resulta de una intuición natural para la mayoría de los niños. Por ejemplo, los estudiantes pueden percibir las deudas como números positivos y no reconocen que pueden usarse números negativos. Los estudiantes a menudo necesitan indicaciones y ayudas, mediante recursos como la recta numérica, cuando se enfrentan a la necesidad de resolver una expresión tal como: 2 - 5 = ?, cuya solución les demanda pensar en los números de manera diferente, y desarrollar el conocimiento necesario para usar números enteros negativos (Wessman-Enzinger, 2015).
Gallardo y Mejía (2015), enfocan el problema desde la noción de obstáculo epistemológico, según la definición hecha por Brousseau, evidenciando que las dificultades de los estudiantes al enfrentar problemas con números negativos, son de origen epistemológico, y que dadas las características de estos conflictos, tales como su persistencia y las semejanzas, son los mismos obstáculos que presentaron históricamente los matemáticos en la conceptualización de los negativos, como señala Artigue (2018).
Brousseau (2007), define un obstáculo epistemológico como las causas que conducen a los errores: “El error no es solamente el efecto de la ignorancia, la incertidumbre, sino que es el efecto de un conocimiento anterior, que, a pesar de su interés o éxito, ahora se revela falso o simplemente inadecuado” citado por Barrantes (2008, p. 3). Así entonces, un obstáculo epistemológico, no hace referencia necesariamente a conocimientos erróneos, sino a tipos de conocimiento que están obstaculizando la adquisición (construcción) de lo nuevo.
En esta investigación hemos seleccionado la Teoría de las Situaciones Didácticas de Brousseau, motivados principalmente por crear condiciones para el tratamiento de la conceptualización de los números negativos en los cuatro niveles señalados anteriormente.
2.1 LA TEORÍA DE LAS SITUACIONES DIDÁCTICAS
Brousseau (2007), señala que los obstáculos didácticos de origen epistemológico son aquellos a los cuales el aprendiz no puede ni debe escapar, por su papel constitutivo en el conocimiento. Se manifiestan por sus errores, que no se deben al azar, no desaparecen espontáneamente, sino que se resisten, resurgen, y se manifiestan por mucho tiempo después de que el sujeto los haya rechazado. Estos errores, para un mismo sujeto, tienen siempre una fuente común: una manera de conocer, una concepción antigua coherente y correcta, que ha tenido éxito en todo un dominio de acciones. Por tanto, un obstáculo epistemológico es siempre un conocimiento, no una falta de este. (Gallardo et al., 2017).
Una situación didáctica es entendida como una situación construida intencionalmente por el profesor para que el estudiante no solo adquiera un conocimiento, sino que además lo utilice y aplique para resolver un problema (Brousseau, 2007). En el desarrollo de una situación didáctica aparecen momentos denominados situaciones adidácticas que, según Brousseau, son situaciones que por una parte no pueden ser dominadas de manera conveniente por el estudiante, sin la puesta en práctica de los conocimientos o del saber que se pretende, y que en contraparte, determinan las decisiones (buenas o malas) que el estudiante toma, en lo concerniente al saber que se pone en juego, y en el cual el estudiante debe interpretar y validar su acción, todo ello bajo un escenario en el cual el docente no interviene.
Como menciona Godino (2020), en estas “…situaciones adidácticas, las interacciones entre alumno y medio se describen como una actividad de producción de conocimiento por parte del alumno. Esta producción es independiente de la intervención explícita del docente en tanto que detentador del saber. Así, el sujeto entra en interacción con una situación-problema, poniendo en juego sus propios conocimientos, pero también modificándolos, rechazándolos o produciendo otros nuevos, a partir de las interpretaciones que hace sobre los resultados de sus acciones” (Godino et al., 2020, p. 150). Aquí es donde la función principal del docente es la devolución, es decir, establecer las condiciones para que el estudiante se apropie de los nuevos conocimientos.
En esta investigación, se propone usar como referente teórico las Situaciones Didácticas (TSD) de Brousseau, según las cuales se postula que un estudiante adquiere un conocimiento, cuando es enfrentado a una situación-problema cuya solución exige un conocimiento adquirido, y es capaz de generarlo en forma de estrategia de resolución de la situación, basándose en un modelo de interacción entre el estudiante y un medio determinado (Chavarría, 2006), que en el contexto de esta investigación se materializa a través de una situación didáctica, en la cual deben programar en Scratch el desplazamiento de un objeto en el plano cartesiano.
Para el análisis de las situaciones didácticas, es fundamental la teoría de campos conceptuales de Vergnaud, que según Moreira (2002), aporta un marco de referencia coherente en el proceso de conceptualización cuando los estudiantes adquieren conceptos, que en este caso son los referidos a los números negativos.
2.2 TEORÍA DE LOS CAMPOS CONCEPTUALES
Diferentes autores Moreira (2002); Moreira et al. (2009); Sureda y Otero (2011); Alfaro y Fonseca (2016) y Barrantes (2006) describen esta teoría, teniendo como premisa que el conocimiento está organizado en campos conceptuales cuyo dominio, por parte del estudiante, ocurre a lo largo de un extenso período de tiempo, a través de la experiencia, la madurez y el aprendizaje.
Esta teoría, plantea que se requiere del dominio de conceptos donde estos no deben ser reducido a una definición, sino más bien, deben plantearse situaciones-problemas con la idea de que el concepto tenga sentido para el estudiante, sustentando el concepto como una terna de conjuntos: 1) Un conjunto de situaciones que dan sentido al concepto; 2) Un conjunto de invariantes (propiedades, las relaciones, objetos) sobre los cuales reposa la operatividad del concepto y 3) Un conjunto de representaciones simbólicas (lenguaje natural, gráficos y diagramas, sentencias formales, etc.) que pueden ser usadas para indicar y representar a esos invariantes. (Moreira, 2002).
Según la teoría, un concepto se torna significativo a través de una variedad de situaciones o tareas, donde el estudiante le da sentido. Es decir es una relación del sujeto con situaciones y significantes, a través de las acciones y su organización, los cuales son evocados por el estudiante para cada situación, y estas acciones y su organización son los llamados esquemas. Estos tienen como ingredientes esenciales aquello que Vergnaud (1990) denomina invariantes operatorios, es decir, conceptos-en-acción y teoremas-en-acción que constituyen la parte conceptual de los esquemas, es decir, los conocimientos contenidos en los esquemas. Según Moreira (2002), se debe prestar atención a los aspectos conceptuales de los esquemas y al análisis conceptual de las situaciones para las cuales los estudiantes desarrollan sus esquemas. Para Moreira, estos esquemas están compuesto por: “1.- Metas y anticipaciones; 2. Reglas de acción del tipo “si... entonces” que constituyen la parte verdaderamente generadora del esquema; 3. Invariantes operatorios (teoremas-en-acción y conceptos-en-acción) que dirigen el reconocimiento, por parte del individuo, de los elementos pertinentes de la situación; y 4. Posibilidades de inferencia (o razonamientos) que permiten “calcular”, “aquí y ahora”, las reglas y anticipaciones a partir de las informaciones e invariantes operatorios que dispone el sujeto” (Moreira, 2002, p. 7).
Son los invariantes operatorios los que hacen la articulación esencial entre teoría y práctica, pues la percepción, la búsqueda y la selección de información se basan enteramente en el sistema de conceptos-en-acción, disponibles para el sujeto (objetos, atributo, relaciones, condiciones, circunstancias...) y en los teoremas-en-acción que subyace a su conducta. Estos conocimientos-en-acción (conceptos y teoremas-en-acción) constituyen la base conceptual, implícita o explícita, que permite obtener la información pertinente, y a partir de ella y de la meta a atender, inferir las reglas de acción más apropiadas para abordar una situación.
Como uno de los elementos centrales de esta investigación es la creación y uso de situaciones didácticas, con el propósito que los alumnos puedan evidenciar sus acciones y la apuesta en uso de sus conocimientos, cuando son enfrentados a resolverlas, es que hemos elegido utilizar el entorno de Scratch para la creación de actividades usando situaciones didácticas. Por las experiencias que hemos venido desarrollando en estos últimos cuatro años en torno de la enseñanza de conceptos de programación, con alumnos de enseñanza básica, hemos constatado las potencialidades que tiene el entorno de Scratch para crear recursos didácticos que favorecen determinados aprendizajes.
2.3 EL ENTORNO DE SCRATCH COMO RECURSO PARA LA CREACIÓN DE SITUACIONES DIDÁCTICAS
Scratch es un ambiente de programación dotado de un lenguaje visual especialmente diseñado para enseñar a programar a niños y adolescentes de entre 8 y 16 años, que facilita la inmersión en el mundo de la programación. Scratch es un entorno de programación diseñado por el Massachusetts Institute of Technology (MIT) (Palma y Sarmiento, 2015).
Scratch, trabaja con una colección de “bloques de programación”, organizados por secciones de diferentes colores, como los de control, movimiento, sonido, operadores, entre otros. Está pensado para que los niños aprendan a pensar creativamente, razonar sistemáticamente, y trabajar en grupo, habilidades esenciales que serán útiles en el futuro, cuando los estudiantes actuales estén en el ámbito de trabajo. (Vidal et al., 2015) (Vidal et al., 2020).
Las características propias del entorno Scratch, permiten el uso y manipulación de variados elementos matemáticos, tales como, operadores aritméticos, relacionales, lógicos, definición y uso de variables, así como diversos elementos geométricos, por ejemplo, control de ángulos, posicionamiento y desplazamiento de objetos en base al manejo de coordenadas del plano cartesiano, entre otros elementos (Acuña, 2018) (Rocha y Azevedo, 2017).
Conforme a las experiencias, hemos verificado que este entorno les invita a explorar y manipular objetos, mediante su programación, instancias en las cuales deben poner en juego conocimientos matemáticos, transformándose las experiencias de programación, en situaciones que llevan a la reflexión en el aprendizaje de la matemática. Una de las principales responsabilidades del docente es el adecuado diseño de actividades con el uso del entorno Scratch, considerando los fundamentos de la teoría de situaciones didácticas, e interpretando a Brousseau (2007), el estudiante aprende adaptándose a un medio que es factor de contradicciones, de dificultades, de desequilibrios, un poco como lo hace la sociedad humana. Este saber, fruto de la adaptación del estudiante, se manifiesta por respuestas nuevas que son las manifestaciones del aprendizaje.
3. METODOLOGÍA
Esta investigación pretende analizar las concepciones que va adquiriendo un estudiante de cuarto año de Enseñanza Básica, sobre los números negativos, cuando es enfrentado a situaciones-problemas a través de modelos concretos usando un medio didáctico tecnológico, mediante el cual se le presentó una situación que fuera familiar para el estudiante, y que para resolverla debía hacer uso de sus conocimientos intuitivos respecto de los números negativos, ya que conforme a su etapa escolar no han tenido enseñanza formal respecto de estos. La intención es estudiar en profundidad situaciones particulares a las que lo enfrentamos y describir su comportamiento frente al uso del conocimiento que posee de estos números.
Debido a la complejidad del análisis se ha optado por realizar una investigación de tipo cualitativa ya que como indican Rodríguez et al. (1996), los investigadores cualitativos “destacan la comprensión de las complejas relaciones entre todo lo que existe”. Para analizar la realidad hay que tener en cuenta que esta es de una alta complejidad y que hay múltiples situaciones que ocurren en forma simultánea y, por tanto, se hace necesario observar y analizar eventos claves para una mejor comprensión de la situación (Hernández-Sampieri y Mendoza, 2018).
Para dar mayor profundidad y exhaustividad a este trabajo, la investigación cualitativa se realiza a través de eventos (situaciones didácticas) y testimonios (cuando tratan con las situaciones didácticas) ya que, con ellos, además de permitir una mejor comprensión del caso estudiado, se facilita la interpretación a partir de los marcos teóricos que sostienen esta investigación. Por esta razón, se ha optado por utilizar el método de estudio de casos, el que, en concreto, está referido a una estudiante, que en lo sucesivo llamaremos Martina (nombre ficticio), confrontada a diversas situaciones adidácticas en las que debe poner de manifiesto la adquisición de concepto de números enteros.
Martina pertenece al cuarto año de Enseñanza Básica del Colegio Luterano Concordia de Valparaíso. La selección de Martina es ideal, por tanto, no aleatoria, y responde al hecho de que solamente ha tenido experiencias matemáticas con números naturales conforme a su etapa escolar.
La información recolectada proviene de diferentes momentos en donde Martina se enfrentó a diversas situaciones adidácticas, actividades que se realizaron en el taller de robótica.
La investigación está basada en la información que se recolecta de las acciones que reflejan los procesos cognitivos que se generan al intentar resolver las situaciones adidácticas a que es enfrentada Martina. Para la recolección de información se usaron grabaciones para registrar los testimonios de las entrevistas y las actividades realizadas por Martina, cuando es desafiada a resolver las situaciones adidácticas. Nuestro interés es realizar un análisis detallado de los hechos, considerando que las grabaciones son una herramienta útil y consistente, para poder recuperar la información de las acciones que ocurren durante el trabajo que realiza. Se sabe, por experiencia, que las acciones que suceden en el taller son complejas y están llenas de matices, desde donde es difícil extraer información solo con una lista de verificación o con notas de campo de quien observa. Por esta razón se piensa que el detalle y la revisión de las actuaciones de Martina, se pueden realizar mejor desde las grabaciones y posterior transcripción de los episodios analizados.
Además de la información obtenida por las grabaciones, se recopilaron sus escritos al momento que desarrolla las guías de actividades en cada situación. La información que se obtiene de estas guías se origina en completación de frases, respuestas a preguntas, dibujos, esquemas, descripción de acciones y llenado de tablas.
Gallardo y Hernández (s.f.), mencionan que coexisten varios modelos de enseñanza propuestos que hablan sobre el uso de modelos concretos para la enseñanza de los números enteros. Se adaptaron dos modelos, el de desplazamiento mediante el uso de la recta numérica y el de equilibrio o neutralización, con uso de fichas de colores, ambos propuestos por Hernández y Gallardo (2006) para la extensión de los naturales a los enteros mediante el modelo concreto de bloques. Con base en estos modelos se diseñaron diversas situaciones adidácticas que son desafiadas por Martina.
La planificación de las actividades se realizó en cuatro etapas. La primera, consiste en determinar el grado de conocimientos de números negativos o enteros que posee Martina usando una entrevista basada en el proyecto Z (Bishop et al., 2014), realizada a 160 estudiantes del nivel K-12 en USA. Se estudió y analizó la encuesta para ser adaptada a nuestra realidad del contexto educativo chileno. Se efectuaron dos pruebas piloto, el año pasado, con estudiantes de cuarto año de Enseñanza Básica del Colegio Luterano Concordia y en la Escuela del Estado de Israel de Valparaíso. Estas pruebas piloto permitieron eliminar preguntas y modificar otras, y mejorar el análisis a priori de las posibles respuestas que los estudiantes entregan.
La segunda etapa se planificó, para su desarrollo, en tres sesiones, en las cuales se utilizó una representación de un modelo del desplazamiento de un ascensor virtual, recreando un ambiente conocido por los estudiantes (ver figura 1). Cada sesión se realiza semanalmente, y tiene un tiempo de duración de 1 hora 30 minutos. La primera sesión concierne a la complejidad, a la que es enfrentada Martina, los nuevos objetos matemáticos, existiendo una nueva notación para los números positivos (+2 = 2), y el signo menos que tiene dos significados, como signo unario y binario. Aparecen nuevas reglas de operatividad. Desde esta perspectiva se trata de unificar el aprendizaje de los números positivos, utilizando las estructuras de adición de los números positivos ampliándolas a nuevos contextos con número negativos, es decir, a + (-b) = c, -a + b = c, -a + (-b) = c. con a, b, c ∈ N.
La primera sesión del desarrollo de estas actividades, en la que se utilizó un juego que simula el desplazamiento de un ascensor virtual, fue significativamente diferente porque se realizó una inducción para la correcta ejecución del juego, incorporando actividades de ensayo, utilizando solamente números positivos, y respecto de cómo debería realizar las anotaciones de los resultados obtenidos en el juego, así como responder a las preguntas planteadas referentes a las acciones realizadas. La ejecución solo con números positivos se incluyó por dos razones: primero, era importante establecer la comodidad, de parte de Martina, para la correcta ejecución del juego, ya que ha tenido instrucción formal referente a estructuras aditivas con número naturales; en segundo lugar, se incluyeron las preguntas solo con números positivos para obtener una perspectiva sobre su razonamiento y conceptos erróneos que, posiblemente, podrían influir en el estudio y la comprensión del número negativo. Recordemos que Martina no ha recibido instrucción de números negativos.
La actividad en el juego asocia las tres dimensiones planteadas por Bruno (s.f.), en referencia al conocimiento numérico: la dimensión abstracta (conocimientos referidos a los sistemas numéricos como estructuras matemáticas y a las formas de escritura de los números); la dimensión de las representaciones (representación de los números sobre gráficos, la recta u otro tipo de diagramas); y la dimensión contextual (aplicaciones, situaciones concretas en las que se usan los números). Este conocimiento numérico abarca, no solo las tres dimensiones, sino también a las traducciones entre ellas. Así, por ejemplo, la suma 2 + 4 = 6 está expresada en la dimensión abstracta al ir desde un nivel a otro. En cambio “el desplazamiento de un ascensor que está en el segundo piso y subió cuatro pisos, y ahora se encuentra en el piso 6o corresponde a lo contextual, y su desplazamiento puede ser representado implícitamente en la recta numérica.
El modelo de desplazamiento del ascensor virtual pretende abstraer a la estudiante de expresiones tales como: 12 - 4 - 5 + 4, como una sucesión de sumas y restas con números naturales interpretando los signos + y - como operaciones binarias, sino que interpretarlas como suma de términos +12, -4, -5 y +4, donde se suprime el signo binario que indica la suma, pasando a que los signos + y - tengan un sentido de signos predicativos o signos unarios. El objetivo de esta sesión es establecer el concepto que no solamente la suma de enteros da como resultado un valor mayor a la suma.
En la segunda sesión de adición de enteros, se hace uso del modelo de neutralización usando fichas, el cual está adaptado para dar continuidad a la actividad de la sesión anterior. Esta sesión está enfocada a la formalización de sustracción de enteros, es decir a - b = c; a - (-b) = c, y -a - (-b) = c.
En los modelos de neutralización, los signos predicativos se refieren a medidas de cantidades de magnitud de sentidos opuestos que se neutralizan entre sí; mientras que los signos operativos binarios y unarios se identifican con acciones de añadir, reunir, quitar, separar, etcétera.
La suma de números enteros, en este modelo, se interpreta como una acción de agregar fichas a un conjunto, generando una reunión de fichas del mismo signo, y la resta se relaciona con la acción de quitar o separar fichas a un conjunto, y el proceso de neutralización para obtener la representación canónica del resultado. El modelo en el cual debe trabajar Martina, está adaptado al modelo de fichas de dos colores, para inducir la operación de sustracción de enteros.
En esta sesión se pretende llevar a Martina a la abstracción numérica, donde debe realizar una extensión de los números positivos y representar la recta numérica estableciendo el orden numérico.
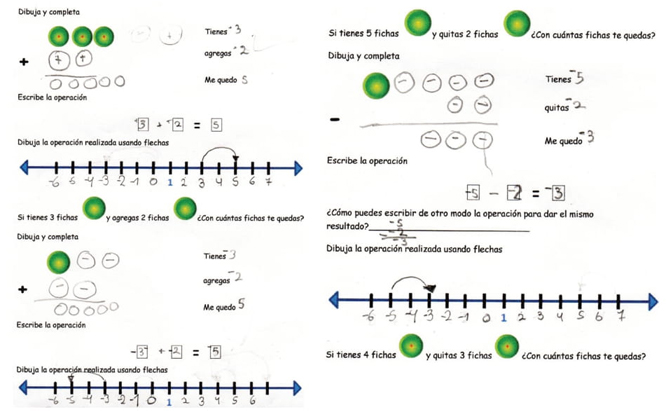
Primero se realiza la adición de enteros, es decir:
Luego en la segunda etapa se realizan actividades para diferenciar el concepto de adición y sustracción de enteros:
La tercera etapa consiste en el desarrollo de la tarea de programar el desplazamiento de un objeto (ratón) para recorrer un laberinto (ver figura 2). Para ello se debe desplazar el objeto en forma vertical u horizontal en el plano cartesiano del escenario de Scratch, para lo cual se debe aplicar la operatoria con números enteros.
Martina tiene conocimientos de programación en Scratch, ya que ha tomado parte activa del taller de robótica, por lo que la propia programación no debe ser vista como una dificultad para el desarrollo de la tarea. Para realizarla debe darse cuenta de la existencia del plano cartesiano, con lo cual para programar el desplazamiento del objeto en el laberinto requiere operar con números enteros en ambos ejes. Ella ha tenido instrucción formal del concepto de plano cartesiano, solamente con números naturales ya que es un contenido de los planes curriculares de cuarto año de Enseñanza Básica.
En la última etapa se realizó una entrevista para mapear la trayectoria del desarrollo de las concepciones de los enteros de los estudiantes.
4. ANÁLISIS Y DISCUSIÓN DE LOS RESULTADOS
Se presentará en primer lugar el análisis y discusión de la primera y segunda entrevista, que se llevaron a cabo en forma previa y de manera posterior a que Martina realizara el conjunto de actividades. En segundo lugar, se presentará el análisis y discusión de los resultados que se obtuvieron de los registros escritos y de las grabaciones de la misma estudiante, al realizar las actividades referidas al desplazamiento del ascensor virtual, al trabajo con fichas. Finalmente, se presenta el análisis y discusión de resultados al realizar la programación para el desplazamiento del objeto recorriendo el laberinto.
4.1 OBSERVACIONES DE LA PRIMERA Y SEGUNDA ENTREVISTA
En la siguiente tabla se presenta de forma resumida, el análisis comparativo de la primera y segunda entrevista, a partir de los resultados de situaciones que se registraron con la estudiante sometida a estudio.
Tabla 1 Análisis comparativo de las entrevistas
| ANÁLISIS COMPARATIVO DE LAS ENTREVISTAS | ||
|---|---|---|
| La primera parte permite determinar si el estudiante tiene conceptos de número negativos en su dominio. La pregunta clave para determinar su dominio de números es: ¿Puedes contar hacia atrás, comenzando desde 5? | ||
| El estudiante puede no saber contar hacia atrás porque no conoce la recta numérica ni tampoco restar -1 por la conceptualización de orden. | ||
| Para que el estudiante contextualice números negativos se presenta una situación conocida mediante un ascensor o los pisos de un edificio. El estudiante puede reconocer los números -1 o -2 pero no asociarlos a la recta numérica. | ||
| Primera entrevista | Segunda entrevista | |
| Martina no tiene preconcepto de número signado, es decir, el signo que precede al número, pero no le asigna ningún significado, solamente lo utiliza para diferenciarlos con respecto de los naturales. Los reconoce porque ve la simbología en la vida cotidiana, por ejemplo, en uso de un ascensor. No tiene claridad del orden a pesar que enumera correlativamente los números al contar en forma descendente. Se puede comprobar al preguntar “Nombra un número pequeño”. Menciona el -5, pero al preguntar por otro más pequeño nombra el 0. | Martina tiene preconcepto de número signado, es decir, el signo que precede al número. Reconoce los números enteros en la cotidiana y los relaciona con la recta numérica, como en el caso del problema 5 cuando se le pregunta por qué no escribió el 0 y responde “No hay piso cero”. Pero si lo hizo en el conteo numérico en la pregunta 3. | |
| Hace la diferencia entre los que son normales (los naturales) y los que llevan un signo menos. Aunque no existen números positivos, ella insinúa que los naturales son de una clase (como si fueran en más) diferente a la otra que contiene el signo menos (como si fueran en menos). No puede decirse que ella entienda estos números como números signados, pues no habla de positivos y negativos. | Reconoce un cierto orden al responder menos diez mil y menos cien mil, a pesar que enumera correlativamente los números a contar en forma descendente. | |
| Hace la diferencia entre los que son normales (los naturales) y los que llevan un signo menos. | ||
| En la segunda parte se le solicita a la estudiante desarrollar expresiones aritméticas, estas expresiones aritméticas permiten determinar el tipo de estrategia o razonamiento que el estudiante aplica para su resolución. Recordemos que estas expresiones aritméticas son la antesala de la conceptualización algebraica. Estos problemas se plantean para confirmar que el estudiante puede resolver expresiones de números abiertos para problemas con términos de números enteros y respuestas de números enteros. La transición de expresiones aritméticas al algebra es un paso importante para llegar a ideas más complejas, que facilitaran procesos matemáticos de nivel superior. | ||
| Primera entrevista | Segunda entrevista | |
| Realiza la operatividad de sumas y resta teniendo en cuenta la noción de número se subordina a la magnitud (en a - b, a es siempre mayor que b donde a y b son números naturales). En la expresión 6 - c=4, opera con elementos concretos utilizando sus dedos. Se observa que invierte el orden del minuendo y sustraendo para poder operar. Esto se comprueba en la expresión c - 4 = 3 donde invierte el orden para obtener el resultado. Se confirma lo anterior en la expresión 3 - 5 = c. Esto se debe a los años de instrucción que ha tenido con operatoria de números naturales y la operatoria de resta. | Realiza la operatividad de sumas y restas teniendo en cuenta la noción de número subordinado a la magnitud (en a - b, a es siempre mayor que b donde a y b son números naturales). Esto lo realiza por procedimiento ya adquirido en la operatoria de naturales durante su enseñanza, se observa en las expresiones c - 4 = 3 , 6 - c=4 y 3 - 5 = c. | |
| El signo “menos” conduce a la estudiante a inventar una resta para darle sentido a estos números. Esta afirmación se comprueba en la pregunta - 3 + 6 = c cuando la estudiante mira la expresión y pregunta por el signo menos de tres. El signo menos lo usa solo para restar cuando el minuendo es mayor o igual al sustraendo, y ambos son números naturales. Por esta razón invierte el orden para responder y se confirma la afirmación en la expresión - 8 + - 3 = c que no puede resolver, aunque invierta el orden de los números. Reconoce el signo “ - “como operación binaria, no como signo unario. | En la expresión c - 4 = 3 se comprueba cuando tiende a realizar la operación como resta invirtiendo los números. Se presenta un obstáculo epistemológico ya tiene conciencia de los negativos y de la necesidad de superarlo esta nueva forma de operar. Se observa que invierte el orden del minuendo y sustraendo para poder operar. Se comprueba al comparar la expresión c - 4 = 3 con la 6 - c = 4, en el modo de resolver dichas expresiones, donde opera con elementos concretos utilizando sus dedos y aplicando una analogía de 4-1=3. Y luego al construir la recta numérica no es capaz de interpretar el significado de -4 como desplazamiento a partir de 1. También lo realiza en el problema 3 - 5 = c tiende a realizar la operatoria subordinando los números a magnitud. Realiza nuevamente una analogía de 5 - 3 = 2. Pero al representar la operación en la recta numérica cuenta los lugares a la izquierda y rectifica su repuesta. Se apoya en el modelo de desplazamiento para rectificar su respuesta. | |
| En el problema 5 - c =8 se tiene un tipo de expresión a- (- b)=c donde a<b a, b ∈ N. A pesar que se trabajó con fichas para representar la sustracción de enteros, solamente se aplicó para el tipo -a- (- b)=c con a > b a, b ∈ N. No puede resolverlo, no tiene claro el inverso aditivo de un número, es decir, -(-a) =a. Para ella es complejo representar esta operación en la recta numérica. A pesar que sabe que debe llegar a 8 tiene que sumar 3 pero no logra visualizar que -(-3)=3 | ||
| La tercera parte consta de problemas de situaciones cotidianas, problemas de contexto, también llamados problemas aditivos de enunciado verbal e implican la resolución de problemas aditivos de números enteros que deben ser modelados mediante estructuras aditivas con números enteros. Uno de los problemas se presenta en el contexto ganar-perder, que tiene poca relación con la representación de la recta numérica. Y los otros problemas, los estudiantes tendrán más éxito cuando emplean la recta numérica ya que la representación en la recta ayuda a razonar la operación que es necesaria para resolver los problemas plateados. | ||
| Primera entrevista | Segunda entrevista | |
| En el problema 18 por desconocimiento de los números negativos como extensión de los naturales, conduce a la estudiante a representar los números naturales en la recta numérica tomando como origen la línea inferior de la figura. | En la resolución del problema 17 es incluso natural para ella que recurre al algoritmo de la adición de números naturales, ya que es posible obtener la solución correcta mediante este procedimiento. Esto nos indica que el contexto deudas, o sea las palabras deber-tener, o ganar- perder no conducen al estudiante a resolver el problema con números negativos. | |
| La respuesta que entrega para este problema no es de extrañar, lo cual indica que conoce o conoce poco la recta numérica siempre que existan números representativos en la figura, los cuales toma como referencia para construir el resto de los otros números, esto se refleja en el problema 19, donde tomó como referencia el -5 para ubicar el 0º C, es decir vincula la cuestión con situaciones cotidianas. Se confirma la afirmación en el ejercicio 5 anteriormente representó los números positivos y negativos tomando como referencia el 1 numerando hacia abajo los negativos partiendo desde el 0, piso que no existe en Chile. | En el problema 18 representa en forma correcta la recta numérica pero no es capaz de realizar la operación referente a la distancia entre las dos magnitudes, es decir, 6-(-5) al igual de lo que ocurre en el problema 19. Resuelve los problemas haciendo uso de la recta numérica, como punto fijo inamovible, esto es, el punto medio de la recta numérica. | |
| En la resolución del problema 17 es incluso natural que ella recurre al algoritmo de la adición de números naturales, ya que es posible obtener la solución correcta mediante este procedimiento. Esto nos indica que el contexto deudas, o sea las palabras deber-tener, o ganar- perder no conducen a la estudiante a resolver el problema con números negativos. | ||
4.2 OBSERVACIONES AL OPERAR EL DESPLAZAMIENTO DEL ASCENSOR VIRTUAL
En la Educación Matemática, el error ha sido objeto de investigaciones, que buscan evidenciar su papel en el proceso de aprendizaje, y con propuestas didácticas, cuyo objetivo es partir del error para estructurar una enseñanza que potencie el aprendizaje, superando el error. El error no se da por desconocimiento, sino por el intento de aplicar determinado conocimiento a una situación diferente de aquella para la cual el citado conocimiento fue concebido, según la teoría de Vergnaud (1990). La construcción del conocimiento está asociada a determinadas situaciones que se dan por medio de un proceso denominado conceptualización. Se puede conjeturar que detrás de un error hay una conceptualización, entendida como el proceso de formación, composición, y elaboración de conceptos.
En esta actividad, las indicaciones de desplazamientos equívocos del ascensor generarán un mensaje de error y, por lo tanto, induce a la reflexión del estudiante para corregirlo. Este es un proceso exhaustivo y que exige atención en la concentración en la determinación de los desplazamientos, dando oportunidad de aprendizaje en la conceptualización de la adición de números enteros.
Martina comete varios errores no forzados en el comienzo de esta actividad del juego como se muestra en la figura 3. Estos se deben a su aprendizaje respecto de la operatoria requerida para establecer el desplazamiento del ascensor, lo que se manifiesta en la cantidad de pulsaciones que hace sobre el botón + para que el ascensor se desplace de nivel, demostrando que el conteo de niveles no es el correcto. Ella cuenta desde el nivel que se encuentra. Por ejemplo, si está en el nivel 3 y debe llegar al nivel 6, pulsa cuatro veces el botón +. Este error lo comete varias veces indicando que no hay una asociación pictórica con la recta y el orden numérico. El error de conteo lo comete tanto para subir como para bajar.
En la figura 4 se muestran las anotaciones que realizó Martina al tratar con las operaciones para determinar los desplazamientos, y se observa que no escribe la operación correcta. En este proceso de conceptualización no asume el significado del signo como unario de los números enteros. Se puede observar que en el 4o y 7o movimiento realiza las operaciones +6 + -4= - 2 y +5+ -5=0. Lo que refleja que asume que más y menos, es menos.
En relación con lo anterior, se le pregunta: "¿Por qué es -2?" Y su respuesta es: "Más, menos es menos", luego borra, lo que evidencia que no asocia los desplazamientos con la recta numérica, representada implícitamente en el ascensor.
En la segunda de estas actividades, comienza a aceptar el signo negativo como unario, es decir, tiende a reconocer que hay otro tipo de número aparte de los naturales, pero no sabe que signo asignar a 0. Hasta el momento le asigna menos como se observa en la figura 4. En las expresiones, no escribe el signo de la operación. Da signo al 0, esto puede deberse a que para ella existe un 1 y un -1, 2 y -2… lo que induce que hay un 0 y un -0, en esta nueva extensión de N.
Al comienzo de las actividades, Martina aplica una estrategia de completar la tabla antes de indicar los desplazamientos del ascensor mediante el conteo. Esto se debe a la motivación de no cometer errores y perder, ya que al momento de subir o bajar el ascensor debe realizar el cálculo. Se le pregunta por esta situación: "¿Por qué estás realizando la tabla?" La respuesta es: "Porque así sé cuánto tengo que pulsar". "¿Cómo lo haces?" Muestra el conteo con los dedos, ver figura 5. Sabe cuándo aplicar las operaciones sumas y cuándo aplicar la de resta. Esto demuestra la adición de naturales, conceptos adquiridos durante los años escolares previos, lo que mostraría arraigamiento de estos conceptos en ella.
Cuando se plantean situaciones con números negativos, Martina ya no puede calcular los valores antes de indicar los desplazamientos, ya que aparecen situaciones como -a + (- b)= -c con a, b, c ∈ N
La determinación de los valores de desplazamiento lo realiza varias veces, para los casos con números negativos. Tiende a pulsar el botón (+) en lugar de pulsar (-). Por ejemplo, para el caso en que el ascensor se encuentra en el nivel -3 y debe desplazarse al nivel -6, pulsa tres veces (+). Martina, tiende a realizar la analogía de 3 + 3 = 6, lo que no es la respuesta correcta. Piensa que es subir, ya que tiende a creer que -6 es mayor que -3. Esto la lleva a cometer errores y a borrar los valores ingresados que no corresponden con los resultados correctos para el desplazamiento.
Una vez construida la tabla (figura 6), responde a la pregunta ¿Cuál es la diferencia con el desafío 1? En la respuesta dada está implícito el concepto de “que sumar números enteros no siempre se obtiene un número mayor”.

Figura 6 Registro de las respuestas de Martina para los niveles negativos y su representación en la recta numérica.
Como se observa, ya no le asigna signo al 0, lo asume como lugar de referencia entre los números positivos y negativos. Esto podría ser un indicio de que ha modificado su estructura cognitiva referida al trabajo con números negativos.
En la figura 7 a continuación, Martina, construye la tabla después de practicar con los desplazamientos del ascensor. Se le pregunta: "¿Cómo te acuerdas de los valores para completar la tabla?" Su respuesta es: "Sumo y resto". "¿Dónde estás?" Su respuesta: "Indica nivel 1". "¿A dónde debes llegar?" Su respuesta: "Al nivel -1", realiza el cálculo y escribe -2. Está asumiendo implícitamente la extensión de los naturales como nuevo conjunto de números negativos.

Figura 7 Registro de Martina del desplazamiento del ascensor para niveles de números positivos y negativos.
En el desarrollo de las actividades se plantean, además, preguntas de reflexión como la que se muestra en la figura 8, en la cual se reafirma el concepto de que “al sumar números enteros no siempre se obtiene un número mayor”.
De lo anterior se desprende que, Martina, ha modificado su campo conceptual respecto a la adición con números.
Para confirmar las conceptualizaciones de número enteros, le realizamos preguntas del tipo: "¿Qué son los números positivos?" Su repuesta es: “Los mayores del cero para arriba”. "¿Y los negativos?" Su repuesta es: “Los menores del cero”. Nótese que en las situaciones planteadas hasta el momento, Martina ha trabajado con la adición de número enteros.
Una vez conocida la operatoria aditiva de números enteros, se le plantea una nueva situación basada en el modelo de neutralización o de equilibrio de enseñanza mediante fichas de colores, adaptado al modelo del ascensor, donde los mismos botones (+) y (-), que se usaron en las situaciones anteriores, ahora sirven de fichas de colores. En este modelo de fichas, enseñar la sustracción de números enteros es más simple. Se basa en las preconcepciones que los estudiantes tienen respecto al ganar-perder. El modelo es adaptado en términos de agregar o quitar energía, es decir, el ascensor debe ganar energía para subir o debe perder energía para bajar.
En esta actividad con fichas, se trabaja, primeramente, la adición y luego la sustracción de enteros negativos. Es decir, se comienza resolviendo situaciones del tipo a + b y -a + (- b) con a, b < 0 para luego introducir situaciones a - b, -a -(-b) con a>b. El objetivo es lograr que la estudiante conceptualice que a + b = a - -b, es decir, el concepto aplicado de -(-b) = b, en la recta numérica, el inverso aditivo de un número b es -b.
En la figura 9 se observa que, Martina, logra realizar operaciones de adición en los conjuntos de fichas de igual signo, representando esta operación en la recta numérica. Esto evidencia que el conocimiento adquirido, lo aplica a esta nueva situación. Aquí se reflejan elementos de la teoría de Vergnaud, en el sentido de que en la medida que Martina va tratando de resolver distintas situaciones con estos nuevos números, va modificando su campo conceptual.
Para la sustracción de números enteros se plantean situaciones en forma análoga al caso anterior, pero para casos a - b, -a - (- b) con a>b. En la anterior, se observa cómo Martina resuelve la situación planteada.
A pesar de que, Martina, representa en forma correcta la operatividad de números, en la pregunta: "¿Cómo puedes escribir de otro modo la operación para dar el mismo resultado?" Responde escribiendo conforme a la instrucción formal que ha tenido en los años anteriores, para resolver restas de naturales, según se muestra en la figura 9, sobre la recta numérica en el lado derecho de la imagen. Esta forma de escribir la respuesta podría estar inducida por la asociación que hace con el dibujo que completó anteriormente en la misma actividad.
4.3 OBSERVACIONES AL REALIZAR LA PROGRAMACIÓN PARA EL DESPLAZAMIENTO DEL OBJETO DENTRO DEL LABERINTO
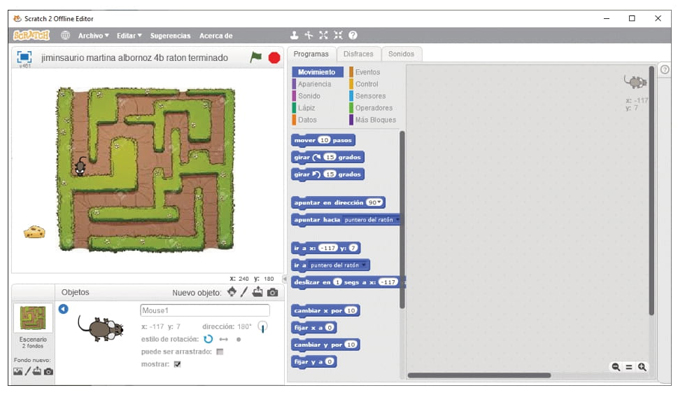
En la figura 10 se muestra la actividad, que consiste en desarrollar la programación en Scratch para conseguir que el objeto ratón, haga el recorrido a través de un laberinto.

Figura 10 Entorno de trabajo en Scratch para la actividad de desplazamiento del ratón en el laberinto.
Scratch presenta en el escenario un plano cartesiano donde el centro de este es el origen (0,0), esta es una de sus características que aprovecharemos para tratar de inducir en Martina la extensión del plano cartesiano que conoce solamente con valores naturales. Tal como señalan Gallardo y Velázquez (2011), los negativos son necesarios para describir completamente el plano cartesiano y las figuras planas con toda su extensión, cuando se trabaja con ecuaciones lineales. Se recuerda que, en la asignatura de matemáticas de cuarto año de Enseñanza Básica, los estudiantes solamente identifican y dibujan puntos en el primer cuadrante del plano cartesiano, por tratarse de coordenadas en números naturales.
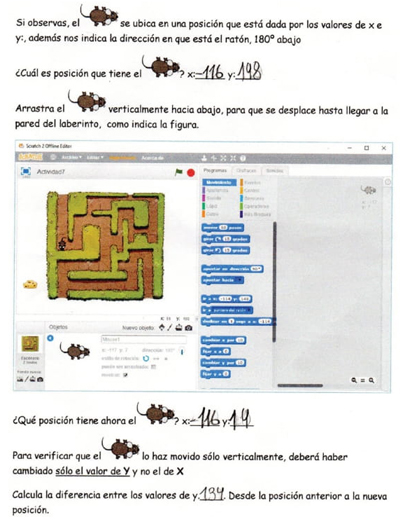
En esta situación, se le presenta a Martina el desafío de ubicar un ratón en una de las entradas del laberinto, y determinar sus coordenadas del punto de partida, para luego desplazarlo vertical u horizontalmente a una nueva posición para realizar el recorrido del laberinto. Para realizar este desplazamiento debe tener presente, que uno de los valores de coordenadas ha cambiado. El desplazamiento del ratón debe ser programado en función al cálculo de la distancia (concepto implícito del valor absoluto).
Martina lee las instrucciones, ubica el ratón al comienzo del laberinto y determina las coordenadas de partida del ratón. Se le pregunta: "¿Cómo sabes cuánto debe desplazarse el ratón?" Su repuesta es: “Cuando baja, debe quedar este igual (al tiempo que muestra la variable x), y cambia la y porque se mueve vertical”.
Luego Martina realiza la diferencia entre los valores de 148 - 14 como se muestra en la figura 11.
Se le pregunta a Martina nuevamente: "¿Cómo obtuviste los valores?" Su repuesta es: “Empecé desde acá arriba, bajé y tenía que cambiar solamente la y. Luego tenía que restar para saber cuánto es la diferencia. Después para ir al otro lado debo girar el ratón, y desplazar horizontalmente para cambia x”.
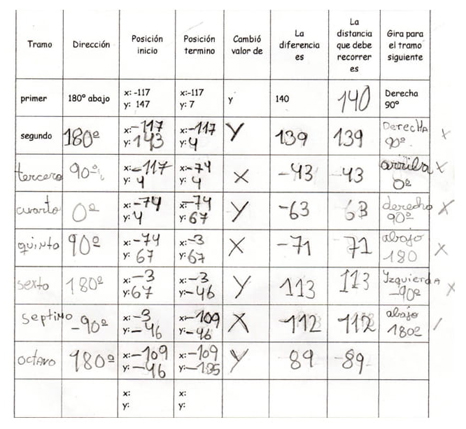
En la figura 12 se observa que, para calcular la diferencia entre los valores toma como minuendo el valor obtenido de la izquierda y como sustraendo el de la derecha. Martina, tiene problemas en la programación, específicamente con los valores negativos, ya que al ser programados con signo menos el movimiento del ratón ocurre en sentido contrario a lo que esperaba. Luego de varios intentos se da cuenta que es la distancia lo que debe calcular y borrar los signos. Aquí está en juego el concepto de diferencia y distancia recorrida, que es la antesala del concepto de valor absoluto.
La operación -3 - (-109) (correspondiente al séptimo y octavo tramo de recorrido del laberinto), la realizó utilizando la aplicación calculadora del sistema operativo. Asumiendo número signado. El acto de ignorar el signo (-) es parte de lo que ocurrió con los matemáticos en la historia, como señalan las investigaciones de Gallardo y Basurto (2010); Cid (2003) (2015), y que también se da en el proceso de la conceptualización que lleva a la aceptación de los números enteros.
5. CONCLUSIONES
Introducir el concepto de números negativos en los estudiantes requiere provocar un cambio en la concepción sobre el número, la cual está profundamente arraigada como resultado de su instrucción formal en relación a los números naturales. Cuando se enfrentan a situaciones que involucran números negativos, se producen cambios conceptuales y de procedimiento que implican el uso de sus conocimientos respecto de los números, es decir, cuando se encuentran con números menores que cero, se produce un rechazo a la aceptación de estos, ya que no tienen un contexto concreto que les permita asimilar y reconocer la existencia de estos. La mayoría de los estudiantes que no están familiarizados con el número como algo concreto experimentan un desequilibrio en su pensamiento cognitivo. Conforme a las evidencias encontradas para el caso de Martina, ella mantiene la concepción de que los números son solo positivos, negando, en principio, la posibilidad de que pueden ser negativos. Sin embargo, al crear situaciones virtuales en contextos que son familiares para ella, reconoce la existencia de estos, sin haber tenido un tratamiento matemáticamente formal respecto de estos números.
Según el resultado del estudio se confirman las dificultades que presentó la estudiante para comprender el número negativo, estos obstáculos se fueron exponiendo en el desarrollo de cada una de las situaciones que la estudiante debió enfrentar. El principal obstáculo que enfrentó, es el relacionado con la aceptación de la existencia de los números negativos. En la primera entrevista manifiesta que reconoce el número solo como un símbolo formal en matemáticas, pero no se da cuenta de que la actividad diaria es la encarnación del número mismo. La naturaleza abstracta del número negativo se convierte en el principal obstáculo epistemológico.
En las fases de interpretación y validación de las situaciones adidácticas en los distintos contextos en que Martina trabajó, le permitió aprender mediante del error, manifestándose como obstáculo epistemológico, llegando a repuestas correctas a partir de las transformaciones conceptuales de la operatoria con números enteros, que se describían en cada situación por medio de una representación pictórica. Logra identificar los números con signos, potenciando su aprendizaje de los números enteros de manera significativa. A la luz de los resultados, la interacción a través de una situación que era familiar para ella, y luego desarrollar la programación en Scratch del desplazamiento del objeto dentro del laberinto, representaron buenas oportunidades para extender su conocimiento en la conceptualización numérica.
Durante el desarrollo de la investigación se observó que, Martina, utilizó el procedimiento de operación de conteo, comprobando que tenía una percepción falsa cuando resuelve operaciones solo con números negativos. Este error de contar no es efecto de la ignorancia, como señala Brousseau (2007), sino que es el efecto del conocimiento adquirido de los números naturales que se reveló inadecuadamente para el caso de los números negativos.
Se muestra en el estudio que, Martina, realizó operatoria de adiciones y sustracciones con números positivos y negativos, trabajando con expresiones de la forma a+(-b) = a -b. Este hecho manifiesta un retorno a los números naturales que le son familiares y abandona los números signados. La aceptación del signo negativo se limita al reconocimiento de este como número sustractivo. Esta condición fue variando en el transcurso de la investigación, evidenciándose que el aprendizaje de números negativos no es una intuición que emerge naturalmente, tal como lo experimentaron los matemáticos en la historia.
Respecto a la última pregunta de investigación, se comprueba que no existen diferencias importantes entre el camino histórico seguido por los matemáticos para la aceptación de los números negativos, y el camino que siguió la estudiante. Sin embargo, es aventurado generalizar los resultados de esta investigación, para afirmar que todos los estudiantes se comportarían de forma similar a los matemáticos históricos. Se está consciente de la necesidad de una investigación más amplia para poder profundizar en las características de estos procesos.
Nos parece interesante, desde una perspectiva metodológica y didáctica, lo que se ha hecho evidente en esta investigación, en el sentido de que Martina logró trabajar con números negativos, a partir de situaciones concretas y contextualizadas que tuvo que resolver, sin antes haber tenido un tratamiento matemáticamente formal de los mismos. Esto puede ser especialmente relevante para tener en consideración cuando en la asignatura de matemática se trate con conceptos que son abstractos, lo que generalmente ocurre en los niveles iniciales de escolarización (cuarto año de Enseñanza Básica en este caso).











 nueva página del texto (beta)
nueva página del texto (beta)