1. INTRODUCCIÓN
El interés por encontrar formas efectivas de estudiar el conocimiento profesional del profesor y comprender los procesos de adquisición, uso y desarrollo de este, lleva a los investigadores a realizar distintas propuestas que permitan indagar sobre la labor del profesor, vista esta como la práctica de un profesional que requiere de conocimientos específicos.
Existen distintos parámetros utilizados para diferenciar las componentes del conocimiento profesional, definidas en función de cómo se genera, sobre qué versa o para qué sirve dicho conocimiento. Shulman (1986), por ejemplo, propone una separación del conocimiento del profesor en tres componentes: el Subject Matter Knowledge, que incluye el conocimiento que requiere el profesor del qué y el porqué de los contenidos referentes a la disciplina que enseña, el Pedagogical Content Knowledge (PCK), que alude a los aspectos de conocimiento referentes a la enseñanza y aprendizaje del contenido que se imparte, y el Curricular Knowledge, que se refleja en los programas, materiales, planeaciones que tienen los profesores. Shulman (1987) destaca el PCK como un elemento de especial interés “because it [. ] is the category most likely to distinguish the understanding of the content specialist from that of the pedagogue” (p. 8).
Con esta propuesta, Shulman provoca un especial interés por profundizar en la comprensión de elementos que conformen el conocimiento profesional de un profesor, de manera que se tenga una mejor conceptualización del constructo y de sus características como un conocimiento propio de la labor de enseñanza (e.g. Carpenter, Fennema, Peterson y Carey, 1988; McDiarmind, Ball y Anderson, 1989). Además, surge la necesidad de buscar características específicas de este conocimiento asociadas al contenido a enseñar, lo que ha llevado a la construcción de modelos de conocimiento que pretenden organizar, definir y analizar los elementos que lo conforman.
Con respecto al conocimiento profesional del profesor de matemáticas, existen distintas propuestas de modelación de dicho conocimiento (e.g. Knowledge Quartet, Rowland, Turner, Thwaites y Huckstep 2009; Mathematical Knowledge for Teaching, Ball, Thames y Phelps, 2008; Proficiency in Teahing Mathematics, Schoenfeld y Kilpatrick, 2008; Profound understanding of fundamental mathematics, Ma, 1999). Esta variedad de modelos pone de manifiesto la complejidad de interpretación y comprensión de la naturaleza de dicho conocimiento, así como la necesidad de establecer mecanismos para operativizar e identificar elementos clave que permitan su análisis.
Dentro de todas estas propuestas y caracterizaciones, a más de 30 años de distancia, el PCK sigue teniendo un papel relevante como uno de los elementos esenciales para la descripción y análisis del conocimiento profesional. A pesar de que las categorías propuestas inicialmente por Shulman han sido reinterpretadas, estas continúan siendo vigentes y siguen siendo consideradas un avance importante en las concepciones sobre el conocimiento del profesor (Vázquez-Bernal, Jiménez-Pérez y Mellado, 2019; Depaepe, Verschaffel y Kelchtermans, 2013).
Sin embargo, la caracterización de este conocimiento depende, en gran medida, de los fundamentos sobre los que se construye el modelo, que suelen quedar ocultos bajo la sombra del modelo mismo y las definiciones de sus componentes.
En este sentido, consideramos importante reflexionar sobre los cambios y/o adaptaciones que sufre el PCK al considerarse parte de un modelo de conocimiento que tiene una filosofía, identidad e intencionalidad propia. Esto proporcionará al lector la posibilidad de adentrarse en este proceso de construcción de un modelo y de la caracterización y adaptación del PCK.
La relevancia de esta propuesta radica en someter a discusión de la comunidad las bases teóricas y metodológicas bajo las cuales se construye esta caracterización, a la luz del modelo de conocimiento especializado del profesor de matemáticas (Mathematics Teacher’s Specialised Knowledge -MTSK-,Carrillo-Yañez, et al., 2018). Consideramos que esta podrá enriquecer la reflexión sobre la utilidad y vigencia del PCK como piedra angular del conocimiento profesional del profesor, así como la discusión sobre la utilidad del MTSK y otros modelos como herramienta de análisis del conocimiento del profesor de matemáticas.
Es importante señalar que, aunque se han presentado otros análisis parciales de algunos de los datos recopilados en esta investigación, estos han estado enfocados a reflexionar sobre el tipo de conocimientos especializados que manifiesta el informante a lo largo del curso (e.g. Escudero-Ávila, et al., 2015) y a resaltar las relaciones existentes entre distintos subdominios de conocimiento (e.g. Carrillo-Yañez, et al., 2018). Sin embargo, en este trabajo nos enfocamos en la descripción del proceso de construcción, justificación y refinamiento de categorías realizado a partir del análisis de este caso. El interés en el contenido matemático concreto queda en un segundo plano, tratándose de un instrumento de trabajo que nos permita ilustrar los subdominios, validar la construcción del modelo y refinar categorías.
2. BASES METODOLÓGICAS
Para definir y caracterizar los elementos del conocimiento didáctico se realizó un estudio de caso de tipo instrumental (Stake, 1995), puesto que la información que nos proporciona el informante sirve para realizar un proceso de abstracción que permita aportar información adicional sobre el funcionamiento y la caracterización del conocimiento profesional del profesor de matemáticas. En este sentido, hemos decidido adoptar un enfoque cualitativo de análisis y posicionarnos en un paradigma interpretativo (Bassey, 2003).
El caso a estudiar se define como el conocimiento especializado del profesor de matemáticas de secundaria que participa en un programa de formación continua a distancia (online). Omar, nuestro informante, es un profesor colombiano de matemáticas de secundaria y bachillerato con más de 25 años de experiencia, que participaba activamente en el curso virtual Teoría de Situaciones Didácticas desarrollado en el seno de un programa de Posgrado en Matemática Educativa (maestría profesionalizante con sede en México).
A lo largo de cinco semanas, Omar realizó aportaciones y reflexiones sobre su trabajo y el de sus compañeros en foros, ensayos y actividades compartidas a través de la plataforma Moodle y por correo electrónico. Uno de los tutores del curso y autor de esta investigación, dio seguimiento y retroalimentación constante al profesor sobre las tareas que se le pedían en concordancia con los objetivos del curso. Una vez terminado el curso, se reconoce la relevancia de la información generada y el potencial para analizar, de estos datos, el conocimiento especializado del profesor en distintos contextos, por la riqueza en cuanto a la justificación matemática y didáctica que Omar vertía en sus participaciones. Se descargaron en formato pdf, y se organizaron y analizaron cinco actividades realizadas, una por semana, en las que se produjeron un total de siete documentos de texto con siete tareas individuales de Omar (A#_ D#) y tres foros de discusión (A#_ F#_P#) en los cuales el profesor interactuaba con otros compañeros de curso y que se separaron en siete conversaciones diferentes. Estos se organizaron y codificaron por actividad y documento como se muestra en la Figura 1.
Dado que las actividades se proponían de acuerdo a la temática del curso, el contenido matemático sobre el que se discute cambia a lo largo de las semanas, aunque se dedica especial atención al desarrollo de una secuencia didáctica que Omar propone centrar en el desarrollo de conocimientos sobre las funciones lineales y cuadráticas. Son estas participaciones y actividades las que utilizaremos en este estudio para ilustrar la caracterización del PCK (Actividades 2, 4 y 5).
Los textos utilizados, para ejemplificar y justificar la caracterización de los subdominios y categorías del PCK en este artículo, han sido modificados con respecto a las participaciones literales de Omar dentro de este curso virtual. Esto con la intención de proporcionar al lector la mayor cantidad de evidencias sobre el conocimiento de Omar y resumir la información que se recolecta a lo largo de cinco semanas de trabajo. Se ha puesto especial atención en crear textos con sentido narrativo que mantengan la literalidad y esencia del discurso en relación con el objeto de estudio. Pueden consultarse los datos completos y codificados en Escudero (2015).
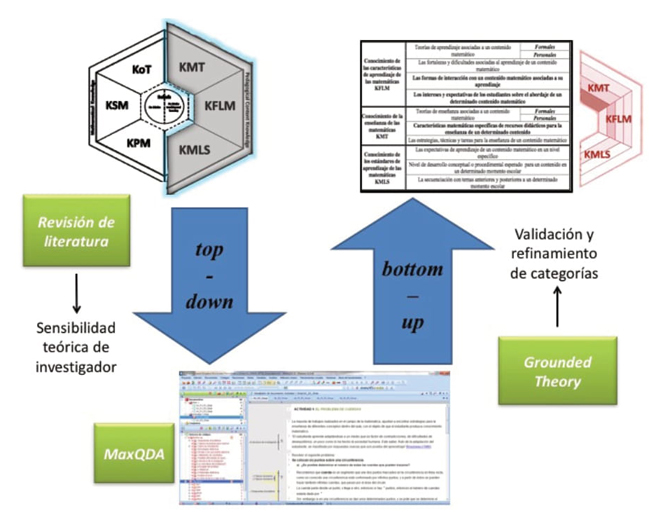
Al respecto del diseño metodológico, inicialmente se utilizó el método top-down: de la teoría a los datos (Niss, 2006), generando una caracterización teórica y muy general del PCK, para lo cual se revisaron y sistematizaron distintas aproximaciones y definiciones de este tipo de conocimiento en la literatura especializada, partiendo de las aportaciones y críticas sobre el modelo de Shulman (e.g. Vázquez-Bernal, et al., 2019; Depaepe, et al., 2013; Flores-Medrano, et al., 2016; entre otros). Apoyados en esta reflexión y en los principios teóricos bajo los cuales se concibe la construcción del MTSK, decidimos imprimir especial énfasis en el reconocimiento de las diferencias entre la naturaleza de este dominio y la del dominio del conocimiento matemático, tomando en cuenta las distinciones en cuanto a los criterios de validez, los procesos de construcción de conocimiento asociados a estos, así como su expresión o manifestación, lo que implica diferentes vías para acceder a ellos. En la siguiente sección entraremos más en detalle en este proceso de construcción.
Posteriormente, recurrimos a una aproximación bottom-up: de los datos a la teoría (Niss, 2006), en la cual se complementa y reinterpreta la definición de los subdominios y sus componentes a la luz del análisis de las producciones de Omar. Además, en este proceso se complementa esa primera caracterización teórica para refinar el modelo con la aportación de categorías específicas de conocimiento (Figura 2), que nos permitan tener una visión más particular de las formas de conocer el contenido que un profesor de matemáticas puede tener y las cuales, en conjunto, le permitirán actuar como un especialista de la educación matemática.
Como explicamos, la metodología top-down y bottom-up utilizada en esta investigación demandaba la generación de categorías de análisis de los datos y su comparación constante. La cantidad de información generada durante el curso y el número de categorías que se utilizaron para el tipo de análisis propuesto requirió del uso del software MAXQDA, como un instrumento que permitía hacer asignaciones de categorías de forma simple y ordenada, haciendo referencia a cualquier tipo de unidad de información (episodios, fragmentos de episodio, frases o palabras una asignación), triangulando distintos momentos del curso y así obtener un análisis lo más completo posible.
3. BASES TEÓRICAS
3.1. EL MODELO CONOCIMIENTO ESPECIALIZADO DEL PROFESOR DE MATEMÁTICAS
Describimos a continuación, de forma sucinta, elementos característicos del modelo de Conocimiento Especializado del Profesor de Matemáticas (Mathematics Teacher’s Specialised Knowledge -MTSK-, Carrillo-Yañez, et al., 2018) con el propósito de contextualizar el proceso de construcción de la caracterización del PCK que se aborda en este estudio, así como explicitar concepciones al respecto del conocimiento profesional del profesor subyacentes en el modelo.
El MTSK es una herramienta teórico-analítica que clasifica aquellos elementos del conocimiento del profesor donde la matemática, como objeto de enseñanza y aprendizaje, es determinante, excluyendo el conocimiento pedagógico general, aunque, naturalmente, reconoce su relevancia (Carrillo-Yañez, et al., 2018).
El conocimiento es entendido en este modelo como una amplia red de conceptos, imágenes y habilidades inteligentes que poseen los seres humanos (Pajares, 1992), disponibles para “usar para resolver problemas, alcanzar metas, o desarrollar cualquier tarea. ¡Nótese que, de acuerdo a esta definición, el conocimiento no ha de ser necesariamente correcto!” (Schoenfeld, 2010, p. 25). La diferencia entre conocimiento correcto o incorrecto es irrelevante si la intención del investigador es saber qué y cómo conoce el profesor, ya que esa es la información que el profesor posee, coincida esta con el referente de verdad del investigador o no. Este posicionamiento responde a la necesidad de crear un modelo de conocimiento que no sea prescriptivo sino descriptivo, con la intención de interpretar el conocimiento desde un punto de vista integral, tomando en cuenta la naturaleza del Conocimiento Matemático (CM) y el Conocimiento Didáctico del Contenido (CDC) y las diferencias que existen en cuanto a los criterios de validez.
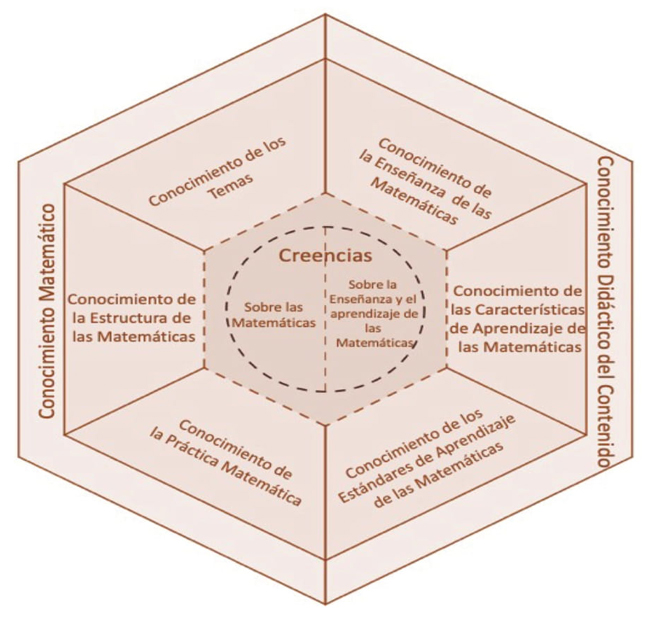
La idea de especialización inspirada en la propuesta que hacen Ball y colaboradores (2008) para el Mathematical Knowledge for Teaching (MKT), se entiende en el MTSK como la integración de los tres grandes dominios vinculados a la enseñanza de las matemáticas (Figura 3): los conocimientos matemáticos (CM), los conocimientos didácticos del contenido matemático (CDC)4 y las creencias y concepciones que tiene el profesor acerca de las matemáticas, su aprendizaje y enseñanza (Carrillo-Yañez, et al., 2018). Mientras que en MKT la especialización se refiere a la exclusividad de uso de conocimiento matemático por parte del profesor frente a otros profesionales, en MTSK procede del uso conjunto de elementos de conocimiento en la enseñanza de las matemáticas, independientemente de que algunos de esos elementos se compartan o no con otros profesionales.
Según Ma (1999) y Schoenfeld, et al. (2008), es evidente la necesidad de que el profesor conozca de manera amplia y profunda el contenido que enseñará. En este sentido el dominio de CM incluye el Conocimiento de los Temas que tiene el profesor sobre las propiedades, definiciones y significados del contenido matemático de manera fundamentada, los procedimientos (cómo se hace, cuándo puede hacerse, por qué se hace así), los distintos registros de representación asociados a dicho contenido, la fenomenología, y aspectos epistemológicos que permiten al profesor comprender diferentes significados atribuibles al contenido. El Conocimiento de la Estructura de la Matemática engloba conocimientos de conexiones inter-conceptuales y conocimientos avanzados y elementales (con respecto al contenido que se atiende). Por último, se incluye un subdominio de Conocimiento de la Práctica Matemática, referente al conocimiento sobre las formas de proceder propias de la matemática, así como, por ejemplo, sobre distintos tipos de razonamientos, incluyendo los contextos matemáticos en que unos son más adecuados que otros (Carrillo-Yañez, et al., 2018).
Otra de las características distintivas de este modelo es la consideración de un dominio de creencias, dejando de manifiesto que estas permean el conocimiento matemático y didáctico del profesor. En este sentido, las creencias y las concepciones sobre la matemática y sobre su enseñanza y aprendizaje en el MTSK serán entendidas como verdades personales, sostenidas individual y/o colectivamente, derivadas de la experiencia o el propio pensamiento, puesto que están basadas en componentes afectivas y evaluativas, sobre las que se pueden tener diferentes grados de convencimiento (Thompson, 1992). Estas pueden, además, estar justificadas con argumentos que no sigan criterios que puedan responder a cánones de evidencia, es decir, no son falsables.
3.2 CONOCIMIENTO DIDÁCTICO DEL CONTENIDO COMO PARTE DEL MTSK
Mostraremos a continuación la fundamentación teórica con la cual se caracteriza el CDC dentro del MTSK, que sirvió para definir subdominios y construir categorías.
En la fase de trabajo top-down se reconoce la importancia que tiene el conocimiento didáctico matemático dentro del MTSK por contar con una entidad propia, con fuentes y referentes diferentes a las del conocimiento puramente matemático. Posee una estructura y naturaleza distintas, puesto que, como menciona Azcárate (1998), está dirigido a la enseñanza de las matemáticas, cuya fuente principal vive en la Didáctica de la Matemática como cuerpo de conocimiento integrador en sí mismo de diversas fuentes de conocimiento.
Parte del proceso de caracterización del CDC dentro del MTSK consistió en la sistematización y análisis de literatura especializada en el desarrollo, comprensión, caracterización y/o reflexión sobre le PCK definido por Shulman y reinterpretado por otros investigadores (e.g. Azcárate, 1998; Ball, et al., 2008; Mitchell, Charalambous y Hill, 2014; Pinto y González, 2008). Consideramos de modo especial el trabajo de Depaepe y colaboradores (2013), cuyo objetivo fue proporcionar una revisión sistemática de la investigación educativa matemática empírica para responder a ¿cómo se conceptualiza y cómo se analiza el PCK en la investigación educativa matemática empírica?
En esta primera revisión se encontró que no existen diferencias claras entre las habilidades o capacidades del profesor y sus conocimientos (Muñoz-Catalán, 2010), por lo que, en el MTSK se caracteriza el PCK como un conjunto de conocimientos, destrezas y habilidades que los profesores necesitan y aplican en el acto de enseñar, ligados directamente con la práctica de aula como actividad principal y a un contenido específico (Depaepe, et al., 2013). Esta definición está en concordancia con la definición de conocimiento, bajo la cual se desarrolla el MTSK y su naturaleza de conocimiento parcialmente tácito, situado, contextualizado, personal, social, dinámico, integrado, complejo y práctico (Climent, 2002; Muñoz-Catalán, 2010).
Como hemos señalado, aunque se han establecido pautas que ayudan a identificar algunas de las componentes de este conocimiento o posibles formas en las que puede desarrollarse, todavía existen discrepancias con respecto a su caracterización. Aun así, Depaepe y colaboradores (2013) identifican algunas componentes de estos conocimientos que surgen en diferentes modelos y aproximaciones teóricas:
[...] (1) knowledge of students’ (mis)conceptions and difficulties, (2) knowledge of instructional strategies, (3) knowledge of mathematical tasks and cognitive demands, (4) knowledge of educational ends, (5) knowledge of curriculum and media, (6) context knowledge, (7) content knowledge, and (8) pedagogical knowledge (p. 15).
Este primer acercamiento a la literatura, junto con la filosofía de base de MTSK que pone en el centro el contenido matemático y deja fuera elementos de conocimiento pedagógico general y de contexto, conduce a una caracterización del CDC organizada a través de tres tipos básicos de conocimiento: el conocimiento del contenido matemático como objeto de aprendizaje, el conocimiento del contenido matemático como objeto de enseñanza y el conocimiento de la organización o secuenciación del contenido matemático desde una visión general de los estándares y objetivos de aprendizaje. A continuación, definimos y ejemplificamos cada subdominio con sus respectivas categorías, poniendo especial énfasis en el proceso de creación y validación de estas.
3.2.1 Subdominio del conocimiento de las características del aprendizaje de las matemáticas (Knowledge of Features of Learning Mathematics-KFLM)
Como hemos visto hasta ahora, distintos autores y modelos de conocimiento expresan la necesidad de identificar los conocimientos que permiten al profesor reconocer, analizar y comprender determinados procesos de aprendizaje de las matemáticas y entender su génesis, lo cual deriva en la capacidad de interpretar las producciones de los estudiantes y anticipar posibles razonamientos, conocer errores frecuentes, dificultades de aprendizaje recurrentes o las concepciones erróneas que podrían tener sus estudiantes.
El foco central del KFLM está en reconocer al contenido matemático como objeto de aprendizaje, por lo que decidimos centrar la atención en los conocimientos del profesor sobre las características de aprendizaje inherentes a un contenido matemático en particular o a la matemática en general. Sus elementos no están orientados hacia el conocimiento de los estudiantes como actores principales en el proceso de aprendizaje. Aunque reconocemos que este enfoque podría restar importancia al papel del estudiante en dicho proceso, resulta necesario focalizar nuestra atención en un aspecto específico del conocimiento profesional del profesor como lo son las características de aprendizaje derivadas de su interacción con el contenido matemático y las características del contenido matemático en sí mismo como objeto de aprendizaje. Esta relación estudiante-contenido pone el énfasis en el conocimiento que tiene el profesor del propio proceso de aprendizaje al observar y analizar las interacciones del estudiante con el contenido matemático (Flores-Medrano, Escudero-Ávila, Montes y Carrillo, 2015).
Con esta definición y basados en literatura de investigación (enfoque top-down), decidimos establecer una primera propuesta de categorías para este subdominio de conocimiento: Errores y dificultades asociados al aprendizaje de un contenido matemático, formas de interacción de los estudiantes con un contenido matemático, intereses y expectativas de los estudiantes y teorías de aprendizaje asociadas a un contenido matemático.
Al respecto de la categoría de errores y dificultades asociadas al aprendizaje de un contenido matemático, es innegable la necesidad de reflexión sobre las posibles dificultades, errores u obstáculos que pueden surgir en los procesos de aprendizaje de un determinado contenido.
En la fase de análisis correspondiente al proceso bottom-up Omar, pone de manifiesto el siguiente conocimiento:
O: La importancia del aprendizaje de la función radica en su papel como herramienta modeladora de fenómenos matemáticos, físicos, químicos, económicos, etcétera. Sin embargo, hay que considerar la complejidad que supone, en este proceso de aprendizaje, la variedad de representaciones que tiene el concepto en diferentes contextos y su forma algorítmica.
Además, Mitchell y colaboradores (2014) presentan un estudio empírico del que concluyen que el conocimiento que requiere el profesor para usar distintas representaciones de un determinado contenido implicadas en diferentes tareas de enseñanza no pertenece únicamente al dominio didáctico, puesto que se requiere articular conocimientos que permitan reconocer las representaciones como recurso para la instrucción y las posibles formas en las que este será usado por los estudiantes, además de reconocer las características matemáticas específicas del recurso. En este sentido, conocer los diferentes tipos de representación de las funciones no implica directamente conocer las dificultades que existen en el aprendizaje de estas, ni conocer estrategias específicas de utilización de una determinada representación, con lo cual es importante hacer una distinción entre el conocimiento profesional del profesor que es puramente matemático (representación de las funciones) y el que es didáctico matemático (dificultades en el aprendizaje de las funciones).
Aunque Omar no lo mencione (incluso lo desconozca), existe literatura en la que se reporta este tipo de dificultades (e.g. Viseu y Menezes, 2014), lo que justifica su inclusión en esta categoría como una dificultad u obstáculo típico relacionado con el contenido mismo. Este conocimiento está ligado directamente al concepto de función, sin embargo, no es conocimiento matemático, sino conocimiento sobre características de este contenido como objeto de aprendizaje.
Por otra parte, el profesor reconoce la importancia que tiene el aprendizaje de este contenido ligándolo con su papel como herramienta de modelación matemática. Esto es importante porque no es el conocimiento de un error o una dificultad asociada a este contenido, sino que podría representar quizá hasta un área de oportunidad para desarrollar ciertos aprendizajes alrededor de este contenido, es decir, valerse de la idea de modelación para trabajar el contenido y potenciar su aprendizaje.
Omar, nos permite reconocer la importancia que tiene que el profesor tenga conocimientos tanto de dificultades como de fortalezas que pudieran estar asociadas a este contenido matemático, de manera que sus herramientas de trabajo profesional se vean enriquecidas, por lo que esta categoría se redefine como: conocimiento de las fortalezas y dificultades asociadas al aprendizaje de un contenido matemático.
A pesar de que la fuente más común de este tipo de conocimiento es la propia experiencia profesional, existe ya una creciente cantidad de investigación cognitiva sobre el aprendizaje del estudiante, que ha producido resultados enfocados, tanto en procesos y algoritmos alternativos de trabajo matemático como en la identificación de concepciones, errores, obstáculos y dificultades de los estudiantes y de su pensamiento matemático.
En la categoría de formas de interacción de los estudiantes con un contenido matemático, se engloban los conocimientos del profesor sobre los procesos y estrategias, tanto los típicos como los no habituales (Sosa, Aguayo y Huitrado, 2013), que podrían seguirse al enfrentar una determinada tarea matemática, así como conocimientos sobre el lenguaje y los procesos a través de los cuales los estudiantes interactúan con el contenido matemático (Flores-Medrano, et al. 2016).
En el caso de Omar, podemos validar esta categoría con evidencias de que el profesor tiene conocimiento de que los estudiantes realizarán ciertos procesos de trabajo matemático asociados a las diferentes representaciones de la función:
O: Al pasar del registro algebraico al gráfico espero que los estudiantes puedan establecer relaciones de variable dependiente con independiente, y que se observe cómo modelar el fenómeno a partir de este recurso gráfico. A través de la tabulación y utilizando métodos como el de solución de ecuaciones simultáneas o el método de diferencias pueden determinar los parámetros de las funciones partiendo de datos dados, con esto pueden proceder a graficar en papel o en hoja milimétrica.
Estas evidencias nos permiten resaltar que Omar tiene un conocimiento de ciertas formas de interacción con el contenido matemático, pero además nos indica que estas formas deben estar ligadas al aprendizaje de este contenido, en este caso el aprendizaje de función. Omar posee conocimiento de que, al pasar de un registro a otro, los estudiantes establecen ciertas relaciones y pueden observar diferentes características de la función, así como asignarle distintos significados.
Esto nos permite reinterpretar el nombre de la categoría como: formas de interacción con un contenido matemático asociadas a su aprendizaje.
En el KFLM se incorpora también la categoría de conocimiento del profesor sobre intereses y expectativas de los estudiantes sobre el abordaje de un determinado contenido matemático. En el caso del conocimiento puesto en evidencia por Omar, se hace evidente que el profesor sabe que la modelación de fenómenos físicos resulta atractiva y motivadora para los estudiantes, puesto que permite generar en ellos un interés en explicar el comportamiento del fenómeno y contextualizar el trabajo matemático que realiza:
O: Las actividades más llamativas para los estudiantes son aquellas que tienen relación con las ciencias naturales, como las relacionadas con caída libre, movimientos y, aquellas donde la medición interviene de una manera primaria. Si se toma a la modelación como herramienta matemática para la solución de problemas reales, es posible realizar simulaciones, aplicando el modelo matemático hallado a situaciones diferentes, favoreciendo que el estudiante las utilice en otras áreas del conocimiento.
Por lo tanto, en esta categoría se valida la necesidad de tomar en consideración los conocimientos del profesor sobre estas expectativas e intereses, así como el conocimiento sobre las preconcepciones de facilidad o dificultad asociadas comúnmente a las distintas áreas de la matemática.
La última categoría a incorporar en este subdominio se refiere al conocimiento sobre teorías de aprendizaje, el cual se refiere a lo que sabe el profesor sobre literatura referente a la Educación Matemática como disciplina científica, específicamente resultados al respecto del aprendizaje de los contenidos matemáticos. Aunque la literatura especializada se menciona como fuente de conocimiento, no se incorpora, en ningún otro modelo que hayamos revisado, su consideración como categoría o subdominio de conocimiento. Sin embargo, esta distinción parece práctica y necesaria puesto que nos permite saber cómo usa el profesor dichos conocimientos e identificar posibles vías de desarrollo de los mismos.
Por otra parte, derivado del análisis de las participaciones en el curso virtual, identificamos que Omar hace referencia a constructos teóricos asociados al aprendizaje de las matemáticas ligados a una teoría específica:
O: Uno de los objetivos principales de la actividad es lograr la resignificación del concepto de función utilizando la práctica de modelación. Dentro de la secuencia trato de apoyarme en las diferentes formas en que se entiende la modelación, entre ellas el enfoque socioepistemológico, recordando que la resignificación es una práctica social.
El análisis de estas participaciones indica que Omar parece transformar el significado de los constructos teóricos que explícitamente relaciona con la Teoría Socioepistemológica (TSE) (Cantoral, 2013), como la resignificación, que define como el proceso por el que se alcanza un aprendizaje significativo de los conceptos y que es uno de los términos centrales de este enfoque teórico. Omar muestra, además, conocimiento sobre la idea de prácticas sociales que, en el marco de la TSE, se refiere a actividades que organizan los procesos de aprendizaje a través de actividades comunes en determinados contextos. Sin embargo, parece relacionar la práctica de modelación con la modelización matemática de fenómenos en contextos reales y no con un proceso de construcción de conocimiento matemático. Esto nos da la oportunidad de identificar que Omar conoce una teoría formal sobre el aprendizaje de las matemáticas como lo es la TSE, pero que la transforma para adaptarla a una teoría personal de aprendizaje basada en una interpretación de estos constructos formales.
Por otra parte, Omar comenta:
O: Siempre he considerado que para un mejor aprendizaje del conocimiento del concepto de función cuadrática es necesario ver primero función lineal. Los ejercicios propuestos en la tarea tienen la intención de resignificar el concepto de función lineal, y por ende está dirigido a recoger todo lo conocido sobre funciones.
Aunque pudiera parecer obvio, Omar enfatiza aquí que, siempre ha considerado más adecuado e importante trabajar el concepto de función lineal previo al de función cuadrática. Este es un conocimiento que pone en juego para el diseño de las tareas, pues considera que una vez que los estudiantes han podido trabajar con las funciones lineales y han reflexionado sobre sus características será más sencillo repetir el proceso para las cuadráticas observando sus diferencias.
Esto lo consideramos, también, como una teoría personal que Omar ha construido sobre el aprendizaje del concepto de función cuadrática, puesto que parece sustentarse en su experiencia personal.
A partir de este análisis bottom-up, esta categoría se define entonces como el conocimiento de teorías formales y/o personales de aprendizaje asociadas a un contenido matemático, englobando aquí lo que sabe el profesor acerca de los posibles modos de aprehensión asociados a la naturaleza misma del contenido matemático y de estructuras cognitivas del estudiante tanto para la matemática en general como para contenidos particulares.
3.2.2 Subdominio del conocimiento de la enseñanza de las matemáticas (Knowledge of Mathematics Teaching-KMT)
Shulman (1986) se refirió a las componentes del PCK como el conocimiento de las formas más efectivas de representación y formulación de un contenido, de manera que este pueda ser comprensible para otros, señalando que estas formas de representación potentes no son únicas, por lo que el profesor debe conocer distintas alternativas para utilizar a conveniencia.
En la fase top-down se identifica que las componentes que suelen asociarse con un conocimiento referente a cuestiones de enseñanza son los conocimientos del profesor sobre estrategias específicas de enseñanza, las formas más efectivas de representación de ideas y el conocimiento de distintas tareas y actividades relacionadas con la enseñanza de un determinado contenido matemático. Además, se hace alusión a distintas representaciones del contenido a enseñar, sus limitaciones, potencialidades y su origen, así como los elementos necesarios para su desarrollo, selección e implementación en el aula (Escudero, 2015; Depaepe, et al., 2013).
Estas componentes han sido utilizadas y reinterpretadas por autores que se han centrado en ampliar la definición de las representaciones como recursos para la instrucción o representaciones instruccionales (Llinares, Sánchez y García, 1994), englobando el conocimiento del profesor de estas representaciones y las formas en las que las interpreta y utiliza en el aula, así como los vínculos que existen entre estos conocimientos y otros de este mismo dominio pedagógico (Pinto et al., 2008).
Como mencionan Bosch y Gascón (2001), la decisión de elegir una representación, recurso, material, formas de instrucción o secuencia para trabajar un determinado contenido, demanda del profesor especial atención en el potencial que tienen para ser usados en la enseñanza, considerando si sus características son las ideales para abordar el contenido matemático.
Esta reflexión teórica deriva en una primera caracterización de este subdominio, que refleja el interés del MTSK en subrayar la integración de matemáticas y enseñanza desde el propio nombre del subdominio, por lo que se incluyen aquí aquellos conocimientos sobre las distintas posibilidades de enseñanza condicionadas por la naturaleza misma del contenido.
Con la intención de clarificar la caracterización de este conocimiento se proponen las siguientes categorías: Estrategias didácticas para la enseñanza de un contenido matemático, teorías de enseñanza asociadas a un contenido matemático y recursos de enseñanza asociados a un contenido matemático.
Es evidente que el profesor necesita tener conocimiento de distintas herramientas con las cuales abordar el contenido y sobre las características matemáticas que pueden tener ciertas estrategias didácticas, así como reconocer la influencia de estas sobre la enseñanza de un contenido matemático en un momento y contexto particular, ya sea positiva o negativamente. En este sentido se define la categoría de estrategias didácticas para la enseñanza.
Sin embargo, en el análisis del caso de Omar se presenta y comenta una actividad diseñada por el profesor con la cual se aborda el concepto de función lineal para trabajarlo con estudiantes de secundaria o bachillerato:
O: Se pretende analizar el llenado de un recipiente a velocidad constante para poder establecer los diferentes vínculos entre distintas variables, a través de preguntas relacionadas con el comportamiento del llenado de un tanque de forma rectangular de 3cm de alto, 2cm de ancho y 5cm de largo, que recibe agua con un flujo constante de 1cm 3 por segundo.
Usando esta actividad los estudiantes pueden llegar no solo a obtener un algoritmo, sino además analizar las diferentes relaciones que se pueden dar entre distintas variables, determinar cómo varía una función con respecto a uno de los parámetros, qué pueden obtener de una gráfica y cuál es el proceso para obtener un modelo matemático. Con todo lo anterior puedo decir que el estudiante logra nuevos significados de función.
Podemos afirmar que Omar conoce una tarea específica con la cual abordar aspectos específicos de las funciones lineales, por ejemplo, las relaciones entre variables y los efectos que tiene la variación de parámetros.
Además, se ponen de manifiesto conocimientos sobre características de esta tarea como: estrategia didáctica propicia para el trabajo con la función lineal, como la conveniencia de considerar la variación y el cambio como foco central de trabajo y la búsqueda de un modelo matemático que represente variaciones propias de este tipo de funciones, así como la flexibilidad de esta tarea para adaptarse a distintos niveles educativos:
O: La tarea dirige al estudiante a inmiscuirse en el contexto variacional, invitándolo a desarrollar una serie de actividades, establecer un modelo matemático y representar los datos en un gráfico, para luego incitarlo a que comience a realizar variaciones fomentando la investigación, y la aprehensión de conocimiento.
La actividad me acerca a la realidad, muestra un fenómeno poco estudiado en el aula, me lleva a establecer relaciones aplicadas a situaciones de la vida diaria; lleva al estudiante a que realice predicciones, y a que dé nuevos significados de la función lineal (resignificación). El objetivo no es el de aprender conceptos de memoria o algorítmicos, sino, a través de procesos de modelación, llegar a un aprendizaje significativo del concepto.
En este diseño, se observa también una explícita intención de guiar los procedimientos de los estudiantes para identificar relaciones específicas por medio de la modelación matemática de fenómenos y el tratamiento y tránsito entre registros de representación de la función lineal.
O: En el caso de esta secuencia se utilizarán las siguientes acciones: elaboración de tablas, utilización de algoritmos, la elaboración de gráficas, comparación, relaciones entre variables, variaciones matemáticas, análisis de datos, consecución modelos, entre otras.
La estructura misma del diseño didáctico pone de manifiesto, además, su conocimiento sobre la modelación de fenómenos como estrategia didáctica asociada al aprendizaje de funciones, y la conveniencia de su uso para generar una secuencia de tareas que permita a los estudiantes trabajar el contenido matemático en contextos específicos.
Al cuestionarlo sobre el uso de la modelación en su diseño de secuencia, Omar comenta:
O: El proceso para obtener un modelo matemático se llama modelación matemática; la modelación matemática se puede ver como el medio para enseñar un concepto matemático y/o como herramienta para generar significados. En el primero se establecen unas secuencias para enseñar cualquier concepto, y en el segundo se generan significados articulando diferentes contextos para reafirmar el aprendizaje.
La modelación como práctica se basa en desarrollar procesos mentales, que lleven al estudiante más allá de aplicar una fórmula o hallar un resultado.
El objetivo de la actividad no es el de aprender conceptos de memoria o algorítmicos, sino llegar a un aprendizaje significativo del concepto a través de procesos de modelación.
Su discurso refleja el peso dado al uso de un contexto real para involucrar a los estudiantes y establecer relaciones a través de la modelación. Sin embargo, este uso de contextos no parece estar ligado directamente al concepto de función lineal, puesto que Omar considera que esta actividad podría trabajarse también con contextos puramente matemáticos sin cambios significativos. Aun así, consideramos que Omar tiene conocimiento sobre las ventajas que tiene el trabajo con la modelación de fenómenos reales como estrategia didáctica para la construcción del concepto de función lineal puesto que identifica características propias de este tipo de estrategia: implica desarrollar procesos mentales que van más allá de aplicar una fórmula o hallar un resultado y requiere que los estudiantes tengan ciertos conocimientos previos que les permitan establecer relaciones entre variables y dar nuevos significados al concepto de función.
O: Al pasar de un registro al otro espero que el estudiante establezca las relaciones de variable dependiente-independiente, y pueda observar cómo se podría modelar el fenómeno a partir de los recursos gráficos.
En el diseño se manejan contextos diferentes como el algebraico, el visual, y el gráfico que unidos fundamentan el aprendizaje de funciones. El juego entre estos contextos permite resignificar el concepto de función través de la modelación.
Se reconocen aquí conocimientos sobre la potencialidad didáctica que tienen los distintos registros asociados a la función, al utilizar el tránsito de un registro de representación a otro como una técnica para abordar el concepto de función, y que identificamos como parte de esta categoría. Esto lo justifica a través de la búsqueda de relaciones entre ellos por parte de los estudiantes para el modelado del problema.
Las evidencias de conocimiento, que extrajimos de las participaciones de Omar, nos permiten reinterpretar esta categoría y refinarla al reconocer la necesidad de distinguir entre estrategias, técnicas y tareas didácticas que permitan al investigador observar los datos desde perspectivas diferentes y analizar cuestiones específicas que ofrecen información sobre las posibilidades de acción que tiene el profesor, así como reflexionar sobre la toma de decisiones que hace sobre su diseño:
- Tarea: Secuencia de llenado de recipiente que permite explorar las características específicas de las funciones.
- Estrategia: Modelación de fenómenos como estrategia didáctica asociada al aprendizaje de funciones.
- Técnica: El tránsito entre distintos registros de representación permite, a través de la modelación, resignificar el concepto de función.
Renombramos entonces el subdominio como el conocimiento de las estrategias, técnicas y tareas para la enseñanza de un contenido matemático.
Así como en el subdominio anterior, se incorpora al subdominio la categoría de teorías de enseñanza asociadas a un contenido matemático. El KMT puede ser un conocimiento fundamentado en resultados de investigación en Matemática Educativa, en la observación y la reflexión sobre la actividad matemática en el aula, en propuestas didácticas que tiene el currículo, así como la experiencia previa del profesor, fuentes con las cuales pueden construirse teorías sobre la enseñanza de las matemáticas que pueden orientar, e incluso condicionar el actuar del profesor y el uso que hace del conocimiento (Schoenfeld et al., 2008).
Del análisis bottom-up se observan algunas evidencias del conocimiento de Omar sobre constructos teóricos provenientes de la teoría SE que le sirven para sustentar y diseñar una determinada estrategia didáctica para la enseñanza de la función.
O: Hago referencia a términos de la Socioepistemología puesto que esta teoría me permite mirar la educación matemática como una actividad en la que se estudia el trasfondo de los conceptos matemáticos y llevarlos a otros contextos, me acerca al mundo real. La investigación en el aula puede trabajarse a partir de la resolución de problemas y de la utilización de fenómenos físicos, químicos o matemáticos donde se tiene que utilizar la práctica de modelación.
La práctica de modelación (que es la que se aplica en este recurso, y sobre la cual se creó la actividad), exige tener conocimiento sobre conceptos como variable dependiente e independiente y, quizá, conocimientos básicos sobre función lineal, de una manera tradicional. La actividad me acerca a la realidad a través de un fenómeno físico, me lleva a establecer relaciones aplicadas a situaciones de la vida diaria; lleva al estudiante a realizar predicciones y, a que dé nuevos significados de la función lineal (resignificación).
Es importante señalar que Omar no hace una asociación directa de la teoría con el tratamiento didáctico de las funciones, pero sí con el entorno de trabajo motivador que se genera con la práctica de modelación y su utilidad como herramienta para generar conocimiento matemático al establecer relaciones con los fenómenos de contextos reales en aula. Esta idea parece ser la que lo lleva a utilizar la práctica de modelación en el diseño y estructura de sus tareas para generar en el estudiante nuevos significados al respecto de la función lineal, estableciendo relaciones entre la modelización matemática y los contextos reales, lo cual parece responder a una influencia significativa de trabajos relativos a SE.
Al igual que en el caso del KFLM, se identifica en Omar la construcción de una teoría personal de enseñanza basada en su conocimiento sobre constructos teóricos de la SE, al utilizar la idea de práctica de modelación como generadora de conocimientos, de ahí la relación que hace con los contextos del mundo real por lo cual reinterpretamos el nombre de la categoría como: teorías formales y/o personales de enseñanza asociadas a un contenido matemático.
La categoría de recursos de enseñanza, se refiere al conocimiento de materiales utilizados para la enseñanza de un contenido particular, manteniendo el foco del análisis en el conocimiento sobre sus características didácticas ligadas específicamente a las matemáticas.
Esta categoría fue especialmente difícil de observar en el análisis. A pesar de que Omar habló varias veces de la posibilidad de usar herramientas tecnológicas como GeoGebra o Cabri, para validar los resultados obtenidos a través del trabajo manual o algebraico de los contenidos, no mencionó la potencialidad que tienen estos materiales para el trabajo matemático, las diferencias entre ellos, ni las ventajas y desventajas de su utilización para trabajar el concepto de función. Lo que sí podemos afirmar es que el profesor conoce dos softwares diseñados específicamente para la enseñanza de las matemáticas, que permiten realizar representaciones gráficas y esquemáticas de contenidos matemáticos.
O: Se usarán recursos de lápiz y papel inicialmente, y para la verificación o validación de la actividad se utilizará un software que puede ser GEOGEBRA o CABRI, para mostrar al estudiante que lo que realizó no solamente lo validan sus pares, sino también una herramienta que además de ser un apoyo visual para mostrar resultados, es como un agente externo al aula que puede decir si lo realizado está bien o no.
Por otro lado, nos muestra conocimiento de una característica específica de los libros de texto como materiales didácticos:
O: Muchos libros de texto se centran en el trabajo algebraico a través de algoritmos, olvidándose de establecer relaciones entre el contexto y otras representaciones a veces necesarias como la graficación.
Esto puede considerarse un conocimiento de características específicas de los libros ligadas directamente a la enseñanza de las funciones, dado que estos conocimientos se suman a los resultados obtenidos anteriormente, acerca de lo que sabe Omar sobre la dificultad que supone la variedad de representaciones de las funciones, y estos conocimientos sirven para motivar el planteamiento de secuencias de tareas en las que se utilizan distintos registros de representación de las funciones.
El análisis y reflexión del caso, nos lleva a repensar la categoría y renombrarla como conocimiento de recursos materiales y/o virtuales de enseñanza asociados a un contenido matemático.
3.2.3 SUBDOMIMIO DE CONOCIMIENTO DE LOS ESTÁNDARES DE APRENDIZAJE DE LAS MATEMÁTICAS (KNOWLEDGE OF MATHEMATICS LEARNING STANDARDS-KMLS)
En la literatura existen discrepancias con respecto a la inclusión del conocimiento del currículum dentro del PCK. Sin embargo, según Depaepe y colaboradores (2013), distintos modelos de conocimiento del profesor reconocen la importancia de tener conocimiento curricular, como parte del dominio didáctico, lo cual identifican como knowledge of educational ends o knowledge of curriculum and media.
Por otro lado, el conocimiento curricular se estudia desde distintas perspectivas: como organizador de contenidos, como modelo de planeación del curso, como el que contiene estrategias de enseñanza, como estándar que ayude a la evaluación de saberes adquiridos o como el que norma lo que se debe aprender y cómo debe aprenderse en el curso (Pinto, 2010).
Dentro del MTSK se define un subdominio que engloba conocimientos sobre contenidos propuestos en las normativas curriculares institucionales, para saber lo que se prescribe en cada etapa, es decir, dar una ubicación temporal y contextual al contenido abordado. Además, respondiendo a críticas sobre el carácter normativo que implica reconocer solo los conocimientos oficiales (Depaepe et al., 2013), se contempla aquí el conocimiento de objetivos y estándares de aprendizaje no oficiales que pueda tener el profesor, así como los procedentes de asociaciones profesionales o de los investigadores, al igual que los que derivan de la experiencia del profesor respecto a los logros de aprendizaje, añadiendo un elemento de juicio y crítica en relación con lo prescrito por la administración educativa.
Esta aproximación top-down, permite proponer las siguientes categorías para el análisis de este tipo de conocimiento: Expectativas de aprendizaje de un contenido matemático en un nivel específico, nivel de desarrollo conceptual o procedimental esperado para un contenido en un determinado momento escolar y secuenciación con temas anteriores y posteriores a un determinado momento escolar.
La categoría de expectativas de aprendizaje de un contenido matemático en un nivel específico, se refiere al conocimiento del profesor sobre lo que se espera que el estudiante aprenda en un determinado nivel escolar. Este puede ser adquirido a través de consultas de un documento rector que indique cuáles son esos contenidos, o como abstracción de las capacidades matemáticas específicas que requieren los estudiantes en ese momento escolar. Por ejemplo, Omar hace algunos comentarios acerca de que en Colombia se aborda el concepto de función como parte de los contenidos del currículum de bachillerato (sexto a undécimo grado) y que se retoman en grados superiores:
O: El concepto de función se aborda regularmente en el bachillerato, además de retomarlo en niveles tecnológicos y universitarios donde generalmente se le da más relevancia.
En el informe no explicito los conocimientos que debe tener el estudiante, debido a que la actividad se diseña para octavo grado (13-14 años) y de acuerdo al currículo el estudiante ya tiene conocimientos suficientes para resolver la actividad. Cuando una actividad se adapta a otros grados diferentes al propuesto, se debe hacer teniendo como referencia que los conocimientos para resolverlo sean conocidos, como es este caso.
Omar señala que los estudiantes de octavo y noveno grado, tienen conocimiento suficiente sobre el concepto de función lineal como para afrontar la actividad exitosamente y, establecer nuevos significados del concepto, aunque no profundiza en cuáles son estos conocimientos. Por otra parte, considera que la tarea es modificable para otros grados y, reconoce que en dicha adaptación se deben tener en cuenta los estándares de conocimiento sobre función lineal y ser consecuente con ello en las adaptaciones que se realicen de la tarea.
Aunque no explicita los conocimientos a los que se refiere para las distintas adaptaciones de la actividad, estos fragmentos nos permiten validar esta categoría, resaltando así la necesidad de contar con conocimiento sobre lo que los estudiantes deberían saber de un determinado contenido en un nivel escolar para realizar un diseño adecuado de tareas.
Cuando Omar menciona que su actividad puede adaptarse a diferentes niveles escolares, es natural preguntarnos qué es lo que hay que modificar y qué conocimientos se requieren para adaptar el recurso al nivel de desarrollo conceptual y procedimental que tengan los estudiantes en octavo, noveno, o undécimo grado, puesto que esto implica reconocer características específicas del desarrollo cognitivo de los estudiantes.
O: Modificaría la actividad agregando algunas preguntas o quitando otras, así se puede ajustar a diferentes cursos sin cambiar el objetivo y la estructura de la actividad.
En general la actividad se puede aplicar a nuestros estudiantes del grado octavo (13-14 años), noveno (14-15 años), y con algunos cambios para grado undécimo (16-17 años) y universidad cuando se hable de integrales.
Omar habla de modificaciones de forma (estructurales sin modificar objetivos), sin profundizar en las modificaciones ligadas específicamente al contenido matemático, a excepción de una mención poco clara a la adaptación para universidad en la que hace alusión a las integrales, lo cual limita el reconocimiento que podemos hacer sobre su conocimiento.
En este sentido reconocemos la necesidad de crear una categoría de nivel de desarrollo conceptual o procedimental esperado para un contenido en un determinado momento escolar, que se refiere al conocimiento del profesor sobre la profundidad con la que debe ser abordado un contenido matemático específico, en relación con un nivel escolar determinado. De manera, que podamos reconocerlo, estudiarlo y caracterizarlo para así poder desarrollarlo posteriormente.
Por último, a pesar de que, entre las narrativas de Omar, no aparece evidencia sobre el conocimiento que tiene de secuenciación con temas anteriores y posteriores a un determinado momento escolar, consideramos importante incluir esta última como una categoría del KMLS. Se refiere al conocimiento sobre la secuenciación de diversos contenidos matemáticos, ya sea dentro de un mismo curso o pensando en cursos anteriores y posteriores. Es imposible no cuestionar la similitud (y preguntarse por las diferencias) de este subdominio con los conocimientos propuestos en el dominio de conocimiento de la Estructura Matemática (del dominio matemático). Su similitud con las conexiones matemáticas es patente. Sin embargo, mientras en el conocimiento de la estructura lo que el profesor conoce son las formas en las que se conectan contenidos (interconceptual o temporalmente), en la categoría que estamos describiendo aquí, la secuenciación de temas matemáticos puede responder a otras especificidades además de su estructura. Por ejemplo, si un profesor conoce que en un grado escolar se ve un tema mediante una actividad y el contexto de esa actividad es continuación para otro tema distinto, entonces el profesor estará evidenciando la secuenciación de temas, cuyo propósito es didáctico y no obedece necesariamente a las conexiones matemáticas (inter o intraconeptuales) existentes entre dichos contenidos.
4. REFLEXIONES FINALES
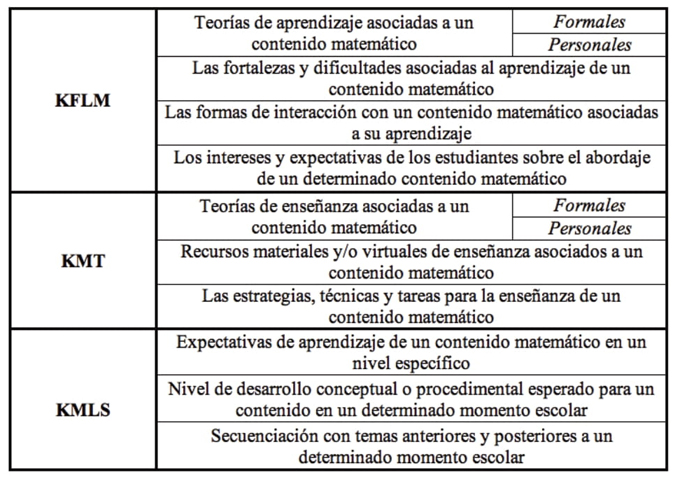
De acuerdo con la descripción que hemos hecho, podemos mostrar al lector la caracterización que se hace del CDC como parte del MTSK (Figura 4), partiendo de subdominios y refinando con categorías de conocimiento:
Consideramos que la definición de estos subdominios y sus categorías supone un refinamiento de los considerados en otros modelos, como el de Shulman o el MKT, en términos del contenido de los subdominios y su conceptualización, focalizando la atención en el conocimiento que tiene el profesor de cómo las matemáticas son aprendidas, enseñadas, o de cuáles son las expectativas de aprendizaje en los diferentes niveles educativos (Escudero, 2015)
Por otro lado, esta caracterización se diferencia de Shulman en tanto que se construye como un modelo integrador (Gess-Newsome, 1999), en el que el CDC no existe como un fenómeno aislado y la enseñanza se considera como el acto de integrar el conocimiento a través de diferentes dominios del conocimiento, lo cual es la esencia del MTSK.
Otra de las críticas al PCK se refiere a si este puede distinguirse teórica y empíricamente del conocimiento del contenido (Depaepe, et al., 2013), sin embargo, consideramos que las evidencias de este estudio permiten observar el potencial que tiene distinguir distintas formas de conocer un contenido para su análisis y sistematización. Por ejemplo, Omar conoce distintos registros de representación para las funciones lineales, además de características específicas de estos registros (KoT) y sabe que esta variedad de representaciones puede suponer una dificultad en el proceso de aprendizaje de este tipo de funciones (KFLM). Además, Omar reconoce el tránsito entre registros como una posible vía de enseñanza que permite analizar las relaciones entre las variables de la función y observar el comportamiento de la misma desde distintos enfoques (KMT). Estos conocimientos tienen una naturaleza distinta, pero en conjunto, permiten tomar una decisión en cuanto a la forma en la que elaborará el diseño de una actividad para trabajar el concepto.
Consideramos importante señalar que hemos mantenido en la traducción al inglés del modelo el término PCK, queriendo aludir a los referentes y bases teóricas de las cuales surge la distinción entre un conocimiento disciplinar y un conocimiento didáctico de la disciplina; no obstante, en la traducción al español hemos decidido hablar de Conocimiento Didáctico del Contenido, que nos parece que conlleva un significado más acorde con nuestra intención de aludir a lo que Azcárate (1998) define como “un conocimiento profesionalizado de las matemáticas que capacite para una intervención didáctica fundamentada” (p. 27).
Esperamos que esta descripción de bases teóricas y metodológicas que subyacen a la construcción del modelo MTSK sirva al lector para reflexionar acerca del potencial que tiene identificar y caracterizar el PCK, así como para discutir y criticar este y otros modelos de conocimiento profesional del profesor de matemáticas. Estamos convencidos de que esto será un paso importante hacia la construcción de programas de desarrollo profesional cada vez más especializados.











 nueva página del texto (beta)
nueva página del texto (beta)