INTRODUÇÃO
Nas últimas duas décadas do século XX, a concepção da aprendizagem como processo mediado por mecanismos psicológicos de pensamento e/ou raciocínio teve muita influência nos cenários de pesquisa, desenvolvimento profissional de professores e produção de materiais curriculares na educação matemática. Essa concepção da aprendizagem tem sua origem em uma visão ontológica do aluno como sujeito autónomo (Radford, 2017b), quer dizer, um indivíduo capaz de aprender por seus próprios meios, sem tanta influência do seu entorno cultural e social. Segundo Radford, essa perspectiva da aprendizagem coloca o aluno “no centro do significado, da conceitualização e da intencionalidade. Tudo emana dele. (...) o indivíduo termina alienado, quer dizer, afastado do mundo concreto e histórico” (p. 151).
Sem dúvida, a perspectiva cognitiva forneceu as primeiras ferramentas conceituais necessárias para enfrentar as contradições geradas na escola por um ensino da matemática orientado à difusão do saber. Porém, o foco sobre o aluno como sujeito autónomo trouxe consigo outros problemas derivados do compromisso do professor com o desenvolvimento individual de estruturas mentais cada vez mais sofisticadas em seus alunos. Nesse cenário, Radford (2017b) sugere que o aluno termina alienado, quer dizer, “preso em suas próprias cavilações” (p. 151). É nesse momento histórico (finais do século XX) que surgem as primeiras teorias educativas socioculturais, que assumem como princípio o fato de os indivíduos não poderem ser concebidos como apartados do mundo e das suas culturas. Por exemplo, os trabalhos de Bartolini-Bussi (1991), Bishop y Pompeu (1991), Boero et al. (1995) e Lerman (1992) convidam a repensar a relação indivíduo-sociedade, abrindo as portas a uma nova conceitualização da aprendizagem matemática como fenômeno social, cultural e histórico.
Desde suas origens, a perspectiva sociocultural tem animado o debate em torno do papel que desempenha a atividade humana no desenvolvimento dos modos histórico-culturais de produção de saberes matemáticos. Desde essa perspectiva, a atividade que acontece na aula de matemática e fora dela, como por exemplo, em cada reunião que professores e alunos realizam em busca da elaboração de simuladores com o GeoGebra (ESG) (Prieto y Díaz-Urdaneta, 2019), começa a ser vista como uma instância social de encontro com os saberes escolares e de posicionamento crítico diante deles. Entretanto, apesar de a atividade considerar a dimensão social no trabalho desenvolvido pelos sujeitos, ainda existem posicionamentos teóricos dentro desta perspectiva que consideram a aprendizagem como “um tipo de adaptação, muito ao estilo de Piaget” (Radford, 2013a, p. 21). É por isso que Radford (2017b) chama a atenção sobre o muito que ainda se tem a fazer para que o social deixe de ser usado como um instrumento de domesticação de consciências e de alienação na atividade matemática da aula.
Embora as reuniões em torno da ESG nunca tiveram como propósito a alienação dos sujeitos que participam nelas, reconhecemos que ela pode estar presente na atividade sem percebê-la, o que faz necessário evitá-la sempre que possível. Uma forma de atingir isso é através do desenvolvimento de pesquisas que permitam ampliar nossa compreensão das implicações e relações entre a atividade humana e a aprendizagem geométrica dos alunos que participam na ESG. Assim, assumindo uma perspectiva histórico-cultural, caracterizamos os processos de objetivação produzidos em uma reunião orientada à ESG, em particular, quando um grupo de alunos e professores de matemática envolvem-se durante a comunicação da técnica de construção de um círculo com o GeoGebra. Para tal, primeiramente nos posicionamos teoricamente no tocante tanto à aprendizagem geométrica na ESG quanto ao desenvolvimento de processos de objetivação.
UM OLHAR SOBRE A APRENDIZAGEM DA GEOMETRIA NA ESG
Nesta pesquisa assumimos uma perspectiva sociocultural da aprendizagem para interpretar este fenômeno em contextos de ESG. Especificamente, adotamos o enfoque histórico-cultural da Teoria da Objetivação (TO) de Radford (2013a) para atingir esse objetivo. Em oposição à perspectiva cognitiva, a TO propõe uma reconceitualização da aprendizagem matemática, não como o resultado da ação do sujeito que constrói o seu próprio saber, senão como “um processo coletivo, cultural e historicamente situado que destaca o papel do trabalho social humano, o corpo, as emoções e o mundo material” (Radford, 2018a). Desde a TO, interessam as práticas sociais “de criação de novos indivíduos capazes de refletir criticamente de maneira matemática sobre as questões urgentes de suas comunidades e do seu mundo” (Radford, 2017b, p. 141).
Assim como acontece com outras teorias educativas, na TO a aprendizagem tem a ver com os saberes matemáticos escolares. Porém, nessa teoria tal fenômeno também diz respeito daqueles seres que se transformam e reafirmam como sujeitos da educação na busca desses saberes. Para estudar como os sujeitos aprendem matemática, a TO introduz duas categorias conceituais na forma de processos de objetivação e subjetivação. Enquanto os processos de objetivação dizem respeito da maneira em que aparece o saber matemático na aprendizagem, os processos de subjetivação têm a ver com o sujeito que aprende e suas formas de colaboração. Em atenção ao propósito deste estudo, nesta parte referimonos à aprendizagem matemática em termos de processos de objetivação. Em outros trabalhos prévios, nosso grupo de pesquisa analisou a outra vertente da aprendizagem matemática em um contexto de ESG.
O significado que tem a objetivação na TO é diferente do significado de coisificação5 da experiência humana, assumido por alguns teóricos sociais. Segundo Radford (2018b), os indivíduos desde que nascem entram em contato com situações, entidades ou coisas que lhes objetam, que lhes parecem estranhas e desconhecidas, mas que fazem parte do mundo dos arquétipos histórico e culturalmente constituídos de pensamento, reflexão e ação que compõem os saberes. A objetivação tem a ver, precisamente, com esses processos sociais, corporais, materiais e simbólicos de tornar-se:
(...) progressivamente e criticamente consciente de uma forma codificada de pensamento e de ação -algo que percebemos gradualmente e ao mesmo tempo atribuímos-lhe significado. São processos de objetivação aqueles atos de perceber significativamente algo que se revela à consciência através da nossa atividade sensorial com a cultura material (Radford, 2013a, p. 23).
A maneira de entender a objetivação proposta na TO revela dois aspectos desse processo que são fundamentais para compreender como se produz a aprendizagem dos saberes geométricos em contextos de ESG. Por um lado, a objetivação é um processo subjetivo, emocional e afetivo de tomada de consciência de algo que se constitui em saber; logo, a tomada de consciência é um reflexo da forma em que cada indivíduo reconhece o mundo objetivo (que lhe transcende) e se posiciona criticamente nele, dentro de uma dinâmica de encontro dialético com as formas codificadas de reflexão, ação e pensamento. Essa tomada de consciência não é contemplativa na medida em que é através da consciência individual que se formam sensibilidades culturais para ponderar, compreender, discordar, objetar e sentir aos outros, a nós mesmos e ao mundo (Radford, 2017a).
Por outro lado, para que a tomada de consciência aconteça é necessário que determinada atividade se coloque em marcha, de maneira que as reflexões e ações dos alunos nela levem a formas de encontro com os saberes. Radford (2017a, p. 125) sugere em chamar trabalho conjunto a essa atividade, definindo-o como “um evento criado por uma busca comum, quer dizer, uma busca que é ao mesmo tempo cognitiva, emocional e ética”. Uma característica chave desse trabalho é a sua natureza social, a qual não desaparece quando se trabalha sozinho (por exemplo, quando um aluno resolve um problema matemático em solitário). Pode-se estar fisicamente sozinho, mas ainda assim o aluno apoia-se em um conjunto de signos (palavras, gestos, inscrições de todo tipo, etc.) e artefatos (calculadora, computador, software de aplicação, etc.) históricos e culturais que fazem do seu trabalho um reflexo da atividade social da aula. Na TO, esses signos e artefatos são chamados meios semióticos de objetivação (Radford, 2006).
Esta última ideia revela outra característica do trabalho conjunto que não podemos passar por alto: a sua manifestação na vida concreta somente “com os meios de trabalho criados pelo próprio ser humano, isto é, artefatos técnicos, ferramentas” (Piedra, 2018, p. 175). Em outras palavras, por meio do trabalho conjunto é possível que os materiais e artefatos culturais revelem a conceitualidade que a atividade humana deposita neles (Radford, 2017a). Por essa razão, a cultura material da época, e particularmente a tecnologia digital, deve necessariamente ser integrada no trabalho conjunto produzido na escola; isso com o fim de fazer aparente o saber que portam esses artefatos tecnológicos criados para professores e alunos. Dada a importância que a TO concede ao trabalho com artefatos, pode-se concluir que a cultura material intervém nos processos de objetivação e ajuda a que estes se materializem.
O TRABALHO CONJUNTO ORIENTADO À COMPREENSÃO DE UMA TÉCNICA
Um olhar da ESG como um ambiente de modelagem matemática exibe a existência de certos processos que orientam as ações dos professores e estudantes envolvidos nela, entre esses o trabalho matemático (Gutiérrez, Prieto, y Ortiz, 2017). O trabalho matemático é um processo cujo propósito é a produção de desenhos dinâmicos que modelam as formas, dimensões e movimentos presentes em objetos da geometria euclidiana, que por sua vez são modelos de objetos da realidade. Ao falar de desenho dinâmico, referimo-nos ao desenho elaborado com um Software de Geometria Dinâmica (SGD) que conserva no seu deslocamento certas propriedades espaciais que dão conta das propriedades geométricas declaradas em sua construção (Laborde, 1997), o que torna esse tipo de desenho “uma instanciação concreta da figura como conceito geométrico” (Sáenz-Ludlow y Athanasopoulou, 2008).
Na produção de um desenho dinâmico intervêm a tarefa de construção e a técnica correspondente ( Sánchez y Prieto, 2017). Por um lado, a tarefa de construção é o problema matemático que os alunos enfrentam durante o trabalho matemático. Por outro lado, a técnica correspondente a uma tarefa é, basicamente, o procedimento aplicado pelos alunos para produzir o desenho dinâmico que dá resposta à tarefa. Quanto à técnica, vale ressaltar a importância dos vínculos entre esse procedimento e o saber histórico-cultural que este mobiliza. Neste sentido, a técnica é portadora de um conteúdo conceitual que apresenta uma perspectiva do objeto geométrico baseado em sua construção.
Quanto aos artefatos, o GeoGebra cumpre um papel fundamental na ESG já que, sendo um artefato cultural, proporciona ao usuário tanto uma série de conteúdos conceituais na forma de ferramentas de construção, medida e outras opções, quanto um espaço de trabalho conjunto estruturado conceitualmente para que o usuário experimente com os conteúdos matemáticos e produça novas formas de construir os desenhos dinâmicos (Radford, 2014). Esse espaço de trabalho é integrado ao software por meio das suas diferentes aplicações (Hohenwarter, Hohenwarter, y Lavicza, 2009), denominadas Gráfico, Janela CAS, Geometria, Janela 3D, Planilha de Cálculos e Probabilidade.
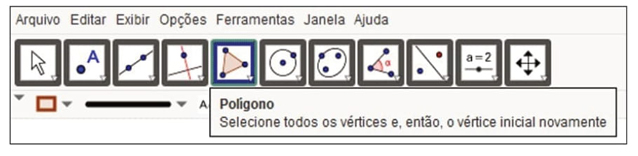
Por exemplo, desenhar um retângulo na aplicação Geometria implica utilizar a ferramenta Polígono, na qual subjaze uma forma de construção dessa figura que precisa informar ao software quais são os vértices que lhe definem (Figura 1). De fato, a ferramenta Polígono é portadora de um conteúdo conceitual (uma maneira de conceituar ao polígono) que faz possível materializar uma técnica de construção particular do retângulo que se espera que seja aprendida. Portanto, assumimos que o uso deliberado das ferramentas de construção do GeoGebra afeta o significado que os alunos produzem dos objetos geométricos que eles tentam representar, uma vez que essas ferramentas sugerem “linhas potenciais de desenvolvimento cognitivo e social” (Radford, 2014, p. 414).
Para que os saberes mobilizados no uso do GeoGebra revelem-se à consciência dos alunos, é necessário que os conteúdos conceituais incrustados em suas ferramentas apareçam durante o desenvolvimento de atividades de reflexão conjunta em torno da técnica de construção de determinado desenho dinâmico. Uma das atividades típicas da ESG tem por objeto a compreensão da técnica de construção (Prieto y Ortiz, 2019), para o qual alunos e professores mobilizam e significam uma variedade de saberes, não só por meio de discursos orais baseados em percepção visual ou em teoria geométrica (Laborde, 1997), senão também por meio de outras formas de reflexão e expressão humana (Radford, 2006).
Este posicionamento teórico aporta os insumos para o estudo da aprendizagem em experiências de ESG, atendendo a uma caracterização dos processos de objetivação em torno dos saberes que se revelam aos indivíduos quando buscam compreenderem uma técnica de construção. Assim, o objetivo desta pesquisa é atingir essa caracterização e, para tal, utilizamos o caminho metodológico descrito a seguir.
METODOLOGIA
A metodologia implementada no trabalho corresponde à de uma pesquisa qualitativa, de natureza descritiva e interpretativa. De acordo com Bogdan e Biklen (2007), a pesquisa qualitativa no campo da educação tem as seguintes características: (i) o ambiente natural é a fonte direta dos dados, (ii) os resultados têm uma forte componente descritiva, (iii) os pesquisadores preocupam-se mais com os processos do que com os produtos, (iv) a análise dos dados é geralmente realizada indutivamente, e (v) o significado é de importância vital nesta abordagem.
PARTICIPANTES E CONTEXTO
A pesquisa envolveu um grupo de alunos de Ensino Médio da Venezuela (entre eles Simão e Edmilson, chamados assim de modo conveniente) com idades entre 14 e 16 anos, e três professores de matemática (chamados Marcelo, Iran e João). No momento da pesquisa, todos estes sujeitos integravam o projeto comunitário Club GeoGebra para la Diversidad, implementado entre os anos 2013 e 2017 em diferentes escolas públicas no oeste do país (Prieto y Gutiérrez, 2017). No contexto desse projeto, os alunos de cada escola reuniam-se semanalmente para participar da ESG com a orientação de um professor de matemática (promotor das aprendizagens) associado ao projeto.
Em meados de 2016, Marcelo e João visitaram o clube orientado por Iran, em que participavam os alunos da pesquisa. O objetivo da visita foi conhecer o trabalho dos alunos naquele ano letivo. Para tal, foi solicitado a cada aluno que comunicasse aos professores visitantes as técnicas de construção aplicadas por eles para produzir os desenhos dinâmicos. Essas técnicas tinham sido produzidas em reuniões prévias à visita dos professores ao clube, e em muitas ocasiões a produção delas implicava o trabalho conjunto do aluno responsável da simulação, seus colegas e o promotor (Iran). Por isso, nessa reunião era possível que o aluno, em situação de comunicação de uma técnica, recebesse o apoio de colegas que possivelmente conhecessem os procedimentos aplicados por ele.
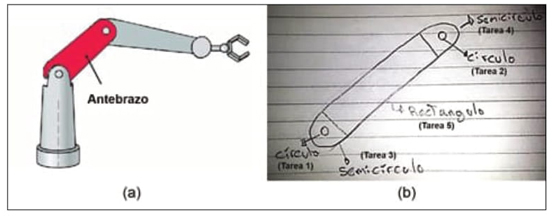
De todas as intervenções que ocorreram nessa reunião, analisamos aquela desenvolvida por Simão, que utilizou o GeoGebra para representar o antebraço que compõe o braço robótico da Figura 2a. Para representar esta parte do mecanismo, o aluno formulou cinco tarefas de construção, que foram resolvidas progressivamente. Essas tarefas estavam vinculadas aos objetos geométricos indicados na Figura 2b.
Especificamente, analisamos o acontecido quando Simão tentava comunicar a João a técnica aplicada por ele para resolver a segunda tarefa de construção: construir um círculo a partir de um ponto exterior. Nesse momento da reunião intervém Edmilson para acompanhar a Simão na comunicação da técnica. Na sequência, explica-se como foram produzidos e analisados os dados no contexto descrito.
PRODUÇÃO DOS DADOS
Diversos autores consideram que, em uma pesquisa qualitativa, os dados são produzidos em lugar de serem coletados, já que eles não somente são capturados pelo pesquisador através dos procedimentos e instrumentos definidos, senão que o pesquisador incide nos dados, percebendo-os e organizando-os com seu próprio olhar (Powell y Silva, 2015).
Assim sendo, nesta pesquisa, a produção dos dados começou com a filmagem em vídeo do trabalho conjunto dos participantes, desenvolvido em torno da intervenção de Simão ao comunicar a técnica de construção do círculo. A intenção de realizar essa filmagem responde a nossa necessidade de capturar a realidade complexa do trabalho conjunto desenvolvido pelos participantes. Posteriormente, a filmagem realizada foi transcrita, excluindo aqueles momentos do trabalho conjunto em que não se discutia o procedimento de construção do círculo. A transcrição foi realizada utilizando um processador de texto; logo, os dados da pesquisa provêm apenas da transcrição realizada não sendo alterados pelos pesquisadores quando esses, por exemplo, decidem excluir determinada informação.
ANÁLISE DOS DADOS
A análise dos dados realizou-se em 3 etapas.
Na etapa 1 realizamos uma primeira leitura da transcrição para identificar, discutir e descrever a técnica de construção de Simão. A finalidade dessa etapa foi reconhecer a particularidade do trabalho realizado por Simão para construir o círculo. Em outras palavras, procurou-se relacionar a conceitualidade da qual é portadora a ferramenta Círculo do GeoGebra com as diferentes ações desenvolvidas pelo aluno para dar resposta à tarefa. Como resultado dessa primeira etapa de análise, ilustramos na Tabela 1 a técnica de construção do círculo, em termos de passos e ações.
Tabela 1 Técnica de construção do círculo aplicada por Simão.
| Tarefa de construção 2: Construir um círculo a partir de um ponto exterior (ponto C) | |
| Ferramenta usada: Círculo dados Centro e Raio | |
| Conteúdo da ferramenta: Selecione o centro e, depois, digite a medida do raio | |
| Passo 1: Determinar o centro do círculo | |
| 1.1 | Traçou-se uma reta a paralela ao eixo x pelo ponto C (Figura 3a). |
| 1.2 | Aplicou-se uma rotação à reta a com centro em C, em um ângulo de amplitude aleatória de 42.6° e em sentido anti-horário, obtendo a reta a´ (Figura 3b). |
| 1.3 | Criou-se o controle deslizante α, com valores mínimo e máximo de 0° y 65°, respectivamente. |
| 1.4 | Aplicou-se uma rotação à reta a´ com centro em C, em um ângulo α (o controle deslizante) e em sentido horário, obtendo a reta a´´ (Figura 3c). |
| 1.5 | Traçou-se uma circunferência centrada em C e raio de 21*k (sendo k uma medida padrão representada por um controle deslizante de tipo número), obtendo a circunferência b. |
| 1.6 | Interceptou-se a reta a´´ e a circunferência b, obtendo o ponto D, centro do círculo (Figura 3d) |
|
| |
| Figura 3. Ações1.1 a 1.6 | |
| Passo 2: Selecionar o raio do círculo | |
| 2.1 | Escolheu-se a medida k como o raio do círculo |
| Passo 3: Traçar a circunferência do círculo | |
| 3.1 | Traçou-se a circunferência do círculo, centrada em D e raio igual a k, obtendo a curva d (Figura 4a). |
| Passo 4: Ilustrar o círculo | |
| 4.1 | Modificou-se a transparência da circunferência do círculo para ilustrar a região interna (Figura 4b). |
|
| |
| Figura 4. Ações3.1 e 4.1 | |
Quanto à conceitualidade da ferramenta Círculo que orientou o desenvolvimento da técnica produzida por Simão, vale a pena ressaltar que essa ferramenta (na versão 5.0 do software) somente representa a circunferência do círculo; logo, o aluno teve que acrescentar mais um passo à sua técnica (passo 4 do procedimento, Tabela 1) para resolver a tarefa.
Na etapa 2 identificamos nas transcrições aqueles fragmentos da discussão entre os participantes em que parecia existir evidências de tomada de consciência de algum objeto geométrico subjacente na técnica, colocando a atenção nas mudanças de foco no discurso. Denominamos segmento destacado (Radford, 2015) àquele conjunto de fragmentos da discussão em que se manifesta um processo de objetivação em torno de algum objeto geométrico.
Na etapa 3 realizamos uma análise multisemiótica (Sabena, Robutti, Ferrara, y Arzarello, 2012) nos segmentos destacados com o intuito de identificar a variedade de significados geométricos e meios semióticos mobilizados pelos participantes durante o trabalho conjunto.
Assumindo o fato de a cognição ter natureza multimodal (Arzarello, 2006; Radford, Edwards, y Arzarello, 2009), focamo-nos na maneira em que os participantes combinaram diferentes signos e artefatos para tentar fazer aparente a conceitualidade que porta a ferramenta Rotação em Torno de um Ponto do software. Denominamos nós semióticos às formas em que os participantes combinam distintos meios semióticos para alcançar um estado de consciência consideravelmente estável sobre algum objeto geométrico subjacente no trabalho conjunto. Radford, Demers, Guzmán, e Cerulli (2003) definem os nós semióticos como “peças da atividade semiótica do aluno, onde a ação, os gestos e a palavra trabalham juntos para alcançar a objetivação do saber” (p. 56).
No início da análise, as etapas 2 e 3 foram realizadas de forma independente por cada um dos pesquisadores. Posteriormente, realizamos reuniões para discutir os resultados obtidos. Finalmente, as discrepâncias no tocante aos resultados obtidos foram solucionadas. Na sequência, apresentamos os resultados da nossa análise.
RESULTADOS
A análise dos dados permitiu reconhecer quatro nós semióticos que revelam processos de objetivação vinculados à ideia de rotação. Esses nós semióticos dizem respeito à rotação de retas na interface do GeoGebra que fazem parte das ações realizadas por Simão para executar o primeiro passo da técnica. A diferença entre as rotações dos nós semióticos encontra-se na natureza do ângulo utilizado em cada ação. Destaca-se que o ângulo de rotação, o objeto a rotacionar e o centro da circunferência são os três elementos que fazem parte da conceitualidade dessa transformação geométrica, da qual é portadora a ferramenta Rotação em Torno de um Ponto. No tocante ao ângulo de rotação, este deve ser informado ao software por meio de um campo de entrada que aparece após selecionar os outros dois elementos. Nesse campo, o usuário deve inserir a medida do ângulo ou a variável (uma letra) que lhe define em sua construção. De acordo com a situação que se apresente, as duas formas de agir levam a formas diferentes de entender a rotação no GeoGebra.
Nos dois primeiros nós semióticos se mostram a discussão que tiveram os participantes quanto à rotação da reta a com um ângulo expressado como medida (ação 1.2 da técnica), enquanto os outros dois nós semióticos referem-se maneira em que os sujeitos reconhecem que a reta a’ foi rotacionada com um ângulo expressado como variável (ações 1.3 e 1.4). Entretanto, a forma como se sucederam os acontecimentos na reunião levou a que ambas as formas de entender a rotação surgissem simultaneamente; logo, é nos últimos dois nós semióticos onde se concretizam tais formas de entendimento dessa transformação no software.
PRIMEIRA APROXIMAÇÃO À IDEIA DE ROTAÇÃO
O reconhecimento da ideia de rotação com um ângulo expressado como medida no GeoGebra começou quando João convidou o Simão a explicar como ele executou as primeiras ações da técnica. Como resposta a esse convite, foi desenvolvido um trabalho conjunto em que se observam diferentes formas de comunicar a rotação da reta a (ação 1.2), que progressivamente se vão aproximando à conceitualidade da qual é portadora a ferramenta Rotação em Torno de um Ponto. Essas formas de comunicar as ações vão surgindo à medida que João orienta a discussão até ao reconhecimento dos elementos característicos do uso da ferramenta mencionada.
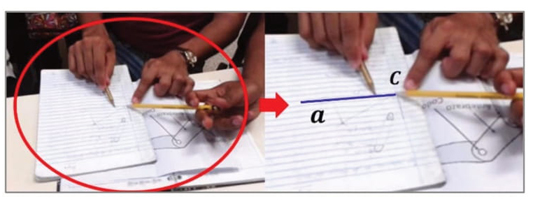
Uma primeira aproximação à ideia de rotação aplicada na ação 1.2 começa a manifestar-se no momento em que Edmilson, motivado pela dificuldade de Simão em expressar as ações realizadas, comunica a João o procedimento que eles utilizaram para atingir o primeiro passo da técnica. Fazendo um uso coordenado de palavras, gestos e indicações sobre o desenho em papel, Edmilson realiza uma descrição das ações 1.1 e 1.2 da técnica sem fazer alusão explícita a cada elemento que caracteriza os objetos geométricos subjacentes a essas ações, em referência às ferramentas do GeoGebra que foram utilizadas para tal (linha 6). Essa situação leva o João a insistir na necessidade de uma nova explicação que considere tais conceitualidades, através de uma pergunta direcionada a Simão (linha 7).
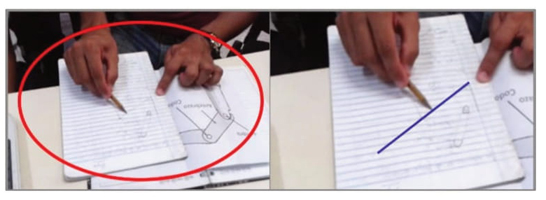
[6] Edmilson: [traçamos] uma reta e a rotacionamos [indica a rotação por meio do giro da mão sob a mesa, em sentido anti-horário (Imagem 1) ], para encontrar esse ponto [centro do círculo].
A nova explicação de Edmilson caracteriza-se por uma maior precisão das qualidades da reta a, enquanto objeto da rotação. Nessa ocasião, Edmilson refere-se à direção dessa reta através de um uso coordenado de palavras e movimentos da sua mão (linha 9). A referência que fez Edmilson da direção da reta a é complementada por João, por meio de uma interpretação do expressado pelo aluno que se apoia no uso do desenho em papel, indicando sobre este meio os procedimentos realizados (linhas 10 e 12). Diante a interpretação realizada, os alunos mostram-se sensíveis e concordam com o dito pelo professor (linhas 11 e 13).
[9] Edmilson: [nós] desenhamos [a reta a] paralela ao eixo y... ao eixo x, e depois a rotacionamos [indica a rotação por meio do giro do lápis que leva na mão (Imagem 2) ]... no sentido anti-horário.
[10] João: Paralela ao eixo x. Tipo assim? [indica a reta desenhada no papel por meio do deslocamento do lápis em direção horizontal e de esquerda à direita].
[11] Alunos: Sim! [acenam com a cabeça, em sinal de aceitação].
[12] João: E depois você a rotacionou assim? [gira o lápis de a até a’, em sinal da rotação].
[13] Edmilson: [acenando com a cabeça em sinal de conformidade]... anti-horário.
A SEGUNDA APROXIMAÇÃO À IDEIA DA ROTAÇÃO
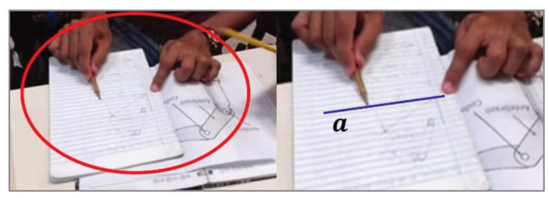
A forma com que Edmilson se aproxima à ideia de rotação não convence a João, que insiste na necessidade de os alunos produzirem um discurso sobre a ação 1.2 da técnica mais próxima à conceitualidade da ferramenta usada. Para tal, e em alusão à reta a’, o professor pergunta aos alunos como desenharam essa reta (linha 20). Em seguida, aproveitando que a reta a’ se obteve da reta a (ação 1.1), João reproduz um discurso sobre a ação 1.1 da técnica que considera a conceitualidade da relação de paralelismo, da qual é portadora na ferramenta Reta Paralela, em uma tentativa de ajudar os alunos a avançarem até um discurso com as mesmas características e que respondesse à pergunta do professor (linha 21). Esse discurso de João combina palavras e gestos, apoiados no desenho em papel, para finalizar novamente na pergunta (linha 22).
[20] João: Mas, como desenharam essa? [refere-se à reta rotacionada, que indica com o lápis sobre o desenho (Imagem 3) ]. Essa é a que eu não entendo.
[21] João: Esta [refere-se à reta a, que aponta com o lápis sobre o papel], sim entendo como a desenharam, porque a fizeram com paralelismo.... Paralela ao eixo x que passasse por aqui [indica o ponto C sobre o desenho]. Este é o ponto C. Está bem, eu desenho essa reta.
[22] João: Mas, como fizeram essa?
Como resposta a essa intervenção, Edmilson refina seu discurso sobre a ação 1.2, fazendo menção por primeira vez da ferramenta Rotação em Torno de um Ponto do software (embora não fosse nesses termos) usada por Simão para aplicar a rotação à reta a (linha 23). A partir disso, João começa um processo de reconhecimento da conceitualidade da rotação, da qual é portadora essa ferramenta, iniciando pela referência ao objeto da rotação (reta a) por meio de palavras e indicações da sua representação no desenho em papel (linha 24. Em sintonia com João, Edmilson menciona o centro da rotação (ponto C) como outro dos elementos característicos da transformação no software, em uma mostra de como o aluno toma consciência da necessidade de explicitar cada elemento característico da rotação no entorno do GeoGebra (linha 25). Continuando com essa dinâmica, João pergunta sobre o ângulo de rotação aplicado (linha 26).
[23] Edmilson: Usamos uma rotação.
[24] João: Você rotacionou essa? [refere-se à reta a, que indica com o lápis sobre o papel (Imagem 4) ].
[25] Edmilson: Com centro nesse ponto [refere-se ao ponto C (Imagem 5) ].
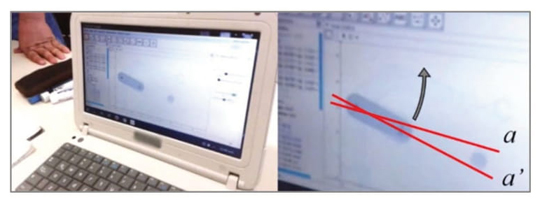
Segundo mostram os dados, Edmilson dúvida em relação à natureza do ângulo utilizado por Simão na ação 1.2. Em meio da sua hesitação, Edmilson assume que Simão vinculou o ângulo de rotação ao controle deslizante α, devido a que nesse momento desconhecia-se alguma medida exata desse ângulo (linha 27). Após comparar as ações descritas por Edmilson com o desenho dinâmico, João percebe visualmente uma contradição no comportamento da reta a’, logo após ser ativada a opção Animar no controle deslizante α (linhas 28, 29 e 30). Em particular, o professor percebe que para certos valores do controle deslizante, a reta a’ tem coeficiente angular negativo,6 questão que não devia acontecer para um ângulo de rotação α que varia entre 0º (posição horizontal) e 65º, em sentido anti-horário (linha 30). A contradição confirma-se quando os alunos se questio-nam entre si e mostram não concordar com o sentido da rotação aplicada (linhas 32, 33, 34 e 35).
[27] Edmilson: Eh, bom, ou seja, fizemos isso com um controle deslizante para... como não sabíamos qual foi o ângulo... sim, o ângulo exato.
[28] João: ¿Está o controle deslizante aí [na tela]? Mostre o controle deslizante, lá nos controles [indica com o dedo indicador a tela do computador].
[29] Simão: [manipula o controle deslizante α e lhe ativa a opção Animar].
[30] João: Bom... mas esse ângulo passa de... ou seja, para aca debaixo [referindo-se a que a reta que rotaciona o faz por debaixo de a (Imagem 6) ].
[32] João: Mas então, o que não entendo é como rotacionaram isso [indica a reta a com o lápis], com respeito a este ponto [referindo-se ao ponto C, que indica com o lápis sobre o desenho], o ângulo que lhes diz o controle deslizante [referindo-se ao controle deslizante α].
[33] Edmilson: Anti-horário.
[34] Simão: Não, horário.
[35] Edmilson: Horário? [mostrando-se incrédulo].
A maneira em que João leva os alunos ao reconhecimento da contradição comentada e, portanto, à tomada de consciência do ângulo que realmente foi utilizado na ação 1.2, explica-se com detalhe no segundo nó semiótico. Tomamos esta decisão dado que esse reconhecimento se realiza ao mesmo tempo em que surge a tomada de consciência da ação 1.4 correspondente ao segundo nó semiótico.
O RECONHECIMENTO DA AÇÃO 1.4 DA TÉCNICA
Como mencionamos no início dos resultados, nos últimos dois nós semióticos evidencia-se uma tomada de consciência sobre a ideia de rotação com um ângulo expressado como variável. Existem duas formas em que uma variável pode representar o ângulo de uma rotação: (i) quando a variável expressa o valor de um ângulo construído previamente na interface do software, e (ii) quando a variável expressa um intervalo de medidas angulares representado por um controle deslizante. Condicionado pela necessidade de representar o movimento do antebraço do braço robótico (Figura 2), Simão executou ações que o levaram a rotacionar a reta a’ com um ângulo como o descrito na segunda forma mencionada, obtendo-se a reta a’’ sobre a qual estaria localizado o centro do círculo que se buscava construir.
Porém, no trabalho conjunto, os dados mostram que Simão e Edmilson parecem ter esquecido a rotação da ação 1.4 da técnica quando vinculam erradamente o controle deslizante (ação 1.3) à rotação da reta a (ação 1.2). Portanto, este terceiro nó semiótico descreve a forma em que os participantes tomaram consciência tanto da existência da rotação aplicada na ação 1.4, quanto da conceitualização desse objeto geométrico depositada na ferramenta Rotação em Torno de um Ponto, com um ângulo expressado como medida (nós semióticos 1 e 2) e como variável vinculada a um controle deslizante.
Os dados mostram que a ação 1.4 da técnica começou a ser reconhecida quando João toma consciência da existência, no desenho dinâmico, de uma reta (reta a’’, ação 1.4) com um comportamento distinto daquela outra descrita por Edmilson e Simão (reta a´, ação 1.2, ver final do nó semiótico 1). Dado o complicado que foi para os alunos reconhecerem essa contradição somente através da observação do desenho dinâmico, João produziu uma nova interpretação das ações descritas por Simão e Edmilson, em que integra o desenho em papel ao repertório de recursos semióticos utilizados nesse momento. Para tal, o professor desenvolve um discurso oral em que usa o lápis para indicar, sobre o desenho em papel, cada um dos elementos necessários para a aplicação da rotação no caso da ação 1.2, até chegar no momento de interpretar o ângulo de rotação (linhas 40 e 41).
A intenção foi fazer com que os alunos pensassem nos efeitos que, sobre o desenho dinâmico, deveriam produzir-se ao definir a ação 1.2 em função de um ângulo de rotação expressado como variável (α) e não como medida. A partir da interpretação realizada sobre a base do desenho em papel, João leva os alunos a observarem o desenho dinâmico e compararem o comportamento da reta a’, segundo o combinado na interpretação realizada (o expressado por Edmilson no seu discurso), com o comportamento observado na tela do computador (linha 42).
[40] João: Logo, vocês me dizem que desenharam essa reta daqui [indica com o lápis a reta a’ (Imagem 7) ]. Por que essa reta é importante? Imagino que é importante porque aí vai estar o outro ponto... a outra circunferência que vocês vão desenhar, ou o outro círculo, acho. Está bom, mas, como desenhei essa reta? Vocês me disseram “rotacionando essa” [refere-se à reta a]. Bom, se a rotaciono, eu entendo vocês. Mas se vocês a rotacionam me devem dizer...
[41] João: Isto é o que eu quero lhes fazer ver. Qual o ângulo aqui? Vocês me disseram: “Não professor, o ângulo não é fixo. O ângulo é um controle deslizante. Usamos um controle deslizante porque, se o manipulamos, vamos conseguir que a reta descenda e ascenda, descenda e ascenda, e isso nos convem”. Eu entendo vocês. Mas se eu vou rotacionar isto [indica com o lápis a reta a sobre o desenho (Imagem 8a), deslocando a mão de esquerda à direita] com respeito... nesse sentido, no sentido anti-horário, um ângulo α, essa reta [a] se mexe de aqui e vai chegar até aqui [indica a rotação da reta a no papel, usando a ponta do lápis (Imagem 8b) ]. Ela não vai baixar [ter coeficiente angular negativo]. Mas eu aí [referindo-se à janela de visualização do GeoGebra] estou vendo que [a reta] baixa.
[42] João: Aqui [na tela do computador]... eu imagino que a reta está aqui [indicando com o lápis o desenho dinâmico na tela (Imagem 9a) ]. Olhem, aí [a reta] chega a ser horizontal, mas depois baixa (Imagem 9b). O que aconteceu aí? Como era a questão [a construção]? Porque eu não a entendi. Simão, não se lembra do que você fez?
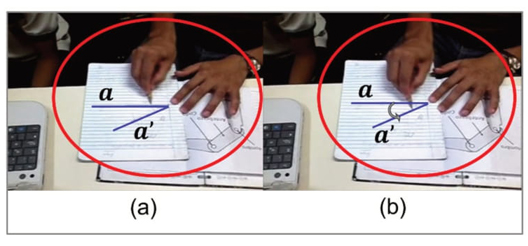
Este uso coordenado de palavras, gestos e inscrições, tanto no papel quanto no software, chega a tornar-se uma oportunidade para reconhecer a existência de a’’ como uma segunda reta presente na construção (e que também foi rotacionada, além da reta a’) no momento em que Edmilson, por vontade própria, decide utilizar a ferramenta Exibir/Esconder Objeto para fazer visíveis todos os objetos construídos até o momento (linha 43). Essa decisão de mostrar todos os elementos da construção revela como o aluno começa a duvidar do seu discurso (linha 44), questão que é aproveitada por João para aprofundar em sua intervenção (linha 47). Vale ressaltar que quando Edmilson fez uso dessa ferramenta, o controle deslizante tinha um valor de 0º; logo, as retas a’ e a’’ encontravam-se sobrepostas e não era possível distingui-las.
Por esse motivo, João solicita a Simão mudar o valor do controle deslizante para visualizar melhor ambas as retas, uma vez que todos os objetos construídos estavam a ser mostrados na tela do computador (linha 47). Essa estratégia foi potencializada pelo próprio professor ao sugerir o uso da opção Animar do GeoGebra sob o controle deslizante α (linhas 48, 49 e 50). Após a ativação dessa opção, foi possível para os alunos não só confirmarem a existência da reta a’’ no desenho dinâmico (como destacou Simão na linha 51), senão também reconhecerem que foi essa mesma reta a que realmente foi rotacionada com um ângulo expressado como variável e não a reta a’, tal como João enfatizou e como Edmilson reafirmou (linhas 52, 54 e 55), o que evidencia a tomada de consciência da ação 1.4 da técnica.
[43] Simão: Localizamos um... [fica pensativo enquanto Edmilson utiliza a ferramenta Exibir/Esconder Objetos].
[44] Edmilson: Olha, essa reta [refere-se à reta que serve de referência à rotação] de quem é linha [homóloga]?
[47] João: [Simão], mexe o controle deslizante de ângulo por favor. Quero ver o que acontece com esse controle deslizante... aí [nessa posição] está bem. Viu? Isso é o que está acontecendo, eu estava imaginando isso. O que estou vendo aí agora [nesse instante], não o enxergava quando α estava em zero. O que estou vendo de especial? [fazendo a pergunta aos alunos]. Já entendi o que este menino [Simão] fez, só com olhar isso [referindo-se ao desenho dinâmico na janela de visualização (Imagem 10) ].
[48] João: [Simão] ativa animação a isso [refere-se ao controle deslizante α].
[49] Simão: Aqui?
[50] João: Isso. Animação. Olhem... olhem.
[51] Simão: É como outra reta. Como se houvesse outra reta ali [refere-se à reta a’’, a qual se mexe à medida que o controle deslizante α toma valores distintos (Imagem 11) ].
[52] João: Exato, olha como se mexe essa reta nova [refere-se a a’’]... Porque, realmente, o controle deslizante não está vinculado com essa reta que vocês desenharam aqui [referindo-se à reta a’] senão com outra [refere-se a a’’].
[54] Edmilson: Ao parecer, essa reta [referindo-se a a’] se desenhou com um ângulo fixo [refere-se ao ângulo de 42,6º], e depois...
[55] João: E a partir dessa [referindo-se à reta a’], vocês desenharam a outra reta [refere-se a a’’].
Nesse preciso momento, além de reconhecerem a existência da reta a’’ na construção, os alunos tomaram consciência do ângulo de rotação que Simão utilizou para executar a ação 1.2. De fato, a linha 54 mostra que os alunos reconhecem que a reta a’ foi rotacionada com um ângulo fixo de 42,6º.
O RECONHECIMENTO DA CONCEITUALIDADE DA ROTAÇÃO APLICADA À RETA a’’
Após reconhecerem a existência da reta a’’ no desenho dinâmico, aquela que verdadeiramente foi obtida com um ângulo de rotação expressado como variável (α), desenvolveu-se um processo de significação da rotação aplicada a essa reta segundo a conceitualidade da qual é portadora a ferramenta Rotação em Torno de um Ponto. Nesse processo, intervém unicamente João para o encerramento da atividade de comunicação da técnica. Neste sentido, ele procede do mesmo jeito que as vezes anteriores, tentando interpretar o que implicou realizar a ação 1.4 da técnica. Na sua interpretação João produz um discurso que, através da com-binação de palavras, gestos e desenhos, refere-se tanto ao objeto a rotacionar quanto ao ângulo de rotação.
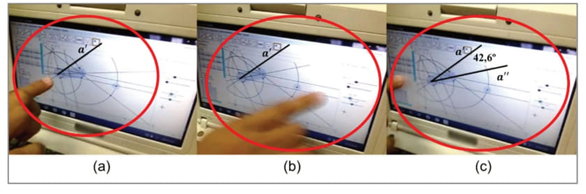
No que diz respeito ao objeto a rotacionar, enfatiza-se que este elemento corresponde a a’ e não à reta a (linha 57). Quanto ao ângulo de rotação, interpreta-se o intervalo de valores que definem α, fazendo ênfases no valor máximo do controle deslizante. Após concluir que esse valor é o dobro do ângulo usado na ação 1.2 da técnica, João justifica essa afirmação retornando ao desenho em papel. Nesse momento, ele tenta mostrar o conjunto de posições possíveis da reta a’’, de uma posição inicial (a ocupada por a’ no desenho) até uma posição final (a ocupada pela reta que é simétrica a a’’ com respeito ao eixo de simetria a), de acordo com o observado na tela do computador (linha 58).
[57] João: E depois que ele [Simão] criou essa reta [referindo-se a a’ (Imagem 12a) ], a rotaciona. Mas não rotaciona a [reta] horizontal, rotaciona essa [indica a reta a’ (Imagem 12b) ]. E a rotaciona por um ângulo α que, eu imagino, terá uma medida máxima igual ao dobro do ângulo que tinha no começo [refere-se ao ângulo de 42,6º (Imagem 12c) ].
[58] João: Por que o dobro? Porque se esse mede 41º [indicando com o lápis o ângulo de 42,6º sobre o papel] e por aqui abaixo [refere-se ao espaço por debaixo da reta a] há mais 41º, [α] chegará até 82º. Imagino que você o fez assim [comentando-lhe a Simão].
Considerando os resultados apresentados, realizamos na seção a seguir uma discussão sobre esses e formulamos nossas conclusões da pesquisa.
DISCUSSÃO E CONCLUSÕES
Nesta pesquisa apoiamo-nos na ideia da aprendizagem matemática que nos fornece a Teoria da Objetivação para dar conta dos processos de objetivação de certos saberes geométricos, mobilizados por dois alunos e um professor de matemática durante a comunicação de uma técnica de construção com o GeoGebra. Por meio de uma análise multisemiótica, identificamos quatro nós semióticos que fornecem informação sobre algumas características dos processos de objetivação do saber geométrico que acontecem em experiências de Elaboração de Simuladores com o GeoGebra. Esses aspectos dizem respeito à atividade semiótica desenvolvida, à atuação do professor durante o trabalho de comunicação e às dificuldades surgidas ao longo desse trabalho comunicativo.
A ATIVIDADE SEMIÓTICA DESENVOLVIDA
Os resultados apresentados nos nós semióticos põem de manifesto a variedade de signos (palavras, gestos, desenhos) e artefatos (lápis, papel, GeoGebra) presentes no trabalho de comunicação da técnica. No que diz respeito aos gestos e desenhos, encontramos que esses recursos tiveram uma função mediadora destacada nos processos de objetivação, uma vez que foram produzidos em sincronia com o discurso oral para revelar as conceitualidades geométricas implícitas nas ferramentas do GeoGebra usadas por Simão no desenvolvimento da sua técnica. Por exemplo, nos primeiros nós semióticos (1 e 2) observou-se o fato de os alunos tomarem consciência, de forma progressiva, da conceitualidade da rotação da qual é portadora a ferramenta Rotação em Torno de um Ponto, para o qual foi necessário conectar a linguagem natural dos alunos, baseada em palavras e gestos, com meios semióticos mais sofisticados como o desenho em papel e o desenho dinâmico.
Para tal, foi necessário desenvolver uma atividade comunicativa multimodal em que intervêm a percepção, os gestos, as inscrições em desenhos e a linguagem natural (Radford, 2013b; Vergel, 2015), para conseguir que Simão e Edmilson reconhecessem tanto os elementos característicos de uma rotação no plano (objeto, centro e ângulo de rotação), quanto as diferenças no tipo de ângulo usado nas ações 1.2 e 1.4, mantendo assim o “equilíbrio” na comunicação das primeiras ações da técnica. Esse conjunto de signos e suas relações é um exemplo do que Arzarello (2006) denomina pacote semiótico (semiotic bundle).
No marco da atividade desenvolvida nos quatro nós semióticos, os gestos foram utilizados naturalmente pelos alunos e o professor para fazer referência (em conjunto com as palavras) aos objetos geométricos, destacando algumas das suas características espaciais ou para recriar os movimentos aplicados a esses objetos, embora não sempre de uma maneira adequada. Por exemplo, nas linhas 6 e 9, Edmilson usa de forma sincronizada as mãos e o lápis, como ferramentas que fazem parte do seu espaço pessoal, para fazer visível a rotação aplicada na ação 1.2 fora dos desenhos em papel e no software. Esse tipo de gestos usados para comunicar as ações 1.2 e 1.4 da técnica estão em correspondência com algumas das categorias de gestos teorizadas por McNeill (1992), especificamente com os gestos de tipo icónico e deíctico.
Particularmente, podemos concluir que a dimensão icónica do trabalho comunicativo esteve presente, já que para os alunos e o professor alguns gestos tinham parecido visual com as entidades que eles pretendiam evocar, como por exemplo, quando Edmilson indicava a direção da reta a’ levantando sua mão com o lápis. Outra dimensão identificada é a deíctica, referida à forma em que os sujeitos indicam um objeto geométrico específico (ou algum dos seus aspectos característicos) representado no desenho em papel ou no software. Ambas as dimensões têm sido reportadas nos estudos de Gómez (2013) e Pantano (2014), embora com diferentes denominações. No caso de Gómez, o autor engloba-os em uma categoria chamada signos cinestésicos. Por sua parte, Pantano é mais específico ao referir-se a esses signos como indicações com o dedo ou um lápis.
Os desenhos também foram recorrentes no trabalho de comunicação, embora não tenham sido usados tão naturalmente pelos alunos como aconteceu com os gestos. Como consta nos quatro nós semióticos, o professor solicitava insistentemente aclarações aos alunos, colocando a atenção deles no desenho em papel, com o intuito de direcionar a discussão até a compreensão da teoria geometria mobilizada. O uso recorrente do desenho em papel (desenho geométrico) durante o trabalho de comunicação é um reflexo da maneira em que o professor evoca uma forma cultural sofisticada e evoluída de comunicar as ideias geométricas (Radford, 2011), em que o desenho geométrico é um meio de legitimação de uma técnica de construção.
Porém, tratando-se de um trabalho de construção realizado em um software dinâmico como o GeoGebra, o desenho em papel pode torna-se insuficiente para legitimar algumas ações da técnica aplicada. Mostra disso encontra-se nas linhas 27 até a 32, em que o professor decide passar do desenho em papel ao desenho no software para validar a rotação aplicada segundo o ângulo de rotação informado por Edmilson, fato que não era possível realizar no primeiro desenho. Assim, nossa pesquisa mostra como o professor se esforçou em ampliar o domínio de funcionamento do desenho geométrico, em relação à rotação, recorrendo ao software para mostrar os efeitos de ter decidido vincular o controle deslizante à rotação aplicada na ação 1.2 da técnica. O fato anterior corresponde-se com as aproximações teóricas de Laborde (1997), ao discutir as possibilidades que oferecem os desenhos dinâmicos no desenvolvimento do trabalho geométrico dos alunos.
A ATUAÇÃO DO PROFESSOR
Os resultados mostram que a atuação do professor durante o trabalho de comunicação teve uma implicação importante na aprendizagem produzida. Ao longo da atividade, ele sintoniza com os meios semióticos de Edmilson (palavras, gestos e desenhos) e os utiliza para fazer com que os alunos tomem consciência da ideia de rotação detrás da ferramenta. Neste sentido, o professor recorre aos desenhos em papel e no GeoGebra, coordenando-os com explicações verbais e gestos, para conseguir que Simão e Edmilson reconhecessem o objeto e o ângulo de rotação como elementos característicos da rotação enquanto objeto geométrico. O anterior pode ser observado em, pelo menos, duas situações evidenciadas nos resultados apresentados.
Por um lado, as linhas 20, 22, 28, 30 e 32 mostram a maneira em que João utiliza de forma coordenada palavras, gestos e os desenhos em papel e no software para questionar a Simão e Edmilson sobre como eles aplicaram a rotação da ação 1.2, em termos da conceitualidade dessa transformação geométrica da qual é portadora a ferramenta utilizada. Por outro lado, nas linhas 40, 41, 42, 47 e 48, o professor combina os desenhos em papel e no software e sintoniza com o uso que Edmilson deu à ferramenta Exibir/Esconder Objetos do GeoGebra para levar os alunos a reconhecerem tanto a existência da reta a’’ no desenho dinâmico quanto a verdadeira rotação (ação 1.4) à qual foi vinculada o ângulo definido pelo controle deslizante.
Dado que as formas de sintonizar com os meios semióticos de objetivação de Edmilson permitiram que este jovem e seu colega tivessem consciência da geometria posta em jogo, podemos concluir que a atuação de João enquanto professor é um reflexo do que Arzarello, Paola, Robutti y Sabena (2009) chamam de jogos semióticos do professor. O fato de o professor ter sintonizado com os meios semióticos do aluno não significa que suas ações didáticas estivessem condicionadas pelas vicissitudes do momento. Ao invés disso, o professor agiu de forma consciente ao longo do trabalho de comunicação, combinando os meios semióticos utilizados com claros propósitos pedagógicos. Este resultado dialoga com as pesquisas realizadas por Manghi (2010), no que diz respeito ao uso não consciente e sim intencionado dos meios semióticos por parte dos professores de matemática no desenvolvimento do seu trabalho.
Outro aspecto característico da atuação do professor durante o trabalho conjunto desenvolvido foi a sua reiterada insistência, sobretudo nos resultados dos primeiros nós semióticos, em fazer com que os alunos produzissem um discurso muito mais próximo à conceitualidade da rotação na ferramenta utilizada. Nesse sentido, as linhas 7, 20, 22 e 26 mostram os diferentes questionamentos realizados pelo professor para fazer emergir, no trabalho comunicativo, os elementos que foram considerados para aplicar a rotação da ação 1.2 da técnica. Essa insistência do professor em conseguir que o anterior se produzisse responde à responsabilidade e ao compromisso, em termos de Radford (2017b), que ele tinha com os alunos e com o próprio trabalho comunicativo.
AS DIFICULDADES SURGIDAS NO TRABALHO DE COMUNICAÇÃO
Apesar de os alunos conseguirem tomar consciência da ideia de rotação ao longo do trabalho de comunicação, podemos concluir que o reconhecimento da conceitualidade dessa transformação, da qual é portadora a ferramenta utilizada por Simão nas ações 1.2 e 1.4, foi um assunto problemático devido a duas dificuldades surgidas no decorrer da atividade. A primeira dificuldade diz respeito ao afastamento da forma de comunicar as ações da técnica por parte dos alunos em relação à forma em que o professor esperava que eles comunicassem. Quanto a isso, o professor buscava que os alunos comunicassem a aplicação da rotação em termos dos elementos solicitados pelo software (uma forma sofisticada de comunicação), fato que não aconteceu nos primeiros momentos da reunião na medida em que os alunos optaram por formas de comunicação mais intuitivas ou apoiadas na linguagem natural deles, como se evidencia nas linhas 6, 9 e 10 do primeiro nó semiótico.
A segunda dificuldade tem a ver com o tempo de separação entre o momento em que Simão produz a técnica de construção do círculo e o momento em que a comunica a João na reunião. O tempo decorrido levou a Simão a esquecer algumas das ações realizadas naquele momento, entre elas, especialmente a ação 1.4. Esse fato explica o porquê Edmilson vinculou o ângulo de rotação expressado como variável à ação 1.2 da técnica e não à 1.4, como verdadeiramente tinha acontecido. Diante disso, o professor recorreu ao desenho dinâmico para visualizar a rotação à que os alunos faziam referência (ação 1.2), observando que de fato foram rotacionadas duas retas, tal como se mostra nas linhas 27, 30, 51, 52 e 54.
Embora os resultados de esta pesquisa representem um avanço na compreensão da aprendizagem geométrica produzida em contextos de ESG, o fato de ter analisado o trabalho particular de comunicação de uma técnica não garante a compreensão aprofundada desse fenômeno. Portanto, consideramos necessário realizar outros estudos focalizados nos processos de objetivação que acontecem durante a ESG, de maneira a que os resultados obtidos possam fornecer contribuições no que diz respeito ao desenvolvimento de habilidades para a gestão de situações de ESG.











 nueva página del texto (beta)
nueva página del texto (beta)