1. EL PROBLEMA DE INVESTIGACIÓN
Las prácticas que se desarrollan tanto en el hacer propio de la disciplina matemática como en el hacer del aula para su aprendizaje, están necesariamente asociadas a prácticas de lectura y escritura. La escritura está relacionada con la posibilidad de crecimiento de las matemáticas. Particularmente la explicitación, la sistematización y la reorganización de conceptos generan nuevas relaciones, nuevos problemas y constituyen parte importante del trabajo matemático. En las clases, los alumnos pueden participar en instancias que les permiten clasificar problemas resueltos o establecer relaciones entre conocimientos que aparentan ser independientes. Se trata de prácticas que se aproximan a la idea de producir y usar modelos matemáticos. Aquí la escritura ocupa un lugar central; al escribir sobre estas relaciones establecidas es posible distanciarse, objetivar el pensamiento y enfrentarse a exigencias lingüísticas que favorecen el progreso en la conceptualización.
La investigación que se presenta estuvo centrada en el funcionamiento de las situaciones de escritura cuyo propósito era explicitar, reorganizar y sistematizar conocimientos que habían circulado en clases de Matemática a partir de la resolución de ciertos problemas. Nos detuvimos en cómo el proceso de escritura posterior a la resolución de los problemas abona a la conceptualización matemática, partiendo de la idea de que el conocimiento matemático se transforma cuando se promueven interacciones sociales a propósito de la escritura durante el proceso de institucionalización.
2. MARCOS TEÓRICOS DE REFERENCIA
El saber a enseñar en la secuencia didáctica implementada involucra prácticas de escritura al servicio de la adquisición de conocimientos matemáticos. Se trata de un saber a enseñar que requiere, para su análisis, de una mirada desde la intersección de dos didácticas específicas en términos de sus contenidos, la Didáctica de la Matemática y la Didáctica de la Escritura.
La indagación se inscribe en la perspectiva de la Didáctica de la Matemática francesa que concibe a las matemáticas como un producto cultural y social, en permanente transformación y construido a través del trabajo de la humanidad al enfrentarse a diferentes clases de problemas. Desde esta perspectiva, la enseñanza de las matemáticas busca generar condiciones para involucrar a los alumnos en procesos colectivos de producción de conocimientos en torno a ciertos objetos matemáticos y de maneras específicas de pensar y producir en esta disciplina (Artigue, 1986; Charlot, 1991).
Un importante marco de referencia para la construcción y análisis de la secuencia implementada en este estudio ha sido la Teoría de Situaciones de Brousseau (1993, 1994, 2007). Sus situaciones de formulación son un referente que nos permite pensar sobre cómo se transforman los conocimientos al ponerlos en palabras para explicitarlos o formularlos por escrito. Apelamos a esta teoría para el estudio de las condiciones didácticas que favorecen que los alumnos produzcan, expliciten y validen sus conocimientos. Además, el concepto de institucionalización como proceso (Perrin-Glorian, 1995; Margolinas, 1993) es central para esta investigación, dado que se pretende analizar cómo funcionan las situaciones de escritura al explicitar, reorganizar y sistematizar lo aprendido.
Un concepto potente para la presente indagación es el de memoria didáctica. Brousseau y Centeno (1991) mostraron que sostener la memoria didáctica evocando la experiencia matemática de los alumnos con relación a conceptos cercanos a los que se están trabajando incide fuertemente en sus aprendizajes. En este estudio, las escrituras producidas en las situaciones de enseñanza resultan un punto de apoyo para el sostenimiento de la memoria didáctica de los alumnos a lo largo de la secuencia implementada.
Otra contribución es tomada de la Teoría Antropológica de lo Didáctico de Chevallard (1997). El autor plantea que los procesos de enseñanza y aprendizaje de las matemáticas son aspectos particulares del proceso de estudio, entendiendo la palabra “estudio” en un sentido amplio que engloba tanto el trabajo matemático del alumno, como el del matemático. Las situaciones de escritura que se incluyen en la secuencia de enseñanza pretenden formar parte de este proceso.
Como marco referencial de la Didáctica de la Escritura se toman aportes del enfoque de base psicogenética que comparte supuestos epistemológicos considerados en el marco proveniente de la Didáctica de la Matemática. En esta línea, Castedo (2003) conceptualiza la escritura como un proceso cognitivo inserto en un contexto histórico y social y señala que enseñar a escribir es enseñar a participar en una comunidad de discurso con tareas auténticas y en interacción con los otros.
La propuesta de incluir situaciones de escritura en las clases de matemática involucra el supuesto de que el proceso de escritura favorece la transformación de conocimientos. Miras (2000) distingue la función epistémica o heurística de la escritura, como función específica en el marco de la función representativa, y subraya su potencia como instrumento de toma de conciencia y autorregulación intelectual y como instrumento para la construcción del propio pensamiento.
Otros estudios que constituyen una referencia conceptual son los que se han ocupado de la enseñanza y el aprendizaje de la escritura como herramienta para la apropiación de contenidos escolares de algunas disciplinas específicas (Vérin, 1988, 2004; García-Debanc, 1995; Lerner, Aisenberg y Espinoza, 2012). Estos parten de la idea de que la producción de escritos por parte de los alumnos puede jugar un papel decisivo en la elaboración del pensamiento, así como facilitar la puesta en juego de las ideas propias y su transformación progresiva. Uno de los trabajos especialmente relevante es el de Chabanne y Bucheton (2002) vinculado con el papel de los escritos de trabajo o “escrituras intermedias” en la construcción del conocimiento en la escuela primaria. Se trata de escritos destinados a acompañar y estimular la actividad reflexiva durante las tareas de recolección o recuperación de la información.
3. DECISIONES METODOLÓGICAS
La investigación reportada consiste en un estudio cualitativo de carácter exploratorio que asume el marco metodológico del estudio de casos y toma algunos aportes de la Ingeniería Didáctica (Artigue, 1995).
La indagación se llevó a cabo a través de la implementación de una secuencia de situaciones de enseñanza de un contenido matemático: los números racionales en su expresión fraccionaria, en un grupo de 5° año de Educación Primaria. Para elaborarla se utilizaron y combinaron problemas matemáticos que involucraban diferentes sentidos de las fracciones extraídos de otras ingenierías (Block, 1987; Block y Solares, 2001), de documentos curriculares y de libros de texto escolares. Para su selección se tuvieron en cuenta la potencia de esos problemas para producir ideas que pudieran ponerse en discusión con las de sus pares, que promovieran rupturas con respecto a los conocimientos anteriores de los alumnos sobre los números naturales y que incluyeran sentidos diversos de las fracciones. En las 17 clases de la secuencia se presentaron distintos momentos de resolución de problemas, de intercambio oral acerca de las resoluciones, así como también instancias de explicitación, reorganización y sistematización de conocimientos en situaciones de lectura y escritura diferentes. Se incluyeron situaciones de escritura individual, en parejas y colectiva por dictado al docente, situaciones de lectura de estas escrituras para recuperar la información y situaciones de revisión y reescritura, todas ellas vinculadas al proceso de institucionalización de los conocimientos matemáticos que circularon en la clase durante la resolución previa de problemas.
Para seleccionar el aula en la que se implementó la secuencia se consideró la formación didáctica del docente,4 su disposición a participar de la investigación, experiencias previas suficientes del grupo de alumnos en prácticas matemáticas y prácticas de escritura con sentido y condiciones institucionales favorables para implementar la secuencia. El contenido elegido fue los números racionales, en su expresión fraccionaria, dado que su estudio supone enfrentar a los alumnos a numerosas rupturas con respecto a los conocimientos construidos en torno a los números naturales (Block, 1987; Centeno Pérez, 1988; Block y Solares, 2001). Supusimos que ello podría potenciar los intercambios y la diversidad de ideas que incluyen los niños en sus escritos.
El diseño de la secuencia se realizó en un espacio de trabajo compartido con el docente en el que, a partir de un esquema de situaciones presentado por el investigador, se hicieron modificaciones de acuerdo al nivel de conocimientos de los niños y al recorrido didáctico ya realizado. Durante la implementación de la secuencia se sostuvo este espacio de intercambio con el docente para realizar ajustes.
Las fuentes para la reconstrucción de la secuencia implementada y su posterior análisis se realizó a partir de un conjunto de insumos: registros de las interacciones que tuvieron lugar en el aula a propósito de la resolución de los problemas y de las escrituras vinculadas al trabajo de explicitación, reorganización y sistematización de conocimientos. Además, producciones escritas de manera colectiva en pizarrón y afiches y las que realizaron los alumnos por sí mismos en sus carpetas.
En este artículo presentamos un recorte de los resultados que forma parte de la dimensión de análisis referida a la transformación de los conocimientos matemáticos en situaciones de escritura ligadas al proceso de institucionalización.5 Entre los numerosos problemas que resolvieron los alumnos seleccionamos, para este recorte, solo uno de ellos denominado en la secuencia repartos de “X” chocolates entre “Y” niños.6 Para llevar a cabo este análisis se confrontaron las formulaciones realizadas por los alumnos en dos situaciones de intercambio, la puesta en común sobre la resolución del problema y la escritura colectiva de conclusiones en la que se proponía a los alumnos que agregaran nuevas ideas al cartel que venían elaborando desde clases anteriores, titulado: “¿De qué maneras puedo resolver un reparto?”.
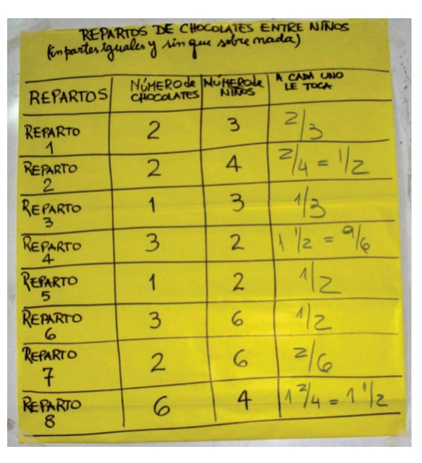
El problema matemático consistía en la comparación de 8 repartos diferentes de chocolates entre niños, en partes iguales y sin que sobrara nada:
| Repartos | Número de chocolates | Número de niños | A c/u le toca |
|---|---|---|---|
| Reparto 1 | 2 | 3 | |
| Reparto 2 | 2 | 4 | |
| Reparto 3 | 1 | 3 | |
| Reparto 4 | 3 | 2 | |
| Reparto 5 | 1 | 2 | |
| Reparto 6 | 3 | 6 | |
| Reparto 7 | 2 | 6 | |
| Reparto 8 | 6 | 4 |
A.¿A los niños de qué repartos les tocará, a cada uno, más de un chocolate?
B.¿A los niños de qué repartos les tocará la misma cantidad de chocolate?
C.¿A los niños de qué repartos les tocará más chocolate que a los del reparto 1?
D.Elijan por lo menos un reparto del que estén seguros que a cada chico le toca lo mismo de chocolate que a cada uno del reparto 5.
Para el momento de resolución se organizó a los niños en parejas. Debían responder en primer lugar las preguntas que requerían el establecimiento de ciertas relaciones entre los números intervinientes en los repartos, sin resolverlos, y posteriormente debían resolver uno de los repartos que era indicado por la docente a cada pareja.
4. RESULTADOS
A continuación se presentan algunos resultados referidos a la resolución del problema en parejas, a la puesta en común de las resoluciones de los repartos y a la escritura colectiva.
4.1. RESOLUCIÓN DEL PROBLEMA EN PAREJAS
Seleccionamos a modo de ejemplo fragmentos del intercambio de una de las parejas, la de Yael que oficiaba de dictante y Natalí que tenía a su cargo la escritura en el papel. Mientras responden la pregunta B, Yael parece tomar conciencia de un conocimiento a partir de enunciarlo para que sea escrito por su compañera.
[1]7 Yael: Acá (señala reparto 2), tiene que ser la mitad. Y en esta, y en esta (señala muy segura los repartos 5 y 6).
(Ambas niñas verifican en la tabla mirando los números, nuevamente sin hacer cálculos, “en esta no…, en esta sí…” y concluyen que los que cumplen la condición solicitada en la pregunta son solo los repartos 2, 5 y 6 que permiten obtener las fracciones 2/4, ½ y 3/6, respectivamente)
[2] Yael: Bueno, poné…, dibujá 2 chocolates. (Da esta indicación a Natalí para representar el reparto de 2 chocolates entre 4 niños). Poné (dicta) les toca la misma cantidad, (dice) porque no es nuestro trabajo poner cuántos sino por qué (no se pedía en la consigna que explicaran por qué). Y abajo ponele el 5, dibujá los chocolates, dibujá los tipitos8 y poné lo mismo, les toca la misma cantidad. Y en el 6 dibujá 3 chocolates y 6…
[3] Natalí: (sigue resolviendo en la hoja sin detenerse, de manera casi automática) después hago una llave y pongo (se autodicta) porque son el doble.
[4] Yael: (dicta) Porque son el doble, (dice) ponele eso… De personas, porque habla de personas y la mitad de chocolate…
(Natalí continúa resolviendo en la hoja y Yael se queda pensando)
[5] Yael: Yo no sabía eso de que si era el doble o la mitad… (se queda pensando)
[6] Natalí: (va diciendo lo que escribe y preguntando) Porque son el doble, ¿de personas?
[7] Yael: Porque son el doble de personas y la mitad de chocolates. De cantidad, que quede eso, de cantidad. Entre paréntesis ponele (dicta) de cantidad.
[8] Natalí: ¿Qué pongo?
[9] Yael: Cantidad. Porque estamos hablando de la cantidad no de la forma.
(Queda escrito: “Porque son el doble de personas y la mitad de chocolate (cantidad)”)
La selección de los repartos que permiten obtener el mismo cociente no parece ofrecer dificultad para estas niñas, dado que con solo mirar los números correspondientes a la cantidad a repartir y a las partes entre las que se reparte esa cantidad, ellas pueden identificar cuáles cumplen la condición solicitada. Yael interpreta la consigna afirmando que no se pide que expliciten cuánto le toca a cada niño en el reparto sino las razones por las que esas fracciones representan la misma cantidad [2]. Al justificar por qué esos cocientes son iguales ambas niñas acuerdan en que se debe a que son el doble de personas y la mitad de chocolates [3] [4] [6] [7]. Durante la textualización compartida de estas ideas, Yael reconoce un aprendizaje nuevo: “Yo no sabía eso de que si era el doble o la mitad…” [5]. Ella parece referirse a que si la cantidad de partes entre las que se reparte -representada en el denominador- es el doble de la cantidad a repartir -representada en el numerador-, o bien, esta última es la mitad de la primera, la fracción resulta equivalente a ½. Esta relación que se había puesto en juego a nivel implícito en la selección de los repartos equivalentes pudo ser identificada por esta niña como un nuevo conocimiento gracias al desafío que supuso dictarlo para que su par lo incluyera en la producción escrita de la resolución.

Figura 1: Detalle de la producción de la pareja de Yael y Natalí para resolver el problema de comparación de repartos de “X” chocolates entre “Y” niños.
Veamos cómo responden la pregunta D.
[10] Yael: Ah, mirá, acabo de descubrir algo. (Señala los números de la tabla, dibuja una rayita en el medio de los chocolates y los chicos en repartos 5 y 3, y lee) Un medio y un tercio.
[11] Camila (niña de la pareja frente a Yael y Natalí): Todos son así, todos son con la rayita. Es como que todos tuviesen la rayita acá (se refiere a que la rayita está entre las columnas de chocolates y de niños). Es así de fácil.
[12] Yael: ¿En serio? (sorprendida) ¿Todos?
[13] Camila: Sí.
(Natalí continúa resolviendo el problema planteado en la consigna D. Yael va haciendo aportes, hace algunos dibujos antes de afirmar que 3/6 es igual a ½ y 2/4 también)
[14] Yael: ¿Sabés qué? Camila me dio una idea. (Va marcando la raya intermedia y va leyendo las fracciones resultantes en cada reparto) Dos tercios, dos cuartos, un tercio, tres dosavos…, no sé, como se diga, ¿entendés? Todos, si les ponés la rayita es el resultado.
(Comienzan a resolver el reparto N°3 que les había sido asignado por la docente. Yael dicta y Natalí escribe cómo lo van resolviendo)
[15] Yael: (dicta) Dividimos el chocolate en 3 y al ser 3 chicos, nos dio justo para 1/3 para cada uno… (dice) Y también anotá eso de la rayita… Es interesante.
(Natalí, que pareció no escuchar la explicación anterior de su compañera, va completando las rayitas que faltaban en la tabla)
[16] Yael: Pero no, las rayitas no, expliquemos algo de eso.
[17] Natalí: Vos explicalo, yo no tuve la idea.
Las relaciones que las niñas iban estableciendo para responder las cuatro preguntas y la disposición de las cantidades en el cuadro de los repartos promovieron que Yael comenzara a observar una regularidad sustancial [10] : los números que indican la cantidad a repartir y la cantidad de partes entre las que se reparte, corresponden respectivamente al numerador y al denominador de la fracción resultante. Si bien este descubrimiento se circunscribió en un principio a los repartos N°3 y N°5, la interacción con Camila [11] [12] [13] facilitó que Yael elaborara la idea de que era posible extender la relación a todos los repartos del cuadro.
Yael intenta compartir el hallazgo con su compañera y propone incluir la explicación -“anotá eso de la rayita”- en la resolución del reparto N°3 porque “es interesante” [14] a [16]. Natalí comienza a completar las rayitas que faltan en el cuadro pero no está dispuesta a incluir la explicación, posiblemente debido a que aún no resultaban claras para ella las razones por las que “funcionaba” tal procedimiento.
4.2. PUESTA EN COMÚN DE LAS RESOLUCIONES DE LOS REPARTOS
Al socializar los procedimientos, algunas parejas comenzaron a explicitar la relación entre las cantidades de chocolates y de niños y los números correspondientes al numerador y denominador de la fracción resultante del reparto. Luca y Ramiro fueron los primeros en hacer circular esta nueva relación a propósito del reparto N°2 (2 chocolates entre 4 niños):
[18] Docente: ¿Ustedes lo pensaron igual?, Luca, ¿cómo pensaron?
[19] Luca: Yo de pronto estaba mirando… Hubo una parte que estaba mirando y vi el número de chocolates y los chicos y dije: 2/4, lo comprobé y me daba. Que si el número de chocolates se pone como el primer número, digamos, de arriba, y el número de chicos se pone como la parte de abajo, da igual.
[20] Docente: ¿Así como está acá, 2/4? (señala el número 2 y el número 4 en la misma fila del cuadro)
[21] Luca: Hice la cuenta, después, sí, daba en todas.
[22] Docente: A ver, ¿qué cuenta hiciste?
[23] Luca: Le fui restando a dos, que es el número de chocolates, le fui restando los 2/4 y me dio justo.
[24] Docente: ¿Y vos te das cuenta por qué llegaste a eso de 2/4?
[25] Luca: Emmm (se queda pensando).
[26] Docente: A ver, miren lo que hizo Luca. Luca sabe que tiene estos dos chocolates (los dibuja en el pizarrón), ¿no? Y él dijo, le voy a dar 2/4 a cada uno. Y él se fijó si sacándole 2/4 a esto (señala los dos chocolates) podía decir si recibía 2/4 cada uno. (A Luca) ¿Cuántas veces le sacaste 2/4 a esto?
[27] Luca: 4 veces.
[28] Docente: 4 veces, ¿por qué?
[29] Luca: Porque son 4 chicos.
[30] Docente: Porque son 4 chicos los que están en el reparto. Pero, ¿yo puedo decir que porque sí, a mí se me ocurrió decir que iba a recibir cada uno 2/4? De algún lado salió, ¿cómo llegaste a eso?
[31] Luca: Llegué porque… primero vi el número de chocolates y después vi el número de chicos y ahí se me vino a la cabeza 2/4. Cuando hice la cuenta sí daba que eran 2/4.
[32] Docente: ¿Entendieron cómo lo pensó él?
[33] Sofía O.: Yo no entendí por qué los 2/4 y no 3 (se refiere a –).
[34] Docente: (A Luca) ¿Por qué hiciste 2/4 y no –?, dice Sofía. ¿De dónde sale ese 2 y de dónde sale ese 4?
[35] Luca: El 2 sale de, del número de chocolates y el 4 sale del número de chicos. (Ramiro va señalando en el cuadro de su hoja los números que menciona Luca para que toda la clase los vea)
[36] Docente: ¿Entendés, Sofi, por qué dijo el 2 y por qué dijo el 4 y no el 3?
[37] Sofía O.: Sí.
[38] Docente: Porque 2 son la cantidad de chocolates y 4 la cantidad de chicos.
La explicación de Luca da cuenta de cierta captación visual de las relaciones entre la cantidad que corresponde al numerador y la cantidad que corresponde al denominador de la fracción resultante: “estaba mirando y vi…” [19], “primero vi el número de chocolates y después vi el número de chicos y ahí se me vino a la cabeza 2/4” [31]. Esta relación que va estableciendo de manera intuitiva necesita ser comprobada para poder ser extendida luego a los demás pares de números [21] [31]. Para validar su conjetura, Luca no realiza el reparto de los dos chocolates entre cuatro chicos sino que efectúa cuatro restas sucesivas de 2/4 a los dos chocolates que tiene para repartir y concluye que es verdadera. Este uso de la resta se vincula con el sentido de partición que tiene el problema. La docente pregunta y repregunta con la intención de que Luca haga cada vez más explícita la relación que elaboró y que se difunda en la clase para que pueda ser comprendida por el resto de los alumnos.
4.3. ESCRITURA COLECTIVA
El intercambio producido en torno al procedimiento que pone en juego la relación entre el reparto de a unidades entre b partes y la fracción a/b despertó gran interés en los alumnos. Antes de pasar a la puesta en común de las respuestas a las cuatro preguntas que iniciaban el problema, la docente propuso registrar por escrito en el afiche que ya venían elaborando la nueva forma de resolución hallada. El afiche estaba encabezado por el título “¿De qué maneras puedo resolver un reparto?”.
El dictado al docente se centró en un primer momento en el grado de generalidad que asumiría la formulación del nuevo modo de resolver para trascender el contexto extramatemático en que se había planteado el problema:
[1] Docente: ¿Cómo puedo poner, Yael?
[2] Yael: (dicta) Si sabés la cantidad de personas entre las que tenés que repartir… (La docente escribe: “Si sabés la cantidad de personas entre las que tenés que repartir”)
[3] Yael: (dicta) Y el objeto que tenés que repartir… (dice) ¿cómo se dice?
[4] Natalí: (dicta) Y el entero.
[5] Yael: (dicta) Y el entero.
[6] Lucas: La cantidad, (dicta) y la cantidad de chocolate.
[7] Natalí: Porque no siempre es un entero.
(Murmullo)
[8] Docente: ¡Paren! Yael dijo, (lee) si sabés la cantidad de personas entre las que tenés que repartir y (dice) ¿el entero? Natalí está diciendo: no siempre es un entero. Macarena dice que podrían agregar ‘la cantidad’, él dijo lo mismo, ¿cómo podemos poner?
[9] Macarena: (dicta) Y la cantidad que tenés para repartir, (dice) lo que pasa que quedaría…(no se entiende)
[10] Docente: ¿Y la cantidad que tenés para repartir? (escribe: “la cantidad que tenés”)
[11] Yael: Porque si no, sería de chocolates pero no siempre son chocolates.
[12] Docente: Escuchen esto que dice Yael. Yael dice no poner la cantidad de chocolates porque no siempre son chocolates.
[13] Natalí: De objetos podés poner.
[14] Docente: ¿Les parece que está bien esto que está diciendo Yael?
(Interrupción)
[15] Docente: (retomando) Ellas están tratando de explicar cómo es que yo puedo poner la rayita y me daba dos tercios para cada nene, ¿sí? Yael dijo, (lee) si sabés la cantidad de personas entre las que tenés que repartir y la cantidad que tenés.
[16] Yael: (dicta) Para repartir, ponés… emmm.
[17] Macarena: (dicta) Ponés la cantidad… (dice) Lo que pasa que queda mucho ‘cantidad’.
[18] Docente: Piensen esto, es un borrador. Uno cuando escribe, por ahí escribe un montón de cosas y no siempre lo primero que escribe es lo que va a quedar, ¿o no? Vamos a ir revisándolo, si hay que tachar tachamos. Si hay que agregar, agregamos. Dale.
[19] Macarena: (dicta) Ponés… la cantidad… de… (dice) no sé.
[20] Varios alumnos: (dictan) La rayita.
[21] Docente: Maca, ¿ponés la qué?, ¿la rayita?
(Murmullos)
[22] Docente: Escuchen, Yael hizo esta introducción, (lee) si yo sé la cantidad de personas entre las que tenés que repartir y la cantidad que tenés para repartir ponés… (dice) ustedes qué tuvieron en cuenta, la cantidad de chocolates y entre la cantidad de personas que se hacía ese reparto, ¿y qué te indicaba cada cosa?
(Algunos niños responden pero no se entiende)
[23] Docente: (destapa el afiche de los repartos del problema y señala allí en la primera fila). Por ejemplo, vos Maca, habías dicho, si es 2 chocolates entre tres nenes es 2/3, ¿sí o no?, bueno, ¿cómo hiciste eso, cómo lo pensaste?
[24] Macarena: No sé, porque yo en realidad primero partí los chocolates dibujándolos y después mirando me di cuenta de que era lo mismo.
[25] Docente: Está perfecto, pero estamos tratando de explicar esta forma. ¿Cómo puedo hacer yo para que entiendan esta nueva forma? Ustedes acá saben la cantidad que tienen para repartir y entre la cantidad que tienen que hacer ese reparto. Yael lo empezó así. ¿Qué es lo que hicieron ustedes?
[26] Yael: La rayita. La rayita entre…
[27] Natalí: La barra.
[28] Lucas: ¡El dominador (sic) y el numerador!
[29] Yael: No entre coso, entre la cantidad de…. repartir…
[30] Docente: ¿A ver, Cami?
[31] Camila: Yo quería poner, por ejemplo, que la cantidad se transforma en el numerador y las personas en el denominador.
[32] Docente: Camila dice que esta cantidad de cosas que yo tengo para repartir se transforma en el numerador y la cantidad de personas que tengo para hacer el reparto se transforma en el denominador. ¿Están de acuerdo con eso?
[33] Varios alumnos: Sí.
[34] Yael: ¿Pero primero no tenemos que anotar qué es el numerador y el denominador?
[35] Docente: Si quieren después podemos poner un ejemplo. A ver, Cami, ponés ¿qué? A ver, dale (invitándola a que continúe con el dictado).
[36] Camila: No sé.
[37] Docente: Como me lo dijiste vos.
[38] Camila: Pero con ‘ponés la’ (era lo último que habían escrito), no sé bien. (dicta) Ponés la rayita entre medio de la…
[39] Docente: Lo que dijiste antes.
[40] Camila: Que después se transforma la cantidad de personas en el denominador y…
[41] Docente: Esperá, ¿’después’, dijiste? (escribe: ”después se transforma la cantidad”)
[42] Camila: Sí.
[43] Docente: ¿La cantidad?
[44] Camila: (dicta) De personas en el denominador.
[45] Docente: ¿La cantidad de fracciones?
[46] Camila: No, de personas.
[47] Docente: ¿Habías dicho de personas? ¿En qué se transforma la cantidad de personas?
[48] Camila: En el denominador.
[49] Docente: (lee mientras escribe) Y después se transforma la cantidad de personas en el denominador. (dice) ¿Y qué más?
[50] Camila: (dicta) Y lo que tenés que repartir en el numerador.
(Queda escrito en el cartel: “Si sabés la cantidad de personas entre las que tenés que repartir y la cantidad que tenés para repartir, después se transforma la cantidad de personas en el denominador y lo que tenés que repartir en el numerador”)
En sus primeras intervenciones Yael y Natalí parecen preocupadas por aludir a la cantidad a repartir usando algún término que no solo refiera a los chocolates que formaron parte del contexto del problema de origen; de allí que proponen “el objeto” o “el entero que tenés para repartir” [3] [4] [5] [13]. La propuesta de Lucas: “la cantidad de chocolate” [6] obliga a estas alumnas a explicitar que puede ocurrir que lo que se reparta no sean chocolates o que ni siquiera sean enteros [7] [11]. Se suceden entonces algunas propuestas que coinciden en escribir “la cantidad que tenés para repartir” sin especificaciones acerca de qué se reparte, aunque la repetición del término ‘cantidad’ no convence demasiado a Macarena [9] [17]. La preocupación que introduce esta alumna no está centrada en el contenido de la producción escrita, sino en un problema de cohesión textual, la pertinencia de la repetición léxica. Cuestiones como esta, vinculadas a la redacción, se intercalan con las que se centran en el contenido de la producción y vuelven a aparecer en el fragmento siguiente del intercambio.
Para superar el escollo que suponía para los niños la formulación en términos algo más generales, la docente se esfuerza por que reparen en la relación entre las cantidades que están intentando diferenciar y los componentes que integran la fracción resultante del reparto [22] [23] [25]. Si bien en principio solo mencionan “la rayita” y dudan al definir las cantidades que corresponden al numerador y al denominador, una de las alumnas, Camila [31], logra enunciar oralmente esta relación: “la cantidad se transforma en el numerador y las personas en el denominador”. A pesar de haber propuesto la idea, ponerla en palabras aptas para poder ser textualizadas no resulta una tarea sencilla; el intercambio producido en las intervenciones [35] a [50] está dedicado a ajustar esta escritura. Es interesante la propuesta de Yael [34] de agregar la definición de numerador y de denominador a la descripción de Camila. Pareciera que esta alumna percibe la necesidad de aclarar estos conceptos ya que se han formulado de manera muy imprecisa en los intentos del grupo por describir el procedimiento encontrado.
El fragmento siguiente incluye intervenciones de los niños orientadas a mejorar la redacción del texto producido y a discutir el alcance de la generalización del procedimiento en cuestión y la información que es necesario incluir para que resulte más clara para el lector. La docente da lugar a todas las intervenciones aunque no todas las propuestas son incluidas en la producción escrita, ya que permanentemente las hace circular para que sean consensuadas:
[51] Docente: A ver, escuchen esto (lee lo que quedó escrito). ¿Están de acuerdo con esto? ¿Albertina?
[52] Albertina: Profe, dice (lee) para repartir, después se transforma (dice) y después hay que poner ‘en, en la cantidad de la que tenés que repartir’.
[53] Valentina: No, para mí está bien. Porque ella dice de poner ‘después se transforma en la cantidad’…
[54] Docente: Porque ¿quién es el que se transforma? ¿Se transforma la cantidad de personas? A ver, dice (lee) después se transforma la cantidad de personas en el denominador y lo que tenés que repartir en el numerador. (dice) ¿Están de acuerdo con eso que dijo Camila? ¿Sofi?
[55] Sofía: Yo le pondría en ‘para repartir’, punto, después… Porque si no, estás…
[56] Lucas: Profe, yo le pondría una rayita. El numerador, por ejemplo el uno, un medio, ¿no? (hace gesto de dibujar la línea de la fracción en el aire)
[57] Docente: Es verdad que ustedes lo pensaron así, agregarle esta rayita. Maca, Yael, Camila, habían pensado en esta rayita (completa las líneas de las fracciones en los repartos del cuadro). Al decir que esta cantidad de chocolate se transforma en el numerador (señala la columna ‘Número de chocolates’) y que las personas entre las que hacen el reparto (señala la columna ‘Número de niños’) se transforman en el denominador, ¿no estamos hablando de que ya es una fracción? De hecho, ¿ustedes no llegaron a hacer todo este tipo de anotaciones (señala la columna ‘A cada uno le toca’ en la que hay diferentes fracciones escritas)? Lucas, lo que estaba haciendo Camila era explicar por qué este 2 que estaba acá (señala el 2 en la columna ‘Número de chocolates’) pasaba acá (señala el numerador de la fracción resultante) y este 3 (señala el 3 en la columna ‘Número de niños’) pasaba acá (señala el denominador de la fracción resultante), ¿sí? ¿Es necesario agregar lo de la rayita? ¿Están de acuerdo con esto? (señala lo que escribieron). Valentino, ¿estás de acuerdo con esta explicación?, ¿sirve para resolver un reparto?
[58] Valentino: En este caso sí, pero por ahí en otro caso, no.
[59] Docente: ¿En otros repartos no sirve?
[60] Valentino: Para mí, no.
[61] Docente: ¿Por qué?
[62] Valentino: Por ejemplo, si no hay un entero de chocolate, hay un medio de chocolate.
[63] Docente: Lo de Camila, sí.
[64] Valentino: No… creo que no sirve.
[65] Varios alumnos: No entiendo lo que dice Valentino.
[66] Docente: Pensando en estos casos (se refiere a los repartos del problema), después vamos a ver qué pasa cuando yo no tengo enteros, pensando en estos casos, yo tengo enteros para repartir entre ciertas personas, ¿me sirvió esta forma?
[67] Varios alumnos: Sí.
[68] Docente: ¿Están todos de acuerdo? ¿No quieren modificar nada más de esta forma?
[69] Yael: Podemos poner un ejemplo.
[70] Docente: ¿Qué ejemplo?
[71] Yael: Y, le ponemos ejemplo y una fracción y le ponemos lo de arriba es el numerador y lo de abajo…
[72] Natalí: Explicar qué es el numerador…
[73] Docente: Nosotros, alumnos de 5°, si leemos que la cantidad de chocolate se transforma en el numerador y que la cantidad de personas por las que yo tengo que hacer el reparto se transforma en el denominador, ¿necesitamos poner qué es el numerador y el denominador?
(Silencio, algunos alumnos dicen que no)
[74] Docente: Les estoy haciendo una pregunta a ustedes, eh, ¿no?, ¿es suficiente con esto?
[75] Martina: Para mí el ‘después’ ese queda un poco de más.
[76] Docente: ¿Qué pongo?
[77] Martina: Tachalo y poné directamente ‘se transforma…’
[78] Docente: Si sabés la cantidad de personas entre las que tenés que repartir y la cantidad que tenés para repartir, se transforma la cantidad de personas en el denominador y lo que tenés que repartir en el numerador.
[79] Fabricio: Para mí en el ‘tenés que repartir’ de abajo va coma, (lee) lo que tenés que repartir, (dice) coma, (lee) en el numerador.
[80] Docente: Yo les había hecho una consulta, en esta forma que ustedes habían puesto (señala el afiche), nosotros ya sabemos que estamos resolviendo repartos. Si yo estoy resolviendo un reparto hay algo para repartir entre algo, ¿no? En los anteriores, ¿necesitaron aclarar esto de que si yo tenía para repartir algo entre tantas personas?
[81] Algunos alumnos: No.
[82] Docente: Fueron directamente a la forma de resolverlo. Pensando en eso, ¿qué podría yo registrar en el afiche?
(Silencio, parecen cansados de la situación, algunos hacen propuestas que no llegan a concretarse)
[83] Natalí: ¿No quedaría mejor: la cantidad de personas se transforma en el denominador y lo que tenés que repartir en el numerador?
[84] Docente: Natalí dice primero poner la cantidad de personas se transforma en el denominador y lo que tenés que repartir en el numerador. Este ‘se transforma’ trasladarlo acá, (subraya ‘se transforma’ y hace una flecha indicando el lugar donde iría, luego lee) la cantidad de personas se transforma en el denominador y lo que tenés que repartir en el numerador.
[85] Varios alumnos: Está bien.
[86] Docente: Lo dejo ahí.
[87] Inv.: Hoy escuché a Valentino que dijo: -pero puede ser que entre los que se reparta no sean personas. ¿Eso sirve para pensar en cambiar algo más o lo dejamos con personas?
[88] Docente: Está diciendo esto que había dicho Yael con respecto a lo que yo tenía que repartir. Algunos dijeron de poner chocolates y Yael dijo que no siempre se reparten chocolates. ¿Y esto que está diciendo Valentino, tiene razón o no? Valentino dijo que no siempre es entre personas el reparto. (Murmullo)
[89] Docente: ¿Entonces cómo puedo poner, qué puedo sacar o qué puedo agregar?
[90] Fabricio: Si sabés la cantidad de cosas para repartir.
[91] Docente: (lee) Si sabés la cantidad de personas entre las que tenés que repartir y la cantidad que tenés para repartir, (dice) ¿a qué se está refiriendo con la cantidad de personas?, ¿son las cosas que yo reparto?
[92] Yael: No, son las cosas que…
[93] Natalí: A quién repartís.
[94] Lucas: En partes que lo repartís.
[95] Docente: ¿Cómo puedo poner esto de las personas para que no quede como que es exclusivo para cuando son personas?
[96] Camila: Son las veces que tenés que…
[97] Docente: ¿Si sabés la cantidad de veces entre las que tenés que repartir, pongo? (lo escribe)
[98] Alumno: Objetos.
[99] Docente: ¿Siempre van a ser objetos?
[100] Alumno: Pueden ser muchas cosas.
[101] Docente: ¿Y no habrá una palabra que reúna todo eso que puede llegar a ser?
[102] Lucas: ¡Seres vivos!
[103] Docente: Esto que los chicos dicen que (lee) Si sabés la cantidad de veces entre las que tenés que repartir y la cantidad que tenés para repartir, (dice) ¿no es suficiente eso?
[104] Sofía O.: Ese ‘se transforma’ abajo para mí iría después de ‘para repartir’.
[105] Docente: Vos seguís con lo de ‘se transforma’. A ver, (lee) después se transforma la cantidad de veces en el denominador y lo que tenés que repartir en el numerador, (dice) o puede quedar (lee cambiando de lugar ‘se transforma’) después la cantidad de veces se transforma en el denominador y lo que tenés que repartir en el numerador. (dice) Puede quedar como la opción 2 o como está así, hace un rato dijeron así, por eso no lo agregué.
[106] Varios alumnos: La 2. Otros: ¡Dejalo así!
[107] Docente: ¿Quiénes prefieren la 2?
(Algunos alumnos levantan la mano, otros gritan: ¡así!).
[108] Docente: ¿Lo dejo así? ¿Me escuchan? No modifica el sentido del texto. Si yo pongo el ‘se transforma’ ahí o donde está la flechita no va a modificar lo que vamos a entender. ¿Lo pongo así en el afiche? (se refiere a copiar lo que estuvieron escribiendo en el pizarrón en el afiche).
[109] Alumnos: ¡Sí!
(Queda escrito: “Si sabés la cantidad de veces entre las que tenés que repartir y la cantidad que tenés para repartir, después se transforma la cantidad de veces en el denominador y lo que tenés que repartir en el numerador”. Posteriormente se pasa en limpio al afiche)

Figura 3: Escritura colectiva en borrador para ser agregada al cartel que lleva el título: ¿De qué maneras puedo resolver un reparto?, sobre el procedimiento que pone en juego la relación entre el reparto de a unidades entre b partes y la fracción a/b
Los intereses de los niños giran en torno a tres núcleos que se van superponiendo. Uno de ellos es la necesidad de incluir información o ejemplos acerca del significado de los componentes de una expresión fraccionaria -numerador, denominador y línea de la fracción-, dado que son conceptos que se mencionan en la explicación del procedimiento que acaban de escribir y no parecen haber sido suficientemente definidos para algunos alumnos. Así, Lucas [56] propone agregar “la rayita” a través de un ejemplo, la fracción ½, a continuación de ‘se transforma la cantidad de personas en el denominador y lo que tenés que repartir en el numerador’. Yael y Natalí [34] [69] [71] [72] insisten en la necesidad de incluir un ejemplo con una explicación sobre qué es el numerador y qué es el denominador. Frente a estas propuestas, la docente [73] explicita quién es el destinatario del escrito y tematiza el problema de la información que es necesario incluir de acuerdo a los conocimientos que supuestamente este ya domina. En este caso el destinatario son los propios alumnos de 5° año, por eso la intervención de la docente pone de relieve la importancia de representarse a sí mismos como futuros lectores del texto que están produciendo y de preguntarse si les han quedado conceptos implícitos que sería necesario desarrollar para comprender el escrito o, por el contrario, si al desarrollarlos, el texto resultaría redundante o sobrecargado porque ya disponen de la información suficiente para interpretarlo.
Otro núcleo del intercambio está centrado en el dominio de validez de la formulación general que han elaborado para describir el procedimiento. Al releer la explicación que han escrito, Valentino plantea que esta forma sirve para este caso pero puede no servir para otros [58]. La preocupación se enlaza con la discusión que había tenido lugar en la puesta en común, a partir de la reflexión de Camila acerca de la imposibilidad de usar “la rayita” para resolver el reparto de ¼ de chocolate entre 2 niños. Si bien la docente pospone el análisis de estos casos para otro momento y propone escribir sobre aquellos en los que se reparten enteros [66], resulta interesante señalar el interés que perdura en algunos niños por incluir en el texto la restricción de la validez de este procedimiento argumentando que no sirve para casos en los que lo que se reparte no llega a ser un entero de chocolate [60] [62] [64].
Un segundo aspecto del interés en la búsqueda de una forma más general de referirse al procedimiento de “la rayita” se retoma al proponer a los niños que reflexionen sobre cómo están expresadas en el texto las partes entre las que se reparte [87] [88], hasta ese momento formuladas en términos de personas: “Si sabés la cantidad de personas entre las que tenés que repartir…”. Valentino había señalado que los repartos no siempre se realizan entre personas, por eso la docente vuelve a plantear de qué modo escribirlo [89] [95] y los niños intentan diferentes maneras de expresarlo: cosas, partes, objetos, seres vivos, entre otras [90] [92] [93] [94] [96] [98] [100] [102], para finalmente reemplazar la palabra ‘personas’ por ‘veces’: “Si sabés la cantidad de veces entre las que tenés que repartir…”.
El tercer núcleo de intereses aparece intercalado a lo largo de todo el fragmento, en este caso los alumnos parecen centrados en la forma y no tanto en el contenido del escrito. Se suceden entonces numerosas sugerencias que apuntan a mejorar la redacción, aunque en el fragor de la discusión varias de ellas no llegan a ser tomadas por la docente. Encontramos un primer intercambio [52] a [54] en el que Albertina sugiere agregar ‘en’ en una parte del texto y Valentina se opone argumentando que es correcta la escritura tal como está; este señalamiento es aceptado como válido rápidamente por la docente dado que el agregado cambiaría el sentido del escrito. Luego Sofía y Fabricio hacen sugerencias de puntuación [55] [79] que quedan diluidas en el intercambio.
Martina hace una indicación explícita para que la docente tache la palabra ‘después’ porque “parece un poco de más” [75] a [78] aunque esta solicitud no aparece reflejada en la producción. En este caso, el señalamiento sobre la redacción sí involucra una cuestión conceptual: al proponer eliminar la palabra ‘después’, la alumna estaría reconociendo que no se trata de dos momentos en el procedimiento de resolución sino que la relación entre los componentes del reparto es constitutiva de la fracción resultante.
Luego, varios alumnos proponen hacer un cambio en el lugar en que se ubica ‘se transforma’ [83] [85] [104] [106] [109]. Esta sugerencia es tomada por la docente en varias oportunidades [84] [105] [107] [108] y dado que los niños no alcanzan un acuerdo se concluye que su ubicación no cambia el sentido del texto.
El fragmento muestra que los niños ponen en circulación conocimientos diversos con el fin de hacer más preciso el sentido de su producción. La preocupación que los alumnos manifiestan por mejorar la escritura contribuye a profundizar la comprensión del contenido involucrado.
Al poner en relación las formulaciones que hicieron los niños en la discusión de las resoluciones de los repartos y en la situación de escritura colectiva para agregar ideas al cartel, identificamos un asunto en común, entre otros, que refiere a la descripción del procedimiento que pone en juego la relación entre el reparto de a unidades entre b partes y la fracción a/b. En la discusión sobre los repartos los niños reconocen haber realizado una captación perceptiva de las relaciones entre los números que parece estar favorecida por la disposición de los datos en el cuadro. Por otra parte, se centran en la ubicación que corresponde a cada uno de los datos en la fracción -“número de chocolates arriba” o “número de chicos abajo” de la “rayita”-, en términos más bien figurativos. Frente a la exigencia de poner este procedimiento en palabras para ser escritas en el afiche los niños hacen intentos por describir el procedimiento con mayor grado de generalidad. Es así que proponen diferentes términos que no remiten al contexto del problema hasta lograr explicitar que la cantidad a repartir se transforma en el numerador y las personas entre las que se reparte, en el denominador. En el escrito ya no se menciona la ubicación espacial en la fracción ni la “rayita” a la que aludían coloquialmente en la puesta en común ya que han profundizado en la conceptualización de la relación hallada.
5. REFLEXIONES FINALES
En las situaciones de escritura de conclusiones, los alumnos mostraron cierta tendencia al uso de formulaciones más generales y descontextualizadas que las utilizadas en las discusiones sobre los problemas. Si bien en diferentes oportunidades a lo largo de la secuencia, el uso de formulaciones con algún grado de generalidad fue promovido por la docente que proponía a los niños escribir ideas que les sirvieran para varias situaciones, consideramos que fue el propósito del escrito el que los convocó a producir numerosos enunciados que no remitían al contexto del problema. El intento por componer un texto en colaboración que incluyera las ideas aprendidas hizo posible cierta profundización en las reflexiones y el establecimiento de algunas nuevas razones o relaciones matemáticas que propiciaron avances en los conocimientos respecto de los que circulaban en la puesta en común de los problemas.
Encontramos situaciones en las que las ideas que los niños incluyeron en la escritura colectiva tenían menor nivel de profundidad que las que formularon en el momento del intercambio sobre el problema. Si bien en esta investigación partimos del supuesto de que la escritura propicia la transformación de conocimientos, coincidimos con otros estudios sobre escrituras al servicio del aprendizaje de contenidos escolares (Aisenberg, 2012; Perelman, 2008) que afirman que las producciones escritas no siempre viabilizan el acceso a los conocimientos de los alumnos en forma completa. Nos permitimos conjeturar que en ciertas ocasiones la preocupación por el proceso redaccional los descentra del contenido que intentan incluir en el texto.
Otro aspecto que nos parece importante subrayar es la preocupación que mostraron los niños en algunos momentos por el modo de escribir. Si bien los textos que produjeron consistían en escrituras intermedias (Chabanne y Bucheton, 2002), cuyo propósito era facilitar el propio estudio, los tenían a ellos mismos como destinatarios y solo serían publicados en el aula, los alumnos propusieron hacer pequeños ajustes en la escritura que les permitieron profundizar en la conceptualización. Por ejemplo, creemos que la tendencia a homogeneizar los verbos en su forma impersonal resultó un efecto de compartir el conocimiento y hacerlo público en la comunidad del aula. De esta manera iniciaron un proceso de despersonalización (Chevallard, 1997), necesario para distanciarse del saber que estaban produciendo y reorganizarlo de una manera cada vez más explícita y objetiva. Los conocimientos que los niños pusieron en circulación con el fin de hacer más preciso el sentido del texto que estaban escribiendo contribuyeron a profundizar la comprensión del contenido involucrado.
Resaltamos también que los avances suscitados a través de estas prácticas de escritura tuvieron lugar bajo ciertas condiciones didácticas sostenidas por la docente. Por ejemplo, si bien no todas las propuestas de los niños pudieron ser incluidas en la producción colectiva, ella habilitó la palabra para que se expusieran y las hizo circular permanentemente para que fueran consensuadas por todos.
Un aspecto no previsto con el que nos encontramos en la implementación de la secuencia fue el modo en que las decisiones que tomaba la docente durante la situación de dictado incidían sobre el proceso de validación tanto de los conocimientos matemáticos como de las formas de expresarlo que usaban los alumnos. Entre la diversidad de textos intentados (Camps et al., 2007) que proponían los niños, la docente iba seleccionando los más avanzados en términos de relaciones matemáticas involucradas, o enunciados de manera más general, o los que más se aproximaban a lo que se esperaba que produjeran, para textualizar en el escrito colectivo. Haber anticipado este modo de validar surgido en las clases nos hubiera permitido prever intervenciones del docente que tuvieran el propósito de tematizar las diferencias entre las propuestas de los niños con la intención de que la validación se produjera a partir del análisis colectivo de las mismas.
Este trabajo puede resultar un aporte a la Didáctica de la Escritura, a la Didáctica de la Matemática y a la producción codidáctica. Numerosos estudios sobre la escritura (Teberosky, 2001; Miras, 2000) y sobre la escritura al servicio de la apropiación de contenidos escolares, especialmente de ciencias naturales y ciencias sociales (Vérin, 1988, 2004; García-Debanc, 1995; Aisenberg y Lerner, 2008; Aisenberg, 2012; Lerner, Aisenberg y Espinoza, 2012, entre otros), han planteado que esta práctica está asociada a la transformación de los conocimientos y que facilita tanto el aprendizaje en estas áreas curriculares como el reconocimiento de los propios procesos de escritura. Esta investigación retoma esas ideas y muestra cómo es posible instalar condiciones didácticas en el aula para que las escrituras favorezcan, del mismo modo, el avance de los niños en sus conocimientos sobre un objeto matemático.
La Didáctica de la Matemática viene produciendo en los últimos años teorías y conceptos que se ocupan de aspectos metacognitivos ligados al estudio, a la toma de conciencia y reflexión sobre el propio saber, así como a los distintos tipos de intervenciones didácticas que propician la explicitación, reorganización y sistematización de los conocimientos (Brousseau, 1986, 1988, 2007; Chevallard, 1991; Margolinas, 1993; Perrin-Glorian, 1995; Chevallard, Bosch y Gascón, 1997; Bosch, Gascón. 2009). El presente trabajo se inscribe en la línea de estos estudios y profundiza en el diseño de situaciones de enseñanza de objetos matemáticos que involucran además, como un componente importante, situaciones de escritura orientadas a la reconstrucción e institucionalización de los conocimientos.
Nos parece primordial insistir en la necesidad de valorar la potencia de la escritura en la transformación del conocimiento matemático para que se incluyan sistemáticamente situaciones de producción, retorno y revisión en las aulas. Creemos que vale la pena el esfuerzo de estudiar las tensiones que enfrentan los niños al escribir en esta disciplina particular para poder planificar y sostener condiciones de enseñanza en las que la escritura se presente como un verdadero problema por resolver y los conduzca a mejores aprendizajes. Quedan pendientes numerosas preguntas para futuras investigaciones sobre las escrituras en las clases de matemática en el marco del proceso de institucionalización que podrían ubicarse en el espacio de confluencia entre la Didáctica de la Matemática y la Didáctica de la Escritura.











 nueva página del texto (beta)
nueva página del texto (beta)