INTRODUCCIÓN
Desde hace muchas décadas, educadores matemáticos han promulgado que una definición no puede ser significativa para un estudiante si no ha participado en la construcción de ésta (de Villiers, 1995). Para que ello sea posible, Tsamir, Tirosh y Levinson (2008) aseguran que se deben estudiar tanto ejemplos como no-ejemplos (contraejemplos) de un concepto, dado que ello ayuda a identificar cuáles son las características esenciales que lo definen. Reconocer que se tiene un no-ejemplo de un concepto requiere identificar cuál atributo definitorio no se cumple, lo que implica establecer que una característica que sí se tiene es la negación de ese atributo. Por ejemplo, si uno de los ángulos de un cuadrilátero es obtuso, ello es la negación de la característica que define a un rectángulo.
Varios investigadores de educación matemática se han preocupado por asuntos que tienen de trasfondo la lógica matemática y su efecto en el desarrollo del razonamiento (Epp, 2003; Selden y Selden, 2009). Se preguntan si, por ejemplo, introducir el estudio de la lógica formal contribuye para aprender a razonar lógicamente, o si, más bien, es suficiente la experiencia con el uso de la lógica en los diversos cursos de matemáticas (Inglis y Simpson, 2008). También ha sido asunto de varias investigaciones determinar qué aspectos específicos de la lógica inciden durante el aprendizaje de la argumentación. Por ejemplo, Antonini (2004), Antonini y Mariotti (2008), Durand-Guerrier (2006) y Stylianides, Stylianides y Philippou (2004) aseguran que el uso de la negación en procesos de argumentación no es intuitivo y genera dificultades para el aprendizaje de la justificación.
Pero, como indican Tall, Yevdokimov, Koichu,
Whiteley, Kondratieva y Cheng (2012), los estudiantes deben llegar a
entender y usar demostraciones por contradicción (i.e. aquellas en las que la
negación del consecuente de la aserción que se pretende demostrar, se añade como
premisa) porque son una herramienta esencial para la matemática avanzada. Ejemplos
de usos tempranos de demostraciones por contradicción son la irracionalidad de la
En el proceso de una investigación que realizamos, cuyo fin era estudiar los argumentos que formulan estudiantes de grado décimo cuando construyen una definición de una figura geométrica, descubrimos que algunos estudiantes usaban espontáneamente la negación de proposiciones, sin ser conscientes de que estaban procediendo de una forma lógicamente válida. Teniendo en cuenta esto y lo expuesto anteriormente, decidimos estudiar con detenimiento los episodios en donde evidenciamos el uso de la negación de proposiciones. Específicamente, buscamos la respuesta a la siguiente pregunta: ¿cuáles son las características del uso de la negación en los argumentos de los estudiantes cuando intentan definir una figura geométrica y justificar su decisión?
1. MARCO DE REFERENCIA
A continuación, presentamos los referentes teóricos utilizados en nuestro estudio. Estos incluyen la caracterización del proceso de definir y de argumentar, además de lo que expresan algunos investigadores sobre su importancia en la formación matemática de estudiantes escolares. También, haremos referencia a la relación entre una proposición condicional y el uso de la negación en el proceso de justificar, y las dificultades que se han reportado respecto a su uso.
EL PROCESO DE DEFINIR
Una definición en geometría puede entenderse como un enunciado que contiene las propiedades necesarias y suficientes para que una figura o relación pueda ser etiquetada por una expresión o una palabra (Herbst, Gonzalez y Macke, 2005). Según Escudero, Gavilán y Sánchez-Matamoros (2014), las definiciones predeterminan al concepto dentro de un sistema teórico de una manera no circular y consistente, y pueden existir definiciones equivalentes para un mismo objeto. Para ellos, aprender a definir significa que: 1) se pasa de asumir la definición como un nombre a entenderla como una lista de características del objeto; 2) se reconoce que una definición incluye unas características mínimas del objeto, y no una lista exhaustiva; 3) se reconoce que a partir de un listado de características se pueden encontrar definiciones equivalentes.
Para definir en geometría, es necesario establecer las diferencias de un objeto con otros similares, pues una definición agrupa a las figuras que comparten un conjunto específico de atributos (Herbst, et al., 2005). Estos investigadores promulgan que para desarrollar el proceso de definir en la clase de geometría, es necesario crear escenarios en los cuales los estudiantes describan figuras geométricas, para determinar atributos comunes que permitan definirlas y diferenciarlas de otras. Estos escenarios también deben promover que los estudiantes generen ejemplos de figuras a partir de un conjunto de propiedades específicas. Precisamente, la geometría dinámica es un escenario en donde el estudiante puede asumir este proceso como una actividad creativa y entender que las definiciones no son parte de un cuerpo teórico inmutable (Govender, 2003). Además, su uso contribuye a generar un ambiente de participación y de interacción en el aula (Perry, Samper, Camargo y Molina, 2013).
LA ARGUMENTACIÓN EN EL PROCESO DE DEFINIR
La argumentación consiste en cualquier enunciación retórica que tiene como fin convencer a alguien de la verdad o la falsedad de una afirmación particular, dentro de un contexto específico. En matemáticas, argumentar es esgrimir razones o puntos de vista, identificar enunciados o proponer referentes teóricos, con el objeto de buscar ideas que conformarán la demostración del enunciado matemático (Douek, 2007) y de esta forma validarlo. La argumentación pretende lograr la aceptabilidad del enunciado dentro de una comunidad específica como, por ejemplo, la conformada por un profesor y sus alumnos o por matemáticos.
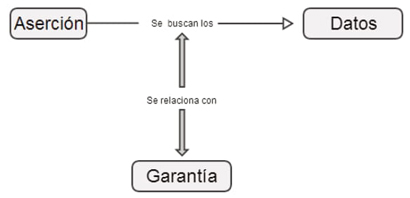
Sobre la naturaleza de los argumentos, Boero (1999) distingue entre argumentos empíricos y teóricos. En un argumento empírico la validez recae en las mediciones, en la evidencia visual y las referencias corporales, si eso lo acepta la comunidad en la que se quiere validar determinada proposición. Mientras que los argumentos teóricos se basan en el uso de elementos que conforman la teoría que dicha comunidad ha establecido como válida: definiciones, postulados o teoremas (figura 1).
Para Toulmin, un argumento está compuesto, principalmente, de tres elementos: datos, aserción y garantía. Los datos y la aserción son proposiciones que se relacionan por medio de una regla general denominada garantía (Molina y Samper, 2019). Los datos son propiedades que en algún momento se asumen como verdaderas. La aserción es una propiedad que se considera consecuencia de los datos, y la garantía son los principios o enunciados, considerados verdaderos, que permiten realizar inferencias que relacionan los datos con la aserción. Los tipos de argumentos que se presentan en la actividad matemática están determinados por el componente principal, de la estructura ternaria, que se concluye. En correspondencia con ello, los argumentos se clasifican en deductivos, abductivos e inductivos.
Un argumento deductivo surge cuando partiendo de los datos se utiliza una regla general como garantía para obtener la aserción (figura 2). Este tipo de argumentos se dan principalmente en el proceso de justificación.
Un argumento abductivo puede surgir en el proceso de conjeturación o de justificación. En este tipo de argumento se asume que la aserción es verdadera. A partir de esto y de posibles garantías conocidas que podrían justificar a la aserción, se concluyen, como posibles, unos datos adecuados. Es importante mencionar que la naturaleza de la regla general (garantía) puede ser diferente: puede ser una regla hipotética que proviene de una exploración empírica o puede ser una regla extraída, por una exploración teórica, del sistema teórico en el que se trabaja (figura 3).
Finalmente, un argumento inductivo surge principalmente en el proceso de conjeturación. En este tipo de argumentos, se tienen varios datos o proposiciones particulares D1, D2, D3,... ,Dn de una proposición general D que producen un mismo resultado, que corresponde a la aserción. Ello conlleva a la formulación de una proposición o regla general. La regla obtenida en este tipo de argumento es provisional, es decir, es una proposición plausible. En este caso, lo que se concluye es la garantía (figura 4).
ACERCA DEL USO DE LA NEGACIÓN EN LA ARGUMENTACIÓN
En un sistema axiomático, una proposición condicional p → q se puede demostrar de forma directa o indirecta. El primer tipo de demostración se da cuando, partiendo de la proposición p verdadera, se deduce que q es verdadera utilizando un sistema teórico de referencia y principalmente el esquema de razonamiento Modus Ponendo Ponens3. El segundo tipo de demostración, llamado por contradicción o prueba indirecta, consiste en introducir la negación del consecuente del enunciado, ¬ q, como una nueva premisa. Si con él se deducen las proposiciones r y ¬r, que por el Principio del Tercio Excluido no pueden ser simultáneamente verdaderas, entonces ¬ q no puede ser verdadero. Como el suponer que el consecuente de la condicional es falso lleva a una contradicción, por el Principio de Reducción al Absurdo se puede concluir que el consecuente de la condicional que se quiere demostrar es verdadero (Caicedo, 1990).
Para demostrar una afirmación condicional (p → q), también se puede validar su contrarrecíproca (¬q → ¬p), pues son lógicamente equivalentes. El método de demostración por contrarrecíproca consiste precisamente en demostrar la validez de una proposición condicional demostrando de forma directa su contrarrecíproca. Finalmente, para demostrar que una afirmación es falsa basta con encontrar un no-ejemplo, es decir, un ejemplo en el cual se cumpla simultáneamente p y ¬q.
Algunas investigaciones, sobre la producción de pruebas indirectas por parte de estudiantes de diferentes grados de escolaridad, reportan que ellos tienen más dificultades para comprender las pruebas indirectas que las directas (Antonini, 2004). Una de las posibles razones de esta situación es que las pruebas directas son más intuitivas que las indirectas. Algunas de las dificultades asociadas a las pruebas por contrarrecíproca son: equivocarse al formular la proposición contrarrecíproca del enunciado que se quiere probar (Antonini, 2004); no aceptar como válidas las pruebas por contrarrecíproca porque consideran que no corresponden a la demostración del enunciado inicial (Antonini y Mariotti, 2008); no diferenciar los datos iniciales de las aserciones del enunciado y asumir que las pruebas por contrarrecíproca son argumentos hacia atrás (Stylianides, et al., 2004). Con respecto a las pruebas por contradicción, algunas dificultades de los estudiantes son: aceptar que la contradicción encontrada permite validar la proposición condicional que se pretende probar, y comprender que algunos de las afirmaciones que se deducen durante este tipo de prueba, teóricamente no se pueden dar (Antonini y Mariotti, 2010). Adicionalmente, asociado al uso de la negación para justificar afirmaciones, Antonini (2004) indica que los estudiantes utilizan de forma intuitiva una relación de equivalencia falsa que consiste en asumir que la proposición p → q es equivalente a su inversa ¬p → ¬q.
LA IMPORTANCIA DE LOS PROCESOS ARGUMENTAR Y DEFINIR EN EL AULA
Furinghetti y Paola (2002) afirman que involucrar a los estudiantes en la actividad de definir tiene un valor didáctico invaluable para la comprensión de la estructura lógica de una proposición condicional, lo cual es un elemento indispensable para la argumentación matemática. Un resultado similar lo reportan Sáenz-Ludlow y Athanasopoulou (2008) cuando señalan la interdependencia entre el conocimiento de la definición de un cuadrilátero y los argumentos que despliegan los estudiantes para justificar afirmaciones que han establecido relacionadas a estos. Douek y Scali (2000) señalan que la argumentación tiene un papel importante en el proceso de construcción de conceptos. Como parte esencial de este proceso es entender la definición, la relevancia de la argumentación se transfiere al proceso de definir. Es por medio de la argumentación que se puede llegar a acuerdos sobre las propiedades que definen un objeto, y sobre los vínculos entre éstas y las propiedades que de su definición se deducen.
2. CONTEXTUALIZACIÓN DEL ESTUDIO
Se describe el contexto de la situación de donde provienen los datos de este estudio. También se expone la metodología que usamos para su análisis.
CONTEXTO
La investigación original se llevó a cabo con siete estudiantes de grado décimo de educación básica secundaria (14 - 16 años), como una actividad extracurricular en la que participaron voluntariamente y que fue dirigida por una de las autoras de este artículo. Para ella, se diseñó una secuencia de tareas que tiene como propósito que los estudiantes aprendan a definir y, requiere el uso de geometría dinámica. Los estudiantes desarrollaron esta secuencia durante siete sesiones de cuatro horas cada una, que fueron grabadas en audio y video. Durante la implementación de la secuencia, los estudiantes trabajaron en dos grupos, dado que sólo había dos computadores. Ellos decidieron con quienes trabajar. El Grupo 1 lo conformaron Saúl, Noé y Néstor, y el Grupo 2 Andrea, Martín, León y Armando.4 Los datos del estudio que estamos reportando se obtuvieron de la séptima sesión, en la cual los estudiantes desarrollaron las últimas tres tareas de la secuencia (tabla 1).
Tabla 1. Objetivos y descripción de las tareas propuestas
Define la Figura Incógnita
Objetivos de enseñanza
Determinar la comprensión de los estudiantes del proceso definir en geometría.
Favorecer el uso de la geometría dinámica para resolver problemas y como medio para la justificación.
Objetivos de aprendizaje
Descubrir, con geometría dinámica, propiedades esenciales de una figura geométrica desconocida.
Definir la figura geométrica desconocida a partir de las propiedades encontradas.
Usar una representación realizada con geometría dinámica como medio para justificar aserciones.
Descripción de la actividad
Abra el archivo Figura Incógnita5 en GeoGebra:
Tarea 1. Escribe las propiedades de la figura.
Tarea 2. Determina conjunto de propiedades que no definen la figura. En cada caso, propón un contraejemplo.
Tarea 3. Determina conjuntos de propiedades que definan la figura. Justifica tu respuesta.
A continuación (tabla 2), se describen los tipos de tareas que conforman la secuencia completa, y la clasificación de las tres tareas descritas en la tabla 1.
Tabla 2 Tipos de tareas con geometría dinámica
| Tarea Tipo I | Tarea Tipo II | Tarea Tipo III | |
| Descripción | Tareas en las cuales el estudiante debe relacionar los pasos realizados para construir una figura con las propiedades exigidas en una definición. | Tareas en las cuales el estudiante explora la representación de una figura para encontrar sus propiedades. | Tareas en las cuales el estudiante representa una figura que cumpla un conjunto de propiedades. |
| Intención | Evaluar posibles modificaciones a la definición, quitando o agregando propiedades. | Proponer posibles definiciones a partir de las propiedades descubiertas. | Determinar si la figura resultante corresponde a la representación de un objeto conocido, para determinar si las propiedades usadas constituyen una definición del objeto. |
La tarea 1 es del tipo II porque los estudiantes tienen que descubrir las propiedades de la Figura Incógnita para poder proponer una definición; la tarea 2 y la tarea 3 son del tipo III porque requieren usar las propiedades elegidas en la construcción de una figura, para determinar si representa o no la Figura Incógnita y así justificar si las propiedades la definen o no. En el proceso de solucionar las tres tareas, surgen tareas tipo I cuando, para construir posibles definiciones de la Figura Incógnita, los estudiantes representen una figura a partir del conjunto de propiedades que seleccionaron, para así determinar cuáles son necesarias y cuáles se pueden eliminar.
METODOLOGÍA DE INVESTIGACIÓN
Los datos que se usan en este artículo son algunas de las trascripciones de las interacciones de los dos grupos de estudiantes cuando intentaban establecer la definición de la Figura Incógnita. El objetivo de nuestro estudio es caracterizar el uso de la negación en los argumentos de los estudiantes, cuando proponen definiciones de la figura a partir de las propiedades que descubren. La metodología de investigación utilizada es un estudio de caso (Stake, 1998).
Para el análisis, tuvimos en cuenta tres asuntos: i) el tipo de argumento que formulan los estudiantes cuando usan la negación (Molina y Samper, 2019); ii) el uso de la negación, desde el punto de vista de la lógica matemática (Caicedo, 1990) y iii) las dificultades respecto al uso de la negación (Antonini, 2004; Antonini y Mariotti, 2008; Stylianides, et al., 2004; Antonini y Mariotti, 2010).
3. ANÁLISIS
En lo que sigue, presentaremos las evidencias que recogimos del uso de la negación de proposiciones en los argumentos de los estudiantes para justificar sus ideas. Se presenta el análisis de tres fragmentos: uno de cada grupo y el tercero de la puesta en común, cuando los estudiantes justifican una posible definición para la Figura Incógnita. Los dos primeros se dieron durante el desarrollo de la primera tarea, cuando los estudiantes están encontrando las propiedades de la figura (tabla 3).
Tabla 3: Propiedades encontradas de la Figura Incógnita
FRAGMENTO 1. EL GRUPO 2 DESCARTA QUE LA FIGURA SEA UN PARALELOGRAMO
En el proceso para determinar cuáles son las propiedades de la Figura Incógnita (figura 5), un integrante del Grupo 2 plantea la posibilidad de incluir como una propiedad de la figura “ser paralelogramo” [86]. En el momento en que se realiza la siguiente intervención, el grupo ya había realizado un proceso exhaustivo de exploración, midiendo los lados y los ángulos de la figura y construyendo las bisectrices de sus ángulos.
| 87. | Armando: | ¿Cómo es un paralelogramo? Son dos líneas paralelas o sea cuatro, o sea dos lados paralelos. | |
| 88. | Profesora: | Para esta figura, ¿cuáles tendrían que ser paralelas? | |
| 89. | León: | Ésta y ésta [señala |
|
| 90. | Armando: | [Traza |
|
| 91. | Profesora: | [Dirigiéndose a Armando] ¿Usted va intentar mostrar que es un paralelogramo? | |
| 92. | Andrea: | Pero no es, porque se encuentran en un punto. Mira [dirigiéndose al profesor al señalar las rectas construidas por Armando] |
|
| 93. | León: | Al parecer se encuentran en un punto. Mira [Armando da zoom y reduce la pantalla y muestra el punto de intersección de las rectas]. No. En este caso ya descartamos que no es un paralelogramo. | |
| 94. | Armando: | O sea, no es un paralelogramo. | |
Se evidencia la construcción de un argumento colectivo, el cual es
deductivo empírico. Los datos
(¬q) son la información visual de la intersección
de las rectas,
En su definición, Armando incluye una conjunción: un par de lados opuestos paralelos y el otro par de lados opuestos paralelos. Trabajan con la negación de sólo una de esas proposiciones, posiblemente sin ser conscientes de que negar sólo una de ellas es suficiente para que quede negada la conjunción, y que por tanto es válido el esquema de razonamiento que usaron. Es decir, procedieron de una forma que es lógicamente válida, aunque no fueron conscientes de ello.
FRAGMENTO 2. EL GRUPO 1 EXPLICA POR QUÉ LA FIGURA NO ES ROMBO
Este fragmento consta de dos momentos: i) establecen y formulan un hecho geométrico que llaman el Criterio de Dos Triángulos Isósceles, que versa sobre los rombos; y ii) usan el Criterio para justificar otra propiedad de la Figura Incógnita.
Momento 1: Noé pasa al tablero para explicarle a sus compañeros de grupo su argumento de por qué la Figura Incógnita no es un rombo [158]. Para ello, dibuja en el tablero un rombo con una diagonal (figura 7). Cuando Saúl le comenta que eso ya lo habían concluido, Noé expresa que “... hay que explicar por qué no es un rombo; no es sólo decir que no es un rombo” [162]. Por tanto, indica las condiciones que deberían cumplir los triángulos isósceles determinados por una de las diagonales del cuadrilátero.
| 168. | Noé: | [...] Tendría que tener dos triángulos equiláteros. | ||
| 169. | Profesora: | ¿Y por qué? | ||
| 170. | Noé: | Porque, es que, digamos el rombo también se puede dar a través de la forma. O sea; yo digo; no sé si esté bien. Digamos como un cuadrado cuando el cuadrado se comprime. ¿Sí? Como el cuadrado tiene todos sus lados iguales, ¿Qué nos formaría eso? Dos triángulos equiláteros. [...] | ||
| 174. | Saúl: | Yo diría que un rombo se forma también con dos triángulos isósceles. [...] | ||
| 176. | Saúl: | Se necesitaría que los dos triángulos isósceles fueran congruentes. O sea... si fueran dos triángulos equiláteros [congruentes], implicaría que esta medida [señala la diagonal del rombo dibujado por su compañero, figura 7(a)] sea igual a ésta [señala un lado del rombo de la figura 7(a)]. Pero, pues también... Pero, pues con ésta [señala los dos triángulos equiláteros de la figura 7(a)] también se puede hacer un rombo. Pero con dos triángulos isósceles también se podría hacer un rombo. Pero no necesariamente esta medida [la de la diagonal] tiene que ser igual a ésta [medida de un lado del rombo]. Digamos, puede ser así y así [dibuja la figura 7(b)]. |
|
|
En la justificación que realizan Noé y Saúl se evidencian varios argumentos. El primer argumento es empírico; tiene como datos visuales que las diagonales del cuadrilátero no determinan triángulos equiláteros [168] (¬p), y como aserción que la figura representada en el computador no es un rombo [158] (¬q); no dan una garantía. La afirmación que resulta del primer argumento de Noé es: Si la diagonal de la Figura Incógnita no determina triángulos equiláteros, entonces la figura no es rombo (Afirmación A). Bajo el cuestionamiento de la profesora, Noé expone tres argumentos deductivos que validan la contrarrecíproca de la afirmación anterior [170].
El primer argumento es una equivalencia que Noé establece: rombo si y sólo si cuadrado comprimido. Esta proposición corresponde a la definición personal de rombo que Noé ha manifestado desde el inicio de la actividad. El segundo argumento es: si el rombo (q) es un cuadrado comprimido (datos) entonces todos sus lados son congruentes (aserción). La garantía implícita es que al comprimir un cuadrado se mantiene la congruencia de los lados del cuadrilátero. El tercer argumento tiene como datos la aserción anterior y concluye que la diagonal determina dos triángulos equiláteros (p), siendo la garantía la definición de triángulo equilátero.
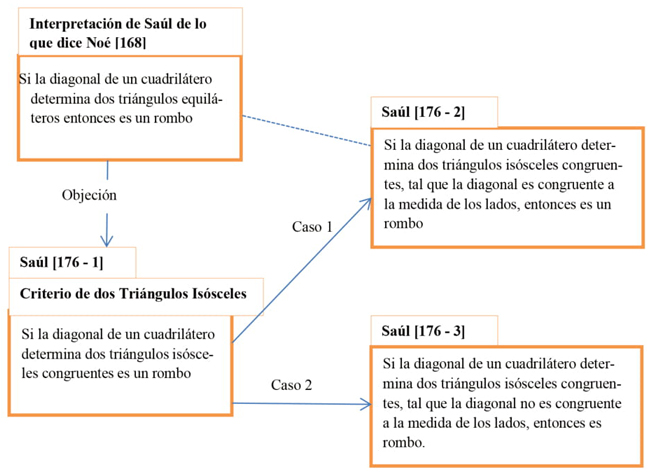
Saúl quiere expresar su acuerdo parcial de lo que expuso Noé, pero enuncia la proposición inversa de la Afirmación A de Noé, sin saber que no son necesariamente equivalentes. Es decir, afirma que: si la diagonal determina triángulos equiláteros entonces es rombo. Con el propósito de justificar su afirmación, Saúl construye una cadena de argumentos [176]. El primer argumento es precisamente el establecimiento de la inversa, convencido de que está reportando lo que dijo Noé. En el segundo argumento, Saúl asevera que si la diagonal del cuadrilátero determina dos triángulos equiláteros (datos), entonces la medida de la diagonal será igual a la medida de los lados (aserción). La garantía implícita de este argumento deductivo es la definición de triángulo equilátero. El tercero argumento, que es empírico, parte del hecho de que si la figura es un rombo (datos), entonces no necesariamente la medida de la diagonal es igual a la de uno de los lados (aserción). La garantía implícita son las representaciones de rombo que hicieron en el tablero. A partir de esto, Saúl establece lo que denominamos el Criterio de Dos Triángulos Isósceles, al cual se va a referir más adelante.
El esquema a continuación ilustra la cadena de argumentos que exponen los estudiantes en la discusión anterior:
La equivocación de Saúl al transformar la Afirmación A es una de las dificultades que identifica Antonini (2004). No es válido, desde el punto de vista de la lógica, usar la inversa para validar una proposición, porque esta no es equivalente a ella. Pero en este caso, como la proposición y su recíproca son válidas, Saúl logró lo que quería.
Momento 2: Con la intención de buscar otras propiedades de la Figura Incógnita, retoman las ideas expuestas en el diálogo anterior. En la siguiente intervención, le justifican a la profesora la validez de una de las propiedades de la Figura Incógnita que quieren incluir en el listado. Como consecuencia de lo que exponen, escriben en la hoja, donde han consignado las propiedades que han encontrado, la siguiente propiedad: “Una diagonal determina dos triángulos isósceles no congruentes”.
| 192. | Saúl: | Sería mejor si sacáramos el Criterio de Dos Triángulos Isósceles. |
| 193. | Profesora: | ¿El Criterio de Dos Triángulos Isósceles?... O sea, tú me dices que, teniendo los dos triángulos isósceles, ¿podemos demostrar qué? |
| 194. | Saúl: | Pero tendría que... O sea, esos dos triángulos isósceles no tendrían que ser congruentes, porque si fueran congruentes se formaría el rombo. |
En la anterior intervención, Saúl intenta justificar por medio de un argumento deductivo teórico que si se tiene la Figura Incógnita (dato), entonces una diagonal determina dos triángulos isósceles no congruentes (aserción). Para construir la justificación, agrega como dato la negación del consecuente, es decir, supone que la diagonal determina dos triángulos isósceles congruentes [194]. Utilizando el Criterio de Dos Triángulos Isósceles [192] como garantía, concluye como aserción que la figura sería un rombo [194]. Con esto Saúl llega a una contradicción, pues anteriormente había afirmado que la Figura Incógnita no es un rombo. Así concluye que la afirmación que negó es verdadera. El esquema de la justificación de Saúl corresponde a una demostración por contradicción. Hizo la demostración indirecta sin dificultades.
FRAGMENTO 3. ¿POR QUÉ LA FIGURA TIENE UN PAR DE ÁNGULOS NO CONGRUENTES?
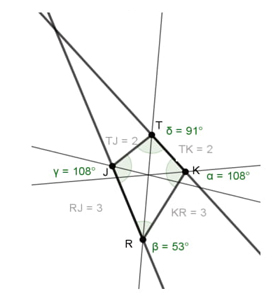
Después de que los estudiantes de cada grupo han trabajado independientemente en la formulación y justificación de definiciones para la Figura Incógnita, es decir para el cuadrilátero denominado cometa, se abre un espacio para la comunicación de resultados. Ambos grupos reportan que una posible definición es: Una cometa es un cuadrilátero con diagonales perpendiculares, tal que solo una biseca a la otra. La profesora cuestiona si la definición que proponen asegura la no congruencia de dos ángulos opuestos (Propiedad 6). El siguiente fragmento corresponde a la justificación dada por un estudiante:
| 216. | Armando: | ¡Eeeh..., bueno! Ya tenemos las dos rectas
perpendiculares. Entonces decimos que “sólo una biseca a la
otra”. Entonces, por consiguiente, los lados son iguales
[señala al |
|
| ||
| 240. | Profesora: | ¿Será que en algún momento el ∠JTK va a ser congruente con el ∠JRK ? |
| 241. | Armando: | No. En ningún momento porque al ser iguales entonces las dos [diagonales] se bisecarían. O sea, al ser los ángulos iguales tendrían que ser las diagonales... las dos diagonales bisecarse, y la propiedad dice que “solo una diagonal biseca a la otra”. |
Lo que pretende Armando justificar es la siguiente afirmación: Si
sólo una diagonal del cuadrilátero biseca a la otra,
entonces el cuadrilátero tiene un par de ángulos que no son
congruentes. En la intervención [216], Armando desarrolla dos
argumentos. El primero, es un argumento deductivo teórico, cuyo
dato es que “sólo una diagonal biseca a la otra” y la
aserción es la congruencia de
Debido al cuestionamiento de la profesora, Armando emite otro argumento [241], usando la negación del consecuente de la condicional que quiere demostrar (datos); es decir, asume que la figura tiene dos pares de ángulos congruentes. Su aserción es que sus diagonales se tendrían que bisecar. Esto, junto con la propiedad que ya se conoce de las diagonales de una cometa, conforman la proposición r y ¬r. Por ello, como si conociera el Principio de Reducción al Absurdo, deduce que los ángulos no pueden ser congruentes. Esto convierte su argumento en una demostración por contradicción, en la que no se presentó alguna dificultad de las mencionadas por Antonini y Mariotti (2010).
CONCLUSIONES
Durante el desarrollo de la secuencia, los estudiantes tenían que proponer diferentes definiciones para una figura desconocida, a partir de las propiedades que descubrieron. Para poder expresar las propiedades de la Figura Incógnita, los estudiantes evocaron propiedades de cuadriláteros conocidos que tenían alguna similitud con la representación de la Figura Incógnita (el paralelogramo y el rombo). Debido a ello, tenían que determinar cuáles de esas propiedades debían dejarse de cumplir para que el rombo y el paralelogramo no fueran ejemplos de la Figura Incógnita. Para expresarlas como propiedades de esta, requirieron el uso de la negación (Ver propiedades 3 y 5 - 11, de la tabla 3).
La estrategia usada por los estudiantes para analizar las propuestas de posibles definiciones de la Figura Incógnita era tratar de construir, con geometría dinámica, figuras que cumplieran las propiedades reportadas. De esta forma, surge el no-ejemplo (el rombo) como herramienta para rechazar algunas definiciones propuestas. Además, los estudiantes vieron la necesidad de justificar por qué la figura que intentaban definir no corresponde ni a un paralelogramo ni a un rombo.
Las características de las tareas propuestas (tabla 2) llevaron a que el uso de la negación surgiera en cuatro momentos: 1) cuando los estudiantes reportaban las propiedades de la Figura Incógnita; 2) cuando querían encontrar un no-ejemplo para indicar que el conjunto de propiedades no podía definir a la Figura Incógnita; 3) cuando justificaban por qué la Figura Incógnita no podía ser clasificada como una figura conocida; 4) cuando tenían que argumentar que una propiedad de la Figura Incógnita, que incluía la palabra “no”, era válida.
Parece que los tipos de tareas diseñados favorecieron el uso espontáneo de esquemas de razonamiento propios de una prueba por contradicción. El surgimiento de este tipo de razonamiento, también se dio porque los estudiantes estaban inmersos en un ambiente que les permitió involucrarse genuinamente en el proceso matemático de argumentar y definir. Dado que la profesora exigía justificaciones, los estudiantes tuvieron la confianza para exponer sus argumentos a los demás, tal vez porque la geometría dinámica les dio soporte empírico para estos. A pesar de que no incluían las garantías, la mayoría de sus argumentos eran deductivos.
No pretendemos que a nivel escolar se dé un tratamiento formal sobre asuntos relacionados con la lógica. Sin embargo, siendo que surgió con tanta espontaneidad el uso de la negación, nos preguntamos si no habría sido pertinente abordar con los estudiantes asuntos relacionados con el porqué de la validez del esquema de razonamiento que utilizaron. Es necesario que el profesor identifique la estructura lógica de los argumentos que formulan los estudiantes, para determinar si corresponden a esquemas de razonamiento válido. Contribuir a que los estudiantes también identifiquen la estructura de sus argumentos, puede llegar a ser una estrategia que le permita al profesor ayudar a que ellos entiendan las formas válidas de justificar en matemáticas.











 nueva página del texto (beta)
nueva página del texto (beta)