1. INTRODUCCIÓN

El presente artículo se perfila, principalmente, como un planteamiento en favor de un diálogo entre la realidad de los estudiantes y el conocimiento que actualmente se brinda en la escuela. Interesa entonces, evidenciar una posible ruta para investigar formas de saberes culturales que poseen los estudiantes de manera que se delimiten marcos de referencia alternativos que pudieran integrar un rediseño del discurso Matemático Escolar (dME) (^{Soto & Cantoral, 2014}).

Como resultado de dicho posicionamiento, no se reduce el problema del desarrollo del pensamiento matemático a la transferencia de conocimientos de lo que se “aprende” en la escuela, sin tomar en consideración las condiciones sociales de su producción o las razones de ser de dichos conocimientos (^{Chevallard, 2013}). Por ejemplo, en la escuela se enseña una manera de multiplicar y de restar; en síntesis, de hacer operaciones de manera “formal” y en gran medida, generalizable. En la escuela suele esperarse que todo aquello que se enseñe a los estudiantes, pueda ser transferido a otras situaciones. Sin embargo, la investigación ha mostrado que esta transferencia se da sólo cuando las situaciones son similares a aquellas que fueron aprendidas; lo cual, en muy raras ocasiones ocurre (^{Cantoral, 2013}).

Ahora bien, algunas investigaciones manifiestan una clara separación entre la escuela y su entorno (^{Carraher, Carraher, Schliemann, 1991}; ^{Arrieta & Díaz, 2015}). Dicha separación, también permite cuestionar sobre aquellos “otros” aspectos del conocimiento matemático que, aunque plausibles, no son aprovechados por la escuela (^{Carraher, et al., 1991}), sino que se soslayan por la supremacía de otras argumentaciones que el dME establece de antemano (^{Soto & Cantoral, 2014}).

Ante este panorama, la investigación en ME puso especial atención en las últimas décadas, a tópicos relativos a la Modelación Matemática y las Aplicaciones con el objetivo de extender las relaciones entre la “realidad” y la “matemática escolar”. Lo anterior con el fin de integrar contextos extra-matemáticos que permitan la creación de acercamientos didácticos innovadores y plausibles para la enseñanza y el aprendizaje de las matemáticas, y con ello, despertar el interés de los alumnos hacia el estudio de las matemáticas. Esto se comprueba, por ejemplo, en el lugar que le brindan a la modelación eventos internacionales de investigación o la amplia literatura especializada que se encuentra disponible (^{García, Gascón, Ruiz y Bosch, 2006}; Niss, Blum y Galbraith, 2007; ^{Almeida, 2018}; ^{Trigueros, 2009}).

De hecho, en diversos currículos de diferentes niveles y países se aprecia una tendencia a integrar mundos extra-matemáticos para enriquecer las actividades y los libros de texto con la finalidad de hacer que las matemáticas sean útiles “fuera” del ámbito escolar. Incluso se proponen acercamientos donde se integra una componente tecnológica informática a través de ambientes experimentales lo cual implica innovadoras estrategias didácticas (ver por ejemplo: ^{Trigueros, 2014}; ^{Rodríguez y Quiroz, 2016}). Sin embargo, se reconoce que aunque la modelación matemática podría jugar un rol importante en las aulas de clases de muchos países y dentro de los planes curriculares, aún existe una brecha importante entre los ideales expresados en las reformas curriculares innovadoras y las prácticas escolares que sustancialmente se desarrollan día a día. Se afirma que es muy complejo encontrar actividades de modelación genuinas dentro del salón de clases de matemáticas (Niss, et al., 2007).

Dentro de las principales posturas de investigación en modelación matemática es clara la búsqueda de un diálogo o “puente” entre las prácticas matemáticas y la realidad. Lo anterior trae consigo también singularidades epistemológicas y cognitivas en las cuales se caracteriza a la modelación y sus funciones durante el proceso de enseñanza-aprendizaje de las matemáticas (^{Kaiser y Sriraman, 2006}). En la tradición clásica, el proceso de modelación matemática se explica generalmente a través de ciclos. Dichos ciclos, inician con proponer sistemas apropiados a ser modelados o de “atractivas” aplicaciones a modelizar con el fin de involucrar e interesar a los estudiantes en dicho proceso (ver ^{Blum y Borromeo, 2009}). Sin embargo, bajo esta postura se atiende solamente una orientación “didáctica” del proceso de modelación: una mirada centrada en lo representacional y en la especificidad, con su consecuente enriquecimiento, de las etapas que conforman los ciclos (Bosh, et al., 2006).

De manera que centrar a la modelación como una aplicación de la matemática donde se conjugan una red de conceptos y representaciones de los mismos que dan lugar a modelos, o como una matematización de situaciones extra-matemáticas, no permite reconocer la naturaleza y la transversalidad del conocimiento matemático en diferentes dominios, es decir, los usos del conocimiento matemático bajo situaciones específicas. Lo anterior significa una problematización del proceso de modelación desde un punto de vista de construcción social, donde el eje de análisis considera una organización basada en prácticas que los individuos utilizan para hallar explicaciones y conformar argumentaciones para explicar fenómenos y tomar decisiones (^{Cantoral, Moreno-Durazo, Caballero-Pérez, 2018}). Este posicionamiento lleva a considerar a la Modelación como una práctica que trasciende y transforma al objeto matemático en cuestión; lo cual significa que la modelación es en sí misma una construcción de conocimiento matemático (^{Cordero, 2006}).

Se asume entonces como problemática de investigación, la manera en la cual se conforma el dME y poca vinculación con la realidad de los estudiantes. Se considera así, que no sólo se trata de proponer aplicaciones de los conceptos matemáticos o de “matematizar” situaciones extra-matemáticas, sino en desarrollar usos del conocimiento matemático que emergen ante el enfrentamiento de situaciones. De manera que se propone a la modelización como la práctica que articularía un diálogo entre el conocimiento matemático y diferentes escenarios donde la matemática sea funcional. Pero para ello, se reformula a la modelación como una construcción en sí misma, esto es, como un proceso de resignificación y de articulación de usos del conocimiento matemático, en tanto funcionamientos y formas asociadas a situaciones específicas.

Con base en los posicionamiento anteriores, en la presente investigación se conforma evidencia empírica sobre usos del conocimiento matemático asociados a las gráficas de las funciones en una situación de movimiento con estudiantes de bachillerato. En el siguiente apartado se describe el instrumento experimental y los elementos teóricos para su diseño y, posteriormente, los resultados de la puesta en escena. Las producciones de los participantes de esta experiencia conforman los datos que se analizan bajo el constructo teórico del “uso de la gráfica” en tanto los funcionamientos (Fu) y formas (Fo) de la gráfica que se involucran en la situación y en la generación de argumentaciones (^{Cordero, Cen y Suárez, 2010}). De esta manera se problematiza a la gráfica y se evidencia una resignificación de la misma en una situación específica (^{Cordero, 2008}).

2. ELEMENTOS TEÓRICOS: LA EPISTEMOLOGÍA DE MODELACIÓN-GRAFICACIÓN

La Matemática Educativa (ME) como disciplina científica, no se remite únicamente a la mejora de los procesos de enseñanza de las matemáticas en ámbitos escolares; sino que también asume como objeto de estudio la organización de una actividad cuya intención declarada sea el aprendizaje de un cierto conocimiento matemático. Su interés es afectar benéficamente al sistema educativo, al pretender que los estudiantes sean capaces de construir un saber vivo que evolucione y principalmente que sea funcional, permitiendo al estudiante resolver sus preguntas (^{Cantoral, 2013}; ^{Cordero, 2008}).

El enfoque asumido en el presente artículo hacia el mencionado objetivo, se basa en un punto de vista sociocultural sobre la naturaleza del pensamiento matemático. Como tal, se asume que dicho pensamiento está íntimamente relacionado con prácticas sociales (PS) desde las cuales se origina. Este supuesto epistemológico desde lo social, pretende construir y modelar explicaciones sistémicas de los fenómenos didácticos en el campo de las matemáticas y se ha denominado Teoría Socioepistemológica (TS). La TS no se centra únicamente en el papel de la semiosis o de las construcciones mentales de estudiantes de una manera aislada, sino que trata con fenómenos de producción, adquisición y de difusión del conocimiento matemático desde una perspectiva sistémica y múltiple. En síntesis, la TS se ocupa del problema que plantea la construcción social del conocimiento matemático y para ello reconoce la incorporación a la investigación de la epistemología del conocimiento, su dimensión sociocultural, los procesos cognitivos asociados y los mecanismos de institucionalización vía su enseñanza (^{Cantoral, 2013}).

La TS reconoce los efectos alienantes de la instrucción escolar basadas en el dME, a partir de modelar las dinámicas del saber o conocimiento puesto en uso (^{Cordero, 2008}; ^{Zaldívar, Cen, Méndez, Briceño, Cordero, 2014}). Así, la TS asume como problemática la falta de marcos de referencia en el dME que resignifiquen el conocimiento matemático en situación escolar. Para ello propone investigaciones donde es pertinente explorar la naturaleza del uso del conocimiento matemático que se involucra en una situación específica.

La TS ofrece entonces un rediseño del dME a través de epistemologías (Argumentaciones) modelizadas por las prácticas sociales. Por lo que el aporte se encuentra en una base de resignificados para la matemática escolar. El posicionamiento de la TS consiste en asumir que el conocimiento matemático tiene un origen y una función social asociados a un conjunto de actividades prácticas socialmente valoradas, compartidas y normativas, pero además pretende el estatus institucional de los saberes matemáticos. Se asume en la investigación “lo institucional” como aquello referido al sistema didáctico, a las prácticas de enseñanza instituidas (la acción didáctica en: aula, familia, comunidad, escuela o vida cotidiana) y a la interacción entre sus componentes: profesor, saber, estudiante; situado en un escenario sociocultural (^{Cantoral, Montiel & Reyes-Gasperini, 2015}).

Así, la TS propone habilitar las PS en el sistema didáctico, con la intención de proporcionar un valor de uso al conocimiento matemático. Para ello, se asume que las PS no se “transfieren” directamente al sistema didáctico, sino que se requiere de una estructura teórica que permita tal cometido. Los trabajos de investigación han propuesto una estructura basada en habilitar Categorías del Conocimiento Matemático, las cuales están equipadas de intencionalidad para su reproducción en el sistema didáctico según las condiciones de este último (ver por ejemplo: ^{Suárez, 2014}; ^{Buendía y Cordero, 2005}). Para ello, el modelo de la TS asume que la PS, propia del grupo humano, se transforma, a través de la intencionalidad didáctica, en una Categoría que se pone de manifiesto en la argumentación dentro de una Situación Específica. Esta última es un escenario didáctico, es decir, vive en lo didáctico, y se referirá al diseño de tareas didácticas (^{Cordero, 2008}; ^{Zaldívar, et al., 2014}).

Un ejemplo de dichas categorías, es la Modelación-Graficación. Esta categoría se propone en los trabajos de ^{Suárez (2014)} y surge a partir del análisis del Tratado de Oresme. Este último representa un parteaguas sobre la comprensión de fenómenos que se estudian a través de las cualidades de figuras geométricas y de las proporciones matemáticas (^{Suárez y Cordero, 2010}). Del estudio de dicho tratado fue posible establecer evidencia que sustenta la conveniencia de desarrollar la modelación de situaciones de cambio a través del uso de las gráficas en situación escolar. Dicha evidencia se traduce en tres datos epistemológicos obtenidos del análisis de la obra de Oresme:

En síntesis, el trabajo de Oresme permitió, en su época, resignificar las figuras geométricas (rectángulos, cuadrados y triángulos) como instrumentos para establecer diferentes tipos de variación (uniforme, deforme, etc.). El estudio de ^{Suárez (2014)} por su parte permitió establecer cómo en el Tratado de Oresme aparecía el uso de las gráficas y reconoce dos elementos indisociables: i) las razones o circunstancias que hicieron posible modelar fenómenos de variación, y ii) la configuración o estructura bajo la cual aparecían. Dichos elementos, definen el binomio Funcionamiento y Forma (Fu-Fo), respectivamente, y se refieren a elementos de construcción que permiten la resignificación del uso de las gráficas en situaciones de variación. Más aún, el trabajo de Suárez y su propuesta centrada en los elementos de funcionamiento-forma para estudiar el desarrollo de usos de las gráficas, permitió establecer que este desarrollo en la obra de Oresme se presentaba en tres momentos. Es decir, en tres conjuntos de tareas que determinan actividades y acciones, así como alternancia de dominios, pero que además definen funcionamientos y formas posibles (^{Suárez y Cordero, 2010}).

A continuación, se describen brevemente cada uno de los momentos de desarrollo del uso de la gráfica en el Tratado de Oresme. Se acompaña cada momento con la descripción de los funcionamientos y formas (Fu-Fo):

Momento I. Establecimiento de la forma del nuevo funcionamiento del uso de las gráficas

El primer uso de la gráfica en el Tratado se refiere a comprender fenómenos de variación a través de figuras (Uso-1). Este uso, determinaba un cambio de paradigma a las formas iniciales (Fo-1) de los conocimientos que en la época se usaban para la teoría del movimiento, donde la geometría y las proporciones estaban como cuerpos de conocimiento ajenos a dicha teoría. De manera que en el Tratado se establece un funcionamiento alternativo para comprender fenómenos (Fu-1), y para ello se establece una nueva forma que consistía en asignar medidas a las variables físicas por medio de segmentos (Fo-2), lo cual constituyó una resignificación de un viejo paradigma.

A su vez, esta segunda forma permitió la emergencia de un nuevo funcionamiento una vez establecida la nueva manera de comprender los fenómenos a través de figuras geométricas. Lo anterior generó el desarrollo a un posterior momento dentro del Tratado.

Momento II. Construcción de argumentos en el uso de las gráficas

La nueva manera de comprender el movimiento a través de formas geométricas y las proporciones, permitió que el funcionamiento de la gráfica (Fu-1) evolucionara hacia establecer relaciones entre las figuras geométricas y las situaciones de variación (Fu-2), pero ello precisa discriminar figuras que representan situaciones de movimiento de las que no lo representan (Fo-2). Se aprecia entonces, en este momento, un cambio hacia un uso de la gráfica más centrado en la construcción de argumentos (Uso-2).

Momento III. Puesta en funcionamiento del uso de las gráficas en la modelación.

Una vez que el nuevo uso de las gráficas se resignifica en el Tratado de Oresme, las construcciones realizadas permiten generalizaciones (Uso-3), como por ejemplo, i) distinguir entre cantidad y cualidad del movimiento, ii) caracterizar puntos extremos de una cantidad que varía y iii) calcular áreas para cuantificar el movimiento a partir de la figura de velocidad (Fu-3, Fu-4 y Fu-5, respectivamente).

En síntesis, en el análisis del Tratado de Oresme se elucida una resignificación de las figuras geométricas para establecer diferentes tipos de variación, lo cual en la época significó un importante avance para entender los fenómenos de movimiento y con ello se estableció un uso de las gráficas alternativo en la época. El análisis del uso de la gráfica en la obra de Oresme estableció las bases para la emergencia de una línea de investigación en la que se discute el estatus epistemológico de las gráficas en la construcción de conocimiento matemático dentro del dME (^{Buendía, 2011}). Así, la Categoría M-G compone una epistemología para el Cálculo escolar y se reconoce su inserción al sistema didáctico a través de una situación específica adaptada a las condiciones escolares-institucionales del ambiente donde profesor y estudiantes interactúen (^{Montiel & Buendía, 2015}). De manera que la quid de la cuestión se halla en el diseño de la situación, es decir, en provocar un escenario propicio para la aparición de la argumentación que responda a la situación.

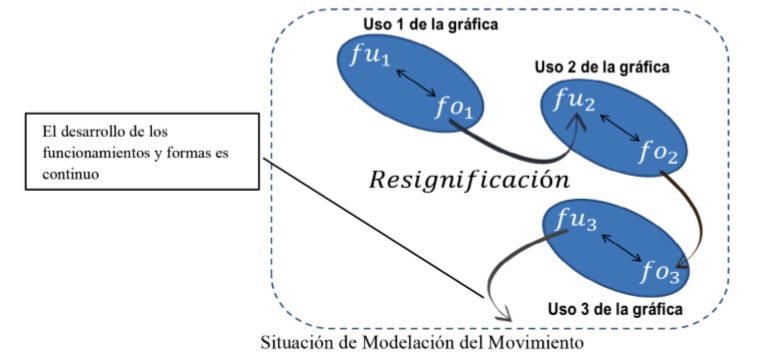
El diseño de la Situación concreta los momentos caracterizados en el trabajo de Oresme, en términos de tareas, acciones y alternancia de dominios; es el producto material dentro del escenario escolar cuya base son los supuestos epistemológicos de la Categoría M-G. A este tipo de situaciones se le convino llamar Situaciones de Modelación del Movimiento (SMM), y su argumento central es la variación de fenómenos de cambio. En la SMM el uso de la gráfica evoluciona en tanto el debate entre los funcionamientos y formas de las gráficas que se desarrollan en los momentos de la situación. A dicha evolución se ha denominado dentro de la TS como una resignificación del uso de la gráfica. La figura 1 ejemplifica a la resignificación de los usos de las gráficas en una SMM, resaltando que dicho proceso no se considera estático, puesto que a través de las tareas que generan diversos funcionamientos y formas a lo largo de los momentos que componen a la SMM, se generan otros usos de las gráficas. De hecho, este modelo teórico considera un desarrollo tal como en la obra de Oresme se puede apreciar.

Figura 1 Modelo de Resignificación en la SMM 

En la siguiente sección se discuten los aspectos metodológicos de la investigación y se resalta el diseño de la SMM que se elaboró con la intención de analizar los usos de las gráficas, que surgen en la modelación de una situación sobre el movimiento de una pesa unida a un resorte. El análisis se realiza con base en los elementos del modelo de resignificación del uso de la gráfica a partir de la delimitación de los funcionamientos y formas de la gráfica.

3. ASPECTOS METODOLÓGICOS: EL DISEÑO DE LA SMM Y LA POBLACIÓN DE ESTUDIO

La SMM se organiza en momentos didácticos, que harán referencia a los momentos referidos por ^{Suárez y Cordero (2010)} anteriormente mencionados. Los momentos no hacen referencia a una estructura temporal del estudio, sino más bien, y en consonancia a Chevallard (1999), son en primer lugar, una realidad funcional del estudio, antes de ser una realidad cronológica (p. 22). Así, un momento didáctico se entiende como el tipo de tareas y formas que se integrarán en el escenario escolar de la clase en términos de cómo se gestiona la situación de aprendizaje en tanto el desarrollo de funcionamientos y formas.

La SMM se organiza en tres momentos, donde se articula el argumento de la situación, a saber, el uso de la gráfica en la variación. Dicha situación problematiza, a través de las gráficas, el comportamiento asintótico y tendencial de un sistema Masa-Resorte. Para ello, se emplean sensores de movimiento y un artefacto físico que representa la situación experimentalmente (figuras 2). De esta forma, la situación provee un marco de referencia donde se resignifica la variación como un comportamiento asintótico y tendencial a partir de los usos de las gráficas pero desde lo que los estudiantes construyen y argumentan.

Figura 2 Instrumentos experimentales: resorte, pesa, calculadora gráfica y sensor de movimiento 

A continuación, se presentan los momentos en los que se gestiona la SMM en el escenario didáctico:

Momento I. Establecimiento de una forma en el funcionamiento de las gráficas

En este momento se espera que los estudiantes construyan argumentaciones desde sus experiencias, con su propio lenguaje y vivencias, de aspectos que tienen que ver con el fenómeno de variación presentado: el movimiento de un resorte cuando se le pone una pesa. La tarea que se les solicita a los estudiantes en este momento es: T1. Dibujar el movimiento del resorte cuando se le pone una pesa en uno de sus extremos, sin realizar el experimento vivencialmente.

Como se puede apreciar, no hay ninguna condición para dibujar el movimiento, incluso no hay una “forma institucional”³ específica bajo la cual se someta a los estudiantes, de manera que estos realicen sus producciones desde sus propias formas culturales que consideren adecuadas. Además, se espera que los estudiantes en este primer momento establezcan argumentos funcionales que permitan modelar el comportamiento del sistema como representaciones pictográficas alusivas al resorte, así como elementos gesticulativos que expliquen el comportamiento.

Momento II. Problematización de las formas de las gráficas a través de la variación

En este momento se cuestionan los modelos que los estudiantes generan en el momento anterior a través de discutir elementos como la anticipación, el comportamiento asintótico y los comportamientos globales-locales del sistema.

Para ello, se ponen en discusión las siguientes tareas:

T2. Explicar si el resorte se detiene y dónde se aprecia en el dibujo del movimiento que se realizó.

T3. Explicar en dónde el resorte se mueve más rápido y dónde más lento en las producciones realizadas.

En este momento de la situación se propone a los estudiantes un “nuevo” grafismo con la intención de establecer una resignificación de las formas iniciales de las gráficas del primer momento. Para ello, se propone el uso de un sensor de movimiento y software, que permite múltiples realizaciones en la modelación y una estructura para producir patrones deseables a través de gráficas cartesianas.

Momento III. Construcción de argumentos en el uso de las gráficas en la modelación

Una vez establecido el nuevo grafismo con base en los elementos tecnológicos y donde la gráfica cartesiana permite hacer referencia a la variación del sistema, a su tendencia y al reconocimiento de puntos de referencia (como el origen), en este momento se espera mantener una estructura más compleja de las argumentaciones sobre la propiedad asintótica del sistema, es decir, la forma en la cual se expresa que el resorte se detiene. El uso de las gráficas entonces en este momento se resignifica como un modelo explicativo, manipulable y predecible de acuerdo a la tarea que se presenta en este momento:

T4. Anticipar cómo es la gráfica del movimiento del resorte posterior a un tiempo determinado

El análisis que se realiza de los Fu y Fo en el uso de las gráficas entre los estudiantes y al dejarles proponer sus formas iniciales, establece una nueva línea de investigación donde es importante reconocer formas culturales de saberes que aparecen en sistemas de usos y que sería posible resignificar por medio de argumentos situacionales. A diferencia del trabajo de Suárez donde se les presentaba de inicio el uso de las gráficas con apoyo de dispositivos tecnológicos (calculadoras y sensores de movimiento) y de ahí se trabajan con las gráficas cartesianas para referirse a ciertos aspectos del Cálculo, la presente propuesta expone que antes de hablar de la gráfica cartesiana es importante reconocer aquello que permite la emergencia de lo cartesiano. Así, el objetivo del análisis de las producciones de los participantes durante la implementación de la situación es identificar la aparición de formas culturales del conocimiento que los participantes pongan en juego al enfrentarse a situaciones donde se problematice la variación, el cambio y los comportamientos con tendencia a través de un uso de las gráficas que se obtienen de modelar una situación de movimiento.

4. DISCUSIÓN DE RESULTADOS

La intención de este apartado es mostrar evidencia de ciertos saberes sobre las gráficas y sus usos, considerados opacados por el dME. Estos saberes conformarán la evidencia de esas formas culturales de saberes que constituyen lo cotidiano para los estudiantes participantes y aunque se trate de un “estudio de casos”, es posible proponer un marco de referencia de los usos de las gráficas para resignificar el comportamiento asintótico en el rediseño del dME.

El análisis es de tipo cualitativo e interpretativo, el énfasis está puesto en las producciones que elaboraron los estudiantes durante la implementación y en la suma de ejemplos, con la finalidad de establecer clases o categorías. Estos elementos son los que permiten la construcción de la evidencia empírica a partir de un estudio de casos, que consiste en caracterizar la aparición, interpretación, descripción, y la lectura que los participantes hacen con las gráficas. El análisis se centra, debido a los datos obtenidos y analizados, en los dos primeros momentos planteados en el apartado 3.

4.1. LA APARICIÓN DE LA TRAYECTORIA

La primera tarea de la situación del resorte consistió en solicitarles a los estudiantes que dibujaran el movimiento de un resorte cuando se le ponía una pesa, sin que se realizara el experimento con el resorte. Esta actividad inicial dio lugar a que los estudiantes formularan respuestas asociadas a dibujos icónicos y en algunas ocasiones dibujos que indicaran una secuencia temporal del comportamiento de la situación.

La manera en la cual se realiza el cuestionamiento a los estudiantes se puede apreciar en el extracto 1. Para efectos del análisis y la presentación de los resultados se utiliza la letra T para hacer referencia al “tallerista” o responsable de la implementación y E1, E2, etc. corresponde a diferentes estudiantes participantes de la actividad. Se indican además las líneas de diálogo para cada intervención de los participantes y tallerista.

[1] T: ¿cómo sería el dibujo del movimiento de una pesa cuando se coloca en un resorte?

[...]

[2] T: aquí tengo la pesa, es una pesa de 50 gramos, puedes tocarla para que veas que no hay truco... es una pesa normal y vamos a colocarla en el resorte... ¿ok?, ¿qué creen que pase?...

Extracto 1. Instrucciones iniciales realizadas por T.

Algunas de las producciones de los estudiantes con base en el cuestionamiento planteado por T se presentan a continuación:

Figura 3(a), 3(b), 3(c), 3(d). El dibujo del movimiento del resorte 

Con base en las producciones realizadas, T solicita a los equipos de trabajo que se conformaron en el grupo, que realicen explicaciones de sus propuestas. En los extractos 2 y 3, se aprecian dos ejemplos de respuestas de los estudiantes.

[1] E1: dibujamos el resorte, que está un poco estirado porque tiene un peso de 50 gramos, hasta abajo. Pero no solo baja, sino que también se puede digamos que mover de un lado al otro <hace referencia la figura 3(c) y señala los paréntesis de los lados> así que si es pesado no solamente para abajo... el resorte, al punto de estirarse también puede <mueve la mano a los lados, de izquierda a derecha no solo de abajo para arriba, para ejemplificar que el movimiento del resorte también podría presentar esa característica>... una vibración...

Extracto 2. Respuesta de un miembro del equipo que realizó el dibujo 3(c)

[1] E2: como su peso es de 50 gramos... y al poner el peso baja y sube <cuando dice esto señala las flechas que aparecen en el dibujo y mueve la mano de “arriba hacia abajo”>

[2] E3: rebota...

[3] E1: rebota como pelota... <realiza un gesto de arriba hacia abajo>... y no está estable...

[4] T: ¿qué significa que no está estable?

[5] E1: pues que no se queda quieto...

Extracto 3. Respuesta de un miembro del equipo que realizó el dibujo 3(a)

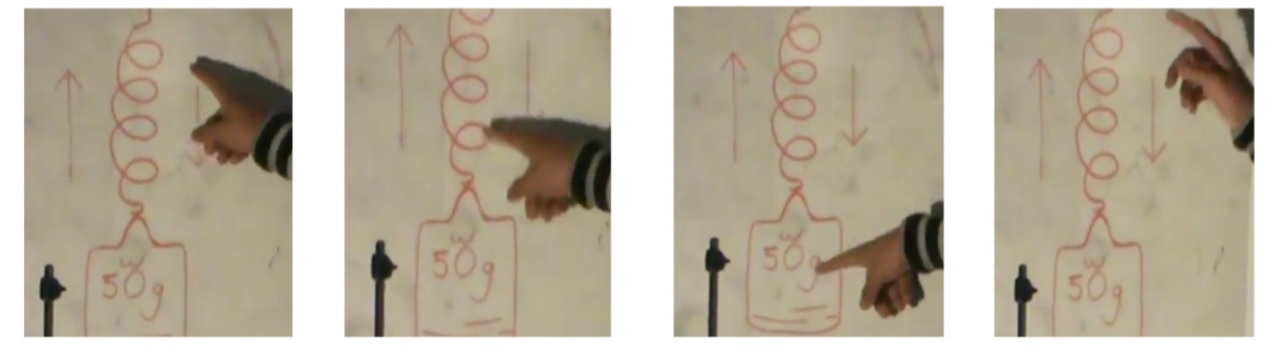
Un elemento a resaltar es que la aparición de estos dibujos icónicos y el discurso de los participantes iba acompañado de gesticulaciones, es decir, de gestos que ocurren en asociación con el discurso (Kendon, 1987 citado por ^{Vergel, 2015}) como por ejemplo uno que hemos denominado la “mano vertical” (extracto 2); gesticulación que aparece en conjunción con el comportamiento y con frases como “sube y baja”, “de arriba hacia abajo”, etc. En la siguiente secuencia de imágenes de la figura 4 que a continuación presentamos, se brinda evidencia de la gesticulación de la mano vertical:

Figura 4  Secuencia de la “mano vertical” para explicar el movimiento del resorte 

Como se puede observar en la secuencia de imágenes de la figura 4, el interés del estudiante es explicarle a T que el movimiento del resorte será “subir y bajar”. Este gesto acompañado del extracto 3, conforman una unidad funcional que permite explicar el comportamiento del movimiento del resorte según la situación planteada a los estudiantes.

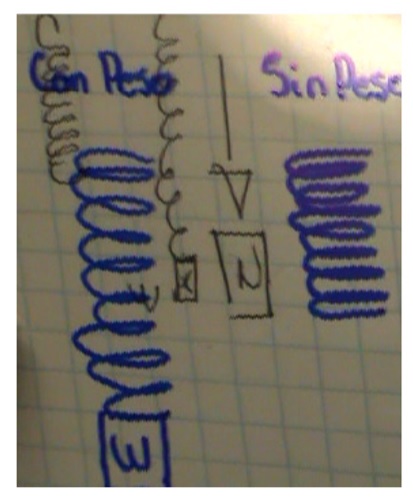
Otro ejemplo de producciones de los participantes incluía una secuencia temporal de lo que observaban, tal y como se puede apreciar en la figura 3(d). Además, este dibujo era acompañado de comentarios como “dibújale antes y después...”, expresado por los estudiantes para referirse a instantes del fenómeno: cuando no tiene peso y después de colocar la pesa (ver figura 5).

Figura 5 Secuencias Temporales: resorte “con peso” y resorte “sin peso” 

A partir de estas clases de ejemplos en este momento de la situación, notamos cómo las producciones de los estudiantes poseen convenciones sociales y culturales asociadas. Este tipo de convenciones y el tipo de respuestas basados en dibujos icónicos y en elementos del discurso, ya se reportaron en otras investigaciones (ver por ejemplo ^{Sherin, 2000}, ^{DiSessa, Hammer & Sherin, 1991}). Por ejemplo, una convención que los estudiantes utilizan es que ellos crean un dibujo para recrear una historia que están intentando contar (figura 3), pero además se apegan lo más posible a ella, sin tomar en consideración e incluir aspectos que “no ocurren o nunca ocurrieron” (^{Nemirovsky, Tierney & Tracy, 1998}). Aunado a todo lo anterior, también se encuentra la relación entre gesto-discurso-dibujo (figura 4) para indicar con todo el cuerpo algo relativo a la dirección del movimiento, de manera que se conforma una unidad funcional que da cuenta del fenómeno.

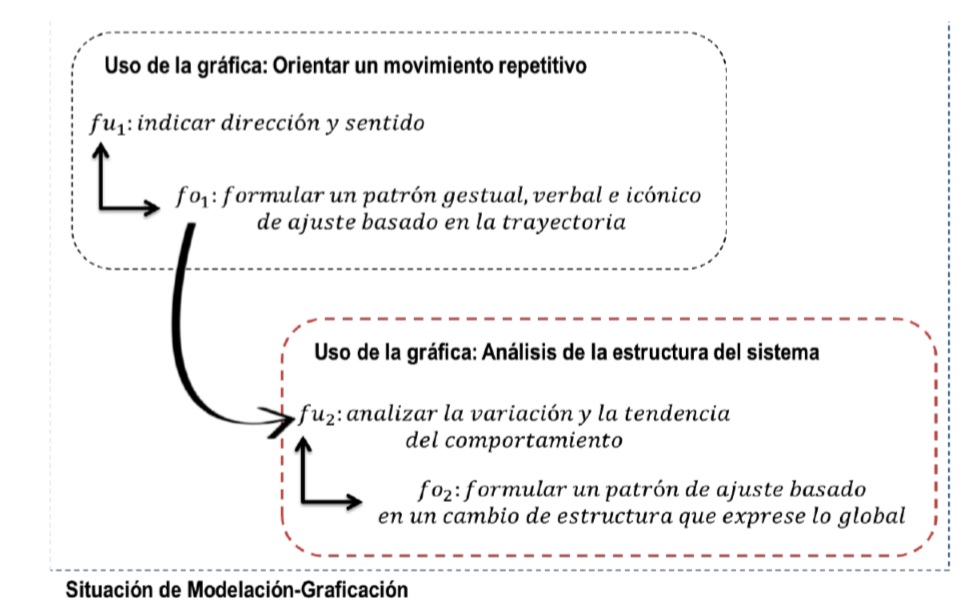
Ahora bien y de acuerdo a el modelo de resignificación del uso de la gráfica hay que tomar una posición importante. El hecho de que no “apareciera” una gráfica cartesiana como configuración para referirse al movimiento, no significa que no hayan usos de la gráfica, puesto que se presentan formas culturales de saberes conformados histórica, cultural y socialmente en esferas de la actividad humana. Las producciones de los estudiantes contienen una carga cultural y social asociada a convenciones para referirse al movimiento, donde la gráfica cartesiana, que es una manera más para referirse a dicho movimiento, pero no la única, de lo cual resultan otros patrones de ajuste válidos y funcionales para los estudiantes, además de que son suficientes para realizar la tarea a la que se enfrentan. De manera que el funcionamiento (Fu-1) de las gráficas en este momento de la situación era para indicar dirección y sentido del movimiento repetitivo, pero a través de formular un patrón de ajuste de tipo icónico, gestual o verbal (Fo-1), por ejemplo mover la mano de “arriba hacia abajo” o utilizar flechas que indicaban si el resorte sube o baja. La argumentación que los estudiantes elaboran de la gráfica la basan en una herramienta que se ha denominado Trayectoria, la cual se define como un patrón de ajuste que hace referencia a aquello que se mueve indicando la dirección del movimiento por medio del lenguaje verbal, icónico o gestual. El uso de la trayectoria es una unidad funcional cuya lectura, interpretación y construcción que los estudiantes utilizan es para referirse a lo observable, en sí es un uso de la gráfica, y resignifica el espacio y el tiempo en un patrón de ajuste donde el tiempo se incrusta en la distancia; por lo que no indica explícitamente variaciones ni tendencias en el comportamiento. Es importante resaltar la postura de que la trayectoria es un uso de la gráfica y no una concepción errónea de la última, dada la postura socioepistemológica, donde se reconoce la validez de todo tipo de saberes ya sean técnicos, cotidianos o cultos.

Ahora bien, a partir de este análisis del uso de la gráfica en esta primera tarea es que emerge una manera de entender la comportamientos asintóticos o con tendencia del sistema en términos de cómo se usa la gráfica, es decir, la trayectoria permite una configuración de algo que permanece sin cambios, debido al tipo de patrones de ajuste que elaboran. Es por ello, que este primer uso de la gráfica detectado se le denomina: orientación del movimiento (Uso-1).

4.2. EL ABANDONO DE LA TRAYECTORIA Y LA APARICIÓN DE LA CURVA

Posteriormente a la tarea inicial, T cuestiona a los estudiantes sobre si el resorte se detiene o no durante su movimiento, con la intención de movilizar las producciones y los argumentos de los estudiantes hacia funcionamientos y formas que hagan emerger explícitamente el comportamiento particular del sistema. En síntesis, consideramos que argumentos como tendencia y variación permiten resignificar a la orientación del movimiento hacia otras formas y funcionamientos de las gráficas. De esta manera se problematizan los patrones de ajuste anteriormente propuestos por los estudiantes. Algunas respuestas de los estudiantes ante la Tarea 2 y la Tarea 3 de la SMM se encuentran en el siguiente extracto:

[1] T: E1, tu dijiste que sí se detiene <refiriéndose al resorte con la pesa>...¿por qué piensas que se detiene?

[2] E1: porque sí se detiene, porque llega a un cierto tiempo en que...

[3] E2: pierde fuerza...

[4] E1: ajá... la fuerza se empieza a hacer más pequeña, más pequeña, más pequeña, más pequeña, hasta que ya... <Mientras E1 explica, realiza un movimiento vertical con la mano pero reduciéndolo cada vez más mientras realiza su explicación, como haciendo que el tiempo “avance”>. (Ver secuencia de imágenes en figura 6).

[5] T: a ver... E3 dice que no se detiene <refiriéndose al resorte con la pesa>, ¿por qué no se detiene?

[6] E3: porque tiene mucho peso, no se va a detener... va a seguir... <se hace referencia a la fuerza de gravedad que siempre jala para abajo>

Extracto 4. ¿El resorte se detiene?

Figura 6  El resorte se detiene: la “mano vertical” se modifica 

Como podemos observar, la problematización de los patrones de ajuste consistía en poner en discusión las argumentaciones iniciales. Específicamente al hacer referencia a la tendencia, a la variación y a aspectos globales del comportamiento, o sobre cómo será el dibujo del movimiento del resorte después de pasados ciertos minutos; o cuando se les solicitaba que reflexionaran sobre cuándo el resorte iba rápido o lento de acuerdo a la propuesta de dibujo que realizaron. Las respuestas de los participantes se inclinan más hacia la necesidad de completar con información escrita y anotaciones en sus producciones; como incluir a un lado del dibujo la frase “muy rápido”, o la palabra “lento”, etc. Esta propuesta también aparece en otras experiencias con otros estudiantes donde muchos dibujos eran complementados con información necesaria para aclarar lo que sucedía (ver por ejemplo: ^{Zaldívar, 2015}; Zaldívar y Cordero, 2012; ^{Briceño y Cordero, 2012}).

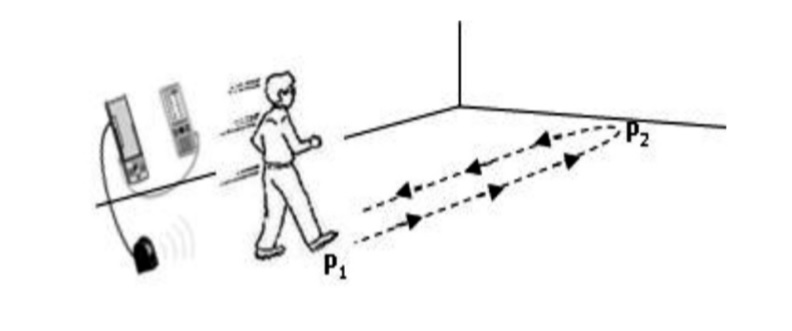
Posterior a estos cuestionamientos y con la intención de una búsqueda de consensos con los estudiantes, se decide emplear un sensor de movimiento y el emulador de la calculadora graficadora TI-Nspire CX como un medio que permite la aparición de un patrón de ajuste distinto al que los participantes emplearon inicialmente. Durante la implementación de la situación, se decide introducir la tecnología a partir de un ejemplo distinto al planteado inicialmente. Para ello se usa un caso presentado en ^{Briceño y Cordero (2012)} de una persona que camina frente al sensor de movimiento en línea recta y se aleja y regresa al punto de partida (figura 7).

Figura 7 Situación de movimiento propuesta 

Se permite que los estudiantes realicen algunos movimientos frente al sensor con la intención de que se familiaricen con el ambiente tecnológico y con el funcionamiento del sensor. Los estudiantes además eligen la manera en la cual se mueven frente al sensor: rápido, lento, etc. Al realizar esta experiencia, los estudiantes visualizan gráficas como la siguiente (figura 8):

Figura 8 La gráfica con el sensor de movimiento 

Las preguntas de T durante este momento de la implementación tienen que ver con dónde estaba ubicado físicamente el participante en puntos específicos de la gráfica: en el inicio, en el valor máximo y en qué momento regresó. La intención de este momento es empezar a reflexionar sobre un punto de referencia.

Durante el caso de la implementación que presentamos en el presente artículo, T no realiza la simulación con el resorte, sino que les solicita a los estudiantes que con base en el funcionamiento del sensor que acaban de experimentar, propusieran cómo sería la gráfica del movimiento del resorte si se usara el sensor (Tarea 4). En este momento, con ayuda de los casos anteriores sobre el movimiento de una persona se esperaba que los estudiantes con ayuda de la tecnología identificaran un punto de referencia menos artificial anclado al origen fenomenológico de la situación de modelación. Para ello, T aclara la manera en la cual ubicará el sensor de movimiento en el sistema físico del resorte (ver figura 9).

Figura 9 Ubicación del punto de referencia del sensor en el sistema físico del resorte 

Desde este análisis de los usos de las gráficas el “abandono” de la trayectoria como patrón de ajuste surge entonces cuando la situación exige un análisis de la estructura interna del sistema a modelar, pero en términos de problematizar explícitamente lo variacional y la tendencia del comportamiento del sistema. Esto implica complejizar el patrón de ajuste basado en trayectorias con apoyo de la tecnología.

Consideramos que los argumentos de variación, tendencia y la ubicación de un punto de referencia provocan, de manera sistémica, una resignificación del uso de la gráfica a partir del momento 1. Así mismo, el ingreso de la tecnología permitió discutir sobre el origen fenomenológico y el cartesiano y sus relaciones, como puntos de referencia necesarios. De esta manera indicar dirección y sentido parece ser insuficiente pero también necesario para explicitar elementos variacionales y tendenciales; puesto que se encuentran en la base de las justificaciones funcionales.

Entre las propuestas que los estudiantes elaboran con respecto a la gráfica del movimiento del resorte, se observan los siguientes ejemplos (figura 10):

Figura 10 Producción del equipo 3 

La explicación que realiza un miembro del equipo sobre la gráfica anterior (figura 10) es la siguiente:

[1] E1: es una gráfica como tipo de ondas senoidal (sic)... pero aquí es el punto donde el resorte está quieto y se le aplica lo que es una fuerza de 50 gramos y aquí desciende… aquí sube y aquí se queda quieto <muestra el corte con el eje de las X>... no... ‘pera... Aquí baja, sube, se queda quieto, sube… vuelve a bajar… y así hasta que queda estable...

[2] T: y esa recta significa qué... <se refiere a la última parte de la gráfica>

[3] E1: que se quedó estable... <realiza un gesto con la mano de forma horizontal (ver elemento encerrado en la figura 10)>

Extracto 5. Explicación de la gráfica del equipo 3

Como podemos apreciar en el extracto anterior, aun cuando el funcionamiento del sensor de movimiento ya se discutió, el punto de referencia establecido como el origen cartesiano no tiene un significado claro, es decir, no se lee como tal, puesto que la curva “corta” al eje horizontal y no se ubica únicamente en el primer cuadrante. De manera que dibujar ejes a manera de representar ejes cartesianos, no implica una lectura funcional entre las variables de correspondencia entre las mismas.

Otro ejemplo es realizado por el equipo 5:

Figura 11 Producción del equipo 5 

Explicación de la producción del equipo 5 con base en la figura 8:

[1] E4: bueno aquí estamos en nuestra gráfica considerando distancia sobre el tiempo <se refiere a los ejes>... entonces, lo que hace aquí es... no consideramos números negativos ni el cuarto cuadrante... Lo que empieza a hacer el resorte al insertar la pesa es... luego luego al instante deja caer la fuerza... y aquí al caer la fuerza va a volver a subir <zona señalada en la figura 11>... va a tener un regreso, así conforme va pasando el tiempo va haciendo la misma... el mismo recorrido y la misma onda, pero mientras más tiempo pasa esta onda va disminuyendo ya que hay un momento en el que va a llegar <con la mano recorre la gráfica sobre ella y con un dedo> a ser estática.

Extracto 6. Explicación de la gráfica del equipo 5

A la luz de nuestro análisis, las producciones de los estudiantes tienen más referencias a un comportamiento asintótico de manera más explícita. Consideramos que este comportamiento se reconoce asociado a la tendencia que presenta el fenómeno, que se expresa en las “curvas” suaves y en las partes de la “curva”. Este significado surge cuando la gráfica se usa para analizar la estructura interna del sistema (Fu-2) y expresar globalidad, variación y en ocasiones tendencia a través de un nuevo patrón de ajuste que denominamos Curva (Fo-2), que es un patrón de ajuste que se lee globalmente e integra elementos tendenciales, más complejos que los que la trayectoria permite analizar. En sínstesis, la curva se convierte en la nueva unidad funcional que expresan los estudiantes. Es importante notar que las referencias al discurso inicial de los estudiantes cuando mencionaban que el resorte “sube-baja”, “rebota”, etc., en este nuevo uso de la gráfica, aparecen más incrustadas en justificaciones con respecto al sistema y su comportamiento. Sin embargo, la lectura, interpretación y construcción que hacen de la gráfica no parece aún contar con las convenciones sociales propias de las gráficas cartesianas, que incluye elementos como escalas, unidades de las variables, ubicación de puntos ordenados (x,y) de coordenadas, y un análisis local de éstos.

Consideramos con base en el análisis de estos casos que las trayectorias como patrón de ajuste no se eliminan del “todo” del uso de la gráfica; la resignificación es progresiva y se está ante elementos que permiten la emergencia del sistema cartesiano, lo cual se logra con la integración de la variación y la tendencia al uso de la gráfica. Sin embargo, los estudiantes no lo logran por completo, ya que existen errores como la ubicación del origen y el uso del espacio de los cuadrantes y los signos que pueden tomar las variables.

En este uso de la gráfica, el análisis de la estructura del sistema (Uso-2) que se discutió anteriormente, se aprecia una necesidad por parte de los estudiantes de “dividir” a sus producciones: “cuando se mueve”, “cuando empieza a detenerse”, “cuando se detiene”. Pero más aún, no existe una necesidad de expresar todo el recorrido, sino su intención es sólo dar una idea general del comportamiento de manera global y anticipar cómo será la forma de la gráfica, que era expresado a través de una línea recta al final de las curvas (ver extracto 7). Tampoco existe un señalamiento claro al punto de referencia, sino indicios. Este uso de la gráfica, sin embargo, ya integra elementos de variación y tendencia.

[1] T: ¿qué pasaría en tu gráfica si yo dejara el sensor durante 10 minutos? <se refiere a la posibilidad de estar tomando datos del resorte durante ese tiempo>

[2] E1: mmm, pues en algún punto se tendría que detener...

[3] T: ¿cómo va a ser la gráfica?

[4] E1: pues como esta... va a ser una línea recta <con la mano dibuja una recta horizontal>

Extracto 7. La línea recta como patrón de ajuste para indicar el comportamiento asintótico del sistema

Posterior a la discusión de las propuestas de todos los equipos, T propone el uso de la tecnología para comprobar las hipótesis de los equipos y confrontar algunas de las producciones. Algunas de las gráficas cartesianas que obtiene con ayuda del sensor se encuentran en la figura 12:

Figura 12 Ejemplos de gráficas obtenidas con el sensor y la calculadora del movimiento del resorte 

Por último y para continuar con la reflexión del comportamiento asintótico del sistema, T propone una gráfica y cuestiona a los estudiantes sobre si esa gráfica podría representar el movimiento de un resorte y bajo qué condiciones. En este momento de la situación se pretende que los estudiantes reflexionen sobre diferentes tipos de amortiguamiento del sistema masa-resorte: amortiguado, sub-amortiguado, críticamente amortiguado (Zill, 1997).

5. COMENTARIOS FINALES

La pregunta que le da nombre al presente artículo implica un reto en la investigación en Matemática Educativa. Implica por un lado, considerar a los estudiantes ya no como sujetos únicamente cognoscentes, sino como individuos con sentimientos, ideas, y partícipes de su propio proceso de aprendizaje de las matemáticas. Pero por otro lado, la pregunta implica reflexionar sobre la noción de aula y encontrar, con base en la investigación, otros marcos de referencia donde el conocimiento matemático se resignifica y adquiere significación en el uso intencional de herramientas matemáticas. Más aún, esos otros marcos de referencia, deben ser tales que permitan un rediseño del dME desde el análisis de los conocimientos de los estudiantes en términos y de su aporte.

El considerar el uso de la gráfica permitió no acentuar la reflexión únicamente en el concepto de función, sino ampliar esa visión e inclusive prescindir, gracias a la modelación-graficación, de referencias a ecuaciones. Pero además, el análisis deja ver que la gráfica cartesiana también subordina en el dME otras resignificaciones y unidades funcionales de la gráfica, como son las trayectorias y las curvas de comportamiento, que compondrían formas culturales de saberes a las que también los estudiantes hacen referencias al enfrentarse a situaciones de movimiento relativo.

En síntesis, el análisis permite ver que la búsqueda de la permanencia (búsqueda de invariantes) en las cosas que varían es parte de la actividad humana relativa a una significación del movimiento relativo, dada la situación específica (^{Zaldívar, 2014}). Sin embargo, esta función podría considerarse opaca en el dME. De manera que las argumentaciones iniciales del comportamiento con tendencia basada en trayectorias, aparecían porque existía, a través de la tarea, una necesidad intencional de buscar la permanencia en el cambio, y un patrón de ajuste lo encuentra en las trayectorias (figura 13).

Al acentuar el análisis en los funcionamientos y formas del uso de las gráficas se deja evidencia de aquello que subyace en la lectura e interpretación de las gráficas, y el porqué los participantes producían el tipo de respuestas, pero también cómo es posible producir resignificaciones progresivas hacia integrar más elementos y complejizar patrones de ajuste iniciales (ver figura 13). Tal función la tuvieron los argumentos variacionales y tendenciales que la situación provocaba.

Figura 13 Marco de Referencia de los usos de las gráficas en la SMM 

Se considera que el comportamiento asintótico deviene entonces de la resignificación del comportamiento tendencial visto como permanencia y constituye un elemento de funcionalidad que se derivó de la orientación y del cambio de estructuras y patrones, por medio de la variación y el reconocimiento de un punto de referencia.

Por último, se requiere el desarrollo de más investigaciones que permitan dejar ver otros marcos de referencia donde el conocimiento matemático se resignifique y que permitan la aparición y habilitación de una matemática funcional en el sistema didáctico. Sin embargo, también esto último precisa de escenarios escolares ad hoc a los avances actuales y que se tensen elementos como los que esta investigación problematizó: el uso del conocimiento matemático por sobre lo utilitario de la matemática escolar.