INTRODUCCIÓN
Al enfrentarse a una tarea algebraica, el alumno puede proceder de distintas formas para realizarla, las cuales han sido estudiadas por diferentes autores. Dichos autores señalan que, de esas formas de proceder, algunas son más eficientes que otras, por implicar un manejo conceptual más profundo y significativo, más reflexivo antes de actuar, procedimientos más cortos y menos propensos al error (Hoch, 2003; Hoch & Dreyfus, 2004; Molina, 2010; Jupri & Sispiyati, 2017). Las formas eficientes requieren de un análisis de la estructura de la expresión, para determinar cuáles serían los procedimientos posibles para trabajar con ella y cuál de ellos sería el mejor. En este sentido, Sfard (2001) considera que, si ser capaz de ver la estructura es útil en cualquier dominio del conocimiento, en matemáticas puede considerarse la esencia misma del aprendizaje. De entre los distintos nombres que se le han dado a estas formas más eficientes de actuar: sentido de estructura (Linchevski & Livneh, 1999), sentido estructural (Vega-Castro, 2013), razonamiento estructural (Harel, 2013), pensamiento estructural (Mason, Stephens, & Watson, 2009), según el autor que se consulte, para esta investigación se usará el de operar con sentido estructural, como lo llama Vega-Castro (2013).
Se pensaría que, al tener identificadas las maneras más eficientes de proceder, y la importancia de que los alumnos las usen, éstas podrían promoverse durante la formación escolar del estudiante y se observarían en sus procesos a su llegada a la universidad. Sin embargo, tanto nuestra experiencia profesional, como diversos artículos consultados, revelan lo contrario. Se han encontrado, por ejemplo, dificultades en el reconocimiento de la estructura de las expresiones algebraicas en alumnos universitarios (Eccius-Wellmann, 2011; Eccius-Wellmann, 2013). A su vez, Chinnappan y Forrester (2014), observaron que los profesores en formación que participaron en su estudio manifestaban un conocimiento más procedimental que conceptual. Godino et al. (2015), por su parte, conjeturaron la presencia de carencias formativas en los estudiantes de magisterio, en particular sesgos sobre pensamiento relacional (estructural). Los estudios presentados en este párrafo fueron relevantes para esta investigación por su enfoque en el sentido estructural de alumnos de nuevo ingreso a la universidad. El que algunos hagan referencia a profesores en formación sugiere la conveniencia de realizar investigaciones posteriores, relacionadas con el sentido estructural de profesores en servicio, como la de Jupri y Sispiyati (2017), quienes observaron en siete profesores de matemáticas en servicio una tendencia a operar expresiones algebraicas sin analizar previamente su estructura, aunque, al pedírseles una forma diferente de proceder, mostraron un mayor razonamiento estructural en dicha forma de proceder. El relacionar el sentido estructural de profesores y alumnos queda fuera del alcance de esta investigación.
Sobre el desarrollo del sentido estructural, al observar que los estudiantes con menor habilidad para reconocer las estructuras eran también los de menor desempeño, Lüken (2012) concluye que necesitan diseñarse acciones instruccionales bien fundamentadas para promoverlo en los alumnos, lo cual puede llevar a mejorar sus competencias matemáticas. A este respecto, Vega-Castro, (2010) considera que algunas formas de enseñar promueven más que otras el desarrollo de dicho sentido, aunque no encontró estudios al respecto en su momento. En Vega-Castro, Molina y Castro (2012) las autoras describen el procedimiento que siguieron para evaluar el nivel de sentido estructural en estudiantes de bachillerato, por medio del análisis de los procedimientos seguidos por los participantes. Sugieren considerar como descriptor del sentido estructural, entre otros, el anticipar la utilidad de las transformaciones algebraicas. Consideran que el sentido estructural es un elemento importante para identificar la utilidad de los conocimientos algebraicos básicos (igualdades notables) dentro de otros temas algebraicos (simplificación de fracciones algebraicas).
La identificación de las carencias y necesidades mencionadas y la escasez de propuestas para desarrollar el sentido estructural, motivó la realización de esta investigación, cuyo objetivo fue el desarrollo de dicho sentido en estudiantes universitarios de nuevo ingreso a las carreras administrativas, mediante la elaboración e implementación de actividades de enseñanza-aprendizaje, específicamente en estructuras algebraicas. Para delimitar el estudio, se trabajó con los temas de simplificación y operaciones con expresiones algebraicas racionales y sus prerrequisitos.
Se eligió, como fundamento teórico pedagógico para orientar la construcción de las actividades de enseñanza-aprendizaje, la Teoría de la Variación de Marton (2015). Su enfoque en los contrastes y variaciones se estima adecuado para promover en el alumno el análisis de las estructuras algebraicas antes de trabajar con ellas, como sugieren Banerjee y Subramaniam (2005). Ellos consideran que desarrollar un sentido estructural de las expresiones requiere el uso de procedimientos y reglas en situaciones y contextos variados, que permitan encontrarle el sentido a las relaciones entre los componentes de diversas expresiones que compartan los mismos aspectos estructurales.
En este artículo se da respuesta a las siguientes preguntas de investigación:
−¿Cómo se puede ponderar el nivel de sentido estructural manifestado en los procedimientos algebraicos desarrollados por los alumnos?
−Con base en la ponderación establecida para este estudio, ¿cómo es el promedio del nivel de sentido estructural en los alumnos, al ingresar a la universidad? Por todos los participantes, por grupo y entre grupos.
−Con base en la ponderación establecida para este estudio, ¿cómo es el promedio del incremento del nivel de sentido estructural en los alumnos que trabajaron con las actividades de enseñanza-aprendizaje diseñadas con base en la Teoría de la Variación, en comparación con el incremento del nivel de sentido estructural en los alumnos que trabajaron con actividades que no contemplen dicha teoría pedagógica?
La primera pregunta se responde en el apartado: Metodología / Descriptores del sentido estructural y su ponderación. La segunda y la tercera se responden en el apartado: Resultados / Nivel de sentido estructural manifestado por los alumnos al ingresar y Cambio en el nivel de sentido estructural, respectivamente.
MARCO CONCEPTUAL
ESTRUCTURAL O PROCEDIMENTAL
Sobre la forma de operar una expresión algebraica, distintos autores han identificado que está guiada por la forma en que se visualiza la expresión. Los alumnos, al enfrentar una tarea algebraica, pueden centrarse en aspectos de tipo procedimental/operacional/instrumental (ver a+b como una suma que debe realizarse) o estructural/relacional (ver a+b como la expresión de la suma de a más b, o la relación de a y b mediante el operador suma, sin que sea obligatorio realizar dicha suma). La manera de visualizar una expresión algebraica tiene diversas implicaciones.
Por ejemplo, Skemp (1976) señala la importancia de enseñar las matemáticas de forma relacional, en la que el alumno comprenda las relaciones entre los elementos antes de operar. Advierte que es fácil enseñar de forma instrumental (seguir reglas sin razonar), con la que se logran desempeños aceptables rápidamente, aunque no perdurables. Enseñar de forma relacional, por el contrario, tiene las ventajas de permitir adaptar lo aprendido a nuevas tareas y de que el aprendizaje sea más sencillo de recordar. Es conveniente que se logre dejar de ver los operadores como una operación que debiera hacerse (interpretación procedimental) y se le dé a la expresión una interpretación estática (relacional) para que las manipulaciones algebraicas, como las sustituciones de variables, puedan hacerse adecuadamente, como sugiere Freudenthal (1983) . Además de los operadores, el signo igual también puede ser visto de forma meramente procedimental, lo cual complica la transición de la aritmética al álgebra. Burgell y Ochoviet (2015) resaltan la importancia de fomentar en los alumnos una visión relacional del signo igual, mediante actividades no estándar.
Se puede tener una concepción operacional de las matemáticas, en la que una entidad es concebida como el producto de un proceso o como el proceso mismo, mientras que en la estructural es concebida como una estructura estática, como un objeto real. La operacional está en las primeras etapas de la formación del concepto y la estructural evoluciona a partir de ella. La operacional es necesaria pero no suficiente para el aprendizaje y la resolución de problemas, mientras que la estructural facilita todos los procesos cognitivos (Sfard 1991).
Por otro lado, Molina (2010) explica que, si al realizar una operación o resolver una ecuación se emplea un procedimiento estándar aprendido, sin detenerse a analizar las características particulares del ejercicio en cuestión, se trabaja bajo un enfoque procedimental. En cambio, si se realiza un análisis previo de las características particulares de las expresiones (su estructura) y al llevar a cabo la actividad se les toma en cuenta, entonces se trabaja bajo un enfoque estructural. Propone, por tanto, promover el hábito de la observación y el análisis de características particulares de las expresiones antes de iniciar la manipulación, con el fin de fortalecer el enfoque estructural, que permita un trabajo más significativo con expresiones aritméticas y algebraicas y evite algunas de las dificultades que los alumnos encuentran en el aprendizaje y transición entre ambas.
SENTIDO ESTRUCTURAL
Aunque el enfoque procedimental/operacional/instrumental es necesario por sí mismo e indispensable para llegar al enfoque estructural/relacional, los alumnos suelen quedarse en el primero por diversas razones, como las referidas por Skemp (1976) previamente en este texto. Es por ello que las investigaciones más recientes, presentadas a continuación, se han centrado en describir y encontrar formas de promover el enfoque estructural.
El concepto de sentido de estructura, introducido por Linchevski y Livneh (1999) , abarca las capacidades de reconocer formas equivalentes de una expresión y de identificar las formas apropiadas de realizar una tarea. Posteriormente, Hoch (2003) lo describe como una colección de habilidades, separada de las habilidades manipulativas, que permiten a los estudiantes hacer mejor uso de las técnicas algebraicas aprendidas previamente. Para ella, las cadenas de símbolos forman estructuras y su interpretación depende del contexto. La conciencia de esas distintas interpretaciones es parte del sentido de estructura. Señala que se denota una falta de dicho sentido al operar sin observar si la estructura permite seguir un proceso más eficiente, como cuando se operan los agrupadores como un primer paso no reflexionado en una transformación algebraica.
La apariencia externa de una expresión revela un orden interno determinado por las relaciones entre las partes que componen su estructura, según Hoch y Dreyfus (2004) , quienes incluyen en la mencionada colección de habilidades: la capacidad de ver una expresión algebraica como una entidad, el reconocer una expresión algebraica como una estructura previamente conocida, sus subestructuras, las conexiones mutuas entre estructuras, cuáles manipulaciones son posibles y, finalmente, cuál manipulación es más eficiente.
Más adelante, los mismos autores formularon descriptores para el sentido de estructura, basados en la complejidad de las estructuras algebraicas operadas, desde las más sencillas, con sub-términos simples, las de complejidad intermedia, con sub-términos compuestos por productos, cocientes y potencias y las de mayor complejidad, con sub-términos compuestos, además, por sumas y restas (Hoch & Dreyfus 2006). A esos descriptores Vega-Castro (2013) propone agregar otro que permita distinguir el sentido estructural mostrado cuando las subestructuras pertenecen a una expresión en un solo nivel y cuando pertenecen a expresiones en diferentes niveles, como en numerador y denominador. Ambas propuestas, y las distintas formas de ver el sentido estructural, referidas en este texto, formaron la base para establecer los descriptores usados en este estudio. Para Vega-Castro (2013), por ejemplo, el sentido estructural es un conjunto de capacidades necesarias para trabajar flexiblemente con expresiones algebraicas, que implican el uso combinado de conocimiento conceptual y procedimental.
Por su parte, Harel (2013) describe el razonamiento estructural como una habilidad combinada de observar estructuras, actuar sobre ellas con un propósito claro y razonar en términos de estructuras generales, no de casos particulares. Harel y Soto (2017) proponen cinco categorías para el razonamiento estructural: generalización de patrones, reducción de una estructura no familiar a una familiar, reconocimiento y operación de acuerdo a la estructura, justificación epistemológica y razonamiento en términos de estructuras generales. Esta categorización presenta algunas similitudes con los descriptores de Hoch y Dreyfus (2006) .
Desde su perspectiva, Mason, Stephens y Watson (2009) identifican como pensamiento estructural la disposición para explicar, conectar y usar las propiedades de una estructura en el pensamiento matemático. La conciencia de dichas propiedades, que dependen de las relaciones entre sus elementos, es el centro del pensamiento estructural. Al desarrollar la conciencia de la estructura matemática en el alumno, se transforma su pensamiento matemático y su compromiso con la actividad matemática.
Según estos autores, el profesor debe ser capaz de reconocer la estructura matemática para poder lograr que sus estudiantes la disciernan, apoyados en las actividades diseñadas por el docente. Una forma de lograrlo es pedirles a dichos estudiantes que señalen, antes de manipular la expresión matemática, cuáles propiedades de su estructura justifican dicha manipulación. Mencionan que el enfoque procedimental o estructural logrado en los alumnos es una decisión pedagógica, esto es, depende de cómo se lleva a cabo la enseñanza. Consideran que se puede desarrollar el pensamiento estructural al trabajar en tareas que se enfoquen en la naturaleza de la relación en vez del cálculo, para que la atención se oriente hacia los aspectos estructurales como propiedades que aplican en muchas instancias; también al usar ejemplos que bloqueen las rutinas familiares. Algo importante acerca de las relaciones estructurales es no convertirlas en el contenido a ser aprendido, sino tratarlas como conciencia a ser traída a la superficie, preferentemente a través del uso de ejemplos cuidadosamente variados, aunque existen casos en los que es necesario hacer del reconocimiento de las estructuras el centro de la actividad, como en el aprendizaje de los productos notables y la factorización (Hoch & Dreyfus, 2007).
Novotná, Stehlíková y Hoch (2006) concluyen en su estudio con estudiantes universitarios que, si se atribuyen las dificultades de los alumnos a su falta de sentido de estructura, es importante enfocarse en desarrollar dicho sentido en esa etapa educativa. Proponen un modelo para evaluar el sentido de estructura en estudiantes que realizan operaciones binarias de álgebra abstracta, que puede servir de base para atender las carencias mostradas por los alumnos en ese tema. Señalan que los modelos para evaluar el sentido de estructura pueden necesitar adaptarse al tema a trabajar, como fue necesario en esta investigación.
Para realizar este estudio fue preciso determinar una forma de valorar el nivel de sentido estructural en los alumnos. Éste se consideró como la suma de las siguientes habilidades: reconocer la estructura algebraica de la expresión que se observa, identificar las manipulaciones que es posible realizar sobre ella, dada su estructura y elegir la más eficiente de todas. Los descriptores establecidos para hacer esa valoración se presentan dentro del marco metodológico.
TEORÍA DE LA VARIACIÓN
La Teoría de la Variación de Marton (2015) está enfocada en las condiciones necesarias para aprender que están relacionadas con el contenido, su elección y secuenciación. Marton y Booth (1997) consideran que adquirir un conocimiento es encontrar nuevas formas de vivir una experiencia relacionada con ese conocimiento. Destacan que una persona ha aprendido un concepto o proceso cuando es capaz de enfocar, de forma simultánea y consciente, aquellos aspectos de ese concepto o proceso que son esenciales a él, dentro de un contexto dado. Mencionan que el aprendizaje es una función del discernimiento, entendido como distinguir, mediante el intelecto, una cosa de otra o varias cosas entre sí, a través de la observación de lo que varía entre ellas.
Los aspectos críticos del objeto de aprendizaje (aquello que se aprenderá) son aquellos que permiten verlo como debe ser visto para ser aprendido de forma adecuada al contexto (Marton, Runesson, & Tsui, 2004). Häggström (2008) , menciona que la persona que discierna más aspectos críticos de un objeto y más relaciones entre ellos, podrá hacer uso de ese objeto de mejores formas, comparado con quien haya discernido menos aspectos críticos. Lo (2012) señala que los estudiantes no pueden discernir de forma natural los aspectos críticos, requieren que el profesor les provea las oportunidades de hacerlo, mediante la elección y organización del contenido. Los aspectos críticos toman valores (no necesariamente numéricos) que varían, llamados características críticas. Para un polinomio que se va a factorizar, por ejemplo, el número de términos (dos, tres, cuatro,...) es un aspecto crítico. Aspectos y características críticas son inseparables y, por tanto, se disciernen de forma simultánea.
Según como sea presentado y percibido, un aspecto se puede discernir de formas más o menos precisas, lo cual afectará la forma en que se entiende y se usa. Una forma más precisa se logra mediante patrones de variación e invariación, según propone Marton (2015) , quien advierte que, para que un alumno pueda discernir un aspecto crítico de un objeto de aprendizaje, es condición necesaria que lo observe variar. Para el autor, el patrón de variación mínimo, base de los demás, es el contraste, en el que se involucran al menos dos aspectos, uno de los cuales varía y el otro no. El que varía es sobre el que se llama la atención del estudiante, es el que se desea que discierna. Por ejemplo, si se desea enseñar a distinguir un trinomio cuadrado perfecto de uno que no lo es, se pueden mostrar estos trinomios:
x 2 -12x+36
x -13x+36
El único aspecto que varía es el coeficiente del segundo término, debido al cual el primer trinomio es cuadrado perfecto (el segundo término es el doble producto de las raíces cuadradas de los otros dos) y el otro no. Mediante este contraste, el estudiante identifica, específicamente en estos dos ejemplos, cuál sería un segundo término de un trinomio cuadrado perfecto y cuál no.
Los contrastes consecutivos llevan a la separación y a la generalización, considerados también patrones de variación e invariación. Después de observar distintos contrastes similares al anterior, el alumno logra separar aquello que hace que un trinomio cuadrado perfecto lo sea y generalizarlo para identificar trinomios cuadrados perfectos entre diversos trinomios con distintas sub-estructuras. Finalmente, el hacer variar dos o más aspectos a la vez, lleva a un patrón de variación e invariación llamado fusión (Marton, 2015). Por ejemplo, la fusión podría lograrse al distinguir un trinomio cuadrado perfecto de una diferencia de cuadrados. Cambia de trinomio a binomio y de un 36 positivo a negativo:
x 2 -12x+36
x 2 -36
Olteanu y Olteanu (2012) , por su parte, sugieren un nuevo patrón de variación e invariación, al que llaman similitud (similarity), el cual permite identificar que dos expresiones tienen el mismo significado, es decir, son dos formas, que se ven diferentes, de expresar lo mismo, como en:
(a+b)(a-b)
a 2 -b 2
Sumado a la determinación de los aspectos críticos y de los patrones de variación con los que éstos se presentarán a los alumnos, el diseño de una actividad o serie de actividades puede incluir un andamiaje, el cual implica pequeñas variaciones que llevan a pequeños avances en el aprendizaje, graduados por las actividades que dirige el profesor, según señalan Gu, Huang y Marton (2004) . Ellos indican que el andamiaje pone énfasis en el proceso y la jerarquía del aprendizaje. Aplicar el andamiaje en el salón, significa que los estudiantes avanzan exitosamente de su nivel actual de conocimiento hacia el siguiente a través de un diseño instruccional efectivo, conocido como Pudian en China (Huang & Li, 2017). En la enseñanza con variación en China se hace, además, una distinción entre la variación conceptual y la variación procedimental en el momento de elaborar las actividades. Lai y Murray (2012) observaron cómo las estrategias de variación procedimental apoyaron el aprendizaje significativo en los alumnos, al enfocar intencionadamente, dentro de las actividades que éstos realizan, conexiones sustantivas y no arbitrarias entre conocimientos.
Por su parte, Kullberg, Kempe y Marton (2017) , señalan que, mediante el análisis de las actividades de enseñanza-aprendizaje bajo el marco de la Teoría de la Variación se puede identificar lo que será más fácilmente discernible por el alumno, por haber sido adecuadamente enfocado y tematizado, y lo que no. Por lo tanto, este marco permite tanto revisar actividades ya existentes para complementarlas para que incluyan las posibilidades de aprender necesarias, como crear actividades completamente nuevas. En este estudio se dieron ambas situaciones al construir las actividades de enseñanza-aprendizaje con las que trabajaron los grupos experimentales.
El que la Teoría de la Variación esté centrada en el contenido hace que sea adecuada para buscar aprendizajes más ordenados, reflexionados, significativos y con un mayor análisis de las estructuras observadas, que, a la vez, eviten cierto tipo de errores mediante la presentación de contrastes de ejemplos y contraejemplos. En ese sentido, Marton (2015) considera que la gran mayoría de los fallos al entender derivan de que el estudiante no observó las diferencias que era necesario que percibiera. También advierte que, si bien el entendimiento no provoca una acción, una acción expresa el entendimiento. Esto puede interpretarse como que los procedimientos de respuesta de los alumnos a los ejercicios muestran las estructuras que discernieron y los procesos que eligieron debido a dicho discernimiento, es decir, muestran su nivel de sentido estructural.
METODOLOGÍA
PARTICIPANTES
Para lograr el objetivo de desarrollar el sentido estructural en estudiantes universitarios de nuevo ingreso, mediante la elaboración e implementación de actividades de enseñanza-aprendizaje para el desarrollo de habilidades para simplificar y operar expresiones algebraicas racionales y sus prerrequisitos, se realizó un cuasi-experimento (dado que los participantes no fueron elegidos al azar) con siete grupos de nuevo ingreso a las carreras administrativas de la universidad sede del estudio, que cursaban la materia de Álgebra. Los alumnos de cuatro grupos, 72 en total, trabajaron con las actividades diseñadas para fomentar el sentido estructural con base en la Teoría de la Variación (grupos experimentales). Los de los otros tres grupos, 62 en total, trabajaron de forma habitual, que no contempla actividades basadas en dicha teoría (grupos de control).
Cabe señalar que los alumnos que estudian en la universidad sede de esta investigación provienen, primordialmente, de diferentes bachilleratos de la Zona Metropolitana de Guadalajara, México y de la región noroeste de la República Mexicana. El historial académico de cada estudiante y, por tanto, su nivel de sentido estructural individual al iniciar sus estudios universitarios puede ser muy diverso.
INSTRUMENTOS
Los reactivos con los que se valoró el sentido estructural en los estudiantes, los mismos antes y después de realizar las actividades de enseñanza-aprendizaje, incluyeron los temas de productos notables, factorización, simplificación y operaciones con expresiones algebraicas racionales, los cuales forman parte de la currícula previa a la universidad, pero se retoman en la asignatura de álgebra que se cursa en el primer año de universidad para homogeneizar los conocimientos de los alumnos. Sin embargo, las actividades diseñadas incluyeron temas previos (elementos neutros, jerarquía de las operaciones, conformación de los términos en el álgebra, leyes de los exponentes y operaciones con expresiones algebraicas), para promover el desarrollo del sentido estructural a lo largo de más clases y crear un andamiaje en el aprendizaje, en el que los nuevos conocimientos se contrasten con los anteriores gradualmente y en todos ellos se haya fomentado el desarrollo del sentido estructural.
La preparación de las actividades se llevó a cabo durante enero-septiembre 2017 y el trabajo de los alumnos con las mismas se realizó durante agosto-octubre 2017. Se construyeron versiones preliminares, con base en la Teoría de la Variación (Marton, 2015) y el andamiaje que se promueve en la enseñanza con variación china (Gu et al., 2004). Los contenidos que constituyeron las actividades fueron seleccionados y secuenciados para promover el desarrollo del sentido estructural a la par del aprendizaje del tema, al fomentar el análisis de las estructuras de las expresiones algebraicas antes de trabajar con ellas. Cada actividad se afinó para incluir aquellos aspectos críticos que se manifestaron en la evaluación diagnóstica y que no habían sido previamente considerados.
A continuación se muestran algunos contrastes que se pidió a los alumnos analizar, los cuales apoyan el desarrollo del sentido estructural. En algunos casos sólo se analizan las diferencias entre las estructuras y en otros se analizan las consecuencias que tienen dichas diferencias en la forma de contestar los ejercicios.
EJEMPLOS DE CONTRASTES EXTRAÍDOS DE LAS ACTIVIDADES DE ENSEÑANZA-APRENDIZAJE
En la tabla 1 se presentan algunos contrastes básicos, que permiten una mejor transición del aritmética al álgebra, al identificar algunas diferencias entre ellas, así como la diferencia entre término y factor y entre reducir y simplificar, con ejemplos y contraejemplos.
Tabla 1 Contrastes básicos
| Contraste | El alumno debe contrastar y/o discernir | |
|---|---|---|
| 3+𝑥 | 3𝑥 | Dos términos vs dos factores. No son equivalentes, por lo que 3 +𝑥 ≠ 3𝑥. |
| +3=3 | 3 +𝑥 ≠ 3𝑥 | El +, cuando es digno, puede omitirse y, cuando es operador, no. |
| 𝑎 * 𝑏 = (𝑎)(𝑏) =𝑎𝑏 | 3 * 5 = (3)(5) ≠35 | El operador multiplicación y los parénte sis en álgebra (al involucrar literales) pueden omitirse, en aritmética no. |
| 3+8=11 | 3+𝑥=3+ 𝑥 | En aritmética una suma siempre puede reducirse, en álgebra puede ser necesario dejarla indicada. |
| (a+b)(c+d) | ab+cd | Dos factores compuestos por dos térmi nos cada uno vs dos términos compues tos por dos factores cada uno. |
|
|
|
Los términos se reducen 2+3=5 (mismo nivel),
los factores se simplifican: |
|
|
|
Sólo se pueden simplificar factores, no términos. |
Fuente: Elaboración propia
En otro tipo de actividad se contrastaron, mediante tablas comparativas que debían completarse, diferentes expresiones con la misma estructura principal.
Se identificaron las subestructuras y se realizaron factorizaciones. La tabla 2 es un ejemplo, con el trinomio cuadrado perfecto como estructura principal. Las variantes de los sub-términos (subestructuras) se basaron en los descriptores de Hoch y Dreyfus (2006) .
Tabla 2 Contraste de distintos tipos de subestructuras
| a2+2ab+b2 | a | b | (a+b)2 |
| m6+2m3n4+n8 | m3 | n4 | (m3+n4)2 |
|
|
|
|
|
| (a+b)2-10(a+b)+25 | (a+b) | 5 | ((a+b)-5)2 |
| 49w2-14w(xy+z)+(xy+z)2 | 7w | (xy+z) | (7w-(xy+z))2 |
Fuente: Elaboración propia
Dado que al realizar una simplificación de expresiones algebraicas racionales se presentan diversos procedimientos, tipos de respuestas y posibilidades de error, se realizó una actividad en la que éstos se contrastaron, como se ilustra en la tabla 3.
Tabla 3 Contraste de casos en simplificación de expresiones algebraicas racionales
| Caso | El alumno debe contrastar y/o discemir | |
|---|---|---|
|
|
para x ≠ -2 | Quedan factores diferentes de 1 en numerador y denominador. |
|
|
para x ≠ -2 | Quedan factores diferentes de 1 sólo en numerador (Ojo, el denominador no desaparece ni es igual a 0, es un 1 implícito). |
|
|
para x ≠ -2 | Quedan factores diferentes de 1 sólo en denominador (Ojo: el numerador no desaparece ni es igual a 0, es un 1 que debe escribirse). |
|
|
para x ≠ -2 | Contraejemplo del anterior. |
|
|
para x ≠ -2, x ≠ 1 | No quedan factores diferentes de 1. No es igual a 0. |
|
|
para x ≠ -2 | Una vez factorizado queda como el primer caso. |
|
|
para x ≠ 1 | Evitar cancelar las 𝑥 como tercer paso. |
|
|
para x ≠ 1 | Sólo pueden simplificarse factores idénticos. |
|
|
para a ≠ -b pero | Identificar correctamente los factores antes de simplificar. |
|
|
Evitar simplificar erróneamente los términos al cuadrado del numerador con los términos a la primera potencia del denominador. Identificar la diferencia de cuadrados para poder factorizar y, posteriormente, simplificar. |
Fuente: Elaboración propia
REALIZACIÓN DE LA PRUEBA
Para llevar a cabo la prueba de la efectividad de las actividades diseñadas, se comenzó por administrar una evaluación diagnóstica (pre-test), con lápiz y papel, en los siete grupos, el primer día de clases. Posteriormente se trabajó con las actividades en nueve clases no consecutivas, cuando dichas actividades coincidían con el temario general de la materia. Se fomentó el análisis de las estructuras y los procesos algebraicos mediante la observación de las diferencias y similitudes entre, por ejemplo, pares o grupos de expresiones algebraicas y sus correspondientes simplificaciones u operaciones, a través de patrones de variación propuestos con ese fin, como los mostrados en las tablas 1 a 3. Para ello se usó tanto el pizarrón como actividades impresas para contestarse de forma individual o cooperativa, todo supervisado por el docente para que los estudiantes se enfocaran en los aspectos críticos correspondientes. En la clase posterior a la última actividad se aplicó una segunda evaluación (pos-test), idéntica a la diagnóstica. En ambas, cada procedimiento de respuesta de cada alumno fue clasificada según la guía de descriptores diseñada para este estudio, mediante la cual se valuaba el sentido estructural manifestado por la forma particular de proceder, según la ponderación de dichos descriptores, que se muestran en el siguiente apartado, seguidos de la guía de evaluación del reactivo 15, como ejemplo. Los reactivos de la evaluación completa se presentan en el Apéndice.
DESCRIPTORES DEL SENTIDO ESTRUCTURAL Y SU PONDERACIÓN
Para responder a la primera pregunta de investigación, ¿cómo se puede ponderar el nivel de sentido estructural manifestado en los procedimientos algebraicos desarrollados por los alumnos?, y determinar las características y la ponderación de los descriptores que permitieran evaluar y comparar el sentido estructural manifestado por los alumnos según sus procedimientos de respuesta, se partió de lo propuesto por Hoch y Dreyfus (2006) y Vega-Castro (2013) . Se adaptó la forma de interpretar el descriptor sugerido por Vega-Castro (2010) a los reactivos propios de este estudio. Se asignaron valores numéricos que ponderaron el sentido estructural mostrado según la complejidad de las estructuras y subestructuras. Se enlistan y explican a continuación los descriptores, acompañados por la ponderación asignada.
SE2 Trata con un término compuesto (subestructura) como una única entidad y reconoce una estructura familiar en una forma más compleja
SE2 a donde el término compuesto (subestructura) contiene un producto o potencia pero no una suma o resta (2 puntos)
SE2 b donde el término compuesto (subestructura) contiene una suma o resta y posiblemente también un producto o potencia (3 puntos)
SE3 Elige manipulaciones apropiadas para hacer el mejor uso de una estructura
SE3 aen su forma más simple (4 puntos)
SE3 b donde el término compuesto (subestructura) contiene un producto o potencia pero no una suma o resta (5 puntos)
SE3 c donde el término compuesto (subestructura) contiene una suma o resta y posiblemente también un producto o potencia (6 puntos)
SE4 Distingue subestructuras dentro de una entidad y reconoce relaciones entre ellas (evita errores de interpretación y uso de las relaciones dentro de la estructura)
SE4 a Las subestructuras forman parte de la misma expresión polinómica o similar (expresión en un solo nivel). Opera sin error pero no contesta la pregunta (7 puntos)
SE4 b Las subestructuras forman parte de diferentes expresiones polinómicas o similares (expresión en dos niveles). Opera sin error pero no contesta la pregunta (8 puntos)
SE4 c Las subestructuras forman parte de la misma expresión polinómica o similar (expresión en un solo nivel). Opera sin error y contesta la pregunta (9 puntos)
SE4 d Las subestructuras forman parte de diferentes expresiones polinómicas o similares (expresión en dos niveles). Opera sin error y contesta la pregunta (10 puntos)
Cada procedimiento de respuesta fue evaluado según los cuatro descriptores (SE1, SE2, SE3 y SE4), ya sea con la letra (a, b, c, d) correspondiente al descriptor mostrado, con un guion, que significa que no puede manifestarse ese descriptor dado el diseño del ejercicio, o una X, que indica que el procedimiento seguido no muestra ese descriptor, aunque el ejercicio estaba diseñado para que se pudiese mostrar. Para valorarlo numéricamente, tanto el guion como la X contaron como 0 puntos, mientras que las letras contaron los puntos que se señalan en el listado previo, que ponderan el grado de dificultad implicado al mostrar ese descriptor.
EJEMPLO DE LA GUÍA DE EVALUACIÓN
Puede observarse en la tabla 4 un extracto de la guía de evaluación para el reactivo 15 y en los párrafos siguientes la interpretación de la misma.
Se eligió este ejercicio porque incluye subestructuras formadas por sumas y puede ser contestado correctamente de formas distintas, con lo que se revela la estructura observada por el alumno y el uso que le dio. Además, se pueden apreciar algunos prerrequisitos según el procedimiento seguido: factorización de un trinomio cuadrado perfecto, binomio al cuadrado, ley distributiva y reducción de términos semejantes. También permite advertir el error de cancelación de elementos que no son factores. Se muestran en la tabla algunas de las opciones de respuesta para este reactivo, que incluyen los cinco casos para los que se consideró un nivel de sentido estructural mayor o igual a 1, así como los dos casos que contemplan el error de cancelación más común que se puede presentar en un ejercicio con esta estructura.
Tabla 4 Guía de evaluación para el reactivo 15
| Planteamiento/ Respuesta | Código | C/S/I | SE1 | SE2 | SE3 | SE4 | SE5 | |
| 15) Expresa en la forma factorizada más simple: |
|
A | C | a | b | c/a | d | 24 |
|
|
|
B | C | a | b | c/a | d | 24 |
|
|
|
C | C | a | - | X | d | 11 |
|
|
|
D | S | a | - | X | b | 9 |
|
|
E | S | a | - | X | b | 9 | |
|
|
|
U | I | X | X | X | X | 0 |
| Otros resultados | UN | I | X | X | X | X | 0 |
Fuente: Elaboración propia
Los procedimientos para llegar a cada respuesta, según su código en la tabla, son:
A Mejor uso de la estructura al identificar el trinomio cuadrado perfecto como estructura principal. Expresar la respuesta como binomio al cuadrado.
B Mejor uso de la estructura al identificar el trinomio cuadrado perfecto como estructura principal. Expresar la respuesta como producto de binomios.
C No elegir el mejor uso de la estructura. Identificar y realizar el binomio al cuadrado, y, posteriormente, reducir y factorizar.
D Sólo realizar la ley distributiva y no continuar.
E No expresar en la forma factorizada más simple.
U Error por cancelar los paréntesis al cuadrado y reducir el resto de la expresión.
UN Error por cancelar los paréntesis al cuadrado más error de signos o de cálculo al reducir el resto de la expresión.
En el segundo renglón de la tabla se presenta el reactivo. En la primera y segunda columnas se observan los procedimientos considerados, en la tercera su código, en la cuarta, identificada como C/S/I, si dichos procedimientos fueron considerados como respuestas correctas / semi-correctas (avance sin error pero sin terminar) / incorrectas (error inicial/avance inicial correcto con error posterior).
En la última columna se presenta el valor que se le da al sentido estructural reflejado por ese procedimiento, con base en las anteriores cuatro columnas, que corresponden a los cuatro descriptores. Como se señaló en el apartado anterior, un guion (-) implica que con esa respuesta no se esperaba que se mostrara ese descriptor y una X implica que sí se esperaba, pero no se observó el descriptor. Cuando el procedimiento lo permite, puede mostrarse un descriptor más de una vez, por lo que hay columnas que muestran más de una letra.
Por ejemplo, la respuesta A implica que primero se vio el numerador de la expresión como un trinomio cuadrado perfecto en el que uno de los términos es un binomio, lo cual muestra un SE2 b. Posterior a la factorización, se redujo la expresión que quedó en el numerador, lo cual muestra un SE1 a. El elegir manipulaciones apropiadas para las estructuras percibidas en ambos casos manifiesta un SE3 c y a respectivamente. Como se contesta correctamente un ejercicio con expresiones en dos niveles, se observa un SE4 d. La suma de los valores correspondientes a los descriptores manifestados indica un nivel de sentido estructural de 24 puntos.
NIVEL DE SENTIDO ESTRUCTURAL POR REACTIVO
Se puede observar en la tabla 4 que, al procedimiento de respuesta del reactivo 15 que manifiesta mayor nivel de sentido estructural, le corresponden 24 puntos. Se muestra a continuación, en la tabla 5, el máximo de puntos que pueden manifestarse en cada uno de los quince reactivos que, en total, suman 371 puntos.
ANÁLISIS ESTADÍSTICO
Para contestar la segunda pregunta de investigación, se calificó el sentido estructural manifestado por cada alumno en cada reactivo en el pre-test, según la ponderación de los descriptores establecidos, y se obtuvo el promedio por grupo. Con esta información, se realizó una prueba Levene para comprobar la homocedasticidad y una ANOVA para probar la hipótesis de igualdad estadística de las medias de todos los grupos:
Posteriormente se calcularon los incrementos de nivel de sentido estructural manifestados por cada alumno en cada grupo (valor en el pos-test menos valor en el pre-test), se promediaron, por grupos experimentales y de control, respectivamente y se realizó una prueba t-student de comparación de medias de muestras independientes para probar la hipótesis correspondiente a la tercera pregunta de investigación:
En caso de rechazo de la hipótesis nula anterior, sería interesante complementar el análisis estadístico mediante una prueba ANOVA de igualdad estadística del promedio del cambio en el nivel de sentido estructural en los grupos, con la hipótesis que se presenta a continuación. Se realizaría una prueba de Levene previa para comprobar la homocedasticidad.
Si se diera el rechazo de la hipótesis nula anterior, se realizaría una prueba Duncan, con la que se compararía el promedio del cambio de los siete grupos, para identificar los subconjuntos homogéneos.
En todas las pruebas se usó un nivel de significancia de 5%. Los resultados obtenidos se presentan y discuten a continuación.
ANÁLISIS Y DISCUSIÓN DE RESULTADOS
Antes de contestar las preguntas de investigación dos y tres se presentan, como ilustración de las problemáticas que se buscaban resolver y del cambio que se buscaba lograr, ejemplos de las producciones de los estudiantes.
ERRORES OBSERVADOS, RELACIONADOS CON UN SENTIDO ESTRUCTURAL POCO DESARROLLADO
Entre los errores que puede cometer un alumno al contestar un ejercicio, hay algunos que tienen una relación más evidente con un sentido estructural poco desarrollado, es decir, que no distinga las estructuras que observa y/o no sepa cuáles son las manipulaciones válidas según dicha estructura, ni cuál de ellas es la más eficiente. Las actividades diseñadas incluyeron un énfasis en contrastes y variaciones que facilitaran a los alumnos discernir las diferencias estructurales y procedimentales que les permitieran evitar dichos errores.
Un ejemplo es el reacomodo y operación o concatenación errónea de elementos en numerador y denominador. Puede verse un caso específico en la figura 1. En problemáticas similares, en los grupos experimentales se vio una disminución de 58% mientras que en los de control sólo de 20%.
Otro ejemplo son los esquemas de tachado no válidos, en este caso de exponentes. Puede verse una muestra en la figura 2. En los grupos experimentales se vio una disminución de errores de ese tipo de 27%, mientras que en los de control sólo de 5%.
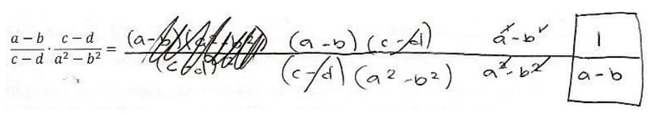
Figura 2 Ejercicio en el que se observa, después de probar con un algoritmo erróneo y reiniciar el procedimiento, una correcta simplificación de factores (c-d), un posterior esquema de tachado erróneo de exponentes, en el que se restan los del denominador menos los del numerador y otro error subsecuente de escribir un único 1 como numerador (además de que se omite el signo igual entre las expresiones)
Un tercer ejemplo son los esquemas de tachado no válidos de términos, los cuales se cancelan. Puede verse un caso en la figura 3. En los grupos experimentales se vio una disminución de 49% mientras que en los de control la disminución fue sólo de 5%. Estos fueron los tres casos en los que fue más notoria la diferencia en la disminución de errores entre ambos grupos.
CAMBIO EN EL PROCEDIMIENTO SEGUIDO
Como ejemplo ilustrativo del cambio observado en la manera de proceder, en la figura 4 se puede observar el reactivo 4 contestado por un alumno que, en el pre-test, muestra poco nivel de sentido estructural (14 puntos, según la guía de evaluación de ese reactivo), ya que comenzó por realizar una acción que le permitiera quitar los signos de agrupación, esto es, expandir los binomios al cuadrado, sin darse cuenta de la estructura externa de diferencia de cuadrados existente. Quitar signos de agrupación como primer paso no reflexionado es común cuando el sentido estructural no está suficientemente desarrollado. En la figura 5 se presenta el mismo ejercicio, contestado por el mismo alumno en el pos-test, en el que manifiesta más uso de sentido estructural (22 puntos), al percibir y aprovechar la estructura de la diferencia de cuadrados.
Aunque el resultado es correcto en ambos casos, se considera que el segundo procedimiento, implica un manejo conceptual más profundo y significativo, más reflexivo antes de actuar y, por tanto, menos propenso al error que el primero (Hoch, 2003; Hoch & Dreyfus, 2004; Molina, 2010; Jupri & Sispiyati, 2017). Esto es, en las figuras 4 y 5 se observa que el trabajo con las actividades propuestas tuvo un efecto positivo en la forma de proceder de este alumno al contestar este ejercicio, lo cual es una muestra del impacto en el cambio en la forma de operar que se logró en los participantes del estudio, según los análisis estadísticos presentados, que se esperaría que afectara en su desempeño en álgebra más allá de este tema.
NIVEL DE SENTIDO ESTRUCTURAL MANIFESTADO POR LOS ALUMNOS AL INGRESAR
La segunda pregunta de esta investigación fue: con base en la ponderación establecida para este estudio, ¿cómo es el promedio del nivel de sentido estructural en los alumnos, al ingresar a la universidad? Por todos los participantes, por grupo y entre grupos. A esta pregunta se da respuesta a continuación.
El promedio del nivel de sentido estructural (SE) inicial manifestado por los alumnos de cada uno de los siete grupos en el pre-test, medido según los descriptores adaptados para ese fin dentro de este estudio, se presenta en la tabla 6. Fue importante acreditar que ningún par de grupos tuvieran promedios estadísticamente diferentes en un inicio, por lo que se realizó una prueba ANOVA (tabla 7) que lo comprobó (significancia 0.428). Previamente se probó, mediante una prueba Levene, que se podían asumir varianzas iguales (significancia 0.159).
Tabla 6 Promedio del nivel de sentido estructural inicial
| Tipo | Grupo | Cantidad de Alumnos | SE (máximo 371) |
| Experimentales | 1 | 20 | 44.35 |
| 2 | 19 | 48.79 | |
| 3 | 15 | 44.67 | |
| 4 | 18 | 83.39 | |
| Control | 5 | 27 | 39.22 |
| 6 | 17 | 45.06 | |
| 7 | 18 | 37.61 |
Fuente: Elaboración propia
Dado que el valor máximo que se puede obtener en el test es 371 puntos, los promedios manifiestan un nivel de sentido estructural pobre con el que llegaron estos estudiantes a la universidad. El promedio obtenido por los 134 participantes fue 48.4 puntos, esto es, 13% del máximo posible. Con esta información se evalúa el sentido estructural manifestado por los alumnos al ingresar a la universidad y se responde a la segunda pregunta de investigación.
CAMBIO EN EL NIVEL DE SENTIDO ESTRUCTURAL
La tercera pregunta de esta investigación fue: con base en la ponderación establecida para este estudio, ¿cómo es el promedio del incremento del nivel de sentido estructural en los alumnos que trabajaron con las actividades de enseñanza-aprendizaje diseñadas con base en la Teoría de la Variación, en comparación con el incremento del nivel de sentido estructural en los alumnos que trabajaron con actividades que no contemplen dicha teoría pedagógica? Para contestarla, se calculó el cambio del nivel de sentido estructural manifestado por alumno, mediante la resta de resultados de ambos test. Se presentan los promedios por grupo en la tabla 8. Puede notarse, en la última columna, que todos los grupos incrementaron su promedio.
Tabla 8 Cambio en el nivel de sentido estructural
| Tipo | Grupo | SE Inicial | SE Final | Cambio en SE |
| Experimentales | 1 | 44.35 | 167.65 | 123.30 |
| 2 | 48.79 | 211.26 | 162.47 | |
| 3 | 44.67 | 179.47 | 134.80 | |
| 4 | 83.39 | 258.22 | 174.83 | |
| Control | 5 | 39.22 | 104.00 | 64.78 |
| 6 | 45.06 | 122.35 | 77.29 | |
| 7 | 37.61 | 119.00 | 81.39 |
Fuente: Elaboración propia
Posteriormente, se agruparon los datos de todos los alumnos en sólo dos grupos: experimental y control. Se observó que los participantes de los grupos experimentales tuvieron un promedio de incremento superior a los de los grupos de control (tabla 9). La prueba t-student de comparación de medias de muestras independientes mostró que la diferencia de los promedios de incremento en el nivel de sentido estructural es estadísticamente significativa (tabla 10, significancia 0.000). Por la prueba de Levene previa se mantiene el supuesto de varianzas iguales (significancia 0.096).
Tabla 9 Estadísticas de los grupos experimentales y de control en conjunto
| EXCO | N | Media | Desviación estándar | Media de error estándar | |
| Cambio SE | Experimental | 72 | 148.92 | 78.812 | 9.288 |
| Control | 62 | 73.03 | 65.063 | 8.263 |
Fuente: Elaboración propia en SPSS versión 23
Con la información de las tablas 9 y 10 se contesta a la tercera pregunta de investigación y se rechaza la hipótesis de que los alumnos que usaron las actividades de enseñanza-aprendizaje basadas en la Teoría de la Variación no tuvieron un incremento en su nivel de sentido estructural significativamente diferente que el que tuvieron los participantes que usaron actividades sin esa base.
Tabla 10 Prueba t-student de comparación de medias de muestras independientes
| Prueba de Levene | Prueba t para la igualdad de medias | ||||||
| F. | Sig | t | gl | Sig. (bilateral) | Diferencia de medias | ||
| Cambio SE | Se asumen varianzas iguales | 2.811 | 0.096 | 6.018 | 132 | 0.000 | 75.884 |
Fuente: Elaboración propia en SPSS versión 23
Para profundizar el análisis estadístico, se llevó a cabo una prueba ANOVA con los promedios de los siete grupos, con la que se confirmó que había al menos un par de ellos cuyas medias no eran estadísticamente iguales (tabla 11, significancia 0.000). Previamente se probó la homocedasticidad, mediante una prueba Levene (significancia 0.119).
Tabla 11 Prueba ANOVA para comparar las medias de los incrementos en el nivel de sentido estructural
| Suma de cuadrados | gl | Media cuadrática | F | Sig. | |
| Entre grupos | 226934.645 | 6 | 37822.441 | 7.233 | 0.000 |
| Dentro de grupos | 664124.311 | 127 | 5229.325 | ||
| Total | 891058.955 | 133 |
Fuente: Elaboración propia en SPSS versión 23
Mediante una prueba Duncan de subconjuntos homogéneos, se determinó qué grupos formaban subconjuntos entre sí (tabla 12). Se recordará que los grupos 1 al 4 son los experimentales y los grupos 5 al 7 son los de control. Puede observarse que se forman cuatro subconjuntos. En el primer subconjunto están solamente los tres grupos de control. El segundo subconjunto es el único que incluye grupos mezclados de experimentales y de control, pues reúne al grupo 1, cuyos resultados fueron los menores entre los grupos experimentales, con los grupos 6 y 7, cuyos resultados fueron los mayores entre los grupos de control. Los últimos dos subconjuntos están formados sólo por grupos experimentales.
Tabla 12 Prueba Duncan de subconjuntos homogéneos para las medias de los incrementos en el nivel de sentido estructural
| Subconjunto para alfa -0.05 | ||||||
| GPO | N | 1 | 2 | 3 | 4 | |
| Duncanab | 5 | 27 | 64.78 | |||
| 6 | 17 | 77.29 | 77.29 | |||
| 7 | 18 | 81.39 | 81.39 | |||
| 1 | 20 | 123.30 | 123.30 | |||
| 3 | 15 | 134.80 | 134.80 | |||
| 2 | 19 | 162.47 | 162.47 | |||
| 4 | 18 | 174.83 | ||||
| Sig. | 0.514 | 0.068 | 0.121 | 0.113 | ||
Se visualizan las medias para los grupos en los subconjuntos homogéneos.
a. Utiliza el tamaño de la muestra de la media armónica = 18.604.
b. Los tamaños de grupo no son iguales. Se utiliza la media armónica de los tamaños de grupo. Los niveles de error de tipo I no están garantizados.
Fuente: Elaboración propia en SPSS versión 23
CONCLUSIONES
Vega-Castro, Molina y Castro (2012) se apoyaron en los descriptores del sentido estructural de Hoch y Dreyfus (2006) , los complementaron y adaptaron para evaluar el sentido estructural en estudiantes de bachillerato en simplificación de fracciones algebraicas que involucraban igualdades notables. Observaron cómo el nivel de sentido estructural mostrado, que fue alto en 40% de los casos y bajo en 36% de los casos, se veía afectado por el tipo de estructura algebraica usada. En la investigación aquí reportada se partió también de la determinación de las características y la ponderación de descriptores que se usaron para evaluar el nivel de sentido estructural de los alumnos. La aportación de este estudio es la propuesta y puesta a prueba de actividades de enseñanza-aprendizaje, con base en la Teoría de la Variación (Marton, 2015), que fomentaran el desarrollo del sentido estructural en alumnos universitarios, las cuales tuvieron un efecto positivo, como se presentó en el apartado de resultados y se comenta en esta sección.
Los resultados obtenidos en el examen diagnóstico permiten concluir que los alumnos llegan a la universidad con un sentido estructural poco desarrollado, ya que el promedio de su nivel fue 48.4, de 371 puntos posibles (13%). De los 134 alumnos, 112 mostraron menos de 100 puntos al inicio de la investigación (57 de los grupos experimentales y 55 de los grupos de control). Esto es congruente con las investigaciones mencionadas al principio de este texto, en las que los participantes mostraban un proceder más operacional que estructural, probablemente debido a las decisiones pedagógicas de sus profesores anteriores (Hoch 2003, Mason et al., 2009 y Skemp 1976). No se encontró ningún grupo cuyo promedio inicial de nivel de sentido estructural fuera significativamente diferente a algún otro.
Este estudio contribuye, por tanto, a la línea de investigación sobre el sentido estructural al identificar que, aunque se ha escrito en publicaciones anteriores sobre la necesidad de desarrollar el sentido estructural en los alumnos a lo largo de todas sus etapas académicas, la problemática persiste, por lo que los esfuerzos para probar estrategias para resolver dicha problemática, como los realizados en esta investigación, deben continuar.
Al analizar los incrementos en el nivel de sentido estructural manifestados por los participantes, con promedios grupales de 148.92 puntos para los experimentales y 73.03 puntos para los de control, se observa que las clases en general promueven el desarrollo de dicho sentido, sin embargo, en las clases con actividades basadas en la Teoría de la Variación (Marton, 2015) se pudo lograr un avance significativamente mayor. Incluso en los cuatro subconjuntos homogéneos formados según el promedio de avance mostrado, sólo en el segundo se incluyen grupos combinados: los dos de control con mayor avance con el experimental con menor avance. Los resultados obtenidos después de la intervención son congruentes con lo que se ha reportado sobre lo complejo y tardado que resulta desarrollar el sentido estructural, ya que requiere abstraer las relaciones dentro de una expresión y entre varias expresiones, como concluyeron Banerjee y Subramaniam (2005) . Kieran (2018) coincide en que desarrollar la capacidad de ver la estructura es un proceso largo que necesita reinventarse con cada nuevo objeto matemático que se observa.
Cabe agregar que, de los 20 alumnos que obtuvieron más de 300 puntos en el pos-test, 18 fueron de los grupos experimentales. Por otro lado, de los 48 estudiantes que obtuvieron menos de 100 puntos en el pos-test, sólo 17 fueron de los grupos experimentales.
Las actividades usadas en la intervención con los grupos experimentales, basadas en la Teoría de la Variación (Marton, 2015) y el andamiaje que se promueve en la enseñanza con variación china (Gu et al., 2004), que incluyeron contrastes, variaciones y andamiajes cuidadosamente planeados, mostraron ser significativamente más útiles para integrar intencionadamente el desarrollo del sentido estructural dentro del aprendizaje de diversos temas algebraicos, en comparación con actividades que no tuvieron ese diseño. Aunque los resultados fueron obtenidos al trabajar con expresiones algebraicas racionales y sus pre-rrequisitos, se considera que pueden conseguirse resultados similares al elaborarse y probarse actividades con diseños semejantes a los usadas en esta investigación, para diversos temas algebraicos, por lo que el aporte a la matemática educativa abarcaría el álgebra en general, no sólo las expresiones mencionadas.
Esta investigación corrobora la presencia de un sentido estructural poco desarrollado en los alumnos de nuevo ingreso a la universidad, lo que sugiere la necesidad de que el desarrollo del mismo sea promovido desde las primeras etapas de la enseñanza-aprendizaje de las matemáticas, con actividades que tengan un diseño con una base similar a la presentada en este estudio, en la que se tomen en cuenta los errores comunes que cometen los alumnos y las características propias de los temas algebraicos para la determinación de los aspectos críticos, los contrastes y los patrones de variación e invariación necesarios para tematizarlos, como propone la Teoría de la Variación (Marton, 2015). Dicha promoción debe continuar durante toda la formación académica de los alumnos, para que éstos aprovechen las ventajas que ofrece el tener un sentido estructural más desarrollado a lo largo de ella y lleguen mejor preparados a la universidad.
La propuesta de intervención a nivel universitario presentada probó ser útil y se considera conveniente continuar esta investigación mediante la elaboración de actividades de enseñanza-aprendizaje para el resto de los temas del curso, con el fin de lograr un desarrollo del sentido estructural aún mayor, en beneficio de los alumnos.











 nueva página del texto (beta)
nueva página del texto (beta)







