Introducción
En Colombia, desde la promulgación de los Lineamientos Curriculares para el área de Matemáticas (1998), se insiste en que la resolución de problemas sea la actividad matemática central en la que se involucren los estudiantes de educación básica y media. Solo así podrán poner en funcionamiento procesos como el razonamiento, la representación y la comunicación de ideas, base para la competencia matemática con la cual enfrentar situaciones cotidianas, profesionales o científicas a lo largo de la vida. Sin embargo, en observaciones de clases de profesores en ejercicio y en descripciones hechas en trabajos de grado de nivel de maestría (v.g. Martínez, 2016), vemos que esta orientación aún no es una práctica usual en las clases de matemáticas y subsiste desorientación sobre cómo organizar currículos alrededor de problemas.
En 2015 y 2016 profesores del grupo de investigación Aprendizaje y Enseñanza de la Geometría (Æ • G), de la Universidad Pedagógica Nacional (Colombia) trabajamos en colaboración con profesores del área de matemáticas del Instituto Pedagógico Nacional, escuela laboratorio de la Universidad, en la preparación y experimentación de secuencias de enseñanza para los grados sexto a noveno, diseñando clases de geometría alrededor de problemas. El objetivo era promover en los estudiantes experiencias académicas de indagación propias de las ciencias, pero no exclusivas de ellas pues pueden estar presentes en situaciones de la vida cotidiana y profesional.
En el marco del trabajo descrito, uno de nuestros focos de interés fue identificar el papel de un software de geometría dinámica (SGD) para apoyar el razonamiento científico de estudiantes y promover por esa vía la actividad matemática. Entendemos esta como el conjunto de acciones, procesos, lenguajes, problemas que se valen de herramientas, técnicas y lenguajes matemáticos.
El interés investigativo surge de estudios que muestran que el uso de SGD favorece procesos de argumentación y demostración (v.g. Samper y Toro, 2017). Lo anterior nos motivó a pensar que este recurso podría apoyar el razonamiento científico y a analizar la actividad matemática de parejas de estudiantes de grado noveno usando indicadores de génesis instrumental y de razonamiento científico. En este artículo pretendemos aportar a la comprensión de la sinergia, o acción conjunta, que se produce entre el razonamiento científico y el uso de un SGD mediante un estudio de caso de una pareja de estudiantes. El estudio muestra que estos dos elementos conforman un dúo útil para la resolución de problemas, que debería explotarse de manera más decidida en las clases de geometría.
Referentes conceptuales
Presentamos los fundamentos teóricos que sirvieron de base para el análisis: la génesis instrumental y el razonamiento científico. Sobre cada elemento adelantamos una revisión de literatura no exhaustiva, con la intención de configurar dispositivos analíticos para el ejercicio.
Esquemas de utilización y actividad instrumentada
Coincidimos con Samper, Perry, Camargo, Molina y Echeverry (2010) al señalar que la presencia de tecnologías informáticas en la enseñanza no garantiza su influencia positiva en el aprendizaje. Se requieren diseños cuidadosos de tareas, basados en la comprensión del proceso de apropiación de las tecnologías, para generar ambientes de indagación que propicien la construcción de conocimiento. Para ello se requieren estudios analíticos que adopten marcos de referencia que favorezcan la interpretación de la interacción entre los individuos y las tecnologías informáticas. Autores como White (2008), Leung, Chan y López-Real (2006) y Trouche (2014) resaltan que la génesis instrumental es un constructo analítico adecuado para examinar el aprendizaje mediado por ambientes tecnológicos.
La génesis instrumental, constructo elaborado por Rabardel (1995), caracteriza el proceso a través del cual los individuos interactúan con artefactos que median su actividad al resolver tareas, los dotan de significado y los incorporan en su labor bajo secuencias de acciones realizadas de manera regular. Los artefactos permiten amplificar o modificar las habilidades humanas para transformar el entorno; están concebidos de forma tal que permiten “materializar”, a través de representaciones, imágenes mentales. El uso de artefactos hace que los usuarios les atribuya funciones, desarrollando formas de uso personales. Cuando esto ocurre, se dice que cada individuo ha construido un instrumento a partir del artefacto (Pérez, 2014). Por ello su valor es inseparable de quien lo usa y específicamente de cómo lo usa (Leung et al., 2006).
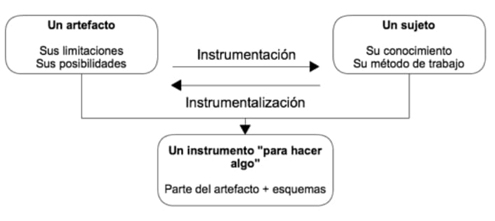
Con base en lo anterior, decimos que un artefacto que interviene en la gene-ración de conocimiento matemático se puede convertir en un instrumento que media el aprendizaje (Samper, Camargo, Molina y Perry, 2013; Trouche, 2014). En este proceso los estudiantes interactúan con artefactos materiales o simbólicos desarrollados con fines determinados, educativos o no, para resolver tareas matemáticas y eventualmente les asignan funciones específicas, haciendo de ellos instrumentos de aprendizaje. Según Rabardel (1995) convertir un artefacto en instrumento requiere de dos procesos interrelacionados, producto de una relación entre el individuo y el artefacto: instrumentalización e instrumentación. En la figura 1 representamos la relación entre los procesos mencionados.
La instrumentalización es el proceso de identificar los componentes de un artefacto y reconocer sus limitaciones y posibilidades para resolver un problema o realizar una tarea. En términos de Verillon y Rabardel (1995, citado en Trouche, 2014) y Alqahtani y Powell (2016), es un proceso en el que el individuo dirige la atención hacia el artefacto y enriquece o modifica las propiedades de este para utilizarlo a favor de sus fines. Tres etapas pueden reconocerse: descubrir y seleccionar funciones relevantes, personalizar/ajustar el artefacto a rasgos característicos personales y transformar el artefacto (Trouche, 2014). A modo de ejemplo, consideremos una cuerda (artefacto) creada por el hombre con el fin de amarrar objetos. El individuo puede aplicarle polvo de color y tensionarla sobre una superficie plana, realizar una pulsación sobre esta y ver cómo queda un rastro sobre la superficie que podría representar una línea recta. En este caso el usuario desarrolla modos de usar la cuerda con un propósito determinado (representar una recta) y este propósito es distinto de aquel con el que fue concebida originalmente (amarrar objetos); en consecuencia, tiene lugar una modificación del significado del artefacto para el usuario.
Por su parte, la instrumentación corresponde al proceso de aparición, desarrollo y adaptación de esquemas de utilización con los que el individuo incorpora el artefacto en la resolución de tareas o problemas. Este proceso señala la influencia del artefacto en el individuo (Trouche, 2014). Entendemos por esquema de utilización, en consonancia con Leung et al. (2006) y Samper et al. (2013), un procedimiento esquemático de acciones que se realizan regularmente al usar un artefacto para un determinado fin. Retomando el ejemplo, la cuerda (artefacto) se pone en funcionamiento con un esquema de utilización (aplicar polvo de color, tensionar y pulsar sobre una superficie plana) y se identifica una vía para trazar rectas cuando no se cuenta con una regla; probablemente así se usará en futuras oportunidades. En este proceso el individuo asocia el artefacto a un esquema particular (Alqahtani y Powell, 2016), deja atrás su utilidad convencional y adopta un nuevo uso de acuerdo con sus necesidades.
Concebimos el instrumento como el conjunto de un artefacto y las formas en que este es usado por un individuo al resolver una tarea (Pérez, 2014). El instrumento existe siempre y cuando haya una relación significativa entre el artefacto y el usuario, en el marco de una actividad específica; de ahí que el instrumento sea una entidad dual. Aclaramos que la relación de un usuario con un artefacto es de carácter subjetivo; en consecuencia, dos individuos pueden enfocar de diferente manera el uso del mismo artefacto, desarrollar distintos esquemas y crear actividades e instrumentos diferentes (Alqahtani y Powell, 2016).
Para efectos del análisis que presentamos, los esquemas de utilización pue-den ser vistos como señales de la actividad matemática de los estudiantes cuando resuelven problemas con apoyo en algún SGD (Samper et al., 2013); esto debido a que los SGD están configurados para reproducir lo más cercanamente posible, atributos y propiedades matemáticas, que se constituyen en invariantes al arrastre de los elementos construidos. Pero ¿cuál es el artefacto en ese caso? Según Pérez (2014), el artefacto podría ser el ambiente computacional en sí mismo, o cada herramienta de este (v.g., rectas paralelas, punto medio). En nuestro trabajo, asumimos artefacto como cada uno de los comandos o funciones provistos por GeoGebra.
Las acciones de los estudiantes guían lo que ocurre en pantalla y esto a su vez los guía a realizar nuevas acciones, produciendo esquemas de utilización, propios de los artefactos de GeoGebra empleados. Al ir convirtiéndolos en instrumentos, los estudiantes pueden utilizar el SGD para resolver problemas. Estudiar la génesis instrumental requiere, en términos de White (2008), no centrarse en los artefactos en sí mismos, sino en el proceso de génesis para usuarios particulares y usos específicos.
Razonamiento científico
Lawson (2004) y Alshamali y Daher (2015) conciben el razonamiento científico como el proceso cognitivo y de procesamiento de información, que se manifiesta en las actuaciones de los individuos, por medio del cual se formulan enunciados condicionales, se construyen explicaciones argumentadas sobre estos, y se realizan inferencias que van más allá de la experiencia directa. Según Morris, Croker, Masnick y Zimmermann (2012), el razonamiento científico efectivo tiene lugar cuando de manera simultánea intervienen formas de pensar inductivas y deductivas. Para ello, los individuos deben comprender cómo evaluar lo que es conocido o creído en la actualidad, desarrollar preguntas comprobables, testar hipótesis, procesar datos y trazar conclusiones apropiadas al coordinar evidencia empírica y teórica. Este razonamiento exige además tratar información sistemáticamente, trazar inferencias razonables a partir de patrones observados y reflexionar sobre el proceso de adquisición y cambio del propio conocimiento que resulta de la actividad de investigar.
Hogan, Nastasi y Pressley (1999) concretan, para el ámbito educativo, el razonamiento científico considerándolo como la construcción conjunta de explicaciones, argumentos y modelos, a partir de observaciones propias y datos obtenidos en contextos de clase. Esta concepción está orientada por la perspectiva social adoptada por algunos educadores matemáticos (Yackel y Hanna, 2003) que se enfocan en los aspectos comunales del razonamiento y la actividad matemática. Desde esa perspectiva, describen el razonamiento matemático como “una actividad comunal en la que los aprendices participan al interactuar entre ellos para resolver problemas matemáticos” (Yackel y Hanna, 2003, p. 228).
Con base en las ideas expuestas entendemos el razonamiento científico como un proceso cognitivo y social mediante el cual se aborda un fenómeno del campo de las ciencias (o un hecho del campo de las matemáticas) con miras a entenderlo, explicarlo y hacerlo parte del bagaje teórico propio. En este se conjuga la exploración sistemática de un problema, la formulación y testeo de hipótesis, la manipulación de variables aisladas y la observación y evaluación de consecuencias (Bao et al., 2009), obteniendo como resultado enunciados relativos al hecho abordado en el problema.
Las ideas presentadas anteriormente nos permiten destacar como relevantes: la valoración del razonamiento científico como recurso para enfrentar la resolución de problemas y el apoyo que puede brindar un artefacto, en la medida que se haga instrumento. Particularmente, nos enfocamos en los esquemas de utilización de los estudiantes al abordar el problema en GeoGebra y en los vestigios del razonamiento científico que se puede evidenciar en su trabajo.
Metodología
Nuestro estudio es una investigación de diseño (Bakker y van Eerde, 2015), motivada por el interés de promover procesos de desarrollo curricular. Organizamos la presentación de la metodología de acuerdo con las fases propias de esta metodología. Por motivos de espacio, incluimos solo información relaciona-da con el análisis específico presentado.
Fase de planeación
Partiendo del interés de profundizar en la posible sinergia entre la génesis instrumental y el desarrollo del razonamiento científico, diseñamos secuencias de enseñanza para los grados 6° a 9° (12-16 años), a partir de problemas de conjeturación en donde los resultados obtenidos al resolver un problema determinan el cuerpo base de conocimiento construido socialmente en la clase para enfrentar la resolución de sucesivos problemas. Las secuencias ofrecen a los estudiantes la posibilidad de formular definiciones de objetos geométricos, establecer relaciones de dependencia, proponer conjeturas y justificarlas.
Los estudiantes de grado noveno conocían herramientas básicas de GeoGebra (v.g. construir puntos, rectas y segmentos, determinar distancias), lo cual, desde nuestro punto de vista, propiciaba la variedad y riqueza de las exploraciones. El enunciado del problema cuya resolución analizamos en este artículo es el siguiente:
Problema de los dos puntos: dados dos puntos A y B, ¿existe una circunferencia que los contiene? ¿Existe otra? ¿Existen más? Si es el caso, ¿dónde se encuentran los centros de las circunferencias que contienen los puntos A y B?
El objetivo del problema es que los estudiantes descubran que los centros de las circunferencias que contienen a los puntos y pertenecen a la mediatriz del segmento. Anticipamos que ellos pueden llegar a dos posibles conjeturas al usar GeoGebra en la resolución del problema:
Conjetura 1 [C1]. Dados dos puntos A y B. Si A y B pertenecen a una circunferencia, entonces, el centro de la circunferencia pertenece a la mediatriz del segmento AB (o cuerda AB).
Conjetura 2 [C2]. Dados dos puntos A y B. Si un punto C pertenece a la mediatriz del segmento AB, entonces C es centro de una circunferencia que contiene los puntos dados.
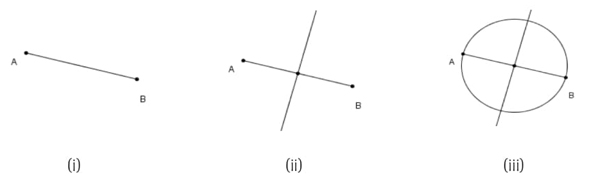
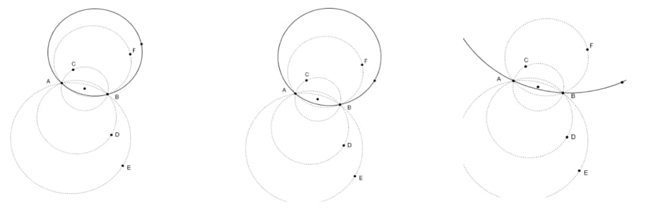
Contemplamos que C1 podía derivarse de una exploración en la que los estudiantes construyeran distintas circunferencias no congruentes y las ajustaran, manipulando su centro, por ejemplo, para que la condición del enunciado del problema se satisficiera. Un número considerable de circunferencias construidas bajo esta condición permitiría evidenciar que los centros pertenecen a la mediatriz del segmento AB (Figura 2).
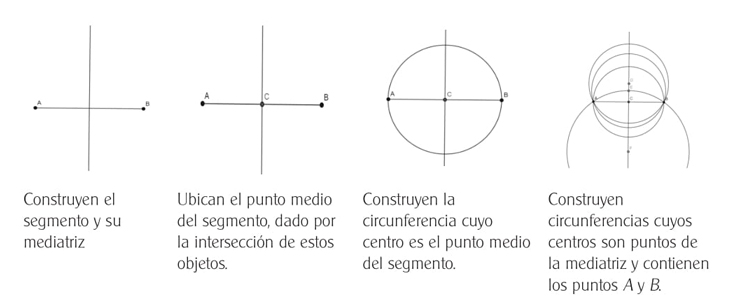
C2 podía darse cuando los estudiantes construyeran el segmento AB y su mediatriz con el fin de obtener el punto medio del segmento, construyendo así la circunferencia para la cual el segmento AB es diámetro. Luego sobre esta recta ubicarían los centros de las otras circunferencias (Figura 3).
Fase de experimentación
La implementación de la secuencia en grado 9° tuvo lugar en un curso de 30 estudiantes, con edades comprendidas entre 14 y 16 años, una vez por semana, durante seis semanas, en sesiones de 90 minutos. Previa la realización de esta, los estudiantes no habían tenido una experiencia similar pues en la clase de geometría no se favorecía la construcción de conocimiento vía realización de experimentos.
En la mayoría de sesiones los estudiantes contaban con computadores que tenían instalado el SGD GeoGebra, que podían emplear a su voluntad. El problema de los dos puntos se propuso en la segunda sesión, después de haber resuelto otro problema que tenía la intención de institucionalizar la definición de circunferencia.3
Video grabamos la interacción de varias parejas de estudiantes con ocasionales intervenciones del profesor que se desplazaba de una pareja a otra para hacer preguntas, atender inquietudes y favorecer la exploración de ideas. Para ello ubicamos una cámara de video atrás de los estudiantes, que registraba su interacción, y las construcciones realizadas en la pantalla del computador. Adicionalmente usamos con una grabadora de audio que
registraba el diálogo. Acopiamos las hojas de trabajo en donde los estudian-tes consignaron exploraciones y hallazgos. Tres miembros del equipo de investigación (P2, P3) y un auxiliar (A1) actuaron como observadores participantes, apoyando al profesor (P1) del curso en la gestión de la clase y tomando notas de campo.
Fase de análisis retrospectivo
La información recogida durante la implementación nos permitió transcribir el proceso de resolución desarrollado por las parejas video grabadas. Enriquecimos la información con anotaciones de los observadores y las producciones escritas. Luego, cada transcripción fue fragmentada según identificábamos el surgimiento y desarrollo de una idea para resolver el problema.
El análisis de los fragmentos se hizo a partir de la caracterización de las acciones e intervenciones de los estudiantes usando los indicadores previstos en los siguientes dispositivos analíticos.
Para estudiar la génesis instrumental, particularmente la forma en que algunos comandos de GeoGebra llegan a convertirse en instrumentos para los estudiantes, construimos los indicadores que se encuentran en la primera columna de las Tablas 1 y 2. Estos surgen de las caracterizaciones dadas a cada proceso de génesis instrumental por los autores referenciados, aunque no descartamos que otras caracterizaciones pudieran dar lugar a otros indicadores. Describimos y ejemplificamos cada indicador en la tercera columna. Como lo señalan Rabardel (1995) y Pérez (2014), si los individuos manifiestan acciones ligadas a ambos procesos, podemos considerar que tiene lugar una apropiación de los artefactos y estos se comienzan a convertir (o se convierten) en instrumentos.
Tabla 1: Indicadores de instrumentalización y ejemplos
| Isa1 | Descubrimiento de posibilidades de un comando | Se descubre, para un comando (o conjunto de estos), nuevas posibilidades y funciones que permiten resolver la tarea y que anteriormente no se conocían. Por ejemplo, al reconocer que el comando simetría central sirve para construir, a partir de los puntos A y B, un punto C de tal forma que B es punto medio de A y C. |
| Isa2 | Identificación de limitaciones de un comando o herramienta | Se identifica que un comando que se quiere usar con un propósito definido o con una idea tentativa no ofrece un resultado afortunado y, en consecuencia, se descarta la posibilidad de asignar esta función al comando. Por ejemplo, ante la necesidad de construir una recta que pase por dos puntos dados, un estudiante construye la recta por uno de ellos y luego arrastra al segundo punto, dejándolo sobre la recta, esperando que esto garantice la solución de la tarea. |
| Isa3 | Personalización y ajuste del artefacto a los intereses personales | Se identifica la diversidad de usos de un comando asociados a intereses específicos. El comando es utilizado según distintos esquemas de acuerdo a los requerimientos de la tarea. Por ejemplo, la función de arrastre, las marcas de ángulo y las marcas de segmento pueden ser usadas con diferentes propósitos. |
| Isa4 | Transformación del artefacto | Se reconoce un artefacto como medio para la obtención de un fin particular en un contexto específico y se usa con un fin igual o distinto a aquel con el que fue concebido. La experiencia del individuo al usar el comando bajo un nuevo esquema le ofrece un nuevo significado del mismo. Por ejemplo, el comando rotación se puede usar para construir ángulos a partir de su medida. |
Tabla 2: Indicadores de instrumentación y ejemplos
| Isa1 | Aparición de un esquema asociado a un conjunto de comandos | Se reconoce un determinado conjunto de pasos, sobre un comando (o conjunto de estos) como efectivo para la obtención de un resultado particular y este es aceptado por el estudiante. Por ejemplo, la construcción de un triángulo equilátero a partir de un segmento AB y dos circunferencias congruentes de radio AB con centros en A y B. |
| Isa2 | Desarrollo de un esquema para la obtención de un resultado particular | Una vez se acepta el resultado de un conjunto de pasos, el estudiante identifica un procedimiento para su uso, con miras a obtener el mismo resultado al incorporar el esquema. Por ejemplo, el estudiante puede reconocer el procedimiento para la obtención de un triángulo equilátero. Cuando quiera este resultado, procederá de la misma forma, descartando otros procedimientos que lleven al mismo resultado. |
| Isa3 | Adaptación de un esquema al resolver un problema | Sucede al modificar un procedimiento, bien sea para incluir algunas acciones a las ya presupuestadas y dar mayor alcance a este o para reducir y refinar el procedimiento inicialmente considerado. Por ejemplo, el estudiante puede ampliar el procedimiento involucrado hasta ahora para construir un rombo, de tal forma que sus lados sean congruentes al segmento AB, o a la mediatriz de este segmento. |
| Isa4 | Uso del comando, en distintas tareas, bajo el mismo esquema | Sucede cuando, de manera rutinaria, en distintos problemas, el estudiante involucra un esquema desarrollado en algún momento. En este punto se puede decir que el artefacto ha sido apropiado bajo un esquema particular y se ha atribuido un papel al mismo en la obtención de un resultado específico. |
Para rastrear el razonamiento científico exhibido por los estudiantes, nos valemos de los indicadores propuestos en la Tabla 3. Los agrupamos de acuerdo a las fases del razonamiento científico sugeridas por Bao et al. (2009).
Tabla 3: Indicadores de razonamiento científico en la resolución de problemas
| Explorar de manera sistemática un problema [ESP] | Procura comprender el enunciado de un problema antes de proceder a resolverlo. Identifica el objetivo general de un problema antes de proceder a resolverlo. Identifica las condiciones que el enunciado del problema provee. Traza un plan de acción para abordar el problema. Ejecuta acciones en correspondencia con el plan delineado. |
| Formular y testar hipótesis [FTH] | Anticipa resultados a las acciones a realizar. Elabora preguntas sobre posibles resultados. Ejecuta acciones con miras a validar o descartar hipótesis formuladas. Utiliza ejemplos concretos con miras a establecer regularidades o resultados. Ejecuta acciones para determinar la generalidad o particularidad de un resultado. Revisa el proceso realizado para contar con certeza de los resultados obtenidos. |
| Manipular variables aisladas [MVA] | Opera datos que provienen de distintas fuentes. Combina distintos datos en búsqueda de relaciones y diferencias. Opera de distintas formas los datos disponibles para solucionar el problema. Utiliza representaciones gráficas que apoyan la comprensión del problema. Establece un orden para operar los datos. |
| Observar y evaluar consecuencias [OEC | Contrasta resultados obtenidos con hipótesis formuladas. Analiza resultados y provee explicaciones a estos. Revisa el resultado de las acciones ejecutadas para evaluar su pertinencia. Provee una justificación a alguna propiedad obtenida antes de usarla de nuevo. Revisa la consistencia de los resultados obtenidos y las condiciones del problema. Formula conjeturas/propiedades, sobre la observación de los resultados obtenidos. |
Por dificultades de espacio no presentamos el análisis realizado al trabajo de cada pareja. Nos enfocamos en los fragmentos de interacción entre los miembros de uno de los casos, escogido porque exhibe de mejor manera la sinergia que queremos presentar. Presentamos ahora los fragmentos de interacción entre los miembros, EA y EB, al resolver el problema de los dos puntos. Utilizamos la denotación dada, en la primera columna de las tablas 1 y 2 o la expresada en paréntesis cuadrado en la tabla 3, para mencionar los indicadores. Cuando se presenten pausas prolongadas en la interacción se utilizará (…).
Análisis
Construcción de circunferencias
Al inicio los estudiantes hablan muy poco. EA utiliza GeoGebra y construye una circunferencia en la que los puntos A y B determinan uno de sus diámetros. El proceso desarrollado involucra determinar el segmento AB y su mediatriz, obteniendo así su punto medio, luego utilizar el comando Compás para construir la circunferencia (Figura 4).
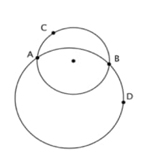
EA construye la primera circunferencia haciendo uso de un procedimiento que parece conocer con anterioridad [Ias1], pues no se entrevé descubrimiento de este ni discusión sobre su efectividad. Luego propone ver si existen otras circunferencias, tratando de construirlas. Oculta el segmento y la mediatriz. Después, construye un punto en la circunferencia distinto a A y B (llamémoslo C y usa la herramienta Circunferencia por tres puntos [C3P] tomando los puntos A y C. Al tomar como tercer punto a B y ver que coincide con la circunferencia que ya tiene, aborta su estrategia. Luego, usa de nuevo el comando C3P, toma los puntos A y B y determina el tercer punto [D] de manera que este no pertenezca a la primera circunferencia (Figura 5). Reitera el proceso, tomando otros puntos exteriores [F y G] y construyendo tres circunferencias (Figura 6).
1 EA Bueno, en este demostramos que existen, (…) pueden existir infinitas circunferencias…
[Utiliza nuevamente la herramienta Circunferencia por tres puntos, mueve el mouse mientras la pantalla presenta distintas circunferencias (Figura 7) y al final determina una cuarta circunferencia que hemos dejado en línea continua].
Para EA tiene lugar la adopción de un procedimiento de construcción de circunferencias bajo las condiciones establecidas [Ias2]. Este involucra el comando C3P y la observación de la variación de la circunferencia, dado el arrastre del tercer punto; lo anterior le permite garantizar que las circunferencias pueden ser infinitas [OEC]. El interés de EA por encontrar “infinitas circunferencias” se evidencia en la ejecución de acciones para determinar la generalidad del resultado [FTH]. En este punto no observamos que los estudiantes reconozcan alguna función nueva para los comandos involucrados; en consecuencia, no hay indicio de instrumentalización.
Determinación de los centros de las circunferencias
Una vez han construido en GeoGebra lo solicitado, P1 les pide determinar la ubicación de los centros de las circunferencias construidas. Los estudiantes tienen en pantalla la construcción realizada (Figura 7) mientras conversan.
2 EA Pues igual que lo hicimos ahorita, con la mediatriz.
3 EB Digamos, para mostrar esto podemos escoger cualquier circunferencia... por ejemplo, esta [con el mouse recorren la circunferencia que contiene a los puntos A, B y D].
4 EA Bueno, borremos las otras y dejemos solo una [con la opción ocultar objeto, oculta todas las circunferencias distintas a la seleccionada [Figura 8].
[Pasan unos minutos mientras piensan cómo abordar el problema. Al parecer no saben cómo determinar el centro vía la mediatriz, idea sugerida por EA al inicio de la conversación].
5 EA O sea, (…), el medio lo determinamos con (…). Con los segmentos (…) al inicio para formar la [primera] circunferencia [construida].
[EB pide a EA “devolver los pasos”, para hacer visibles todas las construcciones que previamente habían ocultado hasta llegar al primer paso de la construcción realizado, esto es, el segmento AB].
Los estudiantes plantean la posibilidad de usar parte del procedimiento que los llevó a construir la primera circunferencia [2] para hallar los centros [ESP]. Sin embargo, aunque dejan visible solamente una circunferencia [4] [MVA] para efectuar el procedimiento sobre esta [ESP], no ejecutan el plan fluidamente, hacen varias pausas. Esto puede ser porque las condiciones son distintas a las que se tenían al momento de construir la primera circunferencia, bien sea por el objeto a construir o por la ubicación de los puntos A, B y C. Surge un limitante al procedimiento [Isa2] que les dificulta su uso. Por eso deciden retomar el proceso desde el inicio.
Retoma de propuestas antiguas
Teniendo únicamente los puntos A y B en pantalla EA comenta a su compañero:
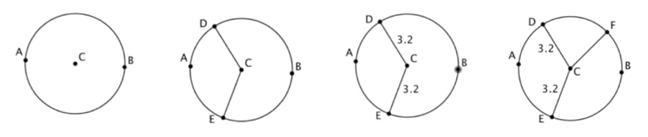
Trazamos el segmento (…) AB. La mediatriz (…) y ubicamos la intersección [la mediatriz y el segmento se ocultan]. Teniendo el punto medio del segmento AB [que llamaron C], podemos utilizar la herramienta Compás para poder ubicar la circunferencia que contenga los dos puntos [realiza la acción seleccionando primero el punto A, el punto B y finalmente el punto medio de nuevo] (Figura 9). Como ya tenemos la circunferencia, y para demostrar4 que el punto (…) C [nombra así el punto resultante] es el punto, ¿ah? Para demostrar que este punto [C] es el punto medio de la circunferencia podemos hacer cualquier segmento [construye un segmento con extremos en el punto C y un punto D sobre la circunferencia distinto a A y B] hasta cualquier punto de la circunferencia [construye el segmento CE de la misma forma] y hallar la distancia, entonces podemos demostrar que la distancia es 3,2 y este otro 3,2 [son valores mostrados en pantalla al utilizar la herramienta distancia en los dos segmentos construidos]. Igual podemos hacer cualquier punto [construye el punto F sobre la circunferencia y lo arrastra sobre esta] y trazar el segmento [CF] y pues también podemos aquí hallar la distancia de este punto a acá [refiriéndose a los puntos C y F] (…) pues lo podemos mover [punto F] y uno se da cuenta que siempre es la misma distancia [idea apoyada en la conservación de la medida], así uno se da cuenta que es el punto medio.
Los estudiantes usan de nuevo el procedimiento para construir la circunferencia para la cual el segmento AB es diámetro. Al parecer, reconocen este procedimiento como efectivo en esta situación [Isa4] y sobre el mismo establecen un orden [Ias2]. A diferencia de la primera vez que lo usaron, involucran un procedimiento adicional para corroborar que el punto C es centro de la circunferencia [Ias3]. Esto último lleva a elaborar una estrategia para corroborar tal propiedad [FTH], apoyados en las herramientas Segmento y Distancia o longitud, acompañado de un discurso que justifica la forma de proceder y el resultado obtenido [Ias1], es decir, que el punto C es efectivamente centro de la circunferencia [OEC]. Luego, EA relee el enunciado del problema donde está la pregunta y EB sugiere reportar los pasos de construcción para responder [ESP], pero su iniciativa no tiene mayores avances y nuevamente quedan sin saber qué hacer. Esto último se debe a la forma en que han sido construidas las otras circunferencias.
Descubrimiento de un nuevo procedimiento
Después de haber manifestado un estado de incertidumbre reiterado, EA encuentra la forma de determinar los centros de las circunferencias construidas con el comando C3P y así se lo comunica al profesor.
24 EA Pues hacemos lo mismo que hicimos ahorita. Trazamos una recta [AB], el segmento AB y la mediatriz [del segmento]. Entonces uno se da cuenta que la mediatriz del segmento AB [con el mouse la señala y recorre] tiene varias intersecciones con las distintas circunferencias que hay (Figura 10). Entonces, pues, ubicamos los puntos de las intersecciones [determina los puntos H e I de intersección de la circunferencia que pasa por los puntos A, B y G] y trazamos el segmento [IH]. Entonces así podemos sacar la mediatriz de este punto [I], (…), de este segmento que acabamos de hacer [IH] y ahí ubicamos el punto medio [determina la intersección del segmento IH y su mediatriz], entonces el punto medio sería este [intersección determinada], de la circunferencia [es decir, el centro de la circunferencia]. Se puede hacer [el procedimiento] con todas [las circunferencias] porque (…) porque las circunferencias que van a resultar siempre van a estar, o sea siempre van a estar ubicadas en línea recta. Porque como ya tenemos los puntos dados [refiriéndose a A y B], digamos, acá [utiliza la herramienta C3P señalando a los puntos A y B y un nuevo punto sobre la pantalla] uno se da cuenta que la circunferencia [manipula la circunferencia que se está determinando por A, B y el puntero del mouse] siempre está ubicada en (…) así [muestran distintas posiciones de la circunferencia].
25 EA Estoy intentando decir que la mediatriz del segmento AB está dividiendo la circunferencia, que siempre la divide de la misma forma, así esté más grande, la circunferencia siempre va a abrir de modo que la mediatriz la divide en dos partes iguales. Entonces así se puede hallar que, utilizando la mediatriz del segmento [AB] para hallar el punto medio [el centro de cada circunferencia], siempre puedo utilizar la mediatriz. Ubicamos las intersecciones acá [determina las intersecciones entre la mediatriz y una de las circunferencias], trazamos el segmento [determinado por estos puntos de intersección] (…) ubicamos las intersecciones. Bueno, trazamos las intersecciones, tenemos el segmento (…)
26 A1 ¿Cuál segmento?
27 EA El segmento (…) es que por medio de la mediatriz ubicamos los dos puntos que intersecan con la circunferencia, con cualquiera de la que estemos utilizando; en este caso utilizamos esta [seleccionan una de las circunferencias ya construidas] y trazamos el segmento [con extremos en las intersecciones con la mediatriz de AB] para poder establecer el punto medio [el centro] pero utilizando la mediatriz [del nuevo segmento]. Ahora del segmento que acabamos de hacer y nos damos cuenta de cuál es el punto medio (…). Ubicamos el punto medio y si lo queremos comprobar hacemos lo mismo que ahorita, con cualquier segmento. Ubicamos cualquier segmento y miramos su longitud.
[Reproduce el procedimiento para corroborar si el punto de intersección del segmento IH y su mediatriz es centro de la circunferencia].
28 EA Nos damos cuenta que efectivamente es el punto medio de la circunferencia que acabamos de estudiar. Ahora dice (…) [Lee] con base en lo realizado escribe la conjetura.
El procedimiento sugerido por EA consiste en determinar, para cada circunferencia, sus puntos de intersección con la mediatriz del segmento AB. Estos puntos determinan un segmento, al cual le construyen su mediatriz (que no es la misma mediatriz del segmento AB), lo que lleva a obtener el centro de la circunferencia. EA afirma dos hechos para este procedimiento: (1) la mediatriz del segmento AB interseca a cada circunferencia en dos puntos [24] y (2) el punto de intersección entre el segmento cuyos extremos son las intersecciones obtenidas en (1) y su mediatriz es el centro de la circunferencia [27].
Los estudiantes descubren un nuevo procedimiento, que les permite determinar el centro de las circunferencias construidas con el comando C3P [Ias1]. Explicitan en su diálogo el esquema asociado a este procedimiento [Ias2] para involucrarlo en adelante. Al mismo tiempo, descubren una función adicional [Isa3] para la mediatriz del segmento5AB, particularmente la obtención de pun-tos de intersección con cada circunferencia; con ello pueden determinar sus centros [Isa1]. Además, reconocen el procedimiento señalado al final de [27] como medio de verificar la propiedad ser centro de la circunferencia en este contexto [Isa4], mencionando además la forma en que este procedimiento se ejecutaría [27], lo que nos lleva a asegurar que han reconocido un procedimiento para usarlo en adelante [Ias2]. La forma en que construyen las circunferencias que contienen a los puntos y involucra nuevamente el comando C3P, lo que da evidencia de que ese comando ha sido asociado a ese producto y lo reconocen, por lo menos EA, como medio para alcanzar ese fin [Isa4].
En términos del proceso de resolución, EA traza y ejecuta un plan [ESP], suministrando una explicación empírica a su proceder [24] que se apoya en el uso de la función de arrastre de GeoGebra para determinar la generalidad de su hipótesis [FTH]. En esa misma intervención EA anticipa los resultados que obtendrá al replicar el procedimiento usado y ejecuta acciones para validar su hipótesis. Además, en [25] utiliza ejemplos concretos con miras a establecer resultados [FTH]. El proceso que EA describe en [24] goza de un orden en su formulación; esto es, EA opera de manera ordenada los datos que provienen de distintas fuentes [MVA] y finalmente suministra una justificación al cumplimiento de la propiedad [OEC] con base en otro procedimiento elaborado previamente [27], [28].
Aun cuando los estudiantes no replican el procedimiento con una nueva circunferencia, aseguran que se obtendrá un resultado similar en las otras circunferencias, construidas con el comando C3P, dada la relación de estas con la mediatriz del segmento AB y su comprobación a través de la función de arrastre de GeoGebra [Isa4].
Establecimiento de una propiedad
Hasta el momento, los estudiantes solo se han enfocado en determinar los centros de cada circunferencia y su construcción es compleja por la cantidad de objetos involucrados (Figura 11; hemos punteado las mediatrices construidas hasta el momento y la recta AB para distinguirlas en la construcción). P2 ahora cuestiona a los estudiantes sobre la propiedad de los centros de las circunferencias:
37 P2 Bueno, ¿pero dónde están esos centros?
38 EB En la mediatriz del segmento AB. Es que mira [señala la pantalla].
39 P2 Listo, […]. Pero mira que lo que tu acabas de decir está bien (…) ¿por qué no lo escribes? [dirigiéndose a EB], ¿qué es lo que acabas de decir? [dirigiéndose a EA], es que se me olvidó. Estaba concentrada en lo que dice tu compañero [EB]; vuélvelo a decir.
40 EA Yo dije que siempre hay intersección (…) es que lo puedo decir de otra forma. Digamos que el centro es la intersección del diámetro con la mediatriz.
41 P2 La intersección del diámetro. Pero mira que, acá en esta circunferencia [refiriéndose a la circunferencia cuyo centro es el punto M] este [segmento AB] no es el diámetro [EA y EB guardan silencio]. Vuélvelo a decir a ver si te entiendo.
43 EA EA Tengo los puntos A y B que están en (…), que pertenecen a la circunferencia (…) el centro es (…) la intersección (…) la intersección del diámetro [con su mano recorre el diámetro de la circunferencia con centro M que es perpendicular al segmento JK] y la mediatriz [mueve su mano de arriba abajo recorriendo la mediatriz del segmento AB].
P2 les pide a los estudiantes que se concentren en los puntos A y B. Les pregunta cómo construirían los centros de las circunferencias que contienen a los puntos A y B. Para responder, los estudiantes reconstruyen el procedimiento en GeoGebra, a partir únicamente de los puntos A y B, pasando por la circunferencia para la cual el segmento AB es diámetro y algunas circunferencias que contienen a los puntos A, B y un tercer punto cualquiera. Al final EA menciona:
44 EA Es que cuando uno utiliza (…) cuando uno construye la circunferencia (…) lo que quería decir es que la mediatriz del segmento [AB] siempre divide la circunferencia [todas las que se han construido] en dos.
En este punto termina el trabajo realizado por esta pareja. Hay cuatro asuntos para resaltar:
- El proceso de construcción empleado para determinar los centros de las circunferencias que contienen los puntos A y B es válido. Es un procedimiento que efectivamente provee los centros de las circunferencias. Aun cuando los estudiantes no dicen el motivo por el cual el procedimiento funciona (en términos teóricos), logran proveer una justificación al resultado de este y verifican que los puntos son centros de las circunferencias, valiéndose de la definición de circunferencia, conocida con anterioridad, a través de un mecanismo que involucra los comandos Segmento y Distancia o longitud.
- Lo que en cada circunferencia construida (distinta a la primera) era para los estudiantes su diámetro, era el segmento determinado por los puntos de intersección entre esa circunferencia y la mediatriz del segmento AB. Los estudiantes no involucraron algún comando para corroborar esto y no suministraron alguna explicación. Esto nos lleva a cuestionar si ellos reconocían este segmento como el diámetro a partir de alguna propiedad conocida o simplemente porque en la representación así lo parecía. Dada la ausencia de una justificación verbal o del uso de las herramientas de GeoGebra para corroborarlo, tenemos inclinación por la segunda opción.
- Destacamos la formulación de cuatro conjeturas durante la conversación que se presentó. Solo una de estas reporta la propiedad de los centros de las circunferencias que contenían tanto al punto A como al punto B [38]. En otra, EA comunica una propiedad que no tiene relación con lo que el enunciado del problema solicitaba [44], aunque retoma una idea que en otro momento permitió garantizar la validez del procedimiento para determinar los centros de las circunferencias construidas con el comando C3P. Aun así, debemos mencionar que esta propiedad reportada por EA es fruto de la observación realizada anteriormente y los resultados corroborados a través de la función de arrastre [OEC]. En las otras dos, EA establece una relación similar entre un segmento y una mediatriz [40, 43]. En las intervenciones afirma que el centro de las circunferencias es la intersección entre estos dos objetos geométricos.
- En una conjetura EA menciona que “el centro es la intersección del diámetro con la mediatriz” [40]. Nos llama la atención la generalidad con la que se refiere a esta propiedad. Da lugar a pensar que está evocando el resultado del procedimiento planteado para determinar los centros de las circunferencias. En consecuencia, EA propone una propiedad en función de las acciones realizadas y corroboradas por él en algún momento; es decir, formula resultados, fruto de la observación [OEC]. Sin embargo, no tenemos evidencia clara para dar peso a esta interpretación debido a que P2 creyó que EA se refería al segmento AB y la mediatriz de ese segmento. Una forma de haber profundizado en la idea reportada por EA hubiera sido solicitar que él explicitara los objetos a los que hacía mención o que explicara el motivo por el cual proponía esta propiedad.
Discusión
La descripción del proceso de resolución del problema por parte de esta pareja nos brinda elementos para interpretar su comportamiento y reconocer la sinergia entre el SGD y el razonamiento científico.
El dúo razonamiento científico y uso de GeoGebra en la resolución del problema
En términos generales, esta pareja involucró comandos de GeoGebra de manera novedosa para abordar el problema propuesto y movilizó aspectos del razona-miento científico. Estos elementos constituyeron un dúo que permitió a los estudiantes llevar a cabo la actividad matemática de resolución de un problema. Presentamos un análisis del dúo generado en esta pareja.
En la Tabla 4 resumimos las acciones realizadas, en correspondencia con los indicadores adoptados para rastrear el razonamiento científico.
Tabla 4 Momentos de resolución
| Acción Momento | Explorar de manera sistemática un problema [ESP] | Formular y testar hipótesis [FTH] | Manipular variables aisladas [MVA] | Observar y evaluar consecuencias [OEC] |
|---|---|---|---|---|
| Construcción de las circunferencias | Cuestionamiento y ejecución de acciones para saber si hay distintas circunferencias que contienen a los puntos A y B. | Se formula una propiedad sobre la existencia de infinitas circunferencias que contienen a los puntos A y B. | ||
| Determinación de los centros | Se establece y ejecuta un plan para determinar centros de circunferencias construidas con C3P. | En pantalla solamente se deja una circunferencia sobe la cual implementar el plan trazado. | ||
| Retoma de propuestas antiguas | Se listan los pasos de un procedimiento para obtener un resultado particular. | Se provee justificación al hecho de que la intersección de un segmento y su mediatriz es centro de la circunferencia. | ||
| Descubrimiento de un nuevo procedimiento | Se traza y ejecuta un plan para determinar un segmento en cada circunferencia que sea diámetro de la misma. | Se involucra la función de arrastre para verificar la validez de una hipótesis: la mediatriz del segmento AB divide todas las circunferencias en dos. Se usan ejemplos particulares. | Las construcciones realizadas atienden a una estructura organizada observada en el discurso de los estudiantes. | Se involucra un procedimiento conocido, sobre el que conoce su validez, para justificar que el resultado obtenido en esta oportunidad es efectivamente el deseado. |
| Establecimiento de una propiedad | Se formulan como propiedades: (i) la mediatriz siempre divide la circunferencia en dos y (ii) el centro es la intersección del segmento y su mediatriz. |
Podemos reconocer cuatro momentos en los que tuvieron lugar acciones correspondientes con al menos un indicador del razonamiento científico. En un primer momento, se formularon hipótesis sobre la existencia de infinitas circunferencias que contuvieran a los puntos A y B. El ejercicio de corroborar esta idea se favoreció por el uso de la función de arrastre de GeoGebra. En un segundo momento, GeoGebra permitió manipular los objetos construidos con el fin de ejecutar el plan trazado, infortunadamente sin resultados favorables para el grupo. En un tercer momento, los comandos Segmento y longitud o Distancia permitieron establecer una estrategia para tener la certeza de un procedimiento que se conocía con anterioridad, lo cual llevó a proponer una justificación empírica sobre su validez. En el cuarto momento, se propuso un plan de acción y este se ejecutó organizadamente, permitiendo que la función de arrastre diera lugar a la observación y formulación de un invariante que conllevaría al establecimiento de un procedimiento para solucionar el problema. Al final, las propiedades que se reportan como solución al problema atienden al proceso realizado con ayuda de GeoGebra. Este recorrido permite apreciar cómo se presentaron aspectos del razonamiento científico, donde el SGD dio elementos para descubrir, verificar y formular propiedades que en conjunto permitieron solucionar el problema.
A lo largo del análisis pudimos evidenciar que los estudiantes desplegaron cuatro procedimientos de acuerdo con sus necesidades: (1) la construcción de una circunferencia para la cual un segmento se convierte en diámetro; (2) la construcción de circunferencias que contengan a dos puntos A y B y un tercer punto tomado al azar; (3) la verificación de que un punto es centro de una circunferencia; (4) la construcción del diámetro de una circunferencia para determinar su centro. La interacción oral no permitió evidenciar que ellos llevaran a cabo un proceso de experimentación; más bien apreciamos un conocimiento previo sobre la forma de utilizar el comando C3P. Sin embargo, cuando los estudiantes tuvieron que afrontar el reto de determinar el centro de las circunferencias construidas con C3P, emergió un procedimiento desconocido por ellos. En esta emergencia, la función de arrastre fue determinante al permitir a los estudiantes experimentar con una de estas circunferencias vista como una representante de una familia, para corroborar su hipótesis. Este resultado fue útil para los estudiantes: pudieron involucrar nuevamente los procedimientos que conocían, modificaron esquemas que habían desarrollado, determinaron los centros de las circunferencias construidas y corroboraron que estos efectivamente satisfacían tal propiedad. Lo anterior muestra que la exploración realizada por los estudiantes con el apoyo de GeoGebra les permitió obtener evidencia empírica de la generalidad de una propiedad y apropiarse de la misma como parte de su conocimiento para poder establecer conexiones con otros resultados conocidos con anterioridad, aspecto característico del razonamiento científico (Klahr y Dunbar, 1988).
El razonamiento científico exhibido en el reconocimiento y uso de las herramientas de GeoGebra nos permitió determinar el grado en que los procesos de instrumentación e instrumentalización tuvieron presencia. En la Tabla 5 se recoge, para cada herramienta involucrada, los aspectos observados de cada proceso.
En términos generales, los estudiantes reconocieron la forma de utilizar los comandos y procedimientos involucrados al abordar el problema o la posibilidad de conectarlos con otros ya conocidos. Este reconocimiento involucró aspectos del razonamiento científico como la planeación de una estrategia, la formulación de hipótesis sobre sus resultados, la operación de las variables involucradas y la observación de resultados con miras a validar o rechazar hipótesis, permitiendo así el reconocimiento de posibilidades para resolver el problema.
Encontramos evidencias del reconocimiento de posibilidades y limitaciones de algunos comandos al involucrarlos para resolver la tarea, asunto que permite asegurar que se dan indicios de instrumentalización. Particularmente, podemos mencionar que tiene lugar la modificación de funciones originales del artefacto mediatriz, utilizado para poder determinar diámetros en las circunferencias. En los otros casos, aun cuando los estudiantes descubren y reconocen artefactos como medios para la obtención de fines, no tuvo lugar una modificación en el uso de estos. De acuerdo con Alqahtani y Powell (2016), creemos que el artefacto se utiliza con el mismo fin para el cual se construyó, lo que no demanda enriquecer o modificar sus propiedades al incorporarlo. Este asunto es motivado por el tipo de problema propuesto, donde se debía repetir el uso del mismo artefacto varias veces. No hicimos observaciones en situaciones donde por limitaciones en el uso de algún artefacto se hubieran buscado otras formas de incorporarlo o de apropiarse de otro que permitiera resolver el problema. Considérese, por ejemplo, que se debiera construir una circunferencia que contuviera dos puntos y que además fuera tangente a una recta. En este caso el comando C3P no podría involucrarse de la forma que se hizo en esta oportunidad.
Tabla 5 Vestigios de instrumentación e instrumentalización
| Comando | C3P | Segmento y longitud o distancia | Segmento, mediatriz y compás | Mediatriz segmento | |
|---|---|---|---|---|---|
| Función | Construir circunferencias que contengan puntos A y B. | Corroborar si un punto es centro de circunferencia. | Construir circunferencia donde un segmento es diámetro y el punto medio es centro. | Determinar diámetro de circunferencia. | |
| Instrumentalización | Ias1 | No. La función del comando se conoce con anterioridad. | No. La función de los comandos se conoce con anterioridad. | Sí. La mediatriz es usada para descubrir puntos que determinan diámetros. | |
| Ias2 | No. No se presentaron limitaciones en su uso. | Sí. Determinar centro de circunferencia dada por C3P | No. No se reconocen limitaciones en su uso. | ||
| Ias3 | No. Solo se reconoció un propósito para su uso. | No. Solo se reconoció un propósito para su uso. | Sí. Se reconocen 2 usos: construir circunferencia donde segmento AB es diámetro y determinar intersección con circunferencias. | ||
| Ias4 | Sí. C3P se utilizó siempre con esa función. | Sí. El procedimiento que Involucraba estas herramientas se reconoció como apropiado en ese contexto para su función. | Sí. Cuando se contaba con los puntos A y B la primera circunferencia se construía de la misma forma. | Sí. Se reconoce que siempre será posible involucrar el procedimiento para las circunferencias dadas por C3P. | |
| Instrumentación | Ias1 | Sí. Se reconoce la posibilidad de involucrar C3P bajo un esquema determinado y obtener circunferencias distintas. | Sí. Se implementa un esquema para corroborar la propiedad “ser centro de circunferencia”. | Sí. Se reconoce un esquema para determinar los diámetros de las circunferencias. | Sí. Se reconoce un esquema para construir una circunferencia para la cual un segmento sea su diámetro. |
| Ias2 | Sí. Se adopta un esquema para involucrar el comando en adelante. | Sí. Se establece un esquema para involucrar el procedimiento en reiteradas oportunidades. | Sí. Es explícito el esquema involucrado para construir la circunferencia. | Sí. Se reconoce un esquema para incorporar el procedimiento aunque solo se involucra una vez. | |
| Ias3 | No. El esquema no se modifica. | No. El esquema no se modifica. | Sí. El esquema se adapta con el fin de corroborar que el punto es efectivamente centro. | No. El esquema no se modifica. | |
| Ias4 | No. Situación poco analizada. Habría que ver el comportamiento al abordar otros problemas. | ||||
Respecto a la instrumentación, podemos decir que aparecieron esquemas de utilización de los comandos involucrados y que esto se favoreció por el desconocimiento de muchas herramientas de GeoGebra. Sin embargo, los esquemas desarrollados no se modificaron, salvo en el esquema desarrollado por la pareja para determinar los centros de las circunferencias construidas con C3P y en las afirmaciones realizadas para respaldar su validez. Al procedimiento que los estudiantes conocían para construir una circunferencia a partir de su diámetro y determinar su centro ellos adhirieron otros pasos que permitieron ampliar su alcance para determinar el centro de otras circunferencias. Es un esquema que tiene validez en casos muy particulares. Sin embargo, a la luz de las ideas propuestas por Samper et al. (2013), este resultado brinda evidencia sobre la actividad matemática exhibida por los estudiantes y el papel que el recurso tecnológico y el razonamiento desempeñaron.
Conclusiones
Nuestro objetivo al presentar el análisis es aportar a la comprensión de la sinergia que se produce entre el razonamiento científico y el uso de un SGD, mediante el estudio de caso de una pareja de estudiantes. En lo que sigue ilustramos esta idea, apoyados en los resultados del estudio realizado.
Con base en las ideas de Samper et al. (2013) y Trouche (2014), sobre la interacción de un individuo con artefactos y la mediación de estos en la gene-ración de conocimiento, mostramos la forma en que una pareja de estudiantes involucró el SGD GeoGebra en la resolución de un problema. Resaltamos que la relación artefactos-individuos se estimula por los procesos de razonamiento ejecutados por los estudiantes, que son promovidos por la tarea propuesta. La naturaleza de la tarea y el desconocimiento de muchas herramientas del SGD los llevó a contemplar estrategias de solución como parte de su actividad matemática involucrando el recurso del que disponían.
Reconocemos en la situación presentada el rol protagónico asumido por GeoGebra para afrontar el problema y la emergencia de esquemas asociados a algunos comandos del software. Las acciones y modos de proceder de la pareja examinada dejan ver el efecto de la sinergia entre el uso de los recursos y acciones propias del razonamiento científico que permitieron a los estudiantes reconocer en algunos comandos, de manera individual o en conjunto, formas para alcanzar propósitos específicos. Este ejercicio permitió identificar artefactos que evolucionaron en instrumentos para los estudiantes. Aun así, resaltamos el carácter subjetivo de la relación artefactos-individuos (Alqahtani y Powell, 2016), asunto evidente en la forma en que la pareja analizada involucró los artefactos y desarrolló para estos esquemas particulares.
La resolución del problema brindó a los estudiantes, gracias al uso del SGD, la oportunidad de experimentar e indagar, apoyándose en objetos y relaciones geométricas no todas conocidas anteriormente por ellos. El abanico de posibilidades que el software ofrece les permite experimentar y someter a prueba ideas, en función de los alcances y limitaciones de los comandos usados, lo cual da evidencia empírica para poder validar o rechazar las ideas y, en consecuencia, ampliar el conjunto de conocimientos que tienen. Uno de los aspectos característicos del razonamiento científico, es la conexión que se establece entre el conocimiento de los individuos y los resultados obtenidos en un proceso de experimentación (Klahr y Dunbar, 1988) y en esta vía, se reconoce al SGD como un promotor de acciones ligadas a este proceso cognitivo.
Las ideas mencionadas anteriormente permiten comprender la sinergia surgida entre el razonamiento científico desplegado por los estudiantes y el uso de GeoGebra, lo que lleva a la conformación de un dúo que impulsa procesos propios de la actividad matemática esperada en la escuela. Como ilustramos, cada proceso de vio favorecido por la actuación conjunta de estos dos elementos. De ahí que se considere la necesidad de explotar dicho dúo de manera más decidida el nivel escolar. Además, el análisis presentado deja ver la necesidad de herramientas apropiadas de las que se pueda disponer para que acciones propias del razonamiento científico puedan emerger, dada la demanda que impone realizar acciones de esta naturaleza. Lo anterior se apoya en la naturaleza de los indicadores propuestos para analizar el proceso de resolución de la pareja de estudiantes y la forma en que el SGD se involucró en este.











 nueva página del texto (beta)
nueva página del texto (beta)