1. EL MINISTRO Y LA REGLA DEL TRES

Hace unos años, un Ministro de Educación francés presentaba su reforma en la televisión. Aceptó, gentilmente, que la periodista lo interrogara acerca de sus “saberes elementales”.³ Ella le propone un problema: “Si 5 lápices cuestan 4 euros y 50 centavos, ¿cuánto cuestan 14 lápices?”. El Ministro titubea, se desorienta y refunfuña: “Yo no lo sé hacer, me muestra?”. La periodista se lanza con el célebre “producto en cruz” y bosqueja una disposición de los números, pero no logra explicar su técnica y termina declarando: “Es necesario, ‘simplemente’, calcular el precio de un lápiz y multiplicar este valor por 14”; evidentemente aquí el problema no es sólo el de calcular a mente el resultado…

Cierto, el Ministro supo dominar la situación y retomar después el episodio como una broma. Se puede incluso encontrar para él una excusa. Pero el incidente reveló públicamente la triste forma como se tratan las cosas que tienen que ver con la enseñanza en modo especial de la matemática.

Este episodio nos interesa aquí porque muestra un fenómeno didáctico importante.

La “regla de tres” nació de una pequeña dificultad que se presenta en el cálculo de las proporciones. El sentido usual conduce a buscar en primer lugar el valor unitario para, en un segundo momento, multiplicarlo por la cantidad de la cual se pide el precio. Pero este método puede conducir a errores si la división inicial “no es exacta”.

Conviene, por tanto, hacer la multiplicación primero y la división en un segundo momento.⁴ Pero, haciendo así, el significado concreto de esta primera operación se vuelve difícil de interpretar pues no es fácil, ni de concebir ni de enunciar, que es lo que se está midiendo en concreto con el resultado de dicha multiplicación. ¿Entonces? ¿Es necesario multiplicar qué número y por qué?

Cuando el significado se escapa, todos nosotros buscamos ayuda en automatismos de memoria: descripciones formales, medios nemónicos, diseños etc., es decir en metaconocimientos o en teorías, la comprensión de las cuales se basa en un significado nuevo, diverso. El aprendizaje de una acción despojada del sentido se centra ahora en la repetición, que tiene dificultad para permanecer estable por las formas equívocas que se presentan.

En el caso de nuestro problema la solución histórica ha sido “la regla de tres”, uno de los medios automáticos de ordenar la sucesión de las operaciones materiales y los cálculos. Por ejemplo, una disposición en una tabla en la cual se escriben en la primera fila los valores conocidos: una cantidad y su precio global; y en la segunda fila la indicación conocida bajo la correspondiente (la nueva cantidad bajo la primera). Sucesivamente, es necesario multiplicar los dos números que se encuentran en diagonal y dividir el resultado por el tercer número. ¿Por qué? ¿Qué mide el número que se encuentra multiplicando el número de lápices, 14, por el precio de 5 de estos? (Sería el precio de 14 confecciones de 5 lápices cada confección).

Para poder entender y, en particular, para explicar este cálculo es absolutamente necesario acompañar este algoritmo con un discurso comprensible.

Una primera solución expresa la conservación de las relaciones fraccionarias y necesita recurrir a la multiplicación de una fracción por un número:

14 son los 145 de 5; el precio de 14 lápices serán los 145 del precio de 5; entonces 145 de 4.5 son 14× 4.55 .

Pero, para los alumnos, que conocen sólo las relaciones naturales, es necesario descomponer la fracción 145 y escribir entre las dos filas una tercera en la cual aparece al inicio “1” y después el precio de la unidad bajo la forma de fracción (sin efectuar la división): 5 lápices cuestan 4.5 €, 1 lápiz 5 veces menos, pero nosotros no calculamos el resultado; y 14 lápices cuestan 14 veces más: 14× 4.55 que escribimos 14×4.55. La multiplicación de esta fracción por el tercer número exige el conocimiento (implícito) del cálculo fraccionario.

Se obtiene así la fórmula correcta acompañada de razones para comprender lo esencial. Pero la formula resta por aprender, a través de numerosas repeticiones de problemas y de explicaciones.

5 → 4.5

5 → 4.5

14 → ? 14x4.55

1 → 4.59 (0.9)

14 → 4.59x14 = 14x4.55

Pero, para sostener la traducción formal de este razonamiento, se requieren de nuevas muletas algorítmicas como: “escribir a la izquierda la magnitud de la cual se conocen los dos valores”. Y si se alcanza a considerar la proporcionalidad inversa, el armazón nemónico se desmorona. Históricamente, se ve el proceso de complejización didáctica que se presentó desde el medioevo, hasta el siglo XX diversos medios que evocaban los ábacos sobrecargando el algoritmo con la alusión a los “productos en cruz” que la buena teoría de la proporcionalidad consagra: el producto de los extremos es igual al producto de los medios. Los estudiantes no pueden hacer nada para entender.⁵

La mejor solución era aquella de botar este dispositivo, que se había convertido en algo inútil, y en treinta años los formadores de docentes lo habían logrado. Pero, ciertos “expertos” de matemática creyeron reconocer en esta situación una preparación inteligente para un futuro teorema del algebra. Propusieron, con insistencia, esta “técnica” a los docentes como un indicador de alta cultura, resucitando así la confusión. El importante número de estudiantes que tropezaron con esta “dificultad” y que no obstante lograron el éxito en sus estudios, lo consagraron, y a pesar de esto se erigió, a prueba discriminante, una piedra de comparación. “¡Por otra parte la regla del tres pertenece a la cultura!

Entonces, es necesario restaurar este tesoro y enseñarlo a más y más niños, y para esto comenzar cuanto antes, cuando los niños son más maleables”.⁶

Este ridículo fenómeno muestra, de todas formas, que para resolver una dificultad, incluso menor, una cascada de procedimientos didácticos puede elaborar progresivamente un proceso que poco a poco se convierte en un monstruo incontrolable.

Hemos identificado los fenómenos de este tipo como deslizamientos metadidácticos.

Se trata de mostrar, en este artículo, otros fenómenos de este tipo y de explicarlos. Son difíciles de evitar y aún más de corregir. Por esto es necesario que sean reconocidos por los docentes y por el público.

Estos fenómenos aparecen después de una derrota, de un fracaso, generalmente inevitable; pero el hecho no es reconocido inmediatamente como tal por los medios de la didáctica espontánea. Los docentes explican, después explican las explicaciones, las ilustran y después explican las ilustraciones… Cada vez los intentos por corregir los fracasos iniciales se revelan inadecuados. El fenómeno se amplifica, además, cuando se somete al juicio del público, aún más ignorante en didáctica. El fenómeno se enquista y rápidamente se vuelve incontrolable. Es así, como en las grandes pandemias del medioevo, algunos aprovechan para acusar todo tipo de prácticas escolares que pretenden renovar mutilándolas, para lanzar al fuego alguna “teoría” y para olvidar los resultados de las experiencias consideradas nefastas.

2. DE LA LÓGICA A LOS DIAGRAMAS DE CONJUNTOS, DESPUÉS A LA CONTRA-INNOVACIÓN

A finales de los años ‘50, la reorganización de los conocimientos matemáticos estaba cerrando un centenar de años de descubrimientos notables. La sociedad, los centros culturales y la enseñanza reconocen la necesidad de adaptarse. Pero la mayor dificultad reside en la introducción de los fundamentos: ¿cómo domesticar la axiomática en una enseñanza acostumbrada a asociar los objetos a sus lenguajes? Necesita un universo de objetos y de relaciones, si es posible adornadas de imágenes y de metáforas. Los analistas tienen necesidad de la lógica bajo una forma apropiada. Pero la lógica formal está en revolución. Proponen usar una teoría ingenua de conjuntos como sustituto de la lógica clásica.

Se trata de un segundo deslizamiento didáctico

Pero, esta vez la “representación” de hecho es sólo una metáfora: los conjuntos no tienen fronteras, mientras que su diseño sí; las uniones de las partes no se ven como “conjuntos”, etc. Sin embargo, también en la enseñanza se necesita conjugar nociones suficientemente definidas con otras que son sólo aproximaciones “transportadas”: las reglas del juego son diferentes, en particular en los primeros niveles en los cuales se requieren reglas de uso bien formulables y consistentes.

Ahora bien, los conjuntos de objetos expresan propiedades de cada objeto del conjunto al cual pertenece; la “y”, que en la vida de todos los días permite reunir dos conjuntos, produce por el contrario una intersección si se usa entre las propiedades. ¡Las canicas de vidrio y las canicas rojas no dan absolutamente como resultado las canicas rojas y de vidrio!

Las colisiones en la escala de los tipos lógicos, que la lengua natural esquiva con pudor, revelan por lo general simas de complejidad. Esta dualidad “propiedad/conjunto” conjuga sus trampas con aquellas de la lengua natural.⁹ En estas condiciones la metáfora de los círculos de Euler no se sostiene.¹⁰

El lenguaje coloquial puesto en juego por la metáfora de los círculos de Euler constituye un nuevo deslizamiento meta.

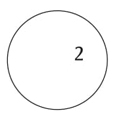
Georges Papy propuso en esa época colorear las fronteras de dichos círculos para identificar así las componentes conexas de un mismo conjunto. Pero la materialización de los elementos a través de los puntos produce nuevas contradicciones.

No se sabe si el signo 2, representado al interior del círculo, es el único elemento, o si es una especie de variable, un elemento identificado a título de ejemplo que evoca otros, por ejemplo todos los pares, no representados, o si está representando el signo “2”. Necesitamos de un vocabulario específico para describir estas figuras.¹¹ Este nuevo vocabulario puede considerarse como un nuevo deslizamiento, y además, muy meta.

Esto crea un cuarto nivel conceptual que obliga a crear sin descanso nuevas convenciones. Estas crecieron tanto o más que los axiomas de Boole, y no se sabe si tienen que ver con el modelo original o con su descripción.

Su formalización creará un quinto nivel conceptual y su meta un sexto. Los estudiantes, los editores, los diseñadores, los docentes y los padres reclaman reglas específicas y precisas que el sistema no puede producir.

Si se quisiera aceptar la metáfora de los conjuntos, para evitar, de un sólo golpe, los deslizamientos sucesivos, se deberían restringir los diseños a un papel solamente ilustrativo, a medio de expresión sin codificarlos, sin enseñar reglas relativas a estos dibujos. Estos habrían formado un conjunto de conocimientos implícitos para representar aquello de lo que se está hablando, para convencerse, y que pueda ser utilizado, pero sin un estatuto de saber significativo, válido, por tanto sin gramática y sin teoría.

Es lo que nosotros llamamos un conocimiento, pero no un saber (véase 7.). Ahora bien, los docentes no pueden manejar un instrumento didáctico de esta dimensión sino de forma furtiva. La sociedad actúa, y les exige a los docentes que actúen, como si todas las condiciones necesarias debieran ser dichas, como si todo lo dicho pudiera ser enseñado y todo aquello que es enseñado debiera ser aprendido, como si todo lo que es aprendido debiera ser comprendido, y todo lo que se ha comprendido debiera asegurar el éxito en situaciones futuras. Esto la sociedad cree y esto exige. Y, hasta ahora, se rechaza toda ciencia que pudiera poner en duda esta creencia. Todo tiene que ser mejorado por el juego simple de la voluntad, de la tradición¹² para los unos (los contra-innovadores), o por el ingenio innovador individual para los otros.

Finalmente, la totalidad de la comunidad matemática se ha visto imposibilitada no sólo de prever, sino también a detener el proceso. Rechazando hacer valer en un auditorio, suavemente potente, los resultados de las investigaciones en didáctica que había suscitado esta misma,¹³ terminó con acusar… ¡El saber mismo! La “matemática moderna” ha sido demonizada y rechazada,¹⁴ y se botaron con esta años de trabajo pedagógico y de cultura, de buenos y útiles conocimientos matemáticos, de dispositivos didácticos muy útiles, de ambiciones educativas y culturales legítimas y perfectamente realizables y de años de trabajo científico pertinente y válido para la enseñanza.

Esta contra-reforma tiene origen en una obstinada ignorancia de nuestros resultados. Los deslizamientos metadidácticos pueden producirse a propósito de cualquier noción matemática.

3. LA HEURÍSTICA DE POLYA Y LA ENSEÑANZA DE LOS MÉTODOS DE PROBLEM SOLVING

Las dificultades que encuentran los estudiantes en la resolución de problemas dejan por lo general a los docentes desarmados. El alumno sabe “sus” saberes, y “sus” teoremas (en ocasiones incluso “sus” demostraciones) y, sin embargo, no encuentra el medio para usarlos en la resolución de los problemas que el docente le propone. Una respuesta clásica a nivel primario consiste en presentarle problemas análogos de forma tal que el estudiante pueda reproducir la solución que le fue enseñada en un caso similar.

El estudiante no tiene necesidad de saber si la respuesta es adecuada, ni el por qué; basta que dicha respuesta sea conforme con el modelo. El estudiante puede así responder en el ámbito de un contrato didáctico sin comprender por qué de su solución correcta. Cualquier cosa que digan, a este propósito, las varias teorías del conocimiento y del aprendizaje que se fundan en el “reconocimiento” del saber y, en la citación de éste, el estudiante simula una resolución que puede incluso no comprender.

En un recorrido más concreto, para guiar a los estudiantes, Polya se prodiga en consejos neo cartesianos para la organización del trabajo de resolución de problemas: comprender el enunciado, conectarlo con los conocimientos, descomponerlo en etapas, Polya sugiere de esta forma intentar pasos aún más heurísticos: buscar similitudes, un ejemplo, un contra-ejemplo, generalizar, comparar. Este trabajo sirvió de fundamento para un intento de enseñanza de la resolución de problemas cuyas bases se encuentran en el uso de estas heurísticas.

Se trata claramente de un deslizamiento metadidáctico: la resolución de problemas se ve, en parte, sustituida por un estudio de procedimientos de dichas resoluciones.

Los ejemplos dados son tales que intentan tranquilizar y hacer competitivos a los estudiantes, pero es evidente que la situación se desplazó sin cambiar la naturaleza: el estudiante busca aplicar sus heurísticas, así como buscaba aplicar sus teoremas y el éxito no es ya asegurado, a menos que se elijan problemas ad hoc. Entonces, ¿es necesario buscar heurísticas de segundo orden? Incluso si el proceso no es recursivo, el engaño es fatal. La única diferencia es que los teoremas son saberes matemáticos que contienen dentro de sí mismos sus condiciones de validez, lo cual no es el caso de las heurísticas que son sólo conocimientos. Tratarlas como saberes es un error epistemológico y didáctico.

4. USOS Y ABUSOS DEL DESLIZAMIENTO METADIDÁCTICO

Entendemos que un error o un fracaso conducen al actor, sujeto o sistema docente/estudiante, a trasladar su atención de la actividad en curso a uno de los medios de control o de conocimiento de esta misma actividad.

Llamamos “meta” a este medio de control.

Por ejemplo, para efectuar una tarea, un actor se sirve de un medio que se revela insuficiente, examina este medio para mejorarlo y transformarlo en instrumento. Este proceso constituye un deslizamiento de actividad que se podría llamar deslizamiento metacognitivo. Este ir y venir, sea o no fructífero, es perfectamente legítimo. Esta es la esencia misma del pensamiento. El deslizamiento inverso podría, por tanto, ser considerado como metacognitivo.

El deslizamiento metadidáctico consiste, para el docente, en cambiar el objeto de su enseñanza de una actividad o de una noción, por uno de sus medios de control. Por ejemplo, el docente de un idioma que sustituye la corrección de un error de sus estudiantes con la enseñanza del enunciado de la regla gramatical que ha sido violada. También esta acción es perfectamente legítima. La desviación teórica es, en ocasiones, indispensable y procura, generalmente, una ganancia de tiempo y de eficacia. También la inmersión en una realización puede tener su interés.

En ocasiones, sin embargo, todo esto puede constituir un cambio de actividad por demás dañino. Los patrones (paterns) de la docencia pierden de vista su proyecto y se olvidan. Nosotros estamos interesados en los deslizamientos que no son el efecto de una falta de habilidad o de un accidente, sino que son el resultado, casi obligatorio, de ciertas condiciones sociales y culturales. Privando a los actores principales de la enseñanza de los medios para rechazar los deslizamientos imposibles de corregir, haciendo estos deslizamientos incoercibles y recursivos.

Este deslizamiento se produce, en particular, cuando el medio es inapropiado o cuando el sistema no puede ni abandonarlo ni rechazarlo, dado que ha sido impuesto por el milieu, por el medio. Es así como la enseñanza de la heurística fue más fácilmente controlada, dado que está subordinada a una comunidad menos vasta y menos dominante que lo que fue el proyecto de la “matemática moderna” o de la “regla del tres”.

Hoy, los medios de control del aprendizaje -los tests- tienden a invadir no sólo el debate sobre la escuela sino también sobre las prácticas escolares. De medio de control de los resultados, se transformaron, en un primer momento, en objetivos, después en medios de enseñanza y por último objeto mismo de enseñanza. Estos tienden a transformar nuestra concepción de conocimiento y de aprendizaje en una especie de preparación a un ‘banal seguimiento’ universal. Se trata por lo tanto, otra vez, de un evidente deslizamiento metadidáctico extremamente potente y peligroso, cuyo estudio hace poco se ha iniciado (sólo 10-12 años). En el sistema escolar, el hecho de controlar un conocimiento lo aísla de su contexto y lo transforma en un “saber a enseñar” que no puede jugar su papel de conocimiento.

5. UN DESLIZAMIENTO BIEN AFINADO

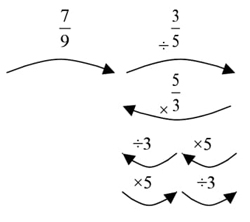
En el curso de una experiencia de enseñanza con estudiantes de 10-11 años,¹⁵ fueron conducidos en el estudio de las fracciones y de los decimales en sus diversas interpretaciones: como medida, como relación, como escalares y por último como aplicaciones lineales racionales. En las clases precedentes, las operaciones y las razones naturales fueron generalmente materializadas a través de flechas:

Su uso se extendió a las fracciones y a sus aplicaciones, que eran construidas matemáticamente en las situaciones que les daban un sentido matemático y un uso independiente de la escritura sagital. Así el símbolo:

representa la función lineal racional de coeficiente 0.75.

Este sistema permite representar fácilmente las composiciones y los inversos de las aplicaciones, que los niños sabían calcular refiriéndose al sentido, y también las ecuaciones dimensionales para la determinación de la unidad. Las flechas permitían, por ejemplo, encontrar el resultado de 79÷35.

o también operar con letras que reemplazaban los números.

Se trata típicamente de un deslizamiento metadidáctico peligroso dado que el interés de la representación sagital se limita tanto al grupo multiplicativo de Q como al semigrupo aditivo, pero no a los dos simultáneamente: esta representación no se hace cargo al mismo tiempo de las adiciones y de los productos de racionales. Es más, concretamente, es el sentido el que controla la validez del grafo y no al contrario. Lo cual nos deja aún más lejos del algebra que se podría, ingenuamente, creer cercana.

Pero en este caso el deslizamiento no ha tenido lugar. Nunca fueron las flechas el objeto de un discurso, de un análisis, de un enunciado, de una regla cualquiera. Los niños nunca fueron interrogados a propósito de su saber acerca de estas flechas. Ellos las usaban cuando esto parecía necesario para acompañar su discurso, su solución etc. El docente se contentaba con rectificar de vez en cuando una representación errónea, pero haciendo referencia a lo que con ésta se estaba representado. Al sentido, no a la representación.

Estos estudiantes se beneficiaron de la facilidad ostensiva que les ofrecían las flechas como un lenguaje privado y nunca recibieron observaciones en el proseguir de sus estudios por parte de sus docentes, como era el caso para algunos con sus métodos de cálculo. Las flechas eran conocimientos, no saberes. La diferencia de estatuto resultaba, por tanto, de aquello que el profesor decía o no decía, comentaba o evitaba de comentar.

Las razones por las cuales los deslizamientos metadidácticos escapan del control de los actores son, en primer lugar, la ausencia de análisis o de específico conocimiento científico en este dominio. En ausencia de una ciencia didáctica, la naturaleza de los fenómenos es ignorada y ciertas soluciones tradicionales inadecuadas causan el empeoramiento de la situación. Sólo los profesionales pueden liberarse de estas soluciones cuando la situación se vuelve absurda. Pero cuando intervienen poderes de regulación externos, su ignorancia los conduce a exigir lo imposible y la situación se degrada sin que nadie pueda hacer nada, ni siquiera entender: fue esto lo que sucedió, de hecho, en el caso de la “matemática moderna”.

6. LOS ABUSOS EN LOS CONTROLES DE EVALUACIÓN

Para reforzar esta declaración, hemos analizado los efectos del uso abusivo de las pruebas de control de la práctica de los docentes y de los resultados de sus estudiantes. Pensamos que una buena explicación de los límites de este sistema y de sus engañosos y decepcionantes efectos, se obtiene mostrando cómo esto disminuye fuertemente las posibilidades del funcionamiento de ciertas formas de conocimiento indispensables para el mejor aprendizaje en beneficio de la adquisición directa de los saberes adquiridos. Ahora bien, la matemática no es producida, pensada o utilizada sin una actividad específica. La adquisición directa se basa en las prácticas de enseñanza, estas mismas fundadas sobre teorías del aprendizaje que ignoran el funcionamiento de la disciplina, y el papel específico de los conocimientos en esta adquisición.

El aprendizaje directo y exclusivo de los saberes matemáticos, por medio de procedimientos formales (la repetición, por ejemplo) conduce a conocimientos que pocos estudiantes pueden poner en juego durante una actividad matemática.

Nosotros fuimos llevados a admitir que una parte de conocimientos (esquemas de acción, de formulación, de argumentos) que no se desarrolla si no en la práctica de actividades auténticamente matemáticas, era indispensable a la práctica y a la adquisición de saberes matemáticos. Fuimos llevados, también, a evidenciar la importancia del papel de la práctica colectiva de matemática, por parte de los estudiantes y de la cultura, que resulta sobre la calidad y la velocidad de los aprendizajes.

7. CONCLUSIONES

Los conocimientos y los saberes forman una pareja de metaconocimientos mutuos. Los conocimientos son los medios implícitos para activar y gestionar los saberes. Los saberes son los instrumentos institucionales y culturales para aprender los conocimientos, los propios y aquellos de los otros. Querer tratarlos de la misma manera, en particular concebir los conocimientos sólo como saberes, constituye deslizamientos metadidácticos permanentes. Cada conocimiento fijado en un saber requiere, para funcionar, nuevos conocimientos que, cuando éstos son de nuevo fijados, no pueden jugar su papel. Resultan errores, malentendidos, fracasos que relanzan exigencias imposibles y prácticas ineficaces. Los conocimientos disponibles en el aula son el capital y sus intereses son los saberes adquiridos. El arte didáctico consiste en distinguir aquello que debe ser dicho de lo que no debe ser dicho. Este arte humano existe desde hace millones de años, implica el juego sutil e incierto de los conocimientos vivos, dudosos, fugaces con los saberes seguros, compartidos, el juego de lo dicho y de lo no dicho.

Antes de pretender “mejorarlo” con medidas sumarias y drásticas, conviene cuanto menos estudiarlo con humildad.