1. INTRODUCCIÓN
Catorce años atrás fue publicado un artículo de gran repercusión en la comunidad internacional de investigadores en Matemática Educativa (ME): Matemática Educativa: una visión de su evolución (Cantoral y Farfán, 2003a, 2003by 2003c). En él se presenta a la ME como una disciplina del conocimiento en la que se pueden encontrar distintas visiones “que buscan cohabitar en pluralidad” (2003a, p. 29) y se describe una evolución de las problemáticas concernientes a los fenómenos didácticos que se suscitan en la enseñanza y aprendizaje de la Matemática, identificando cuatro momentos. El mismo fue escrito con una intencionalidad clara de aportar a la enseñanza: “nos interesa sobremanera esclarecer las condiciones del aprendizaje de ideas complejas en situación escolar con la finalidad de usar dicho conocimiento en la mejora de los procesos educativos” (Cantoral y Farfán, 2003a, p. 29) y es por ello que consideramos puede ser útil para mostrar cómo cambian las propuestas didácticas. En este escrito nos proponemos ejemplificar esos cuatro momentos mediante propuestas que abordan la enseñanza de la trigonometría.
Ya desde su génesis el trabajo tuvo gran aceptación en la comunidad, lo que se evidencia a partir de la aceptación para su publicación casi simultánea en tres prestigiosas revistas: Revista Latinoamericana de Investigación en Matemática Educativa, Revista Educación y Pedagogía y Educational Studies in Mathematics.
Por otra parte, el trabajo ha sido citado en numerosos artículos desarrollados desde la perspectiva de la socioepistemología (Cordero y Flores, 2007; Soto y Cantoral, 2014; Camacho, 2006; Buendía y Montiel, 2011 por citar sólo algunos ejemplos de diferentes revistas o libros) pero también ha tenido repercusión desde otras perspectivas de investigación (Godino, Font, Contreras y Whilhelmi, 2006) e incluso en publicaciones en inglés (Godino, Batanero y Font, 2007). Todo ello demuestra la influencia que el documento tuvo sobre la investigación en el campo.
Pero el mismo Cantoral alude que no es suficiente la sola publicación de un trabajo: “Algunos colegas e instituciones van aún más lejos, al sugerir que la investigación termina sólo cuando el lector entienda el artículo; es decir, que no bastaría con publicarlo, sino que sería necesario además que la audiencia comprendiese su contenido” (2007, p. 312). Nos proponemos en este escrito contribuir con dicho propósito, proveyendo elementos concretos para la comprensión de lo que expresan los autores, en particular en la comunidad de profesores de matemática. Creemos que un acercamiento a diferentes perspectivas didácticas mediante ejemplos concretos de diseños de enseñanza puede enriquecer la mirada del docente: le permite apreciar diferentes modos de abordar un contenido matemático y le ofrece herramientas para reconocer la potencialidad o flaqueza de cada uno de ellos.
Entendemos que de esta manera contribuiríamos, por un lado, a estrechar los vínculos entre investigación y práctica docente, objetivo que la mayoría de los actores involucrados en la enseñanza de la matemática persiguen. Por otro lado, consideramos que este trabajo puede favorecer lo que Shulman (2005) denomina conocimiento didáctico del contenido, uno de los conocimientos bases en la formación del profesor.
2.CUATRO MOMENTOS EN LA EVOLUCIÓN DE LA ME
En Cantoral y Farfán (2003a) se proponen cuatro momentos en la evolución de la matemática educativa como disciplina científica. Los autores se refieren al primero, una didáctica sin alumnos, que se ocupa de la problemática clásica: diseñar presentaciones del contenido matemático escolar más accesibles para estudiantes y profesores, pero sin tomar en cuenta los aspectos cognitivos o afectivos del alumno, así como tampoco su realidad sociocultural. Además, no es sensible al desarrollo histórico de los contendidos a enseñar. Cantoral y Farfán (2003a) afirman que investigaciones de naturaleza cognitiva demostraron que estos enfoques resultan insuficientes para explicar los fenómenos vinculados al aprendizaje y enseñanza de la matemática, precisamente por no considerar al aprendizaje del alumno como factor central para el diseño curricular, así como tampoco al pensamiento del profesor, que incide en la manera en que conduce los procesos de negociación de significados con los alumnos.
El segundo momento que los autores mencionan, una didáctica sin escuela, se caracteriza por considerar los procesos cognitivos de los estudiantes. Mediante la búsqueda de respuestas a preguntas relativas sobre cómo aprenden matemática las personas, se pretende dar pautas para los principios que subyacen al diseño curricular. Los trabajos de investigadores como D. Tall y S. Vinner sobre la imagen conceptual y definición conceptual son característicos de este momento por centrarse en la manera en que aprenden los individuos los objetos matemáticos; sitúan la problemática de estudio en aspectos cognitivos y psicológicos principalmente. Tall y Vinner (1981) es uno de los trabajos utilizados por Cantoral y Farfán (2003) para ilustrar el momento. Los mismos pretenden explicar por qué un estudiante da respuestas contradictorias frente a una misma situación presentada en contextos diferentes. Pero Cantoral y Farfán (2003a) señalan que la sola consideración de la dimensión cognitiva es insuficiente para explicar los fenómenos didácticos, dado que “la vida en las instituciones matiza los procesos del pensamiento” (p. 33). Es decir que para entender la manera en que los estudiantes aprenden, además de considerar el plano cognitivo es necesario tener en cuenta las relaciones que los estudiantes establecen con los saberes matemáticos, mediadas por las representaciones de lo que es la actividad matemática, su aprendizaje y el propio status de alumno. Estas condicionantes son, a su vez, mediadas por la institución de referencia.
El tercer momento, una didáctica en la escuela pero sin escenarios, se caracteriza por su abordaje sistémico: se tienen en cuenta los vínculos entre alumno, maestro y saber, en el seno de una determinada institución. Esta perspectiva de investigación nuclea los trabajos de la denominada Didáctica Francesa, en su mayoría inspirados de alguna u otra manera por los estudios de G.Brousseau. Brousseau (1986) es un ejemplo de ellos. Esta perspectiva aborda la construcción del conocimiento que vive en instituciones, entendida en su más amplio sentido. Ello incluye la consideración de las condiciones en las que surge un conocimiento, lo que a su vez da fundamento para la elaboración de secuencias didácticas. Sin embargo, a partir de investigaciones propias Cantoral y Farfán (2003a) concluyen que puede que no sea conveniente recrear en el aula los mismos contextos que dieron origen al conocimiento, por considerarlos más complejos que el conocimiento que se desea introducir. Ello los condujo a la consideración de aspectos sociales en sus investigaciones, lo que derivó, a su vez, en una resignificación de las restantes dimensiones. En particular, en la dimensión epistemológica se propone poner el foco en las prácticas que dieron origen al conocimiento matemático y no solamente en los conceptos en sí. “No mirar los conceptos y sus diferentes estructuraciones conceptuales en forma aislada, sino tratar con las prácticas que producen o favorecen la necesidad de tales conceptos” (Cantoral y Farfán, 2003a, p. 36).
Es desde esta búsqueda que surge lo que Cantoral y Farfán (2003a) identifican como un cuarto momento: una didáctica en escenarios socioculturales. El mismo se caracteriza por considerar a la matemática como una actividad humana construida socialmente, atiende a los contextos socioculturales en los que surgen los contenidos matemáticos y pone el foco en las prácticas que norman la construcción y difusión de tales conocimientos.
En este artículo proponemos cuatro planificaciones, sobre una misma temática, que podrían corresponderse con esos cuatro momentos, si las pensamos como diseñadas por profesores que utilizan para su planificación insumos de la investigación en ME correspondientes a cada uno de tales momentos. Entendemos que la investigación no siempre brinda diseños específicos de secuencias didácticas ya que no es ese su único objetivo. Schoenfeld (2000) identifica, además del propósito aplicado de la investigación en educación matemática, relativo a mejorar la instrucción matemática, un propósito puro: “Comprender la naturaleza del pensamiento matemático, la enseñanza y el aprendizaje” (p.641). Aún así podemos plantear una especie de “ejercicio” en el que nos imaginamos a cuatro profesores hipotéticos que planifican su clase basándose en aportes de la investigación en ME, cada uno desde una perspectiva diferente.
3.CONTEXTO PARA LA EJEMPLIFICACIÓN
Para ilustrar los cuatro “momentos” en la evolución de la ME identificados por Cantoral y Farfán (2003a), seleccionamos el contenido “Funciones trigonométricas”, para ser enseñado a estudiantes de 15-16 años de edad (nivel 10). En particular nos centraremos en la introducción de la función seno.
Generalmente la trigonometría, como contenido en los currículos escolares, es abordado por primera vez en el nivel anterior (nivel 9, tercero de educación media). En ese curso se abordan las relaciones trigonométricas en el triángulo rectángulo. A modo de ejemplo, el programa uruguayo para ese nivel indica que “El estudio se limitará a las relaciones seno, coseno y tangente de un ángulo agudo, las que serán aplicadas en ejercicios de cálculo de medidas de segmentos y ángulos. Las aplicaciones se referirán a resolución de problemas de convergencia disciplinar.” (ANEP, CES, 2010a).
En el siguiente nivel del mismo plan de estudios se abordan las funciones angulares seno, coseno y tangente, el teorema del seno y coseno, y su aplicación para el cálculo de distancias y áreas.
Se sugiere comenzar el estudio de este tema con medidas de ángulos en grados sexagesimales y centesimales y radianes. En el estudio de estas funciones se determinará dominio, recorrido, ceros, signos y periodicidad… Es necesario insistir en problemas de aplicación al cálculo de distancias, áreas, en figuras planas y en el espacio, y temas relacionados con ciencias y tecnología. (ANEP, CES, 2010b, p. 3)
A juzgar por libros de textos de otros países, consideramos que este abordaje es el que tradicionalmente se presenta en otros contextos: comenzar con el estudio de relaciones trigonométricas en el triángulo rectángulo y en una segunda instancia, ampliar el dominio de las funciones angulares.
4.PLANIFICACIONES DE CLASE
Presentamos a continuación las planificaciones propuestas para ejemplificar cada uno de los momentos. En ellas se detallan los objetivos que el profesor se plantearía, además del desarrollo previsto de la clase, las actividades y su análisis a priori. Entendemos que todos esos elementos pueden dar cuenta de la perspectiva desde la cual se toman insumos de la planificación. Luego de cada propuesta, presentamos un análisis en el que fundamentamos por qué consideramos que la misma se encuadra en el momento correspondiente.
4.1.1 Propuesta didáctica
Tiempo estimado: Una clase de 45 minutos
Objetivos:
Conceptos previos:
Relaciones trigonométricas en un triángulo rectángulo.
Esquema de clase y desarrollo de actividades:
Se comenzará la clase presentando el círculo trigonométrico en el pizarrón, con un punto sobre la circunferencia representado en el primer cuadrante. Se preguntará cómo calcular la segunda coordenada de dicho punto, esperando que representen un triángulo rectángulo y utilicen lo aprendido en el curso anterior. Luego se extenderá lo trabajado en el primer cuadrante para puntos en el segundo cuadrante.

Posteriormente se les entregará la siguiente actividad:
Completa el siguiente cuadro:
Luego se representarán en el pizarrón los valores de seno calculados y se extenderá lo obtenido a valores mayores a 180° y negativos. Se espera mediante la puesta en común llegar a la siguiente representación gráfica:

4.1.2 Análisis de la propuesta
Según Cantoral y Farfán (2003a), la perspectiva clásica en ME se preocupaba por diseñar presentaciones de los contenidos “más accesible para los alumnos y para los profesores que aquellas otras presentaciones llamadas tradicionales” y asumía que ello podría ser logrado “sólo con la reflexión del profesional de la matemática” (p.29). Así, se elaboraron materiales para el trabajo de aula “sin tomar en consideración sistemáticamente otros factores como aquellos de naturaleza cognitiva o afectiva, o bien los relativos a las cuestiones socioculturales del conocimiento” (p. 29).
En este sentido, consideramos que la secuencia que proponemos podría ejemplificar esta situación. Apreciamos un interés por mostrar el contenido en forma secuenciada, de menor a mayor nivel de complejidad teniendo en cuenta la estructura del conocimiento matemático construido en ámbitos académicos. Por otra parte, es el docente quien debe manejar “el arte” de la docencia; el éxito de la actividad queda condicionado a sus habilidades, sin un marco intradidáctico que justifique las decisiones tomadas: no se dan herramientas ni un marco de discusión apropiados para que sean los estudiantes quienes validan las respuestas. El rol del estudiante queda reducido a la ejecución de una actividad elaborada por el docente, que no se origina en sus necesidades de aprendizaje.
No se toma en cuenta la evolución histórica del concepto a enseñar, lo que puede evidenciarse, por ejemplo, en el hecho de trabajar con grados y no con radianes. Tampoco son considerados los conflictos cognitivos relativos al concepto de función que se pueden suscitar en la transición de la representación del punto en el círculo trigonométrico a la representación gráfica de la función seno. La actividad y la implementación propuesta no promueven su explicitación.
4.2.1 Propuesta didáctica
Tema: Trigonometría
Subtema: Función seno
Tiempo estimado: Un módulo de 90 minutos
Objetivo: Ampliar la imagen conceptual relativa al seno, otorgando significado al seno de ángulos fuera del intervalo [0,90] (medidos en grados sexagesimales).
Conceptos previos:
Relaciones trigonométricas en un triángulo rectángulo
Esquema de clase y desarrollo de actividades:
Al comenzar la clase se planteará la siguiente actividad, para resolver individualmente, con el fin de activar los conceptos previos de los estudiantes.
Durante la puesta en común se pondrán de manifiesto los conocimientos previos. En caso de que estos no sean los mismos para todos los estudiantes, por medio de la resolución grupal del problema, se espera que todos recuerden lo trabajado el año anterior.
Luego se pasará a la Actividad 2, en la que se pretende crear un conflicto entre los conocimientos previos y lo que se les presenta. La actividad se realizará en parejas y luego se discutirá grupalmente.
Esperamos que encuentren dificultad al buscar un problema para las partes b y c dado que en cursos anteriores se trabajaron las relaciones trigonométricas exclusivamente en el triángulo rectángulo. Durante la puesta en común se escuchará a los estudiantes, dejándolos debatir entre ellos, sin intervención del docente. Luego se les presentarán las partes a y b de la actividad 3, podrán trabajar en grupos de hasta 4 integrantes para fomentar la discusión y la argumentación por parte de los estudiantes. La parte c se realizará colaborativamente entre toda la clase, luego de la puesta en común de las partes anteriores.
Actividad 3:
En un parque de diversiones hay una rueda gigante de 1 decámetro de radio. Tarda un minuto en dar una vuelta completa y comienza su recorrido en la plataforma que aparece en el dibujo. Un niño se queda en la plataforma esperando a su hermana que estaba en el juego. Al ángulo de vértice el centro de la rueda y cuyos lados pasan, respectivamente, por la plataforma y el punto en que se encuentra la hermana, lo llamaremos α. Desde la perspectiva del niño en la plataforma,
¿A qué altura se encuentra su hermana a los 15 segundos de comenzar el juego?
Completa la siguiente tabla:

| Tiempo transcurrido (en segundos) | Altura a la que se encuentra la niña (en decámetros) |
| 15 | |
| 30 | |
| 45 | |
| 60 | |
| 5 | |
| 20 | |
| 35 | |
| 50 |
c- Bosqueja la gráfica que relaciona el ángulo recorrido por la rueda con la altura de la niña desde la plataforma.
Durante la realización de las primeras partes de la actividad, los estudiantes podrán utilizar los conceptos previos que poseen, y darle un nuevo significado al seno del ángulo, ya que lo utilizarán como herramienta para calcular la altura de la niña respecto a la plataforma.
Luego de comentar los resultados obtenidos en las primeras partes, se intentará realizar la gráfica de la función obtenida con los datos encontrados.
| Tiempo transcurrido (en segundos) | α (en grados) | Altura a la que se encuentra la niña (en decámetros) |
| 15 | 90° | 1 |
| 30 | 180° | 0 |
| 45 | 270° | -1 |
| 60 | 360° | 0 |
| 5 | 30° | 0.5 |
| 20 | 120° | 0.866 |
| 35 | 210° | -0.5 |
| 50 | 300° | -0.866 |

Posibles preguntas:
¿Dónde se encuentra la niña a los 15 segundos? ¿Cuánto mide el ángulo con vértice en la rueda gigante y cuyos lados pasan por el punto en el que se encuentra la niña y por la plataforma?
Cuando pase un minuto y medio, ¿en dónde va a estar la niña?
Si volvemos a la actividad anterior, ¿podrían ahora crear un problema para la parte c?
¿Y para la parte b? ¿Tendrá sentido hablar de ángulo de medida negativa? Luego que tenemos colocados los puntos en el gráfico, se pregunta: ¿Podremos realizar un trazo continuo?
Si la niña estuvo en la rueda durante 3 minutos, ¿qué valores de α se habrían considerado?
Luego de graficar la situación del problema, el profesor será el encargado de extender la función obtenida al caso en el que el dominio es el conjunto de números reales con preguntas como:
Si consideramos el caso irreal en el que la niña está en la rueda gigante durante un tiempo infinito, ¿cuándo volverá a estar a un decámetro de la plataforma?
Y si el ángulo de giro fuera negativo, es decir si gira para el otro lado, ¿a qué altura de la plataforma se encontrará la niña al minuto de comenzado el juego? ¿y a los treinta segundos?
Finalmente se llamará a la nueva función, obtenida durante la puesta en común, como función seno de dominio real.
Después de finalizada la puesta en común de la actividad 3, puede volverse a la actividad 2 para discutir qué respuestas darían ahora a esa situación que antes había resultado novedosa.
4.2.2 Análisis de la propuesta
Esta secuencia está enmarcada en lo que Cantoral y Farfán (2003a) denominan didáctica sin escuela, con un énfasis marcado en los aspectos cognitivos del aprendizaje de la Matemática. En particular utilizamos los aportes de Tall y Vinner (1981). Ellos consideran dos ‘celdas’ referidas a las representaciones que un estudiante puede tener sobre un concepto: la imagen conceptual -fotos mentales, procesos y propiedades asociadas al concepto y que conforman su estructura cognitiva-, y la definición formal -conjunto de palabras utilizado para describir el concepto-. Los autores nos advierten sobre la posibilidad de que se generen conflictos cognitivos entre diferentes partes de la imagen conceptual o entre la imagen conceptual y la definición. Puede que esos conflictos convivan en un estudiante sin ser percibidos, o también pueden hacerse explícitos al evocarse esas partes contradictorias simultáneamente. Los autores afirman que estos conflictos cognitivos pueden impedir seriamente el desarrollo de la teoría formal en la mente del estudiante.
Mediante la planificación propuesta procuramos enriquecer la imagen conceptual de los estudiantes del concepto de seno. Con la primera actividad pretendemos que los estudiantes evoquen la imagen conceptual que tienen; posteriormente intentamos dejar en evidencia las limitaciones de dicha imagen, ya que no les permite realizar lo solicitado en la segunda actividad.
Finalmente, en la tercera actividad esperamos que los estudiantes puedan ampliar la imagen conceptual que poseen sobre el seno. La nueva estructura creada permitirá ver al seno como una función y ya no como algo estático, permitiéndole “rellenar los casilleros” necesarios para resolver los conflictos creados en la segunda actividad; es decir, asimilar y acomodar los nuevos conocimientos para ampliar los esquemas.
4.3.1 Propuesta didáctica
Tema: Trigonometría
Subtema: Función seno
Tiempo estimado: Un módulo de 90 minutos
Objetivos:
Analizar la variación del área de figuras de que poseen el mismo perímetro.
Construir la noción de función seno para ángulos entre 0° y 180°.
Conceptos previos:
Relación entre los lados de triángulos de ángulos: (30°, 60°, 90°) y (45°, 45°, 90°)
Teorema de Pitágoras
Esquema de clase y desarrollo de actividades:
Al comenzar la clase se les presenta a los alumnos un cuadrado formado por cuatro tiras de cartón de igual longitud, unidos por broches mariposa. Se deforma, creando un cuadrilátero “parecido” a un cuadrado.

Luego se les presentará el siguiente problema:
¿Qué información es necesaria para determinar el área del cuadrilátero además de las medidas de las longitudes de sus lados?
Si bien se espera que los estudiantes busquen sus propias estrategias para resolver el problema, a continuación se presentan preguntas que pueden surgir en la discusión o que el docente podrá hacer en caso de resultar necesario.
¿Qué tipo de cuadrilátero es el segundo?
Iniciando con esta pregunta un debate sobre la segunda forma, pueden establecer que es un paralelogramo, específicamente un rombo.
¿El rombo tiene área constante?
Es posible que algunos estudiantes respondan que “el área no cambia ya que los lados no cambian”. En ese caso se mostrarán distintas formas hasta llegar a una que tenga área nula.
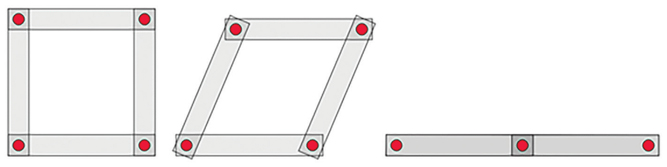
No se espera que los estudiantes recuerden de forma inmediata la fórmula del área del paralelogramo o del rombo, pero esperamos que puedan concluir que no depende solamente de la medida de los lados.
Para ello, en caso de ser necesario se puede trabajar sobre las siguientes figuras:

Se puede observar que, en la primera figura, en la que por compensación se puede deducir que los cuadriláteros ABCD y AB’C’D tienen igual área, la medida de la longitud del segmento DC es menor que la del segmento DC´. Consecuentemente, lo que muestra la segunda figura es que si los lados DC y DC’ son de igual medida, la altura del segundo cuadrilátero es menor al original y de ahí que las áreas ya no sean iguales.
Siguiendo con la idea de compensar se pueden determinar dos triángulos, siendo uno la traslación del otro. El área del paralelogramo en ese caso se determinaría multiplicando la medida de la longitud del lado por la medida de la altura, lo que se explica mediante el siguiente razonamiento.
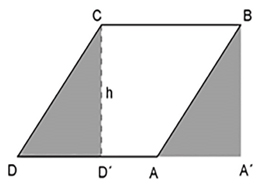
Las áreas de ABCD y A´BCD´ son iguales, y la de este último es igual al producto entre en lado y la altura.
Luego de la puesta en común de los resultados obtenidos consideraremos la variación completa para poder relacionar el área del rombo con el ángulo formado.

Se podría hacer un gráfico que represente la variación del área para un cuadrilátero de lado fijo. ¿Qué podemos elegir como variable independiente? Ante esta pregunta los estudiantes podrán investigar sobre cuál de las variables les conviene utilizar; la altura, o la diagonal son posibles respuestas. Se establecerá que la longitud del lado es 1.
La variación del área será la misma que la variación de la altura (Área=1*h). Finalmente se espera que identifiquen que la altura depende del ángulo formado.
Realicen un gráfico de la variación de la altura en función del ángulo.
Se espera que los estudiantes reconozcan al menos tres puntos. El máximo es 1 para 90° y el mínimo es 0 para 0° y 180°. Ante esto los estudiantes pueden sugerir diversos gráficos, como, a modo de ejemplo, los siguientes:

Analizaremos los gráficos presentados y se les preguntará:
¿Cuánto mide la altura del cuadrilátero si el ángulo formado por dos lados de este es de 45°? ¿Y si es de 135°?
Se espera llegar al menos a que la atura es mayor a ½, pudiendo descartar las dos
primeras gráficas. Puede que algunos estudiantes visualicen el triángulo
rectángulo e isósceles que se forma al interior del cuadrilátero, con catetos de
medida

¿Cuánto mide la altura si el ángulo formado es de 30°? ¿Para qué otro ángulo se obtiene la misma medida para la altura?
Nuevamente se apela a triángulos ya conocidos por los estudiantes. Concluirán que la altura mide 0.5.
¿Cuánto mide la altura si el ángulo formado es de 60°? ¿Para qué otro ángulo se obtiene la misma medida para la altura?
Al finalizar, contaremos con 9 puntos, con los que construiremos nuestra nueva gráfica.
Es probable que algunos estudiantes supongan que el gráfico corresponde a una parábola, si es así se les pedirá que encuentren una expresión algebraica para una parábola que pasa por los puntos (0,0), (180,0) y (90,1), y luego establezcan si el punto (30; 0,5) pertenece a esa parábola.
Para terminar, el docente institucionalizará el nuevo conocimiento dándole el nombre a la función obtenida como: función seno del ángulo.
4.3.2 Análisis de la propuesta
Esta secuencia se enmarca en la didáctica francesa. Ella, así como algunos aspectos considerados en el análisis de la misma, han sido tomados de Berté (1999). Desde esta perspectiva se entiende a los fenómenos de enseñanza-aprendizaje como sistémicos, es decir teniéndose en cuenta los vínculos entre alumno, maestro y conocimiento. Desde este marco es que Brousseau (1986) define la situación didáctica. Según Gutiérrez (1999) una situación didáctica es “un conjunto de relaciones explicita y/o implícitamente establecidos entre un alumno o un grupo de alumnos, algún entorno (incluyendo instrumentos o materiales) y el profesor con un fin de permitir a los alumnos aprender, es decir reconstruir, algún conocimiento” (p. 133). Según esta perspectiva las situaciones didácticas presentan problemas que sólo pueden ser resueltos en la medida en que se construye el nuevo conocimiento.
Creemos que estamos ante una situación didáctica ya que presentamos un problema que sólo podrá ser resuelto en la medida que se construya el concepto de función seno. El docente es el encargado de plantear el problema, pero no interviene en su resolución. Finalmente es quien institucionalizará el nuevo conocimiento construido por los estudiantes.
El material concreto utilizado permite que los obstáculos a los que se van enfrentando los estudiantes puedan ser resueltos por ellos mismos. No es el docente quien determina si la respuesta que se da es correcta o no, sino el propio estudiante en la interacción con el material y la discusión entre pares.
4.4.1 Propuesta didáctica
Tema: Trigonometría
Subtema: Función seno
Tiempo estimado: Un módulo de 90 minutos
Objetivos:
Conceptos previos:
Esquema de clase y desarrollo de actividades:
Al comenzar la clase se organizará a los estudiantes en grupos de a tres y se les dará la siguiente actividad para realizar.
Durante la puesta en común se discutirá lo que hicieron los distintos grupos. Se registrará en el pizarrón las distintas posiciones posibles entre Andrés, Carlos y la fuente que surjan. Se espera encontrar las siguientes:

Luego se discutirá la parte b. Se espera que hallen sin mayor dificultad la distancia entre Andrés y Carlos en el caso en que están alineados y en el caso en el que entre Andrés, la fuente y Carlos se forma un ángulo recto (usando el Teorema de Pitágoras). No se espera que logren hallar la distancia en los casos restantes.
Se les preguntará luego si al menos pueden comparar las distancias de los casos en que no pudieron calcularla. Con esto se espera que noten que dicha distancia depende del ángulo con vértice en la fuente y cuyos lados pasan por Andrés y Carlos.
Al terminar se les dará la siguiente actividad para realizar en los mismos grupos y luego discutir entre todos.
Luego de realizada la actividad se hará una puesta en común. Se espera que los estudiantes calculen lo que se les pidió utilizando proporcionalidad directa.
Después se les entregará una última actividad para realizar en los mismos grupos.
Luego de realizada la actividad, se pondrán en común los procedimientos de cada equipo y las conclusiones a las que arribaron. Finalmente, el docente puede indicar que la función establecida es la función seno.
4.4.2 Análisis de la propuesta
La secuencia presentada se enmarca en la perspectiva socioepistemológica. Desde esta perspectiva se hace énfasis en la matemática como actividad humana, prestándole mayor atención a la evolución histórica de los conocimientos y los contextos y prácticas que impulsaron su desarrollo.
Algunas de estas actividades, así como ciertos aspectos considerados en su análisis, han sido tomadas de Montiel (2013). A continuación desarrollamos brevemente determinados puntos que consideramos importantes a la hora de plantear esta secuencia.
Jácome y Montiel (2007) plantean que:
…para que el alumno no solamente aprenda la noción de razón trigonométrica, sino que la construya y la aplique en casos reales, invitándolo a comprender que su estudio se debe a una necesidad social de conocer distancias y mediar ángulos, y no a un ente que debe ser aprendido porque está anclado en un programa (p. 430).
De acuerdo a estas investigaciones, se destaca la importancia de que las actividades estén orientadas a la construcción de la función trigonométrica a partir del estudio de la variación y el cambio, con el objetivo de utilizar y resignificar la periodicidad y la acotación de esta función por medio de problemas contextualizados, en particular poniendo a los estudiantes en la situación de predecir posiciones futuras de un objeto que se mueve. Es esa la práctica social que norma la construcción del concepto de función trigonométrica.
Otro aspecto importante a tener en cuenta es la utilización de radianes, lo que responde al estudio socioepistemológico llevado a cabo por la autora. Montiel (2005) identifica las prácticas y contextos en los que se construye y desarrolla el saber relativo a las funciones trigonométricas, detectando que es en la astronomía primero, y en el estudio del movimiento en general más adelante, que se desarrolla dicho saber. En estos contextos lo que interesa es conocer la relación entre la medida de la trayectoria del móvil y el radio de la circunferencia que recorre, como en la secuencia que proponemos. De ahí que el radián sea la unidad más conveniente a considerar. En el discurso matemático escolar se ha despojado al saber de las circunstancias que le dieron origen, considerando al grado como unidad angular, dada su simplicidad para realizar cálculos. La autora propone que se trabaje con radianes para respetar la génesis de los conceptos y con ello dotarlos de significado.
Al respecto Montiel (2005) en su tesis concluye:
La dimensión social que hemos incorporado al estudio de la enseñanza-aprendizaje de la función trigonométrica ha afectado a las componentes epistemológica, didáctica y cognitiva que aportaron otras investigaciones, pero más importante que esto fue el hecho de que se modificó su relación sistémica para explicar los fenómenos de su construcción en escenarios escolares. Documentamos que en la escuela se trata a la función trigonométrica como una extensión de las razones y que su única explicación sobre la unidad de medida radica en la equivalencia entre grados y radianes en el círculo trigonométrico. Con esto se despoja de los usos y significados que dan origen a la función trigonométrica, pero más importante, se pierde el vínculo con algunas prácticas de referencia que viven escolarmente en otras asignaturas, como aquella del estudio del movimiento (circular uniforme) en la física (p. 124).
5. CONSIDERACIONES FINALES
En este trabajo hemos abordado el desafío de estrechar vínculos entre los dos propósitos principales de la investigación en Educación Matemática: por un lado, comprender la naturaleza del pensamiento matemático, de su enseñanza y de su aprendizaje, y, por otro, aplicar esa comprensión para mejorar ambos procesos, enseñanza y aprendizaje (Schoenfeld, 2000).
Tomando como referencia básica un documento de gran repercusión en el campo (Cantoral y Farfán, 2003a, 2003b y 2003c), hemos brindado un ejemplo de cómo podría planificarse un tema para su enseñanza, tomando aportes de la investigación de cada uno de los “momentos” detectados en el mismo. Consideramos que este tipo de ejercicio aporta al conocimiento didáctico del contenido, no sólo porque se proponen ideas concretas para la enseñanza sino principalmente porque dichas ideas están sustentadas en investigaciones del campo de la ME.
Confiamos en que este escrito represente un aporte a la comunidad, tanto en el ámbito de la investigación como para quienes se desempeñan en el ámbito de la enseñanza.
El aporte a la investigación consiste en robustecer mediante ejemplos una caracterización realizada de la evolución de la ME. La misma considera como hilo conductor la ampliación de los objetos y métodos de estudio; en este escrito se han ido ilustrando esas ampliaciones mediante planificaciones sobre una temática concreta, en un curso concreto.
En cuanto al ámbito de la enseñanza, esperamos que este trabajo contribuya a mostrar el potencial que tiene tomar aportes de la investigación para diseñar tareas para el aula. En este sentido el trabajo ofrece al docente ejemplos concretos sobre cómo plasmar en una clase aportes de cada una de las diferentes perspectivas mencionadas en Cantoral y Farfán (2003a). Asimismo, esperamos que los profesores puedan apreciar las diferentes repercusiones de tomar en cuenta una u otra perspectiva, especialmente en el tipo de actividad matemática que promueven en el aula cada una de las propuestas didácticas. El escrito pone de relieve las consecuencias de la consideración, o no, de cada una de las componentes del sistema didáctico: los estudiantes, los profesores, el saber y el contexto sociocultural en el que se inscribe dicho sistema.
Invitamos a nuestros colegas, profesores e investigadores, a continuar reflexionando sobre los vínculos entre el ámbito de la investigación en ME y el de la práctica docente y cómo reforzarlos.











 nueva página del texto (beta)
nueva página del texto (beta)





