INTRODUCCIÓN
Un dicho popular mexicano señala que “del dicho al hecho hay mucho trecho”; parafraseando esto, se plantea aquí que del ejercicio convencional al problema de modelaje matemático hay mucho trecho.
El presente artículo muestra que los problemas convencionales difieren de los de modelaje matemático en nueve aspectos (Green y Emerson, 2010). Estos aspectos son utilizados como criterios de evaluación para analizar los problemas encontrados en una muestra de libros de texto de Cálculo a nivel medio superior (alumnos de 16 a 18 años) y superior o universitario (de 18 a 21 años), para posteriormente categorizarlos como problemas convencionales (en adelante PC) o como problemas de modelaje matemático (en adelante PM).
En general, los PC son estructurados en su planteamiento y cerrados en su solución y procedimientos. Involucran contextos matemáticos familiares y son similares a los que se encuentran en clase “para ejercitar la utilización de métodos particulares” (International Association for the Evaluation of Educational Achievement, IEA, 2011: 42). En cambio, los PM no muestran en su planteamiento toda la información necesaria para solucionarlos, y permiten acceder a múltiples soluciones a través de diversos caminos. Además, están enmarcados en situaciones de la vida real, por lo que el alumno requiere “aplicar procedimientos matemáticos en contextos poco conocidos o complejos” (IEA, 2011: 43). En la educación matemática, un PM involucra la representación de la realidad por medio de un modelo matemático.
Por sus características, ambos tipos de problemas difieren en las habilidades matemáticas que se ponen en práctica al enfrentarse a ellos. Las habilidades necesarias para resolver los PC son, generalmente, limitadas o permanecen en un nivel elemental. Aunque esta clase de problemas son apropiados para practicar los procedimientos vistos en clase, no son los más adecuados para desarrollar algunas de las competencias matemáticas necesarias en la actualidad. Los PM tienen mayor complejidad cognitiva y favorecen la relación de dos o más conceptos, el paso de una representación matemática a otra o la implementación de varios procedimientos, por tanto, “representan un resultado valioso de la educación en matemáticas” (IEA, 2011: 44). Este estudio plantea la importancia de investigar a qué tipo de problemas matemáticos están expuestos los estudiantes de Cálculo (PC o PM), analizando los contenidos que plantea una muestra de libros de texto.
El objetivo de este estudio es responder:
¿Qué proporción de los ejemplos y ejercicios planteados en los libros de texto de Cálculo se clasifican como problemas de modelaje matemático y cuántos como problemas convencionales?
¿A cuáles de los criterios o aspectos de los problemas de modelaje matemático (Green y Emerson, 2010) dan mayor énfasis los autores de los libros de texto de Cálculo?
Los resultados obtenidos buscan brindar un panorama general acerca de la ausencia o presencia de los PM en los libros de texto, así como sobre el enfoque que dan los autores a sus ejemplos y ejercicios. Aunque el estudio fue realizado en libros de texto de Cálculo, se espera que los criterios de análisis puedan ser de utilidad para apoyar la evaluación y selección de libros en otras disciplinas donde la resolución de problemas sea una de las principales herramientas de aprendizaje.
DIFERENCIACIÓN ENTRE PROBLEMAS CONVENCIONALES Y PROBLEMAS DE MODELAJE MATEMÁTICO
Cuando los jóvenes finalizan su educación media superior, es de esperarse que no solamente cuenten con los conocimientos matemáticos suficientes para acreditar sus cursos, sino que también sean capaces de utilizarlos para resolver los problemas que pudieran encontrar fuera del entorno escolar (Organización para la Cooperación y el Desarrollo Económicos, OCDE, 2013; Secretaría de Educación Pública, SEP, 2008). La mayoría de las veces este tipo de problemas diferirá de aquellos vistos en el salón de clases, pues estarán situados en un contexto real, no serán planteados de manera directa y permitirán una mayor variedad de aproximaciones y soluciones (IEA, 2011; SEP, 2013). Estas y otras características son reunidas por los PM.
Los PM son problemas abiertos y complejos donde se pueden poner en juego conocimientos previos y habilidades creativas para proponer hipótesis y establecer modelos que logren explicar matemáticamente cómo se comporta un fenómeno (Trigueros, 2006). Al mismo tiempo, promueven la unión de las matemáticas escolares con la realidad de los alumnos (Quiroz y Rodríguez, 2015), o con otras áreas del conocimiento. Al utilizarse en la enseñanza, la modelación matemática refuerza los conocimientos sobre conceptos matemáticos (Muro, Camarena y Flores, 2007), despierta el interés de los estudiantes por las matemáticas frente a su aplicabilidad y estimula la creatividad en la formulación y resolución de problemas (Biembengut, 2006).
Como marco teórico se utiliza la propuesta de Green y Emerson (2010), quienes aportan criterios interesantes para diferenciar los PM de los PC. Los nueve aspectos que proponen pueden dividirse en dos temas: por el planteamiento del problema y por la solución del mismo.
Por el planteamiento del problema
En este tema se encuentran los aspectos: (1) Naturaleza de la evidencia disponible en el planteamiento, (2) Conexión del planteamiento con los procedimientos matemáticos, (3) Tipo de supuestos necesarios y (4) Complejidad del problema.
Con respecto a los primeros tres aspectos, los PC son estructurados en su planteamiento porque presentan toda la información necesaria para su solución, desde las variables implicadas en el problema hasta el procedimiento matemático que debe elaborarse. Por lo anterior, el alumno no requiere introducir nuevas variables ni elaborar una gran cantidad de supuestos y, en caso de realizarlos, estos son de naturaleza matemática. En ocasiones el mismo planteamiento guía al estudiante hacia el procedimiento apropiado; por ejemplo, palabras como “en total” o “ganó” pudieran ser pistas verbales de que debe efectuarse una suma (Nesher y Teubal, 1975). Los estudiantes pueden resolver correctamente problemas rutinarios haciendo uso de estrategias sencillas de memorización; pueden seleccionar y utilizar correctamente los algoritmos y llegar a una solución correcta, aun careciendo de un conocimiento conceptual sólido sobre los conceptos matemáticos (Finney, 2003). Incluso, es común que los alumnos sigan estrategias de solución superficiales, tomando únicamente los números que aparecen en el planteamiento y efectuando cálculos que les son familiares (Blum y Borromeo, 2009).
Los PM son poco estructurados porque pueden no presentar toda la información necesaria para su solución ni dejar en claro el procedimiento matemático que debe realizarse. Es así como el solucionador requiere establecer supuestos matemáticos y supuestos sobre el contexto del problema, poniendo en juego habilidades matemáticas superiores como razonamiento, creatividad, pensamiento divergente, comunicación y la capacidad para plantear problemas (Mevarech y Kramarski, 2014).
En cuanto al cuarto aspecto, la complejidad del PC depende del número de procedimientos matemáticos involucrados para su solución, y dichos procedimientos ocurren únicamente en el dominio matemático, mientras que el PM adquiere su complejidad porque el proceso de solución ocurre entre el dominio matemático y el dominio real. La interacción entre ambos dominios (Niss,Blum y Galbraith, 2007) y el proceso de modelaje matemático se observa en la Figura 1.
Para resolver PC, los estudiantes deben ser capaces de reconocer las técnicas matemáticas que los llevarán a un resultado, hacer cálculos matemáticos básicos y establecer relaciones sencillas entre conceptos. Para resolver PM, el alumno deberá ser capaz de: especificar cuál es el problema (construcción), identificar la información relevante para resolverlo y establecer supuestos cuando no cuente con información suficiente (simplificación y estructuración), representar el problema matemáticamente construyendo un modelo (matematización), manipularlo en términos matemáticos para llegar a una solución (trabajo matemático), dar sentido a los resultados de acuerdo con el contexto (interpretación), evaluarlos (validación) y comunicarlos adecuadamente para poder tomar decisiones (exposición). Estas actividades conforman el proceso de modelaje matemático (Blum y Leiß, 2007) y se muestran también en la Figura 1.
Por la solución del problema
En este tema se encuentran los aspectos: (5) Singularidad de la respuesta, (6) Evaluación, (7) Robustez, (8) Transferencia de las técnicas utilizadas y (9) Tipo de revisión.
El quinto aspecto indica que los PC pueden ser resueltos con un número limitado de métodos que, si son aplicados correctamente, llevan a un único resultado correcto. En contraste, los PM pueden ser resueltos por múltiples caminos que conducen a una gran cantidad de resultados, y es posible que tengan múltiples soluciones o que no tengan solución.
El sexto aspecto señala que, si bien las soluciones de los PC sólo pueden ser “correctas” o “incorrectas”, las soluciones de los PM únicamente pueden ser “más apropiadas” o “menos apropiadas”, dependiendo de las decisiones que tomó el solucionador para determinar el objetivo del problema y los factores que son relevantes para resolverlo, entre otras cuestiones. Entonces, la Evaluación de la respuesta en un PC consiste principalmente en valorar si se efectuaron correctamente los procedimientos matemáticos y si se llegó a una respuesta determinada. En contraste, la Evaluación de una solución de un PM consiste en determinar qué tan apropiada es para el contexto del problema.
Con respecto al séptimo aspecto, la Robustez de la estrategia utilizada para resolver el problema, los PC pueden llegar a ser resueltos simplemente mediante la recuperación y aplicación directa de fórmulas y algoritmos (Finney, 2003), con estrategias de solución sencillas como métodos de prueba y error (Panasuk y Beyranevand, 2010), o copiando el procedimiento de ejercicios similares (Lithner, 2003a). Green y Emerson (2010) observan que estas técnicas llevarían a resultados similares o al único resultado posible. En cambio, la estrategia utilizada para resolver un PM es sensible a cambios en los datos o en el contexto del problema, llevando a que el solucionador adapte sus estrategias de solución.
El octavo aspecto, la Transferencia de las técnicas utilizadas, indica que las técnicas de resolución para los PC son transferibles únicamente a problemas parecidos, en tanto que la resolución de un PM favorece la transferencia de conocimientos y destrezas a nuevas situaciones. Entre estas destrezas se encuentran la identificación del problema, de los supuestos y de la información útil del mismo (Green y Emerson, 2010).
Por último, el Tipo de revisión en un PC se reduce a verificar que se hayan llevado a cabo los procedimientos de manera correcta, mientras que la revisión de un PM necesita que se evalúe el contexto y se considere cuáles datos fueron tomados en cuenta y por qué, entre otras cuestiones.
En el Cuadro 1 se resumen los nueve aspectos presentados, contrastando los PC con los PM.
INFLUENCIA DE LOS LIBROS DE TEXTO EN LA ENSEÑANZA MATEMÁTICA
Adoptar como objeto de estudio a los problemas matemáticos propuestos en algunos libros de texto de Cálculo es relevante debido al papel de esos libros en el proceso de enseñanza-aprendizaje. Los libros de texto constituyen uno de los principales recursos didácticos del profesor para apoyar su trabajo en el aula (Cabero, Duarte y Barroso, 1989; García y Caballero, 2005). En la enseñanza de las matemáticas, el libro de texto es utilizado para seleccionar y organizar los contenidos (Cantoral, Cordero, Farfán e Imaz, 1990), planificar la secuencia y profundidad didáctica del currículo, establecer la definición formal de ciertos términos, así como para ejemplificar y practicar el uso de procedimientos. Los libros de texto también constituyen la principal fuente de los maestros de Cálculo para los ejercicios y problemas vistos en clase, las tareas escolares y los problemas planteados en los exámenes (Bergqvist, 2012). Asimismo, los estudiantes de Cálculo dedican gran parte del tiempo de sus tareas a realizar los ejercicios de los libros, se basan en sus ejemplos o en ejercicios similares para imitar los procedimientos utilizados, y se apoyan en ellos al estudiar para los exámenes (Lithner, 2003a ; 2003b). En pocas palabras, el libro de texto determina en gran medida el tipo de problemas a los que estarán expuestos los alumnos en el aula. En este sentido, es importante conocer en qué proporción se han incorporado los PM a los libros de texto, en contraste con aquellos problemas considerados PC.

El Cuadro 1 es relevante para el análisis, pues se utilizó como instrumento de ponderación y categorización de los ejemplos y ejercicios
Cuadro 1 Contraste entre los PC y los PM (adaptado de Green y Emerson, 2010).
Los problemas y ejercicios constituyen una parte esencial de los libros de texto de matemáticas y, a través de los años, su relevancia ha ido en aumento. Los ejercicios comenzaron a convertirse en un elemento central del aprendizaje para apoyar las explicaciones, representar las matemáticas en estrecha relación con situaciones próximas al alumno, fomentar el interés de los estudiantes y consolidar el aprendizaje (Ruiz de Gauna, Dávila, Etxeberría y Sarasua, 2013). Por su potencial como herramientas para el aprendizaje, “las actividades son uno de los aspectos más valorados por el profesorado a la hora de elegir un libro de texto” (López-Manjón y Postigo, 2016: 86).
Un estudio clasificó los problemas encontrados en libros de texto de matemáticas utilizados en China y en Estados Unidos para secundaria (educación media), y encontró que la mayoría eran PC (Yan y Lianghuo, 2006). En un primer diagnóstico sobre cómo se incorporan los PM en los libros de texto de matemáticas, para educación primaria en México (Quiroz y Rodríguez, 2015) se encontró que la modelación matemática no está presente en la mayoría de las lecciones. En otro estudio se compararon los ejemplos a los que están expuestos los estudiantes de Cálculo, comparando los ejemplos que proponen en clase profesores con distintos años de experiencia (Figueiredo, Contreras y Blanco, 2012). Se descubrió que mientras los profesores nóveles usaron ejemplos situados en un contexto matemático, la profesora experimentada utilizó aplicaciones de las funciones a situaciones matemáticas de la vida real y de modelación en otras ciencias (Figueiredo, Contreras y Blanco, 2012). Dichos estudios dejan abierta la pregunta sobre la presencia de PM en libros de texto, a nivel medio superior y superior. Esta investigación contribuye además a explorar un campo en donde se requiere enseñar mayor conexión entre las matemáticas y la realidad: el Cálculo.
La mayoría de los estudios sobre libros de texto de matemáticas se enfoca en el producto, es decir, en el libro de texto mismo, e ignora la relación entre el libro y variables como el currículo, el profesor y el contexto educativo, entre otras (Fan, Zhu, Miao, 2013). Los libros de texto presentan una propuesta del saber a enseñar y un tratamiento didáctico, por lo que, más allá de ser materiales de consulta, representan una forma de enseñar (Bravo y Cantoral, 2012). Analizar los libros de texto de matemáticas es un primer paso para encontrar relaciones entre el currículum oficial, el impartido, el oculto y lo que realmente es aprendido por los estudiantes de bachillerato (Valenzuela y Dolores 2012). Los problemas propuestos en el libro de texto representan el currículo oficial (los propósitos de las matemáticas), puesto que son el tipo de problemas que se espera que los estudiantes sean capaces de resolver al terminar la instrucción. Al analizar los libros de texto, es posible detectar los modelos de enseñanza y aprendizaje implícitos en ellos (Serradó y Azcárate, 2003). Por ello, otra aportación del estudio es averiguar cuáles de los nueve aspectos que caracterizan un PM (Green y Emerson, 2010) son tomados más en cuenta por los autores al momento de diseñar sus ejemplos y ejercicios.
MÉTODO
Se utilizó una metodología mixta, realizando un análisis de contenido (Bardín, 1986). Primero, fueron definidos los objetivos y las unidades de análisis: los ejemplos y ejercicios de una muestra de libros de texto. Después se determinaron las categorías de clasificación, utilizando como guía los nueve aspectos propuestos por Green y Emerson (2010). Luego contabilizamos con cuántos de los nueve aspectos que definen a un PM cumplía cada ejemplo y ejercicio. Si el ejemplo o ejercicio evaluado no cumplía con las características de los PM, se le ponderaba con cero puntos; si cumplía con una característica se le asignaba un punto y así sucesivamente. Por tanto, se contó con 10 categorías cuantitativas (del 0 al 9). Del análisis también emergieron tres categorías de problemas cualitativas: problemas convencionales, aplicaciones, y de modelaje. Finalmente, calculamos el porcentaje de ejemplos y ejercicios ubicados en cada categoría e hicimos una comparación entre libros.
Para responder a la segunda pregunta de investigación, también se contabilizó el número de ejemplos y ejercicios que cumplían con cada aspecto, con la finalidad de identificar los aspectos a los que se les da mayor importancia en los libros de texto estudiados.
Material analizado
Fueron seleccionados cinco libros de texto sobre Cálculo, de una variable a nivel medio superior y superior. Para simplificar la lectura, de ahora en adelante cada libro será identificado con la abreviatura “LT#” (Libro de Texto #). Los libros analizados y sus abreviaturas son:
LT1: Larson, R., Hostetler, R. y B. Edwards (1994). Calculus of a Single Variable: Early Transcendental Functions. (5a ed.) Boston: Houghton Mifflin.
LT2: De la Borbolla, F. y L. De la Borbolla (1998). Cálculo diferencial e integral. (4a ed.) México: Esfinge.
LT3: Astey, L. (1999). Cálculo diferencial. Programa de complementación de estudios para el ingreso a la educación superior. México: Limusa Noriega Editores, Secretaría de Educación Pública, Colegio Nacional de Educación Profesional Técnica.
LT4: Stewart, J. (2002). Cálculo de una variable. Trascendentes tempranas. (4ª ed.) México: Cengage Learning/Thompson Internacional.
LT5: Thomas, G. (2010). Cálculo, una variable. (12ª ed.) México: Addison- Wesley.
Si bien estos libros no necesariamente representan los que con mayor frecuencia utilizan los profesores de matemáticas, fueron seleccionados con la intención de obtener una gran variabilidad en la muestra. Los más antiguos fueron publicados en los años noventa (LT1 y LT2) y el más reciente en el 2010 (LT5). Hay dos libros (LT1 y LT3) destinados a estudiantes de nivel medio superior y tres (LT2, LT4 y LT5) para alumnos de nivel superior. Dos (LT2 y LT3) pertenecen a dos de las nueve editoriales especializadas en libros de texto con mayor difusión en México (Oficina Comercial de la Embajada de España en México, 2006) y uno de ellos (LT3) fue además coeditado por la Secretaría de Educación Pública (Astey, 1999), el principal editor y distribuidor de libros de texto en el país (Becerril, 2014; Cámara Nacional de la Industria Editorial Mexicana, CANIEM, 2009). Los tres restantes son traducciones de ediciones estadounidenses ampliamente utilizadas alrededor del mundo (Larson, Hostetler y Edwards, 1994) y en Latinoamérica (Thomas, 2010).
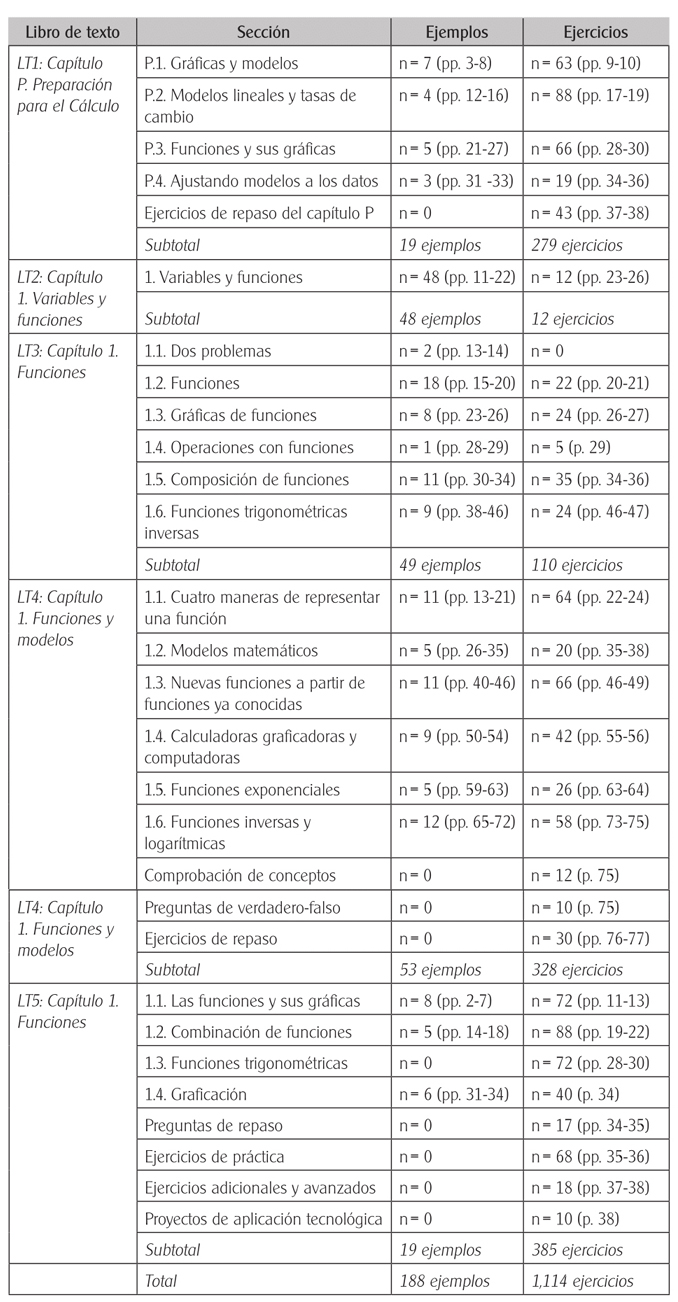
Fueron analizados y clasificados un total de 188 ejemplos y 1,114 ejercicios hallados en la unidad de funciones de los cinco libros (19 ejemplos y 279 ejercicios del LT1; 48 ejemplos y 12 ejercicios del LT2; 49 ejemplos y 110 ejercicios del LT3; 53 ejemplos y 328 ejercicios del LT4 y 19 ejemplos y 385 ejercicios del LT5). Se acotó el análisis a la unidad de funciones por ser un tópico cuya comprensión influye en temas posteriores de Cálculo (García y Vázquez, 2003), común en los cinco libros analizados, y dada la posibilidad del tema para el uso de PM ya que, en un sentido simple, una función es un modelo de una situación.
El Cuadro 2 describe el número de ejemplos y ejercicios encontrados en la unidad de funciones de los cinco libros, así como las páginas y secciones donde se localizaron.
Disciplina de interés
Se optó por el Cálculo diferencial e integral de una variable debido a tres factores. Primero, por su importancia en el desarrollo del pensamiento matemático en los estudiantes, para la solución de problemas en diversos ámbitos y por el éxito académico y profesional (Grattan-Guinness, 1991). Segundo, porque en la educación media superior y superior se presentan los mayores índices de reprobación y deserción escolar de todos los niveles educativos en México (Sistema Nacional de Información Estadística Educativa, SNIEE, 2011) y se ha encontrado que los mayores índices de reprobación y rezago, en muchas instituciones educativas, se presentan en los cursos de Cálculo (Aparicio, Jarero y Ávila, 2007; Riego, 2013; Rubí, Moreno, Pou y Jordán, 2010).
Por último, a causa de que los estudiantes tienen dificultades para conectar el Cálculo con la realidad. La enseñanza tradicional tiende a centrarse en la práctica procedimental y deja de lado la comprensión de los contenidos y cómo son utilizados (Morales y Cordero, 2014). Según la percepción de los jóvenes, los contenidos curriculares matemáticos son poco pertinentes (Alfaro, 2013), el Cálculo es considerado por algunos como una serie de contenidos cuya utilidad no rebasa el salón de clases (Moreno y Ríos, 2006). Como consecuencia, los alumnos no se sienten atraídos ni motivados a aprender, y no son capaces de aplicar dichos conocimientos en la resolución de problemas de la vida diaria (Wilkins, 2000).
Instrumento: criterios de análisis
Utilizando la propuesta de Green y Emerson (2010), clasificamos los ejemplos y ejercicios de acuerdo con el número de características de un PM con las que cumplían. Para ello, se utilizó el Cuadro 1 a manera de lista de verificación o de cotejo. Los ejemplos y ejercicios fueron leídos cuidadosamente y evaluados en cada aspecto. Por cada aspecto de un PM cumplido, se le asignaba un punto. Así, los ejemplos y ejercicios fueron ponderados dentro de un rango de cero (PC) a nueve puntos (PM).
PROCEDIMIENTO
El instrumento utilizado para el análisis es cualitativo, por lo que siempre habrá un grado de subjetividad en la evaluación. A manera de confiabilidad entre jueces, se determinó la Kappa de Cohen ponderada (ĸ = 0.66) para las valoraciones dadas por dos evaluadores.
RESULTADOS
Categorización cualitativa
Del análisis cualitativo emergieron tres categorías de problemas con características comunes: problemas convencionales (PC), problemas de aplicación (PA) (con características intermedias), y problemas de modelaje (PM). A continuación se describen y ejemplifican estas tres categorías.
1. Problemas convencionales (0 a 1 punto)
Los ejemplos y ejercicios que cumplieron con ninguno o con uno de los aspectos de los PM fueron evaluados con cero y un punto, respectivamente. Por el contrario, contaban con nueve u ocho de los aspectos que describen a un PC (con excepción del aspecto 5) y se encontraban situados en un contexto puramente matemático.
Entre ellos encontramos problemas cuya solución se lograba con la aplicación directa de procedimientos sencillos y que, en su planteamiento, daban indicaciones explícitas al alumno sobre cuáles procedimientos matemáticos seguir, por ejemplo aquellos que pedían encontrar el dominio y/o rango de una función, relacionar una lista de ecuaciones con sus gráficas o convertir ciertas funciones implícitas en explícitas.
Algunos de los PC fueron ponderados con un punto pues, al permitir múltiples caminos de solución, cumplían con el criterio de singularidad de la solución (aspecto 5). Tomemos como ejemplo el ejercicio propuesto en LT5, donde los alumnos deben graficar una serie de ecuaciones y explicar “por qué no son gráficas de funciones de x” (Thomas, 2010: 12). Para resolverlo, el estudiante podría utilizar el concepto general de función y hacer una explicación teórica; podría cuestionarse si el valor de la variable dependiente está relacionado con el valor de la variable independiente y podría tabular los valores para comprobar que cada elemento de x tenga una sola imagen en y, entre otras alternativas. Sin embargo, este problema y otros similares son mayormente convencionales al estar situados en un contexto completamente matemático y no cumplir con los otros ocho aspectos de un PM.
2. Problemas de aplicación (2 a 6 puntos)
Estos problemas tuvieron en común que se encontraban situados en un contexto real, por lo cual fueron categorizados como problemas situados o aplicaciones (PA). Debido a ello requerían, como mínimo, que el alumno estableciera conexiones entre el mundo real y el matemático (aspecto 4) y que verificara que su respuesta tuviera sentido en la realidad (aspecto 6), obteniendo dos puntos. Por ejemplo, los problemas que solicitaban la expresión del área o del perímetro de una figura en función de la longitud de un lado, una diagonal o un radio.
Los problemas con tres puntos requerían, además, que el estudiante realizara supuestos tanto matemáticos como del mundo real (aspecto 3), pero en su planteamiento ofrecían toda la información necesaria para su solución (no cumpliendo los aspectos 1 y 2). En el siguiente ejercicio se observa que todos los datos necesarios para su solución son proporcionados, e inclusive se lleva a cabo uno de los procedimientos:
Trescientos libros se venden en $40 cada uno, lo que da por resultado un ingreso de . Por cada aumento de $5 en el precio, se venden 25 libros menos. Exprese el ingreso R como una función del número x de incrementos de $5. (Thomas, 2010: 13).
Blum y Borromeo (2009) encontraron que los alumnos suelen tener problemas para hacer supuestos o asignar valores a variables si estos no han sido definidos en el planteamiento del problema. Ejercicios como el anterior limitan las oportunidades de los estudiantes para practicar estas habilidades.
Los problemas con cuatro, cinco o seis puntos no proveían toda la evidencia necesaria para resolverlos (aspecto 1) ni prescribían los procedimientos (aspecto 2), llevando al estudiante a explorar múltiples caminos de solución (aspecto 5). De igual forma, los alumnos debían evaluar si su solución tenía sentido de acuerdo al contexto (aspecto 6). Algunos PA, como el siguiente, cumplieron con 6 de 9 de los criterios, pero no se consideraron propiamente PM.
El agua fluye a través de un jarrón de 30 centímetros de altura a un ritmo constante. El vaso está lleno después de 5 segundos. Utilice esta información y la forma del jarrón que se muestra en la figura para responder a las preguntas, si d es la profundidad del agua en centímetros y t es el tiempo en segundos. (a) Explica por qué d es una función de t. (b) Determina el dominio y rango de la función. (c) Dibuja una posible gráfica de la función. (Larson et al., 1994: 29).
El estudiante puede justificar de múltiples maneras por qué la profundidad del agua depende del tiempo (aspecto 5), calcular el dominio y rango de acuerdo con el contexto del problema (aspecto 6) y determinar si la figura del jarrón afecta la manera en la que es llenado con agua (aspectos 1, 2, 3 y 4).
3. Problemas de modelaje (7 a 9 puntos)
Estos problemas se consideraron PM al estar situados en la realidad, donde se solicitaba la construcción, selección, análisis, interpretación, evaluación, mejora y/o uso de modelos matemáticos para predecir valores futuros. Por ejemplo, un problema propuesto en el LT1 (Larson et al., 1994: 8) presenta una tabla con datos reales sobre el aumento del dióxido de carbono en la atmósfera entre 1960 y 1990 (en partes por millón), en el Observatorio Mauna Loa, en Hawaii. El problema solicita, como respuesta, que los estudiantes elijan cuál modelo representa “mejor” los datos: (a) Un modelo lineal o (b) Un modelo cuadrático.
Para llegar a una solución, el estudiante debe definir qué significa que un modelo sea “mejor” que otro (aspecto 1) y decidir cuáles criterios va a utilizar para compararlos (aspecto 2). La decisión se basará en los supuestos que establezca el solucionador, en el mundo matemático y en el mundo real (aspecto 3). Matemáticamente, el mejor modelo puede ser aquel cuyo valor del coeficiente de determinación () es más cercano a 1, o aquel donde los valores reales y los valores dados por el modelo sean similares. En el mundo real, el mejor modelo dependerá de si será utilizado para realizar predicciones, representar los datos o expresar la relación entre las emisiones de carbono y el tiempo (aspectos 4 y 6). El alumno deberá elegir entre “dos objetivos (frecuentemente en conflicto): precisión y simplicidad. Esto es, desear que el modelo sea lo suficientemente simple para trabajar con él, pero lo suficientemente preciso para producir resultados significativos” (Larson et al., 1998: 8). De acuerdo con las decisiones tomadas, optará por una estrategia de solución (aspecto 7) y llegará a una de las múltiples posibles (aspecto 5). En el proceso, el estudiante aprenderá estrategias de solución transferibles a problemas similares (aspecto 8) y llegará a una mayor comprensión del contexto y de las limitaciones de los modelos (aspecto 9).
Categorización cuantitativa
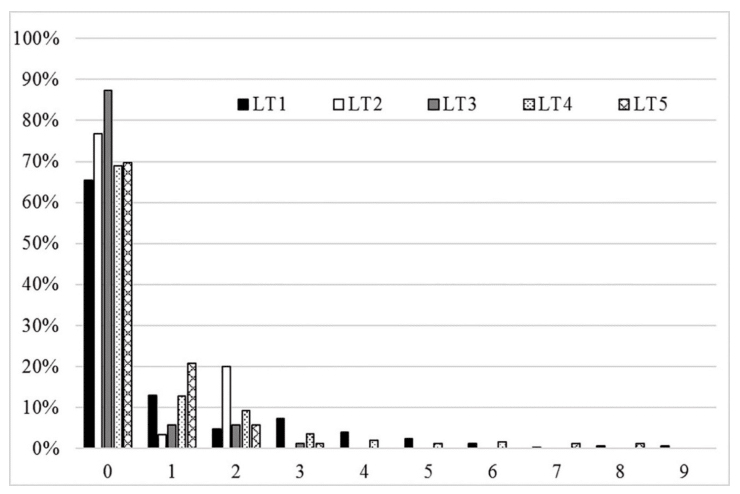
Del análisis cuantitativo se obtuvieron 10 categorías de acuerdo con el número de características que compartían con un PM (del 0 al 9). El Cuadro 3 muestra la proporción de ejemplos y ejercicios en cada categoría, por cada libro. Ll Figura 3 representa la misma información, con la intención de ilustrar la tendencia observada en los cinco libros.

Notas: C= Categoría; PC= Problemas Convencionales; PA= Problemas de Aplicación; PM= Problemas de Modelaje; E1= Ejemplos; E2= Ejercicios; Tot.= Total. Los porcentajes fueron redondeados a enteros. a La proporción de problemas encontrados en esta categoría en relación al total, es cercana a 0%. Todos los demás valores de 0% sí indican que no se encontró un sólo problema en la categoría
Cuadro 3 Porcentaje de ejemplos y ejercicios de los cinco libros, en cada categoría cualitativa (PC, PA o PM) y cuantitativa (del 0 al 9).
En total, la mayoría de los problemas encontrados en los cinco libros (entre 78% y 93%) corresponden a PC, situados en un contexto matemático (0 a 1 punto). Lo anterior implica que los estudiantes están expuestos, en su mayoría, a problemas descontextualizados que pueden ser resueltos con la aplicación directa, y en ocasiones rutinaria, de procedimientos. Estos problemas dificultan que los alumnos comprendan y practiquen las aplicaciones del Cálculo, o bien, que puedan en un futuro identificar situaciones donde el Cálculo puede ser utilizado.
Comparando los totales, se observa que un porcentaje menor de problemas (entre 7% y 20%) son aplicaciones (2 a 6 puntos). Al ser problemas situados en un contexto real, como mínimo cumplen con dos aspectos: llevan a que el alumno establezca conexiones entre el mundo real y el matemático (aspecto 4) y a que verifique su respuesta en relación con la realidad (aspecto 6). Algunos de estos problemas promueven también que practique sus habilidades para establecer supuestos, introducir variables en el problema y proponer diferentes estrategias de solución, entre otras ventajas. Sin embargo, en estos problemas la situación suele estar expresada de manera directa por los autores (por ejemplo, definiendo cuál variable debe estar en función de la otra o expresando matemáticamente en qué consiste la relación entre ambas variables) y esto no permite que el alumno genere o proponga por sí mismo la función o modelo ni que cuestione el modelo dado por los autores, o formule mejores modelos. Si se considera que estos problemas son de una dificultad intermedia, en algunos de los libros no hay suficientes “puentes” o escalafones entre los PC y los PM.
A pesar de que el modelaje matemático es descrito como una herramienta que une la realidad de los estudiantes con las matemáticas (Quiroz y Rodríguez, 2015), en total, un porcentaje aún menor (de 0% a 2%) de ejemplos y ejercicios fueron considerados PM (de 7 a 9 puntos). La mayoría de ellos funcionaba a manera de ejemplos (cumpliendo con un papel ilustrativo o motivacional) y también se encontraron, en menor medida, ejercicios. Así, el modelaje presentado en los libros de texto rara vez cumple con la intención didáctica de que el alumno practique sus habilidades de resolución de problemas abiertos y de construcción o evaluación de modelos.
En la Figura 3 puede observarse que, en los cinco libros, la mayoría de los problemas fueron PC (cero o un punto).
Énfasis dado a cada aspecto
Para responder la segunda pregunta de investigación, sobre los aspectos de un PM que enfatizan los autores al momento de planear y estructurar sus ejemplos y ejercicios, se registró cuántos ejemplos y ejercicios cumplían con cada aspecto de un PM. El Cuadro 4 describe la proporción de problemas que cumplieron con cada aspecto.
El Cuadro 4 revela que en dos de los libros (LT2 y LT3) ningún ejemplo y ejercicio se asemeja a un PM en los aspectos 1, 2, 7, 8 y 9, por lo cual limitan la posibilidad de que los estudiantes aprendan a definir el problema, a identificar posibles estrategias o caminos de solución y a evaluar su solución, más allá de verificar si realizaron los procedimientos de manera correcta, entre otras habilidades importantes.
Los aspectos que los autores enfatizaron pueden observarse con mayor facilidad en la Figura 4. En ella es notorio que la mayoría de los ejemplos y ejercicios cumplieron con los aspectos 3, 4, 5 y 6, es decir que los autores buscan que los problemas estén situados en un contexto real y puedan ser resueltos a través de diversas aproximaciones. No obstante, descuidan los aspectos 1, 2, 7, 8 y 9, prefiriendo “guiar” al alumno en el proceso de solución y limitar el tipo de revisión de las soluciones de los estudiantes.

Notas: Los porcentajes fueron redondeados a enteros. Se encontraron problemas que cumplían con varios criterios, por tanto, la suma de los porcentajes no necesariamente será 100%
Cuadro 4 Porcentaje de ejemplos y ejercicios que cumplieron con cada aspecto de un problema de modelaje matemático.
Los resultados de este estudio indican que escasean los problemas de aplicación y los de de modelaje en los libros de texto analizados. También se observa que, si bien hay problemas que cumplen con algunos criterios de PM, como estar situados en la realidad, hay otros aspectos importantes que no se están tomando en cuenta al planear los libros.
CONCLUSIONES E IMPLICACIONES DIDÁCTICA
La resolución de problemas es un contenido central en la enseñanza-aprendizaje de las matemáticas. Sin duda, gran parte del tiempo de clase es destinado a esta actividad, pues se espera que los estudiantes no sólo posean conocimiento y habilidades matemáticas, sino que también sean capaces de aplicarlos efectivamente dentro y fuera del aula.
En este estudio se explora en qué medida los alumnos están expuestos a PC, en comparación con los PM y aplicaciones. El no contar con suficientes oportunidades para desarrollar y practicar habilidades superiores de resolución de problemas pudiera provocar que los estudiantes no formen suficientes representaciones de los problemas complejos y no puedan recuperar los inicios de solución tentativos correspondientes (Selden, Selden, Hauk y Mason, 1999). A pesar de ello, los libros analizados dedican la mayoría de sus ejemplos y ejercicios a la práctica de procedimientos directos y en menor medida a la aplicación de los conceptos y técnicas matemáticas en una situación real, o al modelaje matemático.
Si bien no es posible “aplicar el cálculo en situaciones de la vida real sin ser capaces primero de comprender y hacer Cálculo” (Larson et al., 1994: IX) y los PC deben formar parte del currículo para practicar, reforzar y posteriormente dominar los conocimientos matemáticos, este tipo de problemas no debe constituir todo el material. La educación matemática debe ir más allá e incluir ejercicios de nivel intermedio y avanzado que logren reforzar el tema mediante aplicaciones y soluciones para el mundo real, que sean de interés para los estudiantes y favorezcan el desarrollo de habilidades de orden superior. Los PM son prácticos, motivan al alumno, facilitan la comprensión de conceptos y le demuestran la clase de situaciones que las matemáticas ayudan a resolver. No obstante, su presencia en los libros de texto analizados no resulta suficiente. Así se pone de manifiesto la necesidad de incorporar en el currículo una mayor cantidad de PA y de PM en la educación matemática (Cordero et al., 2009; Dundar, Gokkurt y Soylu, 2012), además del requerimiento de que investigadores, autores de libros y profesores reflexionemos sobre la clase de problemas con los que nuestros alumnos aprenden y practican nuestra disciplina.











 nova página do texto(beta)
nova página do texto(beta)