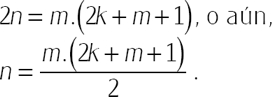1. Introducción
Cuando analizamos los currículos actuales de Matemáticas en las escuelas secundarias iberoamericanas, identificamos con frecuencia la preocupación por la aproximación de las Matemáticas con la vida cotidiana, con el mundo del trabajo y con la búsqueda de contextos aplicados a las otras áreas del conocimiento. En Argentina, según Tauber y Gatiga (2002), una de las preocupaciones es la de que la enseñanza contemple la dimensión social, debido a que las Matemáticas, desde su lenguaje y su método, se han constituido en un medio de comprensión y mejoramiento del mundo científico, industrial y tecnológico. En Chile, según Benavides y Brieba (2002), los objetivos fundamentales transversales del currículo apuntan para el desenvolvimiento de ciudadanos críticos y capaces de solucionar los múltiples problemas que enfrenta la sociedad moderna, y las actividades de aprendizaje deben ser concebidas con flexibilidad por el profesor, quién debe proponer experiencias diversificadas, que consideren conocimientos de otros subsectores de aprendizaje. En España, todos los alumnos reciben una formación básica de carácter profesional en la Educación Profesional Obligatoria y en el Bachillerato, con el foco direccionado para una aproximación entre teoría y práctica, conforme apunta Fernández y otros (2002). Como en los demás países citados, en México hay un reconocimiento de la importancia de la enseñanza de las Matemáticas como transmisión de una parte importante del acervo cultural de la humanidad a los alumnos, pero, los planes y programas de estudio también orientan para que se propicie a los alumnos el conocimiento de nociones y conceptos que les sean útiles para comprender su entorno y resolver problemas de la vida real, como apunta Guzmán y otros (2002). Tanto en Brasil como en Portugal los programas oficiales también señalan la necesidad de aproximación de las Matemáticas con sus aplicaciones, aún como reacción a la fuerte influencia del Movimiento de Matemáticas Modernas de la segunda mitad del siglo pasado, como señalan Carvalho (2002) en el caso portugués y Cyrino y D’Ambrosio (2002) en el brasileño.
La énfasis dada a las aplicaciones de las Matemáticas en contextos aplicados de la vida real, ciertamente constituye un avance en los programas curriculares oficiales de la escuela secundaria, pero, como en una balanza clásica de dos platillos, es importante que no se pierda de vista la relevancia de aspectos del pensamiento matemático que no se limitan solamente a sus aplicaciones prácticas directas. El pensamiento matemático puro puede y debe desempeñar papel importante en el currículo de Matemáticas de la escuela secundaria, especialmente en tiempos modernos de excesiva valoración utilitarista del conocimiento, como apunta Machado (1994).
La teoría de los números es una sub-área de las Matemáticas especialmente rica de situaciones en las que el estudiante puede ser invitado a disfrutar el placer estético del pensamiento matemático, sin que esté necesariamente vinculado al carácter instrumental aplicado a otras áreas de la ciencia. Cuanto a esta forma de ver las matemáticas, se recomienda Lang (1994). En Brasil, muchos temas de la teoría de los números están presentes en los currículos, entretanto, esa presencia aún tiene carácter predominantemente retroalimentador para otros tópicos del currículo de Matemáticas. Por ejemplo, se enseñan números primos y compuestos, factorización, múltiplos y divisores predominantemente con objetivos operatorios para la simplificación de cálculos.
Tal como afirman Zazkis y Campbell (2011), el tratamiento de la teoría de los números en el currículo escolar de Matemáticas puede aparecer de dos formas, que son: con destaque en el contenido en sí, o con destaque en contextos. En el primer caso los temas elegidos son explorados sólo superficialmente teniendo en vista el interés localizado y práctico de su uso como una “regla del juego” de la Aritmética. En el segundo, la teoría de los números aparece directamente enlazada con el desenvolvimiento del pensamiento matemático. Explorar propiedades de los números o de secuencias numéricas está íntimamente relacionado con la idea de conjeturar, probar y generalizar, que son competencias estructurantes del pensamiento matemático (Rico, 2014). Los problemas de la teoría de los números tratados como contexto pueden ser analizados en capas, dejando siempre posibilidades de nuevas investigaciones. Curiosamente, la ausencia de aplicación inmediata de esos problemas no suele ser un obstáculo al interés del alumno, desde que los problemas sean bien elegidos y que haya una buena metodología de trabajo en el aula. Lo que se espera aquí es una especie de retomada del interés de los griegos antiguos sobre propiedades de los números, algo que estaba en el límite entre el placer estético y el gusto por la forma esencialmente matemática de conducir el pensamiento.
A continuación, en el artículo, presento dos temas numéricos: el de los números felices y el de los números educados que, si por un lado no están en los currículos oficiales de las escuelas secundarias, por otro constituyen un rico material para explorar la teoría de los números en su dimensión de contexto. El primer tema explora la teoría de los números en su conexión con la Aritmética, y el segundo en su conexión con el Álgebra. En ambos casos se busca presentar una contribución a las investigaciones propuestas por Campbell (2011).
Terminada la presentación de los temas, concluyo el artículo con breves comentarios sobre una propuesta metodológica de trabajo con alumnos de la escuela secundaria.
2. Números felices: del pensamiento lógico inductivo al ordenador
Elija un número naturale cualquiera como, por ejemplo, 4599. Ahora empieza nuestro divertimento: sume los cuadrados de sus guarismos y, a continuación, sume nuevamente los cuadrados de los guarismos del número obtenido. Siga ese mismo proceso hasta que el juego “pierda la gracia”.
4²+5²+9²+9² = 203, 2²+0²+3²=13, 1²+3²=10, 1²+0²=1, 1²=1,...
El juego perdió la gracia cuando la suma llegó a 1 ya que, de ahí en adelante, nada irá a cambiar, ¿de acuerdo? ¡Verdad! Pero dé una oportunidad al juego e intente con otro número. ¿Qué tal 731?
7²+3²+1²=59, 5²+9²=106, 1²+0²+6²=37, 3²+7²=58, 5²+8²=89, 8²+9²=145, 1²+4²+5²=42, 4²+2²=20, 2²+0²=4, 4²=16, 1²+6²=37,...
Fue más divertido, pero cuando llegó a 37 por segunda vez perdió la gracia porque, de allí en adelante, todo empieza a repetirse cíclicamente: 37, 58, 89, 145, 42, 20, 4, 16, 37, 58, 89,...
A quien le gusta jugar con números quiere hacer nuevos test. ¿Qué será que ocurre con otros números? Pues, entonces, si es ese su caso, pruebe antes de proseguir la lectura.
Curiosamente parece que el proceso siempre termina en la monótona secuencia de unos, o en el intrigante loop 4, 16, 37, 58, 89, 145, 42, 20. A los ojos de las Matemáticas, si tú decides parar el juego con un puñado de ejemplos analizados tendrá, como máximo, una conjetura. Antes de investigar un poco mejor esa conjetura, es hora de decir “al pan, pan y al vino, vino”, eso suele mejorar la comunicación. Bautizaremos de felices los números que terminan el proceso descripto en infinitos números unos, y de infelices aquellos en que eso no ocurre. Pasada a limpio, nuestra conjetura dice que:
Todos los números (acuérdese, sólo estamos hablando de enteros positivos) o son felices o son infelices y presos al loop 4, 16, 37, 58, 89, 145, 42, 20.
Deje por ahora esa conjetura en compás de espera para, antes, investigar la siguiente pregunta: ¿Cuántos números felices, y cuántos números infelices existen?
Si 4599 es un número feliz, también serán felices los números 45990, 459900, 4599000,... El mismo raciocinio se aplica al número infeliz 731 y sus infinitos “seguidores infelices” 7310, 73100, 731000,... Si te parece sin gracia esa estrategia para concluir que existen infinitos números felices e infelices, tal vez te parezca divertida la de pensar en las permutaciones de guarismos de un número, lo que implica decir que también son felices los números 4959, 4995, 5499, 5949, 5994, 9954, 9594, 9549, 9945, 9495, 9459, y también son infelices 713, 371, 317, 173 y 137. Poniendo “ceros a derecha” de cada uno de los números obtenidos con las permutaciones tendremos otros infinitos números felices (e infelices), y diferentes de los infinitos que ya teníamos.
Aun pudiendo listar infinitos números felices e infelices, nuestra conjetura continúa abierta ya que aún no sabemos si existen números infelices fuera del loop 4, 16, 37, 58, 89, 145, 42, 20. Nuestro siguiente divertimento será el de encontrar argumentos matemáticos que puedan transformar esa conjetura en un teorema, o que puedan refutarla por medio, quien sabe, de un contraejemplo. ¡Manos a la obra!
Si n es un número de m guarismos, la suma de los cuadrados de los m guarismos de n necesariamente será un número menor que o igual a 92m, eso porque el mayor cuadrado posible de cada guarismo será 92. Organizando esa idea en una tabla, tenemos:
Ocurre que, para m ≥ 4siempre tendremos 10m-1 > 81 m (¡compruebe!), lo que implica decir que para cualquier n ≥ 1000 (m ≥ 4), llevado al “test de felicidad” con las sucesivas sumas de los cuadrados de los guarismos, las sumas obtenidas a lo largo del proceso:
o constituyen una secuencia estrictamente decreciente hasta que se llegue a la primera suma menor que 1000;
o constituyen una secuencia cuyo primer término (primera suma de los cuadrados de los guarismos del número) es un número menor que 1000.
(a rigor, hay también el caso en que n = 1000, y n es trivialmente feliz)
En último análisis, si n > 1000, entonces, seguramente, en algún momento de la secuencia de sumas de los cuadrados de los guarismos, llegaremos a un número menor que 1000. Sólo para ilustrar esa situación, imagine un número de 15 guarismos. Ese número tendrá, como máximo, el número 1215 (81x15) como primera suma de los cuadrados de los guarismos. Esa suma representa ahora un nuevo n de, al máximo, 4 guarismos. Si n posee 4 guarismos (m=4), que es su límite superior, la suma siguiente de los cuadrados de los guarismos será, como máximo, igual al número 324 (81x4), lo que reduce el nuevo n para un número de, al máximo, 3 guarismos, o sea, un número menor que 1000. De esa manera concluimos que la investigación de la “felicidad” de los números de 1 hasta 1000 es un retrato fiel y preciso de todo lo que ocurre con los demás números, mayores que 1000.
¡Ya raciocinamos bastante! Llegó la hora de pedir ayuda para alguien que piensa mucho menos que nosotros, pero que hace cuentas con velocidad incomparablemente superior a la nuestra: el ordenador. La investigación de la felicidad de los números de 1 hasta 1000 con la ayuda del ordenador nos revela, en fracción de segundos, que en ese intervalo los números o son felices, o son infelices y aprisionados en el loop 4, 16, 37, 58, 89, 145, 42, 20. Listo, ¡ahora tenemos (nosotros y el ordenador) un teorema!
El uso de ordenadores en auxilio a la demostración de teoremas ya ha sido visto con mucho prejuicio en el pasado. Esa cuestión emergió con vigor en 1976 cuando los matemáticos Appel y Haken, utilizando cerca de 1000 horas de procesamiento de un ordenador IBM 360, probaron que cuatro colores son suficientes para colorir cualquier mapa plano dividido en regiones, de forma que “regiones vecinas” no compartan el mismo color. Lo que hasta entonces era conocido como “conjetura de los cuatro colores”, con el auxilio del ordenador ganó el status de “teorema de los cuatro colores”. ¿Será que el uso del ordenador en esa demostración debe ser considerado como violación de los principios de las Matemáticas puras? No es razonable pensar de esa forma, hasta porque la esencia de la demostración no está en el trabajo mecánico de la máquina, sino en el pensamiento de los matemáticos que redujeron un número infinito de posibilidades a un número finito de casos que pudiesen ser verificados uno a uno, aunque con la ayuda de la máquina. Hoy en día, es consenso entre los matemáticos que el ordenador puede tener papel relevante en el auxilio a la demostración de algunos teoremas complejos, y es interesante que esa perspectiva también sea puesta en pauta con estudiantes de Matemáticas escolares.
Un caso emblemático reciente de encaminamiento de una demostración matemática con la asistencia del ordenador se refiere a la conjetura de los primos gemelos, que afirma haber infinitos pares de números primos cuya diferencia es igual a 2 como, por ejemplo, 3 y 5, 5 y 7, 11 y 13 etc. En 2013, el matemático Yitang Zhang consiguió demostrar la existencia de infinitos pares de números primos separados por una distancia de 70 millones. El método usado por Zhang inspiró diversos matemáticos que, con el auxilio de nuevas técnicas y de los incasables ordenadores, consiguieron, en poco más de un año, reducir la distancia de 70 millones para 246. Aún estamos distantes de la distancia 2, que sería lo necesario para transformar la conjetura de los primos gemelos en teorema, pero, el caso de la demostración de Zhang impresiona mucho por dos aspectos: la enorme fuerza actual del trabajo matemático colaborativo, y la gran contribución que los ordenadores pueden dar desde que bien programados por el brillo de la mente humana. Para más detalles sobre la saga de la conjetura de los primos gemelos, desde la primera demostración de Zhang hasta los resultados más recientes, consulte proyecto Plolymath 8b en Internet.
Varias otras preguntas pueden ser formuladas a partir del contexto de los números felices como, por ejemplo: ¿Cuántos números consecutivos felices podemos tener? ¿Podemos tener una secuencia de números consecutivos felices de un tamaño arbitrario cualquiera? Esas preguntas ya han sido investigadas y respondidas por El-Sedy y Siksek (2000).
3. Números educados: del pensamiento lógico deductivo al álgebra
Seguiremos un poco más en el juego de adjetivar números con nuevas definiciones.
Llamaremos de número educado aquel que puede ser escrito como una suma de dos o más números consecutivos. Por ejemplo, 29 es un número educado porque 29 = 14+15. Aquel que no puede ser así escrito, como por ejemplo el 8, será llamado de maleducado.
Exceptuándose el caso trivial del cambio en el orden de los términos de la adición, existen números educados que pueden ser escritos como más de una adición de consecutivos, como es el caso del 18 que es igual a 3+4+5+6, y también igual a 5+6+7. Llamaremos de “grado de educación” de un número educado el total de adiciones diferentes de consecutivos (excepto por el orden). En los ejemplos dados, 29 y 18 tienen grado de educación 1 y 2, respectivamente.
Algunos hechos curiosos pueden ser levantados sobre números educados y su grado de educación. El primero de ellos, es la relación que existe entre números educados y números triangulares. Recordando: un número triangular Tt es tal que
Un número educado mayor que uno siempre será la “diferencia entre pares de números triangulares”, de modo que esa diferencia tiene que resultar en la suma de por lo menos dos líneas consecutivas del “triángulo”. Como han indicado Gamar, Roeder y Watkins (1985), es común llamar los números educados diferentes de 1 de números trapezoidales, debido a la forma de trapecio que aparece con la sustracción de dos números triangulares. Por ejemplo, el educado 18 es trapezoidal, con dos adiciones de consecutivos que son
Vale observar que algunos números educados también pueden ser escritos, además de la diferencia entre pares de triangulares, directamente como número triangular, como es el caso del 36:
En síntesis, un número educado mayor que 1 siempre será trapezoidal y, eventualmente, también será triangular. Sea mirando para la “forma geométrica” de un número educado, o simplemente para la adición aritmética de consecutivos, tenemos en manos una primera idea de algoritmo para hallar todas las adiciones de consecutivos que resultan en un número educado n. Vamos a él:
Arme un número triangular Tn y procure, de la base del triángulo para arriba, sumas de dos o más líneas que resulten en n. A continuación, repita el mismo proceso con Tn-1, Tn-2, ..., T1. Finalice verificando en Tn si alguna suma, de arriba hacia abajo en el triángulo, resulta en n.
Investigaremos ahora el curioso hecho de que una potencia de 2 (diferente de 1) jamás será un número educado. Sea n un número educado en el que la suma de los m números consecutivos, con m>1, empiece por k+1. Entonces, tenemos
Acordando que un número triangular Tt = 1 + 2 + 3 + … + t es la suma de los términos de una progresión aritmética, sigue que  . Tenemos ahora
. Tenemos ahora
Observe la última igualdad. Si m es par, entonces (2k+m+1) será impar, y si m es impar,
entonces (2k+m+1) será par. Sigue entonces que números educados siempre pueden ser
escritos como un producto de un número par  por un número impar (2k+m+1), o de un
número impar m por un número par
por un número impar (2k+m+1), o de un
número impar m por un número par  , lo que saca cualquier oportunidad de una potencia
de 2 ser un número educado ya que, sin usar el 1, las potencias de 2 solo pueden ser
escritas como multiplicaciones de factores pares.
, lo que saca cualquier oportunidad de una potencia
de 2 ser un número educado ya que, sin usar el 1, las potencias de 2 solo pueden ser
escritas como multiplicaciones de factores pares.
Por fin, ahora vamos a demostrar que todos los números, exceptuándose las potencias de 2 (diferentes de 1), son educados. Sea n un número que pueda ser escrito como multiplicación de dos números, siendo uno de ellos impar y diferente de 1 (note que esa es una manera de decir que n es un entero positivo cualquiera, sin ser una potencia de 2 diferente de 1). En ese caso, enseñaremos que n siempre será un número educado.
Como n puede ser escrito con un factor impar diferente de 1, entonces, 2n puede ser escrito como f1 · f2 (con 1 < f1 < f2), con uno de los dos factores (o f1, o f2) siendo impar, y el otro par. Para f1 = m y f2 = 2k + m + 1, que es una representación de un impar y un par, sigue que:
Acabamos de enseñar que todo número que no es potencia de 2 (diferente de 1) puede ser escrito en la forma  y, como ya hemos visto anteriormente, enteros positivos escritos de esa forma son siempre números educados.
y, como ya hemos visto anteriormente, enteros positivos escritos de esa forma son siempre números educados.
El trayecto de la demostración aún nos provino de bonos el camino de un algoritmo, bien más listo que aquel que ya teníamos para representar un número educado como adición de consecutivos. Vamos a él.
Sea n un entero positivo con un factor impar mayor que 1. Si 2n = f1·f2, con f1 =
m, f2 = 2k + m + 1 y 1 < f1 < f2, tenemos: m
= f1 y  ,
con n = (k + 1) + (k + 2) +
(k + 3) + … + (k + m) siendo
un número educado.
,
con n = (k + 1) + (k + 2) +
(k + 3) + … + (k + m) siendo
un número educado.
Vamos a aplicar la idea del párrafo anterior para la obtención de las adiciones de consecutivos del número educado n=60. Para eso, empezamos encontrando todas las multiplicaciones de dos factores en que uno de ellos sea impar (y diferente de 1), y cuyo producto sea 2n=120. Esa búsqueda puede ser hecha analizando los factores primos de 120. De ahí en adelante el proceso es muy sencillo.
Note que el grado de educación de 60 es 3 ya que ha sido posible escribirlo de tres formas diferentes como adición de consecutivos. Es fácil concluir, ahora, que el grado de educación será siempre igual al total de divisores impares mayores que 1 del número educado.
4. Propuesta metodológica para trabajar con los números felices y educados en la escuela secundaria
Los temas de teoría de los números aquí abordados pueden ser explorados con estudiantes de diversas franjas etarias, para eso lo único necesario es que el profesor adecue correctamente el grado de profundidad esperado en cada caso. A continuación presento una secuencia didáctica de preguntas para el trabajo de los temas con estudiantes de 14 a 17 años de edad.
-
1) Elija un número naturale cualquiera como, por ejemplo, 4599. Ahora empieza nuestro divertimento: sume los cuadrados de sus guarismos y, a continuación, sume nuevamente los cuadrados de los guarismos del número obtenido. Siga ese mismo proceso hasta que el divertimiento “pierda la gracia”. Haga esto con varios números.
Ejemplo: 4²+5²+9²+9² = 203, 2²+0²+3²=13, 1²+3²=10, 1²+0²=1, 1²=1,...
2) ¿Cuántos números felices existen? Presente un buen argumento para su respuesta.
3) Elabore una conjetura que relacione los números enteros positivos con los números felices.
Las tres preguntas iniciales exigen la mediación del profesor nombrando a los números felices e infelices y averiguando si todos los alumnos comprendieron bien el carácter cíclico que lleva un número a ser clasificado como infeliz. Específicamente en la pregunta 3, suele ser natural que los alumnos formulen por sí solos la conjetura de que todos los enteros positivos infelices están presos en el ciclo 4, 16, 37, 58, 89, 145, 42, 20. Esa pregunta permite que el profesor discuta con los alumnos la diferencia entre conjetura y teorema en Matemáticas.
La próxima secuencia de preguntas deberá ser contestada colectivamente por el grupo. Cada alumno del aula será responsable por verificar la “felicidad” de tres de los números de 1 hasta 99, de forma que todos los 99 números de esa secuencia sean verificados por el grupo. Enseguida, con los resultados en manos, el grupo debe completar colectivamente los campos en blanco de las tablas a continuación.
Después de rellenar las tablas, pida a los alumnos que discutan, en grupo argumentos que puedan ser usados para investigar la conjetura de la pregunta 3. Alumnos matemáticamente más maduros suelen percibir, aunque con una argumentación insuficiente, que siempre tendremos 10m-1 > 81m. Cabrá al profesor-mediador potencializar las descubiertas de los alumnos a través de la introducción de buenas preguntas estimulando el perfeccionamiento de la argumentación de los estudiantes. Las descubiertas de los grupos deben ser compartidas con los otros compañeros para que haya una validación colectiva de los resultados. Después que esté claro para todos la verificación de la felicidad de los números de 1 hasta 1000 (o, de forma más económica y sin mucho esfuerzo de raciocinio, de 1 hasta 243), se debe discutir con ellos cual sería una forma práctica para hacer esa verificación. Si los alumnos involucrados en la actividad tienen conocimientos básicos de programación de ordenadores es posible solicitar que los interesados hagan un programa para verificar la “felicidad” de los números de 1 hasta 1000.
En el Anexo 1 el lector encontrará un programa, en lenguaje Python, hecho por el alumno Rafael Piacsek, de 14 años de edad, que estudia en el Colégio Santa Cruz (São Paulo/Brasil). El mismo problema también puede ser operado por medio de una hoja de cálculo, por ejemplo, Excel.
Para concluir esa etapa del trabajo, se recomienda que el profesor promueva la discusión con los alumnos sobre la legitimidad o no del uso de los ordenadores en demostraciones matemáticas; la discusión sobre el teorema de los cuatro colores suele ser una buena puerta de entrada al debate.
Seguidamente, el profesor podrá definir números educados, maleducados y grado de educación de un número para después proponer la siguiente pregunta:
6) Localice 8 números educados y 8 maleducados. Determine el grado de educación de todos los números educados encontrados.
Ahora se debe presentar los números triangulares con su representación geométrica a los alumnos que todavía no los conocen. Si los alumnos ya poseen conocimientos básicos de secuencias aritméticas, lo que es deseable para la secuencia de la actividad, las preguntas siguientes deben ser:
7) Determine cuál será el n-ésimo número triangular.
8) Establezca relaciones entre números educados y números triangulares.
9) Establezca una conjetura sobre los números maleducados y, a continuación, argumente de forma consistente para probar o refutar su conjetura.
Después de manipular un poco con números, los alumnos suelen percibir con facilidad que las potencias de 2 son siempre números maleducados, y argumentan satisfactoriamente a ese respeto enseñando geométricamente que una potencia de 2 jamás será un número triangular. La mayor dificultad de los alumnos pasa a ser entonces la de demostrar que todos los demás enteros positivos son números educados. En general, los alumnos buscan argumentar por medio de la representación geométrica de los números triangulares. Esa argumentación es suficiente para probar que las potencias de 2 son números maleducados, pero sola no es suficiente para probar que los demás números son educados. Merece la pena discutir con los alumnos que demostrar que “si un número es triangular o trapezoidal, entonces él es educado” no garante la validez de la recíproca “si un número es educado, entonces él es triangular o trapezoidal”. Si los alumnos no están familiarizados con el uso del Álgebra en demostraciones en la teoría de los números, cabrá al profesor conducir la parte final de la demostración en todos sus detalles. Después de comprendida la demostración por todos, los estudiantes familiarizados con programación suelen interesarse en implementar rutinas de ordenadores para escribir todas las sumas posibles de consecutivos que componen un número educado. Sigue en el Anexo 2 un programa hecho por el alumno Rafael Piacsek con ese objetivo.
Algunas preguntas finales pueden ser usadas para explorar de forma lúdica el contexto de los números felices y educados. Siguen esas preguntas acompañadas de las respectivas respuestas.
10) El año 2016 fue un número “infeliz y educado” (compruebe eso). ¿Cuál será el próximo año “feliz y educado”?
Respuesta:
De hecho, 2016 es infeliz ya que 2²+0²+1²+6² = 41 = 4²+1² = 17 = 1²+7² = 50 = 5²+0² = 25 = 2²+5² = 29 = 2²+9² = 85 = 8²+5² = 89 = 8²+9² = 145 = 1²+4²+5² = 42 = 4²+2² = 20 = 2²+0² = 4 = 4² = 16 = 1²+6² = 37 = 3²+7² = 58 = 5²+8² = 89 (entró en el loop). Y 2016 es educado porque no es una potencia de 2. El grado de educación de 2016 es 5 porque 2016 tiene cinco divisores impares diferentes de 1, que son: 3, 7, 9, 21 y 63. Usando el algoritmo descrito, sigue que:
2016=671+672+673=220+221+...+228=285+286+...+291=86+87+...+106=1+2+...+63.
El próximo año “feliz y educado” será 2019. Vea:
2019 = 2²+0²+1²+9² = 86 = 8²+6² = 100 = 1²+0²+0² = 1, y
2019 = 672+673+674=334+335+336+337+338+339 (grado de educación 2).
11) ¿Cuál será el primer año de la Era Común que es “feliz y maleducado”?
Respuesta:
4096, que es maleducado (4096 = 2¹²), y feliz ya que 4²+0²+9²+6² = 133 = 1²+3²+3² = 19 = 1²+9² = 82 = 8²+2² = 68 = 6²+8² = 100 = 1²+0²+0² = 1.
12) ¿Cuál es el 50º número educado? Esta pregunta se propuso en Lancaster (2015/2016).
Respuesta:
Como todos los números, excepto potencias de 2, son educados, tome los números del 1 al 50, elimine los números 1, 2, 4, 8, 16, 32, y añada los números 51, 52, 53, 54, 55 y 56.
El número también se puede encontrar consultando la “enciclopedia on-line de secuencia de enteros”, indicada en la bibliografía, o aplicando el siguiente teorema: el n-ésimo número educado puede ser escrito como f(n+1), siendo , con representando el mayor número entero menor que o igual al real x. Haciendo las cuentas, sigue que el 50º número educado será f (51)=56.
13) ¡Esa es difícil! Complete el próximo término de la secuencia 313, 331, 367, ____. Para quienes conocen la serie de ciencia ficción Doctor Who, ahí va una pista: vean el episodio 42.
Respuesta:
En el episodio 42 (año 2007) de la serie de la televisión británica Doctor Who, la secuencia 313, 331, 367, ___ tiene que ser completada para el desbloqueo de la puerta de una nave espacial que está a punto de chocarse con una estrella. The Doctor (interpretado en esa temporada por el actor David Tennant) dice que la secuencia debe de ser completada con 379, que es el próximo número primo feliz, y aún ironiza aquellos que creen que su lógica es rara diciendo: “—¿Será que no se enseñan más Matemáticas recreativas en las escuelas?”.











 nueva página del texto (beta)
nueva página del texto (beta)