1. Introducción
El currículo escolar chileno, tanto en el ciclo de enseñanza básica y enseñanza media, organiza la enseñanza de la Matemática a través de cuatro ejes: Estadística-Probabilidades, Números, Álgebra y Geometría. A partir de ellos se promueven cuatro habilidades fundamentales que son: representar, argumentar-comunicar, resolver problemas y modelar (MINEDUC, 2012). Estas habilidades, desarrolladas a través de los contenidos que cada eje incluye en el respectivo nivel de escolaridad, son evaluados a partir de una prueba nacional denominada “Sistema de Medición de la Calidad de la Educación” (SIMCE), y pruebas internacionales tales como el “Programa Internacional para la Evaluación de Estudiantes” (PISA) y el “Estudio de las Tendencias Internacionales en Matemáticas y Ciencias” (TIMSS), (MINEDUC, 2007).
El bajo desempeño que han obtenido los estudiantes chilenos en estos procedimientos evaluativos, ha impulsado la implementación de un ajuste curricular que considera todo el currículo nacional, incluida la asignatura de Matemática. Dicho ajuste pone énfasis, entre otras, en la habilidad de resolver problemas, según se detalla en las Bases Curriculares de dicho subsector (MINEDUC, 2016).
Por otro lado, cabe mencionar que el Ministerio de Educación de Chile busca favorecer el desarrollo del “talento académico” en escuelas y liceos de dependencia municipal a través de la implementación de Programas de Enriquecimiento del Talento Académico (PENTA), dirigidos a la alta capacidad, los que se imparten en algunas instituciones de educación superior del país (MINEDUC, 2010).
Considerando la relevancia que hoy tiene en nuestro país la Resolución de Problemas (RP) y la necesidad manifiesta de promover el “talento académico”, entendiéndolo como una subdivisión del talento, se decidió indagar en las estrategias y procedimientos matemáticos que despliegan estudiantes talentosos de Enseñanza Básica cuando resuelven un problema de matemática. El propósito es describir dichas estrategias y los procedimientos matemáticos que se activan a la luz de los contenidos que declaran los planes y programas de estudio vigentes; de esta manera, se pretende levantar evidencia empírica que permita sustentar una propuesta en RP a nivel escolar.
2. Sobre la investigación
Para dar cuenta de lo anterior, se implementó un taller de RP al interior de un programa para estudiantes talentosos que se dicta en una universidad de la ciudad de Valparaíso, Chile. El taller estuvo dirigido a estudiantes de 12 a 14 años, y su planificación incorporó problemas no rutinarios para estimular el uso de estrategias y procedimientos matemáticos con el propósito de identificar aquellos aspectos inherentes a las cualidades matemáticas que están en juego en la RP (Santos, 1997). En este marco, el objetivo es dar cuenta de aquellos caminos de solución, las nociones e ideas matemáticas que se activan en los estudiantes y las estrategias que se ponen de manifiesto en función del tipo de problema que se plantea (Santos, 2008).
Por otro lado, sin ser exhaustivos, se consideraron algunas investigaciones que dan cuenta de las heurísticas, estrategias y procedimientos matemáticos en la RP, las cuales se diferencian en cuanto al nivel educacional de los estudiantes participantes, el contexto donde se abordó y el respectivo énfasis que se dio a la RP (Jaime y Gutiérrez, 2014; Palacios y Solarte, 2013; Pifarré y Sanuy; 2001; Pino, 2013; Rodríguez y Parraguez, 2014; Valle et al., 2007). En la Tabla 1 se detalla el foco y algunos hallazgos que se dieron en estas investigaciones, antecedentes que ayudaron a enfocar el taller de RP que se implementó.
Cabe destacar, desde los distintos antecedentes que se despliegan en la Tabla 1, el interés que cobra la RP en la formación de profesores con énfasis en la enseñanza de heurísticas y estrategias (Blanco et al., 2015; Palacios y Solarte, 2013; Pino, 2013) y la relevancia de incorporar problemas no rutinarios para estimular el uso de estrategias y procedimientos matemáticos auténticos, sin dejar de mencionar el rol que cumple una olimpiada como instancia para indagar en estos tipos de procedimientos a la luz del contenido disciplinar que se pone en juego según lo que declaran los programas de estudio vigentes a nivel escolar (Rodríguez y Parraguez, 2014; Valle et al., 2007). Por último, se enfatiza en la necesidad de explorar los procesos de enseñanza-aprendizaje en la RP considerando estudiantes talentosos para poder sustentar propuestas de aula que favorezcan a este tipo de estudiantes en su proceso formativo (Jaime y Gutiérrez, 2014).
3. Lineamientos en torno a la resolución de problemas en el marco de esta investigación
Históricamente se hace necesario recordar que la RP se encuentra presente desde los inicios de nuestra civilización en variados contextos de la vida cotidiana, y adquiere un nuevo estatus y posicionamiento como técnica en el trabajo de la matemática gracias a los aportes de matemáticos como Descartes y Wallis, entre otros (Cruz, 2006; Santos Trigo 2007). Desde el punto de vista pedagógico, la RP se sistematizó a partir de las cuatro fases que propuso Polya (1990), a saber: comprensión del problema, concepción de un plan, ejecución del plan y visión retrospectiva, destacando el rol que cumplen las heurísticas y las estrategias en el proceso de resolución (Polya, 1990).
Con la propuesta de Schoenfeld (1994) se incorporan los procesos metacognitivos y el papel de las creencias en la RP. Asimismo, se han impulsado iniciativas que dan cuenta de ésta en otras áreas del conocimiento (Pozo et al., 1994) y el desarrollo de una metodología más bien holística como es el caso de Problem Based Learning (PBL) (Gómez, 2010); inclusive se han hecho propuestas que simplifican las cuatro fases enunciadas por Polya (1990) como lo plantea Mayer (Cit. en Pozo et al., 1994). Por último, cabe destacar que en teorías de la Didáctica de la Matemática, un problema puede ser visto en términos de una tarea o una situación adidáctica (Santos, op. cit.; Rodríguez y Parraguez, 2014).
En atención a los antecedentes que se expusieron en el apartado anterior, y considerando los desafíos que demanda este mundo globalizado, con el impacto de las Tecnologías de la Información y la Comunicación (TIC) en el proceso de enseñanza-aprendizaje (UNESCO, 2013), es posible inferir que la asignatura de Matemática no sólo debe estar orientada a la enseñanza de procedimientos y conceptos matemáticos, sino que además debe promover el desarrollo de un pensamiento matemático (Santos, 2007; MINEDUC, 2007) a través del cual se estimulen aspectos cognitivos, afectivos y metacognitivos y, a su vez, se activen nociones matemáticas, heurísticas y estrategias desde problemas no rutinarios, tal como plantea Santos (2007). En el siguiente diagrama, Figura 1, se explicitan algunos de estos componentes, entre los cuales se encuentra la RP.
Para efectos de esta investigación se ha considerado la propuesta de Santos Trigo, ya citado, quien postula que la RP es una actividad que estimula el desarrollo de habilidades y estrategias en el aprendizaje de la matemática. Además pone de relieve conocimientos previos, procesos cognitivos y metacognitivos. Cobra relevancia en esta mirada la resolución de problemas no rutinarios; es decir aquellos desafíos o tareas que el estudiante entiende pero que no lleva implícito un procedimiento en sí.
4. Antecedentes respecto del talento
El sistema educativo es una realidad compleja al igual que el aula escolar. En ella encontramos estudiantes con diversas características tanto académicas como socio-afectivas (Roget, 2009). En Chile y en particular para la región de Valparaíso, lo anterior no es menos cierto. Existen estudiantes que presentan diversas necesidades durante el proceso de enseñanza y aprendizaje (MINEDUC, 2010), ya sea manifestando dificultades en el aprendizaje o, por el contrario, manifestando un talento (Stainback y Stainback, 1999).
Teóricamente, el talento es reconocido como una habilidad o desempeño excepcional que posee un niño o joven en “una o más áreas que tiene valor para una cultura específica” (Kokot, 1998). Por otro lado Aretxaga (2013), plantea que la evolución del concepto de inteligencia, ya no centrado en pruebas estandarizadas que miden el coeficiente intelectual, ha favorecido el uso de un constructo más amplio, el de altas capacidades, el cual permite referirse no tan sólo a genialidad, en el sentido de la superdotación, sino que además a talento, talento académico, dotación, precocidad por nombrar algunos.
Para algunos autores, es necesario distinguir entre talento y dotación. Gagné (citado en Flanagan y Arancibia, 2005), a través de su Modelo Diferenciador de Dotación y Talento (MDDT), establece la distinción entre ambas nociones, tal como lo exponen las autoras:
La dotación designa la posesión y uso de habilidades naturales no entrenadas y espontáneamente expresadas en al menos una aptitud de dominio intelectual, creatividad, socio-afectiva o sensorio-motriz cuyo desarrollo y nivel de expresión dependen parcialmente de la dotación genética del individuo, pudiendo ser observadas en las diversas tareas de la persona a lo largo de su historia. El talento, en cambio, puede ser definido como el dominio destacado de conocimientos, destrezas o habilidades desarrolladas sistemáticamente en al menos un campo determinado de la actividad humana, en un grado que sitúa al estudiante dentro del 10% superior del grupo de personas de su misma edad que ha cultivado ese campo o actividad (Flanagan y Arancibia, 2005).
El talento ha presentado una evolución conceptual y teórica a través del tiempo, lo que puede desprenderse de los avances de la teoría de inteligencias múltiples desarrollada por Gardner (1993) y la propuesta de Sternberg (1997).
Desde la perspectiva anterior, los estudiantes con talento evidencian características cognoscitivas que los diferenciarían de los demás estudiantes, por ejemplo, una buena memoria, un mayor conocimiento de base, mejores procesos autorreguladores, mayor velocidad en los procesos de aprendizaje, mejor representación de los problemas, mayor uso de estrategias elaboradas en el empleo del conocimiento, gran flexibilidad cognitiva y una mayor preferencia por la complejidad (Jaime y Gutiérrez, 2014; Shore y Kanevsky, 1993). Además, destaca en ellos un alto nivel de atención y concentración (Aretxaga, 2013), habilidades para trabajar con ideas abstractas y una mayor capacidad para establecer relaciones lógicas, sintetizar y efectuar generalizaciones (Artola et al., 2005; Martínez y Guirado, 2012; Aretxaga, 2013). Asimismo, dan cuenta de una mayor perspicacia en tanto son agudos observadores, lo que les permite descubrir con facilidad la idea o aspecto central de algún problema o fenómeno (Aretxaga, 2013).
Si bien el término talento académico entendido como una subdivisión del talento, en el marco de las altas capacidades, es el que prevalece desde un punto de vista educativo, para efectos de esta investigación asumiremos el concepto de talento desde el Modelo Diferenciador de Dotación y Talento (MDDT) propuesto por Gagné (1985), citado anteriormente, y desde el Modelo de los Tres Anillos de Renzulli (1978).
Bajo el modelo de Renzulli, el talento constituye un fenómeno que requiere de tres dimensiones para su adecuado desarrollo, esto es (a) altas habilidades intelectuales, correspondientes a capacidad de pensamiento abstracto, razonamiento verbal, memoria, entre otros, a nivel general, y la capacidad para adquirir conocimiento y desempeñarse favorablemente en ciertas disciplinas y áreas especializadas; (b) compromiso con la tarea, entendido como el interés, motivación y perseverancia con la cual el niño o joven asume y cultiva su talento; y (c) creatividad, vale decir, la capacidad para adaptarse a distintos desafíos y problemáticas, manifestando curiosidad, flexibilidad y originalidad en el abordaje de éstas. De este modo, el autor plantea que los alumnos con alta capacidad “poseen o pueden desarrollar este conjunto de capacidades y aplicarlas a cualquier área potencialmente importante de la actividad humana” (Renzulli, 1978: 184). Lo anterior, en consecuencia, nos permite atender aquellas características relevantes propias del talento que están en sintonía con la RP en matemática.
4.1. Sobre la selección de estudiantes en los programas de enriquecimiento académico
Cabe mencionar que el proceso de selección de estudiantes talentos en Chile se rige por la normativa establecida por el Ministerio de Educación. De acuerdo a lo anterior, los estudiantes seleccionados para ingresar a un programa de enriquecimiento académico deben ubicarse por sobre el percentil 75, comparado con la población de estudiantes en su mismo rango de edad (MINEDUC, 2015). Si bien el modelo de Gagné señala que sólo 10% de la población denota un desempeño superior, otros modelos de talento, como el de Renzulli (1978), indican que este porcentaje puede llegar a operar en el 20% (Artola, Barraca y Mosteiro, 2005).
Por otra parte, considerando los diversos parámetros establecidos en Chile, ubicarse por sobre el 25% superior constituye un antecedente de relevancia para suponer condición de dotación. La tarea a la que son sometidos los estudiantes para definir su nivel de desempeño, se realiza en función de la ausencia del factor verbal, pues éste puede condicionar el logro de aquellos estudiantes que, teniendo las capacidades cognitivas, podrían obtener desempeños deficientes por no presentar el mismo nivel de dominio verbal que sus pares, aspecto que tiene relación con los problemas de acceso a mejores oportunidades educativas, en tanto en Chile se evidencia una situación de segregación a nivel escolar (Mansilla, Vásquez y Estrada, 2012).
5. Preguntas de investigación y metodología
En atención a los distintos antecedentes que se han presentado y el interés particular de trabajar con estudiantes talentosos, dadas sus características particulares, se formularon las siguientes preguntas de investigación:
¿Qué tipo de estrategias ponen de manifiesto estudiantes talentosos al abordar un problema de matemática?
¿Los procedimientos matemáticos que despliega un estudiante talentoso, se articulan con los contenidos disciplinarios que los programas de estudio vigentes plantean?
Para responder a dichas preguntas, durante el segundo semestre del año 2013 se diseñó y presentó al Programa de Buenos Estudiantes con Talento Académico (BETA) el taller denominado “La resolución de problemas y el uso de TIC en matemática”, cuya planificación se encuentra en los anexos. En dicho taller se inscribieron 18 estudiantes cuyas edades fluctuaron entre los 12 y 14 años, lo que corresponde al Nivel 1 en dicho programa.
Para el proceso de identificación y selección de estudiantes se utilizó el Test de Matrices Progresivas Escala General (Raven et al., 2004), mediante el cual se evalúa la capacidad lógica -entendida como la habilidad para inferir relaciones no evidentes de información desorganizada a partir de una cuidadosa observación- y la capacidad reproductiva -que se corresponde con la dimensión de memoria y de acumulación de conocimientos- de jóvenes en un rango etario de 13 a 18 años, procedimiento que ha sido validado a nivel nacional (Fernández, Valera, Martina y Rial, 2012; Mancilla, Vásquez y Estrada, 2012; Raven et al., 2004).
Los problemas que se propusieron en el taller se eligieron procurando escasa referencia a algún conocimiento disciplinar específico y, a la vez, permitieran el uso de diversas estrategias y procedimientos matemáticos declarados en los programas de estudio que están actualmente vigentes (MINEDUC, 2012). En particular, se incluyeron problemas que demandaron distribuir números naturales atendiendo a una condición dada, problemas de criptoarimética y algunos “rompecabezas matemáticos” los que en su mayoría fueron seleccionados de los textos de Recaman (2006) y Emmet (1998). Del estudio que se reporta, se expone un análisis al primer tipo de problemas, distribuir números naturales bajo una condición dada.
Para describir la articulación entre los procedimientos matemáticos, estrategias y el respectivo contenido disciplinar, se consideró un análisis a priori para resaltar los aspectos formales que el problema o tarea involucra, desde un punto de vista matemático, como lo plantean Rodríguez y Parraguez (2014).
Para establecer posibles relaciones entre los procedimientos matemáticos y estrategias utilizadas se incorporó el uso de estadística implicativa, cuyas sigla en francés es ASI (Analyse Statistique Implicative) (Gras et al., 2008; Orús et al., 2009), mediante su herramienta informática CHIC (Cohesive Hierarchical Implicative Classification) versión 6.0. Una de las motivaciones para el uso de este tipo de estadística obedece, fundamentalmente, a que ASI es un método exploratorio no simétrico que permite obtener indicadores como similaridad e intensidad de implicación entre variables analizadas, los que son calculados bajo un enfoque probabilístico (Gras et al., 2008; Orús et al; 2009). La similitud es una medida de correspondencia o semejanza entre las variables que se desean clasificar. Por otro lado, la intensidad de implicación es una medida que se basa en el índice de implicación, el que corresponde al número de contraejemplos que invalida la implicación entre dos variables, en el sentido matemático clásico (Orús et al., 2009).
5.1. Análisis a un problema desarrollado en el curso de RP
Como primera actividad del taller se planteó un problema aritmético para indagar en las estrategias y procedimientos matemáticos. Previamente, se realizó un análisis a priori, en función del nivel escolar de los participantes para establecer posibles procedimientos matemáticos y eventuales estrategias, lo que se detalla a continuación.
Problema: Dados los números del 1 al 24, sepárelos en dos conjuntos, S y P, de tal manera que la suma de los números pertenecientes a S sea igual al producto de los números que pertenecen a P. Explique cómo resolvió el problema.
5.1.1. Análisis a priori al problema planteado
En la Tabla 2 se presenta una posible solución, utilizando un procedimiento que se asocia a un conjunto ordenado de números naturales consecutivos y que, a su vez, permite obtener la suma de dichos números. Procedimiento que el matemático Gauss utilizó en su juventud para obtener la suma de los 100 primeros números naturales.
Considerando la resolución del problema, Tabla 2, se explicitan algunos procedimientos y estrategias que fueron rotuladas, Tabla 3, en términos de variables para ser analizadas con el software CHIC. Dichos procedimientos y estrategias se explicitaron en función del nivel escolar de los participantes del taller y el respectivo programa de estudio.
En atención a la información de la Tabla 3, es posible establecer conjeturas respecto del desempeño de los estudiantes al resolver el problema. Por ejemplo, éstos podrían proceder según la eEe y utilizar el p1 o el p2 sin hacer uso de la eBr. También podrían utilizar el p2 en combinación con la eBr. Por otro lado, como se planteó en la Tabla 2, podrían utilizar el p3 y las eOd y eBr, lo que idealmente debería llevar a una de las respuestas del problema.
5.1.2. Análisis de los datos recopilados utilizando ASI
En la Tabla 4, se presentan las distintas respuestas generadas por los 18 estudiantes al problema analizado. El valor 1 indica que se manifiestan tanto las estrategias como los procedimientos matemáticos que se han declarado y el valor 0, que no se manifiestan. Por otro en la columna R se indica aquellos que presentaron una respuesta al problema planteado.
5.1.3. El árbol de similaridad y la clasificación de los procedimientos y estrategias
Con los datos de la Tabla 4, se obtuvo el árbol de similaridad, Figura 2, generando 6 niveles jerárquicos. En el primer nivel significativo, destacan los procedimientos p2 y p3 con un índice de similaridad de 0,98 y, en un segundo nivel significativo, el procedimiento p1 con las estrategias eBr y eEe con una similaridad de 0,95 (Gras et al., 2008).
En atención al uso de CHIC se determinó que los E2, E7, E8 y E11 contribuyeron para que la primera clase (p2, p3) se configurara. De la misma manera, los E1, E2, E3, E4, E5, E7, E8, E10 y E11 contribuyeron a la conformación de la segunda clase significativa (p1, (eEe, eBr). Cabe destacar que p1, p2, eEe y eBr son, en general, procedimientos y estrategias que se han considerado fundamentales para resolver el problema en cuestión.
La respuesta del E8 en la Figura 3, evidencia una articulación de los procedimientos y estrategias que se trazaron en el análisis a priori. Seleccionar el número mayor y un número central para obtener un producto inferior a la suma máxima, para luego variar los factores en función de dicha suma; lo que supone un ensayo y error con la búsqueda de regularidades. Finalmente, obtiene un tercer factor, el 1, que a su vez es el neutro multiplicativo, aunque no lo manifiesta explícitamente. La actuación del E8 evidencia las características propias de un estudiante talentoso, como se declara en Jaime y Gutiérrez (2014).
De lo anterior, podemos establecer que las técnicas que utiliza el E3 se circunscriben al uso de la operatoria de los números naturales como tecnología y el uso del sistema de los números naturales como teoría, en el sentido de lo planteado por Rodríguez y Parraguez (2014), lo que está en sintonía con lo que proponen los planes y programas del currículo nacional vigente.
En la Figura 4, se aprecia como el E3 obtiene productos y sumas con los números menores del conjunto dado, desde una lista ordenada, que luego compara con la suma de algunos números restantes, desde un proceso de ensayo y error que incorpora la búsqueda de regularidades. Estrategias que le permite determinar la igualdad que se solicita. Al parecer, no se percata de la suma máxima para descontar los factores que asume y luego comparar gradualmente ambos resultados, en atención a lo que realizó el E8. Destaca la originalidad del procedimiento utilizado y su articulación con algunas estrategias. El E3, al igual que el E8, trabaja procedimientos matemáticos que se sustentan en la operatoria de números naturales como tecnología y se enmarca en los números naturales como teoría.
En la Figura 5, se aprecia como el E2 obtiene la suma máxima con el procedimiento de la Tabla 1. Luego intenta componer aditiva y multiplicativamente números de la lista horizontal que genera. Al parecer, no logra relacionar los factores que le permite obtener la suma máxima como los tres posibles factores que están involucrados.
Independiente del nivel de éxito obtenido por los estudiantes, se puede apreciar el uso del ensayo y error en combinación con la búsqueda de regularidades, estrategias que están en sintonía con los procedimientos matemáticos y lo distintos aspectos que promueven los nuevos programas de estudio a nivel escolar (MINEDUC, 2012). Las diferentes actuaciones que se reportan dan cuenta de las características particulares de estos estudiantes en cuanto a talento en el proceso de RP como se manifiesta en Jaime y Gutiérrez (2014).
5.1.4. Sobre el grafo implicativo y las implicaciones que se desprenden
El grafo implicativo, Figura 6, pone de relieve a eEe ⇒ p1 con una intensidad del 95%, lo que denota una influencia de la estrategia eEe respecto del procedimiento p1. También aparece con una menor intensidad eBr ⇒ p1. Ello representa un camino más elaborado, lo que se ve reflejado en el desempeño de los estudiantes E2, E3 y E8.
5.2. Sobre el desempeño en un problema de distribución numérica
A continuación, se analiza el desempeño de los estudiantes en uno de tres nuevos problemas que se les planteó, el que involucró un conjunto de números naturales consecutivos para ser distribuidos en las casillas que forman los lados de una “figura poligonal”, en este caso que se reporta, una “figura pentagonal”.
Problema: Distribuyendo números en una figura
Distribuya los números del 1 al 15 en la figura de tal manera que la suma de los números que quedan en cada lado sea igual a 32.
El problema anterior considera los 15 primeros números naturales, a diferencia del anterior que eran 24. Además, es necesario separar el conjunto en 5 subconjuntos no disjuntos. En el caso anterior, los conjuntos eran disjuntos. En la Tabla 5, se proponen algunos procedimientos y estrategias que se podrían esperar tomando en cuenta lo que los programas de estudio proponen.
En la resolución de este problema, se evidenció el uso de variados procedimientos y estrategias previstos en el análisis a priori. A continuación, en la Figura 7 y Figura 8, se presenta el árbol de similaridad y el grafo implicativo que se generó de la tabulación de los datos obtenidos.
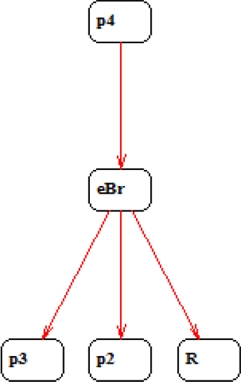
En la Figura 7 destaca la clase (p4, eBr) que pone de relieve un procedimiento y una estrategia cuyo uso articulado demanda de un proceso de sistematización y organización por parte de quien las utiliza. Por otro lado, los estudiantes E3, E10 y E11 contribuyeron a que dicha clase se conformara, los que a su vez tuvieron una participación destacada en el primer problema que se analizó. Esto pone de manifiesto la flexibilidad que existe en este tipo de estudiantes para adaptarse a nuevos requerimientos, variando los procedimientos que están en sintonía con los conocimientos que los programas de estudio vigentes declaran.
En relación al grafo implicativo, Figura 8, se puede deducir que la utilización de un procedimiento más elaborado estimula el uso de otras estrategias y la activación de procedimientos más elementales que inciden en la aproximación de la resolución del problema. En la Figura 9, se aprecia parte del desempeño deE3, quien logra distribuir correctamente los números dados.
Yo puse en 1 de los vértices el primer y último número (igual que antes) pero esta vez eran cinco vértices asi que no podía poner el número del centro, entonces, puse el número en siguiendo algo como un patrón y al ir poniendo los números de la misma forma que la actividad anterior y cuando no podía seguir modificaba a veces los números del los vértices dependiendo de la situación. Al poner el primer y el último número los conecté.
Se puede apreciar cómo la ubicación estratégica del menor y mayor número en los “vértices” de la figura, constituye una idea fuerza que se manifiesta en los otros problemas similares abordados por los estudiantes. La composición aditiva de parejas de números y, a su vez, la composición aditiva de suma de parejas permite, desde la búsqueda de regularidades, equilibrar el paso de números de un lado a otro.
En la Figura 10, se observa parte el desempeño de E3 en un problema similar al problema de la figura pentagonal. Se evidencia en la explicación que ofrece, el uso de las mismas estrategias y procedimientos utilizados en el problema anterior, mediante la descomposición aditiva para la suma dada, y poniendo de relieve una nueva estrategia, esto es “suponer resuelto el problema”. En este caso, el ensayo y error con la búsqueda de regularidades, son una estrategia efectiva a la hora de acercarse a la respuesta.
Distribuí los números del 1-5-9 porque están el principio-medio y final en los vértices y después el número que faltaba para que de 20 lo partía en 2 y después los ponía si otro lado lo necesitaba, lo hacía de nuevo y lo cambiaba.
En la Tabla 6, se presentan algunos procedimientos y estrategias que se manifestaron en la resolución de los problemas que implicaron números naturales consecutivos en una “figura poligonal”.
Discusión
Los problemas que se seleccionaron para este estudio involucran un conjunto de números naturales consecutivos que deben distribuirse según una o más condiciones dadas. Si bien el número de elementos de cada subconjunto es acotado y se conoce la suma y/o producto, no hay un procedimiento explícito para dar con la respuesta en cada caso. Inclusive, uno de los problemas presenta más de una solución.
De las estrategias utilizadas por los estudiantes, se evidenció preferentemente el uso del ensayo y error, búsqueda de regularidades y uso de una lista, las que fueron articuladas y activadas en distintos momentos del proceso de resolución. El ensayo y error se evidenció desde la realización de cálculos aritméticos de manera reiterada que se sistematizó con la búsqueda de regularidades para lograr los distintos objetivos: la misma suma para todos los elementos de subconjuntos no disjuntos, o bien, que la suma y el producto de los elementos de dos subconjuntos disjuntos fuese la misma.
La búsqueda de regularidades se activó comparando los resultados de las operaciones aritméticas que los estudiantes fueron realizaron, para luego organizar sumas o diferencias para lograr “equilibrar” y dar con el requerimiento del problema. En el caso de la distribución de números en una “figura geométrica”, los vértices fueron un punto de referencia a la hora de distribuir los números según su posición en el conjunto, la que se obtuvo gracias al uso de una lista, preferentemente horizontal. La articulación de dichas estrategias y procedimientos se condice con las características de este grupo de estudiantes, señaladas en los antecedentes.
En definitiva, las estrategias ensayo y error, búsqueda de regularidades y haz una lista se utilizaron de manera recurrente en cada uno de los problemas planteados, activando procedimientos como comparar, agregar, quitar y reorganizar números. Destaca, asimismo, el hecho de intercambiar números mayores por números menores para disminuir la suma de sus elementos o el producto de estos, procedimientos que forman parte de la actividad matemática y apuntan al despliegue de un pensamiento matemático, además de constituir insumos para la activación y configuración de procedimientos matemáticos más elaborados como el que se evidenció para obtener la suma máxima en el análisis a priori, procedimiento que se promueve en los programas de estudio, a nivel escolar, como una técnica para trabajar números consecutivos y en la justificación de la suma de una progresión aritmética, en cursos de matemática a nivel de pregrado.
Los procedimientos matemáticos utilizados por los estudiantes fueron acordes a las exigencias de cada problema. Componer o descomponer aditivamente números, o bien, componer multiplicativamente, son procedimientos que se fomentan en la escuela desde tareas específicas y rutinarias que luego se olvidan, pero que en este tipo de problemas se activaron, poniendo en juego, por ejemplo, la “sensibilidad numérica”.
Conclusiones
En primer lugar se destaca la importancia del Análisis Estadístico Implicativo (ASI) en el foco de esta investigación, pues permitió visualizar dos tipos de relaciones entre los procedimientos matemáticos y las estrategias, que se establecieron a priori, y que los estudiantes pusieron de manifiesto: similaridad e implicación. En el primer problema, y mediante similaridad, se muestra que los intentos arbitrarios, o por ensayo y error, quedan alejados de las estrategias que están más cercanas a la resolución correcta del mismo, poniendo de relieve la necesidad de un ensayo y error más sistemático. Las implicaciones no cobran una fuerte intensidad, excepto la que indica que una estrategia de ensayo y error conlleva el uso de un procedimiento de operaciones con números arbitrarios, lo cual era esperable a priori. En el segundo problema, el análisis de similaridad agrupa la resolución correcta con la estrategia de búsqueda de regularidades, y con los procedimientos más organizados, mientras que el análisis implicativo muestra que dicha cercanía entre variables, también es una fuerte relación implicativa, donde el uso del procedimiento p4 implica, en gran medida, que se trata de una búsqueda de regularidades, lo cual conlleva tanto a la resolución correcta, como al uso de los procedimientos p2 y p3. Además de mostrar las relaciones entre variables, estos análisis permiten destacar a los estudiantes que más contribuyen a dichas clasificaciones e implicaciones, lo cual puede servir, en el caso de muestras de mayor tamaño (lo cual no es el caso de esta investigación), para investigar sobre otros factores que intervengan en estos procesos.
Respecto de las estrategias que utilizaron los estudiantes, en función del tipo de problemas que se planteó, están al alcance de un estudiante promedio, dado que el problema de alguna manera lo sugiere: ensayo y error, crear una lista, buscar regularidades. La diferencia radica en la forma en cómo los estudiantes talentosos las utilizan, sistematizando la información que se despliega a medida que utilizan los distintos recursos. En definitiva, poniendo en juego el uso de un pensamiento matemático, en el sentido que se manifiesta en lo antecedentes de este artículo.
Los procedimientos matemáticos que pusieron de manifiesto los estudiantes están en sintonía con los requerimientos del problema y, por otro lado, se articulan con los contenidos que declaran los programas de estudio vigentes. Ello permite señalar que el éxito en la resolución de los problemas analizados requiere de ingredientes cognitivos y el conocimiento necesario de los números en sintonía con los requerimientos del problema. Aspectos que deben considerarse a la hora de articular los distintos ejes que promueve el ajuste curricular en nuestro país.
Como proyección, un aspecto que emerge de la presente investigación para organizar el trabajo de la RP a nivel escolar, en un futuro, es abordar una temática en RP para estimular el desarrollo de un trabajo interdisciplinario y a la vez fomente un pensamiento matemático en el sentido de lo que se plantea en los fundamentos de PISA y TIMSS, es decir, identificar un elemento articulador que caracterice un conjunto de problemas como hilo conductor para el trabajo de procedimientos matemáticos y estrategias, como es el caso de la distribución de números naturales. La cuadrícula es otro ejemplo de una temática en RP que se intentará documentar en un próximo estudio, así como el papel de los problemas de criptoarimética.











 nueva página del texto (beta)
nueva página del texto (beta)