1. INTRODUCCIÓN
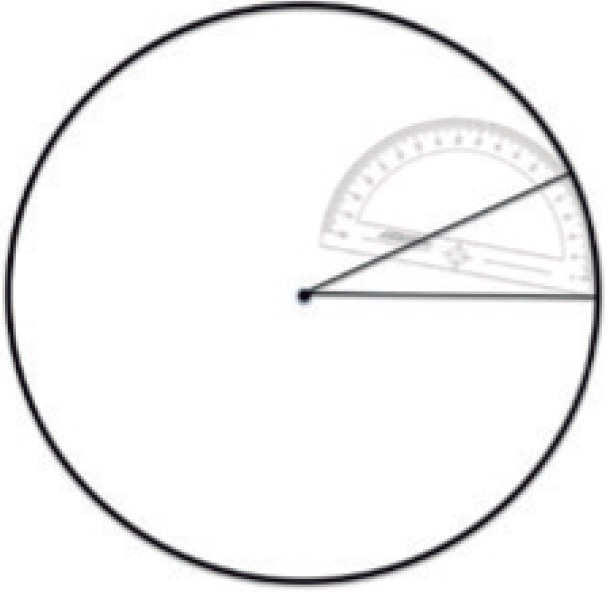
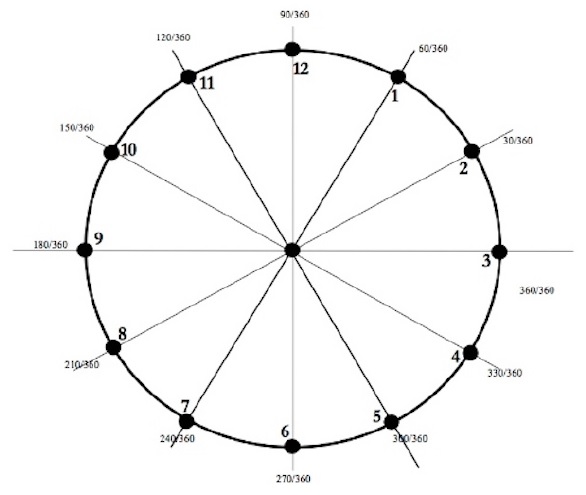
El concepto de ángulo es introducido por primera vez en cuarto grado de la educación primaria del sistema educativo mexicano. Se asume que cuando los estudiantes ingresan a la secundaria son capaces de usarlo, medirlo y aplicarlo en las clases de matemáticas, física y dibujo técnico. Los alumnos se familiarizan con las escuadras del juego geométrico denominándolas como de 30°-60° y la de 45°; sin embargo, por su forma (triangular), en ocasiones no distinguen una de otra, o hacen uso inapropiado de ellas. Por ejemplo, cuando se les solicita que dibujen una línea a 45° suponen suficiente usar la escuadra correspondiente, independientemente de la posición en que se coloque. Uno de los conflictos que más llamó nuestra atención fue el uso que hacen del transportador al medir ángulos en una circunferencia, ya que lo usan como regla para medir la longitud del arco (Figura 1).
A partir de una revisión bibliográfica identificamos que estas dificultades —junto con otros conflictos y malentendidos— se constituyen en un fenómeno didáctico asociado a la particularidad del concepto matemático ángulo, pues se presentan independientemente del país, el contexto o los paradigmas de enseñanza y aprendizaje, de las experiencias educativas e investigaciones hasta ahora reportadas.
2. EL FENÓMENO DIDÁCTICO
Investigaciones como las de Casas (2002), Casas y Luengo (2005), Mitchelmore y White (2000), Clements y Burns (2000), Fyhn (2007) y Munier y Merle (2009) hacen un reconocimiento explícito de la dificultad impuesta por el propio concepto de ángulo, a propósito de su naturaleza multifacética. Analizan conflictos de los estudiantes, diseñan situaciones problema y proponen explicaciones teóricas sobre la construcción del concepto de ángulo. En un panorama general, las dificultades más comunes de los estudiantes están relacionadas con lo siguiente:
La coordinación de las distintas facetas del concepto, por ejemplo como giro (Mitchelmore y White, 1998), o como inclinación (Douek, 1999).
Asumir que la longitud de las rectas que definen al ángulo afecta su medida.
Identificar al ángulo dentro de otras figuras.
Reconocer como ángulos los de medida 0°, 180° y 360°.
Estas dificultades se pueden asociar con el tipo de definición trabajada, así como con el único instrumento utilizado para medirlo: el transportador. Su naturaleza multifacética se refiere específicamente a la diversidad de definiciones que se encuentran en los libros, cada una ajustada a ciertas estructuras matemáticas formales. Tres clases particulares de la definición de ángulo suelen ser las más frecuentes (Mitchelmore y White, 2000: 209):
Cantidad de giro, alrededor de un punto, entre dos líneas.
Un par de rayos con un punto en común.
Una región formada por la intersección de dos semiplanos.
Además de estas clases, se reconoce que el concepto tiene propiedades estáticas o dinámicas asociadas con las definiciones y representaciones usadas como apoyo para la manipulación del concepto en el aula.
Así como existen distintas definiciones en los libros, también se reconocen diferentes definiciones que ha tenido en la historia, dependiendo de la situación matemática donde se trabaje. Keiser (2004) hace una comparación entre el devenir histórico del ángulo y las concepciones de los estudiantes en tres categorías:
¿Qué se mide en realidad cuando nos referimos al tamaño de los ángulos?
¿Los ángulos pueden incluir curvas?
Las dificultades en conceptualizar ángulos de 0°, 180° y 360°.
El autor reconoce la necesidad de trabajar —al igual que en el devenir histórico— en diferentes direcciones, con variedad de representaciones, en distintos contextos y situaciones angulares.
Una forma de abordar la noción de ángulo y beneficiar su aprendizaje es trabajarlo en estrecha relación con situaciones angulares en contextos físicos. En esta dirección se enfocan los trabajos con las sombras (Douek, 1999)), el alpinismo (Fyhn, 2007), la medición del arco del horizonte (acimut) y el campo visual (Munier y Merle, 2009). Todos ellos aportan elementos para mejorar el aprendizaje del concepto en cuestión. Sin embargo, consideramos que sus resultados dependen en gran medida del escenario (extra-aula) en el cual se llevan a cabo las actividades.
Tomando en consideración estos antecedentes y las características particulares del escenario escolar donde identificamos las dificultades de los alumnos, elaboramos un diseño para llevar a cabo una experiencia didáctica que los hiciera transitar por la manipulación, medición y cuantificación del ángulo, para valorar si con esta interacción es posible el aprendizaje del concepto escolar de ángulo o, en todo caso, ampliar su comprensión y vincularlo con las definiciones y aplicaciones escolares trabajadas durante años previos.
3. CONSIDERACIONES TEÓRICAS PARA LA ORGANIZACIÓN DIDÁCTICA
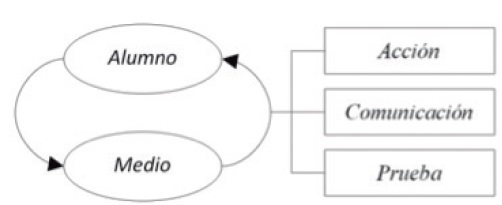
Para orientar la interacción de los estudiantes con el concepto escolar de ángulo, tomamos como referente a Brousseau (2000), quien establece que “el proceso para adquirir un conocimiento matemático pasa por diversas fases y se basa en juegos específicos, donde el actor interactúa con un medio a distintos niveles, evolucionando sus nociones y su lenguaje”. La interacción de un actor con su medio se da en tres niveles (Figura 2).
En la interacción de tipo acción, el actor fija un estado del medio, determina y limita las acciones de otros actores. La interacción de tipo comunicación consiste en modificar los conocimientos de otro actor por medio de mensajes portadores de información y, por último, la interacción del tipo de prueba tiende a la justificación o validación cultural de los actos o declaraciones establecidas. Estas interacciones no pueden ocurrir de manera simultánea, de hecho ocurren en situaciones con características propias y donde el actor juega papeles distintos, utiliza diversas herramientas y produce diferentes mecanismos de comunicación, situaciones que en la Teoría de Situaciones Didácticas (Brousseau, 1997) se conocen como situación de acción, situación de formulación y situación de validación.
El medio con el que interactúan los estudiantes está planeado, organizado y dirigido por el profesor (polo didáctico) que, junto con el saber matemático en juego (polo espistemológico) y los alumnos (polo cognitivo), conforman el triángulo didáctico. Es la interacción sistémica de estos polos la que, en la teoría, se conoce como contrato didáctico y permite planear los niveles de interacción de los estudiantes con el medio en el diseño didáctico.
4. METODOLOGÍA PARA EL DISEÑO
La Ingeniería Didáctica (ID) nace como un modelo para la interacción productiva entre la investigación fundamental y la acción en el sistema didáctico (Artigue, 2014), de ahí que podamos considerarla una metodología para el diseño de recursos didácticos basados en resultados de investigación. La ID se estructura en cuatro diferentes fases: Análisis preliminar; Diseño y análisis a priori; Realización, observación y recolección de datos; Análisis a posteriori y validación.
En lo que sigue, presentamos un análisis preliminar robusto para hacer énfasis en la importancia de la investigación como base del diseño y su puesta en escena. Después, describimos el diseño y el análisis a priori en forma sintética,3 articulados con una narrativa de la experiencia didáctica.
4.1. Análisis preliminar
En esta fase son desarrolladas las consideraciones didácticas, cognitivas y epistemológicas que posteriormente se integrarán en el planteamiento sistémico que sirvió para fundamentar el diseño.
4.1.1. Consideraciones cognitivas
Mitchelmore y White (2000) reconocen la naturaleza multifacética del ángulo en la diversidad de definiciones que pueden encontrarse en los libros, y las asocian con la adaptación del concepto a diferentes estructuras matemáticas formales. Estos autores plantean que la formación del concepto se da a partir de las experiencias físicas que viven los alumnos. Construyen un modelo basado en tres etapas de abstracción que representan una clasificación —progresivamente más refinada— de la experiencia física de los estudiantes: conceptos situados del ángulo, conceptos contextuales del ángulo y conceptos abstractos del ángulo.
En la última etapa, los autores reconocen un concepto estándar que se relaciona con los contextos físicos del ángulo y es el más común entre las construcciones del estudiante: aquel de las dos líneas inclinadas que se encuentran en un punto. Reconocen también que el concepto tiene un desarrollo lento, apto para alumnos de secundaria, y que aún se requeriría de una cuarta etapa para llegar al concepto matemático formal.
4.1.2. Consideraciones didácticas
Producto de la transposición didáctica, el concepto escolar de ángulo se trabaja en un periodo de 10 a 12 años. Las nociones trabajadas en cada nivel educativo están asociadas con ciertas facetas del concepto e incluso es posible identificarlas a partir de las definiciones escolares, pues son acordes al contexto y el tipo de problemáticas. En el sistema educativo mexicano, dos momentos donde el ángulo cobra relevancia son: en cuarto año de primaria (con estudiantes de aproximadamente 9 años de edad) y en primer año de secundaria (alumnos de 12 años, en promedio).
En primaria es introducido con la idea de “partes de vuelta”, sin mencionar el concepto. Posteriormente se nombra la parte de vuelta o giro como ángulo, y es asociada con una medida en grados. La noción es utilizada en años posteriores no sólo como tema, sino como elemento de otras figuras geométricas, siempre considerando que el estudiante ha entendido el concepto y le es familiar su medición. En la secundaria se parte del significado de ángulo como giro y como elemento de otras figuras geométricas para identificarlo en situaciones concretas o contextualizadas. Su medición se hace con el transportador, y para su trazo se incorpora el compás; finalmente, se avanza hacia su clasificación y el reconocimiento de su papel en la tipología de triángulos y paralelogramos. A partir de este nivel se asume el ángulo como aprendido y es usado en otras asignaturas como Dibujo técnico o Física, o relacionado con varios conceptos matemáticos como los de razón trigonométrica y tangente de la recta, entre otros. Es precisamente en este nivel donde situamos la experiencia didáctica aquí reportada.
4.1.3. Consideraciones epistemológicas
En este apartado nos referimos a consideraciones histórico-epistemológicas, en tanto la historia de las Matemáticas, usada como mediador del conocimiento para la enseñanza, puede proveer del contexto que permita ver los tópicos escolares desde una perspectiva diferente a la de la enseñanza tradicional (Furinghetti, 2007). En este sentido, el desarrollo histórico del concepto de ángulo nos permite reorientar la enseñanza: abandonar la perspectiva escolar-tradicional, basada en el manejo de una definición y posterior aplicación, para considerar la apropiación de diversas facetas del concepto a través de su manipulación.
En el desarrollo histórico del concepto de ángulo reconocemos momentos de uso en contextos prácticos, en contextos formales (filosófico-matemáticos) y de debate sobre su naturaleza. En cada una de las definiciones analizadas en la revisión histórica de Matos (1990; 1991) es posible distinguir elementos que le confieren cierto sentido al concepto. Algunas hablan de distancia, sector, contracción, espacio, y todas ellas necesitan de otros objetos para definir o acotar —de toda una figura— lo que es y, en ocasiones, lo que no es un ángulo. Hay casos donde se hace explícito que se le considere cualidad, cantidad y/o relación, aunque es importante señalar que estas categorías tienen una interpretación acorde con la época y la tradición filosófica-matemática de su momento.
A partir de esta revisión Rotaeche y Montiel (2008; 2011) reconocen la naturaleza polifacética,4 del ángulo en su característica de ser una cualidad, por su forma; una cantidad, porque es susceptible de medirse, y una relación, por cómo se acota y define usando otros elementos; y de tener usos y representaciones que le confieren carácter estático o dinámico en diferentes situaciones. De aquí que en el diseño pongamos especial interés en la construcción de ciertas nociones de ángulo en un contexto particular (estático o dinámico), a través del desarrollo de significados específicos (cualidad, cantidad y/o relación).
4.1.4. Integración sistémica para fundamentar el diseño
De inicio, tomamos en cuenta los elementos didácticos relacionados con el acercamiento escolar que se le da al concepto en el nivel primario, es decir, como giro y elemento de otras figuras geométricas. Asumimos entonces que se reconocerían estas nociones de ángulo en sectores de área (significado cualitativo-estático), en los giros (significado cualitativo-dinámico), en la porción de una circunferencia (significado cuantitativo-estático) y en la parte de vuelta (significado cuantitativo-dinámico). En este sentido, es fundamental que los alumnos tengan un manejo amplio de las nociones escolares de proporción, porción, área, fracción, triángulo equilátero, triángulo isósceles, triángulo escaleno, triángulo rectángulo y polígono regular.
A diferencia de las situaciones físicas que trabajaron Mitchelmore y White (1998), hemos considerado el escenario de la escuela y lo que ello implica: las restricciones de tiempo y espacio, los conocimientos previos de los estudiantes, los efectos de los contratos pedagógico y escolar, así como las herramientas de medición con las que cuentan los alumnos, por ejemplo, las escuadras y el transportador. Las situaciones físicas fueron establecidas con el principio de la manipulación y no sólo de la observación a través de materiales recortables y actividades como colorear, superponer figuras y responder a los ejercicios en hojas de trabajo; de ahí que decidimos emplear figuras conocidas por los estudiantes como el triángulo, el cuadrado y el círculo. Estas figuras permiten, en principio, el manejo de ángulos de 30°, 60°, 45° y 90°. Las situaciones se relacionaron con el uso de objetos en los cuales el ángulo está presente, y que los estudiantes trabajan cotidianamente en la escuela.
Los contextos se establecieron según la figura geométrica trabajada: cuadrado, medio cuadrado, triángulo equilátero, triángulo rectángulo, etc. Cuando los alumnos logran generalizar la relación entre la parte de giro con la parte del círculo en cada figura geométrica, sin importar el tamaño de la figura o del círculo sobre el que gira, entonces se dice que han construido concepto contextual. En lo que respecta a los dominios, se consideró lo estático y lo dinámico como parte de la naturaleza polifacética de la noción de ángulo, y se favoreció el manejo de ambos al momento de colorear figuras (naturaleza estática) y al girarlas (naturaleza dinámica).
La etapa de abstracción se dividió en una generalización por parte de los estudiantes y una fase de institucionalización por el profesor. La generalización busca que los alumnos visualicen la división de la circunferencia en 360 partes y le asocien un objeto cotidiano, en este caso, el reloj. Por medio de la institucionalización, el profesor introduce la medición del ángulo en grados, con base en las divisiones construidas en el círculo.
4.2. Diseño y experiencia didáctica
En esta sección mostramos el diseño, su intencionalidad y la narrativa de la experiencia didáctica, con el objetivo de evidenciar el funcionamiento del sistema didáctico, es decir, la interacción de la profesora y los estudiantes en relación con las facetas del concepto escolar de ángulo.
El principio fundamental para el diseño de la secuencia fue dar a los alumnos la responsabilidad de su aprendizaje a partir de actividades concretas en las que se pretende encuentren formas, patrones y relaciones en las diversas situaciones que se les presentan. La secuencia fue dividida en seis partes (SP1, SP2,… SP6), buscando que los estudiantes, paulatinamente, fueran interactuando a través de las actividades, preguntas y materiales empleados con las diferentes facetas del ángulo. En todas ellas se previó que la manipulación del ángulo fuera desde su cualidad estática (como esquina de las diferentes figuras) y dinámica (con los giros de cada uno de los círculos empleados). Intencionalmente nunca se especificó el objetivo de la actividad, con la finalidad de provocar que los estudiantes descubrieran propiedades del ángulo sin estar influenciados por los enunciados de las tareas.
Los materiales empleados fueron: micas circulares (transparentes), tachuelas, figuras geométricas en cartulina y una hoja de fomi, para colocar ahí los materiales anteriores (Figura 3). Las tachuelas permiten fijar la mica sobre la figura geométrica, para que el estudiante pueda girar ambas sin perder la configuración solicitada: que el centro de la circunferencia de la mica coincida con el vértice de la figura de cartulina.
Las actividades buscan la interacción directa con las representaciones de las figuras geométricas, de manera que los estudiantes, guiados por una serie de preguntas, vayan identificando y construyendo características propias del ángulo a través de situaciones angulares. Se pretende que “usen el ángulo” y trabajen con los elementos que lo definen partiendo de la manipulación de materiales, hasta el manejo de definiciones y herramientas institucionales.
Se trabajó con un grupo heterogéneo de 34 alumnos, entre 12 y 13 años de edad, en el aula designada a la asignatura de Matemáticas para toda la escuela, en sesiones de 45 minutos. La experiencia fue grabada en video (120 minutos), y se recolectaron las hojas de trabajo donde resolvieron cada actividad. Con el primer formato de registro, se analizó la dinámica grupal considerando tanto las respuestas como los comportamientos de los estudiantes y de la profesora-investigadora5 (PI) que dirigió la experiencia. Con el segundo formato de registro ejemplificamos el análisis de la producción escrita y gráfica de cada alumnos.
4.2.1. Secuencia Parte 1 (SP1)
Los estudiantes exploran con el círculo y el cuadrado, haciéndolos coincidir por centro y vértice, respectivamente, a fin de identificar cuántas veces puede girar el cuadrado para cubrir el círculo (Figura 4).
Con el primer círculo es posible que se construya el significado angular como “sector” o área, por ello se proporcionan dos círculos más, de distinto tamaño. Así, se espera provocar el significado como “parte de”, que se complemente con el giro para provocar el significado como “parte de vuelta”. El uso de micas circulares de diferentes radios pretende que el estudiante identifique que, sin importar el tamaño, siempre se sombreará la misma parte. En ese sentido, buscamos poner énfasis en la parte de vuelta. Con esta actividad se usarían las cualidades estática (por la parte del círculo) y dinámica (por el giro) del ángulo (Figura 5).
4.2.1.1. Narrativa de la experiencia didáctica
Los estudiantes, orientados por la PI, resolvieron la SP1 paso a paso y con mucho detalle, quizá por ser la primera actividad y ante la novedad de estar trabajando con materiales manipulables en la clase de Matemáticas. La pregunta: ¿qué fracción del primer círculo queda sobrepuesta con el cuadrado?, fue respondida inmediatamente con: un cuarto; y se produjeron tres argumentos:
Partiendo el círculo en cuatro.
Dividiendo en medios y luego otra vez en medios.
Girando el círculo.
Sólo un alumno propuso el tercer argumento, y el docente rescató la idea pidiendo a todos que giraran el círculo para comprobarlo. Esto permitió construir también un significado dinámico. Ante la pregunta “¿son iguales las áreas delimitadas?”, hubo un breve silencio. La PI reaccionó repitiendo la pregunta y acentuando la palabra ‘áreas’. La respuesta grupal fue “No”, pero algunos complementaron la respuesta diciendo que lo que sí era igual era la “fracción” sombreada. La PI preguntó cómo se denominaría a esta vuelta; solamente una estudiante respondió en voz alta diciendo un cuarto de vuelta.
4.2.2. Secuencia Parte 2 a 4 (SP2 a SP4)
Las tres secuencias siguientes son muy parecidas a la anterior. En ellas se busca explorar, de forma similar, la mitad del cuadrado (dividida por su diagonal), el triángulo equilátero y el triángulo rectángulo que se genera al cortar el equilátero por su altura (Figuras 6), 7 y 8), y con micas de diferentes tamaños (Figura 9).

Figura 6 Con el triángulo correspondiente a la mitad del cuadrado, se cubrirá la octava parte del círculo.

Figura 7 En la Secuencia 3, se usará ahora el triángulo equilátero para encontrar sextas partes de vuelta.

Figura 8 En la secuencia 4, se usará la mitad del equilátero para encontrar doceavas partes de vuelta.
4.2.2.1. Narrativa de la experiencia didáctica
En estas tres secuencias, el trabajo fluyó cada vez más rápido que en la SP1, y la estrategia de “girar” el círculo para comprobar la fracción sombreada fue la única que se utilizó. Los estudiantes reconocieron que las áreas en los siguientes círculos serían diferentes y que, en cada caso, la parte sombreada se mantenía, sin importar el tamaño de los círculos (Figura 10). Cuando existían dudas, la PI insistía en el uso del material para comprobar.
Al inicio de cada secuencia, siempre fue importante retomar las anteriores mediante preguntas. Así, al iniciar la SP3, las preguntas de inicio fueron: ¿Qué fracción obtuviste con el cuadrado? ¿Qué fracción obtuviste con la mitad del cuadrado? ¿Qué fracción crees que obtendrás ahora con el triángulo equilátero? Algunos estudiantes contestaron 1/6, otros 1/3. La PI los alentó a comprobarlo con el material, y brindó apoyo a quienes lo requerían.
Con el desarrollo de cada parte de la secuencia, los alumnos lograron predecir las partes de vuelta que se sombrearían en cada caso.
4.2.3. Secuencia Parte 5 y 6 (SP5 y SP6)
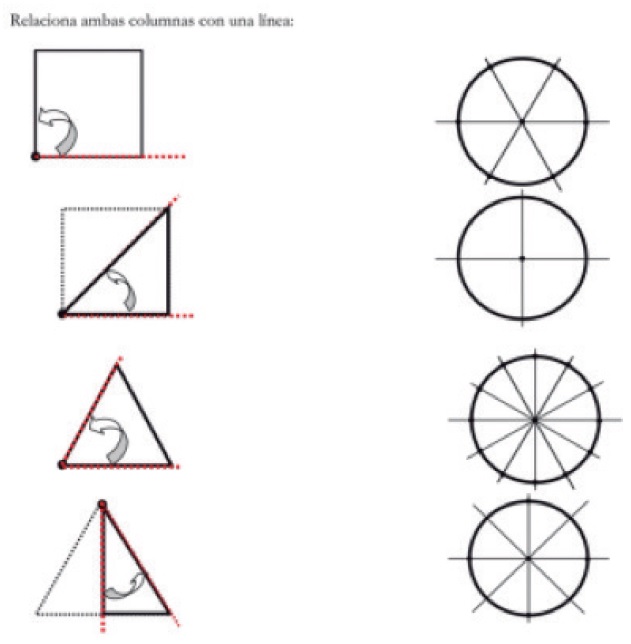
Integrando los aprendizajes anteriores y a manera de conclusión, en SP5 se pide a los estudiantes relacionar las figuras con el giro o parte de vuelta que realizaron con cada una de ellas. Se pretende evidenciar la construcción contextual de ángulo, ver si ellos identifican las cualidades estática y dinámica del ángulo, el giro, sin importar la dirección y cuantificar la parte de vuelta con respecto al todo (Figuras 11 y 12).
Se retoma el círculo dividido en 12 partes para iniciar con ejercicios utilizando una flecha fijada en el centro, y que los estudiantes la giren según se les indique. Cada división tendrá un número como en el reloj, de tal manera que deben realizar giros, por ejemplo, del número 3 al 12, e identificar la fracción de giro que realizaron. No se especificará el sentido, para fomentar el uso de ángulos en ambas direcciones.
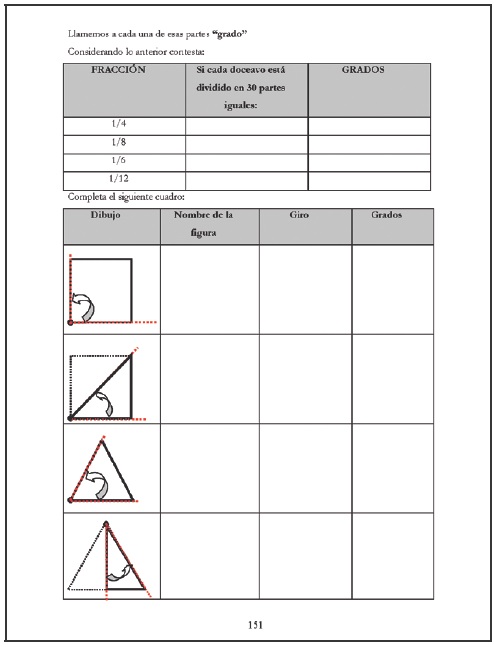
Luego se les da un nuevo círculo, dividido en 12 partes. Los alumnos deben imaginar que cada doceavo está dividido en 30 partes iguales. Con esta actividad se pretende trabajar con giros similares al transportador (Figura 13). Se establecen conclusiones una vez que la PI institucionalice que una de esas 360 partes de todo el círculo equivale a un grado.

Figura 13 Giros con base en las divisiones del reloj y considerando 30 divisiones en cada doceavo, 360 en todo el círculo.
Las conclusiones van orientadas a que los estudiantes determinen el número de pequeñas partes que hay en cada fracción estudiada inicialmente: 1/4 de vuelta, 1/8 de vuelta, 1/6 de vuelta y 1/12 de vuelta, así como los grados correspondientes para cada fracción. La actividad concluye identificando las figuras trabajadas en un inicio, con su fracción de vuelta y el ángulo correspondientes (Figura 14).
4.2.3.1 Narrativa de la experiencia didáctica
Los estudiantes resolvieron la SP5. En las primeras tablas no hubo necesidad de usar los materiales manipulables. Los alumnos relacionaron, sin problemas, la figura con sus partes de vuelta correspondientes (Figura 15).

Figura 15 Tabla para relacionar figura geométrica con las secciones en el círculo que se generan al superponerlas.
A la pregunta “¿qué parte de vuelta equivale el giro que inicia en el punto 3 y termina en el punto 12?”, el grupo dio varias respuestas: 3/4, 1/4 y 3/12. La PI le pidió a una estudiante que pasara a la pizarra y explicara lo que encontró. Ella ubicó el punto de inicio, giró hacia el punto 12 y respondió: éste equivale a 1/4, 3/12… La PI preguntó si todos estaban de acuerdo, y el grupo respondió positivamente. La PI le pidió a otra alumna que compartiera con el grupo su respuesta. Esta explicó que algunos giraron la flecha a la derecha y otros a la izquierda. La PI aclaró que como no se especificó el sentido, el giro podía realizarse en cualquiera de los dos sentidos.
Antes de dar por concluida la actividad, la PI les preguntó a qué les recordaba la figura —el círculo dividido en 12 partes— y retomó la respuesta del “reloj” que dio un estudiante para, a partir de ahí, hablar del “giro en el sentido de las manecillas del reloj”.
En la siguiente actividad de la SP6, por primera vez se presenta un ejercicio abstracto con el que los estudiantes “imaginan” subdividir cada una de las 12 partes en el círculo en 30 partes iguales. A partir de este momento se etiquetaron los giros como “tantas (partes) de 360”, por ejemplo 30 de 360, y lo escribieron en el círculo en forma de fracción (30/600) (Figura 16).
El llenado de la tabla de tres columnas: (1) fracción del círculo, (2) partes de vuelta con la división en 360 partes y (3) equivalente en grados —en donde sólo se les dio la fracción de la primera columna (1/4 1/8 1/6 1/12)—, fue respondido de manera grupal, y la PI fue destacando las respuestas y/o explicaciones de algún estudiante para ampliar la discusión. Por ejemplo, algunos alumnos dan rápidamente la respuesta correcta a cuántas partes de vuelta le corresponden a la fracción 1/8, sin embargo, un estudiante hace un conteo diferente y pasa a la pizarra para mostrar su respuesta. Sucedió que él giraba la flecha en sentido contrario a las manecillas del reloj, contando 8 de las 12 partes en las que está dividido el círculo y ahí coloca la fracción 1/8. Sus compañeros le recomiendan dividir en cuartos y luego en sacar la mitad, pero le resulta difícil imaginarla, quizá porque el círculo ya está dividido. La PI, con el propósito de ir construyendo con él la respuesta, insiste en localizar la cuarta parte y después el octavo, como la mitad de la cuarta parte. Suena la campana que indica que la clase ha concluido, por lo cual la PI le pide a otra estudiante que pase a resolver la pregunta, explicándole al primero cómo lo hizo (Figura 17).
Ella localiza los cuartos y señala cómo los dividió a la mitad trazando dos rectas que cortan al círculo, como se muestra en la Figura 17; enseguida, explica que como el doceavo se divide por la mitad, entonces quedan 15° que, sumados a los 30° del punto A al punto B, dan 45°. Con esto se da por concluida la clase.
Se inicia la nueva sesión haciendo un recordatorio de las actividades resueltas en la anterior, para hacer una vinculación entre las figuras, partes de vuelta y los grados. Al hacer uso de la idea del “reloj y el sentido en el que giran sus manecillas”, se añaden a la revisión algunos ejercicios orales sobre las fracciones que recorre para ir de un número a otro. Recordando la relación del círculo con el reloj, la PI preguntó si tendría algo que ver el tamaño de la manecilla del reloj con el giro que hace y puso como ejemplo dos relojes de diferente tamaño, cuyas manecillas de los minutos van del 1 al 7. Los estudiantes dijeron que no importa el tamaño de los relojes, que ambos dan un giro de 1/2, y argumentaron que es así porque ambos tienen las mismas divisiones.
La PI aprovechó los ejercicios orales para etiquetar el círculo con las partes de vuelta usando fracciones (30/360, 30/360, …, 30/360). Al concluir, preguntó qué les recordaba la figura etiquetada. Los alumnos respondieron que al reloj, a un pastel partido y “a un transformador”; la profesora responsable del grupo les corrigió, señalando que se dice “transportador”. Con esta respuesta, la PI comenzó un discurso explicativo sobre el uso del transportador para medir ángulos, considerando que hay un punto de inicio y un punto final, poniendo énfasis en que esto no cambia si el transportador es de diferentes tamaños.
Para concluir con la SP6, la PI mostró en el pizarrón la división del cuadrado —ya hecha por los estudiantes en la secuencia— de donde “salen” dos escuadras comúnmente denominadas en la escuela “escuadras de 45°” (Figura 18) . De manera análoga, se mostró la división del triángulo equilátero para obtener dos escuadras denominadas de 30°-60° (Figura 19). Con ayuda de las respuestas de los estudiantes, se identificaron y marcaron en el pizarrón los valores de los ángulos interiores de cada escuadra.
También se mostraron escuadras de plástico o madera de diferentes tamaños, para preguntar sobre la medida de los ángulos. Los alumnos aseguraron que eran las mismas, porque ambas son mitades del cuadrado o mitades del triángulo equilátero.
Para finalizar con la SP6, la PI pidió a los estudiantes que escribieran en la parte posterior de su material lo que para ellos era un ángulo. Esta fue la única actividad que respondieron sin compartir respuestas al grupo. Al ver que tenían dificultades para responder, la PI vuelve a preguntar “¿cómo definirían un ángulo?”. Se concluyó la actividad y algunos alumnos aplaudieron.
5. UNA VALORACIÓN INICIAL A LO LOGRADO CON EL DISEÑO
Para valorar si el diseño y su puesta en escena cumplieron con el objetivo de lograr el aprendizaje del concepto escolar de ángulo, o ampliar la comprensión de los alumnos y vincularla con las definiciones y aplicaciones escolares trabajadas en años previos, se llevó a cabo un análisis en dos niveles: la interacción con las facetas del ángulo y la articulación con conocimientos previos.
Considerando que todos los estudiantes se involucraron en la resolución de la secuencia haciendo, respondiendo y argumentando, localizamos momentos de acción cuando ellos manipulan los materiales, por ejemplo al recortar y sombrear; también encontramos momentos de comunicación cuando dan respuesta a las preguntas de cada actividad, pues en la dinámica grupal los estudiantes responden en voz alta y se genera discusión. Finalmente, localizamos momentos de prueba en distintas modalidades:
Al dar respuestas puntuales en actividades no tan familiares para el grupo, por ejemplo al argumentar porqué la parte sombreada corresponde a 1/4 de la circunferencia. El giro se convierte —a partir de aquí— en la estrategia para probar las partes de vuelta, es decir, en una actividad que permite dar respuesta a otras preguntas.
Cuando hay distintas respuestas: se hacen los giros en dos sentidos distintos y se prueba que dos respuestas diferentes son correctas.
Cuando hay elecciones distintas a las que plantea la secuencia: un alumno escoge un vértice distinto para recortar el triángulo isósceles.
Al estudiar estas modalidades de prueba, centramos la atención en la resolución-prueba que hace un estudiante, quien retoma el manejo de los materiales, expone su forma de resolver la actividad y explica el porqué de su respuesta. En conjunto, la PI y el grupo aceptan o cuestionan la respuesta. Para el alumno, fue un descubrimiento paulatino. Usó el ángulo sin saberlo y descubrió que, sin importar el tamaño del círculo usado, la fracción sombreada o el giro realizado siempre sería el mismo. Esto lo trabajó y lo infirió al adelantarse a contestar, para después validar su respuesta con círculos de diferentes tamaños de círculos. Llegó un momento en que ya no tuvo la necesidad de utilizar todos los círculos con todas las figuras, puesto que fue realizando conexiones.
Los estudiantes manejaron el carácter estático del ángulo al sombrear en cada mica la porción encontrada, de acuerdo con la figura trabajada; también lo hicieron en las tablas que completaron, en material impreso que se les entregó y al usar las escuadras del juego de geometría para identificar la fracción correspondiente al vértice de cada una de ellas. El carácter dinámico del ángulo se experimentó al momento de girar las micas para encontrar las diferentes partes de cada figura.
5.1. Interacción con las facetas del ángulo
En esta sección nos referimos a la dinámica grupal en términos de los momentos en los que se ponen en funcionamiento:
Conceptos situados de ángulo y conceptos contextuales de ángulo.
El carácter dinámico o estático de la noción de ángulo.
La noción de ángulo como cualidad, cantidad y como relación.
Hasta la primera tabla de la SP6, se dirige la actividad de los estudiantes para pasar del concepto situado, referido a la parte de vuelta que se sombrea (cualidad de carácter estática) en cada círculo, al concepto contextual. Esto se logra con el reconocimiento de que las porciones sombreadas (cantidad) en los tres círculos es la misma, incluso si la figura geométrica también cambia de tamaño. Se comprueba utilizando el giro (carácter dinámico) como estrategia. La construcción del concepto contextual es reafirmada cuando los alumnos logran asociar las figuras geométricas con las partes de vuelta que les corresponden en el círculo, y con las divisiones en éste.
Hasta antes de la institucionalización, por parte del profesor, de la medida angular “grado”, los estudiantes trabajaron el ángulo como giro (cualidad de carácter dinámico), considerando un lugar de partida y uno de llegada (relación). Reconocemos en esta experiencia el concepto contextual, en tanto los alumnos manejan por igual tanto el giro en el círculo dibujado de las hojas de trabajo como en el círculo, considerablemente más grande, proyectado en la pizarra. En esta actividad, además, cuantifican el giro y distinguen su sentido (derecha/izquierda).
En el desarrollo de la actividad, quizá por la creencia de estar trabajando con fracciones y giros, los estudiantes no tuvieron dificultades para trabajar partes de vuelta mayores a 1 2 (en sentido análogo a la dificultad de concebir un ángulo mayor a 180°), o del giro completo (ángulo de 360°). Sin embargo, por la relación figura geométrica —parte del círculo, carecía de sentido hablar de giros mayores al entero (ángulos mayores a 360°), o de ausencia de giros (ángulo de 0°). Aunque no se introdujo la noción de ángulo negativo en el contexto de la actividad, resultó natural hablar de giros a la izquierda o al contrario de las manecillas del reloj.
El trabajo con círculos de distintos tamaños y la reiterada distinción entre porciones y áreas indica que no hubo conflicto en cuantificar los giros con base en sus tamaños. En las actividades más abstractas, particularmente cuando se reflexionó sobre “el tamaño de las manecillas en relojes de diferente tamaño y su relación con los giros”, los estudiantes no mostraron confusión ni mal manejo de la cuantificación del giro. Por último, el uso de los diferentes términos para caracterizar lo que se hace (porción, área, giro, parte de vuelta) deja claro que en sus desempeños los estudiantes miden ángulos, no áreas ni longitudes.
Consideramos que el concepto abstracto del ángulo se logró sólo a nivel de la subdivisión del círculo en 360 partes y de la manipulación de ellas para realizar giros y cuantificarlos, pero esto de ninguna manera es visto como un concepto formal del ángulo. Reconocemos que las situaciones angulares, escolares o extraescolares, son de naturalezas tan diversas que la noción de ángulo construida en la experiencia puede ser insuficiente sin la organización didáctica que la haga evolucionar hacia una más compleja, o hacia una nueva.
5.2. Articulación con sus conocimientos previos
Presentamos algunas respuestas que dan los alumnos cuando se les pide escribir “lo que para ellos es un ángulo”. Estas -en calidad de respuestas individuales no compartidas con el resto del grupo— fueron analizadas como la articulación que puede lograr el estudiante entre su conocimiento previo y lo aprendido a lo largo de la secuencia. Agrupamos las respuestas en las siguientes categorías:
Expresiones que aluden a líneas rectas unidas en un punto. En esta categoría obtuvimos 14 respuestas; cuatro hacen uso de un dibujo para ilustrar su “definición” o alguna parte de ella. Además, aparecen términos como esquina, abertura, inclinación, vértice, separación.
Expresiones que aluden a figuras. Aunque para algunos es una figura y para otros es parte de ella, ubicamos 10 respuestas en esta categoría. Aquí encontramos dos “definiciones” con dibujo; en cuatro de ellas se le reconoce como medida o tipo de medición.
Expresiones que aluden a las fracciones. Utilizando nociones como unión entre dos líneas, grados o esquina, tres definiciones dan prioridad a la noción de “fracción” para redactar su definición, y ninguna utiliza dibujos para ilustrarla.
Expresiones que aluden a una idea concreta. En esta categoría “miscelánea” ubicamos tres respuestas: una de ellas habla de “abertura medida en grados”, la segunda de porcentajes y la tercera de “partes de un círculo”. Sólo esta última usa un dibujo, pues reconoce que el ángulo puede estar en otro tipo de figuras.
Hubo solamente un alumno cuya respuesta fue “no sé”. No hubo entrevistas posteriores para profundizar el porqué de cada respuesta, debido a que nos propusimos llevar a cabo esta experiencia en un ambiente de clase muy “natural” y, en la medida de lo posible, ir al ritmo escolar tradicional. Sin embargo, es evidente que se puede continuar la investigación en esta dirección, o incluir otro tipo de actividades para “ver en acción” la articulación de los significados angulares construidos con las nociones previas de ángulo que se han trabajado en la escuela.
Con base en los condicionamientos del contrato pedagógico, podemos inferir que al solicitarles una definición de ángulo los estudiantes evocaron, con prioridad, esquemas escolares que hacen alusión a las líneas rectas, los puntos de encuentro, las aberturas, etc., más que a los giros trabajados en las experiencias físicas que plantea la secuencia. Es decir, existe una separación entre lo que hacen para ellos mismos y lo que responden en la escuela.
6. Discusión y reflexiones finales
En (Rotaeche y Montiel, 2008; 2011) hemos planteado, con base en la evidencia empírica, que es posible, como en la historia, usar el concepto de ángulo sin definirlo o presentarlo en sus faceta matemática formal. Sin embargo, a diferencia de la construcción histórica, los estudiantes sólo cuentan con el tiempo limitado de la escuela para la construcción de significados, y es entonces cuando los diseños didácticos llegan a trivializar este proceso.
En el presente documento damos evidencia de que es posible la construcción de significados, representaciones y usos, previo a la formalización del concepto y tomando en consideración la cotidianidad escolar de los alumnos, pero desarrollamos una discusión sobre sus implicaciones en el aula y la imperiosa necesidad de más investigación.
Consideramos que el resultado más importante —relacionado con el aprendizaje de la noción de ángulo— es que los estudiantes sólo logran, con este diseño didáctico, construir ciertos significados angulares. Identificamos que ellos ponen en funcionamiento, de forma oral o escrita, más significados de los que pueden reconocer explícitamente, pero el paso a una abstracción del concepto, articulando estos nuevos significados con los conceptos escolares previos, les resultó una tarea compleja, lo cual nos lleva a pensar que se requiere más tiempo del asignado al tema, o es necesario un enfoque distinto en su enseñanza. Sorprende, por ejemplo, que a pesar de llevar más de cuatro años usando un juego de geometría —que incluye un transportador— el estudiante confunda el nombre de este último y le llame “transformador”, y otro responda, sin broma, que el transportador sirve para transportar.
Del contraste entre el punto de partida —o análisis a priori— y la experiencia, se identifica que se logró que los estudiantes identificaran, cuantificaran y acotaran la angularidad, más que el ángulo como concepto. De forma natural pudieron interactuar con su naturaleza estática y dinámica, a través de las cualidades del ángulo. Pudieron cuantificarla al medir ángulos en ambos sentidos, sin tener que hablar de ángulo negativo o positivo. Además, lograron contextualizarla al identificar similitud entre el reloj y el transportador, y extraer de ahí propiedades del ángulo, por ejemplo que su medida no depende del tamaño de las manecillas del reloj o de la figura geométrica trabajada.
A partir de la evidencia, reconocemos que se debe poner mayor atención a lo que hacen los estudiantes durante el proceso de resolver secuencias didácticas, y evaluar su pertinencia para poner en uso significados. Una visión prospectiva nos dice que, bajo este enfoque, el diseño se ajusta a la dinámica de clase y a la propuesta de construcción de conocimiento; sin embargo, de mantenerse el enfoque que prioriza el dominio de contenido, no cumplirá las expectativas.
Consideramos que es necesario hacer investigación sobre los significados angulares que se ponen en juego en todo el currículo de la educación primaria, posiblemente como una noción transversal. Esto pondría de manifiesto que el concepto no se aprende de una vez y por todas, que no sería posible considerar que el ángulo ya se aprendió en primaria y, en consecuencia, puede “aplicarse” en otros temas u otras asignaturas. Es decir, estaríamos cuestionando que los pilares de nociones más avanzadas —como la razón trigonométrica, la pendiente de la recta, la velocidad angular y el paralelismo, entre otras— sean lo suficientemente robustos para construir estas últimas.











 nueva página del texto (beta)
nueva página del texto (beta)