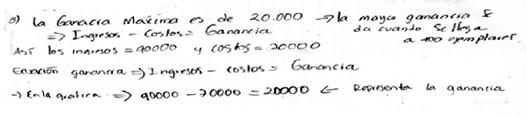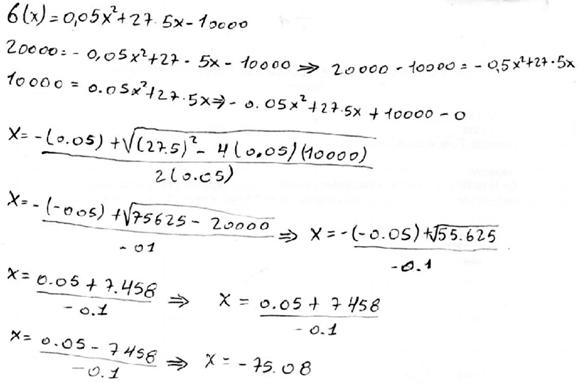nova página do texto(beta)
Espanhol (pdf)
Artigo em XML
Referências do artigo
Tradução automática
Enviar este artigo por email
Citado por SciELO 
Similares em
SciELO 
Permalink
Introducción
La enculturación matemática de niños y jóvenes de las comunidades depende en gran medida de las habilidades y competencias para enseñar que posean las personas que los orientan. En relación con el concepto de función, parece haber un distanciamiento bien marcado entre su comprensión a nivel escolar y su necesidad de uso consciente a nivel social. Es decir, en las prácticas sociales -no académicas- es casi inevitable la utilización de este concepto en contextos cotidianos -aunque sea inconscientemente-, mientras que en contextos académicos los estudiantes parecen no reconocerlo y les cuesta utilizarlo de manera consciente, quizá por no poderlo relacionar con algo conocido. Para el Ministerio de Educación Nacional de Colombia (MEN, 2005), el estudio de las funciones es de suma importancia en el desarrollo de una comunidad, ya que conectan modelos y/o patrones con otros para producir estructuras matemáticas perdurables en el tiempo. Se trata de un concepto que brinda una gran oportunidad para explorar sus representaciones en un mismo ambiente, lo cual facilita su estudio a través del análisis de congruencias e incongruencias entre los elementos de sus representaciones. Así, los escenarios donde este concepto es usado con frecuencia podrían ser los más apropiados como enlace para realizar la conexión entre el concepto a nivel social y su uso y comprensión en contextos académicos.
Son abundantes los trabajos que indagan acerca de las dificultades presentadas por estudiantes y profesores al decodificar información para hacer transformaciones entre elementos de una función (Amaya y Medina, 2013; Hitt, 2003; Marroquín, 2009; Suárez y Cordero, 2010) y sobre los conocimientos didáctico-matemáticos de los profesores en la enseñanza de las funciones (Font, 2011; Godino, Wilhelmi y Bencomo, 2005; Parra y Pino-Fan, 2016). Según Hitt (2003) el problema de los estudiantes y de algunos profesores de enseñanza media para entender el concepto de función es que generalmente se restringen a la manipulación de una representación algebraica del mismo, y esto produce limitaciones en su comprensión. En general, la actividad de conectar diferentes representaciones de un concepto matemático no es considerada fundamental por muchos profesores para su construcción. En particular, las actividades que involucran transformaciones tipo conversión y tipo tratamiento (Duval, 2004) son minimizadas por los profesores al estudiar las funciones, desconociendo que promueven un mejor entendimiento de las funciones y facilitan el desarrollo de procesos de visualización.
De lo planteado por Hitt (2003) se puede inferir que en la enseñanza de las funciones se ha tendido a sobrevalorar los procedimientos analíticos algebraicos y la algoritmización, sin tener en cuenta que el estudio de funciones se potencia si se realiza en un ambiente natural de camaradería y cooperación mutua entre aprendices. Asimismo, el recurrir a diferentes registros es absolutamente indispensable para la comprensión en matemáticas (Duval, 2004) y además, según Duval (2012), esta comprensión requiere de la coordinación y el funcionamiento en sinergia de por lo menos dos registros, y que se pueda pasar espontáneamente de una representación a otra sin siquiera notarlo.
En este trabajo se tuvo como objetivo evaluar el conocimiento matemático de futuros profesores de matemáticas para hacer transformaciones de las representaciones de una función. Concretamente se evalúa el reconocimiento, la producción y transformación de diferentes representaciones de una función, al igual que su uso, con el propósito de resolver una situación problema. Con esta finalidad utilizamos el modelo del conocimiento del profesor denominado Modelo del Conocimiento Didáctico-Matemático (CDM) (Pino-Fan, Assis y Castro, 2015), el cual nos proporciona herramientas teórico-metodológicas concretas para la caracterización de los conocimientos de los futuros profesores, relacionados con la dimensión matemática.
2. Marco teórico
2.1 Sobre los conocimientos necesarios para enseñar matemáticas
Durante las últimas décadas, las investigaciones en Educación Matemática han sido muy fecundas al tratar de indagar sobre los conocimientos matemáticos que debe dominar un profesor para enseñar las matemáticas eficientemente. Entre los trabajos más destacados están los de Shulman (1986, 1987, 2005), Ball, Thames y Phelps (2008), y Godino y sus colaboradores (Godino, 2009; Godino, Batanero, Rivas y Arteaga, 2013; Pino-Fan et al., 2015). Como resultado de estos trabajos, aún no se ha llegado a un consenso sobre un marco teórico que caracterice dichos conocimientos, pero sí se han formulado diversos modelos que han hecho aportes significativos para su caracterización (Pino-Fan y Godino, 2015), uno de ellos es el denominado modelo del Conocimiento Didáctico-Matemático (CDM).
El CDM, inicialmente planteado como un sistema de categorías de análisis de los conocimientos del profesorado (Godino, 2009), se ha ido refinando en diversos trabajos (Godino y Pino-Fan, 2013; Pino-Fan y Godino, 2015; Pino-Fan, Assis y Castro, 2015). El CDM asume del Enfoque Onto-semiótico su sistema de herramientas teóricas, el cual proporciona un sistema de categorías y sub-categorías de conocimientos que el profesor debe conocer, comprender, saber aplicar y valorar, y para las cuales se proponen herramientas teórico-metodológicas que facilitan la operativización de los análisis de los conocimientos incluidos en cada sub-categoría. El modelo del CDM propone tres dimensiones, cada una a su vez compuesta por sub-categorías (Pino-Fan y Godino, 2015): Dimensión matemática, Dimensión didáctica, Dimensión meta didáctico-matemática.
Es de interés en este trabajo la Dimensión matemática, conformada por las sub-categorías conocimiento común del contenido -relacionado con el conocimiento que un profesor moviliza para resolver los problemas que les coloca a sus estudiantes y para verificar que las soluciones dadas a ellos sean apropiadas; más específicamente, se relaciona con el conocimiento que el profesor comparte con estudiantes del nivel donde orienta-, y el conocimiento ampliado del contenido -que permite al profesor realizar las conexiones entre los conceptos que fundamentan lo que se trabaja en un nivel y proyectar lo trabajado hacia lo que se necesita posteriormente, además de permitirle seleccionar y utilizar diferentes representaciones de un objeto, decidir cuál registro utilizar como principal y cuál o cuáles como auxiliares.
La Dimensión matemática es integral, integrada e integradora debido a la naturaleza de sus componentes. Por un lado, el conocimiento común del contenido es absolutamente indispensable en un profesor de matemáticas, quien debe conocer el material que enseña y poderlo modificar para construir situaciones problema, sin que pierda su esencia matemática. El conocimiento ampliado del contenido, en el caso concreto de nuestro estudio, facilita -entre los conceptos- establecer los enlaces, vínculos y conexiones intra e inter registros y representaciones.
Las sub-categorías de la Dimensión didáctica son tanto integradoras como integradas, facilitan el conocimiento del material y de las personas objetivo del proceso de enseñanza-aprendizaje, pero para ser útiles necesitan de la Dimensión matemática, y difícilmente se dan en ambientes aislados de los procesos de enseñanza. El conocimiento de los estudiantes es integrado a los demás conocimientos del profesor y forma parte integral de los demás conocimientos de la Dimensión didáctica. Por lo anterior, la efectividad de los aprendizajes dependerá, principalmente, de la habilidad del profesor para integrar las componentes de cada dimensión.
La Dimensión meta didáctico-matemática hace al profesor consciente de que de su formación y actualización continua y permanente depende, en gran medida, el aprendizaje de sus estudiantes; permite al profesor reflexionar sobre su propia práctica (Pino-Fan, Godino y Font, 2016). Es muy importante si se sopesa el interés en formar personas de bien, versus resolutores de problemas matemáticos, si se quiere que la formación matemática contribuya a la formación de mejores seres humanos y ciudadanos. El establecimiento de este tipo de relaciones entre las dimensiones y su efecto formativo dice mucho sobre la potencialidad del CDM.
2.2 Acerca de las funciones
El objeto matemático función es el resultado de grandes esfuerzos de diferentes pensadores, y en su desarrollo histórico de más de 2,000 años ha sido objeto de diversas acepciones y generalizaciones (Parra y Pino-Fan, 2016). Según Sastre, Rey y Boubée (2008) tiene sus raíces en el desarrollo del concepto de número. En la antigüedad los griegos trabajaron problemas que involucraban funciones, sin reconocerlas como tales, y haciendo sólo representaciones verbales o gráficas. Sin embargo, son aportaciones relevantes de la cultura helénica que, si bien no correspondían explícitamente al concepto de función, sí pueden considerarse los primeros antecedentes en su desarrollo. Para Kleiner (1989) el periodo más fecundo en la realización del concepto de función fue de 1450 a 1650, con grandes hechos como: 1) La extensión del concepto de número al de números reales y números complejos por Bombelli y Stifel; 2) La creación del álgebra simbólica por Vieta y Descartes; 3) Los estudios de problemas de movimiento por Kepler y Galileo; y 4) La unión entre el álgebra y la geometría por Fermat y Descartes. Según Leinhardt, Stein y Zaslavky (1990), el concepto de función tiene un estatus de facilitador en el aprendizaje de las matemáticas, pues permite la interacción de aprendices y objetos matemáticos, a través de actividades que involucran funciones con elementos del medio sociocultural.
El concepto de función es, sin lugar a dudas, un elemento fundamental en el desarrollo histórico de la humanidad, y ha adoptado a lo largo de su evolución histórica al menos seis significados parciales (Parra y Pino-Fan, 2016): 1) La función como correspondencia, 2) La función como relación entre magnitudes variables, 3) La función como representación gráfica, 4) La función como expresión analítica, 5) La función como correspondencia arbitraria, y 6) La función a partir de la teoría de conjuntos. El término "función" fue usado por primera vez en 1673, en una obra de Leibniz; en la literatura frecuentemente alude a:
Una relación de correspondencia entre variables: relación en la que a cada valor en la variable de entrada le corresponde uno y sólo un valor de la variable de salida.
La correspondencia entre elementos de dos conjuntos: una regla en la que cada elemento del conjunto de partida debe estar relacionado con un único elemento del conjunto de llegada.
La dependencia entre dos variables: por cada valor que se le asigne a la variable independiente, existe un único valor de la variable dependiente.
El conjunto de pares ordenados: es un conjunto de pares ordenados, con la condición de que la primera componente no se repita en ningún par del conjunto.
La relación entre dominio e imagen: relación que a cada número perteneciente al dominio D, le asocia un único resultado numérico de entre las imágenes f(x).
El criterio de la recta vertical: si se traza una recta vertical por cualquier parte del plano, si esta sólo corta la gráfica, la corta en una sola parte.
Cada definición se puede mirar como una relación de dependencia entre las variables, y en una representación gráfica, la variable independiente se asocia al eje de las abscisas y la dependiente al eje de las ordenadas. Los registros más comúnmente usados para representar una función son: analítico algebraico, analítico numérico, gráfico, figural, sagital, coloquial, tabular y el fenomenológico.
De acuerdo con el MEN (2005), el estudio de patrones, nociones y conceptos propios del pensamiento variacional -como constante, variable, razón de cambio, dependencia e independencia de una variable con respecto a otra, y con los distintos tipos de modelos funcionales- contribuye a la comprensión y uso de los conceptos y procedimientos de las funciones y sus sistemas analíticos, para el aprendizaje con sentido del cálculo. Con el propósito de desarrollar el pensamiento variacional sugieren analizar diferentes representaciones e intentar formular procedimientos, algoritmos o fórmulas que permitan reproducir el mismo patrón de regularidad, calcular el término siguiente, confirmar o refutar las conjeturas iniciales e intentar generalizarlas. Entre los estándares propuestos por el MEN (2005) para el desarrollo del pensamiento variacional, y los sistemas algebraicos y analíticos, están:
Identifico relaciones entre propiedades de las gráficas y propiedades de las ecuaciones algebraicas (...) Modelo situaciones de variación con funciones polinómicas. Identifico y utilizo diferentes maneras de definir y medir la pendiente de una curva que representa en el plano cartesiano situaciones de variación. Identifico la relación entre los cambios en los parámetros de la representación algebraica de una familia de funciones y los cambios en las gráficas que las representan (p. 87).
En lo sugerido por el MEN (2005) se evidencia la importancia del uso de las representaciones semióticas como fundamento para relacionar los elementos de una función y asignarle significado y sentido a los conceptos. De acuerdo con Duval (2004), las representaciones semióticas son el medio que permite a un sujeto exteriorizar o comunicar sus representaciones mentales. A la transformación de una representación de un objeto sin cambiar de registro se le denomina tratamiento, y cambiando de registro se le llama conversión; es decir, un tratamiento se logra al decodificar la información de un registro y recodificarla en el mismo registro, mientras que en una conversión la información decodificada se recodifica en otro registro. Las similitudes de los elementos de dos o más representaciones permiten establecer las congruencias e incongruencias entre ellos. Duval (1999) asegura que "la comprensión de un contenido conceptual reposa en la coordinación de al menos dos registros de representación y esta coordinación se manifiesta por la rapidez y la espontaneidad de la actividad cognitiva de conversión" (p. 186).
El significado de los objetos estudiados surge de la identificación de los componentes conectados de las diferentes representaciones y la coordinación de las organizaciones cognitivas (Meel, 2003), al ponerlos en paralelo con representaciones fenomenológicas. De lo anterior cabe destacar la función de las representaciones semióticas como andamio en la adquisición de los conocimientos matemáticos, basados en la coordinación tanto intra-registro e inter-registros como trans-registro, es decir, en transformaciones tipo conversión o tipo tratamiento, y al poner en paralelo los elementos identificados en cada representación con elementos socioculturales que se pongan en juego y permitan asignar significado y sentido a los conceptos matemáticos estudiados.
3. Aspectos metodológicos
En este trabajo se evalúa la Dimensión matemática de los conocimientos didácticos-matemáticos de futuros profesores de matemáticas al hacer transformaciones de las representaciones de una función. En otras palabras, se analizan aquellos aspectos que comprenden sobre las funciones y la forma como los comunican. Se propuso un trabajo en dos dimensiones: ontológica y epistemológica. Ontológica por ser una actividad compartida donde la realidad se construye colectivamente a partir de la reflexión de los propios actores, buscando cambios en ellos mismos. Y epistemológica porque la realidad investigada es tratada de forma holística, teniendo en cuenta la relación de los participantes con el entorno educativo en que se forman, y el conocimiento se da como resultado de la interacción entre todos los actores implicados en el proceso (Colás y Buendía, 2004).
La muestra fueron 90 futuros profesores de matemáticas de la Universidad de Sucre, Colombia: 28 del tercer semestre, 28 del sexto semestre y 34 del octavo semestre. Se partió del supuesto que los desempeños de los estudiantes de los tres grupos eran diferentes, teniendo en cuenta la cantidad de cursos de didáctica y de matemática tomados por unos y otros.
Al terminar el tercer semestre los estudiantes han tomado unas 464 horas de formación matemática (dos cursos de Cálculo) y unas 432 horas de la componente didáctica-pedagógica (dos cursos de Didáctica de las matemáticas). Al terminar el sexto semestre han tomado unas 512 horas más de formación matemática (Cálculo III, Ecuaciones diferenciales y Análisis matemático), y unas 288 horas más de la componente didáctica-pedagógica (dos cursos más de Didáctica de las matemáticas). Y al terminar el octavo semestre han tomado unas 192 horas más de la componente disciplinar y unas 224 horas más en la componente didáctico-pedagógica, durante las cuales realizan su práctica docente.
A finales del segundo semestre del 2014 se aplicó un cuestionario con preguntas abiertas y cerradas sobre el mismo enunciado. Se escogió esta situación porque permite relacionar las funciones con el contexto sociocultural, lo cual facilita establecer congruencias entre elementos de dos o más representaciones de las funciones involucradas, comparar sus respectivos significados y encontrarles sentido al utilizarlos mientras se resuelve la situación.
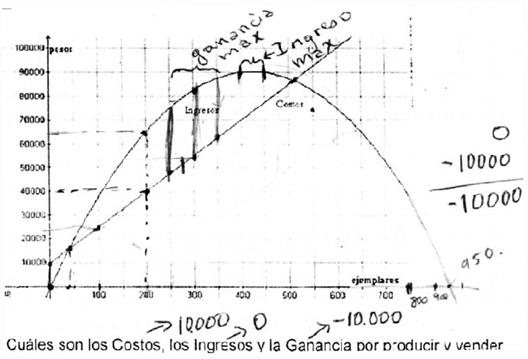
El enunciado del cuestionario es:
En la gráfica se muestran los costos de edición y los ingresos por la venta de una edición facsimilar del poema dramático de Alfonso Reyes, "Ifigenia cruel".
Figura 1 Cuestionario base aplicado a los estudiantes. Original tomado de: http://historiasdeactividades.blogspot.com/2007/09/ifigenia-cruel-de-alfonso-reyes.html
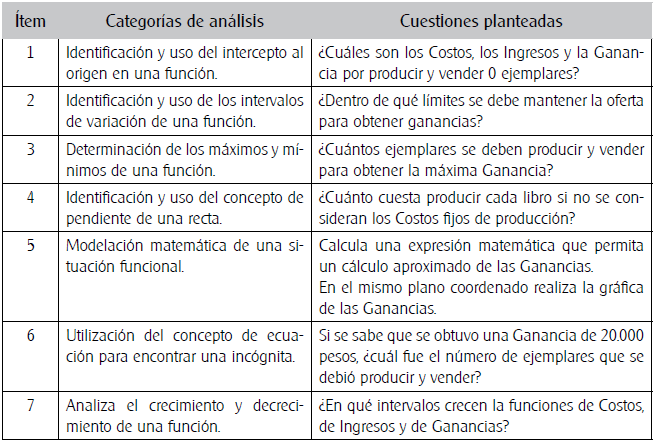
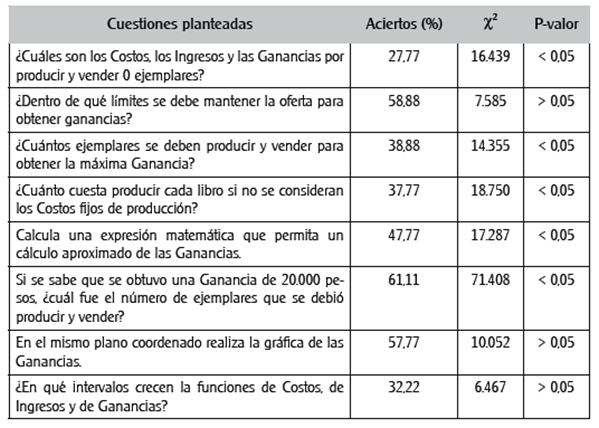
Al enlistar los indicadores que permiten determinar la relación de los elementos de la situación funcional con el contexto sociocultural se obtuvieron las categorías de análisis previas que se muestran en la Tabla 1, con las cuestiones planteadas por cada categoría.
Podría esperarse que al resolver cada ítem/tarea planteada, el estudiante identificara, en la representación gráfica de las funciones involucradas, el elemento por el que se le indagaba y, a partir de esta identificación, hiciera conversiones y/o tratamientos y diera su respuesta. Es decir, que decodificara del registro gráfico los elementos que necesitara de la función y los recodificara en otro o en el mismo registro.
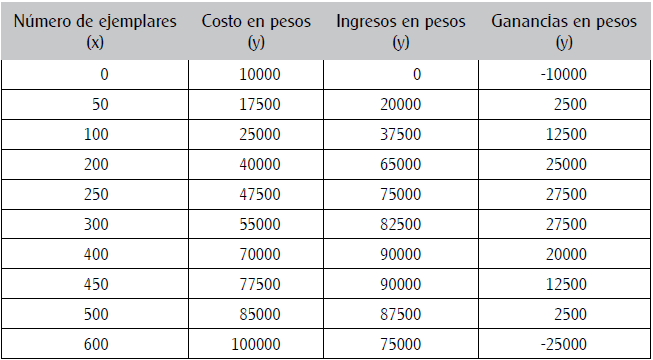
Por ejemplo, para obtener una representación tabular de las funciones involucradas se podían ubicar puntos con igual abscisa sobre las gráficas de las funciones de ingresos y de costos, y luego restar las coordenadas correspondientes (Ingresos - Costos) para obtener algunos valores de la función Ganancias y proceder a elaborar una tabla como la Tabla 2, donde los signos negativos para las Ganancias indican pérdidas. En las representaciones mostradas en este ejemplo se utiliza la siguiente convención de colores: blanco para el Número de ejemplares, verde para los Costos, azul para los Ingresos y morado para las Ganancias.
Asimismo, es posible obtener las representaciones algebraicas de las funciones de Costos,
Ingresos y Ganancias, para ello es necesario realizar algunas transformaciones
tipo conversión y/o tipo tratamiento. Similar a como se hizo para construir la
tabla, se obtienen algunos puntos sobre las representaciones graficas de las
funciones de Ingresos y de Costos, y con esta información se tiene una
conversión al registro aritmético numérico, con la que además se puede construir
una representación cartesiana para cada una de las dos funciones: e. g., Costos
(0, 10.000), (200, 40.000); Ingresos (0,0), (50, 20.000) y (400, 90.0000), y
utilizar esta información para hallar la pendiente de la recta (función de
Costos): 
, que
corresponde al costo de cada ejemplar sin considerar los costos fijos de
producción. Utilizando esta pendiente y el intercepto al origen en el eje Y, se
puede obtener la expresión algebraica: Costos C(x) = 150x + 10.000.
Esto indica que los costos fijos de producción para este libro son de 10.000
pesos, y el costo de edición de cada ejemplar, sin tener en cuenta los costos
fijos de producción, es de 150 pesos.
Para la función de Ingresos se pueden tomar los tres puntos de la representación cartesiana mostrada anteriormente y remplazarlos en la forma general de una función cuadrática: I(x) = ax 2 + bx + c y resolviendo el sistema de ecuaciones: (1) c = 0; (2) 20.000 = 2.500a + 50b y (3) 90.000 = 160.000a + 400b se tiene que a = -0,5 y b = 425 y reemplazando estos valores en I(x) = ax 2 + bx + c se obtiene la función de Ingreso I(x)= -0.5x2 + 425x. Y como:
Ganancias es igual a Ingresos menos Costos [transformación tipo conversión]
G(x) = I(x) - C(x) [transformación tipo conversión]
G(x) = -0.5x2+425x - (150x+10.000) [transformación tipo tratamiento]
G(x) = -0.5x2+425x-150x-10.000 [transformación tipo tratamiento]
G(x) = -0.5x2+275x-10.000 [transformación tipo tratamiento]
Se dice que la transformación es tipo conversión porque se hace un cambio de registro, pasando del registro gráfico al del lenguaje coloquial, y de este al algebraico. Se dice que la transformación es tipo tratamiento porque se hacen transformaciones al interior del registro algebraico, sin abandonarlo.
Con la información anterior, y siguiendo la convención de colores, en la Figura 2 fueron reconstruidas las representaciones gráficas de las funciones involucradas en la situación, y se incluyó la representación gráfica de las Ganancias.
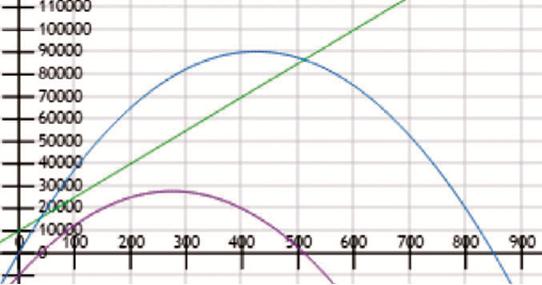
Figura 2 Representación gráfica de las funciones de Costo, de Ingresos y de Ganancias, en diferentes colores.
La convención de colores facilita realizar las congruencias e incongruencias entre los elementos comparables de las representaciones en cada registro, al ponerlos en paralelo y empezar a comparar los elementos ostensibles, tanto en unos como en otros registros y representaciones. Este análisis de congruencias es un fuerte potencializador para la comprensión de las funciones, al hacer el tránsito entre todas las representaciones posibles y relacionarlas con los elementos de las representaciones del registro fenomenológico. De ahí la importancia de poder efectuar transformaciones en matemáticas como herramienta/instrumento para el aprendizaje de un concepto (Del Castillo, 2013).
Con los resultados se hizo un análisis comparativo de las calificaciones medias de los tres grupos al resolver el cuestionario, y utilizando tablas de contingencias, con el coeficiente Chi-Cuadrado de Pearson (α = 0,05), son analizadas las asociaciones entre las respuestas dadas a cada ítem, con el grupo de donde estas provinieran.
Para elaborar el análisis y la caracterización de los objetos matemáticos primarios y procesos presentes en las prácticas matemáticas que desarrollan los estudiantes al resolver el cuestionario, se utilizó la noción de configuración ontosemiótica (Pino-Fan, Godino y Font, 2015), a través de la cual se pueden identificar y describir en detalle elementos lingüísticos, conceptos/definiciones, propiedades/proposiciones, procedimientos y argumentos de los objetos matemáticos implicados, así como sus significados y los procesos incluidos en las prácticas matemáticas institucionales o personales. Aquí solamente se reportan los resultados de la dimensión matemática del CDM de los futuros profesores al resolver el cuestionario.
4. Resultados, análisis y discusión
En la presentación de los resultados se muestra una tripleta (i, j, k) donde "i" (entre 0 y 28) representa la cantidad de estudiantes del tercer semestre, "j" (entre 0 y 28) la de los del sexto semestre y "k" (entre 0 y 34) la de los del octavo semestre que hicieron referencia al tópico analizado en ese ítem. Y se presenta P(r)i, j, ó k donde r = 3, 6 u 8 semestre, para referir a un profesor en formación de alguno de los tres niveles.
4.1 Dimensión Matemática
4.1.1 Conocimiento Común del contenido
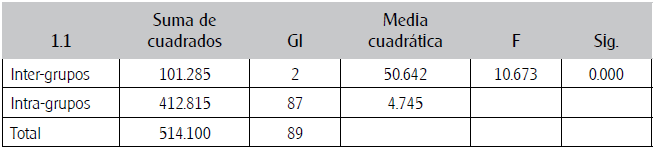
Los resultados del análisis de varianza mostrado en la Tabla 3 y las comparaciones múltiples de la Tabla 4 evidencian que se encontraron diferencias estadísticamente significativas en las calificaciones medias de los estudiantes de sexto semestre con los demás grupos (P < 0.05). Pero llama la atención que no se presentaran diferencias entre los de tercer semestre con los de octavo (ver Tabla 3) y que obtuvieran mejores promedios los de sexto semestre que los de octavo, cuando los de octavo han visto por lo menos 192 horas más de matemáticas, y aproximadamente 704 horas más de matemáticas que los de tercero. Cuestión preocupante, pues los estudiantes de octavo semestre ya cursaron el programa en su totalidad, por lo cual es poco lo que se puede hacer para mejorar su nivel disciplinar, así que ingresarán al mercado laboral con serias dificultades en la dimensión matemática. Que haya diferencias entre los de sexto semestre con los de tercero podría esperarse, puesto que los de sexto en ese momento habían visto aproximadamente 512 horas más de matemáticas que los de tercero, pero a los de tercer semestre les faltan unas 704 o más horas en la componente disciplinar para terminar la carrera, lo que puede ser tiempo suficiente para alcanzar o superar el nivel mostrado por los estudiantes de sexto semestre.
Tabla 4 Prueba DMS de Comparaciones múltiples de las Calificaciones medias al resolver el cuestionario.
A continuación se estudian, por categorías de análisis, los resultados de las respuestas al cuestionario dadas por los estudiantes de los tres grupos.
Identificación y uso del intercepto al origen en una función
En esta pregunta (ítem 1) del cuestionario, se pidió a los estudiantes encontrar los Costos, los Ingresos y la Ganancia por producir y vender 0 ejemplares. Se esperaba que con una inspección visual pudieran encontrar los Costos e Ingresos al producir y vender cero ejemplares, así como inferir, por sustracción, la Ganancias. Sólo 27,7% (8, 13, 4) respondió acertadamente este ítem. La respuesta que predominó entre los estudiantes (44,4%) tenía las dos primeras opciones correctas, Costos e Ingresos, y la Ganancias cero (0), como se muestra en la respuesta del estudiante P(3)2 (Figura 3).
En este objeto los estudiantes (21, 24, 25) utilizan elementos lingüísticos verbales, números naturales y el signo igual, como se observa en la respuesta dada por P(3)2 cuando indica "Costos = 10.000, Ingresos = 0 y Ganancias = -10.000". Entre los conceptos/definiciones que utilizan, destaca el de intercepto al origen; asimismo, entre las proposiciones/propiedades parecen reconocer el punto (0, 10.000) como el intercepto de la recta Y = 150x + 10.000 con el eje Y, evidenciadas ambas representaciones en la respuesta de P(3)2 cuando dice: "punto de corte con eje Y → 10.000". En cuanto a los procedimientos utilizados por los estudiantes (18, 21, 14), parece ser evidente un análisis visual, ya que no muestran ningún procedimiento, como se ve en la respuesta de P(3)2 (Figura 3). En este caso, el análisis visual funcionó a medias porque estos estudiantes, a pesar de que pusieron en juego diferentes representaciones de la situación, no fueron capaces de concebir una Ganancia negativa, lo que pudo impedirles dar soluciones adecuadas al problema (Hitt, 2003). En relación con los argumentos, no hay evidencias explícita de ellos en las respuestas de ningún estudiante de alguno de los tres grupos.
Identificación y uso de los intervalos de variación de una función
En esta pregunta (ítem 2) se pidió encontrar los valores en que se debe mantener la oferta para obtener Ganancias y se esperaba que, a partir de un análisis visual, pudieran identificar el intervalo para dichos valores. 58,8% (13, 20, 20) de los estudiantes dio respuestas acertadas en este ítem, pero mostraron ciertas limitaciones para identificar el dominio de la función Ganancias en el registro gráfico, como evidencia P(8)1 (Figura 4) cuando dice "entre 400 y 450 ejemplares", quien confundió el dominio de la función Ganancias con el intervalo donde se dan los mayores ingresos. Confusiones de este tipo pudieron ocasionar el alto porcentaje de desaciertos (41.2%), quizá por no poder establecer conexiones entre las representaciones semióticas involucradas en la situación (Meel, 2003) y a partir de ahí dar sus respuestas.
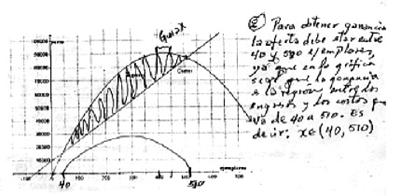
Los elementos lingüísticos empleados por los estudiantes (10, 14, 16) en la identificación y uso de los intervalos de variación de una función fueron mayoritariamente verbales combinados con números enteros, como lo hace P(8)1 (Figura 4) cuando escribe: "entre 400 y 450 ejemplares". Respecto a los conceptos/definiciones, la totalidad de los estudiantes utiliza intervalos como lo hace P(6)4 (Figura 5), quien los expresa de dos formas: "de 40 a 510" o "x∈ (40, 510)". Las proposiciones/propiedades utilizadas, aunque no lo expliciten sí dejan ver que el número de ejemplares para los cuales se tiene Ganancias está entre 40 y 510, esto se hace evidente en el manuscrito de P(6)4 cuando marca sobre el eje x, 40 en un extremo del segmento y 510 en el otro, subrayando además la región del plano correspondiente a las Ganancias en ese intervalo. Los procedimientos usados por los estudiantes parecen ser visuales, como lo manifiesta P(6)4 en su respuesta mostrada en la Figura 5. Y los argumentos son muy escasos en los estudiantes de los tres grupos, sin embargo hay quienes como P(6)4 dan cuenta de estos cuando dice: "para obtener ganancia la oferta debe estar entre 40 y 510 ejemplares, ya que en la gráfica se ve que la ganancia es la región entre los ingresos y los costos que va de 40 a 510".
Determinación de los máximos y mínimos de una función
En esta pregunta (ítem 3) se pidió obtener el número de ejemplares que se deben producir y vender para obtener la máxima Ganancia. Se esperaba que confundieran las Ganancias máximas con los Ingresos máximos. Sólo 38,9% (12, 13, 10) pudo determinar el intervalo donde la Ganancia es máxima. En su mayoría (53,3%) consideraron el intervalo [0, 700] como respuesta, quizá en virtud de que esos eran los extremos visibles en la gráfica y -según lo reportado por Hitt (2003)- los estudiantes tienden a dejarse llevar por lo visual. Sin embargo, no consideraron las representaciones geométricas como complementarias en su proceso de resolución del problema, y como se esperaba (14, 11, 23) terminaron confundiendo la Ganancia máxima con los Ingresos máximos, lo que se evidencia en el manuscrito de P(6)4 (Figura 5), quien marca la Ganancia máxima en la región correspondiente a los Ingresos máximos, tal vez debido a que la gráfica de la función Ganancia no estaba explícita en la situación, por lo cual no pudieron asociarla con algo conocido (Suárez y Cordero, 2010), y en el manuscrito de P(6)1 que dice: "la mayor Ganancia se da cuando se llega a 400 ejemplares".
Los elementos lingüísticos utilizados por los estudiantes en la determinación de los máximos y mínimos de una función fueron verbales combinados con números naturales, elementos gráficos y signos de operación, como lo hace P(6)1 (Figura 6), que afirma: "la Ganancia máxima es de 20.000 → Ingresos - Costos = Ganancia". Entre los conceptos/definiciones empleados están máximos y mínimos, intervalo y función, en particular P(6)1 plantea la estructura aditiva "Ecuación ganancia → Ingresos - Costos = Ganancia", donde se evidencia el uso del concepto de función. En relación con las proposiciones/propiedades, determinan la mayor distancia entre las gráficas de las funciones Ingresos y Costos como la mayor Ganancia, al igual que el intervalo más alto de la función Ingresos como los puntos donde esta función toma sus valores máximos, así lo hace P(3)7 (Figura 7). Respecto a los procedimientos usados, se evidencian procesos de visualización complementados con algunos trazos figurales: P(6)4 (Figura 5), por ejemplo, muestra el punto más alto de la gráfica de Ingresos como la Ganancia máxima y subraya la región correspondiente a las Ganancias, estableciendo con esto congruencias entre elementos de las representaciones gráficas, figural y del lenguaje coloquial. Y en cuanto a los argumentos, no se muestran evidencias claras de ellos, sin embargo P(6)1 en su manuscrito parece querer argumentar su actuar a partir de la serie de pasos que realiza cuando dice: "Así los ingresos = 90.000 y costos = 70.000 ecuación ganancia → Ingresos - Costos = Ganancia → en la gráfica ? 90.000 - 70.000 = 20.000 ← representa la ganancia".
Identificación y uso del concepto de pendiente de una recta
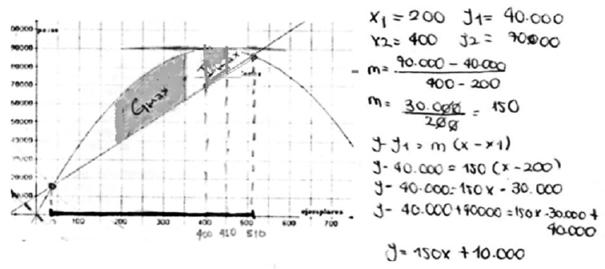
En esta pregunta (ítem 4) se pidió a los estudiantes el costo de producir cada libro si no se consideran los Costos fijos de producción. Se esperaba que identificaran, en el contexto de la situación, la pendiente de la función de Costos, localizaran dos puntos por donde pasa su gráfica y utilizaran la fórmula de la pendiente para encontrarla, como lo hizo P(3)7 (Figura 7). Sólo 37,8% (9, 18, 7) dio respuestas acertadas a este ítem. Otro grupo (12, 4, 14) hizo un análisis visual que no favoreció su avance en la solución de esta tarea (Domenicantonio, Costa y Vacchino, 2011), considerando como respuesta 10.000 -los Costos fijos de producción-, en tanto que otros (7, 6, 13) como P(8)3 (Figura 8) consideraron como respuesta 1500, valor que pudo obtenerse por error al simplificar.
Para este ítem los estudiantes (18, 21, 23) utilizaron elementos lingüísticos verbales y números naturales, expresiones aritméticas, algebraicas y figurales, como lo hace P(8)3 (Figura 8) cuando escribe: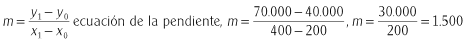 
. Entre los conceptos/definiciones que emplean destaca par ordenado, intercepto al origen, ecuación y pendiente de una recta, como lo muestra P(8)3. En relación con las proposiciones/propiedades, parecen reconocer la pendiente de la recta como determinante de la variación de la función lineal, para el caso P(8)3 señala "θ ← pendiente", quien además establece congruencias entre los elementos de diferentes representaciones semióticas de los registros analítico numérico, gráfico, del lenguaje coloquial y algebraico, como se muestra en los ejemplos anteriores. Respecto a los procedimientos utilizados (19, 10, 27), elaboran una conversión del registro gráfico al analítico numérico, donde hacen algunos tratamientos hasta dar con su respuesta, y usan estos elementos para realizar una conversión al registro algebraico, en el cual efectúan una secuencia de tratamientos hasta obtener la expresión algebraica de los Costos, como puede verse en la solución dada por P(8)3. En cuanto a los argumentos, ninguno los establece claramente.
Modelación matemática de una situación funcional
Para la modelación matemáticamente de una situación funcional, se pidió a los estudiantes resolver dos cuestiones: 1) Calcular una expresión algebraica que permitiera un cálculo aproximado de las Ganancias, y 2) Realizar en el mismo plano coordenado donde estaban las gráficas de las funciones de Ingreso y de Costos, la gráfica de las Ganancias.
1) Ante la primera cuestión (ítem 5) se esperaba que hallaran primero las expresiones algebraicas para los Ingresos y los Costos, y a partir de varias conversiones y tratamientos, encontraran la expresión buscada. Solamente 47,8% (10, 22, 11) de los estudiantes dio respuestas acertadas, con algo de desorden al comunicarlas, como lo hace P(6)11, que denota de varias maneras la función de ingresos y no guarda una secuencia lógica en la presentación de sus resultados. La siguiente opción más respondida correspondió a una función lineal, reforzando lo reportado por Marroquín (2009), quien señala que los estudiantes -al pedírseles modelar algebraicamente una función- tienden a dar como respuesta una función lineal.
Los elementos lingüísticos utilizados por los estudiantes (24, 27, 29) al calcular una expresión algebraica que permitiera un cálculo aproximado de las Ganancias fueron mayoritariamente algebraicos y aritméticos, combinados con números naturales y elementos verbales, como lo hace P(6)11 (Figura 9) cuando anota: "y - 90.000 = 4p (x - 400)2 ecuación de la parábola". Entre los conceptos/definiciones que emplean están: parábolas, rectas, punto, vértice y funciones, como muestra P(6)11 al expresar "G(x) = -0.5x2 + 275x - 10.000", reportando la expresión algebraica que representa las Ganancias. En relación con las proposiciones/propiedades (10, 22, 11), identifican gráficamente el vértice y un punto de la gráfica de la parábola, y los usan para encontrar una expresión algebraica que dan como respuesta; P(6)11, en particular, dice: "(400, 90.000) vértice". En cuanto a los procedimientos usados, en su mayoría (15, 24, 23) identifican el vértice y otro punto por donde pasa la gráfica de la parábola y, utilizando su forma canónica, dan su respuesta, por ejemplo P(6)11, quien encuentra primero las funciones de Costos y de Ingresos, y, a partir de ellas, la de Ganancias. Otros (9, 4, 11) dan como respuesta la expresión algebraica que representa los Costos. Respecto a los argumentos, en ninguno de los tres grupos se evidencian con claridad.
2) Al construir en el mismo plano coordenado donde se presentó la situación, la gráfica de las Ganancias (ítem 6), se esperaba que los estudiantes -a partir de un análisis visual y mediante una serie de conversiones y tratamientos- obtuvieran la gráfica de las Ganancias, al identificar los interceptos de las gráficas de las funciones de Ingresos y de Costos y asociarlos con los cortes de la gráfica de la función Ganancias con el eje de las abscisas, y que su altura la asociaran con la diferencia de las funciones Ingresos y Costos. 57,8% (14, 20, 18) de los estudiantes obtuvo respuestas acertadas. En el análisis de desaciertos se evidencia que apuntaron a que la Ganancia mínima debía ser cero (38,9%), hecho que concuerda con sus respuestas cuando se les preguntó por el intercepto al origen de las tres funciones en el ítem 1, como se muestra en la gráfica elaborada por P(6)2 (Figura 10). Este hecho constituye un obstáculo en el sentido de Brousseau (1999), lo cual pudiera considerarse normal, teniendo en cuenta la sorprendente lentitud de la humanidad en el proceso histórico de construcción del concepto de número negativo (Cid y Bolea, 2007).
Los elementos lingüísticos utilizados por los estudiantes al construir, en el mismo plano coordenado donde estaban las gráficas de las funciones de Ingreso y de Costos, la gráfica de las Ganancias, fueron verbales, gráficos, figurales y números enteros, como lo hace P(6)2 (Figura 10). Entre los conceptos/definiciones que usan destacan funciones, puntos, graficas e interceptos al origen. En relación con las proposiciones/propiedades, parecen reconocer los puntos de corte de las funciones de Ingresos y de Costos y asociarlos con los ceros de la función Ganancias en el eje de las abscisas, como se evidencia en la respuesta de P(6)2 quien además establece congruencias entre elementos gráficos y del lenguaje coloquial cuando señala con una flecha y dice "gráfica ganancia". Según los procedimientos empleados, se puede inferir que lo hicieron por simple inspección visual, en tanto que otro grupo sólo sombreó la región correspondiente a las Ganancias, similar a como lo hizo P(6)2. No hay evidencias claras de los argumentos.
Utilización del concepto de ecuación para encontrar una incógnita
En esta pregunta (ítem 7) se pidió encontrar el número de ejemplares que se debió producir y vender si se sabe que se obtuvo una Ganancia de 20.000 pesos. Se pretendía que identificaran gráficamente dos puntos de igual abscisa, uno para la función Ingresos y otro para la de Costos, de tal forma que su diferencia fuera aproximadamente 20.000 pesos, o que si ya habían obtenido la expresión algebraica de las Ganancias, armaran una ecuación igualándola a 20.000 y que, al encontrar la incógnita, respondieran. 61,1% (14, 21, 20) de los estudiantes dio respuestas acertadas, los restantes cometieron errores al modelar la expresión algebraica de las Ganancias, como lo hizo P(3)18 (Figura 11), quien además comete errores al adecuar la ecuación, antes de aplicar la fórmula general, lo que pudo impedirle responder satisfactoriamente (Domenicantonio, Costa y Vacchino, 2011).
Los elementos lingüísticos que emplearon los estudiantes al usar el concepto de ecuación para encontrar una incógnita fueron mayoritariamente algebraicos, aritméticos y verbales, como lo muestra P(6)6 (Figura 12) cuando expresa: "-0.05(400)2 + 273.5(400) - 10.000 es G(400)". Entre los conceptos/definiciones que utilizan destacan función, polinomio aritmético y ecuación cuadrática, por ejemplo P(3)18 y P(6)6 (Figuras 11 y 12). En cuanto a las proposiciones/propiedades, un grupo amplio (14, 21, 20) identificó puntos en la gráfica de la función de Ingresos y en la de Costos, y los relacionó con elementos del contexto sociocultural donde se plantea la situación. Los procedimientos utilizados son esencialmente los que se previeron: 1) (13, 16, 15) dieron sus respuestas luego de un análisis visual; 2) (12, 13, 14) hacen una conversión al registro algebraico y formulan una ecuación cuadrática e intentan resolverla, como se muestra en el manuscrito de P(6)6 cuando consigna: "Así que al revisar la gráfica nos damos cuenta que si se tienen 400 ejemplares la diferencia entre los ingresos y los costos es de 20.000...", que además dice haber encontrado la expresión algebraica por tanteo. Un grupo muy reducido de estudiantes (0, 3, 1) argumentan sus respuestas, como es el caso del P(6)6, quien expresa: "... por tanto si se tiene una ganancia de 20.000, es porque se tienen 400 ejemplares".
Análisis del crecimiento y decrecimiento de una función
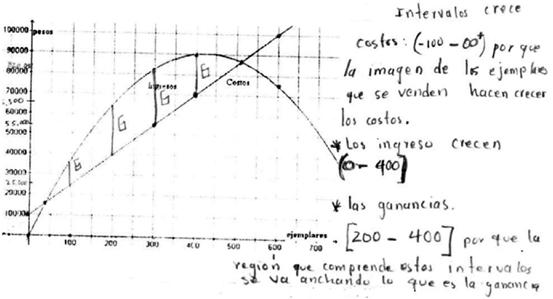
En esta pregunta (ítem 8) se les pidió determinar en qué intervalos crecen las funciones de Costos, de Ingresos y de Ganancias. Se esperaba que los estudiantes identificaran visualmente el crecimiento en cada una de las tres funciones y, a partir de esto aportaran sus respuestas. Únicamente 32,2% (10, 12, 7) de ellos dio respuestas acertadas. Se evidencian serias dificultades con la comprensión del concepto de crecimiento, porque fue mucho mayor el número de quienes hicieron la gráfica de la función Ganancias que los que dieron una respuesta acertada a este ítem y al hacer la gráfica debieron darse cuenta hasta donde crece esta función. La dificultad parece estar centrada en el uso indistinto de la letra como magnitud y como variable generalizada (Font, 2011) y en el obstáculo que genera el análisis gráfico de una situación funcional, y aunque los estudiantes tienen la tendencia de no ir más allá de lo visual (Franco y Ochoviet, 2006), combinaron el uso de la letra como variable generalizada con un análisis visual irreflexivo, como lo muestra la respuesta de P(3)8, que da valores fuera del dominio de la situación funcional "costos (-100, -∞+)", combinados con valores al alcance de su visual cuando dice: "los ingresos crecen (0,400]".
En este ítem los elementos lingüísticos que utilizan los estudiantes (19, 19, 22) son mayoritariamente verbales combinados con números naturales e intervalos, como hacen P(3)11 y P(3)8 (Figuras 13 y 14). Entre los conceptos/definiciones que usan destacan el de intervalo y ejes coordenados, como muestra P(3)8 (Figura 14) al expresar: "de cero a 425 ejemplares". En relación con las proposiciones/propiedades, la mayoría (18, 16, 27) asoció los intervalos solicitados a lo que estaba a su alcance visual, por ejemplo P(3)11, quien hace un análisis visual muy limitado, tanto para la función Costos como para la de Ganancias, mientras que el análisis realizado por P(3)8 (Figura 14) es mucho más completo y adecuado a la situación, asociando el eje Y a cada función analizada cuando escribe: "el eje Y (costos)". Los procedimientos efectuados por los estudiantes de los tres grupos parecen ser solamente visuales. En cuanto a los argumentos, se dan algunos casos aislados como P(3)8 (Figura 14) al decir: "Ingresos: de cero a 425 ejemplares, ya que la función es cuadrática, por lo tanto una parte crece y la otra decrece y en este intervalo donde se aprecia que a medida que se aumenta en unidades sobre el eje X, el eje Y (Ingresos) también lo hace".
A manera de conclusión en cuanto al conocimiento común, las diferencias entre los grupos ocurren en las calificaciones al resolver el cuestionario, mientras que las características de los objetos matemáticos mostrados por estudiantes de los tres niveles, en sus procesos de solución, son muy parejos, tanto intra como inter grupos.
4.1.2 Conocimiento ampliado del contenido
Como hemos visto, el conocimiento matemático es necesario para entender las matemáticas, tanto en el nivel que se orienta como en el nivel posterior (Pino-Fan y Godino, 2015). Permite poner en correspondencia diferentes objetos matemáticos, o hacer conexiones entre representaciones de un mismo objeto matemático. Determina el repositorio de recursos matemáticos usados por una persona ante una situación problema que tenga que resolver.
Las respuestas dadas por los estudiantes de los tres grupos a los ocho ítems del cuestionario son muy diversas. Únicamente (8, 21, 9) de ellos dieron respuestas adecuadas a por lo menos seis ítems, mientras que otro grupo mucho más amplio (20, 7, 25) presentó serias dificultades, tanto en la comprensión de los enunciados de algunos ítems como en la elaboración de los procedimientos; también al tratar de hacer conexiones entre diferentes representaciones de las funciones y en la comunicación de los resultados. Así, se puede decir que los estudiantes del primer grupo poseen un dominio adecuado de la Dimensión matemática para resolver problemas con las características del que se les planteó. Del segundo grupo podemos decir que las dificultades al identificar y relacionar los elementos de una función en uno o varios registros podrían ser un impedimento para el desarrollo del pensamiento variacional, indispensable para el acceso al cálculo (Hitt, 2003).
Que los profesores orientadores de los procesos de enseñanza y aprendizaje de las matemáticas tengan este tipo de dificultades es problemático para la enculturación matemática de las comunidades donde se van a desempeñar, ya que si no poseen sólidos conocimientos de la Dimensión matemática, difícilmente van a poder gestionar de manera adecuada los aprendizajes de sus futuros estudiantes. Sin embargo, se presentaron casos aislados donde se evidencian algunos fundamentos del conocimiento ampliado del contenido: P(6)5 (Figura 14) intentó, por integración, encontrar el área entre las gráficas de los Ingresos y la de los Costos; además, al relacionar los elementos identificados en las representaciones con elementos del contexto sociocultural donde se plantea la situación, hace un análisis trans-registro, proporcionando significado a los objetos estudiados (Pino-Fan y Godino, 2015).
Otro que evidencia algunos fundamentos del conocimiento ampliado del contenido es P(8)9 (Figura 15), pues usa elementos no visuales en la gráfica cuando prolonga tanto el eje de los ejemplares como la gráfica de los Ingresos, conservando la secuencia de los elementos originales, y a partir de ahí da su respuesta; por otra parte, P(3)18 y P(6)13 (Figuras 17 y 18) intentan utilizar la fórmula para resolver una ecuación cuadrática.
Asimismo, fue significativo el número de estudiantes (9, 18, 7) que reconoció la pendiente de la recta en el contexto de la situación. Un grupo amplio de estudiantes (7, 12, 4) realizan varios procedimientos para llegar a una misma respuesta, en más de un ítem, y para designar las Ganancias subrayaron la región del plano correspondiente, hicieron la gráfica, la asociaron con su representación coloquial y encontraron la representación algebraica.
Como puede apreciarse en la Tabla 5, se presentaron altos niveles de homogeneidad al interior de los grupos en 62,5% de las respuestas dadas a las cuestiones planteadas, es decir, la tendencia por grupos fue a dar las mismas respuestas, tanto en los aciertos como en los desaciertos. Que la homogeneidad al interior de los grupos sea alta y que los porcentajes de aciertos en ellos no lo sean, significa que hubo un alto grado de acuerdos, sobre todo en los desaciertos. Y que la homogeneidad al interior de los grupos sea alta y los porcentajes de aciertos también lo sean, indica que hubo un alto grado de acuerdos, sobre todo en los aciertos. Por ello, es muy posible que estos resultados no sean productos del azar, sino que se deban a las creencias y formas de orientar los procesos de enseñanza de algunos profesores, que orientan a algunos grupos y no a otros.
Conclusiones
Al evaluar la Dimensión matemática del CDM de los futuros profesores de matemáticas, se encontraron serias dificultades con la comprensión de la noción función, específicamente con la identificación y uso de los elementos de las funciones involucradas, la identificación de los interceptos al origen sin ayuda gráfica y el análisis de los valores extremos, así como con los intervalos de crecimiento la modelación de las funciones y la identificación de la pendiente de la función lineal. Los objetos primarios y procesos presentes en las prácticas que desarrollan los estudiantes al hacer transformaciones de las representaciones de las funciones involucradas en la situación son muy similares en los tres grupos, a pesar de la diferencia en horas desarrolladas en el programa, en cada uno de los tres niveles.
A pesar de los esfuerzos de los estudiantes por establecer conexiones entre diferentes representaciones de las funciones estudiadas, la generalidad es que privilegian transformaciones tipo conversión hacia un sólo registro, donde recodifican la información, realizan algunos tratamientos y proceden a responder, siendo deseable que establezcan conexiones entre diferentes registros (Duval 2004), ya que según Font (2011), estos ponen en función diferentes procesos cognitivos, cada uno de ellos estrechamente relacionado con otros. Pero además de pensar en los procesos cognitivos que podrían activarse haciendo conexiones entre representaciones, cabe pensar en la representación como una herramienta que posibilita prácticas que sin ella no serían posibles.
Uno de los conflictos epistémicos más marcados en relación con el concepto de función (Godino, Wilhelmi y Bencomo, 2005) es el distanciamiento entre el reconocimiento del concepto a nivel escolar y su uso consciente a nivel social. Esto se manifestó en la no aceptación -por parte de algunos estudiantes- de representaciones como la gráfica, la tabular, la del lenguaje coloquial y la fenomenológica en calidad de representaciones de una función, y por ello no las usaron como apoyo para dar sus respuestas, a pesar de que las actividades propuestas fueron pensadas teniendo en cuenta este tipo de conflictos, reportados en algunos de los antecedentes revisados.
