Introducción
Con el propósito de identificar conocimientos matemáticos implicados en determinadas actividades laborales y de analizar sus posibles vínculos con conocimientos matemáticos escolares, se llevaron a cabo dos investigaciones de manera independiente: por una parte se indagaron los conocimientos sobre la proporcionalidad de menores trabajadores en un medio urbano (Padilla, 2015), y por otra parte se investigaron los conocimientos sobre números y cálculos aritméticos de menores trabajadores agrícolas (Solares, D., 2012).
En el transcurso de las indagaciones los sujetos hicieron referencias a situaciones explícitas de enseñanza (de los trabajadores más expertos a los novatos) o bien, se manifestaron interacciones en el desarrollo de la actividad laboral que daban lugar a formas sutiles de enseñanza, como se mostrará más adelante. Se considera necesario recuperar esas manifestaciones de enseñanza para analizarlas y discutir su papel en los aprendizajes matemáticos de los sujetos que participan en tales actividades laborales. Esta discusión es pertinente por las siguientes razones:
Al parecer, se ha reservado el término "enseñanza" para los espacios escolares, y es ahí donde suelen estudiarse las prácticas de enseñanza. Sin embargo, en las investigaciones que aquí se reportan se identificó que esas prácticas también tienen lugar en situaciones extraescolares.
Se coincide con la perspectiva teórica de la TAD (Chevallard, 1999; Chevallard, Bosch y Gascón, 1998) cuando señala que en las prácticas de enseñanza se ponen de manifiesto conocimientos matemáticos; por lo tanto, se asume que las prácticas de enseñanza identificadas en ambos estudios constituyen un medio propicio para indagar los conocimientos matemáticos que se movilizan en situaciones extraescolares.
El análisis de distintas formas de enseñanza en situaciones extraescolares aporta elementos para profundizar en la indagación sobre los vínculos y/o las distancias entre conocimientos matemáticos de distintos contextos, lo cual ha sido motivo de varias investigaciones en el campo de la educación matemática.
En los siguientes apartados se abordará cada uno de los planteamientos anteriores y se presentará el análisis de la evidencia que los soporta.
Antecedentes teóricos
Los conocimientos matemáticos de poblaciones específicas, en contextos laborales y de la vida cotidiana, han sido documentados por la investigación en educación matemática. Diversos estudios se han dedicado a la exploración de dichos conocimientos con menores trabajadores (Carraher et al, 1995; Solares, D., 2012), adultos no alfabetizados (Ferreiro et al, 1987; Ávila, 1988; Carraher et al, 1995; Soto, 2001; De Agüero, 2006), distintos grupos culturales desde la Etnomatemática (D'Ambrosio, 2002), o "simples personas corrientes (spc,s)" (Lave, 1991).
Aun cuando en esas investigaciones se identifican ciertas relaciones, distancias, conflictos o, incluso, vínculos entre los conocimientos matemáticos provenientes de la escuela y los que se movilizan en otros contextos, poco se ha dicho sobre la enseñanza en contextos extraescolares. Es probable que su papel en la adquisición de nuevos conocimientos se haya visto socavado por el énfasis en los procesos de los aprendices, sin considerar las aportaciones que los expertos hacen a tales procesos mediante distintas formas de enseñanza.
Las dos investigaciones que aquí se reportan (Padilla, 2015; Solares, D., 2012) abordan el estudio de los conocimientos matemáticos en contextos extraescolares, partiendo del análisis de cómo se concibe a las matemáticas, a su aprendizaje y a la misma enseñanza. Para ello, ambas investigaciones se vieron en la necesidad de poner en diálogo perspectivas teóricas distintas, tanto didácticas como no didácticas. A continuación se presentan los aspectos fundamentales de ese diálogo.
El carácter relativo del conocimiento matemático
La Teoría de las Situaciones Didácticas y la Teoría Antropológica de lo Didáctico son teorías didácticas que fungen como marco para ambas investigaciones (en adelante las llamaremos TSD y TAD, respectivamente). Estas teorías aportan elementos que enfatizan el carácter relativo del conocimiento matemático: por el lado de la TSD se plantea que el sentido de un conocimiento matemático está en función de la situación que lo moviliza; el conocimiento matemático tiene utilidad en situaciones específicas y se construye en el proceso de interacción entre el sujeto y un medio(Brousseau, 2000). Lo anterior implica que un mismo conocimiento matemático puede tener distintos sentidos, dependiendo de la situación en que se moviliza.
Por el lado de la TAD, se afirma que la actividad matemática tiene lugar en diversas prácticas concretas que se llevan a cabo en instituciones específicas -no necesariamente escolares- (Chevallard et al, 1998). Las prácticas y saberes matemáticos están determinados por la institución; en consecuencia, el sentido de un mismo saber matemático puede variar entre una institución y otra.
La TAD caracteriza a las matemáticas como una actividad más del conjunto de actividades humanas que se llevan a cabo en la sociedad (Chevallard et al, 1998; (Chevallard, 1999). Para analizar las actividades humanas -incluida la actividad matemática- la TAD propone un modelo praxeológico, el cual consiste, en términos generales, en identificar los "tipos de tareas" que se llevan a cabo en una actividad determinada, las "técnicas" que se emplean para efectuar dichas tareas, la "tecnología" que justifica y explica las técnicas, y la "teoría", que a su vez justifica a la tecnología (Chevallard et al, 1998; Chevallard, 1999). Estos planteamientos son asumidos en las decisiones metodológicas de cada una de las investigaciones que aquí se abordan, como se verá más adelante.
Si bien las dos teorías anteriores aportan planteamientos robustos que han dado lugar a numerosas investigaciones didácticas en diferentes países, el hecho de que ambas teorías estén centradas en las matemáticas que tienen lugar en contextos escolares motivó a buscar otros referentes teóricos que ponen atención a los aprendizajes en contextos extraescolares.
El aprendizaje situado de las matemáticas
El carácter relativo del conocimiento matemático también es reconocido por perspectivas teóricas no didácticas, las cuales asumen al aprendizaje como una práctica social. Particularmente la perspectiva de la Cognición en la Práctica identifica a las matemáticas como una práctica situada (Lave, 1991); plantea que los sujetos problematizan y resuelven determinadas situaciones en función del papel social que juegan tales situaciones, de la interacción entre quienes participan en ellas y de los contextos específicos en los que esas interacciones tienen lugar.
Lave cuestiona la supuesta neutralidad del conocimiento, así como su carácter descontextualizado. Ese planteamiento conlleva una manera particular de concebir las relaciones entre cognición y actividad cotidiana: la autora asume a la cognición como "un fenómeno social complejo", esto es, que los procesos de cognición se construyen en función de las actividades sociales de las cuales emergen.
El foco de esa teoría está en la actividad cotidiana, lo cual implica particularmente para las matemáticas asumir su carácter activo y contextual en la práctica; en otras palabras, como lo señala Lave, es necesario investigar la práctica matemática cotidiana considerando la especificidad situacional de la actividad. Investigar tal especificidad conlleva tomar en cuenta ciertos factores de la situación: las actividades en progreso, la estructura del entorno y sus relaciones (Lave, 1991).
Con base en lo anterior, se asume que el aprendizaje de las matemáticas es una práctica social que está determinada por la interacción con otros y por los contextos específicos en los que esas interacciones tienen lugar. Por ello, en las investigaciones que aquí se reportan se pone atención en "la especificidad situacional de la actividad matemática", particularmente en los factores que influyen en la conformación de problemas que implican conocimientos matemáticos, así como en las estrategias para resolverlos.
La enseñanza de las matemáticas como práctica social
En lo que se refiere a la enseñanza, los hallazgos de las dos investigaciones que aquí se presentan permiten concebirla también como una práctica social que tiene lugar tanto en los contextos escolares como en los extraescolares. Este planteamiento extiende el diálogo entre las perspectivas teóricas anteriormente descritas, poniendo en el centro de discusión la concepción misma de enseñanza.
¿Cómo se comunican los saberes entre los miembros de una misma comunidad, desde la perspectiva de la Cognición en la Práctica? Lave y Wenger (2003) señalan que en las comunidades suele haber miembros más expertos que otros; estos últimos están en proceso de incorporarse a la comunidad. El concepto de Participación Periférica Legítima (en adelante, PPL) da cuenta de cómo los "novatos" pasan gradualmente al centro en la actividad; ese concepto concibe a la participación como el principio epistemológico del aprendizaje. Por esa razón, los autores afirman que en una comunidad de práctica hay poca enseñanza observable, lo que hay es PPL:
Al considerar el aprendizaje como parte de la práctica social, hemos centrado nuestra atención sobre la estructura de la práctica social más que privilegiar la estructura de la pedagogía como fuente de aprendizaje. El aprender, entendido como participación periférica legítima, no es dependiente, necesaria o directamente, de las metas pedagógicas o de la agenda oficial, aun en situaciones en las cuales estas metas parecen ser el factor central (p. e. la instrucción en el salón de clases, la tutoría). (Lave y Wenger, 2003: 92).
Desde esa perspectiva, la enseñanza se circunscribe a la escuela. Sin embargo, como se afirmó anteriormente, las investigaciones con jornaleros agrícolas y con trabajadores urbanos reportan la existencia de relaciones de enseñanza, algunas de ellas menos evidentes que las típicamente escolares (las cuales también tienen formas sutiles de manifestarse), así como otras que presentan rasgos escolares. Es por ello que ambas investigaciones sostienen que la enseñanza puede adoptar distintas formas y, en ese sentido, toman como base el planteamiento de la TAD que considera tanto al aprendizaje como a la enseñanza de las matemáticas como una actividad matemática: cualquier persona que tiene necesidad de resolver un problema matemático -escolar o no- y no sabe cómo hacerlo, puede consultar a alguien más experto o estudiar por su cuenta la cuestión; en ambos casos hay una necesidad de aprender matemáticas y surge, como consecuencia, la actividad de enseñar matemáticas.
Más adelante se presentan las evidencias que sustentan la postura anterior; en las reflexiones finales se retomará este ejercicio de poner en diálogo las distintas perspectivas teóricas que aquí se han comentado.
Metodología
Los aspectos metodológicos que aquí se describen son compartidos por ambas investigaciones; los aspectos más específicos se explican en la presentación y análisis de los datos de cada estudio. En este apartado se hace una descripción general de dos momentos del proceso de investigación: los que tienen que ver con la indagación de la actividad laboral y los que tienen que ver con la exploración de conocimientos matemáticos de los sujetos.
Indagación de la actividad laboral
A partir del planteamiento de la TAD de que "toda actividad humana" puede analizarse en términos de praxeología, se "extendió" el uso de ciertas categorías de esta teoría para analizar actividades laborales que implican conocimientos matemáticos. Como se expuso en el apartado teórico, cada una de las investigaciones se apoyó en la TAD para identificar los tipos de tareas y las técnicas con las cuales se realizan esas tareas. Respecto a la tecnología, (es decir, los discursos en torno a las técnicas, en términos de la TAD), ésta se buscó en los discursos de los trabajadores agrícolas cuando corrigen una técnica o cuando enseñan a alguien una técnica. En el caso del estudio sobre los menores trabajadores del medio urbano, no se hizo una indagación explicita de la tecnología, pero sí se puso atención en las explicaciones y en la forma de evaluar las técnicas usadas por parte de los trabajadores.
Para la indagación de la actividad laboral se entrevistó tanto a adultos como a menores de edad. Considerando los planteamientos de la perspectiva Cognición en la Práctica, se procuró que entre los entrevistados hubiera expertos en la ejecución de las técnicas que la actividad demanda. Asimismo, se observó el desarrollo de la actividad in situ, acompañando a los trabajadores mientras llevaban a cabo sus tareas y documentando quiénes participan en la tarea y qué funciones desempeñan.
En algunos momentos, durante el desarrollo de la actividad, se dio la posibilidad de que los trabajadores (adultos o menores de edad) explicaran a quienes los entrevistaban ciertos detalles sobre las tareas que se llevaban a cabo o sobre las técnicas que usaban para resolverlas. Esa interacción entre investigador y entrevistado se dio en el transcurso de la realización de la actividad sin que ésta se interrumpiera.
Indagación de conocimientos matemáticos de los entrevistados
La exploración a profundidad de los conocimientos matemáticos de algunos de los sujetos se hizo mediante el planteamiento de situaciones problemáticas, las cuales fueron diseñadas con base en las características de la actividad laboral observada
El diseño de tales situaciones problemáticas se hizo, por una parte, con el apoyo de herramientas teórico-metodológicas de la Teoría de las Situaciones Didácticas y, por otra parte, considerando ciertos aspectos sociales de la actividad laboral, los cuales han sido analizados a la luz de los planteamientos de la Cognición en la Práctica.
El hecho de que ambas posturas teóricas subrayen el carácter relativo del conocimiento matemático en función de la situación que lo moviliza, permitió la articulación de herramientas metodológicas en el diseño de las entrevistas: se procuró recuperar ciertas variables que se ponen en juego en la actividad real, pero también se hicieron las adaptaciones necesarias para "llevar al límite" las técnicas de resolución de los entrevistados. Esa decisión metodológica (recuperar ciertas características reales de la actividad y modificar otras) permitió indagar los conocimientos de cada sujeto y, en paralelo, comprender más detalles de la técnica misma.
Enseñar y aprender a llevar las cuentas en un campo de cultivo
Las prácticas de enseñanza que se describen en este apartado son tomadas de un estudio más amplio,1 el cual busca identificar los conocimientos matemáticos que se ponen en marcha en ciertas actividades de las familias jornaleras agrícolas migrantes.
El propósito de ese estudio es aportar elementos que contribuyan al análisis de las posibles relaciones, distancias y/o conflictos entre los conocimientos matemáticos extraescolares y los conocimientos que la escuela promueve.
¿Quiénes son las familias jornaleras agrícolas migrantes? Las estadísticas oficiales señalan que en el 2013 alrededor de 773 300 niños, niñas y adolescentes trabajaban en el sector agropecuario.2 Esos menores de edad son parte de las familias que migran frecuentemente al interior de la República Mexicana para vender su fuerza de trabajo en los campos de cultivo.
Debido a la condición de migrantes y de trabajadores, estos menores interrumpen constantemente la escuela primaria. La reprobación, el ausentismo y la deserción escolar caracterizan las trayectorias escolares de los alumnos jornaleros migrantes, en general (Alvear, 2009). En opinión de maestros que atienden a esta población, los altos índices de reprobación se deben a las dificultades que los alumnos tienen con lectoescritura, mas no con las matemáticas, pues si bien hay alumnos que tienen dificultades para escribir ciertas cantidades de manera convencional, así como para efectuar los algoritmos, consideran que la actividad laboral en la que tempranamente participan estos menores y sus familias les ha permitido adquirir un cálculo mental que compensa tales dificultades.
Con esos antecedentes, se trató de identificar las actividades agrícolas que implican la escritura y el cálculo numérico; para ello, se entrevistó a seis familias migrantes y a cuatro trabajadores con distintas funciones laborales; además, se observó la realización de ciertas actividades agrícolas. Asimismo, se procuró identificar conocimientos específicos de seis alumnos jornaleros por medio del planteamiento de situaciones problemáticas. Los problemas se diseñaron con base en las actividades agrícolas identificadas en la primera parte de la investigación.
Enseguida se describe una de esas actividades agrícolas (el registro del trabajo diario); se explicará en qué consiste la actividad, cuál es su propósito, cómo se realiza y qué discursos hay en torno a esa forma de realizar la actividad. Este último elemento (los discursos) permitirá abordar, un poco más adelante, la enseñanza.
La escritura numérica en los campos de cultivo
El cálculo numérico y la producción de información numérica escrita tienen presencia importante en diferentes campos de cultivo de México. Una de las actividades agrícolas en las se manifiestan es en el registro diario de la producción de cada trabajador. Las personas encargadas de hacer ese registro se denominan "anotadores" o "apuntadores".
Los documentos que los anotadores generan contienen información en la que se manifiestan los distintos significados de los números: se usan como código para identificar a un elemento entre otros (por ejemplo, la clave del trabajador); como cardinal, para indicar una cantidad (número de cajas recolectadas en un día, el salario semanal de un trabajador); como ordinal, para ordenar un conjunto de elementos (por ejemplo, las listas de trabajadores), entre otros.
Los trabajadores en general -adultos o menores de edad- identifican esa diversidad de significados y están atentos a los números que se registran, pues saben que éstos tendrán incidencia en sus pagos. Ese interés lleva a quienes no son anotadores a desarrollar técnicas específicas que les permitan tener un control de su producción personal y/o familiar. En este artículo la atención se centrará en las técnicas de los anotadores del empaque de espárragos.
Es importante destacar que, si bien el interés de la investigación se centró en los menores trabajadores, fue necesario documentar las prácticas de los adultos y de la familia en general. En este texto se recupera lo dicho por dos personas adultas; sin embargo, fueron los niños y las niñas quienes dieron la información sobre qué se escribe, quién lo escribe y cómo lo hace. El siguiente fragmento es un ejemplo de ello:
Roy3 (10 años). [...] mi mamá también mandaba a la gente. Traía una libretita, y los que no iban les daba un regañón ¡machíiin!, los llevaba con don Pablo [el administrador del campo].
Entrevistadora. Los llevaba con don Pablo. ¿Y qué anotaba en la libretita?
Roy. En la libretita anotaba... bueno, como decir, "el Roberto no trabajó lunes, martes ni miércoles", le ponían, 100 pesos, porque no trabajaban no le pagaban el día. [Dice esto mientras hace movimientos con la mano, como si estuviera escribiendo en la libreta].
El registro del empaque de espárragos
El empaque de los espárragos es realizado por mujeres, se les llama "empacadoras" y son pagadas por el número de cajas que logren llenar en una jornada. Los anotadores (hombres y mujeres) registran la producción de cada empacadora como se describe enseguida.
El anotador elabora cuatro documentos a lo largo de una jornada de trabajo: 1) una relación con el nombre de cada trabajadora y el "número de caja" que se asigna a cada una de ellas; 2) una lista con los nombres de las trabajadoras y el número de cheque de cada una de ellas; 3) el registro del número de cajas de cada tipo de empaque que cada trabajadora hace en una jornada; 4) un informe del número total por cada tipo de cajas recolectado.
Para describir la elaboración de esos documentos, la investigación se apoyó en los registros de un anotador y en las explicaciones de una anotadora.
Lucy es la anotadora de las bandas 3 y 4 del almacén donde se hace el empaque de espárragos. Explica que a cada empacadora se le asigna un "número de caja"; todas las cajas que llene una misma trabajadora llevarán ese número.
El registro de cajas se hace según el tipo de empaque (11, 15 y 28 libras) y de espárragos (éstos se clasifican de acuerdo con su "calibre" o diámetro del tallo). La Tabla 1 muestra la variedad de espárragos y de empaques o cajas (la tabla es elaboración de la investigadora, no la usan los anotadores):
Por cada tipo de empaque se hace un registro, en él se precisa además el tipo de espárragos que se está empacando. En la Figura 1 se muestra un fragmento de un registro de cajas de 28 libras:
Como puede apreciarse, en el encabezado se anota el tipo de empaque o de caja (28 libras). En la primera columna (de izquierda a derecha) se anota el número de caja, que a su vez es el número que se asigna a la empacadora. En las siguientes tres columnas se registra cada una de las cajas, según el tipo de espárrago, haciendo grupos de cinco. En la última columna se registra el total de cajas obtenidas por cada empacadora.
Los números que están en lápiz fueron agregados después por la persona encargada de calcular los pagos. Más adelante se explicará esto.
El informe de entrega es el último documento que se elabora al final de la jornada y requiere de varios cálculos por parte del anotador. Lucy explica que lo primero que debe hacer es verificar que las cuentas "le cuadren", para ello hace lo siguiente con cada uno de los empaques de 28, 15 y 11 libras:
Por una parte, se hacen sumas verticales para obtener el total de cajas de cada uno de los tipos de espárragos; luego se suman los totales de cajas de los tipos de espárragos para obtener un nuevo total. La figura 2 es un fragmento de ese registro, ahí se aprecian las sumas parciales obtenidas de manera vertical (large 155, standard 177, small 6). La suma total es 338.
Por otra parte, se suma horizontalmente el número de cajas obtenido por cada empacadora. En la Figura 2 se representan esas sumas en la columna de "Total". Después se suman verticalmente todas las cantidades de la columna de "Total"; esta suma debe coincidir con el total obtenido de las sumas verticales anteriores. A esto se le denomina "cuadrar": el total de las sumas verticales de las columnas debe coincidir con el total de las sumas horizontales de los renglones.
Ya que "cuadraron" los resultados al interior de cada uno de los tres empaques (de 28 libras, 15 libras y 11 libras), entonces se suman los totales de esos tres tipos empaques para obtener un último total.
Una de las personas que recibe esta información es Amalia, la persona encargada de calcular el pago de cada trabajador por toda la semana.
Cómo se aprende a ser anotador y cómo se enseña a los otros
En este apartado se presenta las maneras en que se enseña a los anotadores a realizar sus tareas, para ello se recuperan descripciones de Amalia sobre cómo enseña a los "recién llegados" y se presenta el relato de Lucy respecto a la manera en que Amalia la introdujo en estas tareas.
Amalia es la persona encargada de hacer los cálculos de lo que cada trabajador recibirá como pago; para ello, se apoya en los registros de los anotadores.4 También se encarga de coordinar a los anotadores, de revisar que hagan bien su trabajo, de elegir a los candidatos a anotador y de enseñarles a hacer los registros.
Cuando hay apuntadores principiantes que se muestren temerosos, Amalia procura animarlos, les repite las indicaciones sobre qué deben anotar y permanece a ratos con ellos mientras hacen su labor. Amalia comenta que les dice lo siguiente:
Amalia: No te preocupes, no es difícil, yo te voy a ayudar en lo que pueda, yo te voy a enseñar y ahí vamos a estar apoyándote. [...] Se le pone la fecha [al documento], el día de hoy y lo que estamos haciendo, si está podando, pues podando, si están con azadones, pues azadones.
Lucy tiene 19 años, viene de Lázaro Cárdenas, Michoacán y es anotadora en el empaque de espárragos. Describe cómo Amalia le enseñó a ser anotadora; en su descripción se advierten dos aspectos de la enseñanza: al aprendiz se le presenta una tarea un poco más sencilla de lo habitual (en este caso se le pide que registre la producción de sólo una banda de empacadoras, en lugar de dos), y hay una persona más experta que acompaña al aprendiz de manera "intermitente":
Lucy: Ahí tardó un buen rato conmigo (se refiere a Amalia)... ahí pues... como estaban ya las empacadoras y nomás era una banda... dijo no pus, una banda dice pa' que te enseñes porque siempre son dos (...) y ahí estuvo conmigo, me explicó, y así me dijo: cualquier duda, pus, como no voy a estar, dice, le preguntas al de un lado, al apuntador del otro lado... y cuando tenía una duda le preguntaba...
La enseñanza como medio para "dar razón" de las técnicas empleadas
En las descripciones que Amalia hace sobre cómo los anotadores deben registrar aparecen aspectos que dan cuenta de la técnica empleada; se trata de "discursos tecnológicos" que, en términos de la TAD, justifican, explican y producen las técnicas. Sin embargo, algunos de esos aspectos son sumamente pragmáticos, atienden detalles que van más allá de justificar o explicar las técnicas en términos generales, como se verá enseguida. Para analizar la especificidad pragmática de esos discursos ha sido necesario recurrir a los planteamientos de Castela y Romo (2011), quienes desde el marco de la TAD proponen otras funciones del discurso tecnológico, a saber: describir, facilitar, motivar, explicar, validar y evaluar la técnica. Enseguida se mostrarán algunas de esas funciones presentes en el discurso de Amalia mientras enseña y/o corrige la técnica del registro con los anotadores. Sus discursos se centran en dos técnicas: registrar las cajas haciendo grupos de cinco, y verificar el total de cajas registradas "cuadrando" las cantidades.
a) La técnica de agrupar de cinco en cinco es "visible"
Se han identificado distintas formas de registrar la producción en los campos de cultivo. Al parecer, la que predomina es la que consiste en hacer grupos de cinco elementos, como se muestra en las imágenes anteriores. El argumento central de Amalia sobre el por qué de esa elección, es que disminuye la posibilidad de errores, pues se considera un sistema de registro fácil y ordenado; en caso de que llegaran a ocurrir errores, es fácil identificarlos debido a que este sistema es "visible". Evitar errores e identificarlos rápidamente en caso de que ocurran es sumamente importante, pues permite a los anotadores enfrentar los posibles reclamos de los empacadores. El conflicto aparece aquí como un elemento que moviliza la puesta en marcha de técnicas y de discursos sobre esa técnica.
Amalia: Aquí tenemos este sistema, más fácil de encontrar un error [...] Nosotros ya nos acoplamos tanto con esto. Siento que son menos fallas y se ve más visible, porque todo tiene que ver ¿eh?... Cuando hay un apuntador... y yo creo que es normal... los que están empacando a veces desconfían del apuntador entonces si van y ven que un apuntador tiene su trabajo sucio, está muy borronado... desconfían, dicen a la mejor se les pasaron cajas, a la mejor esto, a la mejor otro...
Amalia piensa que al marcar con rayas en grupos de cinco es más fácil encontrar un error (la técnica facilita la tarea) y les da elementos a los anotadores en caso de que haya reclamos. Según Castela (2011), facilitar la técnica comprende saberes que "permiten a los usuarios utilizar la técnica con eficacia pero también con un cierto confort. Son portadores de mejorías pero también de advertencias que evitan errores y torpezas frecuentes" (Castela 2011: 170).5
Asimismo, Amalia trata de motivar a los anotadores a que lo hagan de la manera en que ella se los indica porque eso les permite tener un trabajo más ordenado, pues si los empacadores ven que el trabajo está "sucio" (con borrones) entonces no tendrán confianza y es más probable que cuestionen el trabajo del anotador:
Amalia: Entonces [...] siempre cuando yo voy les explico [a los apuntadores]: miren traten de hacer el trabajo [...] si alguien viene y ve su trabajo y lo ve que está ordenado, y si reclama algo, entonces ustedes tienen un fundamento para decir: sabe qué, pues yo creo que he estado apuntando bien, está ordenado, además de que se cuadra esto, ¿eh?, al final de la jornada se cuadra esto, cuántas cajas salieron y cuántas cajas vinieron del campo...
Respecto a la función pragmática de "motivar el uso de la técnica", Castela precisa: "Las funciones de evaluar, facilitar y motivar están algunas veces íntimamente asociadas: la puesta en evidencia de ciertas dificultades (evaluar) puede comportar al cabo de cierto tiempo la producción de mejorías (facilitar) [...] la motivación se nutre entonces de la evaluación" (Castela 2011: 170).
b) Si las cuentas "cuadran", la tarea estuvo bien hecha y la técnica funciona
Las últimas líneas expresadas por Amalia en el fragmento anterior, destacan el asunto de "cuadrar" como la prueba última a la que recurren los anotadores para verificar si su trabajo estuvo bien hecho. Si los números "cuadran" el apuntador muestra a sus superiores que su trabajo estuvo bien hecho y puede confrontar las posibles diferencias con los otros trabajadores.
Como puede advertirse en los párrafos anteriores, la enseñanza se pone de manifiesto en distintos momentos: cuando se corrige y/o se precisa una técnica en el transcurso de la ejecución de la actividad; cuando se modifica la actividad para hacerla más accesible al aprendiz; cuando se motiva a los trabajadores a llevar a cabo las tareas de una manera determinada. Asimismo, en esos momentos de enseñanza se comunican ciertos aspectos de las técnicas (los discursos tecnológicos) que consolidan a la técnica empleada y, al mismo tiempo, consolidan los conocimientos matemáticos que pudieran estar implícitos en esa técnica. Esa diversidad de manifestaciones de la enseñanza y los conocimientos que la enseñanza comunica, se hacen presentes en otros contextos extraescolares, como se mostrará enseguida.
Conocimientos matemáticos de menores trabajadores en el contexto de la venta de agua
Las prácticas de enseñanza que se describen en este apartado provienen de una investigación sobre los conocimientos matemáticos que menores trabajadores de la zona conurbada de la Ciudad de México6 ponen en marcha en sus actividades laborales (Padilla, 2015)
El objetivo de la esta investigación fue identificar específicamente las tareas y las técnicas matemáticas que los menores movilizan al efectuar su actividad laboral. Se hicieron observaciones y entrevistas. Las observaciones permitieron identificar algunas de las tareas matemáticas que los menores resuelven en su actividad (Padilla y Solares, A., 2013; Padilla, 2015), las cuales son variadas y complejas, entre ellas se identificaron tareas aditivas, multiplicativas y de medición (cálculos de alturas de castillos, áreas de paredes, capacidades de recipientes); el estudio se centró en las que involucran relaciones de proporcionalidad. En las entrevistas se buscó profundizar en el análisis de las técnicas que los menores aplican; para diseñarlas, se modificaron las características de las tareas observadas, como tipos de números y relaciones entre datos e incógnitas.
¿Quiénes son los menores trabajadores con los que se llevó a cabo esta investigación? Se contactó a 20 menores de entre 8 y 15 años de edad. Todos ellos fueron localizados en sus lugares de trabajo. La mayoría asistía a la escuela; estudiaban primaria, secundaria en diferentes modalidades (técnica, telesecundaria, para adultos), o alguna carrera técnica. Se les encontró vendiendo golosinas y otras mercancías de forma ambulante; atendiendo puestos de dulces, aguas o puestos de frutas y verduras; lavando y cuidando coches; cargando bolsas de mercancía o rentándose como diableros7 en mercados; recolectando productos reciclables en los basureros; siendo cobradores en camiones de transporte de pasajeros; trabajando como chalanes8 de albañilería; o como empleados en la fabricación de cohetes.9
Si bien los menores fueron los protagonistas principales de esta investigación, desde las primeras observaciones se contactó a expertos (también llamados maestros, como los "maestros albañiles") para indagar sobre las características de las tareas y de las técnicas en juego en las actividades laborales de los menores. Se contactó a expertos (en su mayoría adultos) en distintas actividades, recolección de basura (llamada en México pepena), albañilería y venta de agua. Aun cuando estos adultos tienen diferentes maneras de participación que las de los menores, comparten el desarrollo de la actividad y tienen numerosas interacciones en las que se movilizan y comunican conocimientos matemáticos.
De acuerdo con los resultados obtenidos, los menores trabajadores disponen de una amplia diversidad de técnicas para enfrentar las tareas que les demanda su actividad (Padilla y Solares, A., 2013; Padilla, 2015; Solares, A., Padilla y Solares, D., en proceso). Dichas técnicas se aplican, comunican y propician en las interacciones entre expertos y menores. Este apartado se enfoca en presentar justamente la enseñanza de estas técnicas.
La actividad laboral de la venta de agua
A continuación se presentan algunos de los datos obtenidos en la actividad de la venta de agua. Específicamente, se discuten resultados de las observaciones y la entrevista realizadas con Roberto, un menor de 13 años que, en el momento del estudio, estaba recursando el primer año de telesecundaria. Se eligen estos datos porque permiten dar cuenta de momentos en los que las prácticas de enseñanza se hacen explícitas.
Roberto llevaba dos años trabajando como ayudante de una pipa que vende agua en la colonia donde vive, en el municipio de Chimalhuacán, en la zona conurbada de la Ciudad de México. Hablar de esta colonia es hacer referencia a un escenario en el que habita un amplio sector de población que ha sido segregado a áreas no incorporadas al sistema de servicios urbanos, por lo regular en viviendas improvisadas y sobre terrenos ocupados ilegalmente. Estas condiciones dan lugar a diferentes formas de trabajo en las que se puede insertar un menor, como la venta de agua potable.
Las pipas se llenan de agua en los pozos de la zona de Chimalhuacán. Ahí, Roberto (R) espera a que algún chofer de pipa, también llamado pipero (un experto vendedor de agua), lo llame para ir a vender. Roberto es responsable de calcular los costos por llenar los recipientes, cobrar el dinero por cada venta y dar el cambio a los compradores.
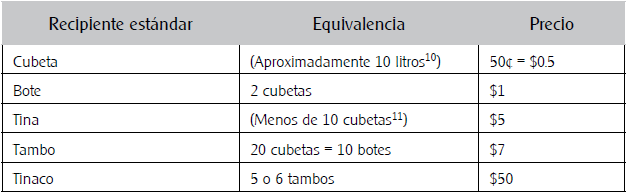
Roberto: Haz de cuenta, el sábado es el día que conviene ir por la pipa porque es cuando casi todos necesitan agua y entonces la compran... Ahí [en esa colonia] es de a 7 pesos "el tambor" [el tambo de agua]. Haz de cuenta, pus [pues] un tinaco, si es grande, muy grandote, son diez tambores, o seis por uno mediano. Y pues ahí está, calculo y ya. Así, cobras.
En esta actividad el sistema "oficial" de unidades de capacidad (litros), es transformado para realizar de manera eficiente la medición y el cobro por los recipientes que los compradores piden llenar. Se usan tambos, cubetas y botes como unidades "estándar". La Tabla 2 presenta los tipos de recipientes estándar, su equivalencia y el precio que usualmente se cobra por llenarlos.
En combinación con las técnicas de cálculo de capacidad, el sistema de medidas que se usa en esta actividad permite determinar los costos a cobrarse por el agua.
Es importante señalar que en la aplicación de las técnicas matemáticas observadas en la venta de agua se involucran numerosos conocimientos no matemáticos, como el saber los días en que es conveniente ir a vender agua a una colonia; o el priorizar que no se pierda dinero, pero saber que si se vende muy caro hay riesgo de no vender todo el contenido de la pipa. Estos conocimientos matemáticos dan forma a la aplicación de las técnicas y sentido a las tareas que se resuelven (Padilla, 2015).
A continuación se describen algunas técnicas de cálculo de capacidad de los recipientes y las maneras en que Roberto las ha aprendido.
Las técnicas matemáticas involucradas en la venta de agua y su enseñanza
En este apartado se presentan algunas de las prácticas de enseñanza que se manifiestan en la actividad de la venta de agua. Entre ellas destacan las maneras en que los expertos vendedores de agua (piperos) enseñan a los aprendices (chalanes) los precios de los recipientes más comunes en la actividad; sus intervenciones para corregir o validar la aplicación de alguna técnica; y la introducción de una técnica específica para el cálculo de la capacidad de recipientes. Para ello se recuperan las descripciones de Roberto sobre cómo aprendió a vender agua.
Roberto: A nosotros nos enseñan a calcular, bueno a los chalanes porque el conductor nomás va arriba, o hay veces que te ayuda como El Gato [uno de los piperos con los que Roberto trabaja usualmente].
Si bien Roberto es responsable de determinar el costo del llenado de los recipientes y cobrar, los expertos de la venta de agua intervienen en numerosas ocasiones ayudando en la aplicación de una técnica o corrigiendo alguna solución.
Para ser chalán en la venta de agua se requiere, para comenzar, saber los costos de las unidades estándar. "No se trata nada más de subirse a la pipa", dice Roberto; "¡a todos!, a todos, a todos se les enseña cuando van abrir un pozo, a todos se les enseña. Si vas a ser pipero, a todos se les enseña", insiste Roberto.
En su descripción de cómo le enseñaron a vender agua, Roberto dio cuenta de una pequeña "situación de enseñanza" mediante la cual se enseña a los aprendices los costos de las unidades estándar y de los recipientes más comunes.
Entrevistadora: ¿Alguien te enseñó a "medir" la capacidad de los recipientes?
Roberto: El señor del pozo de Corregidora. Tiene formados todos los botes de diferentes litros y... pasa así el señor y te dice: 5 [pesos], 4 [pesos]; no te dice... ni te explica...así, nomás te dice: 5, 4, 3, 2... así, 7 [pesos]. No te dicen ni cuántos litros, sólo te dicen 5, 4, 7 así te van diciendo; rápido.
Chalo [un pipero para quien Roberto trabajaba] me dijo: "Primero tienes que pasar a que te enseñen". Estaban otros tres [aprendices] y yo, y así te van diciendo. Pero nos dicen: "y si no aprenden pus ya no es mi problema". Ya si no te los aprendes te regañan.
Lo narrado por Roberto da cuenta de que esta "situación de enseñanza" es organizada de modo intencional para comunicar conocimientos matemáticos entre los expertos y los aprendices. Un rasgo de interés de esta situación es que se lleva a cabo al margen de la actividad, como preparación para los nuevos chalanes, antes de salir a vender.
Pero no basta con aprender los costos de los recipientes estándar para la medición de capacidad ni de los recipientes más comunes. Como se señaló antes, los compradores tienen recipientes de las más diversas formas y tamaños: desde tinas de baño, vasijas de barro o cubetas lecheras,12 hasta grandes contenedores o, incluso, cisternas. Para continuar aprendiendo es de vital importancia la interacción con los demás participantes de la actividad. Además de la interacción con los expertos, la interacción con los compradores es otra fuente importante de retroalimentaciones.
Entrevistadora: ¿Te regañan... si... si cobras más?
Roberto: Ajá.
Entrevistadora: No creo que te regañe El Gato ¿o sí?
Roberto: No, pero sí se dan cuenta, si se dan cuenta, sí te regañan. Haz de cuenta si la dueña te dice "no pues por estos, no pus otra pipa me la cobra más barata" se dan cuenta.
Entrevistadora: Y ¿por qué te regañan?
Roberto: Porque tienes que aprender
Entrevistadora: ... si no, van a perder
Roberto: No, pero así aprendes. Como la primera vez que fui, haz de cuenta ahorita, te paras, no nada más es de subirse a la pipa, no nomás es de decir "vámonos" [se refiere nuevamente a que hay que saber cosas antes de comenzar a vender agua]. También te van explicando: "tal, tal, tal, tal", y si no te lo aprendes, si cobras más o menos, ya te lo van descontado, si es menos te descuentan.
Entrevistadora: O sea si cobras de menos... ¿Y si es más?
Roberto: Si es más... porque hay veces...allá arriba nos tocó una señora, una vez le llené y le cobré más y ya después pasaba la pipa y aunque no tuviera agua no nos compraba; por eso también te regañan, porque se dan cuenta, no te reclaman, no te reclaman pero se dan cuenta y ya cuando volvemos a pasar ¡no te compran!
Durante las observaciones también se pudo identificar varias intervenciones en que el pipero sugería la aplicación de alguna técnica, indicando, por ejemplo, efectuar alguna operación. Se identificaron otras intervenciones en las que los expertos introducían técnicas para realizar cálculos específicos, como la técnica "se lo come" que Roberto usa para establecer la capacidad de algunos recipientes.
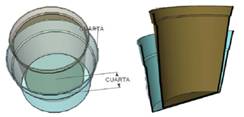
La técnica "se lo come" consiste en comparar la capacidad de dos recipientes que pueden ser puestos uno dentro de otro, como se muestra en la Figura 3 con los recipientes A y B.
La comparación se lleva a cabo estableciendo compensaciones entre las dimensiones de los recipientes. En este caso, Roberto dijo que lo que la altura de B superaba a la altura de A, se compensaba con lo que el tamaño de la base de A superaba al tamaño de la base de B. Para mostrar que estas partes efectivamente se compensaban, Roberto midió con cuartas13 (él dice cuartadas) la longitud de la altura que sobresalía y la distancia entre los bordes de los recipientes (ver Figura 4).
Roberto: Mira... toda esa "cuartada" es lo que se lo come. [Roberto abre su mano y considera la distancia que hay entre la punta de su dedo pulgar y el meñique, una cuarta. Con esta "unidad de medida" mide la longitud que la altura del tambo (recipiente B) sobresale por la altura de la tina (recipiente A); esta longitud es de una cuarta. Luego, la compara con el espacio que queda entre el tambo y la tina, midiendo la distancia de separación entre las paredes de los dos recipientes, que también es de una cuarta]. (Ver Figura 4).
Roberto: Si la vaciamos [el agua del tambo, si estuviera lleno] es lo que va a quedar al ras de ésta [de la tina, recipiente A] porque es lo que "se lo come".
De acuerdo con lo que Roberto señaló, esta técnica le fue enseñada por uno de los piperos, como se describe en el siguiente episodio.
Entrevistadora: Oye, y alguien más... ¿algunos otros niños o chalanes miden así... con cuartadas?
Roberto: ¿Con cuartadas?, sí. Así se les llama, cuartadas.
Entrevistadora: ¿Quiénes más miden así?
Roberto: Nomás, haz de cuenta como El Gato luego así mide... una cuartada... [...] Lo mides así y así [la medida en forma horizontal y vertical]. Más rápido así, a que te digan así, como el señor [el señor del pozo de Corregidora], "7 [pesos]... así" pues no le entiendes, muchas veces te equivocas, te dicen éste $2 [mira un bote de 20 litros], y estos 3 [pesos] [señala otro recipiente un poco más grande que el bote]. Vas a decir éste 3 y éste 2 [señala los recipientes intercambiando el costo].
Y no, y no te acuerdas. Y El Gato, no. El Gato nos enseña así [ejemplifica poniendo una cuarta con su mano de manera horizontal] y pa' arriba [poniendo una cuarta con su mano de manera vertical].
Entrevistadora: ¿Y al Gato quién le habrá enseñado?
Roberto: Pues él ya es pipero, ¡uy de tiempo!, ajá.
Si bien se restringe a la comparación de recipientes como los mostrados en el ejemplo, la aplicación de la técnica "se lo come" permite resolver situaciones de duda o conflicto. Por ejemplo, dice Roberto que cuando "ponen una cubeta de 20 litros y un bote más altito de 20 litros", algunos piperos cobran un peso por la cubeta y dos por el bote, aunque les quepa lo mismo; pero "el chiste es que es lo mismo. Y así... Y El Gato te los mide".
Las técnicas expertas
Identificamos algunos casos en los que, cuando hay alguna dificultad especial en las características de la tarea o hay conflicto con el cliente, se cambian las técnicas o, incluso, los responsables de realizar la tarea. Por ejemplo, generalmente el chalán se encarga del cálculo del precio y el cobro por la venta de agua, siempre y cuando los recipientes no sean "muy grandes". Pero cuando hay que llenar cisternas,14 es el pipero quien se encarga de sacar la cuenta, como narra Roberto:
Roberto: Ah sí, pero por cisterna, esa sí ya no te la saco [refiriéndose a obtener el costo por el agua de la cisterna]; te saca la cuenta el patrón porque, por decir, ya no nomás le caben tambores; le caben tambores y le caben tinacos.
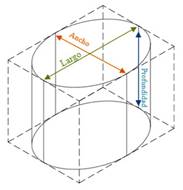
El experto recurre a técnicas propias para determinar estos costos; por ejemplo, se fija cuánto baja el nivel del agua en el interior de la pipa o le pregunta al cliente cuánto le cobran generalmente por llenar su cisterna. Pero, cuando hay algún conflicto con el cliente, puede recurrir a la técnica de cubicar, que consiste en "sacar un metro", tomar las medidas de largo, ancho y profundidad de la cisterna y calcular la capacidad de la cisterna multiplicando las medidas de estas dimensiones, como si fuera un prisma rectangular (ver Figura 5).
A manera de ejemplo, en la Figura 5 se muestra una cisterna con forma de cilindro recto de base circular, pero la cisterna puede tener cualquier forma. El prisma rectangular que circunscribe a la cisterna permite efectuar la cubicación, aproximando la capacidad de la cisterna "por arriba" (es decir, la capacidad del prisma es siempre mayor que la de la cisterna, pues la circunscribe).
En el siguiente episodio de la observación, Ernesto, uno de los piperos, describe la aplicación de la cubicación para el cálculo de la capacidad de una cisterna. Este episodio también da cuenta de la motivación principal para la aplicación de la técnica: la solución del conflicto con el cliente.
Ernesto: Entonces lo conveniente es medirla, tanto para el cliente como para nosotros, porque yo le puedo decir: "le cobro tanto", y probablemente se lleve más agua de la que yo tengo contemplada, o menos. ¡Qué te digo!, ya con la práctica pues ya más o menos vas sabiendo.
Entrevistadora: Ahí nomás como...
Ernesto: ... como a ojo de buen cubero, a ojo de buen pipero, podría decirse (Ernesto completa el dicho), no pus a esto le cabe tanto. Te digo la cisterna hay que cubicarla y cada metro cúbico pues son 1000 litros, el metro cúbico de agua, y te digo por lo regular son 60 o 70 pesos, dependiendo de a dónde tenga que ser (dependiendo del lugar al que haya que trasladarse para llenar la cisterna).
Entrevistadora: ¿60 o 70 pesos por metro cúbico? [...] ¿Y no te ha llegado a pasar que, por ejemplo, la gente te diga: "me estás cobrando de más"?
Ernesto: Bueno, pues ahí ya entra la polémica con el cliente ¿no?: "no que aquí le cabe tanto, no pues que le cabe tanto, o que mi abuelito la hizo y él me dijo que le cabía tanto..." (Risas) Y ya por eso te digo, luego por eso muchas veces conviene traer un metro y ahí: "a ver mire, dos por dos son cuatro, por dos... son ocho [se refiere a medidas supuestas sobre una cisterna] lo que equivale a ocho metros cúbicos, ocho mil litros, entonces yo le tengo que cobrar 'tanto'..."
Entrevistadora: Ah, ya...
Ernesto: Para que también quede contento el cliente.
La técnica de cubicación y su forma de aplicación fueron corroboradas por otro experto pipero, El Gato.
Además del cálculo de la capacidad mediante la fórmula largo por ancho por profundidad, en la aplicación de esta técnica se usa el sistema de unidades "oficial": se cobra el metro cúbico o los 1 000 litros a "60 o 70 pesos, dependiendo de a dónde tenga que ser", dice Ernesto. Se trata de la presencia de conocimientos típicamente escolares usados en la actividad de la venta de agua, en este caso, a diferencia de las situaciones anteriores donde las técnicas y los conocimientos que se ponen en marcha no tienen rasgos escolares.
Las descripciones de las situaciones donde es conveniente aplicar la técnica y de su motivación, de las unidades propias de su uso y los responsables involucrados en su aplicación dan cuenta del discurso tecnológico que se genera en la actividad laboral en torno a la cubicación.
Reflexiones finales
En la investigación educativa es común encontrar el término "enseñanza" referido a espacios escolares, y muchas veces restringido a ellos. De hecho, es en la escuela donde suelen estudiarse las prácticas de enseñanza. Sin embargo, las investigaciones presentadas en este capítulo identifican prácticas de enseñanza sistemáticas e intencionales que tienen lugar en situaciones extraescolares.
Estas prácticas de enseñanza nos muestran, por una parte, aquellos conocimientos matemáticos que los participantes de la actividad consideran esenciales que los aprendices tengan para incorporarse al desarrollo de la actividad: las tareas más comunes, las técnicas más adecuadas para resolverlas y los discursos que justifican, motivan o validan su aplicación. Las prácticas se presentan ya sea durante el transcurso de la actividad (puede suceder que se modifique un poco la tarea para que ésta sea más accesible para el aprendiz y que la presencia del experto sea intermitente), o a través de situaciones que se organizan, de manera intencional, al margen de la actividad (como la situación de enseñanza descrita por Roberto, para preparar a los ayudantes antes de salir por primera vez a vender agua).
Por otra parte, además de poner de manifiesto conocimientos matemáticos, las prácticas de enseñanza generan discursos tecnológicos para la comunicación de las técnicas. Es decir, al explicar, facilitar, motivar y evaluar las técnicas, la enseñanza hace explícitas las "razones de ser" de esas técnicas, lo cual permite consolidarlas y, al mismo tiempo, consolidar los conocimientos matemáticos que están implicados en ellas. Esto confirma lo señalado por la Teoría Antropológica de lo Didáctico (TAD), la cual atribuye tanto al aprendizaje como a la enseñanza de las matemáticas el carácter de actividad matemática (Chevallard, 1999; Chevallard et al, 1998).
Así como la enseñanza pone en evidencia ciertos conocimientos matemáticos y contribuye en su conformación, también hace evidente la existencia de otros conocimientos no matemáticos relacionados con el objetivo de las tareas, con los propósitos de quienes participan en ellas y con las condiciones en las que las tareas se realizan (por ejemplo, en la venta de agua no se debe perder dinero, pero también se debe satisfacer al cliente; en el registro de espárragos se debe anotar rápidamente lo producido por varias empacadoras, pero el registro debe ser claro, por si se presentan reclamos). Esos otros conocimientos son comunicados también a través de la enseñanza e inciden en la conformación de los mismos conocimientos matemáticos.
La consideración de esos otros aspectos que se ponen en juego en el aprendizaje de una práctica determinada, ha sido en buena medida gracias a las aportaciones de los estudios de la Cognición en la Práctica, a la cual recurren ambas investigaciones, así como a otros estudios derivados de la TAD (Castela y Romo, 2011) que apoyaron la investigación sobre jornaleros migrantes. Este enriquecimiento del marco teórico y metodológico subraya la necesidad no sólo de extender las referencias teóricas sino también de buscar un "cruce de miradas" entre las distintas perspectivas.
En ese diálogo entre posturas teóricas distintas resalta el papel y el concepto mismo de enseñanza en los aprendizajes que tienen lugar más allá de la escuela. Si bien el concepto de Participación Periférica Legítima (Lave y Wenger, 2003) permite comprender la gradual participación de los aprendices en una práctica concreta, no destaca suficientemente el papel de los expertos en ese proceso gradual, particularmente no considera las interacciones entre aprendices y expertos en las que estos últimos ponen de manifiesto su intención de enseñar. Esas manifestaciones son diversas, algunas muy explícitas, otras más sutiles, lo cual da cuenta de la complejidad de la enseñanza -tanto escolar como extraescolar- y cuestiona que se le conciba como una simple transmisión unidireccional de contenidos.
Finalmente hay que señalar que estas investigaciones se adhieren al interés por tender puentes entre la escuela y las actividades matemáticas que se realizan fuera de la escuela, en particular las relacionadas con el trabajo.
Entre los hallazgos, es importante destacar la presencia de conocimientos matemáticos con rasgos escolares usados en espacios extraescolares. Es el caso de la técnica de cubicación para la venta de agua: cuando hay conflictos con el cliente por el precio del llenado de una cisterna, los expertos pueden echar mano de conocimientos matemáticos sobre el cálculo de la capacidad de prismas rectos -conocimientos con fuerte presencia en la escuela- para solucionar un problema extraescolar. Las explicaciones que los expertos dan del uso de la cubicación muestran además las motivaciones, las formas de aplicación y los alcances de esta técnica; es decir, dan cuenta del discurso tecnológico que se construye en los espacios laborales extraescolares. Ese hallazgo de la investigación abre la pregunta: ¿cómo dialogan -si es que se establece ese diálogo- esos discursos extraescolares con los discursos que la escuela elabora en torno a ese mismo conocimiento matemático?
Respecto al interés compartido de ambas investigaciones por recuperar conocimientos matemáticos extraescolares para la escuela, los resultados presentados en este capítulo permiten sostener, por una parte, que es indispensable caracterizar las actividades extraescolares en las cuales tienen lugar ciertas tareas y técnicas matemáticas: se requiere identificar en qué condiciones se desarrollan esas actividades, quiénes participan, cuáles son sus propósitos y de qué medios disponen para alcanzarlos. Por otra parte, y como consecuencia de esa caracterización, no puede afirmarse que los objetivos, retroalimentaciones y formas de validación de las actividades extraescolares sean "transferibles" a la escuela. Transferirlas implicaría que perdieran su naturaleza, los significados dados justamente por los contextos en los cuales viven.
¿Cómo la escuela puede entonces sacar provecho de los conocimientos matemáticos que circulan en otros contextos? Si bien esa pregunta sigue quedando abierta, los hallazgos de estas investigaciones aportan elementos para seguir esbozando una respuesta e, incluso, para abrir otras preguntas: ¿qué sentido tendría que la escuela considere las formas de enseñanza identificadas en los espacios extraescolares? En el entendido de que la transferencia de formas de enseñanza tampoco es posible -ni deseable- la pregunta anterior contribuiría más bien en la profundización del estudio de cómo funcionan los conocimientos matemáticos en distintos contextos, considerando que esos conocimientos se van conformando en el transcurso de su enseñanza y de su aprendizaje.











 nueva página del texto (beta)
nueva página del texto (beta)