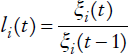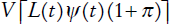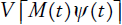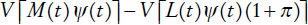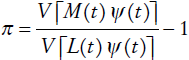Introducción

El riesgo de longevidad, que se define como la probabilidad de que las personas sobrevivan más allá de lo esperado, genera un daño financiero a los programas de pensiones en general, ya que se traduce en la potencial subestimación de las reservas, y por lo tanto, implica un riesgo de déficit de recursos financieros para cumplir las obligaciones de pago futuras. Este riesgo afecta a los programas de pensiones de beneficio definido a cargo de organismos gubernamentales, aunque no es exclusivo de ellos, todo sistema pensionario en el que exista una obligación de pago vitalicia es afectado por el riesgo de longevidad.

Una forma de manejar este riesgo es la utilización de productos derivados financieros, por medio de los cuales es posible transformar la longevidad en un activo que genere rendimientos a inversionistas e instituciones que deseen comprarlo o venderlo. Este tipo de mecanismos, entre los cuales se incluyen futuros, opciones, swaps y combinaciones de ellos, permiten la dispersión de este riesgo entre varios actores dispuestos a tomarlo para cancelar sus posiciones contrarias de longevidad, que buscan posiciones en activos con riesgos no correlacionados o simplemente que quieren obtener ganancias especulativas.¹

En este artículo se propone la utilización de un swap para manejar el riesgo de longevidad relacionado con las obligaciones pensionarias, ya que de todos los productos derivados financieros que se podrían utilizar para reducir el riesgo de los sistemas de pensiones, los swaps de longevidad son los más sencillos de construir e implican un costo menor de implementación. Tienen como desventaja que se deben estructurar caso por caso, lo que provoca que no sean instrumentos líquidos, situación que no debería generar problema en el caso propuesto, al no tener un elemento especulativo.

La principal contribución de este artículo es la generalización de un modelo de estructuración y valuación de un swap de longevidad, por medio de la construcción de un índice de longevidad proporcional y una variable de monetización, que permiten usar el derivado financiero referido en un amplio rango de sistemas de pensiones en los cuales existen trabajadores activos, tomado en cuenta las particularidades de cada caso.

También se propone el uso de la metodología modificada para disminuir la exposición del gobierno federal mexicano al riesgo de longevidad, por medio de un swap de longevidad, el cual se puede estructurar como un instrumento fuera del mercado (OTC, por sus siglas en inglés) entre el gobierno federal y el sector de aseguradoras y reaseguradoras de vida, tanto nacional como internacional.

El resto del documento se divide de la siguiente manera. Se inicia con la revisión de la literatura relevante relacionada con la utilización de swaps para cubrir posiciones de longevidad (sección I). A continuación, se hace una revisión histórica de la experiencia internacional en instrumentos financieros y su utilización para el manejo del riesgo de longevidad (sección II). Posteriormente, se propone un índice de longevidad proporcional, aplicable a grupos de pensionados que tienen crecimiento por trabajadores activos y se realiza la estructuración y valuación del swap de longevidad, agregando una variable de monetización a la formulación general prevaleciente en la literatura (sección III). En seguida se analiza la propuesta de aplicar el swap de longevidad en México, en particular en lo relacionado con los pasivos pensionarios derivados de la reforma a la Ley del Seguro Social de 1997 (sección IV). Luego se desarrolla una simulación referida a México del modelo presentado en este documento con el fin de ilustrar los conceptos vertidos (sección V). Por último, se presentan las conclusiones y la discusión final.

I. Revisión de la literatura

La idea de utilizar productos derivados financieros para manejo del riesgo de longevidad se ha discutido en la literatura desde hace algunos años. Por ejemplo, en ^{Blake et al. (2006)} se analiza el uso de instrumentos financieros ligados a la mortalidad y su utilización por las empresas de los ramos asegurador, pensiones y rentas vitalicias para manejar su exposición al riesgo de longevidad. Dentro de su análisis se describen los swaps de mortalidad, como un acuerdo para intercambiar un flujo de efectivo en el futuro, basados en el resultado de un índice de mortalidad, haciendo referencia al artículo de ^{Cox y Lin (2004)} y su análisis del hedge natural que ocurre entre una aseguradora de pensiones y una aseguradora de vida, cuando la mortalidad disminuye respecto a un escenario esperado.

En particular, ^{Cox y Lin (2004)} proponen utilizar el hedge referido de dos maneras: la primera, dentro de una sola compañía que ofrezca los dos productos, seguros de vida y pensiones, lo que le permitiría un manejo de riesgos más eficiente y el cobro de menores primas; y la segunda, la transferencia de riesgos entre dos aseguradoras con diferentes posiciones respecto a la variación en mortalidad por medio de un swap, que es justo la propuesta que se retoma en el presente artículo. Adicionalmente, ^{Cox y Lin (2004)} realizan una propuesta de construcción y valuación de un swap de longevidad, en la cual consideran las diferencias generadas por un fenómeno de selección adversa para construir los flujos a ser intercambiados, partiendo del supuesto de que las personas con buena salud tienen incentivos para comprar rentas vitalicias y las personas con mala salud tienen el incentivo de comprar seguros de vida. Tomando las diferentes experiencias de mortalidad derivadas de este problema de información, ^{Cox y Lin (2004)} construyen los flujos a intercambiar y valúan el swap igualando su valor a cero. Sin embargo, su metodología pudiera ser de difícil aplicación, ya que implicaría la elaboración de dos o más índices de longevidad para cada contrato de un swap de longevidad.

A este respecto, ^{Dowd et al. (2006)} presentan una formulación más sencilla. Ellos construyen un modelo de estructuración y valuación del swap basado en un solo índice de mortalidad, al balancear las diferentes perspectivas sobre longevidad generadas por el problema de selección adversa, mencionadas por ^{Cox y Lin (2004)}, por medio de una prima que iguala el valor del swap a cero al inicio del contrato. Debido a que este enfoque tiene una estructura más sencilla, en el presente documento se adopta la idea de usar el hedge natural que ocurre entre las aseguradoras de vida y los sistemas de pensiones propuesta por ^{Cox y Lin (2004)}, pero utilizando el modelo general de estructuración y valuación de ^{Dowd et al. (2006)}.

Cabe señalar que el modelo de ^{Dowd et al. (2006)} fue desarrollado para un fondo de pensiones cerrado, es decir, con un número fijo de pensionados, los cuales se van reduciendo con la mortalidad y con un monto de pensión fijo. Estas dos características son un obstáculo para aplicarlo en un sistema de pensiones que tenga un número de miembros creciente y otras características particulares que hagan difícil monetizar un índice de longevidad, como lo es un monto de pensión variable.

Por ello, en lo que representa la principal contribución de este artículo a la literatura, se realizan modificaciones a la propuesta general de estructura y valuación de un swap de longevidad de ^{Dowd et al. (2006)}, enriqueciéndola al construir un índice de mortalidad que permite el crecimiento de la población pensionaria e introduciendo una variable para monetizar los flujos de longevidad. Con ello, el modelo modificado tiene un rango de aplicación mayor, lo que se muestra más adelante cuando se construye una propuesta de un swap de longevidad para el manejo de este tipo de riesgo en el sistema de pensiones de la Ley del Seguro Social anterior, que está a cargo del gobierno federal en México.

II. Experiencia internacional

En cuanto a la experiencia internacional con instrumentos financieros para el manejo del riesgo de longevidad es necesario mencionar que los resultados han sido mixtos, con algunos instrumentos como los bonos catastróficos de mortalidad y los swaps de longevidad, que son en general bien recibidos por el mercado, mientras otros, como los bonos de longevidad, no han generado el suficiente interés en los mercados financieros.²

Por un lado, respecto a los ejemplos en donde se utilizan bonos para transferir riesgo, el tipo de instrumentos que han sido exitosos en los mercados de capital son los bonos catastróficos de mortalidad, diseñados para dar protección a aseguradoras y reaseguradoras sobre eventos catastróficos con gran impacto (e. g., epidemias, terrorismo, desastres naturales). Estos bonos se caracterizan por un vencimiento de tres a cinco años, por lo que en realidad no cubren el riesgo de longevidad como se entiende en el contexto de la literatura. Como un ejemplo particular de un bono de mortalidad catastrófica está el bono, con una madurez de cuatro años, emitido en 2003 por Swiss Re, que recaudó 400 millones de dólares, y cuyo principal estaba ligado a escenarios adversos de mortalidad.³

Por otro lado, el tipo de bonos cuya colocación ha sido problemática son los bonos de longevidad, que se caracterizan porque el pago de cupones cae conforme se eleva un índice de mortalidad. El primer intento de emisión privada fue un bono de longevidad a 25 años, estructurado por BNP Paribas y emitido por el European Investment Bank en 2004, el cual se canceló por falta de interés. El segundo intento lo realizaron el Banco Mundial y la Superintendencia de Valores y Seguros de Chile en 2010, que tampoco logró el éxito esperado, y tuvo que cancelarse al no percibirse interés por parte de las compañías aseguradoras, un riesgo base alto y problemas burocráticos en el país andino.⁴

En lo relacionado con la utilización de productos derivados financieros para el manejo del riesgo de longevidad, el más exitoso ha sido el swap de longevidad, el cual, de acuerdo con lo reportado en ^{Oppers et al. (2012)}, ha registrado la mitad del valor del mercado de transacción de riesgos en el Reino Unido, un mercado que negoció 8 000 millones de libras esterlinas promedio por año en el periodo 2008-2010, elevándose a 9 000 millones en el 2011. Adicionalmente, en los Países Bajos se llevó a cabo un swap de longevidad de 12 000 millones de euros en el 2012 entre Aegon y Deutsche Bank.⁵

^{Blake et al. (2013)} mencionan que el primer swap de longevidad exitoso en los mercados de capitales se realizó en el Reino Unido, entre JP Morgan y Canada Life, mismo que difiere del swap propuesto en la presente investigación, en términos de la población cubierta. El swap realizado por JP Morgan involucra la mortalidad observada de 125 000 pensionados, mientras que en la propuesta desarrollada en este artículo el índice de longevidad proporcional se mide sobre pensionarios y trabajadores activos que todavía no entran en etapa de retiro.

Como es posible identificar en la literatura presentada, se tiene un mercado de longevidad cada vez más activo, principalmente por medio del uso de swaps de longevidad y bonos catastróficos de mortalidad, en mercados financieros en donde existe experiencia con la estructuración y comercialización de productos derivados financieros.

Desafortunadamente este tipo de transacciones no se han presentado de manera exitosa en mercados emergentes, en donde existe un elevado potencial de incremento de la longevidad, ya que es posible que con mejoras relativamente sencillas en atención médica se pudieran tener fuertes ganancias en la esperanza de vida. Por ejemplo, en el caso de México, las ganancias de esperanza de vida a los 65 años han crecido menos que en sus pares de la Organización para la Cooperación y el Desarrollo Económicos (OCDE). En el periodo 1990-2009 la esperanza de vida a los 65 años de los hombres en México creció en medio año, mientras que Canadá mostró una mejora de 3.1 años; Francia, 2.9 años; Alemania, 3.2 años y los Estados Unidos, 2.7 años. Conforme mejores protocolos de atención a los adultos mayores se generalicen en países en vías de desarrollo, se podrían tener ganancias en esperanza de vida relativamente rápidas.⁶

Otra posibilidad de ganancias potenciales en la esperanza de vida la presenta el estudio de ^{Litchenberg (2005)}, quien realiza un análisis econométrico del efecto del lanzamiento de nuevos medicamentos en la longevidad de 52 países en el periodo 1982-2001. ^{Litchenberg (2005)} concluye que 40% del incremento de esperanza de vida en el periodo se debe al lanzamiento de nuevos medicamentos. Un ejemplo de este tipo de ganancias rápidas en esperanza de vida y la pérdida financiera asociada se vivió con el desarrollo de nuevos medicamentos en la lucha contra el virus de inmunodeficiencia humana (VIH).⁷

A pesar de esta necesidad manifiesta de manejar el riesgo de longevidad, es difícil que el mercado de derivados financieros relacionados con la longevidad se consolide por sí mismo en países en vía de desarrollo, en donde los mercados de derivados están en general poco desarrollados o son poco líquidos. Para que esto ocurra se requiere una intervención gubernamental, como lo sugieren ^{Antolin y Bloommestein (2007)}, quienes proponen los dos papeles que pueden tomar los gobiernos en la promoción de mercados cobertura de longevidad. El primero es emitir bonos de longevidad; y el segundo, el desarrollo de índices de longevidad, que es uno de los componentes de la propuesta presentada en este artículo.

En las siguientes secciones se modificará la metodología de ^{Dowd et al. (2006)} con el desarrollo de un índice de longevidad proporcional y con la inclusión de una variable de monetización y, posteriormente, se desarrollará la propuesta de swap de longevidad para que el gobierno federal pueda cubrir el riesgo de longevidad relacionado con la reforma de la Ley del Seguro Social de 1997.

III. Estructuración y valuación del SWAP de longevidad

Como se mencionó anteriormente, la formulación más factible, por su relativa sencillez, para la estructuración y valuación de un swap de longevidad encontrada en la literatura es la expuesta por ^{Dowd et al. (2006)}. Sin embargo, esta propuesta está desarrollada para un fondo de pensiones con un número fijo de pensionados el cual se va reduciendo con la mortalidad y con un monto de pensión fijo. Estas dos características son un obstáculo para aplicar esta formulación a sistemas de pensiones como el que surgió de las reformas a la Ley del Seguro Social de 1997 en México. Por ello se realizan modificaciones al modelo de ^{Dowd et al. (2006)}, al introducir un índice de longevidad proporcional, que permite aplicar la metodología cuando el grupo de pensionados crece por la presencia de trabajadores activos, y agrega una variable de monetización, que adapta la metodología a las condiciones específicas del plan de pensiones.

1. Desarrollo del índice de longevidad proporcional

La variable clave para establecer un swap de longevidad que sea atractivo para los participantes es el establecimiento del índice de longevidad sobre el cual se llevará a cabo el contrato, ya que el retorno esperado del instrumento, y por lo tanto el precio, están basados en él. En este sentido, ^{Dowd et al. (2006)} establecen un índice de supervivencia S(t) que equivale a los pensionados vivos al tiempo t, por medio del cual se miden las mejoras observadas en la esperanza de vida, al recoger el riesgo de longevidad. Para que esta medida refleje adecuadamente el riesgo de longevidad debe utilizarse en grupos cerrados de pensionados, es decir, que no tienen entradas de nuevos pensionados, y por lo tanto, el número de pensionados varía año con año solamente por la mortalidad observada.

Si bien esta medida simplifica los cálculos, no es adecuada para un grupo de pensionados con crecimiento, como es el caso de los pensionados a cargo del gobierno federal mexicano a raíz de la reforma de la Ley del Seguro Social en 1997 o en algún otro sistema de pensiones abierto, en el cual existen entradas constantes de nuevos pensionados al grupo, debido a que existen asegurados activos, que cumplen la edad, o cotizaciones necesarias para tener derecho a las pensiones en el tiempo. Por ello, en este caso se tienen dos factores que afectan el tamaño del grupo de pensionados: la mortalidad de los pensionados y las nuevas entradas.

Para superar este problema, en este documento se construye un tipo de índice de longevidad, el cual llamaremos índice de longevidad proporcional, en el cual se toman en cuenta la supervivencia proporcional de un grupo de pensionados agrupados por edad a su entrada al grupo.

Para ello se utiliza la variable ξ _i (t) que se define como el número de pensionados que ingresaron al sistema de pensiones en el año i ∈[i,i-, ], que está determinado por los años que se consideren para el contrato del swap, y que está vivo en el año t. Como se mencionó anteriormente, para evitar la distorsión generada por la contabilización de pensionados entrantes a cada generación se propone utilizar una medida de proporción de sobrevivencia una vez que entraron al grupo, la cual se define como:

(1)

que representa la proporción de pensionados vivos que ingresaron al sistema en el año i, que estaban vivos al cierre del año t - 1 y que están vivos en el año t.⁸

Finalmente, se agregan todas las generaciones en el índice de longevidad, ponderado por la estructura poblacional, el cual se describe por la siguiente ecuación:

(2)

donde β _{i t,} es un ponderador que representa la estructura de edades calculada con la composición de los grupos de edad basados en las proyecciones del Consejo Nacional de Población (Conapo) que cumple la siguiente formulación:

(3)

y que tiene las siguientes características:

(4)

La principal crítica que pudiera surgir a este índice de longevidad es el uso de un ponderador fijo β _{i ,t} , que pudiera, en caso de ganancias extremas de longevidad, ser una fuente de riesgo base. A este respecto, y para contrarrestar esta posibilidad, en el contrato del swap deben establecerse revisiones periódicas para este ponderador y los supuestos bajo los cuales puede ser modificado. En lo relacionado con el riesgo base, en el caso particular de México, una medida para minimizarlo es usar la experiencia de mortalidad del Instituto Mexicano del Seguro Social (IMSS) en la construcción del índice, ya que esta institución tiene en registros administrativos el número de observaciones suficientes para construir un índice de longevidad proporcional robusto.

Un punto a considerar es que las medidas de longevidad tienen que ser calculadas por una institución independiente, con una capacidad técnica comprobada y reconocida por las partes del acuerdo. Para ello, en México destacan dos opciones, el Instituto Nacional de Estadística y Geografía (INEGI) o la Bolsa Mexicana de Valores (BMV). Este tema es relevante, ya que este índice pudiera utilizarse como base para otro tipo de productos derivados financieros que tiene como subyacente la longevidad y pudiera ser la base para un mercado de derivados de longevidad más profundo y líquido. Es importante notar que la experiencia de mortalidad del IMSS es usada como referencia regular en la valuación de los productos relacionados a pensiones y vida en México, por lo que la adopción de un índice de longevidad de este tipo en el mercado pudiera ser mayor.

2. Estructura y valuación del swap de longevidad

Derivado de la formulación descrita en las ecuaciones (1) a (4) se establecen dos series de longevidad, la primera, un índice L(t) que representa el comportamiento proporcional de la longevidad ex ante, es decir, el índice de longevidad proporcional esperado al inicio del periodo del swap, y segundo, un índice de longevidad proporcional que refleja la experiencia de longevidad ex post M(t), que es una variable aleatoria y es donde se incorpora el riesgo de longevidad, el cual se define al momento de iniciar el contrato del swap como:

(5)

donde ζ(t) es una variable aleatoria independiente e idénticamente distribuida que replica un shock de longevidad.⁹

Dado que este tipo de contratos trabaja principalmente con flujos netos y los índices tienen un valor proporcional, una cuestión que se debe considerar es la monetización de la diferencia entre los índices. En el contrato del swap se debe integrar una pensión en pesos y un número de pensionados sobre los cuales se aplicaría el swap. Todo ello se resume en la variable de monetización, ψ(t), que se define como la multiplicación de la pensión vigente, en pesos nominales, al inicio del año t por el número de pensionados vivos al inicio del año t. La pensión se modificará de acuerdo con las reglas establecidas por la Ley del Seguro Social en términos de actualización de las pensiones, pagos de aguinaldo, grupos familiares y otras particularidades del sistema de pensiones, mientras que el número de pensionados se modifica por dos vías: la sobrevivencia del stock de pensionados y la entrada de pensionados nuevos. Un supuesto adicional que se hace sobre la variable de monetización ψ(t) es que se conoce su distribución ex ante.

Una vez definidos el índice de longevidad proporcional y la variable de monetización, se puede continuar con la estructuración y valuación del swap de longevidad, si se sigue la formulación de ^{Dowd et al. (2006)}.

El valor de la parte fija del swap de longevidad estaría determinado por el valor presente de los flujos pagados por el organismo público de pensiones obligado a pagar la longevidad esperada (ex ante) y se representa con:

(6)

El primer término de la ecuación (6) es el índice de longevidad esperado al momento de la firma del swap; el segundo término es la variable de monetización que transforma el diferencial entre los índices de longevidad en dinero; y el término π, representa el premio a pagar que se establece con el fin de evitar el arbitraje.

Por otro lado, el valor de la parte aleatoria del swap, el cual es cobrado por el organismo de pensiones, se define por el valor presente del índice de longevidad ex post, transformado en pesos por su multiplicación con el segundo término, la variable de monetización, tal como se presenta a continuación:

(7)

Con ello, es posible determinar el valor del swap de longevidad como la diferencia de las dos partes, es decir, el valor del swap es el valor presente neto del diferencial de los dos flujos, los pagos esperados ex ante (fijos) y los cobros esperados que se definen ex post (variables), como se ve en la siguiente formulación:

(8)

Es aquí donde se define el valor de la prima, π, con la condición de no arbitraje que iguala el valor de swap a cero. Realizando manipulaciones matemáticas simples obtenemos:

(9)

que es similar a la ecuación (8) de ^{Dowd et al. (2006)}, siendo la principal diferencia que los índices de longevidad están expresados de manera proporcional, lo que permite medir la longevidad con poblaciones pensionarias crecientes y la utilización de una variable ψ(t) que monetiza las diferencias en el índice de longevidad proporcional y sirve para reflejar las condiciones particulares del monto pensionario del contrato que se modele. Estas características hacen que el modelo de estructuración presentado sea más general y aplicable a diversos fondos de pensiones, más allá del ejemplo propuesto más adelante en este artículo.

Una cuestión a considerar es que debido a que la distribución de las ganancias de longevidad es desconocida en el momento de la firma del swap, para poder calcular el valor de π se utiliza la transformación propuesta por (^{Wang 2000} y ²⁰⁰²) en la parte aleatoria de la ecuación (9), en la que se asigna un precio de mercado al riesgo. Un tema relevante es que el tamaño del shock de longevidad asumido es muy importante para el precio final del swap.¹⁰

IV. Propuesta para México

En el pasado, el gobierno federal mexicano ha transferido el riesgo de longevidad y otros riesgos relacionados con los sistemas de pensiones por medio de las reformas a los dos grandes sistemas, el IMSS en 1997 y el Instituto de Seguridad y Servicios Sociales de los Trabajadores del Estado (ISSSTE) en 2007. Al incorporar a los asegurados y futuros pensionados en el esquema dual de ahorro para el retiro en cuentas individuales, durante la etapa de acumulación, y los retiros programados o la compra de rentas vitalicias, en la etapa de desacumulación, el riesgo de longevidad se transfirió del gobierno federal hacia los trabajadores y hacia las compañías privadas que otorgan las rentas vitalicias.

Sin embargo, en la reforma que dio como resultado la Ley del Seguro Social de 1997 se incluyeron dos artículos transitorios: el XI y el XII, que establecen que los asegurados inscritos en el IMSS antes de la reforma podrán elegir el régimen bajo el cual se pensionan, el de 1973 (reparto) o el 1997 (rentas vitalicias), y que el gobierno federal se hará cargo de las erogaciones relacionadas con el régimen de reparto. De acuerdo con los cálculos presentados en ^{Alonso et al. (2014)}, esto representa un pasivo equivalente a 27.4% del producto interno bruto (PIB) nominal de 2012 y alcanza su nivel máximo de compromiso de recursos fiscales alrededor del año 2045, cuando el gobierno federal estará pagando un nivel superior a 1% del PIB en la nómina de pensiones.¹²

Para ejemplificar la aplicación de esta metodología se propone al gobierno federal de México el manejo del riesgo de longevidad relacionado con los pasivos pensionarios mencionados por tres razones:

La alternativa específica que se propone en este documento es la utilización de un swap de longevidad de largo plazo (50 años), en el cual el gobierno federal, con una posición natural corta en longevidad, entra en un acuerdo con un consorcio de aseguradoras y reaseguradoras de vida, nacionales e internacionales, que tienen una posición natural larga en longevidad, para intercambiar flujos de efectivo de acuerdo con el comportamiento de un índice de longevidad proporcional construido por un agente independiente, que pudiera ser el INEGI o la BMV, utilizando la experiencia de mortalidad experimentada por el IMSS.¹³

Para una mejor visualización de la propuesta, se presenta el Diagrama 1, en la cual se ejemplifica la situación actual de las obligaciones del gobierno federal y cómo los movimientos de flujos del swap de longevidad propuesto le ayudan a disminuir ese riesgo.

Diagrama 1 Swap de longevidad 

Como se mostró previamente, el gobierno federal tiene una obligación legal de pago de las pensiones derivadas de la Ley 73, flujo que es inevitable y que crece conforme al comportamiento de una variable incierta, que es la disminución de la mortalidad observada en la población pensionaria. El riesgo de longevidad para el gobierno federal proviene de las mejoras no esperadas en la esperanza de vida, ya que si la población vive un tiempo mayor, sus obligaciones se elevan.

En contraparte se tiene a un consorcio de aseguradoras y reaseguradoras de vida, las cuales tienen una exposición opuesta al riesgo de longevidad, es decir, si la población vive más de lo esperado, sus obligaciones financieras se reducen. El swap de longevidad aprovecha esta exposición opuesta para contrarrestar los riesgos de ambos agentes.

En el swap de longevidad propuesto, el gobierno federal recibiría un flujo de efectivo en el caso de que la mortalidad observada fuera mayor a la mortalidad esperada para cada periodo, en caso contrario, si la mortalidad observada fuera menor a la mortalidad esperada el gobierno haría un pago a su contraparte, lo que ayudaría a las aseguradoras y reaseguradoras de vida a enfrentar sus pasivos contingentes.

V. Simulación

En esta sección se llevará a cabo la simulación del proceso completo de la construcción del swap de longevidad propuesto para el gobierno federal mexicano y las compañías aseguradoras y reaseguradoras de vida. Para este ejercicio se considera un swap de 50 años, que inicia en 2017 y termina en 2066.

Este proceso va desde la construcción del índice de longevidad base L(t)y la simulación de la longevidad aleatoria M(t) por medio de una distribución asumida del shock de longevidad, hasta la estructuración y valuación del swap de longevidad, y finalmente la simulación de los flujos.¹⁴

Se comienza con el índice de longevidad proporcional base L(t), que indica la longevidad esperada ex ante (parte fija del swap). Por simplicidad y sin pérdida de generalidad, en la simulación solamente se modela el fenómeno de mortalidad en el género masculino, para lo cual se utilizan las tablas de mortalidad EMSSAH-97 publicadas por la Comisión Nacional de Seguros y Fianzas (CNSF), con las que se puede construir directamente la variable l _i (t).¹⁵

Para determinar la proporción fija de la población β _i,t se utilizan las proyecciones oficiales de población por edad del Conapo, las cuales llegan hasta el año 2051. Los años del periodo 2052-2066 se cubren con estimaciones propias. Los resultados se muestran en el Cuadro 1.

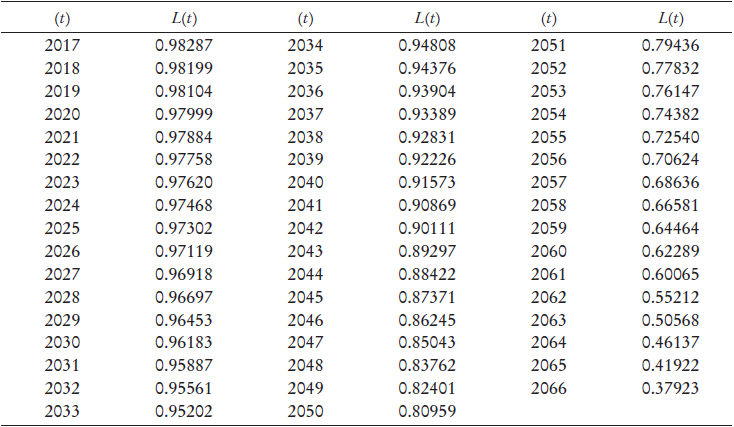
Fuente: cálculos propios con base en la ENSSAH-97 y en estimaciones de población de la Conapo.

Cuadro 1 Estimaciones del índice proporcional de longevidad 

Con el fin de determinar ζ(t) se llevaron a cabo 200 000 iteraciones Montecarlo en Crystal Ball© de Oracle. Los resultados de los índices de longevidad se presentan en la Gráfica 1, en donde se observa el comportamiento esperado de la longevidad L(t), así como los intervalos superior e inferior con una confianza de 90% del índice de longevidad con el shock.

Gráfica 1 Índice proporcional de longevidad 

En la simulación de shock de longevidad aleatorio, con el que se construye el índice de longevidad proporcional M(t), se tomó una aproximación similar a la simulación del error de medición utilizada por ^{Cheng y Wang (2001: 710)} para ejemplificar su modelo de estimación de supervivencia. Esto en el sentido de que el shock de longevidad (error de medición) es aditivo sobre el modelo de supervivencia utilizado (^{CNSF, 2015}) y se comporta como una distribución normal desplazada hacia la derecha -lo que podría ser el resultado de una combinación de dos distribuciones normales-. Sin embargo, para desarrollar la simulación presentada en este artículo se adiciona el resultado de la distribución simulada directamente sobre el modelo de supervivencia base (^{CNSF, 2015}), tal como se establece en la ecuación (5). Es importante notar que la distribución utilizada en esta simulación está construida ad hoc con el fin de mantener el ejemplo simple, sin embargo, al momento de estructurar el swap no se conoce la distribución de las mejoras en longevidad y los supuestos que se realicen sobre la misma tienen un impacto importante en el costo del swap, por lo que se requiere que los parámetros de la distribución de las ganancias en longevidad se deriven de los datos base de mortalidad que existen en los registros administrativos del IMSS.¹⁶

Siguiendo con la simulación, con el supuesto de una distribución conocida de las mejoras de longevidad podemos establecer los flujos provenientes del contrato. Para ello se requiere definir la variable ψ(t), que es lo que permite la monetización del índice de longevidad proporcional. Para efectos de la simulación se establece el número de pensionados iniciales en 300 000 y una tasa de crecimiento de 6% anual de nuevos pensionados, calculada respecto a los pensionados vivos al final de cada año t. Respecto a la pensión, se estableció un valor inicial de 10 000 pesos, con una tasa de crecimiento anual de 4%, que equivaldría al crecimiento esperado de las unidades de salario mínimo.¹⁷

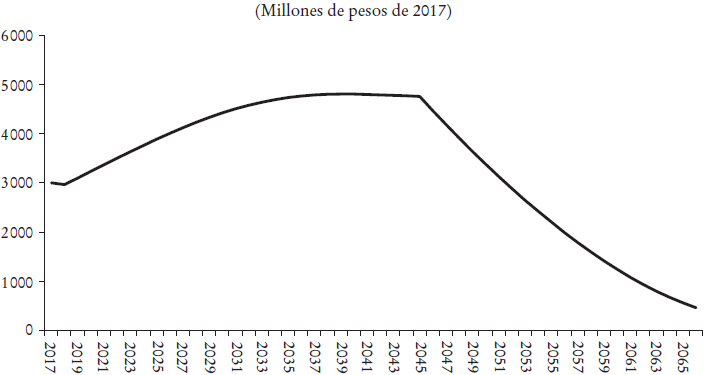
La variable ψ(t) se presenta en la Gráfica 2, en donde es posible observar el comportamiento en el tiempo de la variable de monetización de las obligaciones del esquema pensionario simulado, en el cual existe, tal como ocurre con el esquema de pensiones de la Ley del Seguro Social de 1973, un compromiso financiero creciente, tanto en número de pensionados, como en el monto individual de la pensión, con el fin de alcanzar el máximo nivel alrededor del año 2040. Esto ocurre porque las entradas de nuevos pensionados al esquema son crecientes, logran su máximo nivel en el año 2034, en donde si bien siguen entrando pensionados al cumplir la edad y requisitos, estas entradas comienzan a ser decrecientes. Dado que el monto de la pensión continúa siendo creciente, la variable de monetización ψ(t) continúa elevándose por unos años más, hasta conseguir su máximo alrededor del año 2040.

Gráfica 2 Valor de ψ(t) 

En el modelo utilizado se cierra la entrada a nuevos pensionados en el año 2044 y, a pesar de que el monto de pensión individual sigue creciendo, al cerrarse el grupo, la mortalidad asociada va disminuyendo la obligación financiera total del fondo de pensiones simulado.

Es importante notar que cuando se considera el monto completo de las obligaciones base del gobierno federal usadas en la simulación, es decir L (t)ψ(t) , existe una coincidencia del modelo simulado en este artículo con los resultados presentados por ^{Alonso et al. (2014)}, en lo que se refiere a que el nivel máximo de compromiso de recursos fiscales para pensiones ocurre alrededor del año 2045.¹⁸

Para calcular el costo de la protección para el gobierno federal se utilizan las ecuaciones (8) y (9) y una tasa libre de riesgo de 3.5% para descontar los flujos de efectivo generados por la simulación. El resultado es que el gobierno federal debería pagar una prima (π) equivalente a 1.1198% del flujo descontado total diferencial sobre los 50 años que estaría vigente el acuerdo.

El tamaño de la prima está relacionado con los supuestos que se hicieron en la distribución de las ganancias en longevidad, dentro de los cuales existe un sesgo hacia la derecha en el valor esperado de la distribución. Como se comentó previamente, se asumió una distribución ad hoc con propósito de ilustrar el funcionamiento del swap. En el momento de llevar a cabo las estimaciones para el contrato de swap se tendrían que calcular los parámetros de la función de distribución con los datos de mortalidad del IMSS.¹⁹

Es importante notar que en este tipo de contratos no existe un pago por adelantado, por lo que esta erogación es equivalente a un recargo en el índice de mortalidad. Ya que se espera un sesgo a la alza, el gobierno federal compensa en el flujo esta prima, la que equivale en valor presente neto a 1.1198%.

Existen al menos dos puntos que se pudieran discutir sobre este tema. El primero es que, como se comentó previamente, ésta es la alternativa más eficiente y, por lo tanto, la menos costosa para cubrir este tipo de riesgos, ya que se toma ventaja de una posición diferenciada contra el riesgo de longevidad de dos contrapartes. El segundo, es que el nivel de protección contra el riesgo de longevidad logrado con la simulación es notable. Para ilustrar este último punto se presenta el Cuadro 2, en el cual se muestran los resultados para el año 2045, que de acuerdo con la simulación realizada y los resultados presentados por ^{Alonso et al. (2014)} es el año en el cual la obligación fiscal del gobierno federal será mayor.

Fuente: cálculos de simulación con las variables especificadas.

Cuadro 2 Cobertura de flujos derivados del riesgo de longevidad en el año 2045 

En este año en particular, el resultado más extremo en ganancias de longevidad simuladas ocurre cuando el índice de longevidad proporcional alcanza 0.91371. En caso de que el gobierno federal no tuviera contratado un swap de longevidad, éste tendría un gasto adicional de 190.2 millones de pesos de 2017 con respecto al escenario base. Este gasto adicional tendría que provenir directamente de recursos fiscales, ya que, como se explicó previamente, estas obligaciones pensionarias no están fondeadas y mucho menos protegidas contra el riesgo de longevidad. En caso de que el gobierno federal hubiese contratado un swap de longevidad como el propuesto, y se diera el escenario de alta longevidad, el gobierno federal recibiría un pago del consorcio de aseguradoras y reaseguradoras de vida de 143 millones de pesos de 2017, con lo que se cubre 75.5% de las obligaciones adicionales comparables al escenario sin cobertura. Por otro lado, si la longevidad proporcional se reduce al mínimo nivel simulado, 0.85371, y se hubiese contratado el swap de longevidad, el gobierno federal tendría un compromiso de flujo hacia las aseguradoras y reaseguradoras de vida de 142 millones de pesos del 2017, el cual sería financiado en 67.1% por los ahorros en pensiones del gobierno federal, producto de la mayor mortalidad entre la población pensionaria. Una cuestión importante que se debe observar es que los pagos están sesgados hacia el sector asegurador y reasegurador de vida porque el riesgo de longevidad está sesgado hacia arriba, por lo que las aseguradoras y reaseguradoras de vida estarían tomando un riesgo mayor al entrar al swap y son compensadas por ello por medio de la prima (π).

Es importante notar que el valor esperado ex ante de la cobertura es cero, tanto para el gobierno federal como para la contraparte, por definición la prima se establece para que el valor del swap sea ex ante cero, como se pude observar en la ecuación (9). No obstante, el costo real para el gobierno federal será determinado ex post, conforme se vaya reportando la mortalidad de la población pensionaria y se calculen los flujos. Por ejemplo, si se consideran los cálculos de la simulación del Cuadro 2, se tiene que el costo para el gobierno federal, sin importar el escenario de longevidad que ocurra, es de 46.5 millones de pesos de 2017 durante ese año. Si se hace un análisis similar, si se consideran los 50 años de vida del swap, y se toma en cuenta el valor esperado de la distribución simulada y su comparación contra el escenario sin protección, el costo ex post del swap para el gobierno federal sería de 1 622 millones de pesos de 2017.

De este ejercicio de simulación podemos concluir que la contratación de un swap de longevidad provee una cobertura del riesgo de longevidad notable, ya que cuando se considera un escenario de longevidad desfavorable, los flujos del swap cubren un porcentaje relativamente alto de los compromisos adicionales. Sin embargo, por esta cobertura se tiene que pagar un costo, el cual tiene un recargo en contra del gobierno federal por construcción.

La distribución de ganancias de longevidad está sesgada a la derecha y refleja el comportamiento observado en la literatura de longevidad. Una cuestión que se debe considerar es el costo real de cobertura (ex post) para el gobierno federal, el cual se determina por la diferencia entre la distribución de longevidad propuesta en el contrato para la mejora del riesgo de longevidad y la longevidad realizada, la cual se puede estimar o simular, pero sobre la que no existe certidumbre.

Conclusiones

El riesgo de longevidad implica un daño financiero potencial para los sistemas de pensiones y retiro que tengan a su cargo obligaciones vitalicias, ya sean gubernamentales o privados. En la búsqueda de alternativas para transferir ese riesgo de longevidad hacia el sector privado por medio del mercado de capitales, se concluyó que el swap de longevidad es la mejor alternativa existente para este tipo de riesgos, retomando una idea de ^{Cox y Lin (2004)}, acerca de utilizar el hegde natural existente entre los sistemas de pensiones y las empresas aseguradoras y reaseguradoras de vida con el fin de realizar un swap de longevidad más eficiente.

A partir de esta idea, se modificó la metodología de estructuración y valuación de un swap de longevidad de ^{Dowd et al. (2006)} en dos sentidos. Primero, se introdujo un índice de longevidad proporcional, que permite medir la longevidad en poblaciones pensionarias crecientes y, segundo, se adicionó una variable de monetización que se aplica sobre los diferenciales de los índices de longevidad (fijo y variable). Estas dos modificaciones permiten ajustar el modelo de estructuración del swap a las condiciones contractuales de diferentes sistemas de pensiones, como es el caso de las obligaciones pensionarias a cargo del gobierno federal mexicano, derivadas de la reforma de la Ley del Seguro Social de 1997.

Adicionalmente, se presenta una propuesta para llevar a cabo esta primera transacción en mercados emergentes, que genere un nuevo mercado financiero en México, y que permite al gobierno federal mexicano un traslado eficiente del riesgo de longevidad hacia un consorcio de aseguradoras y reaseguradoras de vida. Para ejemplificar esta propuesta se simula la estructura y valuación del contrato y se concluye que el swap de longevidad le da una cobertura notable a los flujos contingentes del gobierno federal. El costo ex ante es cero, sin embargo, el verdadero costo se definirá ex post, es decir, una vez observada la mortalidad, lo que se ejemplifica en la simulación con el sesgo en la longevidad hacia arriba, que refleja la evidencia conocida en el comportamiento de la longevidad.

Existen dos aspectos que deben considerarse en investigaciones futuras. El primero, relacionado con un mercado secundario de longevidad que puede surgir de la contratación de un swap de longevidad como el propuesto; y el segundo con las aplicaciones potenciales de este tipo de productos en otras instituciones financieras relacionadas al retiro. Respecto al primer punto, otros instrumentos derivados financieros de longevidad relacionados al swap, como swaptions, caplets y floorlets pudieran ayudar a diluir el riesgo para las dos contrapartes del swap de longevidad, por medio de su transmisión al mercado financiero, y con ello impulsar un mercado secundario de dispersión de riesgo. En cuanto al segundo punto, si bien las aseguradoras de pensiones que proveen rentas vitalicias bajo la Ley del Seguro Social vigente en México tienen en su precio algunos elementos para cubrir el riesgo de longevidad, éstas pudieran tener el potencial de ser más competitivas en las subastas de rentas vitalicias organizadas por el IMSS si utilizan este tipo de productos para cubrir su riesgo de longevidad. Otro caso interesante son las Afores, que de acuerdo con la misma ley, pueden ofrecer un tipo de retiro llamado retiros programados, en el cual el riesgo de longevidad lo absorbe el trabajador retirado, ya que puede quedarse sin ingreso de extender su vida más allá de lo esperado. Por medio de los esquemas mencionados en este artículo, las Afores pudieran hacer vitalicios los retiros programados.

El potencial de utilización de los productos derivados financieros de longevidad en México es alto. Las condiciones institucionales y de mercado existentes son suficientes para que dichas transacciones se lleven a cabo, y representan también las condiciones necesarias para iniciar un nuevo mercado financiero en el que se incorporen las instituciones de pensiones, seguros y ahorro para el retiro. En conjunto, este tipo de desarrollos con productos derivados pudieran contribuir a tener sistemas de pensiones y seguros más eficientes alrededor del mundo, considerando las tendencias esperadas en longevidad en los años por venir.