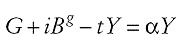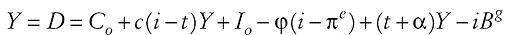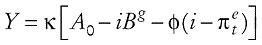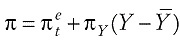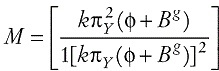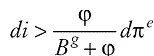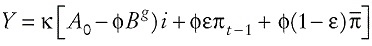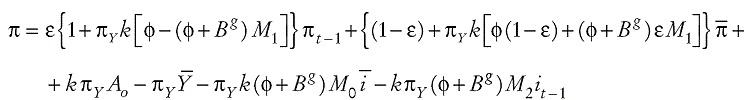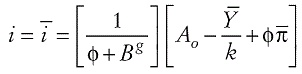Introducción

En este trabajo se presenta un modelo donde la política monetaria se basa en un sistema de metas explícitas de inflación, con la tasa de referencia para los mercados interbancarios como instrumento de política y la cantidad de dinero endógena; mientras que la política fiscal opera con un límite sobre el déficit fiscal como porcentaje del PIB, siendo el gasto público endógeno. En la regla de política monetaria, el parámetro de suavizamiento que vincula la tasa de interés de referencia con su rezago, se desprende de la conducta optimizadora del banco central¹.

El modelo permite mostrar la dinámica macroeconómica que se produce en dos escenarios extremos, de credibilidad completa en la meta de inflación del banco central, y de credibilidad nula, y se encuentra que i) puede haber convergencia hacia el equilibrio estacionario, incluso si no se cumple el Principio de Taylor; y ii) si hay credibilidad completa en el banco central, una política monetaria contractiva puede producir un undershooting de la inflación.

El artículo consta de las siguientes secciones. En la siguiente sección se presentan los antecedentes teóricos del modelo. En la sección II se presenta el modelo, el cual contiene un subsistema dinámico y un subsistema del equilibrio estacionario. En la sección III se hace un ejercicio de estática comparativa para evaluar los efectos de una política monetaria contractiva (una reducción de la meta de inflación) sobre la producción, la tasa de interés y la inflación. Por último, en la sección IV, se presentan algunas conclusiones e implicancias para la política macroeconómica.

I. Antecedentes

Este modelo está inspirado en la corriente neokeynesiana marcada por el trabajo de ^{Clarida, Galí y Gertler (1999)} e iniciada por ^{Taylor (1993)} . Este marco impone rigidez de precios en el corto plazo, con lo cual la política monetaria tiene efectos reales en el corto plazo; el instrumento de la política monetaria es la tasa de interés, no algún agregado monetario; el banco central busca minimizar una función de pérdida que está en función a las desviaciones de la inflación y la producción respecto a los niveles deseados; y, por último, las expectativas juegan un rol protagónico.

La política monetaria en estos modelos se basa en la regla propuesta por ^{Taylor (1993)} . De acuerdo a la regla de Taylor, la tasa de interés de la Reserva Federal americana (FED) es una función lineal de una constante de 4 % (la tasa de inflación meta implícita más la tasa de interés real natural), la brecha del producto y la brecha de la inflación (la inflación observada menos la inflación meta implícita del FED, de 2 % anual). Según el Principio de Taylor, la tasa de interés real de corto plazo debe elevarse cuando la inflación está por encima de su nivel meta; o, lo que es lo mismo, la tasa de interés nominal debe subir en una proporción mayor que la inflación.

La influencia del trabajo de Taylor ha sido notable. En ^{Asso, Kahn y Leeson (2007}, 2010) y ^{Taylor (1999)} se hace una reseña comprensiva de su influencia sobre la investigación macroeconómica y el diseño de la política monetaria. En particular, destaca la importancia de la regla de Taylor en las discusiones del Federal Open Market Committee (FOMC) del FED para tomar las decisiones de política monetaria durante el periodo 1993-2001. ^{Bernanke y Mihov (1998)} muestran que el uso de la tasa de interés como instrumento de política monetaria, en lugar de algún agregado monetario, es el rasgo general de la política monetaria del FED desde 1965, con excepción del periodo 1980-82 de Paul Volcker, así como de los principales bancos centrales del mundo.

Este nuevo paradigma de política monetaria ha sido expuesto en términos del esquema tradicional de la Macroeconomía por ^{Romer (2000)} , ^{Walsh (2002)} y ^{Carlin y Soskice (2005)} . En este esquema, el equilibrio en el mercado de bienes es representado por la curva IS; la oferta agregada, por la curva de Phillips, la curva CP, y el equilibrio en el mercado monetario, la tradicional LM, es reemplazada por la Regla de Política Monetaria, la RPM, que es obtenida a partir de la conducta optimizadora del banco central.

La regla de política monetaria tiene dos características distintivas. En primer lugar, el parámetro que multiplica a la brecha de inflación (la diferencia entre la inflación esperada y la inflación meta) es mayor que uno, con el objetivo de que la elevación en la tasa de interés nominal sea más que proporcional al de la inflación esperada de manera tal que pueda alterarse la tasa de interés real. Es el Principio de Taylor.

En segundo lugar, de acuerdo con ^{Clarida, Galí y Gertler (1999)} , y ^{Woodford (1997)}, en la práctica, los bancos centrales ajustan la tasa de interés más cautelosamente que lo que predice la regla de Taylor. De esta manera, los bancos centrales tienden a ajustar sus tasas de interés gradualmente, hasta alcanzar el nivel fijado como objetivo. Por eso, las reglas de política monetaria que reproducen la conducta de la mayoría de los bancos centrales incorporan la tasa de interés rezagada como uno de los determinantes de la tasa de interés actual.

Hay varias explicaciones de por qué los bancos centrales suavizan los movimientos en la tasa de interés². En primer lugar, como la producción y los precios no dependen de la tasa de interés de corto plazo, sino de la de largo plazo, que está asociada a las expectativas sobre las tasas de corto plazo; una manera simple de afectar a las tasas de largo plazo es establecer la reputación de mantener la tasa de corto plazo alta, una vez que se ha empezado a subirla, o mantenerla persistentemente baja, una vez que se la ha bajado. En segundo lugar, en la toma de decisiones de política monetaria la incertidumbre está siempre presente, lo que obliga a un manejo cauteloso de la tasa de interés. En tercer lugar, la regla lineal de política monetaria puede producir grandes fluctuaciones en la tasa de interés, atentando contra la restricción de no negatividad de la tasa de interés nominal de corto plazo. Por último, grandes movimientos en la tasa de interés pueden tener efectos desestabilizadores en los mercados financieros.

^{Rudebusch (2006)} tiene una explicación alternativa. La disputa no es sobre si la inercia en el movimiento de la tasa de interés existe, sino acerca del origen de esa inercia. El ajuste lento de la tasa de interés de corto plazo puede estar reflejando simplemente la lenta acumulación de información relevante para tomar la decisión de modificar la tasa de interés. En cualquier caso, como adelantaron ^{Clarida, Galí y Gertler (1999)} , entender por qué los bancos centrales mueven la tasa de interés menos de lo que la teoría predice es un importante tema aun no resuelto.

También en el Perú, ^{Rodríguez (2008)} y el modelo de proyecciones de corto plazo del Banco Central de Reserva del Perú ^{(BCRP, 2009)}, en un sistema de metas explícitas de inflación, incorporan, desde fuera del modelo, el rezago de la tasa de interés como un argumento de la RPM. El modelo que presentaremos, siguiendo a ^{Woodford (2002}, ²⁰⁰³⁾, incorpora un objetivo adicional para el banco central, el de suavizar los movimientos en la tasa de interés, de manera tal que la presencia de la tasa de interés rezagada en la RPM se desprenda de la conducta optimizadora del banco central.

Por otra parte, en los modelos reseñados, se abstrae el sector fiscal o solo se lo incorpora a través del efecto del gasto público o la tasa impositiva en la tasa de interés natural, que es un argumento de la RPM. En nuestro modelo, se asume que la política fiscal se conduce a través de una regla que impone un límite al déficit fiscal, como porcentaje del PIB³. Esta regla endogeniza el gasto público no financiero, el que será una función directa de la meta de déficit fiscal, de la presión tributaria y del nivel de actividad económica; y una función inversa de la tasa de interés y del stock de deuda pública.

En este sistema, cuando el banco central eleva la tasa de interés, no solo afecta a la tasa de interés real y a la inversión privada, sino también al gasto público no financiero. Por lo tanto, el banco central puede cumplir con su rol estabilizador, aun cuando no se cumpla el Principio de Taylor.

Por último, se hace una presentación de las expectativas de inflación de manera que puedan simularse los efectos de una política monetaria contractiva en dos escenarios extremos; de completa y nula credibilidad en la meta de inflación anunciada por el banco central. Una consecuencia de la credibilidad perfecta es que una política monetaria contractiva puede producir un undershooting de la tasa de inflación en el corto plazo.

II. El modelo

Este es un modelo de economía cerrada que incorpora el sistema de políticas macroeconómicas vigentes en el Perú. La política monetaria opera con un sistema de metas explícitas de inflación y tiene como instrumento la tasa de interés de referencia para los mercados de crédito interbancarios. La política fiscal trabaja sobre la base de un tope del déficit fiscal como porcentaje del PIB, convirtiéndose el gasto público no financiero en una variable endógena.

El modelo contiene dos subsistemas. En el subsistema dinámico, la inflación esperada está asociada a su rezago y a la inflación meta, y en la regla de política monetaria aparece la tasa de interés rezagada. En el subsistema del equilibrio estacionario, la inflación es igual a la inflación meta, la tasa de interés alcanza su nivel natural y el producto es de pleno empleo. La estructura del modelo no parte de micro fundamentos (preferencias o acervo de tecnología de los agentes económicos). Está compuesta por ecuaciones de comportamiento lineales que pueden obtenerse a partir del comportamiento óptimo de los agentes.

1. El subsistema dinámico

El banco central tiene como objetivo central mantener la estabilidad de precios y el instrumento de política es la tasa de referencia para el mercado interbancario. Además, como en la literatura que gira alrededor de la Regla de Taylor⁴ el banco central, ante una elevación de la inflación por encima de su meta, reacciona a través de una serie de pequeñas alzas sostenidas en la tasa de interés, y no de un alza fuerte, por una sola vez, de dicha tasa. Es consecuencia, puede asumirse que la autoridad monetaria opera como si buscase minimizar una función de pérdida (Ω) que tiene como argumento no solo el diferencial entre la inflación observada y la inflación meta π-π-, sino también el diferencial entre la tasa de interés de referencia y su valor rezagado i-it-1. ⁵

(1)

En el mercado de bienes asumimos que la producción Y se determina en función a la demanda D, cuyos determinantes son el consumo C, la inversión privada y el gasto públic G o. Suponemos que el consumo responde solo a un componente autónomo Co y al ingreso disponible Yd1-tY; y la inversión responde a un componente autónomo I0 y a la tasa de interés real, que es igual a la tasa de interés nominal ajustada por la inflación esperada i-πe.

Por otro lado, el gasto público no financiero G se determina de acuerdo con una regla que impone un límite máximo de déficit fiscal como porcentaje del PIB α. El déficit fiscal, la diferencia entre los gastos (no financieros y financieros) y los ingresos del gobierno, que son una fracción del producto, equivale a:

en que Bg es el momento de deuda pública, que se supone exógeno. Entonces, el gasto público no financiero es endógeno:

Si se considera la demanda como la suma de las distintas funciones de comportamiento (consumo, inversión y gasto público), el equilibrio en el mercado de bienes viene dado por:

Esta ecuación, la curva IS de esta economía, puede también representarse como:

(2)

Donde A₀ es el gasto privado autónomo, de consumo e inversión, y k=11-c1-t-α es el multiplicador keynesiano, de signo positivo, para garantizar la convergencia asintótica hacia el equilibrio estacionario.

La oferta agregada está representada por la curva de Phillips (CP). La inflación (π) está asociada a la inflación esperada πte y a la brecha del producto (Y-Y-).

(3)

En el contexto de este modelo, la respuesta de política monetaria óptima la obtenemos minimizando la función de pérdida del banco central, sujeta a las restricciones establecidas por la IS y la CP. De este procedimiento resulta que si la inflación está por encima de su nivel meta, el banco central debe elevar la tasa de interés por encima de su nivel anterior.

(4)

Necesitamos incorporar, en lugar de la inflación, sus determinantes. Para este objetivo, se resuelve el sistema compuesto por las ecuaciones del mercado de bienes, la curva de Phillips y la regla de política monetaria (ecuaciones 2, 3 y 4), y se incorpora este valor en la ecuación (4). De esta manera, se obtiene la regla de política monetaria óptima del banco central.

(5)

En la que

En la regla, uno de los determinantes de la tasa de interés es la tasa natural o tasa de interés del equilibrio estacionario. Esta tasa la obtenemos a partir de la ecuación del mercado de bienes, cuando la economía está en equilibrio estacionario. Por definición, en el equilibrio estacionario, la inflación esperada es igual a la inflación observada πte=π y la tasa de interés es igual a su valor rezagado i=i-1 . Cuando se cumplen estas dos condiciones el producto alcanza su nivel potencial y la inflación esperada es igual a la inflación meta (Y=Y-;πte=π-) . Por lo tanto, partiendo del equilibrio en el mercado de bienes (ecuación 2) e introduciendo los resultados anteriores, la tasa de interés natural (i) viene dada por:

(6)

⁷

De (6), se obtiene:

(6.1)

Reemplazando (6.1) en (5), obtenemos, finalmente, la Regla de Política Monetaria Óptima (RPM):

(7)

en la que:

;

En la RPM, los valores M₀ y M₂ , que vinculan la tasa de interés con la tasa natural y la tasa de interés rezagada, respectivamente, tienen los valores usuales, que fluctúan entre cero y uno. El parámetro M₂, que permite la suavización de la tasa de interés, no se introduce desde fuera del modelo, como es usual, sino que se desprende de la conducta optimizadora del banco central y por eso contiene parámetros estructurales del modelo.

El Principio de Taylor establece que el parámetro que relaciona la tasa de interés con la brecha de inflación, M₁, debe ser mayor que 1. La razón es que los bancos centrales persiguen alterar la tasa de interés real (la tasa de interés nominal menos la inflación esperada), para afectar al gasto privado. Cuando la inflación esperada se eleva en un punto porcentual, la autoridad monetaria debe elevar la tasa de interés nominal en más de un punto porcentual.

En nuestro modelo, no es necesario que se cumpla el Principio de Taylor para que la política monetaria tenga un rol estabilizador. La razón es que el alza de la tasa de interés no solo afecta al gasto privado sino también al gasto público, porque afecta al pago de intereses de la deuda pública y en consecuencia al gasto público no financiero. Podría ser posible, entonces, que ante un alza de la inflación esperada, la tasa de interés real no se eleve y aún así el banco central consiga su objetivo de bajar la demanda agregada. La ecuación (2) nos ayuda a entender por qué no es indispensable que se cumpla el Principio de Taylor.

Suponiendo que la inflación esperada se eleva (dπe>0) para que la producción se reduzca (dY<0) la tasa de interés nominal debe elevarse. ¿En cuánto? De la ecuación (2) se deriva que:

Es decir, basta que la tasa de interés nominal se eleve por encima de la fracción ϕBg+ϕ para que la demanda y la producción se reduzcan.

El modelo completo viene dado por el equilibrio en el mercado de bienes (la IS), la regla de política monetaria (la RPM) y la curva de Phillips (la CP).

(2)

(7)

(3)

El papel de las expectativas. En el subsistema anterior tanto la inflación esperada como la tasa de interés rezagada están dadas. Sin embargo, luego del impacto inicial de los cambios en las variables exógenas, en el tránsito hacia el equilibrio estacionario, tanto la inflación esperada como la tasa de interés rezagada deben empezar a ajustarse, hasta alcanzar sus nuevos valores de equilibrio estacionario.

¿Cuáles son las ecuaciones que reflejan la dinámica de la tasa de interés y la inflación esperada? La dinámica de la tasa de interés ya está presente en la ecuación (7), la RPM. Para la dinámica de la inflación, hay que postular hipótesis sobre el comportamiento de la inflación esperada.

Como en ^{Birch y Jorgen (2005, Cap. 21)} , asumiremos que el público tiene en parte expectativas estáticas - esperan que la inflación será igual a su valor previo-, y en parte perfecta certidumbre- esperan que la inflación igualará a la meta anunciada por el banco central-. Cuanto mayor sea la ponderación de la inflación meta, más "anclada" estará la expectativa de inflación alrededor de la inflación meta⁸.

(8)

⁹

Por lo tanto, el sistema dinámico completo, con la inflación esperada endógena, introduciendo la ecuación (8) en las ecuaciones de la IS, la RPM y la CP , viene dado por:

(9)

(10)

(11)

Las variables endógenas de este subsistema son la producción, la tasa de interés y la inflación. Los instrumentos de la política fiscal son la tasa impositiva y la meta de déficit fiscal. El único instrumento de la política monetaria es la inflación meta. Las otras variables exógenas no instrumentales son el gasto privado autónomo y el producto potencial.

2. El tránsito hacia el equilibrio estacionario

Para evaluar las condiciones para la convergencia al equilibro estacionario, hay que construir un sistema de ecuaciones en diferencias para las variables tasa de interés e inflación. La primera ecuación (la 10) corresponde a la regla de política monetaria, donde la tasa de interés es una función su rezago. Esta es una ecuación en diferencias, lineal y de primer grado. Para construir la segunda ecuación, la de la inflación, hay que combinar las ecuaciones (9), (10) y (11). Reemplazando (10) en (9), e introduciendo el resultado en (11), obtenemos:

(12)

En consecuencia, el sistema dinámico está compuesto por dos ecuaciones en diferencias de primer grado:

(10)

(12)

3. El subsistema del equilibrio estacionario

En el contexto de este modelo, en el equilibrio estacionario, la inflación esperada debe igualar a su valor efectivo y la tasa de interés debe estabilizarse. Es decir, i)πe=π y ii) i=i-1

Imponiendo estas condiciones en el subsistema compuesto por las ecuaciones (2), (7) y (3) llegamos a la siguiente presentación del modelo en su forma reducida:

(6)

(13)

(14)

Es decir, en el equilibrio estacionario, la tasa de interés converge a su valor natural, la inflación a su nivel meta y la producción a su nivel potencial.

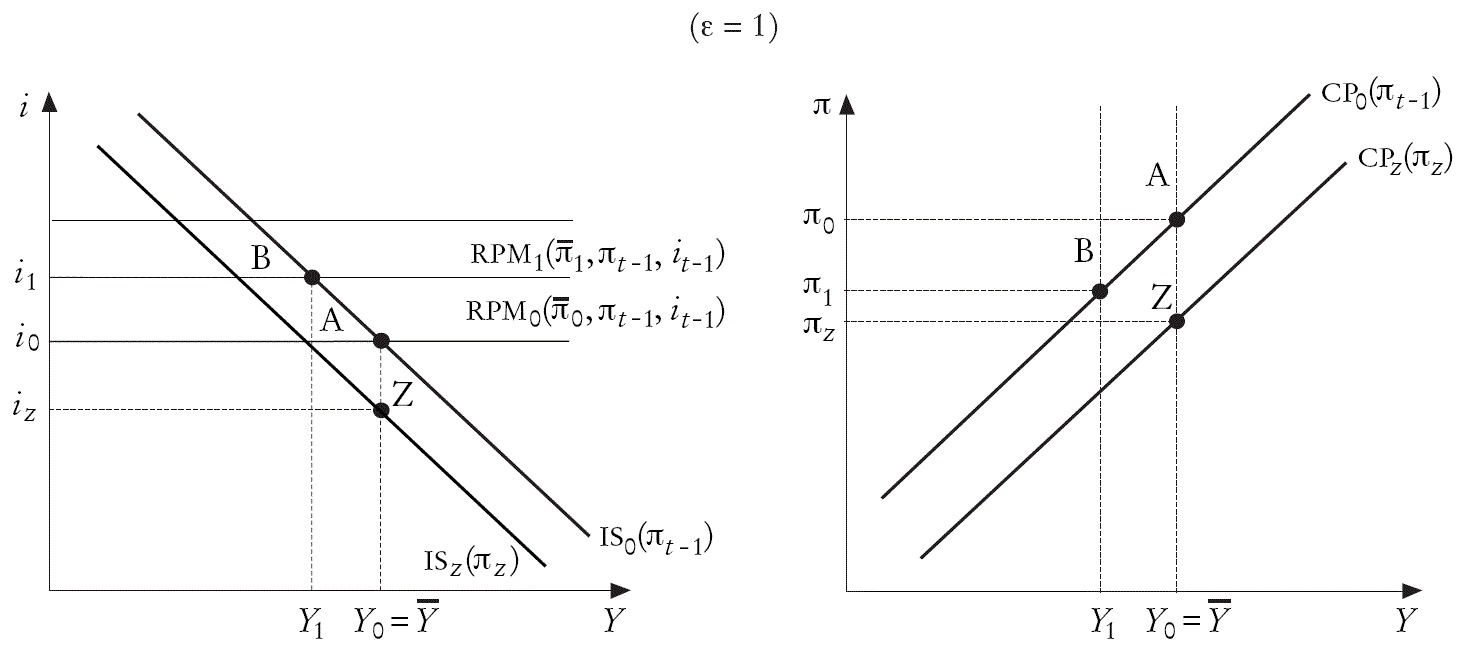
El modelo completo, que conjuga el sistema dinámico y el equilibrio estacionario, se representa en la Gráfica 1. En el plano superior, en la intersección de las curvas IS (la combinación de tasas de interés y producción que mantiene en equilibrio el mercado de bienes) y la RPM (la ecuación de la Regla de Política Monetaria) se muestran los valores de equilibrio de la tasa de interés nominal y la producción. Dada la producción, en el plano inferior, a través de la CP (la ecuación de la oferta agregada), se halla el valor de equilibrio de la inflación. Los valores de equilibrio inicial son valores de equilibrio estacionario. Es decir, la tasa de interés está en su nivel natural, la producción alcanza su nivel potencial y la inflación es igual a la inflación meta.

Gráfica 1 El modelo 

Los parámetros de las curvas son variables exógenas o endógenas rezagadas, y son estas últimas las que introducen dinámica en el modelo. Así, cada vez que se altera una variable exógena, en el periodo de impacto, se modificarán los valores de la tasa de interés, la producción y la inflación. En el siguiente periodo, como la inflación y la tasa de interés han cambiado, las curvas IS, RPM o CP empezarán a desplazarse, hasta que el sistema alcance un nuevo equilibrio estacionario.

III. Dinámica macroeconómica con metas de inflación y déficit fiscal¹⁰

En esta sección, se simulan los efectos de una política monetaria contractiva consistente en una reducción de la meta de inflación sobre el nivel de actividad económica, la tasa de interés y la inflación, en el periodo de impacto, en el tránsito al equilibrio estacionario y en el equilibrio estacionario. Respecto a la expectativa de inflación, nos situaremos en dos casos extremos. En el primer caso, se asumirá que la credibilidad de la autoridad monetaria es nula: la inflación esperada responde únicamente a la inflación rezagada (ε=1). En el segundo caso, supondremos que existe plena credibilidad en la autoridad monetaria: la inflación esperada responde únicamente a la inflación meta (ε=0).

Caso 1: (ε=1) Una política monetaria contractiva (reducción de la inflación meta), tiene los siguientes efectos, en el primer periodo o periodo de efecto. Como las expectativas de inflación dependen solo de la inflación rezagada, la inflación esperada permanece constante. Sobre la tasa de interés nominal hay dos efectos en sentido opuesto. Por un lado, una menor inflación meta eleva el diferencial entre la inflación esperada y la inflación meta, lo cual empuja al alza de la tasa de interés. Por otro lado, la reducción de la inflación meta hace caer la tasa de interés natural, lo que empuja a hacer bajar la tasa de interés. Puede mostrarse que el primer efecto descrito es más fuerte que el segundo, por lo que la tasa de interés se eleva; es decir, una menor inflación meta eleva la tasa de interés.

La mayor tasa de interés genera los siguientes efectos en el mercado de bienes. Como la inflación esperada no varía, sube la tasa de interés real, conduciendo a la caída de la inversión privada, y como se ha elevado el pago de intereses de la deuda pública, se reduce el gasto público no financiero. Ambas fuerzas hacen caer la demanda y por tanto el nivel de actividad económica y la brecha del producto. La inflación baja como consecuencia de la menor brecha del producto. Los resultados matemáticos del modelo muestran que la inflación cae, en el periodo de impacto, en una proporción menor que la reducción de la inflación meta.

En el segundo periodo, las variables endógenas reciben el impacto tanto de la mayor tasa de interés, como de la menor inflación rezagada. La mayor tasa de interés rezagada conduce a una nueva elevación de la tasa de interés. Sin embargo, la menor inflación rezagada, induce a la reducción de la tasa de interés, y este efecto es el dominante, lo que reduce la tasa de interés. La menor tasa de interés eleva la inversión privada y el gasto público, lo que reactiva la economía. Este efecto es debilitado, pero no anulado, por la menor inflación esperada (inflación rezagada), que eleva la tasa de interés real y reduce la inversión privada y la producción. La mayor producción, con el producto potencial constante, eleva la inflación.

Por otro lado, la menor inflación rezagada, en el lado de la oferta, tiene un efecto directo y de uno a uno sobre la inflación. Este efecto sobre la inflación es más potente que el producido por el mayor nivel de actividad económica. Es decir, la inflación en el segundo periodo continúa reduciéndose.

Para que el tránsito hacia el equilibrio estacionario sea dinámicamente estable, en los periodos siguientes la inflación debe seguir bajando, para converger al nuevo nivel meta; la tasa de interés debe seguir descendiendo, luego de haber subido en el periodo de impacto, pues en el nuevo equilibrio estacionario tiene que alcanzar su nuevo nivel natural, que es menor a su nivel natural inicial; y la producción debe continuar elevándose, hasta volver a su estado original, equivalente al producto potencial.

En la Gráfica 2, se parte del equilibrio estacionario inicial (punto A), con la producción en su nivel potencial, la tasa de interés igual a la tasa natural y la inflación en su nivel meta. En el periodo de impacto, una reducción de la inflación meta traslada la RPM, de RPMM₀ a RPMM₁, dadas la inflación y la tasa de interés rezagadas. El equilibrio de corto plazo se alcanza en B, con una tasa de interés más alta y una producción más baja. En la figura inferior, el de la oferta agregada, el equilibrio de corto plazo también se traslada de A a B, con una menor inflación. En el nuevo equilibrio estacionario(Z), la producción vuelve a su nivel potencial, la tasa de interés nominal baja a su nuevo nivel natural, que es más bajo que el inicial, y la inflación se reduce, hasta alcanzar su nuevo nivel meta.

Gráfica 2 Política monetaria contractiva 

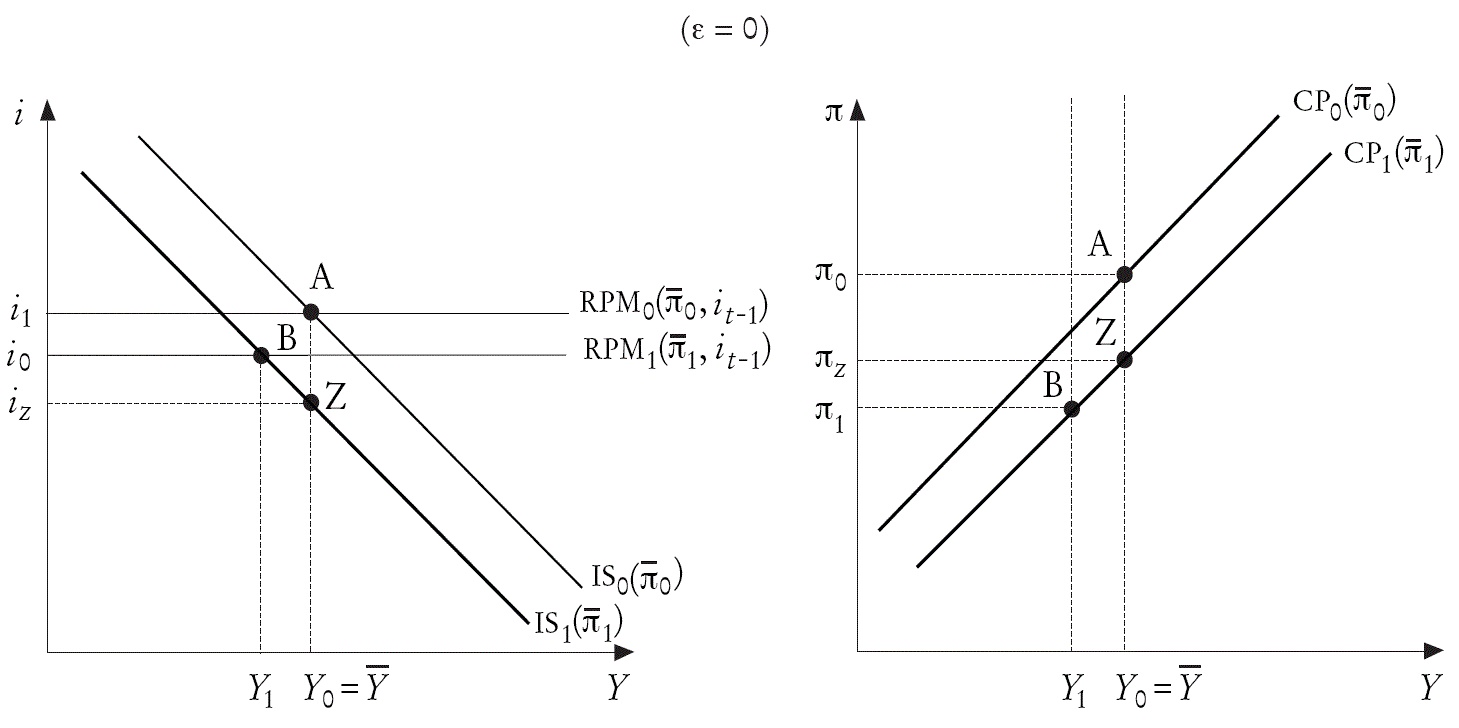
Caso 2: (ε=0). En el caso de que la inflación esperada responda únicamente a la inflación meta (ε=0), la dinámica de ajuste es distinta y se inicia en el periodo de impacto. En este periodo, la menor inflación meta reduce la inflación esperada. La menor inflación esperada, en el mercado de bienes, eleva la tasa de interés real y reduce la demanda. Pero la menor inflación meta, en la regla de política monetaria, también conduce al descenso de la tasa de interés natural, lo que reduce la tasa de interés, elevando la demanda en el mercado de bienes. Para que la convergencia al equilibrio estacionario sea dinámica estable, el efecto que prevalece es el primero, con lo cual se reduce la demanda y en consecuencia el nivel de actividad económica.

La menor actividad económica reduce la brecha del producto y como consecuencia la inflación. La inflación cae también por el efecto directo de la inflación meta en la Curva de Phillips. Por consiguiente la inflación cae en una proporción mayor que la inflación meta: hay un undershooting de la inflación respecto a su nivel del equilibrio estacionario. En los siguientes periodos el comportamiento de la tasa de interés define toda la dinámica de ajuste. De acuerdo a la regla de política monetaria, como la tasa de interés se redujo en el periodo de impacto, en el segundo periodo vuelve a caerse. La menor tasa de interés, por un lado, eleva el gasto público y, por otro lado, como la inflación esperada se mantiene constante, reduce la tasa de interés real, elevando la inversión privada. La mayor demanda eleva el nivel de actividad económica y en consecuencia la inflación.

Esta dinámica de tasa de interés en caída y nivel de actividad económica e inflación en alza continúa hasta que la inflación iguala a su nuevo nivel meta, que es más baja que la original; la tasa de interés alcanza su nuevo nivel natural, que también es más bajo que en la situación inicial; y la producción vuelve a su nivel inicial, el potencial.

En la Gráfica 3, en el corto plazo, la RPM se traslada de RPM₀ a RPM₁ , y la IS de IS₀ a IS₁ , por el descenso de la inflación meta. El equilibrio de corto plazo se alcanza en B, con una tasa de interés y una producción más bajas. En el gráfico inferior, la CP se desplaza de CP₀ a CP₁ , con una menor inflación, que cae por doble motivo, por el desplazamiento de la oferta agregada y por la recesión undershooting. En el nuevo equilibrio estacionario, la producción recupera su nivel potencial, la tasa de interés alcanza su nuevo nivel natural, más bajo que el inicial, y la inflación iguala a s u nuevo nivel meta, inferior al inicial.

Gráfica 3: Política monetaria contractiva 

Conclusiones

En este artículo se ha presentado un modelo con metas de inflación y déficit fiscal, y con la tasa de interés rezagada como un argumento de la RPM.

En el modelo, hemos simulado los efectos de una política monetaria contractiva en dos casos extremos, de credibilidad nula sobre la meta de inflación (ε=1)y de credibilidad completa (ε=0). En ambos casos, el resultado en el equilibrio estacionario es el mismo: cae la inflación y la tasa de interés nominal, y no se altera la producción. En el periodo de impacto, los resultados cualitativos son también similares: caen la tasa de interés, la inflación y la producción.

Sin embargo, cuando la credibilidad sobre la meta de inflación es completa, la reducción en la tasa de inflación es mucho mayor que cuando la credibilidad es nula, y se da un undershooting de la inflación en el periodo de impacto. Son tres las implicancias que se desprenden de lo encontrado. En primer lugar, en un sistema macroeconómico como el descrito, no es indispensable que se cumpla el Principio de Taylor para que la política monetaria sea estabilizadora. En segundo lugar, cuando la credibilidad en la meta de inflación es completa, la política monetaria contractiva puede contribuir a un descenso rápido de la inflación en el corto plazo, incluso por debajo de su nivel de equilibrio estacionario, y con menores impactos recesivos de corto plazo, pues la menor inflación meta produce un choque de oferta favorable.

Por último, en el modelo descrito, el parámetro que permite la suavización de la tasa de interés, no se introduce desde fuera del modelo, como es usual, sino que se desprende de la conducta optimizadora del banco central y por eso contiene parámetros estructurales del modelo, que podrían ser estimados para servir como guía de la política monetaria.