Introducción

La justificación para este trabajo, de naturaleza teórica y metodología analítica, se puede deducir enteramente de su título. ¿Por qué funciones de Leontief? En el lado de la oferta, porque su empleo a nivel académico es generalizado y, en el lado de la demanda, por el famoso resultado de ^{Mantel (1999)} según el cual ─para un número suficiente de mercancías─ cualquier economía se puede reducir a una descrita por individuos con estas utilidades ¿Por qué dos variables? Porque la exposición se simplifica, sí, pero también porque son suficientes. Dada la tradicional técnica, válida en ausencia de incertidumbre e inter-temporalidad, mediante la cual, la mercancía de interés se separa de las otras ─a las cuales se agrupa en una mercancía compuesta.

Lo más importante: ¿Por qué es necesaria una nueva perspectiva? La lógica tras las funciones de producción de esta clase se halla en el corazón mismo del modelo matricial insumo-producto de ^{Leontief (1941)}: si requiere una proporción fija y positiva de todos los insumos con el fin de producir una cantidad unitaria de cierta mercancía¹, entonces el nivel de producción maximizador equivale a la relación entre la cantidad del insumo contratada y la proporción de uso en el mecanismo productivo². Por consiguiente, puede producir tanto ─cota tecnológica superior─ como el mínimo de estos cocientes.

De lo anterior se sigue que, cuando a cada insumo se le interpreta como un producto intermedio de otra industria, se alcanza la forma lineal de coeficientes técnicos (determinados) que ponderan el producto de cada empresa representativa como elementos necesarios para el de otra. Una implicación directa es que cualquier economía, constituida por empresas cuya función de producción sea neoclásica, poseerá una representación bajo el modelo de insumo-producto.

En efecto, si F(Z→) ─donde Z→≔(z1,…,zm) describe el vector de los “m” insumos que toma en consideración la empresa─ es una función de producción neoclásica ─por ende, derivable y homogénea de grado 1 con respecto a todos sus argumentos─, el Teorema de Euler sobre funciones homogéneas conduce a FZ→=∑i=1mzi∂FZ→∂zi. Como FZ→ es una función de rendimientos constantes a escala, sus productividades marginales dependen de las proporciones de los factores de producción en lugar de su nivel absoluto; así, para cada nivel determinado de intensidades de uso, ∂FZ→∂zi ∀{1,…m} será una constante. Y como a cada uno de los insumos (excepto el trabajo, por los supuestos Leontiefianos que se explicitan después) se le puede interpretar como el producto de otra industria, tendremos los arreglos lineales que usa el modelo.

Lo anterior simplifica y generaliza ─en el sentido de que no exige agentes racionales; en ningún momento se acudió a un proceso de optimización─ el resultado que se presenta en ^{Bour (2010)}. Empero, no puede enfatizarse lo suficiente el que es incorrecto designar a aquella como una representación válida para cualquier combinación de precios relativos ─el resultado se alcanza para una relación de uso determinada─; el conocido Teorema de No-Sustitución brinda las condiciones en las cuales sí lo es. Este asegura que “[…]con un único factor primario (trabajo) y sin producción conjunta […]”, la constancia de los coeficientes técnicos no se distorsiona por alteraciones en las demandas de los consumidores (^{Bour, 2010, pp.663-667}).

Ahora no resulta extraño que a las funciones de Leontief se les considere el espacio de la ortodoxia en que sobrevivió la teoría Marxiana. Si cada uno de los argumentos en la función de producción de mínimos han de igualarse entre sí, es inmediato que todo valor real (es decir, no mediado por el precio) de una mercancía puede expresarse en términos del tiempo laborado. Además, en el modelo insumo-producto todo precio depende de la cantidad de mano de obra empleada en la producción de su mercancía. Sin embargo, este último hecho puede oscurecer el de que, como bien apunta ^{Cameron (1952)}, solo es resultado de que se asuma al trabajo como único factor escaso. Como recopila ^{Bour (2010)}, es consecuencia de las restrictivas circunstancias que exige el cumplimiento del Teorema de No-Sustitución; en el mundo real el trabajo no es homogéneo, todos los bienes son escasos, la producción a veces es conjunta y los métodos de esta son múltiples.

En otras palabras, la supervivencia de la teoría del valor-trabajo en el paradigma vigente se debe a la propia teoría del valor subjetivo: si solo sobre el trabajo pudiera ejercerse análisis de escasez relativa, los agentes ─en última instancia─ tomarían sus decisiones estáticas con base en él.

Es todo esto (la fijeza de lecturas anacrónicas y la difusión implícita de axiomas inapropiados) lo que obliga a revisar las funciones de utilidad de complementos perfectos. Esta investigación y sus tres simples resultados, contrario a la interpretación convencional y a las propias intenciones de Leontief (en ^{Robles, 2007}) al plantearla, descubren que esta función puede encajarse en la lógica usual del marginalismo ─tanto productivo como subjetivo─ y la eficiencia competitiva.

I. Teoría del consumidor: la Tasa Marginal de Sustitución

Es sabido que si definimos min{a,b}, donde “a” y “b” son valores reales, como

Entonces

En consecuencia, podemos aproximar una función de utilidad de tipo Leontief “clásica” -ux,y- de complementos perfectos como

Donde “x” y “y” son dos mercancías; las utilidades marginales de ambas pueden expresarse como

Claramente, (4) y (5) son no-negativas. Ergo, las mercancías son “neutras” o “bienes” dependiendo del consumo más grande, como es conocido³. Aquí, en términos teóricos, logramos un gran avance: se prueba que las funciones de Leontief son totalmente compatibles con el marginalismo y sus conceptos de valoración por la contribución diferencial. En términos prácticos, también se alcanza una mejora: el loable análisis de ^{Diewert (1971)} para generalizar esta clase de formas funcionales, si bien para la producción, deja expresiones mucho menos manejables y su diferenciabilidad depende en gran medida de la de la función de costo mínimo.

Ahora bien, para una curva de indiferencia arbitraria⁴, sabemos que

Donde u-∈R es un nivel cualquiera de utilidad. Entonces podemos designar

Y por el Teorema de la función implícita

Como u- es constante

De este modo, hemos descubierto la pendiente de las curvas de indiferencia de una función de utilidad de proporciones fijas.

Ahora es trivial el hecho de que la Tasa Marginal de Sustitución Subjetiva de “x” con respecto a “y” (TMSSx,y)⁵ se describe por

Si el agente consume más “x” que “y”, no valora “x” y no está dispuesto a ceder consumo en “y” para subir el de “x”. Si “x” es menor que “y”, valora “x” inmensamente en términos relativos y está dispuesto a ceder mucho de “y” para obtener “x”.

De esta forma se complementa el trabajo de ^{Voorneveld (2014)}, quien demuestra el orden preferencial compatible con estas funciones de utilidad ─concretamente, lo que llama “meet preservation” es la característica medular: es la que hace al individuo preferir unas canastas a otras solo cuando consume en una complementariedad tan estricta─, en el sentido de que todos los conceptos de la teoría subjetiva del consumidor encajan, al fin, en este escenario (p.200). Asimismo, se alcanza una forma simplificada y más informativa que la que se obtiene a partir de la función de utilidad de elasticidad de sustitución constante en (12). Además, (11) aporta una mayor intuición económica, al ser apreciables las características supra mencionadas.

La representación amplia de una función de Leontief de dos variables, como se estudia en los próximos apartados, es la que se aprecia en (13). Donde f(·) y g(·) son funciones uni-variables, de valor real y estrictamente crecientes.

Como primer acercamiento a (y como justificarán) las secciones a continuación, es menester acotar que ─dado que el comportamiento es idéntico─ las conclusiones alcanzadas a lo largo del texto son generalizables al problema individual de una empresa competitiva con esta tecnología, a una sociedad con función de bienestar social Rawlsiana, entre otros.

II. Teoría del productor: Eficiencia tecnológica del equilibrio competitivo

Suponga una economía con dos sectores (como antes, uno produce el bien “x” y el otro produce el bien “y”) que requieren dos insumos: trabajo (L) y capital (K). Cada sector posee una función de producción, respectivamente, descrita por

Donde fx(·), fy(·), gx· y gy(·) son funciones estrictamente crecientes de valor real.

Como el comportamiento es idéntico al caso del problema del consumidor ─conforme crece un argumento más que otro, se malgasta presupuesto al no crecer utilidad, así que el óptimo se consigue al igualar los argumentos─ con las demandas hicksianas, se sabe que cada industria posee las siguientes demandas condicionadas:

En este caso, conforme uno de los dos argumentos crece más que el otro, no hay incremento en la producción; se desperdician insumos y la empresa busca eliminar esa situación para minimizar sus costos, lo cual consigue cuando ambas entradas se igualan. El equilibrio competitivo exige que la demanda por insumos agote la dotación de estos y operacionalmente se consigue la cantidad producida en el sector “y” en términos de la producida en el sector “x”.

El sistema de ecuaciones en (17) es el resultado que alcanza la acción empresarial. Si, en cambio, se considera a un “dictador benevolente” que busca una producción óptima y factible, se encara el problema

Este se puede simplificar en un problema de solo una restricción

Y como la producción se maximiza sin desperdiciar recursos cuando los argumentos de la función de producción se igualan, se ve que las asignaciones eficientes de trabajo y capital en el sector “y” son

Por lo tanto, la Frontera de Posibilidades Máximas de Producción (FPMP) coincide con lo encontrado en (17)

Así se demuestra que a nivel estático-microeconómico (el dinamismo macroeconómico, cuando se ignoran las preferencias de la población, puede ostentar resultados no deseables como el conocido subempleo perpetuo del modelo Harrod-Domar de crecimiento económico), cuando las empresas disponen de tecnologías de proporciones fijas, el que el empresariado busque maximizar sus beneficios hace al agregado de la economía operar eficientemente a nivel tecnológico.

Debe acotarse que ^{Ten Raa (2008)} demuestra que el coeficiente de utilización de Debreu-Diewert proviene de preferencias del tipo Leontief; con ello (como bien afirma con anterioridad) confirma la intuición Diewertiana según la cual, esta clase de preferencias, suprimen del coeficiente de utilización de Debreu la porción de ineficiencia en la asignación de recursos ─al estar fija. Esto, junto con (17) y (20) permite que una economía competitiva sea eficiente a cabalidad cuando tanto el lado de la oferta como el de la demanda están descritos por esta especie de funciones. Es decir, que el que los deseos y las condiciones industriales conduzcan a la rigidez de las asignaciones, no evitan la eficiencia mixta.

En concordancia y como ligamen del apartado previo, nótese que (20) permite observar FFPMP no lineales ─como las que se obtienen de la forma común de las funciones de mínimos. Pero, incluso si aquel fuera el caso, ^{Jiang, Fan y Tian (2020)} demuestran que se puede curvar una frontera de transformación lineal al añadir funciones de Leontief con nuevos insumos primarios. Dato que empata con las inferencias gráficas de ^{Robles (2007)}, según las cuales, las isocuantas de complementos perfectos adquieren una convexidad suavizada conforme se agregan formas funcionales de complementos perfectos con diferente ponderación por insumo, sin necesidad de ampliar el número de factores.

En síntesis, la forma funcional de tipo Leontief no es un óbice para la lógica de la productividad marginal decreciente. Tampoco lo es para el estudio de la utilidad marginal decreciente; ese es el sentido de las funciones p-Leontief que estudia ^{Garg (2017)} al incorporar aditivamente funciones de mínimos insertas en funciones de máximos ─estas últimas tienen un comportamiento de solución de esquina idéntico al caso de sustitución perfecta.

III. Teoría del equilibrio general: Existencia de infinitos equilibrios de Pareto en una economía de intercambio

Considérese ahora una situación tecnológicamente más simple, pero no menos relevante: una economía de intercambio de dos individuos (1 y 2) cuyas preferencias sobre los mismos bienes de antes ─es decir, la economía es representable por una caja de Edgeworth─ se describen, respectivamente, por

Donde f1(·), f2(·) , g1· y g2(·) son funciones de valor real y estrictamente crecientes. Como puede verse en la Figura 1, las curvas de indiferencia de uno y otro individuo se “tocan” siempre en el área encerrada por⁶ g1-1f1x1 y g2-1f2(x2) ─como esto ocurre tanto antes como después de intersecarse sus rayos de expansión, es evidente que ocurriría lo mismo en una situación en que los rayos de expansión no lleguen a cruzarse; no importa el tamaño relativo de las dotaciones. Aquí hay coincidencia de intereses y ningún individuo puede mejorar su situación sin empeorar la del otro (óptimos de Pareto).

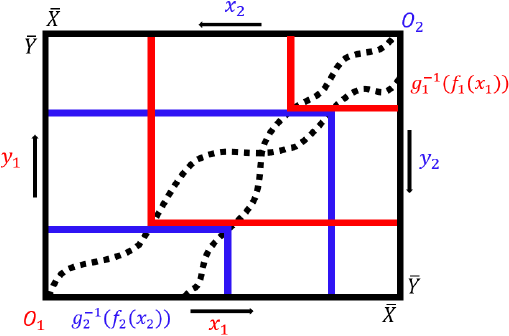
Fuente: Elaboración propia.

Figura 1 Caja de Edgeworth representativa con dos individuos de preferencias Leontief arbitrarias 

Por lo tanto, es claro que la región de contratos es

Como se sabe que la inversa de toda función estrictamente creciente es estrictamente creciente y como se sabe que toda función monótona es Riemann integrable en un intervalo cerrado, (23) existe (^{Ugalde, 2015}). Aunado al escenario trivial en que los rayos de expansión de ambos individuos coinciden en la caja de Edgeworth (en cuyo caso, los múltiples óptimos de Pareto son todos los puntos de la senda de expansión) (23) demuestra que en una economía de intercambio ─de dos bienes y dos individuos con preferencias del tipo Leontieff─ existen infinitos óptimos de Pareto. Se pueden apreciar como el continuo de puntos en cualquier parte de la región de contratos que tome en cuenta; la locación final particular dependerá de las habilidades de negociación de cada persona.

Sin embargo, esta proposición también muestra lo laxo que puede llegar a ser el concepto Paretiano de eficiencia. ^{Nicolò (2004)}, en un marco más propio de la teoría de juegos, caracteriza y descarta el desperdicio de recursos que prevalece en las asignaciones en las que ninguno de los dos agentes consume sobre su rayo de expansión (id est, no deberían tener desincentivo para revelar sus preferencias y ceder poder de negociación a la vez que cantidad de una de las dos mercancías). No debe obviarse el hecho de que (23) prueba que la eficiencia no se basa en la unicidad del equilibrio Walrasiano, sino en que este es la consecuencia de las decisiones conscientes y, hasta cierto punto, mutuamente beneficiosas de los individuos.

Finalmente, se puede verificar con sencillez (dada la desigualdad triangular del valor absoluto) que las preferencias como las descritas en (3) tienen un comportamiento convexo en la diagonal, de modo que ─por el Teorema del Hiperplano de Minkowski─, cuando los rayos de expansión de dos individuos coinciden, hay un hiperplano de separación entre sus curvas de indiferencia. Y, gracias a que todas las asignaciones de dicho separador están contenidas en la caja de Edgeworth (no exceden las dotaciones de la economía) y a que están ubicadas en el rayo de expansión de ambos individuos (en el que cada uno se encuentran maximizando su utilidad), el hiperplano de separación lo define un vector no negativo de precios.

Como dichas asignaciones son Pareto-eficientes (se aprecia desde el figura 1), se comprueba el cumplimiento del Segundo Teorema Fundamental del Bienestar para aquella clase especial de preferencias de Leontieff ─si nos restringimos a la coincidencia de rayos de expansión, claro está. Empero, lo más destacable de esto es que ─mientras el centro de la caja de Edgeworth se incorpore en las sendas de expansión de ambos individuos─, el equilibrio competitivo es capaz de obtener una asignación totalmente igualitaria y eficiente; una asignación que satisface condiciones normativas más exigentes que la eficiencia Paretiana, como las señaladas por ^{Li, J. y Xue, J. (2013)}: ausencia de envidia y de incentivos para reservarse información.

Conclusiones

La eficiencia económica y las cavilaciones marginalistas sobre el valor, a diferencia de la teoría Marxiana del valor-trabajo cuando se la aleja de supuestos inconsistentes, encaja a la perfección con las funciones de tipo Leontief en la oferta y en la demanda. Tanto los juicios en términos de los aportes diferenciales de un elemento a una categoría de interés determinada, como los juicios que conciernen a las valoraciones relativas de dos variables cualesquiera, pueden ser incorporados a las preferencias y tecnologías de proporciones fijas. Asimismo, sea en condiciones de producción o de intercambio puro, esta clase de funciones alcanza resultados ─incluso una infinidad de estos─ socialmente eficientes sin coerción sobre las adquisiciones.