1. Introduction
In recent decades, most of the economies in the world have been impacted by the presence of speculative bubbles in asset prices, to name some cases: the “kamikaze” bubble generated in the real estate sector in Japan exploding in 1990; the “dot-com” bubble occurred in the late 90’s related to new technological firms; and, of course, the subprime bubble bursting in 2007 that had its gestation in the real estate sector in the United States. Despite the recurring presence of this kind of phenomena, its study still represents innumerable questions related to the origin, detection and convenience of government intervention to stop the evolution of bubbles in financial markets. Even the definition itself is not yet exempt from controversy. Regarding the causes that can explain the formation of a speculative bubble, there are many studies that point to different factors. Some papers focus on the analysis of behavioral finances. As an example, we mention the investigations from Shiller (1984), Flood and Hodrick, (1990), Lux (1995), Case and Shiller (2003), Scheinkman and Xiong (2003), and Chuang and Lee (2006), The common issue in these works is human behavior and its effect on the evolution in asset prices. The inefficiencies in the behavior of the agents generate distortions like excess of optimism, herd behavior and self-fulfilling prophecies that break with the efficiency of financial markets.
Another research framework studies the relationship between monetary policy and formation of speculative bubbles. This topic has gained much interest since Mishkin’s (2011) paper, which deals with the transmission mechanisms between monetary policy and explosive growth in asset prices. In this regard, Galí (2013) studies the relationship between monetary policy and rational asset price bubbles, and Detken and Smets (2004) analyze the effect of both real and nominal variables in a time window around an explosive growth in asset prices. On the other hand, Bordo and Landon-Lane (2013) study the relationship between monetary policy, credit expansion, and low inflation with a sharp increase in the prices of financial assets. Finally, Gilchrist and Saito (2006) argued that a monetary policy that responds strongly to inflation could be enough answer to stop a bubble. Particularly in the subprime bubble scenario, some studies, as Aoki et al. (2004), Ahearne et al. (2005), Calza et al. (2009), and Dokko et al. (2009) have examined the impact of monetary policy on the evolution in real estate prices.
Greenspan (2004) and Trichet (2005) point out the repercussions of price stability within the financial market. The managing of monetary policy has focused in pursuing price stability, and in most cases the goal has been successfully achieved; at least in a certain period. However, its effects and repercussions have transcended beyond the own objectives of the monetary authorities. Greenspan (2004) states that the paradoxical result of the successful control of inflation in the United States was the formation of the dot-com bubble in the late nineties. In this respect, Trichet (2005) emphasizes that an accurate understanding of the links between speculative bubbles, prices of financial assets and monetary policy has been one of the most intricate challenges faced by central banks in the early twenty-first century.
While there are many studies that address the relationship between monetary policy and speculative bubbles, the results obtained do not allow the formulation of general conclusions and may even be in many cases contrasting. The view expressed in this work is that this kind of studies cannot be approached with linear techniques. In other words, the behavior of financial markets cannot be represented by linear structures or linear transformation. In contrast to the classical assumptions, this paper uses of a new analysis tool, called the mutual information coefficient. The main advantage of this indicator is that it can be used without assumptions about normality or linearity. This fact represents an important advance because financial markets do not adapt to these classical assumptions.
This work mainly follows the guidelines from Minsky’s (1992) theory, under the assumption that an increase in the amount of money generates high public expectations. Therefore, the continuous growth in asset prices seems to be justified. Even more, once inflation begins to affect financial assets, the same system feeds back the bubble leading to Ponzi financing systems. Thus, according to the financial fragility proposed by Minsky, the following hypothesis is proposed: if an expansionary medium-term monetary policy is implemented in an economy, then important deficiencies can be generated within financial markets, which will be reflected in a smaller amount of information shared by the monetary policy and the financial markets represented by lower values of the mutual information coefficient. Hence, the loss of information in the market is the process that generates the speculative bubble.
The general objective of this research is to apply the mutual information coefficient to demonstrate the existence of an information system between monetary policy and the performance of financial markets. This information is not constant over time, so there are periods in which the variables are disconnected, which generates deficiencies in the valuation of asset. This objective is to measure, by using the mutual information coefficient, the individual effect of each of the monetary transmission channels represented by the interest rate, real money supply, inflation rate, and the number of total loans. Regarding the performance of the financial market, it was taken as a reference the Down Jones Index. This study period covers the complete evolutionary cycle of two of the most recent bubbles, the dot-com and the subprime, occurred within the period from 1992 to 2013.
This investigation provides useful information-theoretic tools for analyzing the predictability of a financial market and the way in which the market incorporates information to the price system. This methodology is based on the principle of entropy, term used physical sciences that was adapted by Shannon (1948) as a measure to quantify the amount of information emitted by a source. Recent studies have used different variants of the concept of entropy as an attempt to quantify the efficiency of financial and real estate markets. For instance, Wang, Xie and Han (2012) and Álvarez, Rodríguez and Álvarez (2012) study the hypothesis of efficient financial markets through the concept of Shannon’s (1948) entropy, and Risso (2008) applies the concept of Shannon entropy to measure the evolution of the US housing market behavior.
The concept of entropy is taken up in various investigations, for the study of systems in which a pair of variables share information. For instance, Darbellaya and Wuertzc (2000) use the coefficient of mutual information as a measure of statistical dependence. In the same way, Dionisio et al. (2004) use joint entropy, conditional entropy, and the coefficient of mutual information. The concept of the mutual information coefficient responds to the essential assumption that the market reaction to similar stimuli is consistent over time. That is, if the market is understood as a dynamical system, it generates a stable alphabet built on a finite number of symbols (outcomes provided by a time series realization). Under this framework, it is assumed that: 1) the market gradually incorporates available information; 2) the agents are not homogeneous in analytical capacity and risk tolerance; and 3) the rate at which information is incorporated and disseminated is not homogeneous for all agents. This is, undoubtedly, related to what Keynes called “Animal Spirits”.
As it was previously stated, the channels through which monetary policy influences on asset prices are very diverse and with very different temporality. Thus, a linear analysis such as that of standard econometrics may not capture properly the interdependence between variables. To deal with the nonlinearity of the phenomenon under study, this study proposes, based on the coefficient of mutual information, an alternative methodology to quantify the efficiency with which financial markets respond to the implementation of different instruments of monetary policy.
The present work is organized as follows. Section 1 presents a review of different theories that address the study of monetary policy. The theoretical framework used in this research is based on Minsky’s financial fragility. Additionally, other complementary theories are mentioned, such as the structuralist and horizontalist that contribute with important elements for understanding the feedback process that follows a bubble. Section 2 introduces the concept of the mutual information coefficient, the properties of this indicator, and its background with the theory of information and entropy formulated by Shannon (1948). Section 3 contains the empirical application by calculating the mutual information coefficient and the discussion of the results obtained. Finally, the conclusions of the results obtained are presented.
1. Monetary policy and financial markets efficiency
The hypothesis of efficient financial markets, introduced by Fama (1970), states that an efficient financial market is one in which the prices of financial assets reflect always and completely, all available information. Fama, also refers to an efficient financial market as one in which the changes in asset prices are of random type; more specifically prices follow a random walk. In the presence of high randomness, a financial market would be working at full efficiency because it reflects the entire spectrum of expectations formed from the existing information on the economic and financial situation. Under this framework, in an efficient market, at any point of time, the price of an asset will always be a good estimate of its intrinsic value. Therefore, it is not possible to observe periods of revaluation in which asset prices rise away from their core values. In other words, there are not “irrational” speculative bubbles. It is, generally, accepted that markets hardly meet the mentioned conditions. There are several theories trying to explain the reasons why a financial market may lose efficiency. This paper argues that the implementation of an expansionary monetary policy influences public expectations and, therefore, can transfer distortions affecting the ability of agents in valuing asset prices.
In what follows, we will describe some of the transmission mechanisms. First, we analyze the effect of inflation in financial markets. This issue can be approached from different. First, the Austrian school vision will be used, which indicates that the bubbles are more likely to occur in scenarios where monetary policy has created an environment of confidence in price stability. In this regard, Greenspan (2004) highlights that the low levels of inflation contribute to exacerbate the value of financial assets, attributing an important role to expectations. According to Greenspan (2004) inflation control generates expectation of increasing macro-economic stability by helping to reduce the perception of risk and exacerbating optimism among the investing public. This allows increasing profit expectations among analysts, accelerating stock prices increases. Several empirical studies as Christiano, Ilut, Motto and Rostagno (2010), and Bordo and Landon-Lane (2013) have shown the correlation between low levels of inflation and bubbles in asset prices. We will show later that the estimates obtained by this research indicate that periods of low inflation are consistent with a sustained loss of information, which leads to the loss of efficiency in financial markets.
In this paper, it is also argued that the expansion of the money supply also fueled the bubble formation. This is consistent with the financial fragility hypothesis from Minsky (1992). Under this hypothesis, an increase in the amount of money in the economy creates a feeling of prosperity that generates high public expectations about the future asset returns (Delgado-Selley, 2011). In this way, the continuous rapid growth in asset prices seems to be justified. The certainty that asset prices will continue to grow leads firms to request higher levels of funding. In fact, as the boom moves on, the increase in asset prices will be the main way to pay credits. According to the second theorem of the financial fragility, in the long run most of the firms will be involved with unstable funding systems (Ponzi type), which results in the need to obtain higher future cash flows to hire new loans.
Under the above framework, it can be observed that a credit expansion generates short- and medium-term expectations that give rise to shift investment towards risky assets. This process remains in the long-term due to the dynamics of the financial system in which the debt backed with risky assets is used for getting funds to accomplish the projects or make them financially viable through the cost of the money because debt is usually cheaper than capital. Once the new project is funded, its expected future cash flows will appreciate the price of the firm’s stock, allowing it to go to a new debt round (because the higher value of the collateral) creating the Ponzi scheme lending which is the main argument for explaining the formation of the stock bubbles in the Minsky’s (1992) hypothesis.
In the above context, it would be reasonable to think that a simple application of a restrictive monetary policy would reduce the exacerbated optimism of the public. The mainstream vision says that raising the interest rate would increase the cost of money and would stop the processes of lending and investing. However, the process is not being completely stopped. As we will see later, once expectations are generated, they are fed back by the money created by the banks and by the financial markets. This feature is explained by the ability of commercial banks to lend resources to firms for the production process. Additionally, we argue that this creation of money is also made by the financial markets. We contend that the process of the creation of money in the market begins with the rise of stock prices (also because of cheaper money from low interest rates). Therefore, the stocks are sold and money with low interest rates) is reintegrated to the net credit in the economy, measured by M1.
It could be argued that the money created in the stock markets is destroyed by other person’s loss, but this is not monetized until the sale is made. Also, there is a chance for using some derivative instrument that can help the investor to hedge possible loss. In this process, in the long run, the market is expanding, and thus creating and monetizing wealth, and with it, creating market bubbles until all this monetary richness is destroyed when the debt is not repaid, the asset’s prices drop and the market crashes as an adjustment mechanism for the non-fulfilled expectations on the investment projects.
To empirically prove our contention, the mutual information coefficient will be used to measure the common information between key monetary variables (loans for companies, interest rate, M1, and inflation) related to the previously explained mechanism of monetization and the market. The first part of our hypothesis is related to the Ponzi scheme defined by Minsky (1992), and it will be measured the common information (the mutual information coefficient) between the Dow Jones Industrial Average (DIJA) (the market) behavior and the loans obtained by commercial entities.
The second part of the analysis will use the mutual information coefficient between the interest rate and the returns of the stock market (DIJA). This is done by examining the relation between the principal instrument of monetary policy and the stock market when this is not volatile. Under these conditions, the investment decisions are made based on the cost of the money and the associated risk. As we will be showing later the paper, the common information between the two alphabets (the realizations of both time series are used as realizations of a dynamic alphabet) diminishes when the market becomes volatile. This process of sharing information between the financial market and the monetary instruments is finally transmitted to the amount of money in the economy when the capital gains are taken (by selling the stocks or derivatives settlement) and the monetary richness created in the market is pumped to the real economy. This point of our contention is proved by using the mutual information coefficient between the net credit on the economy, M1, and the financial market returns of the DIJA. Moreover, this paper analyzes the mutual information between the inflation rate and the returns on the market. Here, it is found a slightly stronger relation between the market crashes and the amount of information related to the inflation rate, and practically there are not changes when the bubble is being formed.
Putting all the analysis elements together, central bank has the main assignments of promoting employment and maintaining price stability; being the interest rate the main control instrument. Theoretically, an increase in the interest rate must slow the investment process and consumption (slowing also economic growth), and then stopping the inflation (the process must be inverse with a fall in interest rate). In practice, there is a “quantitative easing” environment, with a long run inflation stability and a lot of cheap money in the market that may be used to invest in real projects or in the stock market. If the economic agents decide to invest in real projects, they may achieve a return rate that covers at least their capital cost (payment to the shareholder) and cover the incurred expenses (debts, salaries, costs, etc). This can be easily accomplished if the market is plenty of money due to the “quantitative easing”; in this case, the risk-free interest rate is almost zero.
Under these conditions, a lot of new projects may be started and funded, despite their profitability or risk exposure. When the firms going to the market to get funds, the Ponzi scheme begins, and the money is allocated into the firms (as savings or investments) preventing them to get into the real economy and not causing short run inflation. When these Ponzi loans are defaulted, the money is destroyed, and the real economy enters a recession (due to the monetary constraint) instead of having inflation (money has been destroyed).
The combined effects of mutual information of the M1 and the financial market reveal the reinvestment process (originated by a low interest rate) that fuels the expectations on the financial market, through the commercial loans, during the bubble formation and the monetary wealth destroyed in the financial turmoil; this is a measure of the Ponzi scheme stated by Minsky (1992). This means that monetary wealth is not fully reaching the net credit, M1, so it can generate inflation. Instead of that, it is being reinvested in the financial market and, when monetized creates recessions on the real economy to clear the money of the loans that are not backed by real production since the central bank holds the interest rate artificially low. One possible explanation for the inertial credit expansion can be found under the post Keynesian view of monetary economics, which is concerned with studying the relationships between money, uncertainty and time. Lavoie (2007) points out that the main feature of the post Keynesian monetary economics is the existence of endogenous money. This feature is explained by the ability of commercial banks to lend resources to firms for the production process.
The above ideas became popular under the vision of the post Keynesian school. There are two approaches, one under the name “horizontalists” and the other known as “structuralists” or theory of liquidity preference. In both paradigms the challenge is how to conduct policy in a world of endogenous money. Garcia (1991) describes the effect of the preference for liquidity if credit supply is not infinitely elastic because of the existence of uncertainty in the market. The perception of risk requires banks to add a surcharge to the cost of credit. In response firms will be forced to maintain higher levels of profitability and show larger collateral for contracting new debts.
In other words, for getting new loans firms must present higher future income flows. In this context, the discretionary nature of monetary policy, as conceived under the vision of the quantity theory of money is lost and, therefore, it is also lost the ability of an opportune intervention in the market to change the public expectative. Additionally, in the presence of risk and uncertainty, firms tend to revalue their assets by an increase in credit or market risk, which requires a surcharge to boost the prices of financial assets. Consequently, the monetary authorities cannot control the associated liquidity excess. If the process coincides with a period of uncertainty that creates the perception of risk among agents, then there is a requirement of a surcharge and the need to show more valuable collaterals for contracting new debts feeding back the formation of speculative bubbles. The explosive growth of credit, basic feature of post Keynesian monetary analysis, transforms bonanza into fragility as firms are committed to a high percentage of debt. At this point, the prices of assets that have been used as collateral are irrationally away from their fundamental value. Therefore, the bubble is evident but also unmanageable, which coincides with times of low mutual information between market returns and loans.
In summary, the concept of uncertainty to which the post Keynesian vision describes as causing liquidity preference appears to be the explanation of the formation of speculative bubbles. This uncertainty can be explained in various ways. The post Keynesians attributes it to credit risk, i.e., to the default caused by the huge volume of credits backed by the money issued by the central bank. This study did not use the number of defaults on commercial loans because, unfortunately, their timing does not match the rest of the variables used in this work.
In the next section, we provide a brief review of the main concepts on Shannon’s (1948) information theory, emphasizing the idea of the mutual information coefficient and its use to measure market efficiency. Subsequently, we select the macroeconomic variables for this study, and see how they may explain the timing of the transmission mechanism previously described.
2. Efficiency in the financial markets and the coefficient of mutual information
Shannon (1948) proposed, in his theory of information, a reformulated concept of entropy, which is useful on measuring information in coding alphabets. In his research, entropy is described as the mean value of the information provided by symbols emitted by a source. More precisely, let X be a discrete random variable with mass probability density p(x), then entropy is defined as
Under the above framework, average entropy is a measure of the randomness or uncertainty in the behavior of the random variable, and it is understood as the predictability of the tested process. In fact, if the analyzed information source provides constant values, the new information issued is null and therefore the entropy is zero leading to a perfect knowledge by traders in the market.
The entropy of an information source is not negative and is bounded above. This means that the source cannot lose information and cannot submit an unlimited amount of information (for a limited number of symbols). Within financial theory, this means that agents have not forgotten, and they have increasing flows of information, which is currently modeled by an increasing filtration.
H(X) = 0 if for some x' p(x') = 1. In this case, the remaining probabilities are zero and, therefore, there is no surprise and entropy become zero, coinciding with the loss of randomness in the formation of both price and total loss of market efficiency.
2). H(X) = ln(N) Û p(x) = 1/N " x. When all symbols are equally probable, the uncertainty of what will happen will be high, reaching the upper limit of entropy.
Thus, it is expected that in an efficient market, agents use all information provided by the market. In this context it is not possible the existence of trends in the prices of financial assets and entropy will reach its maximum value. If the price evolution begins to be deterministic, the entropy decreases showing the possible formation of speculative bubbles. The loss of randomness implies the existence of events that strongly influence public expectations. Cruz-Aké, García-Ruiz and Venegas-Martínez (2014) describe entropy as a measure of adaptation to the economic environment. A phenomenon that provides much information responds with a high degree of randomness, while a quasi-deterministic economic event can be understood as a separated process from the rest of the system. In this regard, Wang, Xie and Han (2012) use entropy as a statistic to quantify the disorder and uncertainty of a complex dynamic system.
The concept of entropy has several variants. In this paper is assumed that there are two discrete random variables, whose behavior is conditioned on a reciprocal basis through a system of mutual information. More precisely, mutual entropy I(X; Y) for a pair of discrete random variables with joint mass probability density p(X, Y) is defined by
The above coefficient defines the relationship between two random variables and has the following properties:
I(X; Y) ≥ 0, that is, the coefficient of mutual information is a positive quantity and can only be zero when events X and Y are independent. In this circumstance a zero value for the coefficient of information indicates that monetary policy and the market return are independent phenomena.
I(X; Y) = I(Y; X), that is, the coefficient of mutual information is symmetrical in X and Y. This parameter quantifies the relationship between variables but does not specify the direction of causality between variables.
When the dependency between variables is complete, the coefficient of mutual information is equal to the entropy of any of them.
The next section presents the results of the empirical analysis based on mutual information distributed by different instruments of monetary policy and financial market performance.
3. Transmission of Monetary Policy on the Formation of Speculative Bubbles: Empirical Evidence
This section examines the dynamics of the coefficient of mutual information of several relevant variables related to the performance of the Dow Jones Industrial Average (DIJA) during the period 1992-2013. In this period were located two significant bubbles, the dot-com occurred in the second half of the nineties and the housing bubble or subprime bubble that burst in 2008.
To assess the impact of monetary policy on the efficiency with which financial markets perform and according to the exposed theoretical framework four variables are analyzed: money supply in real terms (M1), interest rate of Treasury Bills of a three-month term (r), inflation rate (π) and industrial and commercial total loans granted by commercial banks (L).
Monetary policy in the United States, according to Greenspan (2004), was characterized by a context aimed at controlling inflation, among the main characteristics in such a policy stand out: 1) the higher degree of competitiveness from the processes of globalization, 2) the rapid increase in productivity, and 3) the direction of economic policy to promote price stability. For the period of study, the policy generally was characterized by being discretionary during subsequent recessions to crises of 1987, 2000 and 2008, aimed to restore economic activity. The evolution of the main monetary instruments analyzed in this work is shown in Figure 1.

Source: Authors’ own elaboration with data from the Federal Reserve Bank of St. Louis.
Figure 1 Evolution of monetary variables (loans, interest rates, M1 and prices) from 1992 to 2013
Now, we proceed to analyze whether the increases in money supply, the low interest rates, the credit expansion and the low inflation, reflect the decreases of efficiency in the market by using the coefficient of mutual information. To better understand the obtained results, it is worth remembering that if some or all the instruments of monetary policy, discussed here, influence public expectations, these expectations will tend to exacerbate the price of financial assets diminishing the randomness in them. In other words, the asset prices tend to show constant revaluation periods causing a speculative bubble. This behavior should be reflected in a steady decline in the medium and long-term levels of mutual information (the unit of measure for the rate of information is expressed in “nats” because we are using the natural logarithm in coding).
The results for the coefficient of mutual information and confidence intervals obtained, at the 95% level, for the variables: loans, interest rates, money supply (M1) and inflation, relative to the market return represented by the Dow Jones Industrial Average index are shown in Figure 2. We emphasis on confidence intervals to give the reader a clearer picture of the level of the coefficient of mutual information with respect to its historical values, without making assumptions about the distributions of the data.
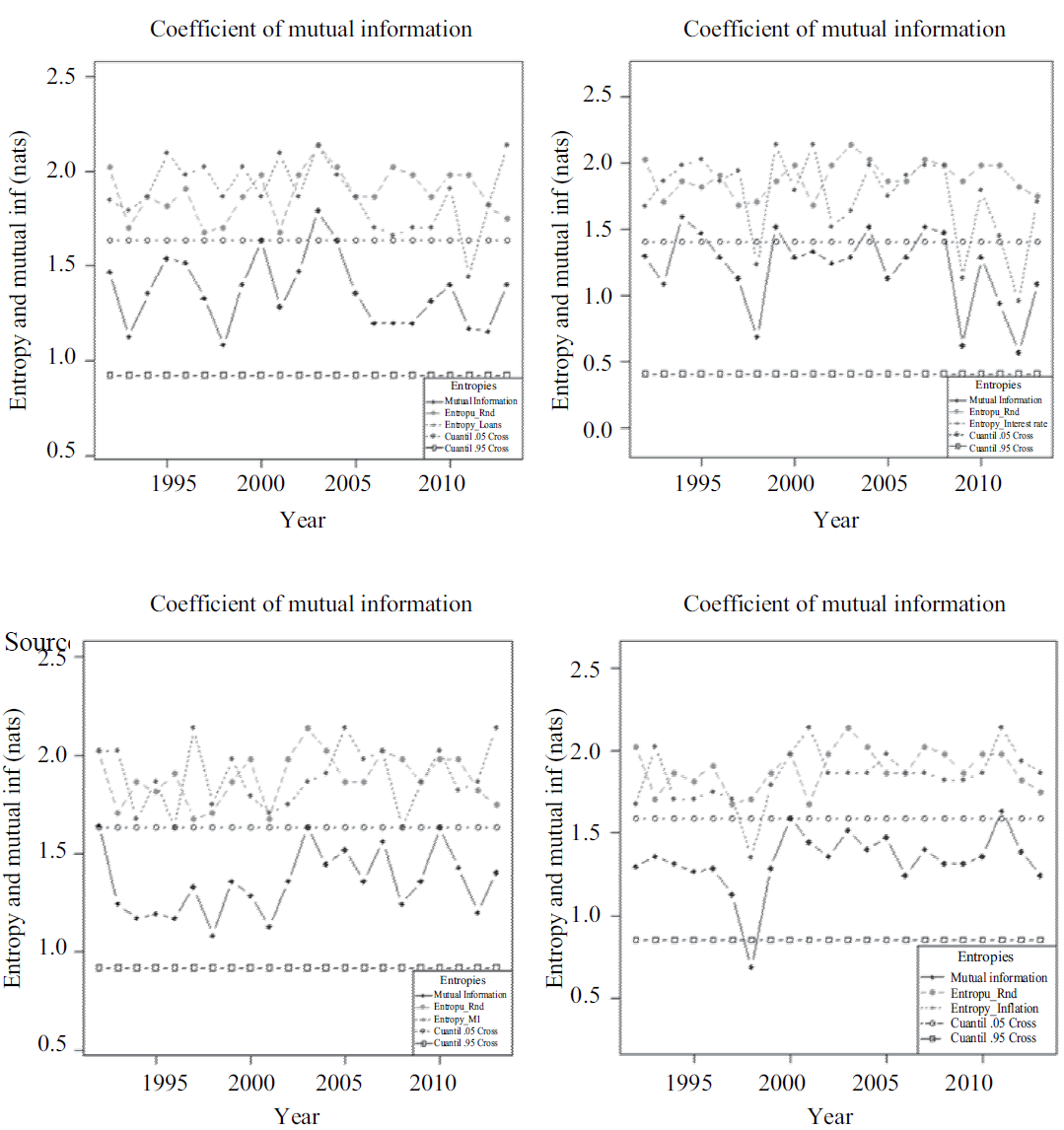
Source: Authors’ own elaboration using data from the Federal Reserve Bank of St. Louis.
Figure 2 Coefficients of mutual information for loans, interest rates, M1 and inflation relative to the stock market
As it can be seen in panel 2(a), there is a clear relationship between credit growth and overtrading of the dot-com and subprime bubbles. There are two periods of loss of efficiency, the first one from 1995 to 1998 in which the mutual information coefficient falls 30%, and the second from 2003 to 2007, period in which the coefficient of information falls 33%. Another important issue is that the decrease in the rate of credit growth or the negative evolution of the rate itself is reflected in increasing levels of efficiency for two periods, 2001-2003 and 2008-2010.
On the other hand, it is particularly interesting the recovery of efficiency between 1998 and 2000. The rate of credit expansion is diminished slightly; however, the credit crisis was not enough to reduce optimism of the public in the pre-bubble burst dot-com years. Moreover, when in 2008 the credit expansion decreases more than 50%; the indicator of efficiency remains constant, i.e., the market becomes indifferent to the conduction of monetary policy in times of increasing euphoria, which is consistent with the transmission mechanism previously exposed.
The obtained empirical results lead to the conclusion that variations in the amount of credit have a direct effect on the efficiency of financial markets. This conclusion is consistent with the studies from Detken and Smets (2004) that analyze the financial and monetary policy conditions for 38 periods of increasing prices of financial assets in 18 oecd countries. Their findings show strong correlation among asset prices, real credit and real money before and during the rise of the growth rates and decline significantly in the two years following the outbreak of bubble. It is worthy pointing out that although credit contractions have a positive impact, this effect is not enough to reconnect the formation of expectations with market information. This fact provides empirical evidence on the fact that a tight monetary policy cannot return the financial market efficiency, as initially stated in this investigation.
In panel 2(b), it is also observed that there is a relationship between loss of efficiency and decreasing interest rates. This is especially true for the period 1995-1998, which corresponds to the overtrading of the dot-com bubble. Now then, regarding the effect on the gestation period of the subprime bubble it is interesting to note that this effect is quantitatively less even though there is a persistent influence of low interest rates on market efficiency, but the effect remains to be the same during the period 2000-2003. This finding can be explained by the extremely low interest rates reached at the end of the period with levels below 1%. This argument is reinforced for period 2010-2012, during which another significant drop in efficiency levels is evident and now with interest rates close to zero. This situation, according to Keynesian analysis, is a characteristic of an economy that has fallen into a trap for liquidity, i.e., interest rates have reached a level at which the elasticity of money demand with respect to the interest rate becomes infinitely elastic. On the other hand, if we consider the consequences of an increase in interest rates, the result of efficiency appears to be marginal, while interest rates increased 48%, the coefficient of information only increases 14% from 2005 to 2006. In brief, unlike the mechanism of bank loans, the interest rate does not seem to be a good tool to regain the levels of efficiency, especially when these have become too low, as the market becomes indifferent to changing interest rates. Gali (2013) offers a different point of view in explaining the appearance of low rates of interest. This author emphasizes that fluctuations in interest rates can encourage further increases in asset prices, so he considers that it can be a positive factor to reduce the interest rates facing to the growth of a bubble.
Regarding the effect of transmission of an increase the money supply, Panel 2(c), the results show that efficiency losses are consistent with the formation periods of both studied bubbles; periods 1992-1994 and 2000-2001. The same observation is considered in Detken and Smets (2004) that find that real money growth is strong enough before and during the explosive growth in asset prices and with a sharp fall in the next two years of this events. These results are also consistent with Minsky’s (1992) theory in the sense that an increase in the money supply affects public expectations. It is also important to highlight that from 1998 to 1999 there was a significant recovery in efficiency levels corresponding to the reduction in the money supply. However, again, monetary tightening is not enough to realign the market behavior and prevent the collapse of the bubble in the late 2000s. Additionally, it is interesting to note that while in times of prosperity a monetary expansion can influence public optimism, in times of uncertainty and economic instability, monetary expansion may become a discretionary measure used to restore stability in the financial system as occurred in 2008-2010 when efficiency was recovered by increasing the amount of money in circulation.
For the overtrading of the dot-com bubble, it can be seen a significant drop in efficiency during the period 1993-1998, in panel 2(d). This trend is consistent with a period of low and stable inflation levels; while prices fell 36%, information ratio fell 49%. Despite inflationary pressures in 2000, from the end of this year and until 2002 it was again observed a return to price stability and a constant loss in the mutual information coefficient, the same relation is found between 2007 and 2009.
According to the obtained results, the price mechanism transmits significant deficiencies in financial markets. However, its effect lasts only during the initial stages of the formation of a bubble; as public expectations adapt to price stability. The indicator loses efficiency to give signals in the market and only becomes important when inflationary pressures are observed, as in the cases of 2000 and 2007, when the coefficient of information increases significantly with market movements.
It is now convenient to jointly study all information coefficients obtained for each of the variables. As already was demonstrated, the inefficiency market changes with monetary policy; however, the relationships become complex in varying significantly between periods. As it can be observed the timing between each specified period is different, and the duration and depth of effect is also different.
Figure 3 allows us to observe the different temporalities of each of the transmission mechanisms. As mentioned before, there was a displacement and overtrading of the dot-com bubble, occurred between 1992 and 1994. During this period the efficiency loss begins, as stated in Minsky’s (1992) theory with the implementation of a monetary expansion from 1992. This is reflected in the sharp decline of the coefficient of mutual information since 1993. Under the expectation of economic recovery, it begins the decline of interest rates and credit expansion. These events feedback optimism in the public causing the formation of expectations even more disconnected from economic fundamentals. The decrease in the coefficient of information is maintained from 1994 to 1998 for interest rates and from 1995 to 1998 for the credit expansion.

Source: Authors’ own elaboration using data from the Federal Reserve Bank of St. Louis.
Figure 3 Coefficients of mutual information for loans, interest rates, M1 relative to stock market prices
Regarding the evolution of the subprime bubble, again, low levels of inflation and monetary expansion are present during displacement and overtrading. The effect of these variables on market efficiency is observed in 2001 and 2002, respectively. But now their influence is much less marked, the monetary instrument that now transmits greater inefficiencies to the market is the credit expansion, which causes a significant and sustained decrease in the coefficient of information from 2003 to 2007. Finally, the strong effect on loans and the marginal effect of interest rates during the period 2000-2003 can be explained by the low interest rates. In December 2003, the three-month treasury-bill rate reached the level of 0.90%, the lowest level since 1960
Conclusions
The results obtained are consistent with the proposed hypothesis. As it was observed, monetary policy provides information about the performance of financial markets. This can be confirmed because the values obtained for the mutual information coefficient for each of the different transmission mechanisms that were measured, gave non-zero results. In other words, among the variables studied it can be said that there is a dependency relationship. We can also confirm that the periods recognized in the literary consensus as the origin of the bubble, match with important decreases in the values of the mutual information coefficient. This is particularly right for the monetary supply variable because, as it could be observed, the value of the mutual information coefficient decreases drastically in the periods 1992-1994 and 2000- 2001; periods that were recognized at the beginning of the dot-com and subprime bubbles, respectively. According to these results, the hypothesis was verified. An expansive monetary policy generates deficiencies in the financial market that can be represented by lower levels of the mutual information coefficient.
Regarding the general objective, it can also be considered that the coefficient of mutual information is successfully applied, as it was stated. It was shown that each transmission mechanism has a temporality and different magnitude. In relation to the specific objective, the money supply transmission mechanism acts in both episodes of bubble formation; however, the effect is lower in the period 2000-2001.
For the dot-com bubble the inflation seems to have had the most important effect, and this fact is completely in line with the paradox of the Central Bank mentioned above. The variable loans do not seem to have a significant impact on the gestation of any of the bubbles. However, its effect is very important in the feedback process. We may point out that the periods 1995-1998 and 2003-2006 had significant decreases in the information coefficient. It is notable because in both mechanisms seems to be deactivated in the periods before the bubble burst.
The transmission mechanism associated with the interest rate did not have important effects at the beginning of the studied process. In the case of the episode corresponding to dot-com, a drastic fall in the information coefficient was obtained between 1995 and 1999. However, for the subprime bubble the effect practically disappears for all stages. This can be easily understood by the low levels of the interest rates handled by the Federal Reserve. In other words, low levels of interest rates lead the market to the liquidity trap.
According to the obtained results, we can also verify that the process begins, as described by Minsky (1992), under the implementation of an expansionary monetary policy that generates public expectations of economic prosperity. Also, it was shown that public optimism is fed back by other routes of transmission. This is understood as the management from monetary authorities of interest rates and credit expansion, which are present at different times. These mechanisms vary considerably at each moment of time, so when the monetary authorities pretend control the exacerbated atmosphere, what Keynes called the “animal spirits”, it is not enough to apply restrictive monetary measures, as supported by classical quantity theory, to recover efficiency without generating costs.
Regarding the effect of credit growth, this is a characteristic of the over-trading of the dot-com and subprime bubbles. Inefficiencies in the market caused by this instrument are of considerable importance and even if the authorities try to restrain the growth rate of bank credits to burst the bubble; the market efficiency increases only marginally or remains practically indifferent.
In general terms, the proposed objectives are successfully achieved. However, some disadvantages of the methodology used must be noted. In first place, the mutual information is a bidirectional indicator, so that the order of the dependence between the variables cannot be differentiated. Secondly, it is not possible to establish with exactitude the times in which each one of the evolutionary phases of the bubble occurred, reason why we use the periods generally recognized in the literature of the subject.
Finally, it was shown that the coefficient of mutual information adequately represents the variations in the efficiency of a financial market, even in stages where an incipient drop of this indicator can provide alarm signals. In this sense, the coefficient of mutual information is a useful measure for the evolution of market behavior. It is important for future investigations to establish average values that could provide an early warning regarding the occurrence of inefficiencies in the markets.











 nueva página del texto (beta)
nueva página del texto (beta)


