Introducción
A lo largo de la historia de la humanidad, el estudio y medición del riesgo por mortalidad ha sido de suma importancia. Una de las primeras contribuciones al área de predicción de mortalidad es la llamada “Ley de mortalidad de Gompertz” (Gompertz 1825). En Yan, Peters y Chan (2018) se presenta información basta sobre las leyes de mortalidad que se han propuesto a través de los años. Además, en ese artículo los autores proponen una nueva forma de predicción considerando una estructura de datos de mortalidad de largo plazo.
Actualmente, una de las formas más comunes de medir la mortalidad es a través de tablas de mortalidad (tabla de las probabilidades de muerte, en un plazo de un año, por edad para una población determinada) o tablas de vida, las cuales son una herramienta básica para describir la mortalidad a través de una estructura por edades, estas se empezaron a utilizar desde Halley (1693). Sin embargo, una tabla de mortalidad es solo una alternativa cuando no hay una ley matemática (de probabilidad) disponible. Existen diversos factores que pueden influir en la probabilidad de muerte de una persona; el factor más extensamente considerado es la edad cronológica pero existen otras características relevantes como el sexo, el historial clínico, tabaquismo, antigüedad de la póliza, estilo de vida, hábitos alimenticios, entre otros. Por su parte, Zuev et al. (2000) muestran cómo la edad fisiológica influye en la mortalidad a través de un índice de vitalidad en modelos de supervivencia.
Una vertiente para estudiar la modelación de la mortalidad es a través de las distribuciones tipo fase (PH, por sus siglas en inglés). Las distribuciones PH son utilizadas para modelar el tiempo de arribo al estado absorbente de un proceso de saltos de Markov (PSM) con espacio de estados finito. De tal forma que si el PSM representa el proceso de envejecimiento (que a su vez considera factores fisiológicos) de un individuo a través del tiempo y la muerte es el estado absorbente, la distribución PH modela el tiempo hasta la muerte del individuo. La idea de construir modelos de mortalidad utilizando procesos de Markov y distribuciones PH ha sido utilizada en décadas recientes. Por ejemplo, Gavrilov y Gavrilova (1991) utilizan un proceso de Markov para derivar una fórmula Gompertz-Makeham bajo supuestos especiales. En Alen (1995) se explora el potencial teórico de utilizar las distribuciones PH al modelar de forma diferente las tasas de riesgo, lo que sugiere que en tal modelo se puede encontrar una mayor aplicación en análisis de supervivencia.
En lo referente a la modelación del proceso de envejecimiento utilizando la edad fisiológica y las distribuciones PH se encuentran principalmente dos artículos. El primero de ellos es el de Lin y Liu (2007), donde modelan la mortalidad humana a través de un proceso de Markov con espacio de estados finitos y un estado absorbente. Dado que el PSM tiene un solo estado de absorción, el tiempo hasta la muerte sigue una distribución PH. Su modelo posee muchas propiedades analíticas deseables útiles para el análisis de mortalidad, incluyendo fórmulas cerradas para cantidades de interés, como las probabilidades de supervivencia condicional del momento de la muerte y los valores actuales actuariales del seguro de vida y la anualidad.
Este modelo se extendió en Esparza y Baltazar-Larios (2018) donde los autores proponen un PSM con espacio de estados finito pero donde es posible la transición entre edades fisiológicas no consecutivas, característica que el modelo de Lin y Liu no posee, pues ahí solo se da la transición a la siguiente edad fisiológica o bien a la muerte. En ese artículo los autores presentan una forma de construir las edades fisiológicas y para construir la tabla de mortalidad, resuelven el desafío de estimar el generador infinitesimal del PSM con base en los registros del proceso de envejecimiento. Esto se ha hecho a través de varios algoritmos como los son el esperanza-maximización (EM) estocástico o bien a través de Cadenas de Markov vía Monte Carlo (MCMC) (Esparza y Baltazar-Larios 2018 y Baltazar-Larios y Esparza 2019).
Por otro lado, la construcción de tablas de mortalidad como función de la edad se ha tratado como un problema determinístico, de tal manera que se eliminan las irregularidades de las tasas de mortalidad observadas mediante un procedimiento de suavizamiento (graduación). En fechas recientes, los enfoques de modelación han incluido la parte de la aleatoriedad, resultando así, la modelación estocástica de la mortalidad. Por ejemplo, Plat (2009) propone un modelo de mortalidad estocástica combinando características “agradables” de otros modelos ya existentes, al tiempo que elimina las desventajas de esos modelos. Su modelo se ajusta muy bien a los datos históricos, es aplicable a un rango de edad completo, captura el efecto de cohorte, tiene una estructura de correlación no trivial, no tiene problemas de robustez y tiene estructura relativamente simple. Además, incorpora la incertidumbre de los parámetros en el modelo.
En México, García-Guerrero y Ordorica-Mellado (2012) aplicaron el método de Lee-Carter para proyectar la mortalidad, suponiendo una relación lineal entre el logaritmo natural de las tasas centrales de mortalidad y la edad y el tiempo; combinando un modelo demográfico con pocos supuestos y análisis de series de tiempo. Les fue posible medir la incertidumbre asociada con la mortalidad y así calcular intervalos de confianza.
Actualmente, es indispensable contar con una nueva metodología que mida de forma más precisa el riesgo de mortalidad debido a su importancia para comprender y pronosticar la esperanza de vida y la mortalidad (entre otros factores) que impactan de manera significativa en el cálculo de primas y reservas en seguros, valuaciones actuariales en sistemas de seguridad social, cálculo de pasivos pensionarios, análisis poblacional y proyecciones demográficas, entre otros. Todos ellos necesarios y relevantes en la toma de decisiones personales, empresariales y en la implementación de políticas públicas. Además, la solvencia y la estabilidad financiera de las instituciones depende, entre otros aspectos, de tener herramientas apropiadas que permitan una medición precisa de la siniestralidad asociada con este riesgo, así como con sus posibles desviaciones.
El estudio de la mortalidad ha sido un tema principalmente demográfico. En este artículo se propone un análisis interdisciplinario, desafiante pero factible, para profundizar el estudio de la mortalidad visto desde un punto de vista actuarial, es decir, como un proceso estocástico, incorporando factores (enfermedades, hábitos alimenticios, salud mental, accidentes, práctica de ejercicio, etc.) que afectan el riesgo de mortalidad, obteniéndose así un análisis más complejo de su representación social. Es por eso que en este modelo es necesario un pensamiento interdisciplinario para analizar la mortalidad, pues el asesoramiento coherente de diferentes tipos de profesionales de la salud (epidemiólogos y médicos), economistas, sociólogos, psicólogos, matemáticos, estadísticos, entre otros, contribuye a un mejor entendimiento del tema.
En México, la construcción de nuevas tablas de mortalidad, considerando la mayoría de los factores (edad cronológica, alimentación, ejercicio físico, estrés, accidente, entre otros) que las afectan con datos recientes es de interés para varios sectores gubernamentales y privados del país. Es por ello que, en este trabajo, nuestro objetivo es adaptar la metodología propuesta por Esparza y BaltazarLarios (2018) para desarrollar, implementar y calibrar una metodología para construir un proceso de envejecimiento (un PSM) donde los estados transitorios sean las edades fisiológicas y el estado absorbente sea la muerte con registros del 2000 al 2015 de población y mortalidad de México. Además, este método contempla cómo definir las edades fisiológicas, las transiciones entre estas y la estimación de los parámetros de la distribución PH con base en registros de mortalidad en tiempo discreto, que es el tipo de información que se tiene documentada.
En este artículo, bajo la consideración de que se tienen registros de algunas dependencias como lo es el Instituto Nacional de Estadística y Geografía (INEGI), la Secretaría de Salud y el Instituto Nacional de Salud Pública (INSP), a través de algunas de sus encuestas como lo es la ENSANUT, se propone estimar tablas de mortalidad para México basadas en la teoría de estimación de las distribuciones PH. A través de esta construcción de tablas de mortalidad, se podrá, en particular, obtener la esperanza de vida de México. Estos resultados son de interés particular en el sector asegurador en México, pues no hay tablas de mortalidad con experiencia mexicana que consideren los factores que se consideran en la presente propuesta.
Este artículo está organizado de la siguiente manera. En la sección 1 se presenta un breve resumen del estudio de la mortalidad en México. El proceso de envejecimiento y la edad fisiológica se presentan en la sección 2. En la sección 3 se presentan las distribuciones PH. El modelo propuesto para la obtención de la tabla de mortalidad se presenta en la sección 4, mientras que en la sección 5 se presenta la construcción de dicha tabla con experiencia mexicana de 2000 a 2015. Las conclusiones se presentan en la sección 6.
1. La mortalidad en México a través del tiempo
Cuando el sector asegurador entró en funciones en México (a principios del siglo XX), la primera tabla de mortalidad utilizada fue la “American Experience” construida en 1868 por Sheppard Hormans, debido a que en México no existían estudios que permitieran construir una tabla de mortalidad con experiencia mexicana (Huerta y Reynaud 2009).
En 1927, Alfredo Wulf y Sotero Prieto construyeron la primera tabla de mortalidad basada en experiencia mexicana, sin embargo, esta fue usada solo por la compañía “Seguros de Latinoamérica” y no pudo ser utilizada por otras compañías debido a que no fue publicada por ningún órgano regulador (Huerta y Reynaud 2009).
En México se continuó utilizando tablas de mortalidad basadas en experiencias extranjeras, hasta que en 1968 se crea la primera tabla con experiencia mexicana de los años 1962 a 1967. Dicha tabla fue presentada en 1969 en el IV Congreso de Actuarios de la Asociación Mexicana de Actuarios (AMA) y publicándose posteriormente con el nombre de Experiencia Mexicana 62-67 en las memorias de dicho congreso. Esta se utilizó hasta 1989, cuando fue remplazada por la tabla Experiencia Mexicana Individual (EM 82-89) elaborada por la Comisión Nacional de Seguros y Fianzas (CNSF). Estas primeras dos tablas con experiencia propia se produjeron con técnicas de graduación determinísticas basadas en el modelo de Gompertz-Makeham para las tablas básicas y con un margen de protección (sobrestimación de la mortalidad para garantizar solvencia) para obtener las tablas modificadas (las que se utilizaban en la práctica).
La tabla EM 82-89 se utilizó durante diez años, hasta que en 1999, la CNSF elaboró y publicó la tabla CNSF 2000-I con experiencia de 1992 a 1998. Para la graduación de esta se utilizó un modelo estadístico que toma en cuenta la variabilidad de las observaciones anuales (Mendoza, Contreras y Gutierrez 2015).
En 2005 se realizó una evaluación, con información de 1999 a 2003, para saber si debía actualizarse la tabla CNSF 2000-I. El análisis correspondiente sugirió que hay evidencia suficiente, debido a la sobrestimación de la mortalidad (Mendoza, Contreras y Gutierrez 2015).
Dado que hasta la fecha en México no se ha modelado la mortalidad utilizando la edad fisiológica y por tanto los factores que la constitiyen, en este artículo se propone una forma de construir las edades fisiológicas con base en datos reales. Además, se adapta el modelo de Esparza y Baltazar-Larios (2018) para establecer cómo evoluciona el proceso de envejecimiento en estas edades y así modelar el tiempo hasta la muerte por medio de una distribución PH que nos permita la construcción de las tablas de mortalidad.
2. Proceso de envejecimiento y edad fisiológica
El envejecimiento es un proceso que evoluciona de forma continua en el tiempo desde el nacimiento hasta la muerte, que abarca cambios físicos, sociales, psicológicos y espirituales (Hunt 2004). Así, el envejecimiento es la acumulación progresiva de cambios en el tiempo que están asociados o son responsables de la susceptibilidad cada vez mayor a la enfermedad y a la muerte que acompaña a la edad avanzada. Algunos de estos cambios se anticipan con respuestas positivas o negativas. Cada etapa de la vida tiene sus propias ventajas y desventajas, a veces, en la vejez, el equilibrio parece inclinarse más al lado negativo, pero esto no se debe al proceso natural de envejecimiento.
A nivel biológico, el envejecimiento resulta del impacto de la acumulación de una amplia variedad de daños moleculares y celulares a lo largo del tiempo. Esto conduce a una disminución gradual de la capacidad física y mental, un riesgo creciente de enfermedad y, en última instancia, a la muerte. Pero estos cambios no son lineales ni consistentes, y solo se asocian con la edad de una persona en años. Por ejemplo, mientras que algunas personas de 70 años disfrutan de una salud y un funcionamiento extremadamente bueno, otras de 70 años son frágiles y requieren la ayuda significativa de otros (WHO 2018).
La edad fisiológica, también llamada edad biológica, es una medida de qué tan bien o mal funciona el cuerpo en relación con la edad real del calendario (edad cronológica). Por ejemplo, se puede tener una edad cronológica de 65 años, pero debido a un estilo de vida saludable y activo (evitando amenazas de longevidad como el tabaco y la obesidad), el cuerpo sería fisiológicamente más similar a alguien con una edad cronológica de 55 años. La edad biológica sería, por lo tanto, 55 (Basaraba 2020).
Hay varias formas en que se puede determinar la edad biológica, pero ninguna es definitiva o verdaderamente precisa. Sin embargo, hay ciertos factores de salud que podrían devolverle años en la esperanza de vida promedio. Si las personas tienen un estilo de vida con hábitos saludables pueden tener un impacto significativo en su longevidad y edad biológica. Estos incluyen: hábitos de ejercicio, alimenticios, niveles de estrés, consumo de alcohol, nivel de educación, cantidad de sueño, relaciones sexuales y románticas, tabaquismo y exposición a otras toxinas ambientales.
La modelación del proceso de envejecimiento ha sido de interés para matemáticos, biólogos, estadísticos, demógrafos, actuarios, entre otros. En particular, modelar la mortalidad a través del proceso de envejecimiento juega un papel muy importante. En este artículo, se propone un modelo para estudiar la mortalidad de México a través del envejecimiento y la edad fisiológica, donde el mayor reto es el poder determinar las edadades fisiológicas en las que la vida humana está particionada ya que implica tener información sobre el estado de salud (entre otros factores) de la población en estudio. Esta modelación está basada en la teoría de las distribuciones PH, que se describen en la siguiente sección.
3. Distribuciones tipo fase
En esta sección se presentan las distribuciones PH, las cuales se utilizarán para modelar el proceso de envejecimiento. Dado que esta clase de distribuciones se basa en la teoría de los procesos estocásticos, en particular de los procesos de saltos de Markov, se comenzará con una breve descripción ellos.
3.1 Procesos de saltos de Markov (PSM)
En probabilidad definimos los procesos estocásticos como un concepto matemático que sirve para caracterizar una sucesión de variables aleatorias que evolucionan en función de otra variable, generalmente el tiempo. Una de las clases de procesos más estudiados y con mayor aplicación en diversas áreas son los procesos de Markov. En esta sección presentaremos las propiedades básicas de un tipo de procesos de Markov, los PSM, también llamados cadenas de Markov a tiempo continuo; que serán utilizados para modelar al proceso de envejecimiento necesario para la construcción de las tablas de mortalidad.
Definición 3.1.1 El proceso estocástico {X(t)} t≥0 es un PSM si es un proceso de Markov continuo en el tiempo (un proceso que evoluciona en el tiempo de forma continua y que tiene la propiedad de Markov, es decir, el estado actual del proceso posee toda la información del pasado de este) y que toma valores en un conjunto E (llamado espacio de estados) a lo más numerable.
En este trabajo se considerará el caso donde el espacio de estados es finito, es decir, E = {1, 2, …, n}. Sin importar el conjunto de valores que pueda tomar el proceso a través del tiempo, siempre se pueden asignar etiquetas y así trabajar con el conjunto {1, 2, …, n} para el caso finito.
La evolución de un PSM en el tiempo está caracterizada por las siguientes propiedades.
Proposición 3.1.1 Sean T1, T2, … los momentos donde el PSM {X(t)} t≥0 salta de un estado a otro y definimos a T 0 = 0, entonces:
Dado X (T n ) = i, el tiempo de estancia en ese estado i se distribuye exponencial con parámetro dependiente del estado, es decir, T n +1 - T n ~Exp (𝜆 i ) para todo i ∈ E.
Si X (T 0) = i o, X (T 1) = i 1, …, X (T n ) = i n entonces los tiempos de estancia en cada estado dados por T 1 - T 0, T 2 - T 1, …, T n +1 - T n son variables aleatorias independientes.
Condicionado a X(T n ) = i, la probabilidad de que exista un salto del PSM en un intervalo de tiempo infinitesimal [T n , T n + dt ] es 𝜆 i dt.
Dado X (T n ) = i y si se presenta un salto en el PSM al tiempo T n + t > 0 con t > 0, la probabilidad de que este salto sea al estado j ≠ i es p ij donde p ij es la ij-ésima entrada de la matriz de transición de la cadena de Markov a tiempo discreto definida por el PSM en los momentos de saltos, es decir, {X (T n )} n ≥0 .
De las dos propiedades anteriores, tenemos que, dado X (T n ) = i, la probabilidad de que exista un salto del PSM en un intervalo de tiempo infinitesimal [T n , T n + dt ] y ese salto sea al estado j ≠ i es p ij 𝜆 i dt.
La prueba de esta proposición se puede encontrar en el teorema 1.2 de Asmussen (2003).
De acuerdo con el parámetro que rige el tiempo de estancia en cada estado, estos se pueden clasificar según los siguientes criterios:
Decimos que i es un estado transitorio si 0 < 𝜆 i < ∞.
Decimos que i es un estado repelente si 𝜆 i = ∞.
Finalmente, i es un estado absorbente si 𝜆 i = 0.
La interpretación de un estado transitorio es que si el proceso visita lo visita, eventualmente saldrá de él, sin embargo, no hay certeza de que sea visitado. Un estado absorbente es aquel que una vez que el proceso llega a él, permanece en este el resto del tiempo. En este trabajo se restringe el espacio de estados excluyendo a los estados repelentes.
Sea 𝜆 ij : = p ij 𝜆 i dt, para j ≠ i, la intensidad de saltar del estado i al estado j y definamos 𝜆 ii = -∑ j ≠ i 𝜆 ij , luego llamaremos Λ = {𝜆 ij } i,j ∈ E al generador infinitesimal o matriz de intensidad del PSM {X(t)} t≥0 . Además, denotemos por p ij (t ) a la probabilidad de transición del PSM {X(t)} t ≥0 del estado i al estado j al tiempo t > 0, cuya matriz de transición correspondiente la denotaremos por P (t ) = {p ij (t )} i,j ∈ E .
El siguiente resultado permite calcular la matriz de transición en cualquier tiempo a partir del generador infinitesimal lo que nos será de utilidad para el cálculo de probabilidades de muerte a distintos horizontes de tiempo.
Proposición 3.1.2 Sea {X(t)} t≥0 un PSM con espacio de estados E y genererador infinitesimal Λ. Para cada t > 0 se tiene que: P (t ) = exp(tΛ), donde exp(tΛ) es la matriz exponencial definida por la expansión de Taylor correspondiente.
Ver el Teorema 3.4 de Asmussen (2003) para su demostración.
3.2 Distribuciones tipo fase
Una distribución PH puede ser interpretada como una variable aleatoria que representa el tiempo de absorción de un PSM con un único estado absorbente (generalmente). Esta clase de distribuciones fueron definidas por Marcel Neuts en los años setenta (Neuts 1975 y Neuts 1981). Las distribuciones PH pertenecen a la clase de distribuciones matriz-exponenciales (ME) (Asmussen y Bladt 1996), donde estas últimas se definen como aquellas que tienen transformada de Laplace racional, pero su interpretación probabilística es menos clara.
Las distribuciones PH han ganado mucha popularidad en modelación estocástica por su gran aplicación en áreas como teoría de colas, confiabilidad, finanzas, salud, ciencias de la computación, entre muchas otras. Además, esta clase de distribuciones PH es densa en la clase de distribuciones definidas en los reales positivos, lo que significa que las PH pueden aproximarse a cualquier distribución no negativa (Asmussen 2003).
Antes de presentar la definición formal consideremos lo siguiente. Sea {X(t)} t≥0 un PSM con espacio de estados finito E = {1, 2, …, n, n + 1}, donde el estado {n + 1} es un estado absorbente; con distribución inicial 𝜶 = (𝛼1, 𝛼2, …, 𝛼 n ), tal que ∑ n i =1 𝛼 i = 1 y 𝛼 i = P(X(0) = i ), y generador infinitesimal
donde Q es una matriz de dimensión n × n, r es el vector (columna) de salida de dimensión n × 1 y que cumple con r = - Qe donde e es un vector de 1’s de dimensión apropiada. 0 es un vector de ceros de dimensión 1 × n.
La distribución inicial del PSM {X(t)} t≥0 indica que el proceso solo puede inicializar en alguno de los estados transitorios {1, 2, … , n} y no en el estado absorbente. Las intensidades entre los estados transitorios se rigen a través de la matriz Q y el vector de salida r registra las intensidades al estado absorbente.
Definición 3.2.1 El tiempo hasta la absorción 𝜏 = inf {t ≥ 0:X (t ) = n + 1}, se dice que tiene una distribución PH, y escribimos 𝜏~PH (𝜶, Q ).
El conjunto de parámetros (𝜶, Q ) se dice que es una representación de la distribución PH. La siguiente proposición presenta propiedades necesarias en el cálculo de probabilidades de muerte y esperanza de vida.
Proposición 3.2.1 Supongamos que 𝜏~PH (𝜶, Q ):
La función de densidad de 𝜏 está dada por: f (s) = 𝜶 exp( Qs ) r , para s > 0.
La función de distribución de 𝜏 está dada por: F (s) = 1 - 𝜶 exp( Qs ) e , para s > 0.
El n-ésimo momento de 𝜏 está dado por: E(𝜏 n ) = (-1) n n ! 𝜶 Q -n ) e . Así, la media y varianza de 𝜏 están dadas por: E (𝜏) = -𝜶 Q -1 e y Var (𝜏) = 2𝜶 Q -2 e - (𝜶 Q -1 e )2, respectivamente.
Véanse los teoremas 4.1, 4.2 y 4.3 de Bladt (2005) para la demostración de estas propiedades.
Así pues, para la modelación del proceso de envejecimiento, entendido este como la progresiva y esencialmente la disminución irreversible con el paso del tiempo de la habilidad de un organismo o una de sus partes para adaptarse al ambiente, se utilizará un PSM con espacio de estados finito y un único estado absorbente. Para nuestro modelo, el número de edades fisiológicas es una constante determinada de acuerdo con la información con la que se cuenta para construir dichas edades.
En este PSM los estados transitorios son las edades fisiológicas, interpretadas como un índice relativo de salud que representa el grado de envejecimiento de un individuo y considerando la muerte como el estado absorbente. Dado que se tiene un espacio de estados con un único estado absorbente y los demás transitorios es seguro que eventualmente el proceso llegue al estado absorbente, lo que es incierto es el momento en que esto ocurre. Entonces, el tiempo de vida de una persona sigue una distribucion PH. Los detalles del modelo se presentan en la siguiente sección.
4. Modelo de mortalidad tipo fase
Para modelar el tiempo restante de vida (o el tiempo de muerte) de una persona utilizando una distribución PH, donde las fases -estados- sean las edades fisiológicas del proceso de envejecimiento y este sea modelado por un PSM con estados transitorios y un único estado absorbente -la muerte-, son necesarios los siguientes supuestos.
Supuestos 4.1 Dada una población de individuos, supongamos que se cumple que:
La vida de cada individuo puede ser segregada en una cantidad finita de edades fisiológicas.
El tiempo que cada individuo permanece en cada una de las edades fisiológicas puede ser modelado por una variable aleatoria exponencial de parámetro dependiente de cada edad.
El proceso de envejecimiento es irreversible, es decir, es imposible transitar desde una edad fisiológica con cierta calidad de vida a una de mejor calidad.
El tiempo transcurrido en cierta edad fisiológica puede ser ilimitado, así pues, es suficiente conocer la edad fisiológica actual del individuo (independientemente de su evolución en el pasado) para determinar su evolución futura, es decir, este proceso presenta un comportamiento Markoviano, por lo que es natural suponer que el tiempo en cada estado (edad fisiológica) tiene un comportamiento exponencial. Con esto se satisface el inciso 2 de los supuestos 4.1.
Así pues, supongamos que la vida de una persona puede segregarse en n edades fisiológicas y la muerte está representada por el estado {n + 1} (inciso 1 de supuestos 4.1). Consideramos un PSM con espacio de estados finito E = {1, 2, …, n, n + 1}, donde el tiempo de muerte sigue una distribución PH.
En cuanto a la transición entre las edades fisiológicas, consideramos la siguiente evolución para el proceso de envejecimiento propuesto por Esparza y Baltazar-Larios (2018). Si una persona tiene edad fisiológica i ∈ {1, 2, …, n}, suponemos que el tiempo que está en esa edad se distribuye exponencialmente con parámetro 𝜆 i tal que 0 < 𝜆 i <∞.
Por otra parte, para una persona en edad fisiológica i ∈ {1, 2, …, n - 1} consideramos los siguientes cuatro escenarios en un intervalo de tiempo [0, T ], T > 0, es decir, al final del periodo de tiempo:
La persona se queda en edad fisiológica i, con intensidad 𝜆 i = -𝜆 ii , donde 0 < 𝜆 ii < ∞.
La persona presenta un desarrollo natural del proceso de envejecimiento, en este caso la persona pasa a la siguiente edad fisiológica i + 1, con intensidad 𝜆 i,i +1 , donde 0 < 𝜆 i,i +1 < ∞.
El proceso de envejecimiento de una persona se ve afectado por un incidente inusual (accidente automovilístico, epidemias, etc.) que causa una disminución de su capacidad para continuar la calidad de vida que tenía, pero la persona no muere. Sin embargo, la persona transita a alguna edad fisiológica j ∈ {i + 2, i + 3, …, n}. La intensidad de esta transición se denota por 𝜆 ij , donde 0 < 𝜆 ij < ∞.
La persona muere con intensidad r i , con 0 < r i < ∞.
La matriz de subintensidad del PSM que modela el proceso de envejecimiento está dado por:
La distribución inicial para una persona en edad fisiológica i es 𝜶 = e i , siendo e i el i-ésimo vector unitario.
Sea q i (T) la probabilidad de muerte de una persona a edad fisiológica i en el intervalo de tiempo [0,T], T > 0, luego si denotamos a 𝜏 i como la variable aleatoria que modela el tiempo hasta la muerte de una persona a la edad fisiológica i, tenemos que 𝜏 i ~PH ( e i , Q ) y entonces por la proposición 3.2.1 se tiene
Para calcular esta probabilidad de muerte, se necesitan conocer los parámetros de la distribución PH, calcularlos o bien estimarlos (Asmussen, Nerman y Olsson 1996). En este trabajo, considerando que se tienen datos de población y mortalidad en tiempos discretos, se obtendrán estos parámetros, requeridos para la construcción de las tablas de mortalidad; tema que se aborda en la siguiente sección.
5. Construcción de tablas de mortalidad con experiencia México 2000-2015
En esta sección, se utilizarán datos reales de salud, población y mortalidad en México que, bajo los supuestos 4.1, se crearán las edades fisiológicas, se generan las transiciones entre ellas utilizando la matriz de transición del correspondiente generador infitesimal del PSM, y con base en este se construye la tabla de mortalidad modelando el tiempo de muerte por medio de una distribución PH.
5.1 Datos de población y mortalidad en México 2000-2015
Para construir la tabla de mortalidad para la población mexicana que obedezca la ley tipo fase se tomaron datos de INEGI, INSP y Secretaría de Salud correspondientes a los años 2000 a 2015.
Los registros de población se obtuvieron de las bases de datos del INEGI del año 2000 y 2010 prorrateada mediante un prorrateo simple de aquellos cuya edad no fue especificada y se calculó la población para los siguientes años considerando la tasa de crecimiento poblacional obtenida del mismo instituto. Los registros de las defunciones se obtuvieron de la Secretaría de Salud y fueron prorrateadas me diante un prorrateo simple de aquellos cuya edad no fue especificada.
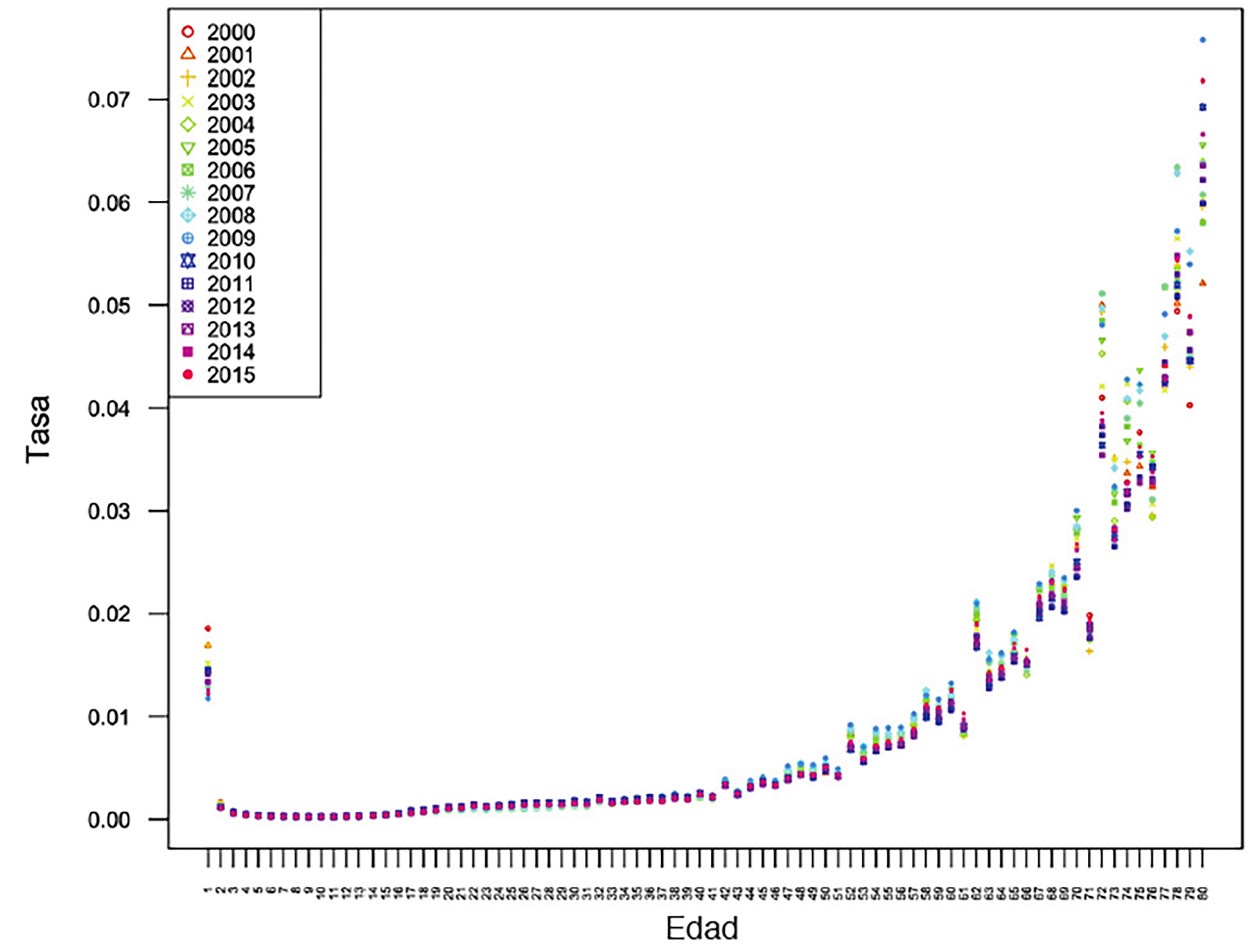
La base de datos consta de información anual de la población y mortalidad del 2000 a 2015 en México. En cada año, la información está clasificada en 101 edades (0, 1, 2, …, 99, ≥ 100). Para efectos de este artículo tomando en consideración una cota superior de la esperanza de vida promedio de los mexicanos,1 y la información de la Encuesta Nacional de Salud y Nutrición del año 2012 (ENSANUT 2012) solo se consideraron 81 edades (n = 81) correspondientes a las edades 0, 1, …, 80. En la Figura 1 se muestran las tasas de mortalidad observadas por edad para los años 2000 a 2015.
Denotemos por μ
i
(j) a la probabilidad de muerte observada (tasa de mortalidad) de una persona de edad i ∈ {0, 1, …, 80} en el año j ∈ {2000, 2001, …, 2015} y definamos
5.1 Construcción del generardor infinitesimal del proceso de envejecimiento
Dado que la edad cronológica es el factor más importante para la construcción de las edades fisiológicas, usaremos el mismo número de edades fisiológicas que cronológicas. Para la construcción de las edades fisiológicas es necesario establecer la ley de transición (anual) entre dichas edades, denotemos por p ij a la probabilidad de que una persona de edad i transite (en un año) a la edad j para i, j ∈ {0, 1, …, 80}. Para lograr dicho objetivo, usaremos el método propuesto en Esparza y Baltazar-Larios (2018).
Es necesario, para la construcción de las probabilidades de transición p ij , obtener la proporción de población con hábitos saludables (vida saludable) para cada edad, la cual denotaremos por s i para i ∈ {0, 1, …, 80}. Para obtener esta proporción se consultó la ENSANUT 2012. A pesar de que existen datos disponibles de la Encuesta Nacional de Salud 2000 (ENSA 2000) y la Encuesta Nacional de Salud y Nutrición 2006 (ENSANUT 2006) no se utilizaron los datos debido a que las encuestas se realizaron con cuestionarios diferentes que no son comparables. Las categorías de la ENSANUT 2012 que se consideraron son:
Componente de salud para obtener información sobre fumadores.
Componente de nutrición (bases trabajadas) para obtener información sobre actividad física, antropometría y hábitos alimenticios.
En el artículo de Loprinzi, Branscum, Hanks y Smit (2016) se menciona que una persona lleva una “vida saludable” cuando tiene las siguientes características: realiza al menos 150 minutos de ejercicio a la semana, consume una dieta con al me nos el 40% del índice de alimentación saludable, tiene un porcentaje de grasa corporal inferior al 20% (para hombres) o 30% (para mujeres), y no fuma. Con base a los resultados obtenidos en esa investigación se considera s i = 0.027 para cada una de las edades en Estados Unidos de América (EUA).
Basados en Loprinzi, Branscum, Hanks y Smit (2016) y en ENSANUT se obtuvieron los datos que aparecen en la Tabla 1, donde se reportan los porcentajes de la población adulta de EUA y México que fuma, que realiza alguna actividad física semanalmente, que tiene sobrepeso u obesidad y que lleva una vida sedentaria.
Tabla 1 Vida saludable de EUA y México.
| Rubro | EUA | México |
| Fumadores | 25% | 28% |
| Actividad física | 40% | 43% |
| Sobrepeso | 66% - 75% | 60% - 70% |
| Obesidad | 26% - 35% | 34% |
| Sedentarismo | 25% | 23% |
Fuente: Elaboración de los autores con base a datos de Loprinzi, Branscum, Hanks y Smit (2016) y ENSANUT.
En la Tabla 1 podemos observar que los principales factores que influyen para considerar un estilo de vida saludable en las personas residentes en EUA y México es similar, por lo que usaremos el mismo índice (s i = 0.027) para la población mexicana.
Por otro lado, las causas de defunción contenidas en las bases de datos abiertos de la Secretaría de Salud se clasificaron, basándonos en Esparza y BaltazarLarios (2018), en 4 grandes grupos: suicidios, accidentes, enfermedades y otras causas. En este trabajo consideraremos solo las tres primeras causas y distribuimos el cuarto rubro entre los tres primeros de manera uniforme. Así pues, se han clasificado las causas de defunción de manera general en autolesiones intencionales, daños intencionales y enfermedades.
Denotemos por il a la probabilidad de que una persona de edad i presente un incidente tipo l ∈ {1, 2, 3} (1 = intento de suicidio, 2 = accidente y 3 = enfermedad). Es importante mencionar que dicho incidente, en caso de no causar la muerte, tiene como consecuencia que la persona que lo padeció pierda cierto nivel de capacidad para adaptarse al medio y por tanto la probabilidad de morir se incremente. Estas probabilidades se pueden calcular de la siguiente forma
y denotamos por γ i a la probabilidad de que una persona de edad i presente al menos un incidente, es decir,
De esta forma, las probabilidades de transición son:
donde bajo el supuesto de que si la persona presenta un incidente, pero no muere, la probabilidad de transición entre edades es inversamente proporcional a su distancia (para obtener este valor se necesitan incidentes históricos para cada edad fisiológica), y entonces en este trabajo se consideró
Una vez obtenida la matriz de transición P = {p ij }, si hacemos Γ = log( P ), el generador infinitesimal Λ del proceso de envejecimiento que seguirán los individuos de la población, está dado por:
donde Γ ij es el ij-ésimo elemento de la matriz Γ.
5.2 Tabla de mortalidad tipo fase con experiencia mexicana 2000-2015
A continuación se presentan dos implementaciones del modelo, la primera de ellas utiliza los datos del 2000 al 2015 para estimar las probabilidades de muerte y la segunda implementación utiliza los datos del 2000 al 2014 para estimar 2015 y así comparar las estimaciones para el año 2015 del modelo propuesto con los datos reales observados en el mismo año.
Implementación 1
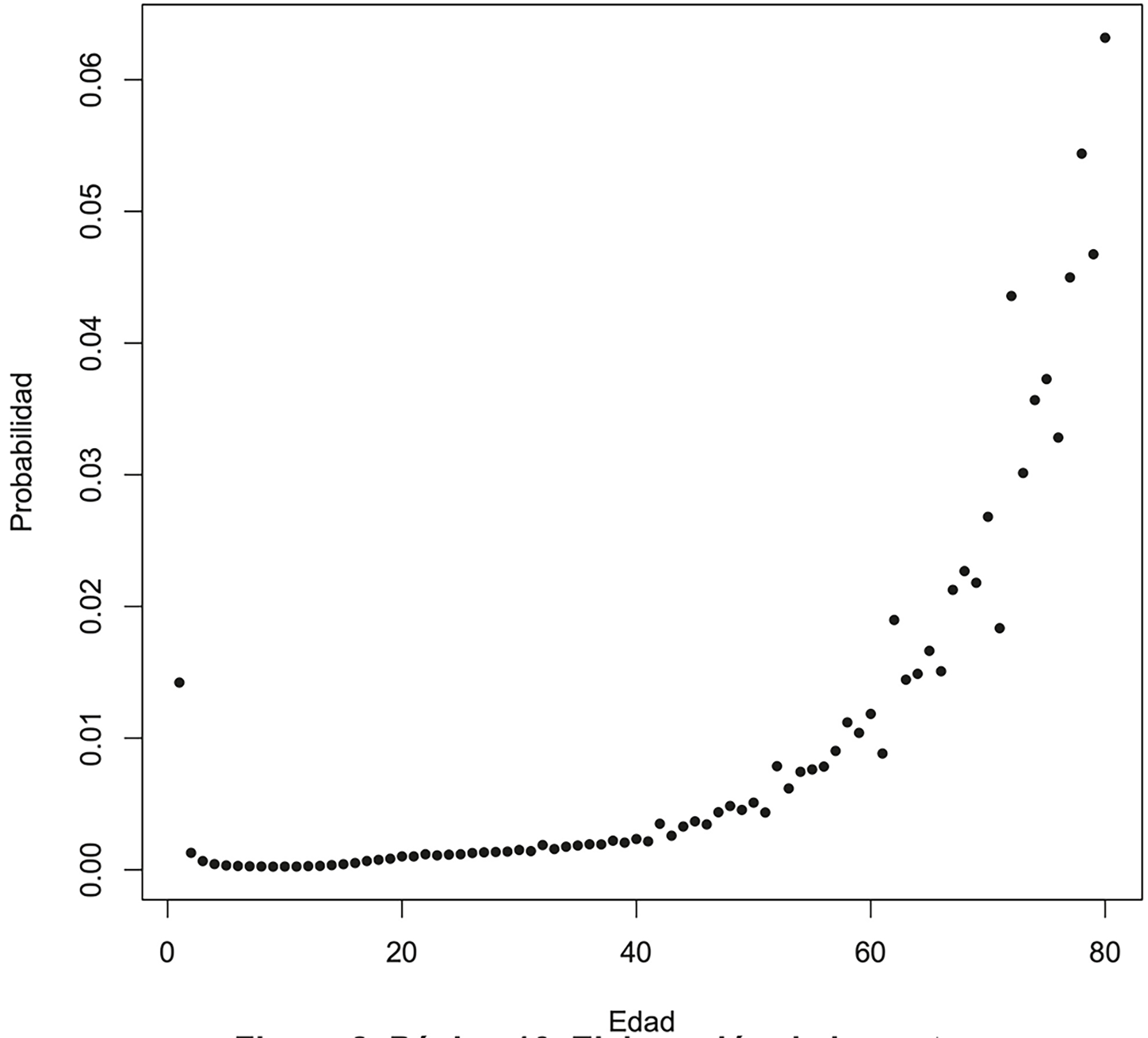
En esta primera implementación, siguiendo la ecuación (2) se calcularon las probabilidades de transición p ij utilizando como probabilidades de muerte observada al promedio de muerte observado de 2000 a 2015 (ver Figura 2) y las probabilidades de sufrir un incidente calculadas con la información obtenida de la Secretaría de Salud durante el mismo periodo de tiempo (ver Figura 3).
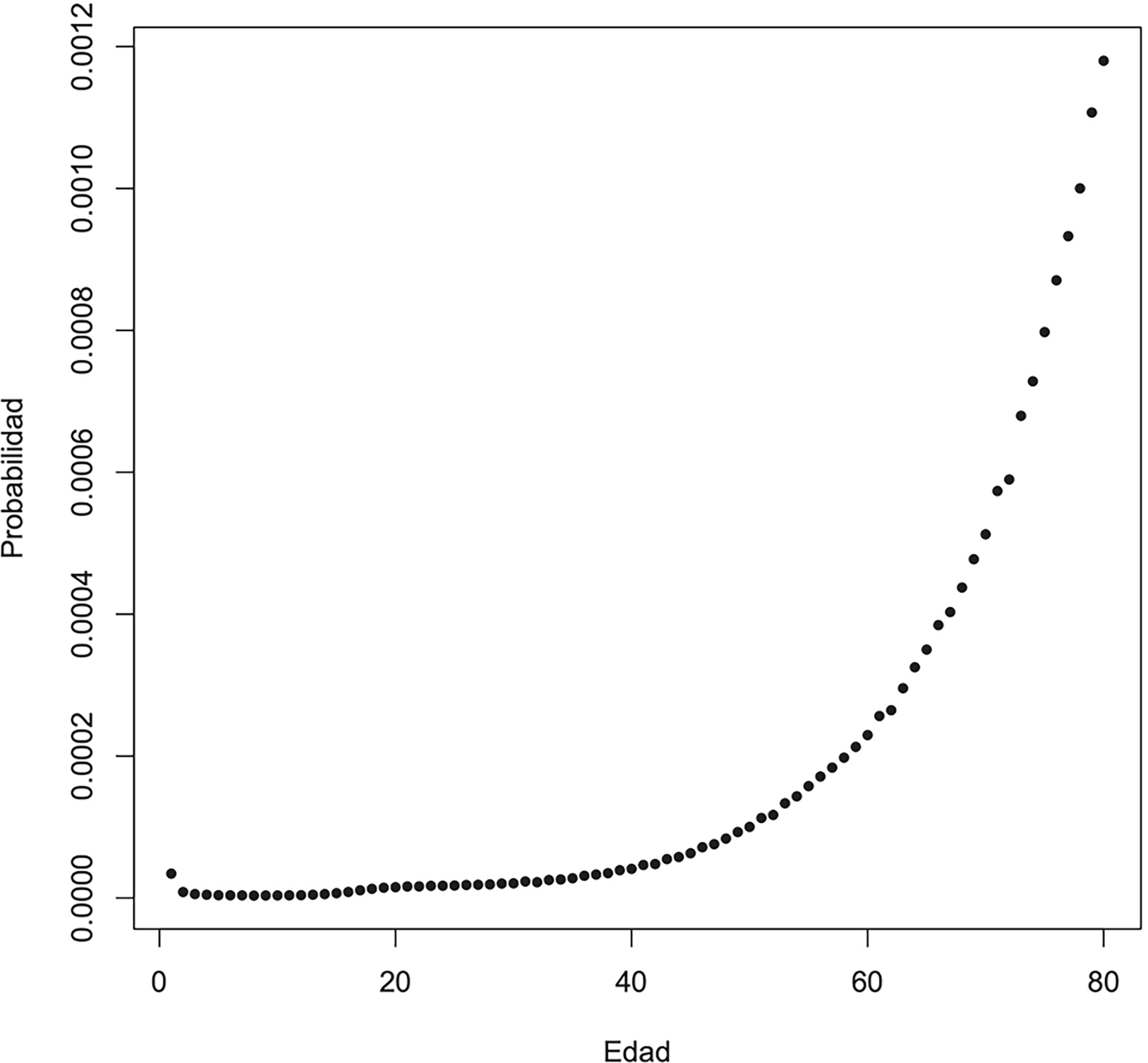
Fuente: Elaboración de los autores.
Figura 3 Probabilidad de sufrir al menos un incidente de acuerdo con cada edad con datos de 2000 al 2015.
Con las probabilidades de transición, usando la expresión (3), se obtiene el correspondiente generador infinitesimal. Dado este generador y utilizando la expresión (1) con T = 1, tenemos que las probabilidades de muerte se calcularon de la siguiente manera:
donde Q es la correspondiente matriz de subintensidad.
En la Figura 4 se muestran las probabilidades de muerte promedio para un año calculadas con el generador infinitesimal estimado y usando el modelo PH presentado en este trabajo (ver anexos). Además, la Figura 4 compara las probabilidades de muerte en un año, q i (1), i = 0, 1, …, 80, con el promedio de probabilidad de muerte observado entre 2000 y 2015.
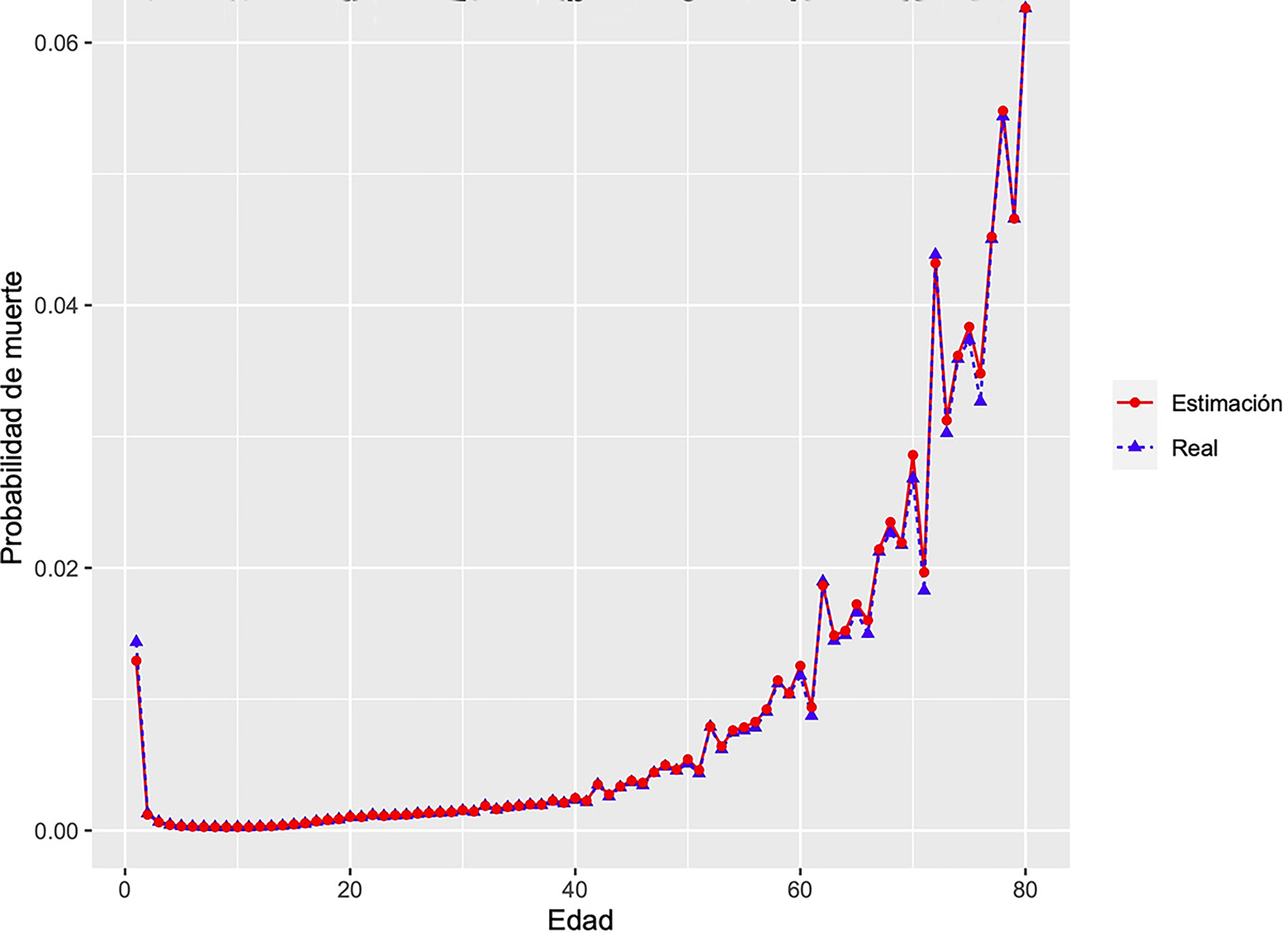
Fuente: Elaboración de los autores.
Figura 4 Probablidad de muerte real y estimada obtenida a través de la implementación 1.
Para efectos de comparación entre los valores estimados y los reales se obtuvo el error cuadrático medio (ECM), en la Figura 4 se puede observar que la estimación de la probabilidad de muerte utilizando el método presentado en este trabajo es bastante buena pues se obtuvo un ECM de 2.335285 × 10-7. Por otro lado, se puede observar que para algunas edades entre 60 y 80 años, el método propuesto sobrestima ligeramente la probabilidad de muerte observada y esto puede ser a consecuencia de utilizar el mismo índice de vida saludable para toda la población. Debido a la naturaleza de los registros era de esperarse un mejor ajuste para edades (2-60 años) donde los registros son más confiables. Es importante señalar que esta estimación mejoraría si se usaran registros más detallados y desglosados por edad para el índice de vida saludable.
Implementación 2
Datos de entrenamiento 2000-2014 y datos de prueba 2015
Ahora se presenta una implementación análoga a la anterior, pero para calcular las probabilidades de transición p ij se utilizaron como probabilidades de muerte observadas, al promedio de muerte observado de 2000 a 2014 y a las probabilidades de sufrir un incidente, se calcularon con la información obtenida de la Secretaría de Salud correspondiente. El objetivo de esta implementación es estimar la probabilidad de muerte para el 2015 utilizando el modelo propuesto en este trabajo y compararla con la probabilidad de muerte observada en 2015.
La Figura 5 presenta la comparación entre las probabilidades de muerte estimadas y observadas para el año 2015.
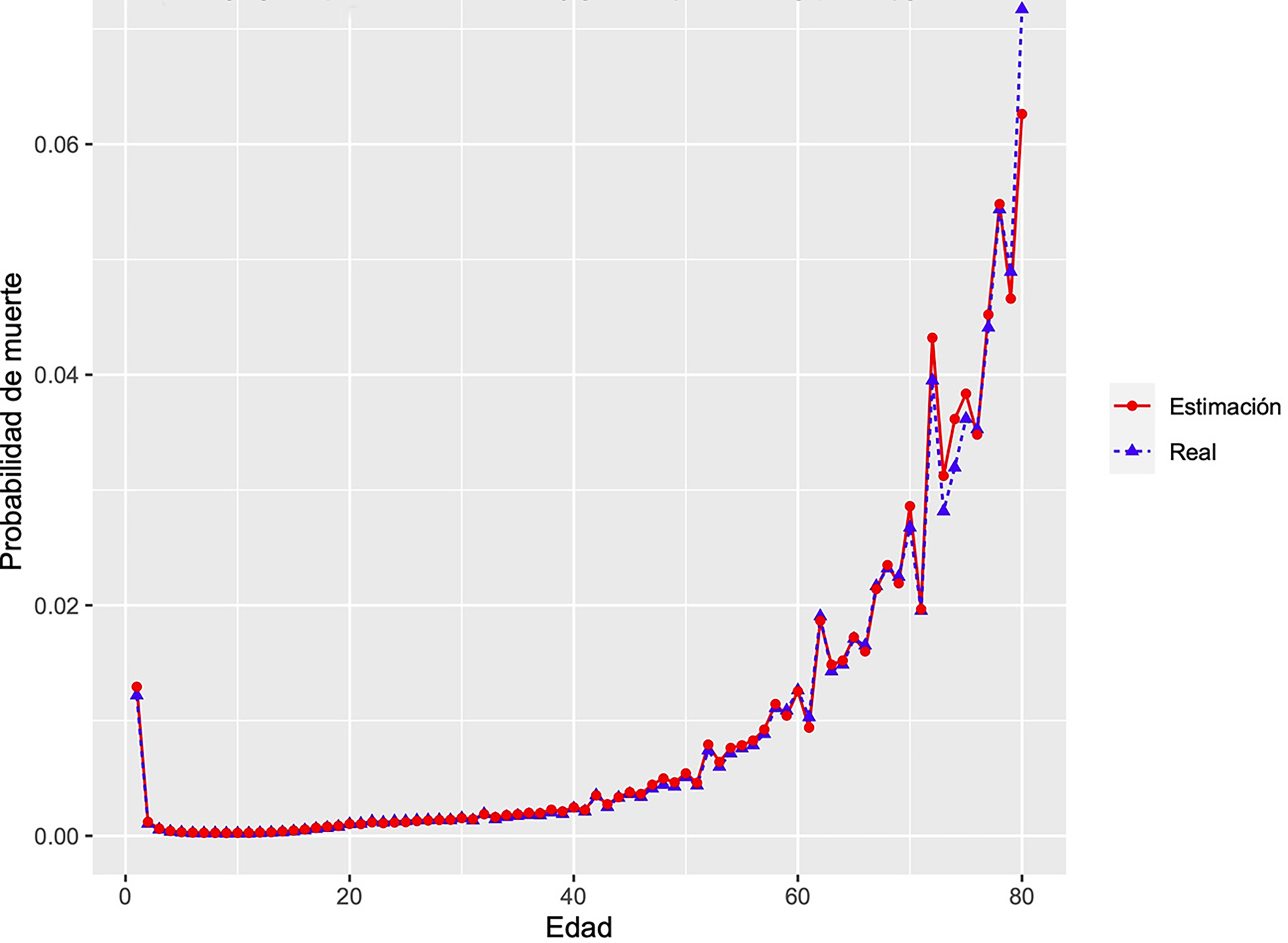
Fuente: Elaboración de los autores.
Figura 5 Probablidad de muerte real y estimada para el año 2015 utilizando la implementación 2.
De acuerdo con lo observado en la Figura 5, la estimación de la probabilidad de muerte utilizando el método propuesto es satisfactorio pues se obtuvo un ECM de 1.801983 × 10-6. En particular, podemos concluir que se mejoró la estimación para casi todas las edades haciendo solo el cálculo para un año y utilizando el generador infinitesimal de la información de los años anteriores. Sin embargo, es importante señalar que la estimación mejoraría bajo las condiciones señaladas en la implementación anterior.
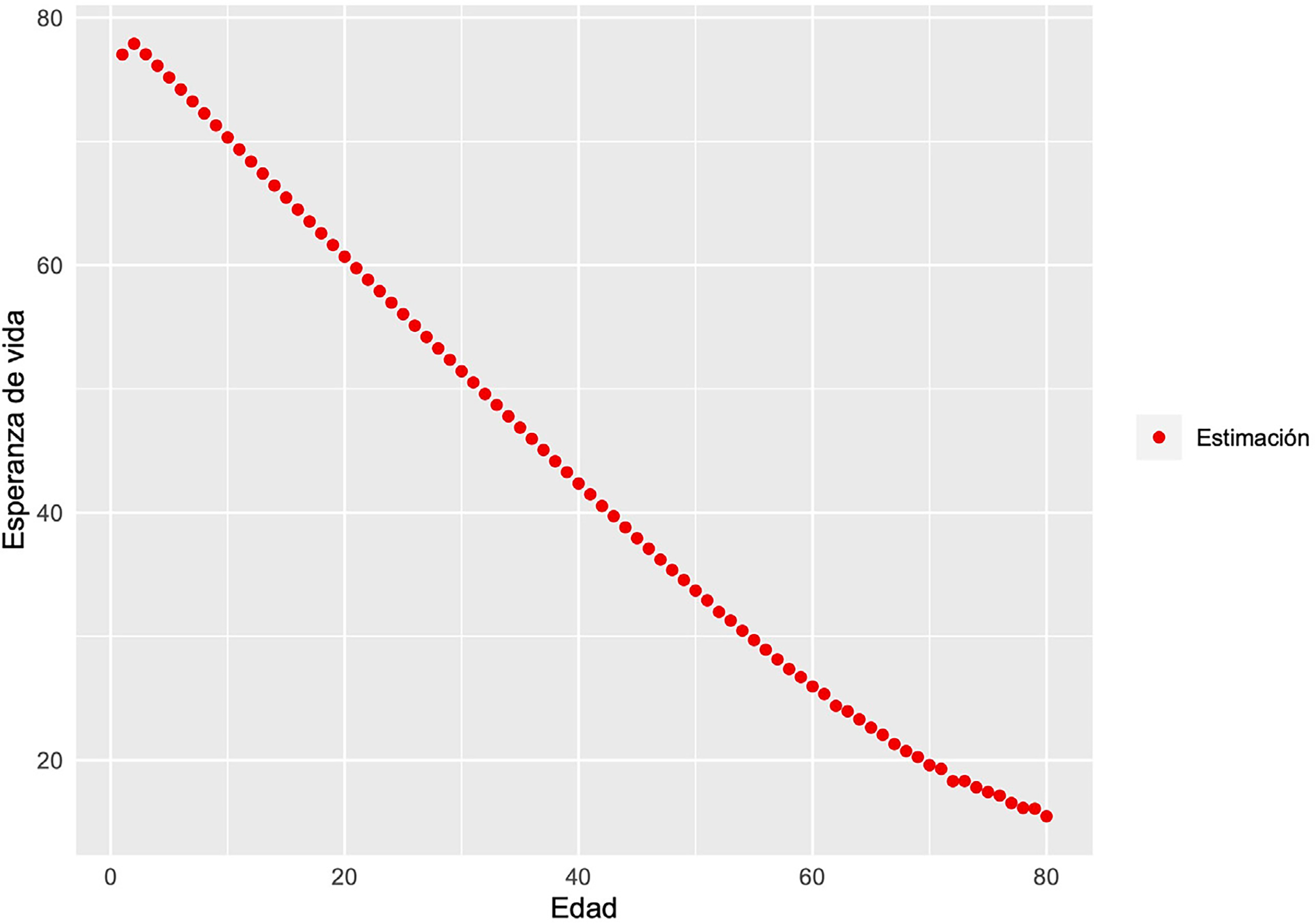
Por otro lado, conociendo los parámetros de la distribución PH que modela el proceso de envejecimiento para la población de México podemos calcular las esperanzas de vida. En la Figura 6 se grafican estas esperanzas por edad para el año 2015.
Conclusiones
Este artículo presenta una propuesta para actualizar las tablas de mortalidad de México con experiencia de población y mortalidad de 2000 a 2015 utilizando el proceso de envejecimiento a través de la edad fisiológica. Debido a que existe información disponible por parte de instituciones gubernamentales, en nuestro caso información valiosa para la construcción de un índice de edad fisiológica, se utilizó esta para proponer una manera de construir las edades fisiológicas y el generador infinitesimal que rige la transición entre estas edades, obteniendo así el proceso de envejecimiento correspondiente. Dado que el proceso de envejecimiento es modelado por un PSM con espacio de estados finito y considerando a la muerte como único estado absorbente, el tiempo hasta la muerte sigue una distribución PH. Con la propuesta de modelación presentada en este trabajo se tiene información completa de la distribución de probabilidad que sigue la mortalidad y se tienen fórmulas cerradas para calcular probabilidades de muerte en cualquier horizonte de tiempo, para estimar esperanzas de vida y a su vez permite incorporar información en cualquier momento para actualizar el generador infinitesimal del proceso de envejecimiento.
Una de las principales ventajas de utilizar este modelo es que considera factores que influyen de manera determinante el riesgo de mortalidad, por lo cual representa una manera más precisa de medir el riesgo. Es importante mencionar que para que el modelo sea más preciso es indispensable contar con información detallada por edad y género para el índice de vida saludable y para el tipo de incidente. En particular, cuando no se tiene información de este tipo es imposible implementar este método.
La actualización de las tablas de mortalidad de cualquier país es crucial para contar con una herramienta que mida con precisión el riego por mortalidad. El modelo propuesto en este artículo se puede actualizar (automáticamente) cada vez que se cuente con información nueva sobre población, mortalidad desagregada por causas e índice de vida saludable.
Por otro lado, los resultados obtenidos al implementar la metodología para construir el proceso de envejecimiento con experiencia mexicana de 2000 a 2014 y estimar la mortalidad para 2015 y compararla con la mortalidad observada para el mismo año, muestran evidencia de que el método propuesto ajusta de manera adecuada para edades con registros más confiables.
Finalmente, es importante mencionar que este modelo se puede mejorar en función de la calidad y detalle de los insumos. Una posible extensión de este modelo es permitir que el proceso de envejecimiento pueda transitar entre todas las edades fisiológicas, pero es necesario tener evidencia sólida de que esos escenarios se presentan en la población de estudio.











 nova página do texto(beta)
nova página do texto(beta)