Introducción

Las Leyes de escalamiento ocurren en muchos fenómenos naturales y sociales tan diversos como temblores (^{Bak et al. 2002}; ^{Heimpel 1997}), precipitaciones atmosféricas (^{Dickman 2003}; ^{Peters y Neelin 2006}), erupciones solares (^{Parnell et al. 2009}; ^{Boffetta et al. 1999}), la intensidad de las guerras medida en términos del número de víctimas (^{Spagat et al. 2006}), el número de personas infectadas en epidemias (^{Pastor-Satorras y Vespignani 2001}; ^{Antonio et al. 2014}; ^{Fredrik Liljeros, Edling y Amaral 2003}), el tamaño de las ciudades medido en número de habitantes (^{Gabaix 2016}), la distribución de la riqueza en una sociedad (^{Churchill 1997}; ^{X. Gabaix 2008}; ^{Ogwang 2011}) y la dinámica neuronal en el cerebro (^{Plenz y Thiagarajan 2007}), por mencionar solo algunos ejemplos. El significado e interpretación de las leyes de escalamiento varían de un sistema a otro, pero generalmente, cuando se encuentra una ley de escalamiento en un sistema hay dos posibles interpretaciones no necesariamente excluyentes. La primera es que algún aspecto de este sistema se repite a muy diferentes escalas, lo que trae como consecuencia que cada parte del sistema sea similar al sistema completo. Y la segunda consiste en que eventos que se consideran “raros” en realidad no son tan raros y pueden ocurrir con más probabilidad de lo que uno esperaría. Para ilustrar estas dos interpretaciones tomemos como ejemplo la observación hecha en la década de los años 20’ del siglo pasado, por el economista Vilfredo Pareto, consistente en que la riqueza sigue una ley de escalamiento respecto a la forma en la que se distribuye entre los miembros de una sociedad (^{Churchill 1997}). Pareto descubrió que si se considera una sociedad cualquiera, se encuentra que aproximadamente el 45% de la riqueza total de la sociedad está en manos del 5% de sus habitantes. Y esta proporción se cumple más o menos independientemente de la escala a la que estemos viendo la sociedad: a la escala de una ciudad, de un estado, de un país o del mundo entero. En este sentido, la distribución de la riqueza en cada parte del sistema se parece al sistema total. Pero además, como veremos más adelante, la ley de escalamiento de Pareto tiene una consecuencia importante y es que las personas muy muy ricas, aunque son pocas, no son tan pocas como lo imaginamos. Hay más ricos acaparadores de riquezas de lo que creemos.

¿Cómo surgen las leyes de escalamiento en un sistema? Es decir, ¿qué tipo de interacciones se deben establecer entre los elementos de un sistema para que este desarrolle una ley de escalamiento? No lo sabemos de forma general para cualquier sistema, pero hay dos mecanismos importantes que ciertamente generan leyes de escalamiento. Uno es el enlace preferencial introducido por los físicos Albert-Lasló Barabási y Reka Alber, en 1999, para describir la formación de redes complejas (^{Barabási y Albert 1999}), y el otro es la criticalidad dinámica, la cual fue estudiada de forma sistemática por muchos físicos (entre ellos Michael Fisher, Leo Kadanoff y Kennett Wilson) en las décadas 70’ y 80’ del siglo XX (^{Hohenberg y Halperin 1977}; ^{Wilson 1983}; ^{Stanley 1999}). La criticalidad dinámica se refiere a un estado muy particular de un sistema que está a punto de sufrir una transición en su comportamiento, pasando de un régimen ordenado a uno desordenado (o viceversa). Justo en este punto de transición en el que el sistema está decidiendo si se comporta ordenadamente o desordenadamente, surgen leyes de escalamiento en casi todas las propiedades que caracterizan el sistema (^{Stanley 1999}). En este trabajo describiremos el surgimiento de las leyes de escalamiento por medio de la criticalidad porque es este mecanismo el que definitivamente confiere mayor riqueza a las leyes de escalamiento. En particular, nos enfocaremos en la dinámica de formación de opiniones y en la dinámica neuronal pues, aunque aparentemente son sistemas muy diferentes (grupos de votantes versus grupos de neuronas), veremos que tienen muchas propiedades en común.

Sin embargo, antes de ver los mecanismos que generan leyes de escalamiento, es necesario comprender cómo se describen matemáticamente dichas leyes. Para esto, consideremos una función y(x) que relaciona dos variables x e y. Decimos que la función y(x) es escalable si al cambiar la escala en x lo único que ocurre es que también se cambia la escala en y, pero no se cambia la forma de la función. Lo anterior se describe matemáticamente de la siguiente forma. Supongamos que cambiamos la escala en x multiplicando esta variable por un factor de escala a. Entonces, decimos que y(x) es escalable si se cumple:

donde b es otro factor de escala. Es importante enfatizar que la ecuación anterior significa que el único efecto de haber cambiado la escala en el eje x (por un cierto factor a) es simplemente el de cambiar la escala en el eje y (por otro factor b), pero la función y(x) no cambia su forma después de haber llevado a cabo estos escalamientos. Se puede demostrar formalmente que las únicas funciones que satisfacen la condición de escalamiento dada en la Ec. (1) son necesariamente de la forma:

donde A es una constante y γ es el exponente de escalamiento. A las funciones definidas en la Ec. (2) se les llama leyes de potencia y son las únicas funciones con la propiedad de escalamiento definida en la Ec. (1), es decir, son las únicas funciones que al escalarlas se siguen viendo iguales (solo que a una escala distinta). Es importante enfatizarlo: la propiedad de escalamiento no se cumple para otras funciones como la exponencial, el logaritmo, las funciones trigonométricas o ninguna otra función. Por lo tanto, cuando decimos que existe una ley de escalamiento en algún sistema significa que algunas de las variables que describen el comportamiento de dicho sistema se relacionan a través de leyes de potencia como la dada en la Ec. (2).

Volvamos al caso de la distribución de la riqueza en una sociedad. Pareto encontró que la probabilidad y(x) de que una persona tenga un salario igual a x está dada por:

donde A=xmα-1(α-1) es la constante que garantiza la normalización de la probabilidad, α = 2.36 es el exponente de escalamiento, y x _m es el valor del salario mínimo (en principio, nadie debería tener un sueldo menor al salario mínimo). La ecuación anterior contiene mucha información sobre cómo se distribuye la riqueza en la sociedad. Por ejemplo, si u(x) es la fracción de personas con un salario mayor que x, entonces:

Por otro lado, la riqueza total R en la sociedad es:

mientras que la riqueza R _q acumulada por las personas con un salario mayor que x _q es:

Como la fracción q de las personas con un salario mayor que x _q es, de acuerdo con la Ec. (4), q = u (x _q ) = (x _q /x _m )^α-1, entonces, de las ecuaciones (4), (5) y (6) se deduce que la fracción r _q = R _q /R de la riqueza total que han acumulado estas personas está dada por

Para el caso que encontró Pareto, con α = 2.36, se desprende que para q = 0.05 entonces r _q = 0.45 (el 5% de las personas tiene el 45% de la riqueza). Peor aún, si hacemos q = 0.01 en la ecuación anterior obtenemos r _q = 0.30, lo cual significa que el 1% de la población más rica en la sociedad tiene el 30% de la riqueza total. Esto es increíble, pues para México quiere decir que el 30% de la riqueza del país está en manos de aproximadamente un millón de personas. Es decir, no solamente son los grandes millonarios famosos que todos conocemos (Carlos Slim, Emilio Azcárraga, Luis Miguel, etc.) los que han acaparado la riqueza de México. Si la ley de escalamiento de Pareto es cierta, hay por lo menos un millón de personas extraordinariamente ricas en México de las cuales ni siquiera hemos oído sus nombres.

¿Por qué son importantes las leyes de escalamiento?

La ley de escalamiento de Pareto discutida anteriormente nos da una idea de las consecuencias de que la riqueza esté distribuida en la sociedad de acuerdo con una ley de potencias. Para entender bien el significado de esta distribución, comparemos con lo que ocurriría si los sueldos estuviesen distribuidos gaussianamente¹ de tal forma que la probabilidad de que una persona gane un sueldo x estuviese dada por y(x) = Ae-(x-μ)2/2∆2. Tomemos el caso hipotético en el que la desviación estándar es igual al promedio: μ = ∆, y tomemos el mismo promedio que el que se obtiene para la ley de Pareto dada en la Ec. (3), que para α = 2.36 nos da μ = 3.77 (en unidades del salario mínimo, es decir, haciendo x _m = 1). La Figura 1 muestra una gráfica log-log con las curvas que representan la distribución de Pareto (en negro) y la distribución gaussiana (en rojo), ambas con el mismo promedio y por lo tanto correspondientes a la misma riqueza total en la sociedad. Lo que es importante es el comportamiento de estas distribuciones en las “colas”, es decir, para valores grandes de x. Puede observarse que cuando x crece, la distribución gaussiana tiende a cero mucho más rápidamente que la ley de potencias. Esto tiene implicaciones importantes. Por ejemplo, en el caso de la ley de potencias, 12 de cada mil personas tendrán sueldos de más de 25 salarios mínimos (lo cual no es para nada difícil de imaginar en la sociedad en la que vivimos), mientras que para el caso gaussiano solo 1 de cada catorce mil millones de personas ganaría más de 25 veces el salario mínimo. Es decir, si la riqueza estuviese distribuida gaussianamente no habría ningún ciudadano en nuestro planeta que tuviese un sueldo de más de 25 salarios mínimos, lo cual es claramente irreal. Debido a que las distribuciones gaussianas decaen muchísimo más rápido que las leyes de potencia, a las primeras se les llama distribuciones de “cola corta”, mientras que a las segundas se les llama de “cola larga”.

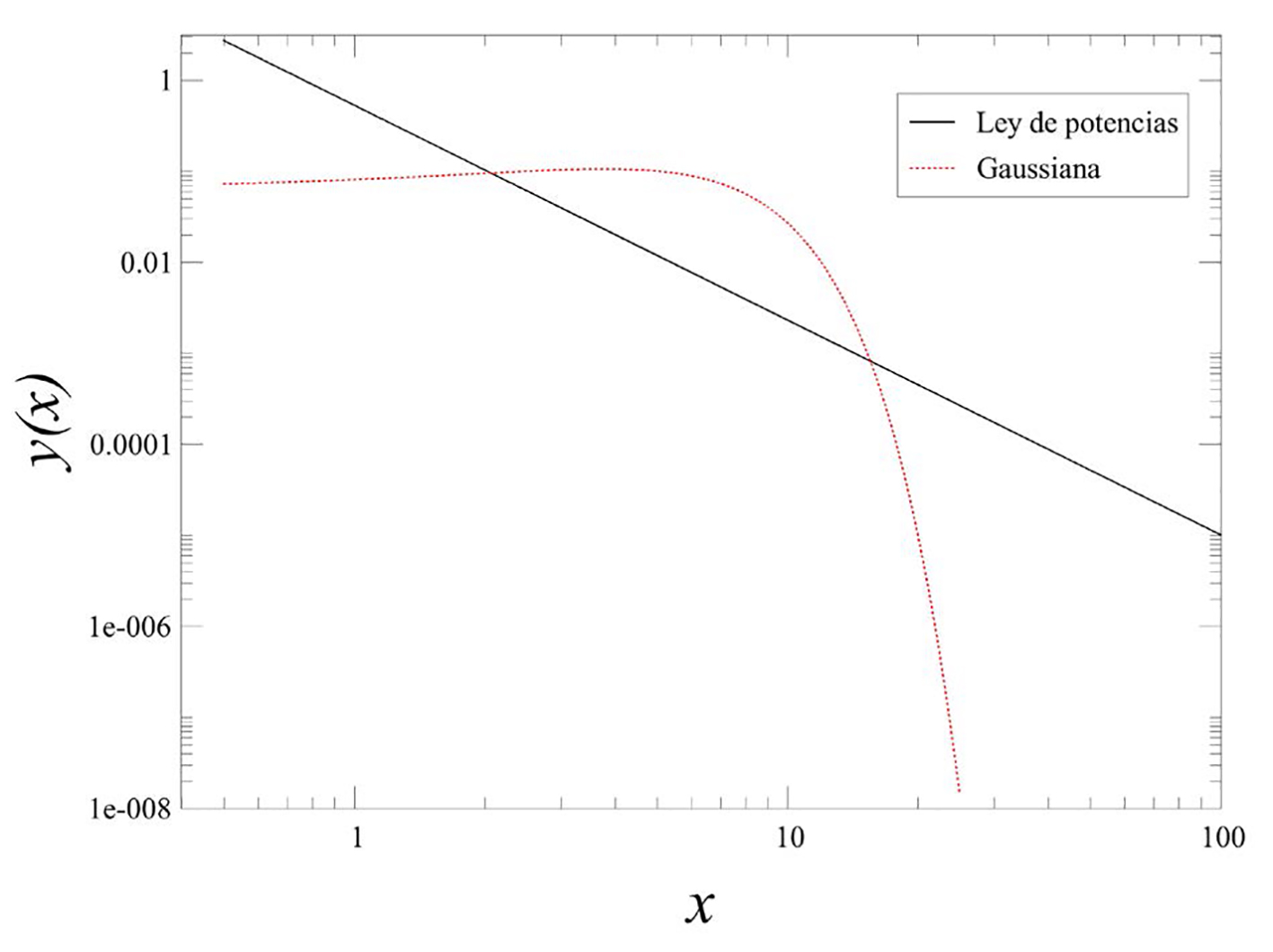
Nota: Ambas distribuciones corresponden al mismo valor de la riqueza total dado en la Ec. (5). Obsérvese cómo para valores grandes de x la distribución gaussiana decrece muchísimo más rápido que la ley de potencias (tuvimos que cortar la curva gaussiana en x = 25 o no hubiera cabido en la figura.

Fuente: Elaboración del autor.

Figura 1 Gráficas log-log de una distribución ley de potencias y(x) = Cx ^-α (curva negra) y una distribución gaussiana y(x) = Ce-(x-μ)2/2∆2 (curva roja punteada). 

Como ya hemos dicho, Pareto encontró que la riqueza en las sociedades reales se distribuye de acuerdo con una ley de potencias de la forma y(x) = Ax ^-α . En este caso, la desigualdad en la distribución de la riqueza es enorme debido a que la probabilidad de los “eventos raros” (es decir, de que haya personas extremadamente ricas) es mucho mayor que para el caso gaussiano (o que para cualquier otra distribución de “cola corta”). La distribución de la riqueza es solo un ejemplo que presenta una ley de escalamiento. En la Tabla 1 se dan más ejemplos de leyes de escalamiento en sistemas muy diferentes. Como puede verse de esta tabla, las leyes de escalamiento frecuentemente ocurren en la función y(x) que determina la probabilidad de alguna variable x. De particular importancia son los casos cuando el valor del exponente está en el intervalo 1< α <3 (como en todos los ejemplos listados en la Tabla 1), porque entonces el sistema presenta fluctuaciones infinitas. Efectivamente, si x es una variable aleatoria y y(x) = Ax ^-α es la función de probabilidad de esta variable, se puede demostrar que la varianza de x es proporcional al siguiente término:

Este límite solo existe cuando α > 3. De lo contrario, si α ≤ 3 resulta que σ² = ∞. En la práctica ningún sistema es infinito, por lo cual hay que interpretar cuidadosamente el hecho de que la varianza de un sistema se haga infinita. Cuando la varianza de un sistema “explota” o diverge significa que no hay ningún valor representativo del comportamiento promedio del sistema, debido a que las fluctuaciones alrededor de cualquier promedio calculable ocurren a todas las escalas, desde fluctuaciones pequeñas hasta fluctuaciones tan grandes como el sistema completo. Por ejemplo, si consideramos las guerras habidas a lo largo de la historia de la humanidad y de las que tenemos registro histórico, no existe un número representativo del promedio de víctimas mortales en cada una, puesto que han habido guerras que tienen desde unos cuantos muertos (como el Niger Delta Conflict) hasta otras en donde los muertos se cuentan por decenas de millones (como la Segunda Guerra Mundial). Aunque es posible calcular el promedio aritmético de los muertos en todas esas guerras (puesto que uno siempre puede calcular el promedio de cualquier conjunto finito de números), dicho promedio no sería representativo de ninguna guerra, pues debido a que las fluctuaciones son infinitas, no existe tal cosa como una “guerra promedio” representativa. La ley de escalamiento en este caso (cuyo exponente es 2.5 (^{Spagat et al. 2006})), nos dice que han habido guerras de todas las escalas, chicas, medianas, grandes y más grandes, de tal manera que ningún promedio es representativo de ninguna guerra, y el hecho de que la varianza explote quiere decir que podría incluso haber una guerra en la que el número de muertos sea casi del tamaño del sistema completo (esto es, del total de habitantes de la Tierra).

Lo mismo ocurre con los temblores (el exponente en este caso es α ≈ 1 (^{Bak et al. 2002})), pues hay desde temblores muy suaves hasta terremotos muy intensos, sin que haya un valor “promedio” representativo para la intensidad de un temblor. O el número de parejas sexuales distintas que una persona pueda tener (el exponente es α ≈ 2.31), ya que hay desde aquellos que solo han tenido una (o ninguna) pareja sexual en toda su vida, hasta los más promiscuos que han tenido cientos o miles de parejas sexuales diferentes (principalmente trabajadores sexuales) (^{Liljeros et al. 2001}; ^{Fredrik Liljeros, Edling y Amaral 2003}).

La importancia de las leyes de escalamiento, cuando aparecen en funciones de probabilidad, radica en dos puntos:

Criticalidad dinámica: El modelo de votantes

No existe un mecanismo universal que genere leyes de escalamiento en la Naturaleza. Cada sistema físico, biológico, social o económico puede obedecer a diferentes reglas de interacción y organización que serán las que generen leyes de escalamiento en el sistema específico bajo consideración. Sin embargo, un mecanismo muy importante es la criticalidad dinámica, que ocurre cuando en un sistema existe una transición de fase entre estados ordenados y estados desordenados (^{Stanley 1999}). El punto en el que se da dicha transición se llama “punto crítico” y es justo allí, en el punto crítico, donde aparecen las leyes de escalamiento en las propiedades que caracterizan al sistema. La importancia de la criticalidad dinámica radica en que la existencia de los puntos críticos solo depende de propiedades muy generales de las interacciones que hay entre los elementos que conforman el sistema, y no de los detalles específicos de dichas interacciones. Por lo tanto, puntos críticos muy similares pueden observarse en sistemas muy diferentes, tales como, por ejemplo, la dinámica neuronal, el comportamiento magnético de un imán o la formación de opiniones en una sociedad.

Para ilustrar el concepto de criticalidad consideremos un modelo de una sociedad de N personas en la que se está llevando a cabo un proceso de votación respecto a un tema que tiene dos posibles opciones. Por ejemplo: “estás a favor o en contra del aborto”. La opinión de cada persona la podemos entonces representar por una variable binaria σ que puede tomar solo los valores +1 o -1. La sociedad está representada por el conjunto de variables {σ₁, σ ₂, …, σ _N }, en donde la variable σ _n representa la opinión del n-ésimo individuo. Las personas en la sociedad forman una red de amigos que intercambian opiniones, lo cual representamos por una red de N nodos como la mostrada en la Figura 2, en donde los nodos son las personas y las conexiones entre ellos son relaciones de amistad. Supongamos que el nodo σ _n tiene k _n amigos que influyen en su opinión, los cuales representaremos por σ1n, σ2n, …, σknn. Sin embargo, no todos estos amigos influyen de la misma manera en la opinión de _n , pues habrá algunos que influyan más que otros. Es más, algunas de estas influencias podrían incluso ser negativas (como cuando alguien siempre hace lo contrario de lo que dice su mamá). Por lo tanto, a las conexiones de esta red hay que asignarles pesos (o intensidades) para determinar qué tanto influye un nodo en la opinión de otro. Denotaremos como w _nm a la intensidad de la interacción entre el nodo σ _n y su m-ésimo amigo σnm y llamaremos a este número la influencia que tiene σnm sobre σ _n . La red consiste entonces en un conjunto {σ₁, σ ₂, … , σ _N }, de N variables conectadas entre sí, siendo σ1n, σ2n, …, σknn los nodos con conexiones entrantes² al nodo σ _n y wn1, wn2, …, wnkn) las correspondientes influencias de estas conexiones (Figura 2). Existen muchísimas maneras de crear una red. Aquí supondremos que los k _n amigos del nodo σ _n están escogidos al azar dentro de la red, y que las influencias correspondientes w _nm también están escogidas al azar a partir de una función de probabilidad P(w) gaussiana con promedio μ y varianza ẟ ², como se ilustra en la Figura 2. Es importante notar que la fracción de influencias negativas (región sombreada en la curva gaussiana de la Figura 2) depende del parámetro α = μ/ẟ, al cual llamaremos parámetro de influencia. Entre más grande sea α, menos influencias negativas hay en la red, y, viceversa, entre más chico sea α, más influencias negativas habrá.³

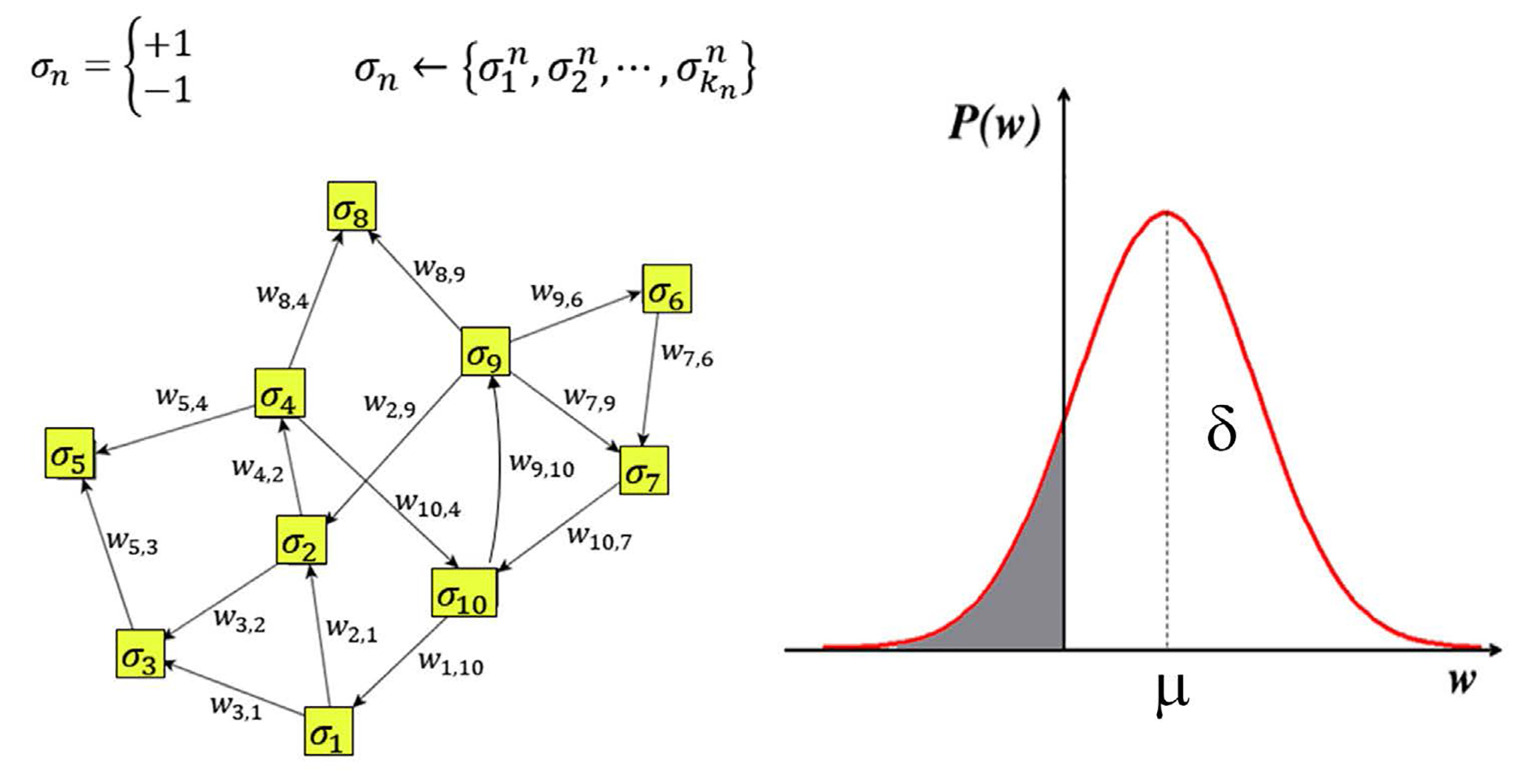
Nota: La red social se representa por un conjunto de N nodos {σ ₁,… ,σ _N }, cada uno adquiriendo el valor +1 o -1 dependiendo de la opinión de la persona a la que representa. Cada nodo σ _n recibe opiniones de un conjunto σ1n, …, σknn de otros nodos de la red (sus “amigos”, representados por las flechas entrantes). Las conexiones están ponderadas por los factores de influencia w _nm , los cuales se seleccionan aleatoriamente de una distribución gaussiana con promedio μ y varianza δ ², como la mostrada en la parte derecha de la figura. La región sombreada bajo la curva gaussiana representa la fracción de influencias negativas y su tamaño depende del parámetro α = μ/δ.

Fuente: Elaboración del autor.

Figura 2 La red social representada por un conjunto de nodos. 

El proceso dinámico de formación de opiniones que simularemos es el siguiente: supongamos que cada persona σ _n se reúne con sus amigos σ1n, σ2n, …, σknn periódicamente cada cierto tiempo τ para discutir el tema en cuestión e intercambian opiniones. Después, el nodo σ _n se va su casa para reflexionar, ponderando las opiniones de sus amigos y formándose así su propia opinión. Después de ponderar las opiniones recibidas, muy probablemente este nodo adquirirá la misma opinión que tienen la mayoría de sus amigos (por eso son sus amigos, ya que seguramente comparten muchas cosas en común). Pero existe la posibilidad de que después de reflexionarlo, el nodo σ _n adquiera la opinión contraria a la que tienen la mayoría de sus amigos. Esto lo modelamos haciendo que el valor de la variable σ _n cambie en el tiempo de acuerdo con la siguiente regla dinámica:

donde la función signo Sig(x) se define como Sig(x) = 1 si x > 0 y Sig(x) = -1 si x < 0. El término ∑m=1knwnmσmn(t) es la suma ponderada de las opiniones de los amigos de σ _n . Por lo tanto, la ecuación anterior nos dice que después de reflexionar durante un tiempo τ, el nodo σ _n adquiere la opinión de la mayoría (ponderada) de sus amigos con probabilidad p, o bien adquiere la opinión contraria a la de la mayoría con probabilidad q = 1 - p. Este parámetro p, al que llamaremos parámetro de empatía, es entonces la probabilidad de estar a favor de la opinión mayoritaria, y representa qué tan independiente es la opinión de cada persona respecto de lo que opinen los demás (q sería entonces el parámetro de discordia, ya que es la probabilidad de ir en contra de la opinión mayoritaria).

Para determinar si la sociedad en conjunto ha llegado o no a un consenso respecto al tema por el que están votando, definimos el parámetro de orden M como:

lo cual es simplemente la opinión promedio de todas las personas en la sociedad al tiempo t. Si |M(t)| ≈ 1 quiere decir que la gran mayoría de las personas tienen ya la misma opinión (ya sea +1 o -1), mientras que si |M(t)| ≈ 0 entonces aproximadamente la mitad de las personas tienen la opinión +1 mientras que la otra mitad tienen la opinión -1, las opiniones están divididas y la sociedad en su conjunto no ha llegado a ningún consenso. La Figura 3 muestra gráficas típicas de M(t) como función del tiempo para una red en particular y distintos valores de los parámetros σ y q. En las simulaciones que se realizaron para generar las curvas de la Figura 3, la red comenzaba con una condición inicial en la que aleatoriamente el 50% de los nodos tenía el valor +1 y el otro 50% el valor -1. Como puede verse, hay combinaciones de los parámetros σ y q para los cuales la sociedad alcanza un consenso (|M(t)| ≈ 1, curva negra), mientras que hay otras combinaciones para las cuales la sociedad nunca alcanza un consenso y las opiniones permanecen siempre divididas (|M(t)| ≈ 0, curva roja). A la región de parámetros para los cuales |M| > 0 la llamaremos fase ordenada, mientras que la región de parámetros para los cuales M = 0 será la fase desordenada.

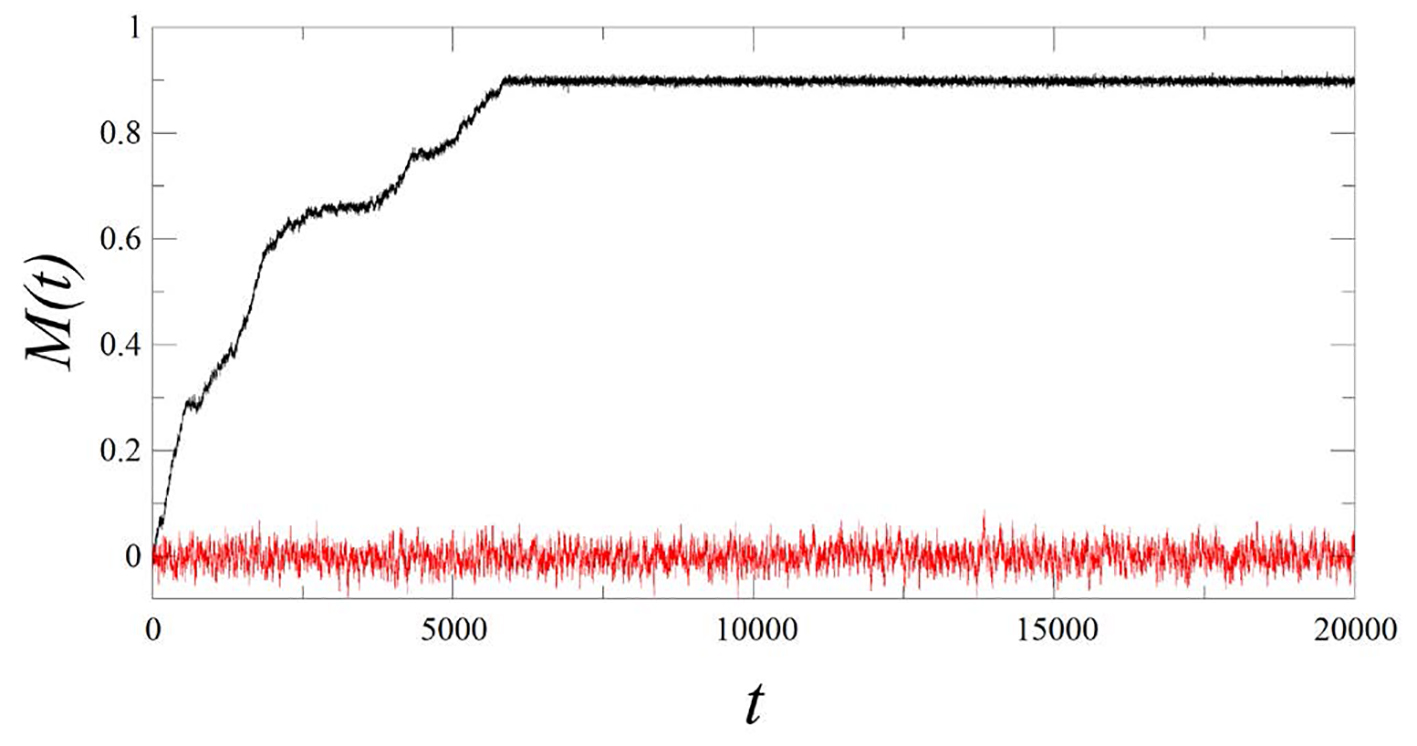
Nota: La curva negra corresponde a q = 0.05 y α = 1.5, mientras que la curva roja se calculó con q = 0.25 y α = 0. En ambos casos el sistema parte de una condición inicial aleatoria en la que aproximadamente la mitad de los nodos tiene el valor +1 y la otra mitad el valor -1. Nótese cómo para el primer conjunto de parámetros la red alcanza un estado ordenado estacionario con un valor promedio M = 0.9, mientras que en el segundo caso la red nunca sale del estado desordenado.

Fuente: Elaboración del autor.

Figura 3 Parámetro de orden M(t) como función del tiempo para dos conjuntos diferentes de valores de parámetros. 

¿De qué depende el que la sociedad alcance o no un consenso? La respuesta esencialmente es la siguiente: el parámetro de activación α y el parámetro de empatía p deben ser grandes. ¿Pero qué significa “grande” o “pequeño” en este contexto? Es decir, ¿grande o pequeño respecto a qué?

Un análisis riguroso de campo promedio⁴ de la dinámica dada en la Ec. (8) muestra que la evolución temporal del parámetro de orden está dada por (^{Aldana y Larralde 2004}):

donde Erf(x) es la función error y k es el número promedio de conexiones de entrada de cada nodo. Lo primero que puede observarse de la ecuación anterior es que si α = 0, entonces la única solución posible es M(t) = 0 (pues Erf(0) = 0). El que α = 0 significa que la distribución gaussiana que determina las influencias w _nm está centrada en cero, es decir, habrá la misma cantidad de influencias positivas como negativas. No es de extrañar entonces que el consenso en la sociedad nunca pueda alcanzarse si la mitad de las personas que influyen en nuestra opinión lo hacen de forma positiva, y la otra mitad lo hacen de forma negativa.

Para encontrar soluciones no triviales de la ecuación (10) utilizamos métodos numéricos, lo cual nos permite resolverla de forma muy sencilla. Sobre todo, queremos resolverla para el valor estacionario de M(t). Como puede verse en la Figura 3, después de un cierto tiempo transitorio, el parámetro de orden M(t) se estabiliza y alcanza un valor estacionario promedio. En el estado estacionario, el parámetro de orden ya no cambia (salvo pequeñas fluctuaciones inducidas por la probabilidad q que tiene cada individuo de ir en contra de la mayoría); de tal forma, en el estado estacionario se cumple que M (t + τ) = M(t) = M. Es en este régimen donde resolvemos la Ec. (10) obteniendo M como función de q, α y k. La Figura 4a muestra la gráfica de M (q, α, k) como función de q para para una red con una conectividad promedio k = 5 y el valor fijo de α = 5. Puede observarse que cuando q es pequeño, es decir, cuando la probabilidad de ir en contra de la mayoría es pequeña, la sociedad alcanza un estado ordenado en el que M ≈ 1. Sin embargo, al incrementar el valor de q, el consenso en la sociedad va disminuyendo gradualmente hasta que se anula completamente en un valor crítico q _c ≈ 0.2145. Si seguimos incrementando el valor de q por arriba de este valor crítico, resulta que M = 0 siempre. Lo anterior significa que si la opinión de cada persona es muy independiente de lo que digan los demás, entonces nunca podremos ponernos de acuerdo en ningún tema. La Figura 4a muestra entonces una transición entre la fase ordenada y la fase desordenada conforme el parámetro de discordia crece. La transición ocurre justo en valor crítico q _c .

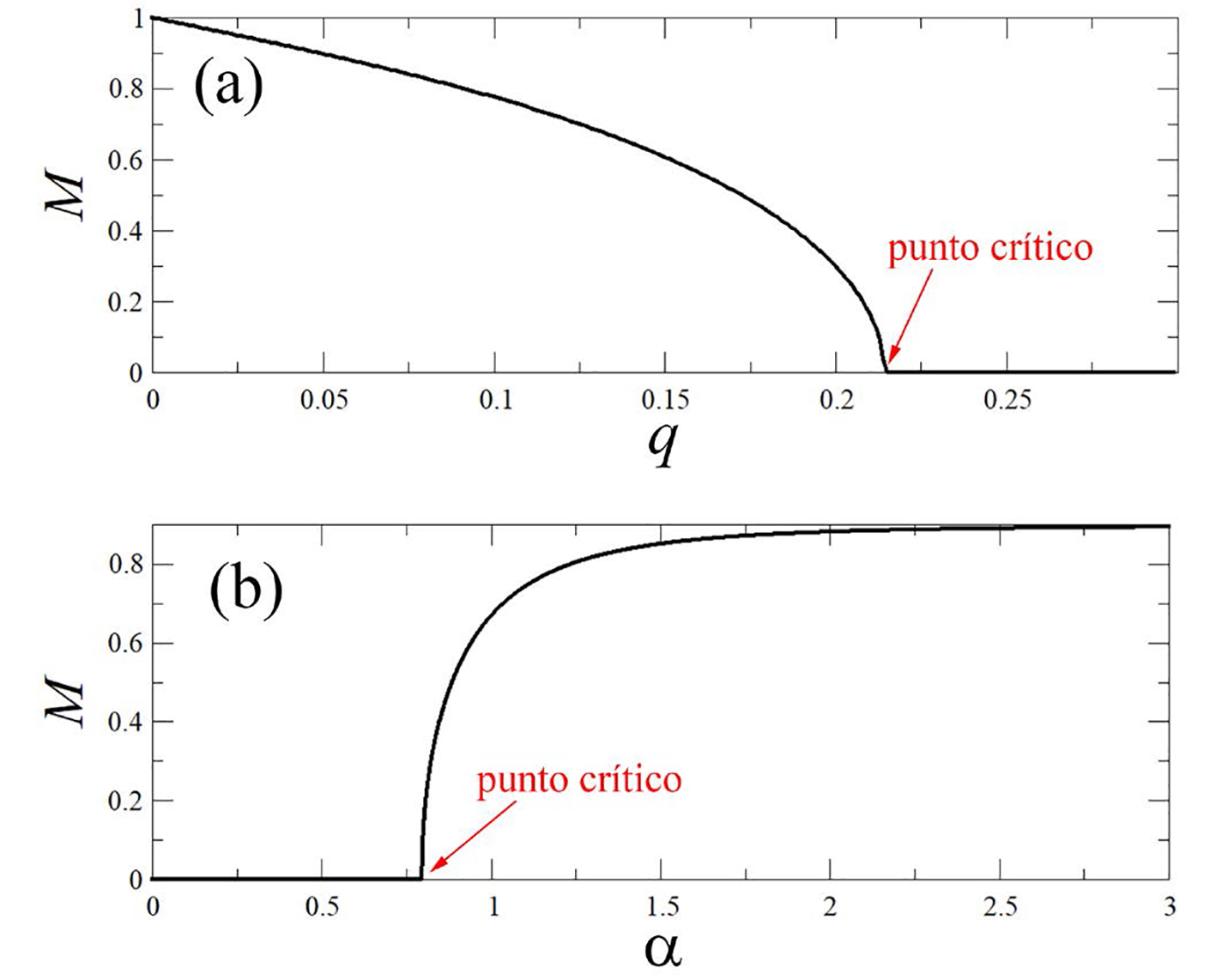
Nota: (a) Al dejar fijo el valor del parámetro de influencia en α = 5 y variar el parámetro de discordia q, el sistema pasa de una fase ordenada para la cual M > 1 a otra fase desordenada en donde M = 0. La transición de fase ocurre en el punto crítico q _c = 0.2145. (b) Una transición de fase análoga se obtiene ahora al dejar fijo el valor de q = 0.05 y variar el parámetro de influencia α. Nótese que en este caso, para valores menores al valor crítico α _c = 0.795 no hay orden en la sociedad. Se necesita que la fracción de influencias positivas exceda un cierto valor crítico (determinado por α _c ) para que la sociedad llegue a un consenso.

Fuente: Elaboración del autor.

Figura 4 Curvas de transición de fase para el modelo de votantes con una conectividad promedio K = 5.  

Por otro lado, también existe una transición entre la fase ordenada (M > 0) y la fase desordenada (M = 0) al variar el parámetro de influencia α y mantener fijo el parámetro de discordia en el valor q = 0.05, como se muestra en la Figura 4b, en donde la transición ocurre en el valor crítico α _c ≈ 0.796. Ya habíamos señalado antes que para α = 0 el sistema se encuentra en la fase desordenada. Al ir aumentando el valor del parámetro α el sistema se mantiene en la fase desordenada hasta que justo en el valor crítico α _c se da la transición a la fase ordenada y la sociedad comienza a llegar a un consenso. Esto significa que si queremos que haya un consenso en la sociedad, el número de influencias negativas en las relaciones interpersonales no puede exceder de un cierto valor crítico.

La Figura 5 muestra el diagrama de la transición de fase completa como función de los parámetros q y α. Se puede ver que hay toda una curva de puntos críticos (q _c , α _c ) en la que el sistema pasa de la fase ordenada a la fase desordenada. En estos puntos críticos, aunque el parámetro de orden se anula igual que en la fase desordenada, el sistema tiene un comportamiento dinámico muy interesante. La Figura 6 muestra imágenes del sistema en las tres fases: ordenada, crítica y desordenada. Cada cuadrito representa un nodo de la red, y se ha dibujado en verde si el valor del nodo correspondiente es +1, y negro si es -1. En la fase ordenada la sociedad ha llegado a un consenso, de tal forma que la imagen se ve mayoritariamente verde excepto por aquellos pocos individuos que van en contra de la mayoría. En la fase desordenada se ve una mezcla homogénea de cuadros verdes y negros pues, en promedio, la mitad de las personas tienen la opinión +1 y la otra mitad tienen la opinión -1, y los unos y los otros están más o menos mezclados de manera uniforme en la sociedad. Sin embargo, en el punto crítico el sistema forma dominios de opinión, es decir, grupos de nodos contiguos del mismo color. Dentro de estos dominios los nodos están altamente correlacionados. Así, aunque M = 0 en el punto crítico igual que en la fase desordenada, la estructura interna del sistema es muy distinta.

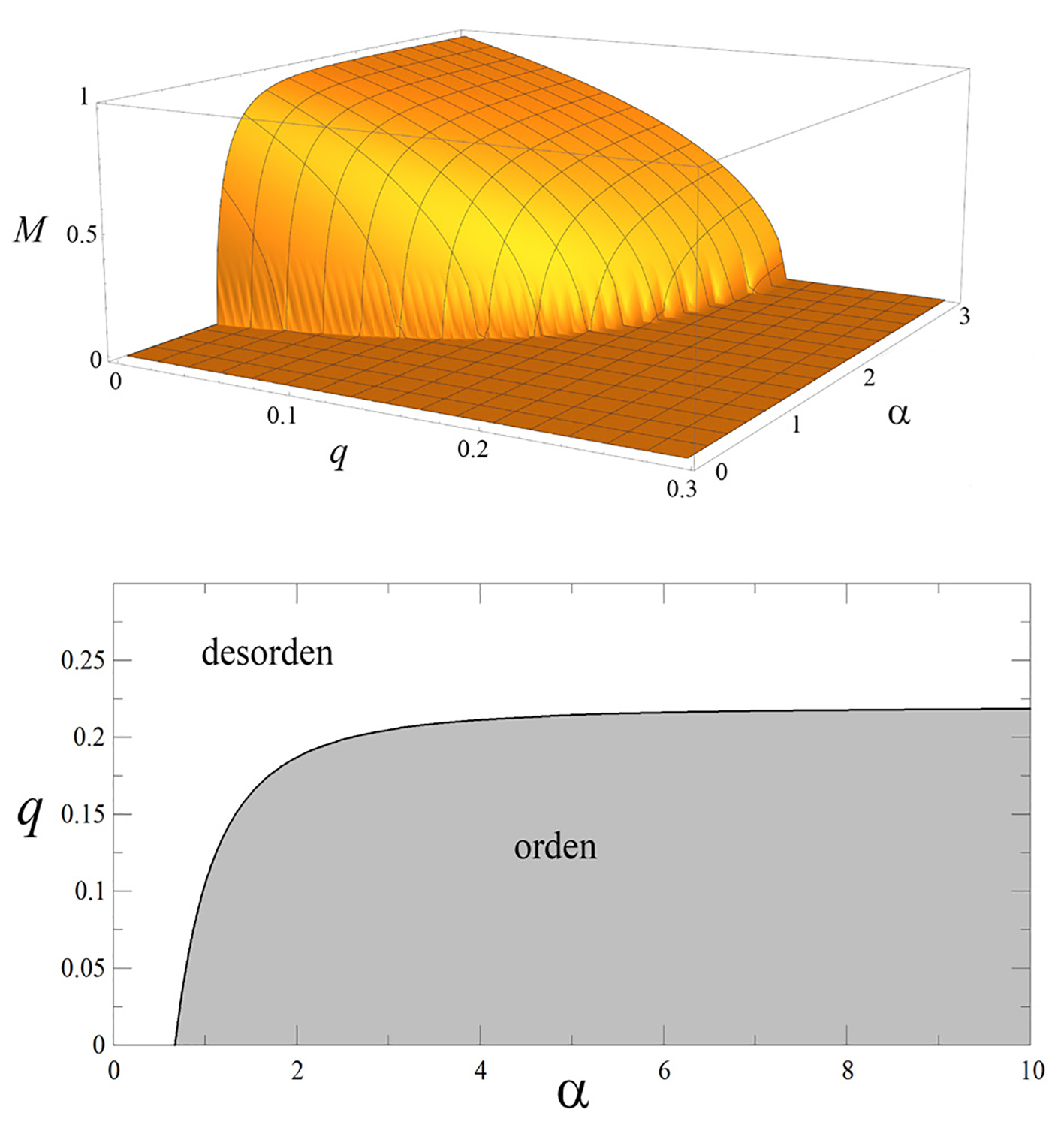
Nota: (a) El panel superior muestra el parámetro de orden M como función de los parámetros de control q y α; también muestra el diagrama de fases indicando las fases ordenada (M > 1) y desordenada (M = 0). La curva que separa estas dos fases (panel inferior) es la curva crítica. Es decir, cualquier punto de esta curva es un punto crítico.

Fuente: Elaboración del autor.

Figura 5 Parámetro de orden M y diagrama de fase. 

Nota: Observe la estructura de dominios de todos los tamaños (verdes y negros) que aparecen en el punto crítico. La existencia de estos dominios en punto crítico es una muestra clara de que la longitud de correlación entre nodos se hace del tamaño de todo el sistema (diverge).

Fuente: Elaboración del autor.

Figura 6 Estructura del sistema en las tres fases dinámicas: ordenada, crítica y desordenada. 

Observando detenidamente la Figura 6 vemos que en el punto crítico ocurren dominios de todos los tamaños, desde dominios pequeñitos (casi puntos aislados), dominios de tamaño intermedio, hasta dominios enormes que abarcan todo el sistema (invitamos al lector a encontrar un camino que atraviese toda la imagen sin salirse de un dominio verde o de uno negro). Por el contrario, en la fase ordenada solo existe un gran dominio verde que abarca casi todo el sistema salpicado por puntos negros, mientras que en la fase desordenada los dominios negros o verdes son muy pequeños. Si ignoramos el dominio enorme de la fase ordenada que siempre va a estar presente, puede demostrarse que la probabilidad G(s) de encontrar un dominio de tamaño s se comporta de la siguiente manera:⁵

donde β depende del valor específico de los parámetros q y α. Lo anterior nos dice que, exceptuando el dominio enorme de la fase ordenada, es muy poco probable encontrar dominios grandes en las fases ordenadas y desordenadas pues la probabilidad decae exponencialmente. Sin embargo, en el punto crítico la distribución del tamaño de dominios es una ley de potencias, por lo que podemos encontrar dominios de todos los tamaños, desde los muy pequeños hasta los que cruzan todo el sistema de lado a lado.

Dentro de un dominio, los nodos están altamente correlacionados. Eso significa que si forzamos a un nodo a cambiar su valor, esta perturbación puede propagarse a todos los nodos que están dentro de ese dominio, como una especie de efecto dominó. En la fase desordenada, el perturbar alguno de los nodos no tiene casi ningún efecto, pues solo se verían afectados los nodos que estén dentro de su dominio, pero como en dicha fase los dominios son muy pequeñitos, las perturbaciones no llegarían muy lejos, extinguiéndose de forma prácticamente inmediata. Lo mismo pasa en la fase ordenada. Aquí, aunque existe un dominio enorme, las perturbaciones también desaparecen rápidamente precisamente porque ese dominio enorme no permite que los nodos cambien de opinión. Imaginemos una sociedad en la que la gran mayoría de las personas están convencidas de algún tema, (por ejemplo, de que el aborto debería ser una opción legal). Si de pronto perturbamos a una de estas personas convencidas presentándole cierta evidencia que la haga estar en contra de la opinión mayoritaria, muy probablemente esta perturbación no durará mucho ni se propagará a más personas, puesto que los amigos de la persona que perturbamos la volverán a convencer de estar a favor. Y si por casualidad esa persona llegó a convencer a alguno de sus amigos de estar en contra, los amigos de los amigos los volverán a convencer de estar a favor, pues en esta fase la gran mayoría de los nodos están a favor y eso presenta una resistencia enorme para los que quieren cambiar de opinión. Esto ocurre no porque los nodos estén fuertemente correlacionados en la fase ordenada, sino por la enorme presión social para estar a favor de un tema.

En el punto crítico, la situación es radicalmente diferente, pues aquí, aunque las opiniones están divididas mitad y mitad, sí existen correlaciones muy fuertes entre los nodos que están dentro de un mismo dominio. Por lo tanto, si dentro de un dominio verde perturbamos a un nodo obligándolo a hacerse negro, esta perturbación se propagará a los amigos del nodo perturbado, los cuales transmitirán la perturbación a sus amigos, y así sucesivamente. El resultado es que en el punto crítico la perturbación se propagará a través de todo el dominio cambiando el valor de los nodos que pertenecen a él. Debido a que en el punto crítico existen dominios de todos los tamaños, ocurre que una sola perturbación puede cambiar el estado de dominios pequeños, de dominios medianos o incluso de dominios enormes que abarcan todo el sistema.

Otra propiedad que se convierte en una ley de potencias en el punto crítico es la correlación estadística entre los nodos. Supongamos que los nodos σ _m y σ _n están separados por una distancia r. La función de correlación se define como C(r) = 〈σ _m σ _n 〉 - 〈σ _m 〉〈σ _n 〉 donde los paréntesis angulares 〈∙〉 denotan el promedio sobre todas las parejas de nodos que están separados por la misma distancia r. Puede demostrarse que cerca del punto crítico, la función de correlación se comporta como:

En esta expresión η es un exponente cuyo valor solo depende de la estructura de la red social, mientras que ξ es la longitud de correlación que determina la distancia a partir de la cual los nodos dejan de estar correlacionados. Esta longitud de correlación depende del valor de los parámetros q y α de la siguiente manera:

donde ν es un exponente positivo. La implicación importante de la ecuación anterior es que al acercarnos al punto crítico, es decir, cuando α → α _c y q → q _c , se tiene que ξ → ∞. Es decir, en el punto crítico la longitud a la cual los nodos se correlacionan se hace infinita (del tamaño de todo el sistema). Esto queda manifiesto en la Figura 6 con los dominios verdes y negros que atraviesan todo el sistema. La existencia de esos dominios se debe precisamente a que la longitud de correlación se hace infinita, de donde resulta también, a partir de la ecuación (12), que en el punto crítico la función de correlación queda como una ley de potencias: C(r) ≈ r ^η . La Figura 7 muestra la gráfica de C(r) en la fase ordenada y en el punto crítico. Como puede verse, en la fase ordenada la correlación entre nodos decrece muchísimo más rápido con la distancia que en la fase crítica. Por lo tanto, aun cuando en la fase ordenada existe un gran dominio que abarca uniformemente todo el sistema, eso no significa que los nodos en este dominio estén fuertemente correlacionados.

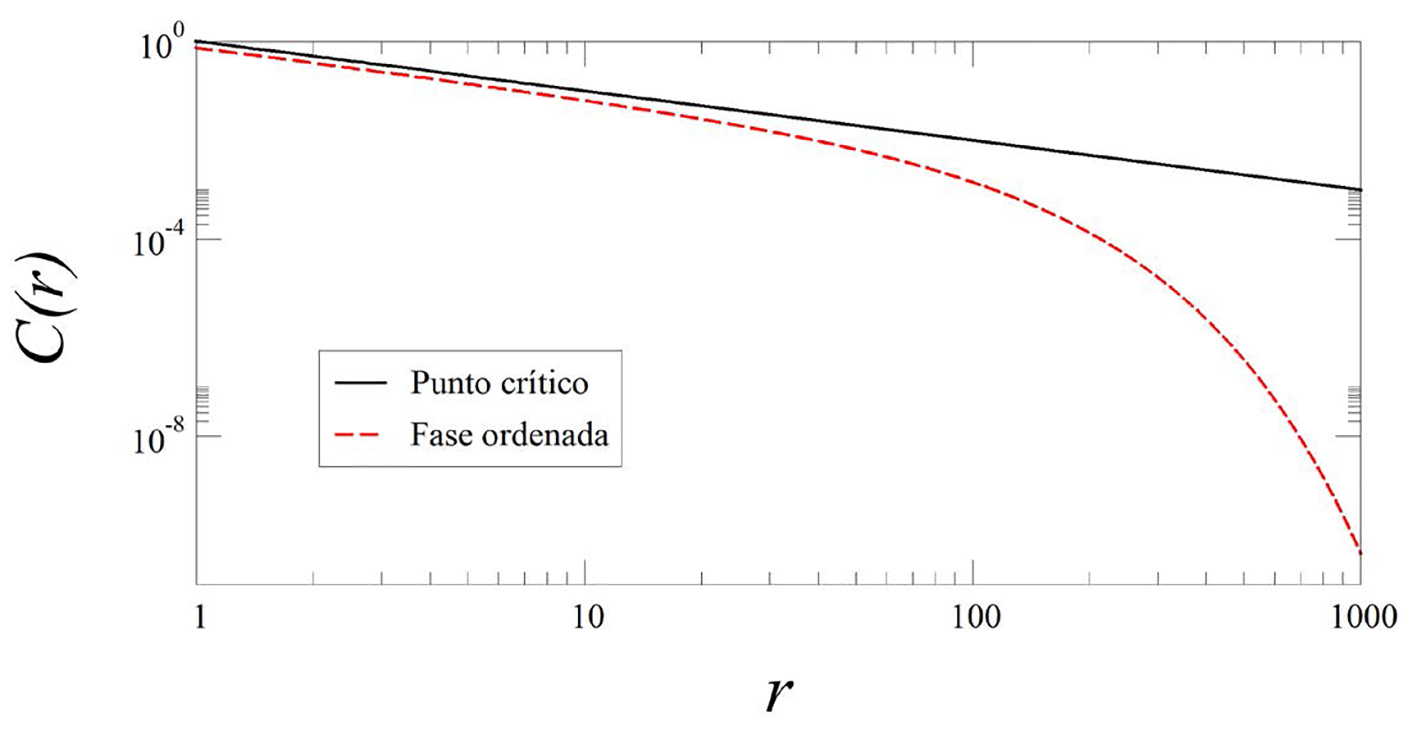
Nota: La curva negra corresponde al punto crítico y la curva roja corresponde a la fase ordenada con q = 0.2 y α = 5 (es decir, no muy lejos del punto crítico, véase la Figura 4a). Es importante observar que la función de correlación decrece mucho más rápido en la fase ordenada que en el punto crítico.

Fuente: Elaboración del autor.

Figura 7 Función de correlación entre nodos como función de la distancia que los separa. 

Desde nuestro punto de vista, la propiedad más importante de la dinámica en punto crítico es la siguiente:

Debido a que en el punto crítico las correlaciones se hacen infinitas, un sistema operando con dinámicas críticas puede responder de forma colectiva a las perturbaciones, propagándolas incluso a través de todo el sistema.

Finalmente, quisiéramos hacer notar que el modelo de votantes que presentamos en esta sección y cuya dinámica está dada por la Ec. (8) también puede considerarse como un modelo de red neuronal. De hecho, el modelo que presentamos aquí es una generalización de un modelo que formularon Warren ^{McCulloch y Walter Pitts en 1943} para describir la dinámica de redes neuronales en el cerebro (McCulloch y Pitts 1943; ^{Maass 1997}). Es este contexto, cada variable σ _n representa el estado de activación de una neurona, adquiriendo el valor +1 si la neurona está activa 0 -1 si la neurona está inactiva. La neurona σ _n recibe impulsos eléctricos de otras k _n neuronas con las que está conectada (el conjunto σ1n, σ2n, …, σknn), y si la corriente total recibida es mayor que un cierto umbral, la neurona σ _n se activará, de lo contrario, permanecerá inactiva. En este caso, los pesos w _nm serían las intensidades de las conexiones sinápticas entre las neuronas, y pueden ser positivos o negativos dependiendo de si la conexión sináptica es activadora o inhibitoria, respectivamente. El parámetro σ determinaría en este caso la fracción de conexiones activadoras versus las inhibitorias, por lo que en este caso se llamaría parámetro de activación. Por otro lado, el parámetro q determina la probabilidad de que una neurona no se active a pesar de que recibe una señal eléctrica que en principio debería activarla. Esto ocurre porque hay fluctuaciones aleatorias en el potencial eléctrico de la membrana de la célula, por lo cual podría ocurrir que la neurona se active cuando no debería activarse y viceversa.

Aun cuando el modelo de McCulloch-Pitts es muy sencillo, contiene muchos aspectos que sí se observan en la dinámica neuronal. En particular, es de interés preguntarse si en el cerebro existe algo parecido a la transición de fase orden desorden de la que hemos estado hablando, lo cual nos lleva a la siguiente sección.

Leyes de escalamiento y criticalidad en la dinámica neuronal

Es generalmente conocido y aceptado que el cerebro tiene una estructura funcional modular, de tal manera que regiones distintas del cerebro se encargan de diferentes tareas (^{Nicolini y Bifone 2016}; ^{Russo, Herrmann y de Arcangelis 2014}). Actualmente, la técnica de Imagen por Resonancia Magnética Funcional (FMRI, por sus siglas en inglés) permite ver en tiempo real las diferentes regiones del cerebro que se activan cuando realizamos diferentes tareas. La Figura 8 muestra un ejemplo de este tipo de imágenes, obtenidas de una persona a la que se le puso en un simulador de manejo bajo diferentes condiciones (^{Schweizer et al. 2013}). Se puede ver como se activan regiones distintas dependiendo de si la persona manejaba en línea recta sin distracciones, o cuando tenía que dar una vuelta hacia la derecha o hacia la izquierda con y sin tráfico, con y sin música, etc. Estas regiones miden algunos cuantos centímetros y se activan o desactivan casi instantáneamente cuando la persona cambia de actividad. Hasta aquí todo parece normal y consistente con la estructura modular del cerebro. Sin embargo, cuando consideramos que cada centímetro cúbico de tejido cerebral contiene aproximadamente 60 millones de neuronas (^{Witelson, Glezer y Kigar 1995}; ^{Azevedo et al. 2009}), cabe preguntarse con asombro cómo le hacen los cientos de millones de neuronas contenidas en cada una de esas regiones cerebrales, para activarse o desactivarse casi instantáneamente y de forma simultánea ante diferentes estímulos. Cada una de estas regiones es como un árbol de navidad en el que las luces se prenden y apagan de forma sincronizada al recibir diferentes estímulos. La diferencia con el árbol de navidad es que cada una de estas regiones contiene, como ya hemos dicho, cientos de millones de “foquitos”. Claramente, dentro de estas regiones cuyo tamaño va desde 1 cm hasta 15 cm, las neuronas están fuertemente correlacionadas. Aunque 1 cm no parece ser una longitud muy grande para nosotros, desde el punto de vista de una neurona, cuyo tamaño típico es de 2 × 10^-3 cm, estas regiones correlacionadas son enormes. Para tener una idea más concreta, si nos hiciéramos del tamaño de una neurona, una distancia de 1 cm equivaldría aproximadamente a 1 Km. Es enorme. Además, la densidad neuronal también es muy grande, pues sería equivalente a tener a todos los habitantes de México (que son como 120 millones) viviendo en una ciudad pequeña como Morelia. ¡Y todas estas neuronas están correlacionadas!

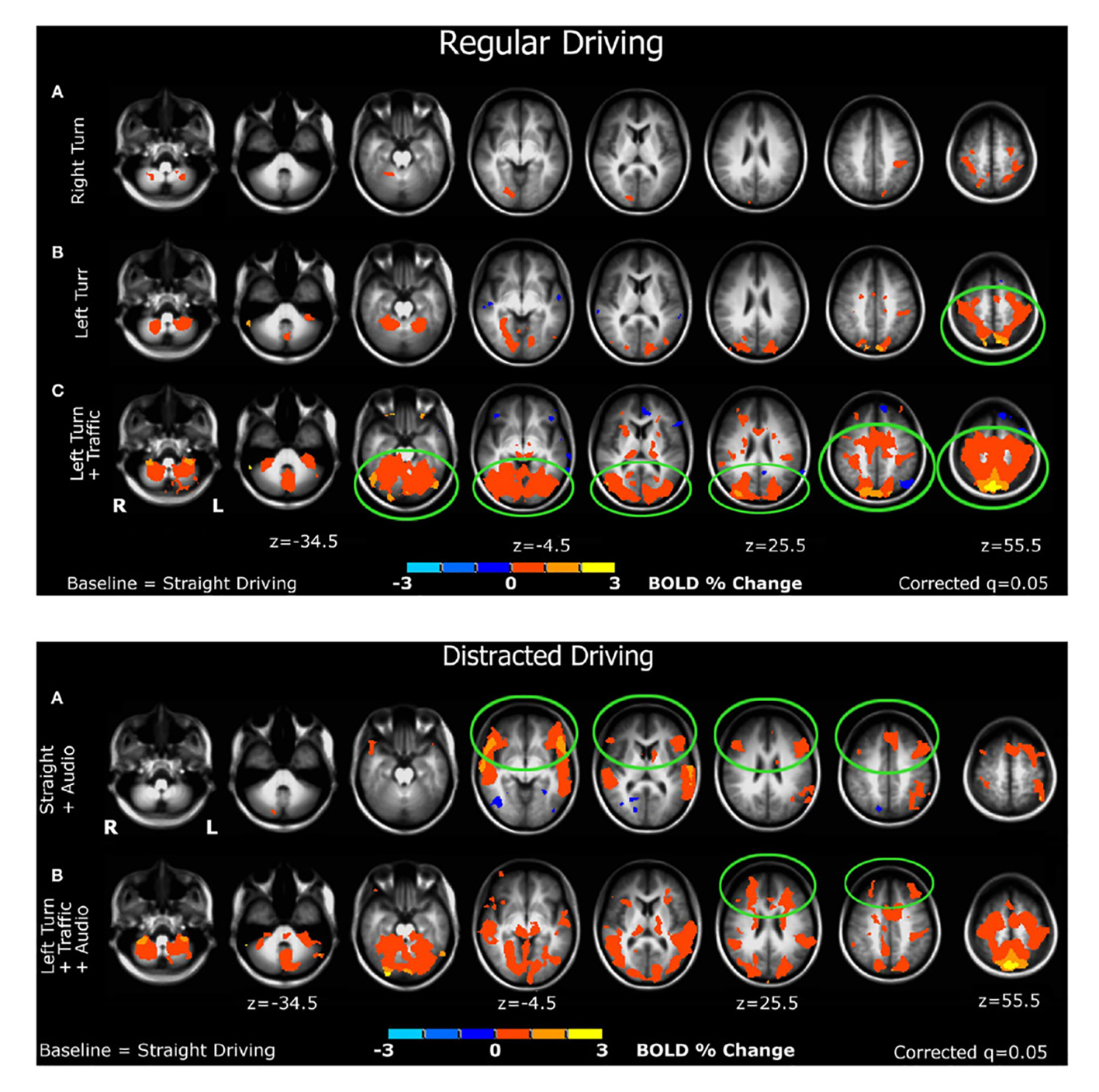
Fuente: Tomada y adaptada de ^{Schweizer et al. (2013)}.

Figura 8 Imágenes de resonancia magnética funcional que muestran diferentes regiones del cerebro activándose o desactivándose conforme una persona en un simulador de manejo cambia de actividad. 

¿Qué mecanismos dinámicos existen que puedan generar correlaciones entre neuronas a tan grandes distancias? No muchos. De hecho, nosotros conocemos solo dos: (i) la topología de mundo pequeño (^{Strogatz 2001}), y, (ii) las dinámicas críticas que, como vimos antes, generan correlaciones de muy largo alcance. Se sabe que ambos mecanismos están presentes en el cerebro, pero aquí discutiremos solamente la evidencia que muestra la existencia de dinámicas críticas en la actividad neuronal.

Uno de los principales promotores de la hipótesis de que el cerebro opera en punto crítico ha sido el Dr. Dante Chialvo, precisamente porque las correlaciones que se miden entre las diferentes regiones cerebrales son compatibles con lo que uno esperaría obtener en dinámicas críticas (^{Chialvo 2004}, ²⁰⁰⁷ y ²⁰¹⁰). Las primeras observaciones experimentales que confirman la hipótesis del cerebro operando en punto crítico las llevó a cabo el Dr. Dietmar Plenz y su grupo, al medir las avalanchas de actividad en tejido neuronal de rata (^{Beggs y Plenz 2003}; ^{Plenz y Thiagarajan 2007}). Para esto, tomaron rebanadas muy delgadas de la corteza cerebral de la rata y las mantuvieron vivas en cajas de Petri. Para medir la actividad neuronal espontánea del tejido neuronal colocaron numerosos electrodos a lo largo de la rebanada. La actividad registrada es “espontánea” en el sentido de que la rebanada de cerebro, al estar completamente desconectada de cualquier órgano sensorial, no recibía estímulos externos. Era simplemente la actividad espontánea de las neuronas, que de forma aleatoria se activan, la que se registró en los experimentos de Plenz. Cuando una neurona espontáneamente se activa, envía una señal eléctrica a las neuronas que están conectadas con ella, las cuales pueden a su vez activarse mandando señales eléctricas a otras neuronas a las que están conectadas, y así sucesivamente. Por lo tanto, la activación espontánea de una neurona puede (o no) generar una avalancha de activación, cuyo tamaño se mide en términos del número de neuronas que se activaron durante la avalancha. Con los electrodos se midió la distribución del tamaño de las avalanchas, obteniéndose los resultados que se muestran en la Figura 9a. Sorprendentemente, se obtuvo que la probabilidad P(s) de que ocurra una avalancha de tamaño s obedece una ley de escalamiento: P(s) ≈ s ^-3/2, lo cual es consistente con dinámicas críticas. Sin embargo, para corroborar que efectivamente esta ley de potencias es resultado de dinámicas en punto crítico, fue necesario sacar al sistema del punto crítico y medir las avalanchas en las fases ordenada y desordenada. Pero, ¿cuál es el parámetro que pone al sistema en punto crítico?

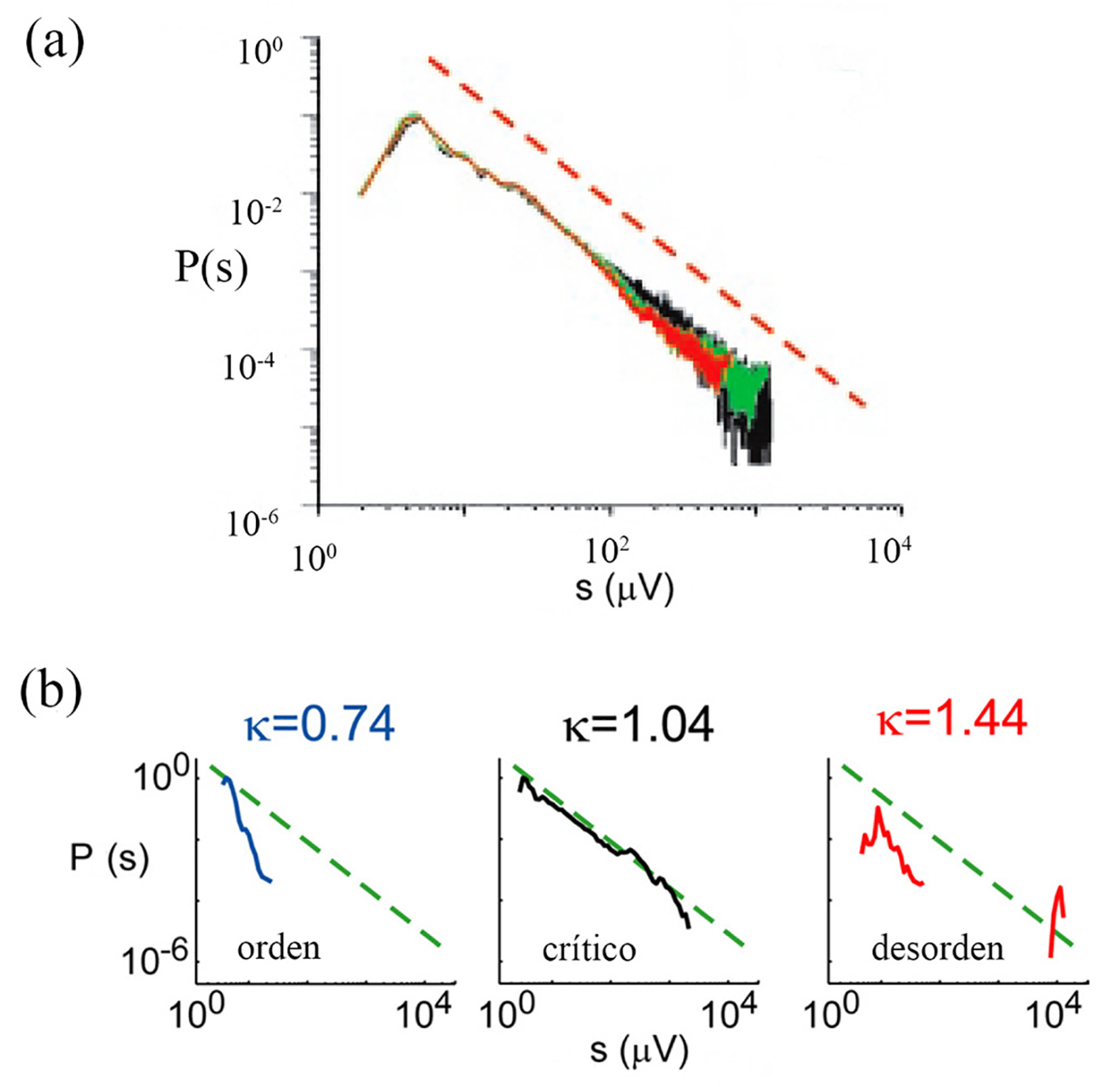
Notas: (a) En tejido neuronal normal, la distribución de avalanchas obedece a una ley de potencias P(s) = Cs ^-1.5. Las diferentes curvas corresponden a diferentes cultivos del tejido neuronal (la curva punteada es una guía que muestra la ley de potencias exacta). (b) Cuando se bloquean los receptores de glutamato o de ácido γ-aminobutírico se puede cambiar la fracción de conexiones sinápticas activadoras versus inhibidoras, llevando así al sistema neuronal a la fase ordenada o a la fase desordenada. El parámetro κ es una medida de qué tan alejada está la dinámica del punto crítico, con κ < 1 correspondiendo a hipo-activación (fase ordenada), mientras que κ > 1 corresponde a hiper-activación (fase desordenada). El punto crítico se tiene para κ = 1. Como puede verse, en la fase ordenada las avalanchas son muy pequeñas, mientras que en la fase desordenada hay avalanchas muy grandes (nótese el pico arriba de s ≈ 10⁴. Solo el tejido neuronal “normal” (sin ningún tipo de bloqueador, lo que en los experimentos corresponde a κ = 1.04) está en punto crítico, pues la distribución de avalanchas obedece una ley de potencias.

Fuente: Estas gráficas fueron tomadas y adaptadas de las referencias ^{Beggs y Plenz (2003)}; ^{Shew, Yang, Yu, Roy y Plenz (2011)}.

Figura 9 Distribución del tamaño de las avalanchas de actividad eléctrica espontánea en tejido neuronal de la corteza cerebral de rata.  

Estudiando un modelo teórico de red neuronal, en 1999, Vreeswijk y Sompolinsky mostraron que la proporción entre activación e inhibición en las conexiones neuronales puede cambiar drásticamente la dinámica de la red, llevándola de dinámicas ordenadas a dinámicas caóticas al variar dicha proporción (^{van Vreeswijk y Sompolinsky 1996}). Trabajos posteriores han mostrado que el balance entre excitación e inhibición en los circuitos neuronales puede, efectivamente, cambiar el estado dinámico de la red neuronal, llegándose incluso a correlacionar con disfunciones mentales y motoras (^{Yizhar et al. 2011}; ^{Atallah y Scanziani 2009}). Estas observaciones son consistentes con lo que mostramos anteriormente para el modelo de votantes, que al variar el parámetro de activación (o de influencia) α, uno puede hacer que la red pase de la fase ordenada a la fase desordenada. Tomando esto en cuenta, Plenz y su grupo cambiaron experimentalmente la proporción entre las conexiones sinápticas activadoras y las inhibidoras simplemente bañando el tejido neuronal con soluciones que contenían moléculas antagonistas de los receptores de glutamato en el primer caso, y de ácido γ-aminobutírico (GABA) en el segundo caso. De esta forma, variaron el parámetro de activación α que determina la proporción de conexiones activadoras versus inhibidoras (^{Shew et al. 2011}). Los resultados se muestran en la Figura 9b, de donde se observa que solo para el tejido normal (es decir, sin antagonistas de ninguna especie) las avalanchas de actividad espontánea siguen una la ley de potencias P(s) ≈ s ^-3/2, mientras que para el tejido alterado con antagonistas, ya sea que promuevan más o menos activación de lo normal, las avalanchas definitivamente no siguen una ley de potencias, pues son generalmente muy pequeñas o muy grandes.

Estos resultados, aunque no constituyen una demostración definitiva, sí sugieren fuertemente que el cerebro opera de forma natural con dinámicas en punto crítico, lo cual permitiría entender cómo es que se generan correlaciones entre grupos tan grandes de neuronas. Además, hay evidencia de que alteraciones en el balance activación/inhibición entre las conexiones neuronales, respecto a lo que se observa en un cerebro “sano”, están asociadas con desórdenes mentales y cognitivos como la esquizofrenia, el autismo o la esclerosis múltiple (^{Rubenstein y Merzenich 2003}; ^{Dickinson, Jones y Milne 2016}; ^{Lewis, Hashimoto y Volk 2005}; ^{Kehrer 2008}; ^{Yizhar et al. 2011}; ^{Manson et al. 2008}). Pareciera que a lo largo de la evolución esta fracción entre activación e inhibición en las conexiones sinápticas se fue ajustando para poner la dinámica cerebral en punto crítico, y alteraciones que sacan al cerebro de la criticalidad generan desórdenes graves.

Aparte de las correlaciones de largo alcance que se forman en punto crítico y que hacen posible que grupos muy grandes de neuronas se sincronicen, existen otras consecuencias cognitivas de la criticalidad en el cerebro. Una de ellas es la enorme capacidad que tiene el cerebro para distinguir entre diferentes estímulos auditivos, visuales y sensoriales que ocurren en rangos muy amplios de intensidad. Por ejemplo, somos capaces de distinguir estímulos visuales muy débiles (un objeto negro sobre una mesa negra en un cuarto oscuro por el que apenas entra la luz de la luna por la ventana), o bien muy intensos (un conejo blanco sobre un paisaje nevado en un día soleado). El intervalo de intensidades de un estímulo dado en el que dicho estímulo puede distinguirse sin ambigüedad se conoce como rango dinámico. El ojo junto con el cerebro forman un sistema con un rango dinámico muy amplio que ningún sensor de cámara fotográfica ha podido alcanzar hasta la fecha. Es por esto que muchas veces nos decepcionamos al ver las fotografías que tomamos de paisajes que nosotros recordamos como hermosos, coloridos y llenos de contrastes, pues dicha riqueza visual no aparece en las fotografías. Muy frecuentemente en las fotografías el cielo se ve blanco, o el follaje casi negro, o los paisajes nevados aparecen como manchas blancas sin estructura, o una persona frente a una ventana aparece como una silueta negra. Esto es porque el rango dinámico del sensor de la cámara es comparativamente pequeño y no alcanza a distinguir diferentes tonos de grises claros, o diferentes tonos de grises oscuros. ¿Cómo es posible que el cerebro tenga un rango dinámico tan amplio?

En un trabajo pionero, Kinouchi y Copelli analizaron la dinámica de un modelo de red neuronal en el que las neuronas, además de tener actividad espontánea, también se activan debido a la presencia de un estímulo externo (^{Kinouchi y Copelli 2006}; ^{Gollo, Kinouchi, y Copelli 2009}). En dicho modelo el parámetro de control σ es el número promedio de neuronas que una neurona activada a su vez puede activar en ausencia del estímulo externo (cuando se aplica el estímulo, las neuronas pueden prenderse no de forma espontánea, sino precisamente por la influencia del estímulo; por lo tanto, la definición del parámetro de control σ se hace tomando en cuenta solo la actividad espontánea de las neuronas, sin introducir el estímulo externo). Así, por ejemplo, si una neurona que está activa a su vez puede activar en promedio a otra única neurona, entonces σ = 1; si una neurona activada a su vez activa en promedio a otras dos neuronas, entonces σ = 2, y así sucesivamente. Variando este parámetro, al que se le denomina parámetro de ramificación (o branching ratio) se puede hacer que la red transite de una fase en la que toda su actividad espontánea se extingue después de un cierto tiempo (lo cual corresponde a σ < 1), a otra fase en la que la red nunca deja de tener actividad espontánea (lo que ocurre para σ > 1). Justo cuando σ = 1, es decir, cuando cada neurona activada es capaz de activar en promedio a otra única neurona se tiene el comportamiento crítico en donde la red está al borde de apagarse pero no se apaga (o bien, tarda mucho en apagarse). De hecho, si medimos la probabilidad P(τ) de que la actividad espontánea de la red dure un tiempo τ antes de apagarse completamente (en ausencia del estímulo externo), resulta que para σ < 1 se tiene P(τ) = Ae ^-ατ (un decaimiento exponencial), mientras que cuando σ = 1 se tiene P(τ) = Cτ  ^-γ (una ley de potencias). La Figura 10a muestra la fracción F ₀ de neuronas que se mantienen activas de forma espontánea como función del tiempo para tres valores del parámetro de ramificación σ. En esta Figura se pueden observar las tres fases, una de actividad espontánea corta que se obtiene para σ < 1; otra de actividad espontánea infinita que surge para σ > 1, y, un punto crítico de transición entre ellas que ocurre justo cuando σ = 1.

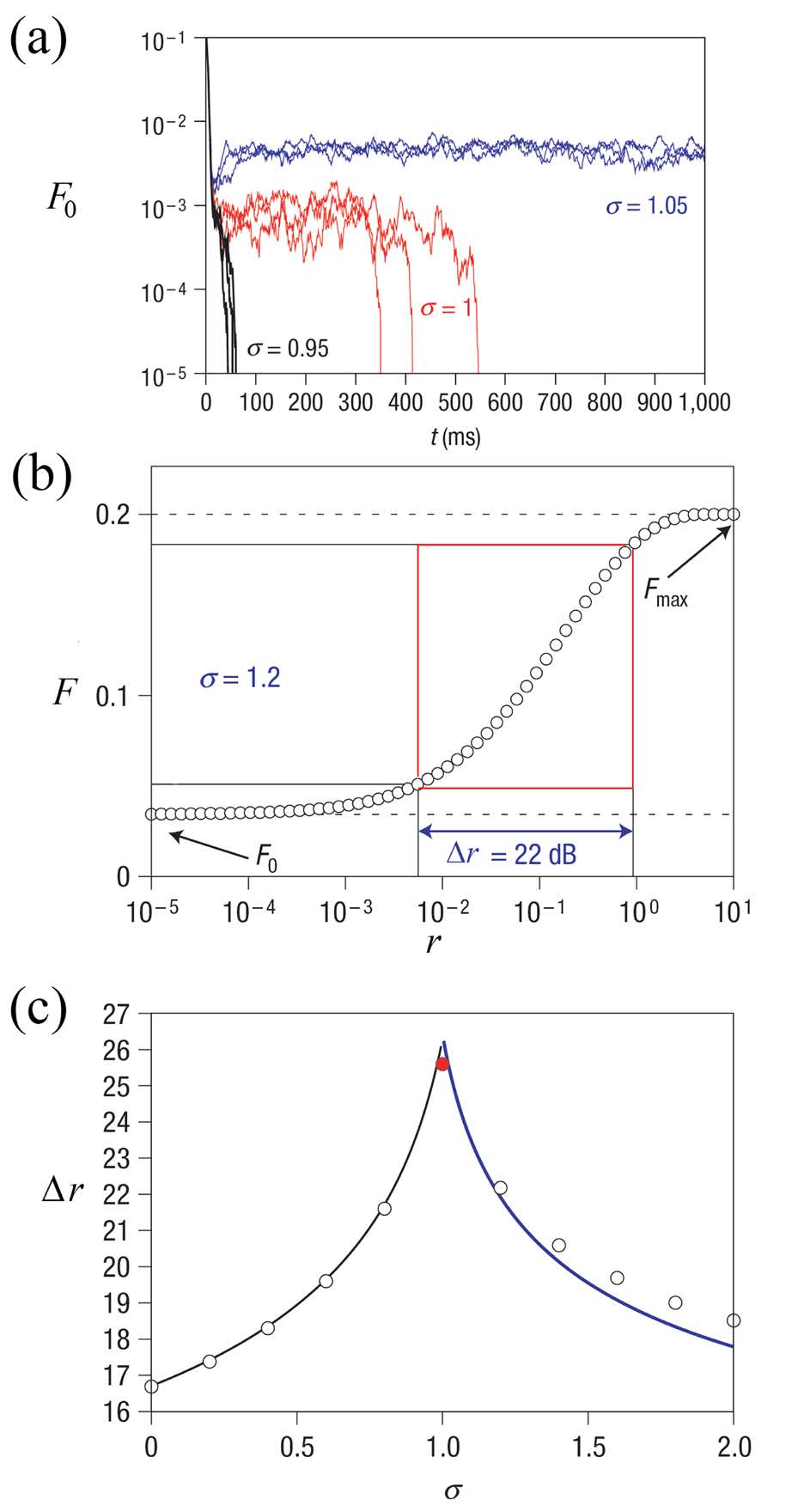
Nota: En el modelo de Kinouchi-Copelli de red neuronal, las neuronas además de tener actividad espontánea, pueden activarse debido a la presencia de un estímulo externo de intensidad r. (a) Fracción F ₀ de neuronas espontáneamente activas como función del tiempo en las tres diferentes regiones dinámicas: subcrítica (σ < 1), crítica (σ = 1) y supercrítica (σ > 1). (b) Fracción F de neuronas activas como función de la intensidad r del estímulo para una red operando en régimen supercrítico. El recuadro rojo muestra el intervalo donde la red responde al estímulo sin saturarse, lo cual define el rango dinámico ∆r. (c) Gráfica del rango dinámico en función del parámetro de orden σ. Nótese que el rango dinámico alcanza su máximo valor justo en el punto crítico σ = 1.

Fuente: Estar gráficas fueron tomadas y adaptadas de ^{Kinouchi y Copelli (2006)}.

Figura 10 Modelo de Kinouchi-Copelli de red neuronal.  

Al aplicar el estímulo externo se van a prender más neuronas de las que se hubieran prendido de forma espontánea. Por lo tanto, si denotamos como F a la fracción de neuronas prendidas en presencia del estímulo externo, y como F ₀ a la fracción de neuronas que se hubieran prendido espontáneamente en ausencia de dicho estímulo, la diferencia ∆F = (F - F ₀) es una medida de qué tanto responde la red al estímulo. En la Figura 10b se muestra una gráfica típica de F como función de la intensidad r del estímulo. Como puede verse, para intensidades bajas F se mantiene prácticamente constante e igual a F ₀, mientras que para intensidades altas F se satura alcanzando un valor máximo F _max y ya no cambia a pesar de que sigamos aumentando la intensidad r del estímulo. El rango dinámico ∆r es justamente la región de intensidades en las cuales F no permanece constante, sino que cambia apreciablemente al cambiar la intensidad del estímulo. La región que define el rango dinámico se indica con un recuadro rojo en la Figura 10b.

El resultado importante del trabajo de Kinouchi y Copelli es haber demostrado que el rango dinámico de la red alcanza un valor máximo justo en el punto crítico σ = 1, como se ilustra en la Figura 10c. Es decir, que es justo en el punto crítico en donde la red tiene la capacidad de distinguir más eficientemente entre estímulos de diferentes intensidades, tanto los muy tenues como los muy intensos. Esto sugiere que el enorme rango dinámico del cerebro, tanto para percibir estímulos auditivos como visuales, puede deberse a que está operando en punto crítico.

Conclusiones

Probablemente la propiedad más importante de los puntos críticos es que generan leyes de escalamiento en la función de correlación. Esto hace que grupos muy grandes de elementos puedan estar correlacionados y responder de forma colectiva a perturbaciones o estímulos externos. Una ley de escalamiento entraña una propiedad de auto similitud en la que todo el sistema se parece a cada una de sus partes, y esto es cierto en particular para las funciones de correlación. Por lo tanto, en los puntos críticos emergen correlaciones en grupos de todos los tamaños, desde los muy pequeños hasta los muy grandes, lo cual queda de manifiesto en el panel central de la Figura 6 correspondiente al punto crítico, donde pueden apreciarse dominios pequeños que van desde casi un “pixel” aislado hasta dominios que atraviesan todo el sistema de un lado al otro. Por lo tanto, en los puntos críticos el sistema puede montar respuestas a perturbaciones externas que pueden ser pequeñas, medianas o grandes. En el contexto de la dinámica neuronal, esta capacidad de respuesta a diferentes escalas es de la mayor importancia, debido a que el cerebro está constantemente recibiendo estímulos sensoriales procedentes de muy diversas fuentes y en rangos de intensidades muy amplios. Gracias a que está operando en punto crítico, el cerebro puede montar respuestas colectivas, es decir, en las que participan decenas o centenas de millones de neuronas, a todos estos estímulos sin saturarse. El cerebro es un sistema complejo⁶ que ha evolucionado interaccionando con un entorno que también es complejo. Aparentemente esta evolución ha puesto al cerebro en punto crítico precisamente para que pueda responder a los estímulos provenientes de un entorno complejo. Interesantemente, se ha demostrado que la evolución de un sistema que tiene que aprender tareas nuevas sin olvidar las tareas ya aprendidas con anterioridad lo conducen directamente a dinámicas críticas (^{Torres-Sosa, Huang y Aldana 2012}).

Sin embargo, no todas las leyes de escalamiento son generadas por puntos críticos. Como se mencionó en la introducción, otro mecanismo importante de generación de leyes de escalamiento es el enlace preferencial. Este mecanismo consiste, esencialmente, en que en una red que está creciendo los nuevos nodos que se incorporan a la red eligen preferentemente a los nodos más conectados para conectarse. Por ejemplo, cuando se es estudiante, muy probablemente uno quiera hacer la tesis con el investigador más reconocido en el área que nos interesa, lo cual aumenta aún más el reconocimiento de dicho investigador (al incrementar su número de estudiantes graduados). Así, la red de colaboraciones científicas va creciendo de acuerdo con una ley de potencias respecto al número de colaboraciones de cada investigador, en donde los investigadores más reconocidos son también los más conectados (^{Albert y Barabási 2002}). La existencia de leyes de escalamiento en redes sociales, como por ejemplo las redes de formación de opinión, no necesariamente significa que dichas redes estén operando en punto crítico. Sin embargo, cabe preguntarse si la sociedad en su conjunto está en punto crítico, es decir, al borde de una transición entre orden desorden. No lo sabemos. No obstante, hay evidencia de que las redes sociales están en la fase ordenada respecto a la dinámica de formación de opiniones, pero las fluctuaciones alrededor de esta fase ordenada (es decir, los cambios de opinión) exhiben dinámicas críticas (^{Moussaïd et al. 2013}).

La gran moraleja de las leyes de escalamiento, ya sean generadas por puntos críticos o no, es que los sistemas que las presentan tienen respuestas colectivas a perturbaciones externas y estructuras internas que están lejos de lo que se esperaría por puras interacciones aleatorias. Por eso son importantes.