Introducción
La elaboración de horarios de actividades es un problema que se presenta en diversos ámbitos, en especial en las instituciones educativas, su complejidad radica en el gran número de combinaciones de horarios que se pueden presentar, y seleccionar el mejor o encontrar una buena solución en un tiempo razonable, que cumpla con las necesidades de la institución, es una tarea que consume una gran cantidad de tiempo, aún para problemas con unas cuantas materias, aulas y profesores.
En la literatura existente sobre la asignación de horarios en las universidades se han reportado diferentes enfoques de solución a través del uso de modelado matemático, destacando principalmente la búsqueda de buenas soluciones en tiempos cortos a través de diferentes métodos, o bien, la utilización de técnicas exactas en la búsqueda de una solución óptima.
La elaboración de un horario universitario se clasifica como un problema NP-duro debido al gran número de combinaciones presentes, ocasionando que el tiempo en la búsqueda de una solución se incremente drásticamente (Bardadym, 1996; Even, Itai y Shamir, 1976). Por lo anterior es necesario un tratamiento que reduzca el espacio de soluciones.
Una estrategia para acotar el espacio de búsqueda es la elaboración del horario escolar por etapas, la cual se ha implementado con éxito en otros casos de estudio reportados en la literatura. Se debe señalar que, bajo este enfoque de solución, se han utilizado como máximo dos etapas para resolver el problema.
En la mayoría de los estudios presentados en la literatura concernientes a la construcción de horarios universitarios, no se considera la asignación de profesores, o bien, pareciera no ser un problema para algunas universidades en el mundo; en este trabajo sí se toma en cuenta dicha asignación, esto tiene su origen en los nuevos lineamientos que solicitan, por un lado, aprovechar al máximo la plantilla de profesores de tiempo permanente en la institución, y por otro, los recortes de presupuesto que limitan la contratación de nuevo personal docente.
Este artículo presenta como principal aportación una estrategia para elaborar un horario universitario en tres etapas a través de la descomposición del problema original en tres modelos matemáticos, usando variables binarias de dos índices, a diferencia de otros estudios donde se pretende resolver el problema con uno o dos modelos matemáticos. Otra contribución es el desarrollo de un método heurístico para definir los coeficientes en la función objetivo de la etapa I, éste elimina la necesidad de plantear restricciones relacionadas con intervalos de tiempo sucesivos en el modelo matemático. Además, a diferencia de otros artículos, donde sólo se limitan a mencionar que se cumple con las restricciones del problema, en éste se muestran gráficamente las bondades de generar el horario universitario con la estrategia implementada.
El artículo se encuentra organizado de la siguiente manera: primero, se lleva a cabo una revisión de la literatura de los artículos relacionados con la problemática analizada; además, se mencionan las características más importantes a considerar en la elaboración de horarios universitarios; más adelante, se describe el problema del caso de estudio; posteriormente, se desglosa paso a paso la metodología implementada en la búsqueda de una solución y aparecen los modelos matemáticos desarrollados en cada etapa; enseguida, se muestra la experimentación, así como los resultados alcanzados en el cumplimiento de objetivos y el análisis computacional en problemas de gran tamaño; por último, se declaran las conclusiones de la investigación realizada.
Revisión de la literatura
A lo largo del tiempo se han reportado diferentes enfoques de solución en la elaboración de horarios escolares. Los primeros trabajos corresponden a modelos de asignación (Appleby, Blake y Newman, 1961; Csima y Gotlieb, 1964) y la técnica de coloreo de grafos (De Werra, 1985; De Werra, Asratian y Durand, 2002; Welsh y Powell, 1967).
En otra vertiente, diversos autores han optado por el empleo de programación matemática en la búsqueda de una solución óptima, destacando lo realizado por Lawrie (1969), quien comienza catalogando a los grupos de estudiantes en lo que él llama layouts, para luego utilizar Programación Entera (PE) en la elaboración del horario escolar. Además, Tripathy (1984) emplea Programación Entera Binaria (PEB) y relajación lagrangiana en la búsqueda de una solución.
Más adelante, Daskalaki, Birbas y Housos (2004) desarrollan un modelo matemático usando variables binarias y subconjuntos en la planeación de un horario universitario. Luego, Schimmelpfeng y Helber (2007) generan un modelo basado en Programación Entera Mixta (PEM) para asignar materias universitarias. Después, Bakir y Aksop (2008) intentan programar el horario de una universidad a través de PEB, sin embargo, no encuentran una solución óptima al problema. Por su parte, Kristiansen, Sørensen, y Stidsen (2015) obtienen los horarios en escuelas preparatorias a través de PEM y el formato XHSTT. Además, Lindahl y Mason (2016) desarrollan un modelo multiobjetivo tomando en cuenta PEM, para asignar materias en aulas de una universidad. Recientemente, Sánchez-Partida et al. (2017) emplean Mediation Software para organizar las materias de acuerdo con las necesidades de una institución universitaria y utilizan un modelo de PEB para generar el horario.
En años recientes se han empleado otras estrategias que han permitido alcanzar soluciones de buena calidad en menor tiempo, a problemas de gran tamaño. Entre éstas destacan el uso de métodos de búsqueda local (Demirović y Musliu, 2017; Goh, Kendall y Sabar, 2017; Saviniec, Santos y Costa, 2017; Savienic Santos y Costa, 2018; Song et al., 2018), las técnicas metaheurísticas de búsqueda tabú (Goh et al., 2017; Lü y Hao, 2010; Saviniec et al., 2018) y algoritmos genéticos (Beligiannis, Moschopoulos y Likothanassis, 2009; Feng, Lee y Moon, 2017; Junn, Obit y Alfred, 2018; Khonggamnerd e Innet, 2009); soluciones basadas en mínima perturbación (Barták, Müller y Rudová, 2003; Lindahl, Stidsen y Sørensen, 2019; Phillips et al., 2017), hyper-heurísticas (Ahmed, Özcan y Kheiri, 2015; Junn et al., 2019) y el algoritmo de Late Acceptance Hill-Climbing (Fonseca, Santos y Carrano, 2016).
En otro enfoque de solución, autores han optado por elaborar el horario escolar por etapas, lo que ha permitido disminuir en gran medida el número de variables empleadas en el modelado matemático, agilizándose la búsqueda de la solución. Birbas, Daskalaki y Housos (2009) resuelven un problema de horarios de una escuela preparatoria a través de dos etapas, haciendo uso de modelos basados en PEB: en la primera asignan turnos de trabajo a profesores con base en sus preferencias y en la segunda se define el horario escolar. Por su parte, Sørensen y Dahms (2014) emplean una estrategia similar considerando modelos de PEM; asignan inicialmente materias a intervalos de tiempo, luego definen las aulas para cada materia.
Lindahl, Sørensen y Stidsen (2018) proponen una heurística matemática para resolver problemas de horarios universitarios con modelos de PEM a través de dos etapas; en la primera establecen a cada materia un intervalo de tiempo, en la segunda a cada materia se le asigna un aula. Por último, Yasari et al. (2019) implementan dos etapas para elaborar un horario universitario, por medio de modelos de programación estocástica y considerando las probabilidades de apertura de materias.
Existen dos líneas de investigación sobre los problemas de programación de horarios universitarios: en la primera se proponen estrategias de solución para casos particulares de universidades, departamentos o facultades (ver Tabla 1); por otro lado, la segunda se enfoca en desarrollar algoritmos que satisfagan los requisitos establecidos por la International Timetabling Competition 2007 (ITC) en el congreso internacional del Practice and Theory of Automated Timetabling (PATAT), para demostrar la potencia de éstos en la búsqueda y calidad de soluciones generadas, tomando en cuenta bases de datos definidas, sin resolver la problemática de una institución educativa en particular. El presente trabajo sigue la primera línea.
Tabla 1 Artículos consultados en la programación de horarios universitarios
| Autor | Aspectos considerados | Metodología | Modelos matemáticos | Caso de estudio | País | Facultad o departamento | |||
|---|---|---|---|---|---|---|---|---|---|
| Estudiante | Materia | Aula | Profesor | ||||||
| Daskalaki et al. (2004) | * | * | * | * | PEB | 1 | Universidad de Patras | Grecia | Ingeniería eléctrica |
| Schimmelpfeng y Helber (2007) | * | * | * | * | PEM | 1 | Universidad de Hannover | Alemania | Economía |
| Bakir y Aksop (2008) | * | * | * | * | PEB | 1 | Universidad de Gazi | Turquía | Estadística |
| Khonggamnerd y Innet (2009) | * | * | * | Algoritmo genético | 1 | Universidad de la Cámara del Comercio | Tailandia | Ingeniería | |
| Lindahl y Mason (2016) | * | * | * | PEM | 1 | Universidad de Udine | Italia | -------- | |
| Feng et al. (2017) | * | * | * | Algoritmo genético hibrido y PEM | 1 | Universidad de Corea del Sur | Corea del Sur | -------- | |
| Goh et al. (2017) | * | * | * | Búsqueda local y búsqueda tabú | 1 | Bases de datos del *ITC2007 | -------- | -------- | |
| Phillips et al. (2017) | * | * | * | Mínima perturbación y PEB | 1 | Universidad de Auckland | Nueva Zelanda | -------- | |
| Sánchez-Partida et al. (2017) | * | * | * | PEB | 1 | Universidad UPAEP | México | Medicina y biología | |
| Junn et al. (2018) | * | * | * | Algoritmo genético | 1 | Universidad UMSLIC | Malasia | -------- | |
| Lindahl et al. (2018) | * | * | * | Dos etapas, heurística matemática y PEM | 2 | Bases de datos del *ITC2007 | -------- | ------- | |
| Song et al. (2018) | * | * | * | Búsqueda local | 1 | Bases de datos del *ITC2007 | -------- | ------- | |
| Junn et al. (2019) | * | * | * | Hyper-heurística | 1 | Universidad UMSLIC | Malasia | -------- | |
| Lindahl et al. (2019) | * | * | * | Mínima perturbación y PEM | 1 | Bases de datos del *ITC2007 | -------- | ------- | |
| Yasari et al. (2019) | * | * | * | Dos etapas y modelos de programación estocástica | 2 | Universidad Ferdowsi de Mashhad | Irán | ------- | |
| Estudio presentado | * | * | * | * | Tres etapas y PEB | 3 | Tecnológico Nacional de México en Celaya | México | Ingeniería Industrial |
Fuente: elaboración propia.
La Tabla 1, muestra un resumen de los artículos consultados en la elaboración de horarios universitarios, en ella se observa que, en gran parte de éstos, no se considera la asignación de profesores, o bien, pareciera no ser un problema en algunas universidades. Dicha tabla también detalla la metodología empleada, el número de modelos matemáticos, el caso de estudio, así como el país de origen de la institución educativa y, en algunos casos, el departamento o facultad considerados.
Características de la programación de horarios universitarios
El problema de la elaboración de horarios en universidades consiste en programar las materias que se dictan en un periodo académico determinado (año, semestre o trimestre), considerando los profesores necesarios, los grupos de estudiantes, los días e intervalos de tiempo, las aulas o laboratorios, de tal manera que se satisfagan las restricciones establecidas por la institución educativa.
Estos problemas se pueden dividir en dos clases: horarios de materia y horarios de examen, los cuales están sujetos a una gran variedad de restricciones catalogadas como duras y suaves. Las restricciones duras se aplican estrictamente y no deben ser violadas, mientras que las restricciones suaves son aquéllas que son deseables, pero no absolutamente esenciales (Babaei, Karimpour y Hadidi, 2015; Burke et al., 1997).
Ejemplos de restricciones duras:
En cada intervalo de tiempo por aula, sólo un grupo de estudiantes y un profesor podrían asistir.
Un profesor o estudiante no puede asistir a dos clases al mismo tiempo.
La capacidad de las aulas no debe ser excedida por el número de estudiantes asignados en cada materia.
Ejemplos de restricciones suaves:
El profesor tiene la opción de sugerir prioridad de ciertos intervalos de tiempo para sus materias.
Un profesor puede solicitar un aula especial para una materia.
Las materias deben programarse de manera que los intervalos de tiempo vacíos, de los profesores y estudiantes, sean minimizados.
La programación de materias debe realizarse preferentemente en el turno de la mañana.
Descripción del problema en el caso de estudio
Para la generación del horario escolar se tomó como caso de estudio el Tecnológico Nacional de México en Celaya, Guanajuato. Esta universidad brinda 10 licenciaturas en distintas áreas de ingeniería y oferta un promedio de 1 000 materias cada semestre. En la elaboración del horario universitario participan 18 personas cuyo criterio es la asignación a prueba y error de los recursos, con un tiempo estimado para su elaboración de un mes.
La generación del horario comienza con los coordinadores de cada licenciatura, los cuales asignan a cada materia un intervalo de tiempo, posteriormente, el departamento de planeación escolar, asigna a cada materia un aula considerando la demanda de los estudiantes. Por último, un responsable de cada licenciatura establece los profesores encargados de impartir las materias.
Uno de los grandes problemas que se presenta con la forma actual de establecer el horario es la programación de materias de un mismo semestre y grupo a lo largo de todo el día; esto ocasiona que gran parte de los estudiantes asistan a la universidad por la mañana y por la tarde, teniendo un número considerable de horas libres en sus horarios de clase.
Por otro lado, al igual que la mayoría de los centros educativos públicos del nivel superior en México, esta institución enfrenta un reto importante cada semestre en la asignación de profesores, ya que en promedio sólo la mitad de ellos trabaja de forma permanente en la universidad, mientras que los demás son contratados temporalmente, por lo que no se garantiza tener el mismo personal docente en cada ciclo escolar.
Las restricciones y consideraciones que se toman en cuenta para elaborar el horario de clases son las siguientes:
Las materias se imparten de lunes a viernes en 14 intervalos de tiempo; siete correspondientes a los días lunes-martes-jueves, y siete a los días lunes-miércoles-viernes (ver Tabla 2).
Las materias tienen distintas horas de clase a la semana (cuatro, cinco o seis horas). Cuando éstas superan las cuatro horas, se utiliza el día lunes para impartir las horas restantes (ver Tabla 2).
Las materias que llevan el mismo nombre pero pertenecen a grupos diferentes, deberán ser asignadas preferentemente en intervalos de tiempo distintos, con la intención de que profesores titulares puedan impartirlas.
Las materias del mismo semestre y grupo deben ser asignadas en intervalos de tiempo distintos.
Se tiene un número limitado de aulas para cada licenciatura.
Se tiene como prioridad asignar las materias en los intervalos de tiempo de la mañana.
Existe una junta de academia para profesores permanentes en la universidad los días miércoles, lo que impide que éstos impartan clase en el intervalo de tiempo 11 (13:00 - 15:00 horas).
En un aula no se pueden asignar dos materias en el mismo intervalo de tiempo.
El número de estudiantes por materia no debe exceder la capacidad de las aulas.
Las materias deberán asignarse a los profesores afines. Existen tres categorías de profesores; titular de la materia, secundario (o segunda alternativa) y tercera alternativa.
Sólo se debe asignar un profesor por materia.
Las materias deben ser asignadas a los profesores de acuerdo al número de horas de su contrato temporal, o bien de su plaza (tiempo permanente).
Las materias sólo serán asignadas en los intervalos de tiempo que disponga cada profesor.
No deben existir empalmes de clases en las materias programadas a cada profesor.
Tabla 2 Intervalos de tiempo por turno
| Intervalo de tiempo | Turno | Lunes | Martes | Miércoles | Jueves | Viernes | ||
|---|---|---|---|---|---|---|---|---|
| Materias de 4 horas | Materias de 5 horas | Materias de 6 horas | ||||||
| 1 | Matutino | 8:00-9:00 | 7:00-9:00 | 7:00-9:00 | 7:00-9:00 | |||
| 2 | Matutino | 10:00-11:00 | 9:00-11:00 | 9:00-11:00 | 9:00-11:00 | |||
| 3 | Matutino | 12:00-13:00 | 11:00-13:00 | 11:00-13:00 | 11:00-13:00 | |||
| 4 | Matutino | 14:00-15:00 | 13:00-15:00 | 13:00-15:00 | 13:00-15:00 | |||
| 5 | Vespertino | 16:00-17:00 | 15:00-17:00 | 15:00-17:00 | 15:00-17:00 | |||
| 6 | Vespertino | 18:00-19:00 | 17:00-19:00 | 17:00-19:00 | 17:00-19:00 | |||
| 7 | Vespertino | 20:00-21:00 | 19:00-21:00 | 19:00-21:00 | 19:00-21:00 | |||
| 8 | Matutino | 7:00-8:00 | 7:00-9:00 | 7:00-9:00 | 7:00-9:00 | |||
| 9 | Matutino | 9:00-10:00 | 9:00-11:00 | 9:00-11:00 | 9:00-11:00 | |||
| 10 | Matutino | 11:00-12:00 | 11:00-13:00 | 11:00-13:00 | 11:00-13:00 | |||
| 11 | Vespertino | 13:00-14:00 | 13:00-15:00 | 13:00-15:00 | 13:00-15:00 | |||
| 12 | Vespertino | 15:00-16:00 | 15:00-17:00 | 15:00-17:00 | 15:00-17:00 | |||
| 13 | Vespertino | 17:00-18:00 | 17:00-19:00 | 17:00-19:00 | 17:00-19:00 | |||
| 14 | Vespertino | 19:00-20:00 | 19:00-21:00 | 19:00-21:00 | 19:00-21:00 | |||
Fuente: elaboración propia.
Actualmente no se tiene una división de horarios por turno, matutino y vespertino, la propuesta que se presenta en este estudio promueve trabajar de esta manera, con la finalidad de que los estudiantes no tengan horarios mixtos y disminuyan sus horas libres entre clases. Por tal motivo, se consideraron siete intervalos de tiempo para cada turno (ver Tabla 2).
Metodología: estrategia de asignación en tres etapas
El número de combinaciones de un modelo matemático con variables binarias es 2 n , donde n es la cantidad de variables. Para acotar el espacio de búsqueda se propuso como estrategia resolver el problema por etapas, como lo han hecho otros autores en la elaboración de horarios escolares (Birbas et al., 2009; Lindahl et al., 2018; Sørensen y Dahms, 2014; Yasari et al., 2019), lo que ha permitido disminuir el número de variables. El estudio de Sørensen y Dahms (2014), muestra los teoremas teóricos matemáticos que ilustran las ventajas de trabajar un problema binario por etapas, fundamentando las bondades de esta estrategia para su aplicación en otros casos de horarios escolares.
A diferencia de los estudios mencionados, donde se utilizó un máximo de dos etapas, la estrategia desarrollada consideró la elaboración de un horario universitario en tres etapas, usando variables binarias de dos índices, además de emplear una heurística en el establecimiento de coeficientes de la función objetivo en la etapa I.
Todo inició con el ordenamiento de la lista de materias a impartir, por semestre y grupo. Posteriormente, se implementó la estrategia que asigna a cada materia un intervalo de tiempo, un aula y un profesor de manera consecutiva, a través de tres modelos matemáticos (ver Figura 1).
La Tabla 3 muestra una comparativa entre plantear un modelo matemático para elaborar un horario universitario, como los estudios presentados en (Bakir y Aksop, 2008; Daskalaki et al., 2004; Sánchez-Partida et al., 2017; Schimmelpfeng y Helber, 2007) los cuales emplearon PE y técnicas exactas en la búsqueda de la solución, o bien, la propuesta elaborada en este artículo de utilizar tres modelos matemáticos, tomando en cuenta 126 materias, 14 intervalos de tiempo, 9 aulas y 21 profesores. Como se puede observar, cuando el modelado se descompone en tres etapas, el número de variables se reduce en un 98.34 % y sólo es necesario utilizar dos índices en cada variable, lo que simplifica en gran medida la complejidad del problema.
Tabla 3 Comparativa del número de variables binarias utilizadas, al elaborar el horario con uno y tres modelos matemáticos
| 1 Modelo Matemático | 3 Modelos matemáticos | ||||||
|---|---|---|---|---|---|---|---|
| Modelo 1 xijkl | Modelo 1 xij | Modelo 2 yik | Modelo 3 zil | ||||
| Variable binaria 4-índices | Variable binaria 2-índices | Variable binaria 2-índices | Variable binaria 2-índices | ||||
| i Materia | 126 | i Materia | 126 | i Materia | 126 | i Materia | 126 |
| j Intervalo de tiempo | 14 | j Intervalo de tiempo | 14 | k Aula | 9 | l Profesor | 21 |
| k Aula | 9 | Variables (i x j) | 1 764 | Variables (i x k) | 1 134 | Variables (i x l) | 2 646 |
| l Profesor | 21 | ||||||
| Total de variables binarias (i x j x k x l) 333 396 | Total de variables binarias 5 544 | ||||||
Fuente: elaboración propia.
Al igual que en Daskalaki et al. (2004) se utilizaron subconjuntos en cada uno de los modelos matemáticos, con la intención de separar materias por grupo e intervalo de tiempo, permitiendo que el modelado de ciertas restricciones fuera más fácil y disminuyera la iteración entre las variables. Además, se emplearon coeficientes en la función objetivo de manera intencional para agilizar la búsqueda en variables binarias.1
Etapa I: asignación de materia-intervalo de tiempo
En esta etapa, se asignan las materias a un intervalo de tiempo considerando las primeras siete restricciones mencionadas en la descripción del problema.
La construcción del modelo matemático toma como base subconjuntos que contienen siete materias de un mismo semestre y grupo, considerados en la carga académica de la retícula escolar. Una parte esencial en el desarrollo del modelo matemático es el establecimiento de coeficientes en la función objetivo αij de manera intencional con los propósitos de:
Saturar los intervalos de tiempo disponibles del turno matutino, antes de considerar la asignación de materias en el turno vespertino.
Asignar materias pertenecientes a un mismo semestre y grupo en intervalos de tiempos consecutivos. De esta manera se suprime la necesidad de plantear restricciones en el modelado matemático, a diferencia de los trabajos presentados en (Bakir y Aksop, 2008; Daskalaki et al., 2004; Feng et al., 2017; Phillips et al., 2017; Saviniec et al., 2018; Schimmelpfeng y Helber, 2007).
Asignar materias del mismo nombre, pero de distintos grupos en intervalos de tiempo diferentes, para que profesores titulares puedan impartirlos.
Disminuir la asignación de materias en el intervalo de tiempo 11, donde se tiene programada una junta de academia cada semana, que afecta la disponibilidad de profesores de tiempo permanente.
Método heurístico para definir los coeficientes en la función objetivo αij
Antes de establecer los coeficientes αij, se calcula el mínimo de aulas requeridas para la generación del horario, a través de la ecuación (1) redondeando al entero superior el valor obtenido:
Una vez definido éste, se establece el número de aulas disponibles físicamente para elaborar el horario, obviamente este número tiene que ser igual o mayor al cálculo que se realizó en la ecuación (1) para generar una solución factible, como se muestra en la desigualdad (2):
Posteriormente, se determina el número de subconjuntos de los grupos de materias que serán asignados en el turno matutino. Tomando en cuenta que las aulas tienen diferentes capacidades y las horas de clase de las materias son distintas, se propone establecer un número de aulas de tolerancia, con la intención de tener intervalos de tiempo disponibles cuando se tengan conflictos en la asignación de materia-aula; se recomienda iniciar con el valor de cero. En caso de no asignar todas las materias a un aula en la etapa II, se podrá modificar el número de aulas de tolerancia y se reiniciaría el proceso desde la etapa I. La ecuación (3) determina el número de subconjuntos del turno matutino:
Enseguida, se definen los coeficientes de la función objetivo αij para cada una de las materias, considerando los intervalos de tiempo por turno en el formato de la Tabla 4.
Tabla 4 Formato para el llenado de coeficientes de la función objetivo α ij
| Coeficientes de la función objetivo αij | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Número del subconjunto | Subconjunto | Materia | Intervalos de tiempo para el turno matutino | Intervalos de tiempo para el turno vespertino | ||||||||||||
| T1 | T2 | T3 | T4 | T8 | T9 | T10 | T11 | T5 | T6 | T7 | T12 | T13 | T14 | |||
| w | Im | 1 | C11 | C12 | C13 | C14 | C15 | C16 | C17 | C11 | C12 | C13 | C14 | C15 | C16 | C17 |
| 2 | C21 | C22 | C23 | C24 | C25 | C26 | C27 | C21 | C22 | C23 | C24 | C25 | C26 | C27 | ||
| 3 | C31 | C32 | C33 | C34 | C35 | C36 | C37 | C31 | C32 | C33 | C34 | C35 | C36 | C37 | ||
| 4 | C41 | C42 | C43 | C44 | C45 | C46 | C47 | C41 | C42 | C43 | C44 | C45 | C46 | C47 | ||
| 5 | C51 | C52 | C53 | C54 | C55 | C56 | C57 | C51 | C52 | C53 | C54 | C55 | C56 | C57 | ||
| 6 | C61 | C62 | C63 | C64 | C65 | C66 | C67 | C61 | C62 | C63 | C64 | C65 | C66 | C67 | ||
| 7 | C71 | C72 | C73 | C74 | C75 | C76 | C77 | C71 | C72 | C73 | C74 | C75 | C76 | C77 | ||
Fuente: elaboración propia.
Los coeficientes αij ponderan el grado de compatibilidad de cada materia i con un intervalo de tiempo j, considerando el valor de tres como primera opción, el valor de dos para segunda opción, el valor de uno en tercera opción y menos uno cuando no es favorable a la materia. Éstos se establecen por parte del responsable de la programación del horario, tomando en cuenta el número del subconjunto w como criterio para el llenado de coeficientes por turno, siguiendo la secuencia del diagrama de flujo de la Figura 2; una vez definidos, se sustituyen en el modelo matemático de la primera etapa.
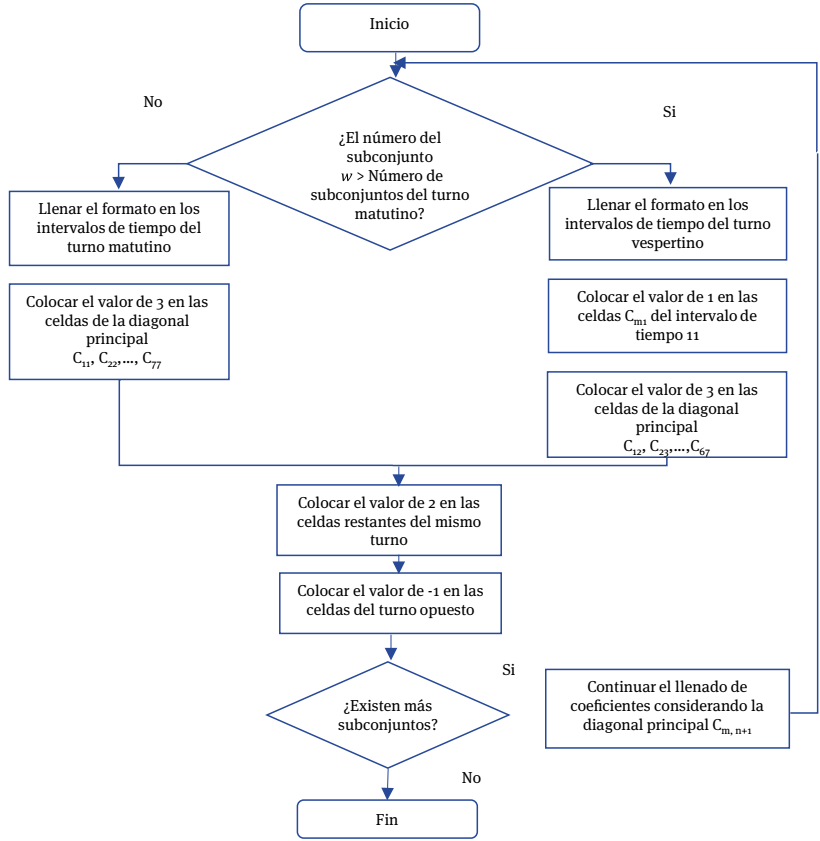
Fuente: elaboración propia.
Figura 2 Diagrama de flujo para el llenado de coeficientes en la función objetivo αij
Modelo matemático 1: asignación de materia-intervalo de tiempo
Sujeto a:
La función objetivo (4) busca maximizar la asignación de materias en los intervalos de tiempo, considerando los propósitos establecidos para los coeficientes
Las restricciones consideran que:
(5) Cada materia debe ser asignada en no más de un intervalo de tiempo.
(6) Las materias de un mismo semestre y grupo (subconjunto) deben ser asignadas en intervalos de tiempo distintos.
(7) Las materias asignadas por intervalo de tiempo, no deben exceder el número de aulas disponibles.
El resultado de esta primera etapa define la asignación de materias en los subconjuntos In e Io que serán utilizados en las etapas II y III.
Etapa II: asignación de materia-aula
En esta segunda etapa se asignan las materias a un aula, considerando las restricciones ocho y nueve definidas en la descripción del problema. La construcción del modelo matemático toma como base 14 subconjuntos formados por materias asignadas a un mismo intervalo de tiempo (siete correspondientes a los lunes-martes-jueves In y siete a los lunes-miércoles-viernes Io). A continuación, se muestra el modelo matemático utilizado.
Modelo matemático 2: asignación de materia-aula
Sujeto a:
La función objetivo (9) busca maximizar el número de horas-clase en cada aula, además penaliza la diferencia entre la capacidad de ésta y el número de estudiantes de la materia asignada, con la intención de generar soluciones donde se aprovechen los espacios disponibles.
Por su parte, las restricciones establecen que:
(10) Cada materia debe ser asignada en no más de un aula.
(11)-(17) Los pares de materias asignados en los intervalos de tiempo 1-8, 2-9, 3-10, 4-1, 5-12, 6-13 y 7-14 en la misma aula, no deben sumar más de 10 horas de clase, evitando empalmes el día lunes.
(18)-(19) En cada aula no deben asignarse grupos mayores a su capacidad.
(20)-(21) En cada aula no debe asignarse más de una materia en un mismo intervalo de tiempo.
Etapa III: asignación de materia-profesor
En esta última etapa se asignan las materias a un profesor considerando las restricciones 10-14 mencionadas en la descripción del problema. La construcción del modelo matemático toma como base los mismos subconjuntos de la etapa II.
En esta tercera etapa, se busca maximizar la compatibilidad de cada materia con los profesores disponibles, para lo cual se establecen de manera intencional coeficientes en la función objetivo γil con distinta calificación. El valor de cinco corresponde a profesores titulares de la materia (este valor solamente lo pueden alcanzar, los profesores considerados de tiempo permanente en la universidad), el valor de cuatro se establece a profesores catalogados como segunda opción y el valor de tres se otorga a los que son considerados como la última alternativa. Cuando el profesor no es apto para impartir la materia se le asigna un valor negativo.
Una vez definidos los coeficientes γil por parte del coordinador de la licenciatura, se sustituyen en el modelo matemático 3.
Modelo matemático 3: asignación de materia-profesor
Sujeto a:
La función objetivo (23) busca maximizar la compatibilidad de cada una de las materias con los profesores disponibles.
Las restricciones determinan que:
(24) Cada materia debe ser asignada a no más de un profesor.
(25) Debe asignarse al menos la mínima cantidad de horas de clase por profesor.
(26) La asignación no debe exceder la máxima cantidad de horas de clase por profesor.
(27)-(33) Los pares de materias asignados en los intervalos de tiempo 1-8, 2-9, 3-10, 4-11, 5-12, 6-13 y 7-14 de cada profesor no deben sumar más de 10 horas de clase, evitándo empalmes el día lunes.
(34)-(35) Las materias deben ser asignadas en los intervalos de tiempo que disponga cada profesor.
(36)-(37) Cada profesor no debe impartir más de una materia en un mismo intervalo de tiempo.
Experimentos y resultados
La programación del horario universitario en el Tecnológico Nacional de México en Celaya, se lleva a cabo por licenciatura. Para demostrar la efectividad de los modelos matemáticos desarrollados en cada etapa, se eligió la carrera de Ingeniería Industrial, en el ciclo escolar enero-junio 2019. Esta carrera cuenta con la mayor matrícula de estudiantes inscritos dentro de la institución, por lo que la utilización eficiente de los recursos es muy importante.
Para la validación del modelado matemático, se realizaron diez experimentos en los que se consideró un máximo de 168 materias, 14 intervalos de tiempo, 12 aulas y 33 profesores (21 profesores de tiempo permanente y 12 profesores de tiempo parcial).
Se utilizó una computadora con un procesador Intel Celeron 2.16-GHz N2840 CPU con 4 GB de RAM, empleando el sistema Windows 10 Home. Las matrices de datos fueron programadas en Excel, las cuales se ligaron al software Lingo 17 donde se capturaron los modelos matemáticos y se les dio solución a través de la técnica exacta de ramificación y acotamiento.
En la Tabla 5 se muestran las condiciones empleadas en cada experimento. Cabe mencionar que en todos los casos fue posible obtener una solución óptima en cada modelo.
Tabla 5 Condiciones consideradas en cada experimento
| Experimentos | Materias | Intervalos de tiempo | Aulas | Profesores |
|---|---|---|---|---|
| 1 | 42 | 14 | 12 | 33 |
| 2 | 56 | 14 | 12 | 33 |
| 3 | 70 | 14 | 12 | 33 |
| 4 | 84 | 14 | 12 | 33 |
| 5 | 97 | 14 | 12 | 33 |
| 6 | 109 | 14 | 12 | 33 |
| 7 | 122 | 14 | 12 | 33 |
| 8 | 135 | 14 | 12 | 33 |
| 9 | 151 | 14 | 12 | 33 |
| 10 | 168 | 14 | 12 | 33 |
Fuente: elaboración propia.
La Figura 3 y las Tablas 6 y 7, presentan gráficamente el grado de cumplimiento de las condiciones establecidas en la etapa I.
Tabla 6 Materias asignadas por intervalo de tiempo en los diferentes experimentos
| Turno | Intervalo de tiempo | Experimentos | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| Matutino | T1 | 6 | 8 | 10 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| Matutino | T2 | 6 | 8 | 10 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| Matutino | T3 | 6 | 8 | 10 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| Matutino | T4 | 6 | 8 | 10 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| Matutino | T8 | 6 | 8 | 10 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| Matutino | T9 | 6 | 8 | 10 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| Matutino | T10 | 6 | 8 | 10 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| Vespertino | T5 | 0 | 0 | 0 | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| Vespertino | T6 | 0 | 0 | 0 | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| Vespertino | T7 | 0 | 0 | 0 | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| Vespertino | T11 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 3 | 7 | 12 |
| Vespertino | T12 | 0 | 0 | 0 | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| Vespertino | T13 | 0 | 0 | 0 | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| Vespertino | T14 | 0 | 0 | 0 | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
Fuente: elaboración propia.
Tabla 7 Materias asignadas por intervalo de tiempo en el experimento 10
| Intervalos de tiempo del turno matutino | Intervalos de tiempo del turno vespertino | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Semestre | Grupo | T1 | T2 | T3 | T4 | T8 | T9 | T10 | T11 | T5 | T6 | T7 | T12 | T13 | T14 | Grupo | Semestre | |
| 1 | A | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 86 | 87 | 88 | 89 | 90 | 91 | 85 | A | 5 | |
| B | 14 | 8 | 9 | 10 | 11 | 12 | 13 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | B | |||
| C | 20 | 21 | 15 | 16 | 17 | 18 | 19 | 105 | 99 | 100 | 101 | 102 | 103 | 104 | C | |||
| 2 | A | 26 | 27 | 28 | 22 | 23 | 24 | 25 | 111 | 112 | 106 | 107 | 108 | 109 | 110 | A | 6 | |
| B | 32 | 33 | 34 | 35 | 29 | 30 | 31 | 117 | 118 | 119 | 113 | 114 | 115 | 116 | B | |||
| C | 38 | 39 | 40 | 41 | 42 | 36 | 37 | 123 | 124 | 125 | 126 | 120 | 121 | 122 | C | |||
| 3 | A | 44 | 45 | 46 | 47 | 48 | 49 | 43 | 129 | 130 | 131 | 132 | 133 | 127 | 128 | A | 7 | |
| B | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 135 | 136 | 137 | 138 | 139 | 140 | 134 | B | |||
| C | 63 | 57 | 58 | 59 | 60 | 61 | 62 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | C | |||
| 4 | A | 69 | 70 | 64 | 65 | 66 | 67 | 68 | 154 | 148 | 149 | 150 | 151 | 152 | 153 | A | 8 | |
| B | 75 | 76 | 77 | 71 | 72 | 73 | 74 | 160 | 161 | 155 | 156 | 157 | 158 | 159 | B | |||
| C | 81 | 82 | 83 | 84 | 78 | 79 | 80 | 166 | 167 | 168 | 162 | 163 | 164 | 165 | D | Extra | ||
Fuente: elaboración propia.
La Figura 3 muestra el porcentaje de materias asignadas por turno en cada prueba. En ella se observa que a partir del experimento cinco, fue necesario considerar la asignación de materias en el turno vespertino, ya que se habían ocupado todos los intervalos de tiempo del turno matutino. De los resultados se deduce que bajo las condiciones actuales, la asignación buscará saturar el primer turno del día antes de considerar el segundo.
Además, la Tabla 6 registra el número de materias asignadas en cada intervalo de tiempo, en los diferentes experimentos. Los intervalos de tiempo mas utilizados fueron los correspondientes al turno matutino; por otro lado, el menos empleado en la asignación fue el T11, donde se presenta la junta de academia programada para profesores permanentes.
La Tabla 7 ilustra la asignación de las materias del experimento 10, en éste se alcanzó la ocupación total de los intervalos de tiempo disponibles. A las materias que llevan el mismo nombre en un determinado semestre se les dio un color con la intención de verificar que, en los distintos grupos, se asignaron en intervalos de tiempo diferentes, preferentemente consecutivos, lo que permite que profesores titulares puedan impartirlas. Además, se aprecia que, por turno, cada grupo de materias se asignó en intervalos de tiempo sucesivos, disminuyendo las horas libres de los estudiantes.
Las Tablas 8-9 y la Figura 4, muestran el grado de cumplimiento de las condiciones planteadas en la etapa II.
Tabla 8 Número de materias asignadas por aula en cada experimento
| Experimento | Aulas | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Total | |
| 1 | 6 | 3 | 7 | 7 | 7 | 7 | 4 | 1 | 0 | 0 | 0 | 0 | 42 |
| 2 | 7 | 5 | 7 | 7 | 7 | 7 | 7 | 4 | 1 | 0 | 4 | 0 | 56 |
| 3 | 7 | 7 | 7 | 5 | 5 | 7 | 6 | 7 | 6 | 7 | 3 | 3 | 70 |
| 4 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 84 |
| 5 | 13 | 10 | 11 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 97 |
| 6 | 13 | 13 | 10 | 8 | 7 | 7 | 8 | 8 | 10 | 11 | 7 | 7 | 109 |
| 7 | 14 | 13 | 12 | 10 | 8 | 9 | 11 | 10 | 10 | 11 | 7 | 7 | 122 |
| 8 | 14 | 14 | 13 | 11 | 11 | 11 | 10 | 11 | 12 | 14 | 7 | 7 | 135 |
| 9 | 14 | 14 | 13 | 13 | 13 | 14 | 14 | 14 | 14 | 14 | 7 | 7 | 151 |
| 10 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 168 |
Fuente: elaboración propia.
Tabla 9 Número de estudiantes promedio asignados por materia en cada aula
| Aulas | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Experimento | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| C: 30 | C: 30 | C: 35 | C: 35 | C: 35 | C: 35 | C: 35 | C: 35 | C: 35 | C: 35 | C: 40 | C: 40 | |
| 1 | 30.00 | 30.00 | 33.86 | 34.00 | 35.00 | 35.00 | 35.00 | 35.00 | NA | NA | NA | NA |
| 2 | 30.00 | 30.00 | 32.57 | 32.43 | 34.00 | 35.00 | 35.00 | 35.00 | 35.00 | NA | 37.00 | NA |
| 3 | 30.00 | 30.00 | 33.57 | 35.00 | 33.80 | 31.86 | 34.17 | 33.14 | 33.83 | 34.29 | 37.00 | 37.00 |
| 4 | 30.00 | 30.00 | 34.57 | 33.57 | 33.86 | 32.71 | 34.00 | 33.57 | 33.57 | 35.00 | 33.29 | 33.57 |
| 5 | 30.00 | 30.00 | 34.18 | 34.14 | 32.57 | 33.29 | 33.43 | 33.43 | 34.43 | 35.00 | 33.57 | 33.29 |
| 6 | 30.00 | 30.00 | 35.00 | 34.25 | 32.86 | 32.86 | 33.13 | 33.63 | 33.00 | 33.27 | 32.57 | 34.29 |
| 7 | 29.64 | 30.00 | 33.58 | 32.90 | 33.25 | 32.67 | 32.55 | 32.90 | 32.70 | 32.64 | 33.57 | 33.29 |
| 8 | 28.93 | 30.00 | 32.54 | 32.45 | 32.91 | 32.27 | 31.70 | 32.73 | 32.67 | 33.50 | 32.57 | 34.29 |
| 9 | 27.79 | 29.29 | 32.85 | 30.92 | 32.15 | 30.79 | 32.29 | 31.57 | 32.79 | 33.29 | 34.29 | 32.57 |
| 10 | 27.71 | 27.86 | 30.43 | 30.79 | 32.07 | 31.71 | 30.14 | 32.71 | 33.07 | 31.71 | 28.21 | 28.71 |
Nota: NA no asignado.
Fuente: elaboración propia.
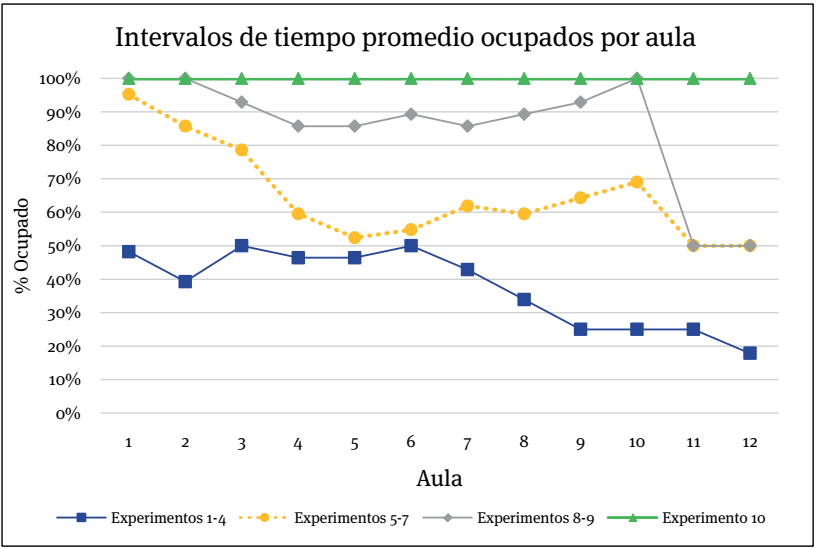
Fuente: elaboración propia.
Figura 4 Porcentaje de ocupación de los intervalos de tiempo por aula en los experimentos
En la Tabla 8 se establece el número de materias asignadas por aula, por su parte en la Tabla 9, se aprecia el número de estudiantes promedio asignados por materia en cada una de ellas, respetando en todo momento su capacidad (C) y aprovechando el espacio disponible. A su vez, en la Figura 4 se ilustra el porcentaje de ocupación de los intervalos de tiempo por aula.
En gran parte de los experimentos, las aulas menos empleadas fueron 11 y 12, ya que éstas, al tener una mayor capacidad, se consideraron como la última opción ya que si se asignaban en ellas materias con un bajo número de estudiantes sería un desperdicio de espacio. En el experimento 10 todas las aulas se ocuparon en los 14 intervalos de tiempo.
Las Figuras 5 y 6 señalan gráficamente el grado de cumplimiento de las condiciones planteadas en la etapa III.
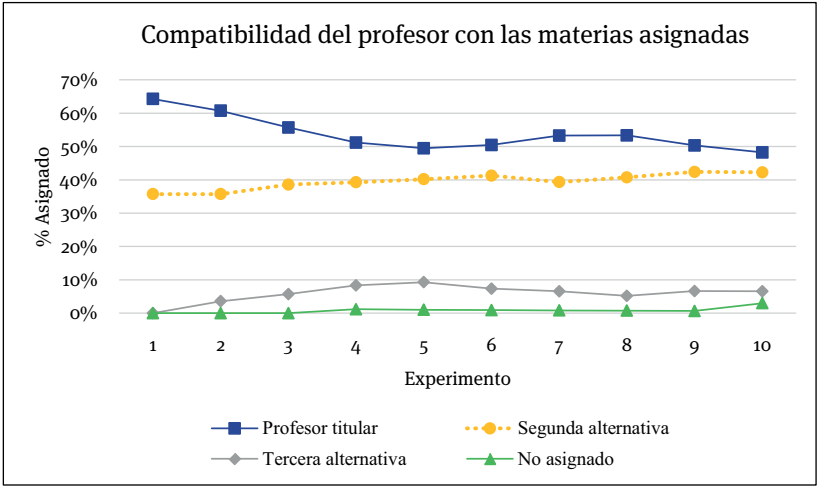
Fuente: elaboración propia.
Figura 5 Compatibilidad de los profesores con las materias asignadas en los diferentes experimentos
En la Figura 5 se observa que la mayor parte de los profesores asignados a las materias son los considerados como titulares. Cuando no fue posible realizar esta asignación, se tomó en cuenta a profesores de segunda y tercera alternativa respectivamente. Las condiciones impuestas por el problema imposibilitan el asignar a todas las materias un profesor en los experimentos 4 al 10.
La Figura 6 muestra que la asignación más alta de materias se presentó en profesores de tiempo permanente en la universidad, aprovechándose de esta manera al personal con el que cuenta la institución educativa y aminorando la necesidad de contratar profesores de tiempo parcial.
Es importante destacar que la estrategia implementada, permite que el tiempo que antes se empleaba en la construcción del horario ahora se utilice en el análisis de escenarios, favoreciendo la identificación de los factores que afectan el horario resultante y facilitando la toma de decisiones por parte de los responsables de la programación de materias.
Resultados computacionales
Con la intención de evaluar los modelos matemáticos binarios propuestos en diferentes instancias, se resolvieron cinco problemas de gran tamaño, en los que se consideró un rango de 126 a 504 materias, de 9 a 36 aulas, así como 21 a 84 profesores. El número de variables binarias, restricciones, non-zeros y los tiempos empleados en la búsqueda de una solución óptima en cada etapa se muestran en la Tabla 10.
Tabla 10 Tamaños de problemas resueltos con el modelado matemático
| Problemas | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Tamaño del problema | Materias | 126 | 252 | 308 | 406 | 504 |
| Intervalos de tiempo | 14 | 14 | 14 | 14 | 14 | |
| Aulas | 9 | 18 | 22 | 29 | 36 | |
| Profesores | 21 | 42 | 53 | 68 | 84 | |
| Variables binarias | Etapa I | 1 764 | 3 528 | 4 312 | 5 684 | 7 056 |
| Etapa II | 1 134 | 4 536 | 6 776 | 11 774 | 18 144 | |
| Etapa III | 2 646 | 10 584 | 16 324 | 27 608 | 42 336 | |
| Total | 5 544 | 18 648 | 27 412 | 45 066 | 67 536 | |
| Restricciones | Etapa I | 393 | 771 | 939 | 1 233 | 1 527 |
| Etapa II | 442 | 883 | 1 079 | 1 422 | 1 765 | |
| Etapa III | 904 | 1 807 | 2 270 | 2 923 | 3 613 | |
| Total | 1 739 | 3 461 | 4 288 | 5 578 | 6 905 | |
| Non-zeros | Etapa I | 7 056 | 14 112 | 17 248 | 22 736 | 28 224 |
| Etapa II | 5 670 | 22 680 | 33 880 | 58 870 | 90 720 | |
| Etapa III | 18 522 | 74 088 | 114 268 | 193 256 | 296 352 | |
| Total | 31 248 | 110 880 | 165 396 | 274 862 | 415 296 | |
|
Tiempo en segundos para encontrar la solución |
Etapa I | 8 | 27 | 28 | 54 | 92 |
| Etapa II | 7 | 9 | 10 | 16 | 29 | |
| Etapa III | 14 | 106 | 1 110 | No se encontró solución | No se encontró solución | |
| Total | 29 | 142 | 1 148 | -------- | -------- | |
Fuente: elaboración propia.
En la etapa III (asignación de profesores) de los problemas cuatro y cinco, no fue posible encontrar una solución óptima después de 12 horas de ejecución por lo que se decidió detener la búsqueda; si bien no fue posible generar la solución completa de estos problemas, definir el horario por etapas tiene la ventaja de seguir generando soluciones parciales al asignar materia-intervalo de tiempo-aula.
Otra de las bondades que ofrece la estrategia es la reducción en gran medida del número de variables binarias y en consecuencia el espacio de soluciones. La Tabla 11 muestra una comparativa del número de variables necesarias para resolver los problemas, considerando un solo modelo matemático, o bien, los tres modelos de la estrategia por etapas. En la parte final de la tabla se establece el porcentaje de reducción de variables que acota el espacio de soluciones de cada problema como resultado de la nueva estrategia implementada.
Tabla 11 Comparación de variables binarias entre uno y tres modelos matemáticos
| Modelos matemáticos | Problemas | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 1 Modelo | 333 396 | 2 667 168 | 5 027 792 | 11 208 848 | 21 337 344 |
| 3 Modelos (tres etapas) | 5 544 | 18 648 | 27 412 | 45 066 | 67 536 |
| % Reducción de variables | 98.34% | 99.30% | 99.45% | 99.60% | 99.68% |
Fuente: elaboración propia.
Conclusiones
En este artículo se presentó una nueva estrategia en la elaboración de un horario universitario, a través de tres etapas de asignación y el uso de variables binarias de dos índices; el problema se descompone en más de un modelo matemático simplificándose en gran medida la complejidad de éste, lo que permite obtener soluciones en poco tiempo, a diferencia de resolver todo el problema en un solo paso.
Para agilizar la búsqueda de soluciones, la estrategia expuesta contempló la descomposición del problema original en tres modelos matemáticos, lo que redujo, considerablemente, el número de combinaciones posibles. Se utilizaron además subconjuntos que separaron por grupo e intervalo de tiempo las materias, facilitando el modelado de ciertas restricciones; así como la determinación de los coeficientes de las funciones objetivo de cada modelo.
Utilizando como caso de aplicación la programación del horario universitario en el Tecnológico Nacional de México en Celaya, se ejemplifica el proceso de análisis, construcción del modelo y solución; este problema administrativo se resolvía mediante prueba y error, lo que implicaba invertir una gran cantidad de tiempo por parte del personal administrativo; con la propuesta desarrollada en este estudio, la automatización del proceso ahora es posible y el tiempo se invierte en analizar escenarios.
El estudio presentado consideró la problemática que enfrentan la mayoría de los centros educativos de nivel superior en México, que es la contratación de profesores de forma temporal en cada ciclo escolar para cubrir las necesidades de la institución. Éste demostró que es posible generar soluciones donde se aproveche a los profesores de tiempo permanente en la universidad y se disminuya la contratación de profesores de tiempo parcial.
La propuesta descrita en este artículo, puede ser adoptada por otras instituciones educativas, principalmente las que forman parte del sistema de Institutos Tecnológicos de México para programar sus horarios escolares. En futuras investigaciones sería interesante estudiar el impacto de esta estrategia en el análisis de otros problemas combinatorios.











 nueva página del texto (beta)
nueva página del texto (beta)





