Introducción
En los procesos productivos industriales existe infinidad de operaciones desarrolladas directamente por el ser humano, cada una de las cuales debe estar balanceada según las diferentes necesidades del proceso productivo, de ahí que sea importante tener un balanceo de líneas adecuado para cumplir con las demandas estimadas del producto. Al respecto, Orejuela y Flórez (2019) destacan que los primeros diseños de líneas de ensamble se desarrollaron para obtener eficiencia y eliminar costos de producción en operaciones que comúnmente trabajan contra inventarios. Por eso, se han desarrollado investigaciones para crear métodos óptimos de asignación de tareas en las estaciones de una línea de ensamble, a los cuales se les denomina problema de balanceo de la línea de ensamble (ALBP).
Las líneas de montaje pueden ser de tipo lineal y tipo U; estas últimas ofrecen una productividad y una calidad mejoradas, por lo que se consideran una de las mejores para implementar sistemas just-in-time (JIT). Aunque existe un creciente interés en la literatura para organizar líneas de montaje rectas o lineales como líneas en forma U para mejorar el rendimiento, los trabajos literarios aún siguen siendo limitados. El problema de balanceo de la línea de ensamble tipo U (UALBP) es una extensión del problema de balanceo de la línea recta (SALBP), en el que las tareas se pueden asignar desde ambos lados del diagrama de precedencia (Baykasoğlu y Özbakır, 2006).
Los problemas de balanceo de línea se dividen en dos tipos: tipo 1 y tipo 2. En el primero ya se conoce el tiempo de ciclo, por lo que se asignan las tareas a las estaciones de trabajo para minimizar el número de estaciones. En el problema tipo 2 se busca disminuir el tiempo de ciclo cuando el número de estaciones es fijo.
Las técnicas heurísticas y metaheurísticas han permitido el desarrollo de metodologías de solución para los problemas de balanceo de líneas de ensamble que no pueden ser atendidos con métodos convencionales. Por ejemplo, Gallego et al. (2015) mencionan que las técnicas metaheurísticas son de gran utilidad para resolver problemas de optimización, los cuales no pueden ser solventados por otro tipo de técnicas
Las metaheurísticas operan mediante algoritmos no de orden común, sino especiales porque, básicamente, no se rigen por un patrón predictivo, ni causal, ni organizado, sino aleatorio. Este algoritmo adquiere su forma óptima a través de itinerancias o pruebas que aproximan la solución. “Los algoritmos más conocidos en metaheurística son los algoritmos genéticos, la búsqueda tabú, algoritmo de colonia de hormigas (ACO), recocido simulado, optimización con enjambre de partículas (PSO)” (Maldonado, 2016, p. 173).
Los algoritmos genéticos fueron desarrollados originariamente por J. Holland. Estos tienen la capacidad de aprender, lo que constituye el rasgo más determinante en la evolución de cualquier sistema vivo o que exhiba vida. Esta técnica de búsqueda usa una población de soluciones que son manipuladas independientemente (Maldonado, 2016).
Actualmente, en la mayoría de los estudios del ALBP se consideran parámetros determinados. Sin embargo, en los procesos de fabricación real siempre existe incertidumbre, ya que puede haber variaciones en los tiempos de operaciones manuales y de la maquinaria. Por eso, para minimizar los efectos negativos de todos estos problemas inesperados se ha aplicado la teoría estocástica en el SALBP y el UALBP (Zhang et al., 2018).
Ahora bien, aunque en los últimos años diferentes autores han propuesto metodologías para resolver el ALBP, la presente investigación se desarrolla dentro del enfoque estocástico en el balanceo de líneas en forma de U tipo 1. Los algoritmos genéticos, al ser métodos más eficientes, nos proporcionan más opciones de posibles soluciones al problema de equilibrado estocástico de líneas en forma de U tipo 1. En ese sentido, Martínez (2015) desarrolló y publicó un nuevo algoritmo que emplea técnicas metaheurísticas mediante algoritmos genéticos con reglas heurísticas, las cuales pueden ayudar a resolver ALBP y UALBP, pues proporcionan una o más soluciones buenas, y en algunos casos óptimas, para aplicar a cualquier proceso.
Para resolver el UALBP tipo 1 estocástico, el algoritmo es adaptado incorporando ecuaciones para calcular las probabilidades de que los tiempos en las estaciones de trabajo excedan los tiempos de ciclo. El desempeño del algoritmo es evaluado y comparado con las soluciones existentes en la literatura de Adil Baykasoğlu y Lale Özbakır (2006) “Stochastic U-line balancing using genetic algorithms” (p. 139).
Métodos y materiales
Algoritmo genético
Para Cortez (2004) un proceso computacional, también llamado proceso algorítmico o algoritmo, es fundamental para la ciencia de la computación, puesto que un computador no puede ejecutar un problema que no tenga una solución algorítmica. Evaluar la eficiencia de los algoritmos, por ende, tiene mucho que ver con valorar la complejidad de estos. En este sentido, la teoría de la complejidad computacional es la parte de la teoría de la computación que estudia los recursos requeridos durante el cálculo para resolver un problema. Los recursos comúnmente estudiados son el tiempo (número de pasos de ejecución de un algoritmo para resolver un problema) y el espacio (cantidad de memoria utilizada para resolver un problema). Un algoritmo que resuelve un problema, pero que tarda mucho en hacerlo, difícilmente será de utilidad.
Los algoritmos genéticos forman parte de las llamadas técnicas evolutivas, propuestas originalmente en los años 50, que tienen una estructura básica común: realizan la reproducción, llevan a cabo variaciones aleatorias, promueven la competencia y ejecutan la selección de individuos de una población determinada. Siempre que estos cuatro procesos están presentes, ya sea en la naturaleza o en una simulación informática, la evolución es el producto resultante.
En las simulaciones informáticas -según Gallego et al. (2015) - los algoritmos genéticos, al igual que otras técnicas evolutivas, simulan un proceso de selección natural para obtener la solución de problemas de optimización. En este caso, el problema por resolver desempeña el papel del entorno y cada individuo de la población está asociado a una solución candidata. De este modo, un individuo estará más adaptado al entorno siempre que corresponda a una solución más eficaz del problema.
La computación evolutiva presenta la ventaja de poder resolver problemas a través de descripciones matemáticas simples. “De este modo, la computación evolutiva debe ser entendida como un conjunto de técnicas y procedimientos genéricos y adaptables, para ser aplicados en la resolución de problemas complejos, para los que otras técnicas conocidas son ineficaces o no aplicables” (Gallego et al., 2015, p. 6).
Los algoritmos evolutivos son técnicas basadas en una población de individuos, los cuales están en constante comunicación y compartiendo información a través de operadores de reproducción y mutación. La población está formada por varios individuos, que generalmente se representan mediante una cadena binaria llamada cromosoma, donde cada bit de esta cadena se conoce como gen (Esparza, 2009).
Algoritmo de codificación directa modificado para resolver el UALBP estocástico tipo 1
En la codificación directa el algoritmo genético es alimentado con los datos específicos de cada problema. Los problemas de balanceo tienen un número de tareas, tiempos de tareas, restricciones y precedencia de estas, así como un tiempo de ciclo determinado. En el algoritmo de codificación directa cada gen representa una tarea, es decir, el número de genes es equivalente a la cantidad de tareas. Los datos mencionados previamente se introducen al algoritmo y este generara una población inicial; luego comienza la búsqueda de un cromosoma ideal (uno que genere un número óptimo de estaciones de trabajo). Si no se encuentra dicho cromosoma, nuevas poblaciones son generadas utilizando operaciones genéticas de reproducción, cruce y mutación (Martínez, 2015).
Codificación
Como lo comenta Martínez (2015), el primer paso para construir un algoritmo genético es definir una representación genética denominada codificación. Así, cada tarea se enumera secuencialmente en el orden en que se asignará a las estaciones de trabajo, y cada gen del cromosoma contiene el número de tarea que representa (Martínez, 2015).
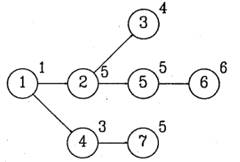
El cromosoma es simbolizado por un gráfico lineal o diagrama isomórfico, denominado de esta manera en la teoría de gráficos. El diagrama isomórfico contiene la misma configuración respecto a precedencia relacionada al diagrama original, es decir, el diagrama isomórfico es equivalente al diagrama de precedencia. Este se utiliza para construir un cromosoma.
El método utilizado para construir una secuencia aleatoria válida de genes en el cromosoma (diagrama isomórfico) es el siguiente:
Paso 1: Generar un cromosoma vacío con un número de genes igual al número de tareas.
Paso 2: Seleccionar un conjunto de tareas que no tenga precedencia.
Paso 3: Seleccionar una tarea disponible de manera aleatoria y agregarla al cromosoma.
Paso 4: Eliminar del conjunto de tareas sin precedencia la tarea seleccionada.
Paso 5: Agregar todas las tareas sucesoras inmediatas a la tarea agregada, siempre y cuando todos sus predecesores ya estén en el cromosoma.
Paso 6: Si aún existen tareas sin asignar, regresar al paso 3; de lo contrario, terminar el cromosoma.
En las figuras 1 y 2 se muestra el diagrama de precedencia y la representación isomórfica, respectivamente, para el problema de Mertens.
Población inicial
La población inicial de cromosomas se genera de forma aleatoria, y el número de cromosomas por utilizar es definido por el usuario. Muchas de las posibles combinaciones de genes son irrelevantes porque violan las restricciones de precedencia. Para generar la población inicial se utiliza el método de construcción del diagrama isomórfico. Así, se garantiza que los cromosomas generados mantengan una secuencia válida de genes. En la tabla 1 se muestra un cromosoma para el problema de Mertens.
Tabla 1 Cromosoma para el problema de Mertens
| Cromosoma | Genes | ||||||
| 1 | 4 | 7 | 2 | 3 | 5 | 6 | |
Fuente: Elaboración propia
Dado que cada cromosoma es representado por un diagrama isomórfico, este se puede utilizar para mostrar de forma gráfica cómo estaría representada la línea en forma de U una vez que se haya solucionado el problema. En la figura 3 se muestra la representación gráfica en forma de U para el problema de Mertens.
Decodificación
Los cromosomas son generados de tal manera que la secuencia no viole las restricciones de precedencia, lo cual permite que las tareas sean asignadas de múltiples formas a las estaciones de trabajo en lugar de una (Martínez, 2015). El proceso de decodificación se refiere al procedimiento mediante el cual los genes de cromosoma (tareas) son asignados a las estaciones de trabajo y la manera en que estas se van generando.
Cuando este proceso termina se obtiene una solución, la cual muestra un índice de aptitud (número de estaciones de trabajo), un índice de suavidad y un tiempo computacional.
Las siguientes notaciones utilizadas por Baykasoğlu y Özbakır (2006) son empleadas para el desarrollo del algoritmo.
N |
Número de tareas |
T |
Tiempo de ciclo |
µi(Tj) |
Tiempo medio de proceso de la tarea i |
σi |
Desviación estándar del tiempo de proceso de la tarea i |
Pk |
Probabilidad de que el tiempo de la estación exceda el tiempo de ciclo |
Zk |
Variable aleatoria con media de 0 y desviación estándar de 1 |
F(Zk) |
Valor acumulado de la función Zk |
α |
Límite superior de la probabilidad de que el tiempo de la estación exceda el tiempo de ciclo |
Kα |
α cuantil de la distribución normal estándar |
σi² |
Varianza del tiempo de proceso de la tarea i |
El método utilizado para decodificar el cromosoma se describe a continuación:
Crear una estación de trabajo vacía.
Seleccionar la tarea inicial y la final, y asignar una de ellas a la primera estación de trabajo.
Calcular la probabilidad de que el tiempo de la estación exceda el tiempo de ciclo utilizando las ecuaciones 1 y 2 (Baykasoğlu y Özbakır, 2006).
4. Si la probabilidad de que el tiempo de la estación exceda el tiempo de ciclo es menor al valor de α, se continúa con la asignación de tareas a la estación.
5. Si la probabilidad de que el tiempo de la estación exceda el tiempo de ciclo es mayor al valor de α, se abre la siguiente estación y se continúa con la asignación de tareas.
6. Se agregan las tareas del extremo izquierdo si sus antecesores ya están en el cromosoma, y se agregan las tareas de los extremos derecho si sus sucesores ya han sido asignados.
7. Regresar al paso 3, y repetir el proceso hasta terminar la asignación de tareas; posteriormente, finalizar el proceso.
Generación de la varianza
La literatura del problema de balanceo de líneas en forma de U estocástico es muy limitada. Si bien las metodologías que se han propuesto muestran el desarrollo del método para llegar a la solución, no enseñan valores específicos para la media y la varianza de las tareas. En tal sentido, Armin Scholl (1993) propuso un conjunto de problemas, los cuales han sido utilizados por distintos autores en soluciones al problema de balanceo de líneas; sin embargo, resulta complicado encontrar problemas en la literatura que muestren los valores específicos para la varianza de las tareas; en consecuencia, fue necesario desarrollar un método y combinarlo con el enfoque de Carraway utilizado por Urban y Chiang (2006) para la generación de dichas varianzas.
La varianza se genera aleatoriamente empleado parte del enfoque de Carraway. En este se generan valores aleatorios de varianza en dos intervalos [0, (Ti/4)²] para baja varianza y [0, (Ti/2)²] para alta varianza y utilizando los tiempos de ciclo mínimos para generar un rango de valores aleatorios. Para mostrar el procedimiento se utiliza el problema de Mertens. La tabla 2 muestra la media del tiempo de las tareas para este problema.
Tabla 2 Media del tiempo de tarea para el problema de Mertens (1967)
| Tarea | Media del tiempo de tarea |
|---|---|
| 1 | 1 |
| 2 | 5 |
| 3 | 4 |
| 4 | 3 |
| 5 | 5 |
| 6 | 6 |
| 7 | 5 |
| Tiempo de ciclo 8 |
Fuente: Elaboración propia
1. Los valores máximos de Zk fueron determinados como 1.28, 1.645, y 1.96 (Urban y Chiang 2006). Utilizando la ecuación 2, se pueden desarrollar las siguientes ecuaciones y determinar un valor máximo de la varianza para cada tarea.
2. Cálculo de varianza tarea 1.
Se observa que la varianza menor calculada es para el valor de Zk de 1.96. Este es el valor que se selecciona como máximo de varianza para esta tarea. Además, se usa como valor máximo para el intervalo de valores aleatorios para la varianza de esta tarea. Este es seleccionado debido a que cualquier valor mayor de varianza no generaría ninguna solución, es decir, no existe manera de asignar la tarea (en este caso, la 1 a alguna estación de trabajo9, ya que una varianza mayor excedería la probabilidad de que el tiempo de la estación exceda el tiempo de ciclo. Se realiza el mismo procedimiento para las tareas faltantes. A continuación, en la tabla 3 de resultados se incluye el enfoque de Carraway para la selección del intervalo de la varianza.
Tabla 3 Resultados para la varianza calculada
| Tarea | Rango de varianza Carraway | Desviación estándar (σ) para los valores de Zk | Varianza (σ²) | |||
|---|---|---|---|---|---|---|
| [0,(Tj/4)²] | Z=1.96 | Z=1.645 | Z=1.28 | σ² Calculada | σ² Aleatoria | |
| 1 | 0.0625 | 3.571 | 4.255 | 5.469 | 12.755 | 0.017 |
| 2 | 1.5625 | 1.531 | 1.824 | 2.344 | 2.343 | 0.165 |
| 3 | 1 | 2.041 | 2.432 | 3.125 | 4.165 | 0.257 |
| 4 | 0.5625 | 2.551 | 3.040 | 3.906 | 6.508 | 0.541 |
| 5 | 1.5625 | 1.531 | 1.824 | 2.344 | 2.343 | 0.987 |
| 6 | 2.25 | 1.020 | 1.216 | 1.563 | 1.041 | 0.976 |
| 7 | 1.5625 | 1.531 | 1.824 | 2.344 | 2.343 | 1.556 |
Fuente: Elaboración propia
3. Se comparan los valores de las columnas [0,(Tj/4)²](rango de varianza Carraway) y σ² calculada, y se seleccionan los valores menores. En este ejemplo, se seleccionan los valores de la columna [0,(Tj/4)²], dado que son los menores para las tareas 1, 2, 3, 4, 5 y 7; para la tarea 6 se selecciona el valor de la columna σ² calculada. En la tabla 4 se observan los intervalos de la varianza y los resultados aleatorios para la misma.
Tabla 4 Resultados aleatorios para la varianza
| Tarea | Valores máximos para la varianza | Intervalo de la varianza | σ² Aleatoria |
|---|---|---|---|
| 1 | 0.0625 | 0 - 0.625 | 0.017 |
| 2 | 1.5625 | 0 - 1.5625 | 0.165 |
| 3 | 1 | 0 - 1 | 0.257 |
| 4 | 0.5625 | 0 - 0.5625 | 0.541 |
| 5 | 1.5625 | 0 - 1.5625 | 0.987 |
| 6 | 1.041 | 0 - 1.041 | 0.976 |
| 7 | 1.5625 | 0 - 1.5625 | 1.556 |
Fuente: Elaboración propia
4. Con los datos de varianza generados de manera aleatoria se crea la tabla 5 con los valores de la media y varianza para el algoritmo.
Tabla 5 Datos para el algoritmo
| Tarea | Media del tiempo de tarea | Varianza |
|---|---|---|
| 1 | 1 | 0.017 |
| 2 | 5 | 0.165 |
| 3 | 4 | 0.257 |
| 4 | 3 | 0.541 |
| 5 | 5 | 0.987 |
| 6 | 6 | 0.976 |
| 7 | 5 | 1.556 |
Fuente: Elaboración propia
Desarrollo del algoritmo
Los pasos para la solución del cromosoma generado se describen a continuación:
Colocar las posibles tareas asignables (1,6) a la estación del trabado 1.
Seleccionar una de las tareas de forma aleatoria.
Determinar la probabilidad de que el tiempo de la estación exceda el tiempo de ciclo.
Si la probabilidad de que el tiempo de la estación exceda el tiempo de ciclo es menor al valor de α, se continúa con la asignación de tareas a la estación 1.
Si la probabilidad de que el tiempo de la estación exceda el tiempo de ciclo es mayor al valor de α, se abre la estación 2 y se continúa con la asignación de tareas.
Para ejemplificar el proceso de solución del algoritmo se utiliza el cromosoma previamente mostrado en la tabla 1 y se utilizan los datos de la tabla 5. En la tabla 6 se muestran los pasos para la solución del cromosoma mencionado. El tiempo de ciclo propuesto es de 10 y la probabilidad propuesta es de 95 % (α = 0.05).
Tabla 6 Solución del cromosoma
| Probabilidad 95 %, α = 0.05, CT = 10 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Tareas asignables | Tarea seleccionada | µ | Σµ | σ^2 | Σσ^2 | √Σσ^2 | Pk | Estación de Trabajo |
| 1,6 | 1 | 1 | 1 | 0.017 | 0.017 | 0.130 | 1-F((10-1)/0.130) = 0 | 1 |
| 4,6 | 6 | 6 | 7 | 0.976 | 0.993 | 0.996 | 1-F((10-7)/0.996) = 0.001 | 1 |
| 4,5 | 4 | 3 | 10 | 0.541 | 1.534 | 1.239 | 1-F((10-10)/1.239) = 0.5 | 2 |
| 7,5 | 5 | 5 | 8 | 0.987 | 1.528 | 1.236 | 1-F((10-8)/1.236) = 0.052 | 3 |
| 7,3 | 3 | 4 | 9 | 0.257 | 1.244 | 1.115 | 1-F((10-9)/1.115) = 0.184 | 4 |
| 7,2 | 7 | 5 | 9 | 1.556 | 1.813 | 1.346 | 1-F((10-9)/1.343) = 0.228 | 5 |
| 2 | 2 | 5 | 10 | 0.165 | 1.721 | 1.312 | 1-F((10-10)/1.312) = 0.5 | 6 |
Fuente: Elaboración propia
Cálculo de la probabilidad de que el tiempo en la estación 1 exceda el tiempo de ciclo utilizando las ecuaciones 1 y 2 con la tarea 1 asignada:
Valor P de la tabla Z:
Valor P de la tabla Z:
Valor P de la tabla Z:
Al finalizar la operación 3 se observa que la probabilidad de que el tiempo de la estación 1 exceda el tiempo de ciclo es mayor al valor de α; por lo tanto, se abre la estación 2.
Las operaciones para cada una de las tareas seleccionadas para ser asignadas a las siguientes estaciones se realizan de la misma manera. La solución para este cromosoma da como resultado seis estaciones de trabajo.
Solución computacional
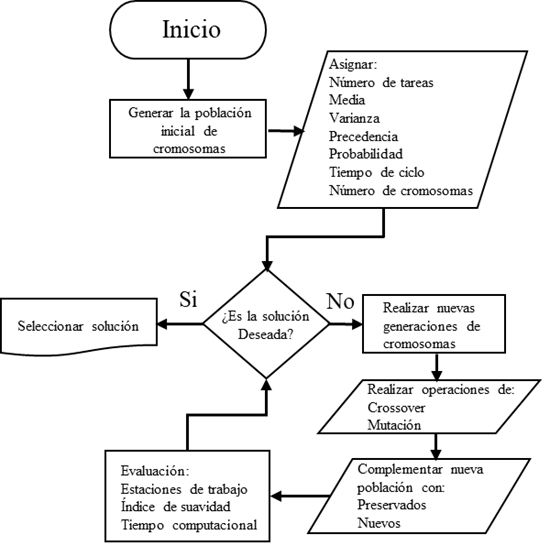
El algoritmo computacional desarrolla soluciones buscando cromosomas que generen soluciones factibles mediante operaciones genéticas. El proceso implica lo siguiente: el usuario define las poblaciones iniciales, se seleccionan los cromosomas más adecuados para realizar la operación de cruce, se realiza una selección aleatoria de cromosomas para la operación de mutación, y se complementa la nueva población con cromosomas más adecuados para ser conservados y con nuevos cromosomas. Este proceso continúa hasta alcanzar el número de generaciones establecido. El diagrama de bloques de la figura 4 representa el proceso del algoritmo.
Resultados
Para evaluar el algoritmo para el problema de balanceo de líneas en forma de U tipo 1 estocástico se utilizó el conjunto de problemas de balanceo de línea presentado por Armin Scholl (1993), el cual ha sido utilizado por varios autores para probar diferentes metodologías de solución al problema de balanceo de línea. Este conjunto de problemas propone tiempos de tarea, los cuales fueron considerados como la media del tiempo de la tarea (µi).
Siete categorías de problemas son utilizadas para la evaluación del algoritmo: Mertens (7 tareas), Bowman (8 tareas), Jaeschke (9 tareas), Jackson (11 tareas), Mitchell (21 tareas), Heskiaoff (28 tareas), y Killbridge (45 tareas). Los problemas se evalúan en dos rangos de varianza (alta y baja varianza), lo que permite visualizar el impacto en las soluciones con diferentes rangos en la varianza de las tareas. Las probabilidades de finalización de tareas se ajustaron a 0.90, 0.95 y 0.97 (Kα = 1.28, 1.645, y 1.96, respectivamente). La combinación de estas categorías con su tiempo de ciclos respectivos, los rangos de varianza y las diferentes probabilidades generan un total de 165 problemas. Estos fueron resueltos con una computadora personal de 2.3 GHz. En las tablas 7 y 8 se muestran los resultados resaltados en negritas del desarrollo computacional del algoritmo y las soluciones existentes en la literatura de Baykasoğlu y Özbakır (2006).
Tabla 7 Resultados del desarrollo computacional del algoritmo baja varianza
| Baja varianza | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Problemas | N.° de tareas | Tiempo de ciclo | K(1-α) = 1.96 Probabilidad 97.5 % | K(1-α) = 1.645 Probabilidad 95 % | K(1-α) = 1.28 Probabilidad 90 % | ||||||||||||
| SI | Solución WS | CPT | SI | Solución WS | CPT | SI | Solución WS | CPT | |||||||||
| Existente | Existente | Existente | Existente | Existente | Existente | ||||||||||||
| Mertens | 7 | 8 | 1.354 | 6 | 5 | 0.118 | 0.203 | 1.354 | 6 | 5 | 0.053 | 0.281 | 1.354 | 6 | 5 | 0.049 | 0.078 |
| 10 | 1.414 | 5 | 4 | 0.102 | 0.17 | 1.414 | 5 | 4 | 0.053 | 0.201 | 2.179 | 4 | 4 | 0.045 | 0.18 | ||
| 15 | 0.577 | 3 | 3 | 0.11 | 0.079 | 0.577 | 3 | 3 | 0.056 | 0.203 | 0.577 | 3 | 3 | 0.049 | 0.22 | ||
| 18 | 0.707 | 2 | 2 | 0.112 | 0.281 | 0.057 | 2 | 2 | 0.707 | 0.155 | 0.707 | 2 | 2 | 0.043 | 0.187 | ||
| Bowman | 8 | 20 | 5.082 | 6 | 6 | 0.141 | 0.172 | 5.082 | 6 | 6 | 0.045 | 0.203 | 2.75 | 5 | 5 | 0.037 | 0.094 |
| Jaeschke | 9 | 6 | N/S/F | 8 | N/S | 0.172 | N/S/F | 8 | N/S/F | 0.203 | N/S/F | 8 | N/S | 0.156 | |||
| 7 | 1.541 | 8 | 7 | 0.161 | 0.157 | 1.541 | 8 | 7 | 0.113 | 0.172 | 1.62 | 8 | 7 | 0.055 | 0.23 | ||
| 8 | 1.62 | 8 | 7 | 0.058 | 0.172 | 1.62 | 8 | 7 | 0.032 | 0.09 | 1.927 | 7 | 7 | 0.032 | 0.171 | ||
| 10 | 2.12 | 6 | 5 | 0.181 | 0.141 | 2 | 5 | 5 | 0.152 | 0.141 | 2 | 5 | 5 | 0.109 | 0.13 | ||
| 18 | 0.816 | 3 | 3 | 0.187 | 0.14 | 0.816 | 3 | 3 | 0.127 | 0.11 | 2.08 | 3 | 3 | 0.057 | 0.203 | ||
| Jackson | 11 | 9 | 1.414 | 8 | 7 | 0.097 | 0.17 | 1.414 | 8 | 7 | 0.055 | 0.204 | 1.5 | 8 | 7 | 0.048 | 0.2 |
| 10 | 1.69 | 7 | 7 | 0.151 | 0.063 | 1.69 | 7 | 7 | 0.071 | 0.183 | 1.69 | 7 | 7 | 0.068 | 0.172 | ||
| 13 | 1.095 | 5 | 5 | 0.137 | 0.14 | 1.414 | 5 | 5 | 0.066 | 0.204 | 1.264 | 5 | 5 | 0.066 | 0.13 | ||
| 14 | 1.264 | 5 | 4 | 0.132 | 0.188 | 1.264 | 5 | 4 | 0.073 | 1.1 | 0.707 | 4 | 4 | 0.057 | 0.24 | ||
| 21 | 0.816 | 3 | 3 | 0.126 | 0.187 | 0.816 | 3 | 3 | 0.069 | 0.14 | 0.816 | 3 | 3 | 0.063 | 0.157 | ||
| Mitchell | 21 | 15 | 2.774 | 10 | N/S/F | 0.153 | N/S/F | 1.632 | 9 | N/S/F | 0.101 | N/S/F | 1.563 | 9 | 9 | 0.101 | 0.297 |
| 21 | 1.647 | 7 | 6 | 0.173 | 0.5 | 0.707 | 6 | 6 | 0.105 | 0.843 | 0.707 | 6 | 6 | 0.103 | 0.26 | ||
| 26 | 1.183 | 5 | 5 | 0.154 | 0.34 | 0 | 5 | 5 | 0.128 | 0.344 | 0.183 | 5 | 5 | 0.126 | 0.234 | ||
| 35 | 1.5 | 4 | 4 | 0.254 | 0.28 | 5.408 | 4 | 4 | 0.227 | 0.21 | 2.692 | 4 | 4 | 0.167 | 0.281 | ||
| 39 | 8.139 | 4 | 4 | 0.301 | 0.21 | 1.29 | 3 | 4 | 0.225 | 0.235 | 1.29 | 3 | 3 | 0.218 | 0.156 | ||
| Heskiaoff | 28 | 205 | 12.69 | 6 | 6 | 0.138 | 11.031 | 14.85 | 6 | 6 | 0.166 | 3.297 | 10.23 | 6 | 6 | 0.131 | 0.343 |
| 216 | 12.11 | 6 | 6 | 0.134 | 1.97 | 17.34 | 6 | 6 | 0.186 | 0.1 | 23.54 | 6 | 6 | 0.171 | 0.25 | ||
| 256 | 12.88 | 5 | 5 | 0.311 | 0.405 | 18.15 | 5 | 5 | 0.183 | 0.36 | 23.75 | 5 | 5 | 0.202 | 0.328 | ||
| 324 | 18.61 | 4 | 4 | 0.282 | 0.453 | 20.84 | 4 | 4 | 0.205 | 0.25 | 28.52 | 4 | 4 | 0.216 | 0.454 | ||
| 342 | 29.77 | 4 | 4 | 0.247 | 0.328 | 36.78 | 4 | 4 | 0.197 | 0.32 | 65.6 | 4 | 4 | 0.239 | 0.406 | ||
| Killbridge | 45 | 79 | 6.073 | 9 | 9 | 0.346 | 0.39 | 6.904 | 9 | 9 | 0.275 | 0.39 | 8.062 | 9 | 8 | 0.289 | 5.203 |
| 92 | 11.34 | 8 | 8 | 0.349 | 0.594 | 5.707 | 7 | 8 | 0.353 | 0.391 | 5.644 | 7 | 7 | 0.294 | 1.37 | ||
| 110 | 4.163 | 6 | 6 | 0.395 | 0.4 | 5.887 | 6 | 6 | 0.334 | 0.4 | 5.228 | 6 | 6 | 0.336 | 0.594 | ||
| 138 | 9.777 | 5 | 5 | 0.412 | 0.578 | 12.17 | 5 | 5 | 0.407 | 0.2 | 21.24 | 5 | 5 | 0.42 | 0.39 | ||
| 184 | 33.79 | 4 | 4 | 0.48 | 0.391 | 42.05 | 4 | 4 | 0.437 | 0.112 | 47.15 | 4 | 4 | 0.399 | 0.45 | ||
| N/S/F No se encontró solución factible | |||||||||||||||||
Fuente: Elaboración propia
Tabla 8 Resultados del desarrollo computacional del algoritmo alta varianza
| Alta varianza | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Problemas | N.° de Tareas | Tiempo de ciclo | K(1-α) = 1.96 Probabilidad 97.5 % | K(1-α) = 1.645 Probabilidad 95 % | K(1-α) = 1.28 Probabilidad 90 % | ||||||||||||
| SI | Solución WS | CPT | SI | Solución WS | CPT | SI | Solución WS | CPT | |||||||||
| Existente | Existente | Existente | Existente | Existente | Existente | ||||||||||||
| Mertens | 7 | 8 | 1.354 | 6 | N/S/F | 0.134 | N/S/F | 1.354 | 6 | N/S/F | 0.055 | N/S/F | 1.354 | 6 | 5 | 0.056 | 6.172 |
| 10 | 1.354 | 6 | 5 | 0.078 | 0.1 | 1.354 | 6 | 5 | 0.032 | 0.18 | 2.489 | 5 | 5 | 0.031 | 0.14 | ||
| 15 | 0.577 | 3 | 3 | 0.141 | 0.13 | 0.577 | 3 | 3 | 0.071 | 0.125 | 0.577 | 3 | 3 | 0.03 | 0.11 | ||
| 18 | 0.577 | 3 | 3 | 0.149 | 0.09 | 0.577 | 3 | 3 | 0.11 | 0.078 | 0.707 | 2 | 2 | 0.049 | 0.075 | ||
| Bowman | 8 | 20 | 6.928 | 7 | 6 | 0.07 | 7.12 | 5.016 | 6 | 6 | 0.032 | 0.171 | 5.016 | 6 | 6 | 0.108 | 0.2 |
| Jaeschke | 9 | 8 | 1.62 | 8 | 7 | 0.132 | 0.922 | 1.62 | 8 | 7 | 0.036 | 0.531 | 1.62 | 8 | 7 | 0.033 | 1.47 |
| 10 | 1.927 | 7 | 7 | 0.033 | 0.125 | 1.927 | 7 | 7 | 0.071 | 0.219 | 2.121 | 6 | 7 | 0.059 | 0.187 | ||
| 18 | 0.816 | 3 | 3 | 0.152 | 0.234 | 0.816 | 3 | 3 | 0.121 | 0.175 | 0.816 | 3 | 3 | 0.1 | 0.3 | ||
| Jackson | 11 | 10 | 1.414 | 8 | N/S/F | 0.068 | N/S/F | 1.581 | 8 | N/S/F | 0.024 | N/S/F | 1.5 | 8 | 7 | 0.027 | 0.203 |
| 13 | 1.732 | 6 | 5 | 0.098 | 2.04 | 1.732 | 6 | 5 | 0.074 | 0.985 | 1.095 | 5 | 5 | 0.036 | 1.402 | ||
| 14 | 1.095 | 5 | 5 | 0.068 | 0.891 | 1.095 | 5 | 5 | 0.084 | 0.25 | 2.236 | 5 | 5 | 0.1 | 0.772 | ||
| 21 | 0.816 | 3 | 3 | 0.116 | 0.766 | 0.816 | 3 | 3 | 0.044 | 0.187 | 0.816 | 3 | 3 | 0.035 | 0.31 | ||
| Mitchell | 21 | 21 | 1.274 | 8 | 8 | 0.08 | 0.344 | 1.362 | 7 | 7 | 0.083 | 0.231 | 1.647 | 7 | 7 | 0.093 | 0.516 |
| 26 | 2.121 | 6 | 6 | 0.196 | 0.782 | 1.957 | 6 | 6 | 0.092 | 0.344 | 2.366 | 5 | 5 | 0.092 | 1.89 | ||
| 35 | 0.866 | 4 | 4 | 0.257 | 5.468 | 0.866 | 4 | 4 | 0.173 | 0.562 | 0.866 | 4 | 4 | 0.16 | 0.281 | ||
| 39 | 2.692 | 4 | 4 | 0.269 | 0.174 | 6.224 | 4 | 4 | 0.219 | 0.235 | 6.576 | 4 | 4 | 0.185 | 0.344 | ||
| Heskiaoff | 28 | 205 | 17.41 | 8 | 8 | 0.298 | 0.547 | 20.37 | 8 | 7 | 0.143 | 1.641 | 14.75 | 7 | 7 | 0.101 | 0.437 |
| 216 | 25.95 | 8 | 7 | 0.491 | 1.976 | 27.15 | 7 | 7 | 0.135 | 0.563 | 23.76 | 7 | 6 | 0.128 | 5.593 | ||
| 256 | 23.12 | 6 | 6 | 0.2 | 0.48 | 18.75 | 6 | 6 | 0.157 | 0.53 | 24.06 | 6 | 5 | 0.149 | 1.453 | ||
| 324 | 19.57 | 5 | 5 | 0.15 | 0.691 | 41.19 | 5 | 4 | 0.184 | 0.328 | 13.1 | 4 | 4 | 0.114 | 0.531 | ||
| 342 | 48.67 | 5 | 4 | 0.249 | 0.531 | 5.787 | 4 | 4 | 0.192 | 0.657 | 11.25 | 4 | 4 | 0.21 | 0.18 | ||
| Killbridge | 45 | 92 | 10.65 | 9 | 8 | 0.198 | 0.61 | 4.769 | 8 | 8 | 0.201 | 5.547 | 7.632 | 8 | 8 | 0.172 | 0.594 |
| 110 | 8.115 | 7 | 7 | 0.288 | 0.609 | 9.433 | 7 | 7 | 0.214 | 0.984 | 21.42 | 7 | 6 | 0.226 | 4.14 | ||
| 138 | 22.61 | 6 | 6 | 0.313 | 0.782 | 4.289 | 5 | 6 | 0.302 | 0.39 | 8.148 | 5 | 5 | 0.276 | 0.797 | ||
| 184 | 11.85 | 4 | 4 | 0.345 | 0.593 | 14.35 | 4 | 4 | 0.331 | 0.781 | 31.6 | 4 | 4 | 0.302 | 0.593 | ||
| N/S/F: No se encontró solución factible | |||||||||||||||||
Fuente: Elaboración propia
Al finalizar el proceso de evaluación el algoritmo muestra los siguientes resultados:
El índice de suavidad muestra qué tan cercano está el cromosoma (solución) generado de lograr el equilibrio de la línea de producción. Un número más cercano a cero es mejor, pues entre más pequeño sea este valor, significa que se está más cerca de lograr un equilibrio perfecto. El número de estaciones de trabajo indica la cantidad de estaciones de trabajo que se generan por cada cromosoma. El tiempo computacional indica el tiempo que consume el algoritmo para generar los cromosomas (las unidades de tiempo se muestran en nanosegundos). En la figura 5 se observa un ejemplo de la solución computacional del algoritmo.
Discusión
De los resultados obtenidos se realiza una tabla comparativa con las soluciones existentes de Baykasoğlu y Özbakır (2006) para alta y baja varianza, donde se muestra la cantidad y porcentaje para los siguientes resultados:
Ws mayor. Problemas en los cuales se generó una WS (estación de trabajo) más.
WS similar, menor CPT. Problemas en los cuales la cantidad de WS es similar con un CPT (tiempo computacional) menor.
WS similar, mayor CPT. Problemas en los cuales la cantidad de WS es similar con un CPT mayor.
WS menor. Problemas para los cuales se generó un número de WS menor.
No se encontró solución factible. Problemas para los cuales no se encontró solución.
Total de problemas. Numero de problemas realizados.
Tabla 9 Comparación de resultados para alta y baja varianza
| Baja varianza | ||||||
|---|---|---|---|---|---|---|
| WS Mayor | WS Similar Menor CPT | WS Similar Mayor CPT | WS Menor | No se encontró solución factible | Total de problemas | |
| 18 | 52 | 16 | 1 | 3 | 90 | |
| % | 20.0 | 57.8 | 17.8 | 1.1 | 3.3 | |
| Alta varianza | ||||||
| WS Mayor | WS Similar Menor CPT | WS Similar Mayor CPT | WS Menor | No se encontró solución factible | Total de problemas | |
| 18 | 46 | 5 | 6 | 0 | 75 | |
| % | 24.0 | 61.3 | 6.7 | 8.0 | 0.0 | |
Fuente: Elaboración propia
Del análisis de los resultados, podemos afirmar que el algoritmo evaluado brinda mejores soluciones para los problemas de alta varianza, pues únicamente para el resultado WS mayor se observa una diferencia de 4 %. En cambio, en los resultados restantes los porcentajes son mejores. Además, se puede observar que se encontraron seis soluciones mejores a las existentes. En este sentido, las soluciones para algunos problemas muestran variación por una tarea adicional como máximo, aunque en la mayoría el número de las estaciones de trabajo son similares a las existentes. Respecto a los tiempos computaciones de las soluciones, no se observa gran diferencia, pues la mayoría de los tiempos está por debajo de 1 segundo. La tabla 10 enseña los promedios de los tiempos para ambas varianzas.
Tabla 10 Promedios de los tiempos computacionales
| Promedios de los tiempos computacionales | ||
|---|---|---|
| Varianza | Soluciones del algoritmo | Soluciones existentes |
| Baja | 0.177 | 0.522 |
| Alta | 0.146 | 0.991 |
Fuente: Elaboración propia
En definitiva, se puede observar que los tiempos promedios de las soluciones del algoritmo son mejores a los existentes, lo cual muestra la capacidad del algoritmo para encontrar las soluciones en un tiempo computacional menor.
Conclusiones
La realización de este trabajo reafirmó la efectividad de los algoritmos genéticos computacionales para solución de problemas complejos, pues mediante la validación se hallaron resultados similares a los existentes en la literatura.
Por otra parte, cabe indicar que en muchos casos el balanceo de líneas se realiza basándose en la experiencia del personal a cargo de esta tarea, es decir, no se emplean metodologías basadas en la metaheurística u otra herramienta. Un balanceo empírico, por ende, no siempre resulta lo más adecuado, ya que puede implicar incrementos en los costos de producción. Sin embargo, con esta nueva herramienta basada en algoritmos genéticos se puede realizar un balanceo más adecuado en las líneas en forma de U con tiempos de tarea estocásticos. Una de sus características más destacada es la versatilidad, pues permite variar distintos parámetros para obtener una cantidad considerable de soluciones. Esto sirve para experimentar y observar los diferentes aspectos que pueden mejorar u optimizar la operación, con lo cual se puede lograr un balanceo con la menor cantidad de recursos humanos posible.
Asimismo, la validación del algoritmo fue un proceso muy extenso, ya que los problemas realizados se desarrollaron con diferentes valores de probabilidad y rangos de varianza. Esto fue muy importante porque permitió someter el algoritmo a diferentes escenarios para conseguir una comparación lo más pareja posible.
Finalmente, es importante destacar que las varianzas de ambas soluciones fueron generadas aleatoriamente, por lo que resulta difícil concluir que un algoritmo brinde la mejor solución al problema de balanceo de línea en forma de U estocástico tipo 1. Por ello, para tener una comparación más realista, sería necesario realizar el estudio computacional con varianzas iguales.
Futuras líneas de investigación
Con los resultados obtenidos se tiene una idea más clara de las soluciones que puede mostrar el algoritmo. De hecho, como medida de evaluación de la solución el algoritmo muestra el SI (índice de suavidad), aunque también existen tres medidas que ayudan a evaluar la solución. Un trabajo futuro, por tanto, podría mejorar el algoritmo e incorporar estas tres medidas de evaluación de la solución:











 nueva página del texto (beta)
nueva página del texto (beta)