Introducción
En los cursos de matemáticas, cuando el alumno tiene un acercamiento con las funciones algebraicas, desde ese momento se le pide que grafique una función lineal o una cuadrática. A esto se le agrega que el estudiante debe ser capaz de diferenciar la variable dependiente de la independiente. Asimismo, en el salón de clase, el alumno debe aprender qué es el dominio y qué es el contradominio. A la vez, debe saber distinguir cuando se trata de una relación o una función entre estos conjuntos. Esto es lo que de manera tradicional se maneja en la educación secundaria o media superior, sin embargo, ahí se encuentra escondido el Discurso Matemático Escolar (DME).
En la enseñanza de las matemáticas, el DME es el lenguaje que se maneja en clase, es el sistema de razón que produce violencia simbólica debida a la imposición de los argumentos, significados y procedimientos (Soto, Gómez, Silva y Cordero, 2012; Soto y Cantoral, 2014). Es todo lo que permanece sin cambios a pesar de las modificaciones que supuestamente se realizan, ya que en realidad no se modifican los conceptos que se están enseñando (Cantoral, Montiel y Reyes, 2015). Algo similar ocurre con los libros de texto que se emplean en las clases de matemáticas: están influenciados por el DME (Cantoral et al., 2015).
La huella del DME se ve en los libros de texto que se utilizan en diferentes áreas, no únicamente en la enseñanza de la matemática escolar. Por ejemplo, en el área de la ingeniería de control (Ogata, 2003; D’Azzo, 1995) no cambia la manera en cómo se expone la forma de determinar una función de transferencia. A esto le podemos agregar que estos argumentos no cambian comparando una edición anterior contra una actualizada de la misma obra.
Lo mismo ocurre si comparamos el graficado de funciones revisando dos libros de diferentes autores (Barnett, R. (1994); Stewart, 2007) y lo mismo podemos decir si comparamos estas obras contra sus versiones actualizadas con diferencia que se han agregado recursos pedagógicos y manejo de la tecnología como el manejo de software matemático (Barnett, 2012; Stewart, 2012). Sin embargo, hay autores que han utilizado otros procedimientos, ya sea agregando o mostrando caminos distintos que llevan al mismo resultado. Por ejemplo, en (Gómez, 2017; Ogata, 2003) se presentaron los procedimientos alternativos de descomposición de fracciones parciales mediante el método de Heaveside reemplazando la metodología de los coeficientes indeterminados que se manejan en los cursos tradicionales de cálculo integral y precalculo (Ayres et. al., 1994; Purcell, et. al., 2007; Edwards y Penney, 2007; Barnett, 2012).
En (Sandoval-Hernandez, et. al, 2019a) se realizó un análisis de polarización en corriente directa para dos diodos rectificadores en serie, donde se presentó una solución algebraica en términos de los parámetros de los componentes del circuito. En este artículo se evitó el DME que impera en los cursos de electrónica básica, ya que de manera tradicional, la polarización de un diodo rectificador se halla de manera gráfica, es decir, el cruce de la curva característica del diodo rectificador contra la recta de carga del circuito. Esta metodología tradicional aparece en (Boylestad y Nashelsky, 2003). De manera alternativa se puede obtener el punto de polarización para este circuito con el método de Newton-Raphson (Burden y Faires, 2005; Chapra, 2004).
Además, en el trabajo (Sandoval-Hernandez, et. al, 2019b) se propusieron dos aproximaciones en términos de funciones elementales, una para la función error y otra para la función acumulativa normal, las cuales pueden ayudar en las clases de estadística mostrando caminos alternativos en su determinación comparado contra las tradicionales tablas en donde se encuentra involucrado el DME (Spiegel,1994).
De igual manera en (Sandoval-Hernandez, et. al, 2021a) se superó el DME que ha imperado en los libros de algebra en la deducción de la formula general para resolver ecuaciones de segundo grado presentando una alternativa para esta fórmula por medio de la sustitución de un numero complejo. Asimismo, ahí se presentó un análisis de dígitos significativos cuando se decide racionalizar la formula general para hallar las raíces. Este mismo análisis se hizo para una solución por medio de series de potencias cuando existe un pequeño valor perturbativo (Holmes, 2012) en el término lineal una ecuación cuadrática
En ese trabajo proponemos unir dos o más funciones elementales por medio de una función que permite graficar una combinación de funciones trascendentes y/o algebraicas que represente funciones definidas por trozos, conocidas como piecewise (Chua et. al.,1987) evitando el uso de comandos especializados de software matemático como Maple (Fox, 2011; Barnes, 2014), Octave (Lie. 2019) o Matlab (Barnes, 2014; Nakamura,1997), etc. Esta metodología se puede implementar en los cursos de precálculo como algebra y trigonometría en bachillerato, en donde la mayoría de los alumnos aún no poseen conocimientos de lenguajes de programación (Joyanes-Aguilar, 2001) o software matemático avanzado.
Graficado de funciones
El primer contacto que tienen los alumnos con las gráficas, sean histogramas, esquemas y graficas cartesianas es en la educación básica (Cordero y Flores, 2005). En la enseñanza tradicional donde el DME está presente, para graficar una función les decimos a los alumnos que deben comenzar por hacer una tabla de valores (Baldor, 2011, Olvera, 1991). Por lo general, les damos a los alumnos el dominio, es decir, el conjunto de valores que la variable independiente x va tomar. En algunos casos, sin decirles por qué se han elegido esos valores (nuevamente el DME está presente) y entonces procedemos como se muestra en la Figura 1.
En la Figura 1 se muestra cómo se grafica una función, esto es, a partir de una tabla con los valores de x. Después se procede a realizar una tabulación para formar los puntos coordenados, los cuales pondremos en el plano cartesiano. Por último los unimos con una línea.
Este procedimiento mostrado es utilizado cuando se le enseña a los estudiantes como graficar funciones algebraicas y trascendentes. En la actualidad se dispone de software matemático educativo para estos propósitos y uno de ellos es GeoGebra (Sánchez, 2019). De esta manera, haciendo uso de software matemático el problema presentado en la Figura 1 se puede graficar fácil y rápidamente introduciendo las coordenadas y la ecuación de la recta. Sin embargo, si quisiéramos graficar una función f 1 (x) = 0 y después una función f 2 (x) = sin(x) a mano o en algún software matemático, tendríamos que graficar por separado indicando el intervalo en donde va a quedar cada una de las funciones, lo que haría necesario entonces introducir dos ecuaciones y graficarlas de manera independiente.
Por ejemplo, se desea graficar la función
Esta es un función tipo piecewise (Chua et. al.,1987). En este ejemplo se tienen dos funciones, una recta y la función seno que son válidas en cada uno de los intervalos señalados. Para graficar esta función f(x) en Maple tendríamos que introducir los comandos
˃with(plots);
˃f:=x;
˃g:=sin(x);
˃recta:=plot(f, x=0..3.14, color=red):
˃seno:= (f, x=0..3.14..9.9, color=blue):
˃display(recta, seno):
Esto puede superarse si utilizamos un comando avanzado que permita graficar este tipo de funciones. Para este propósito el comando piecewise resuelve el problema. Utilizando las funciones f, g en Maple y agregando los comandos
se resuelve el problema. Sin embargo, esto implicaría que los alumnos conozcan un poco programación y del software Maple. Desafortunadamente muchos alumnos en el bachillerato y alumnos universitarios de semestres iniciales no los poseen. En la Figura 2 se tiene la función graficada en Maple.
Metodología
Este trabajo comenzó con una investigación documental del software matemático más conocido que incorporan funciones interconstruidas para graficar funciones piecewise.
La investigación incluyó la ayuda y libros de los programas matemáticos Maple (Fox, 2011; Barnes, 2014), Octave (Lie. 2019) o Matlab (Barnes, 2014; Nakamura,1997) en donde se buscaron los comandos para graficar funciones elementales.
Materiales
Las gráficas y los ejemplos que se presentan en este artículo se realizaron con el software matemático Maple 2015 y gfortran GNU en Linux para medir tiempos de cómputo. La computadora utilizada en este trabajo de investigación cuenta con sistema operativo Linux Ubuntu (Version 18.04.05 LTS), procesador Intel I7-7700@ 3600GHz x 8 y tarjeta gráfica NVIDIA GeForce GTX 1050Ti/PCIe/SSE2.
Resultados
En la investigación documental se encontró que los comandos de graficación incluidos en varios programas de cómputo matemático son plot y piecewise. El primero generalmente se utiliza para hacer graficas en dos dimensiones, una función en términos de la variable dependiente y la variable independiente. Esta función por lo general cuenta con varios argumentos para personalizar la gráfica, por ejemplo el color y el tipo de fuente que se utilizará. El segundo comando se utiliza para construir y definir las funciones definidas por trozos. Este comando también cuenta con argumentos adicionales para definir varias funciones por trozos y el intervalo donde será válido cada una de las funciones que formarán parte de la función piecewise.
En la Tabla 1 se presenta un listado de programas matemáticos tanto de licencia como libre que incorporan las funciones interconstruidas plot y piecewise para elaborar las gráficas.
Tabla 1 Comandos de graficado en software matemático
| Software | Comando | Tipo de Software | |
| Plot | Piecewise | ||
| Maple | Si | Si | Licencia |
| Matlab | Si | Si | Licencia |
| Octave | Si | Si | Libre |
| Wolfram | Si | Si | Licencia |
| Python | Si (plt.plot) | Si | Libre |
| Maxima | Si (plot2d) | * | Libre |
| Excel | ** | ** | Licencia |
| Descripción general de los comandos | plot(f,x) Crea una gráfica en dos dimensiones, la funcion f y la variable independiente. | piecewise(cond_1,f_1, cond_2,f_2, ..., f_otherwise) Crea gráficas continuas por pedazos. La semantica es que si cond_1 es verdadera se gráfica f_1, en caso contrario cond_2 es verdadera se gráfica f_2, y asi sucessivamente. De otro modo f_otherwise se gráfica. | |
| Nota | |||
| * | Se define la función matemática a graficar como piecewise utilizando el condicional if then else | ||
| ** | Los gráficos se generan por medio de un menú de opciones o programando una macro en Visual Basic para Aplicaciones | ||
Fuente: Elaboración propia
De la Tabla 1 se puede advertir que los comandos plot y piecewise tienen prácticamente la misma sintaxis para elaborar gráficas. En Maple (Fox, 2011; Barnes, 2014) para construitr una función piecewise primero debe definirse cada una de las funciones incorporadas y los intervalos de graficación, posteriormente se utiliza el comando plot para graficarla.
En el caso de Maxima, la función definida por trozos, puede definirse incorporando simultáneamente el intervalo de graficación para cada trozo y posteriomente utilizando el comando plot2d o wxplot2d.
En el caso de Excel las gráficas se pueden generar a través de un menú interactivo con el cual interactúa el usuario. Estas gráficas se personalizan según el interés de la persona. Sin embargo es posible escribir una macro en Visual Basic para Aplicaciones para realizar distintos tipos de gráficas (Torres-Remon, 2016). Esto último representa una gran desventaja si el usuario no tiene conocimientos de programación.
La sintaxis del código que se escribe en Matlab y Octave es prácticamente el mismo con la diferencia que Matlab es software de licencia (Lie. 2019; Nakamura, 1997), sin embargo los comando de graficación que se utilizan en estos programas tienen una sintaxis de graficación muy parecida al que utiliza Maple.
El método de la ventana
Analizaremos el comportamiento de la función logística dada por
que es muy utilizada en modelos de crecimiento de poblaciones, propagación de epidemias, entre otros (Zill et. al., 2002).
El método de las ventanas que se propone consiste en primer lugar, utilizar la propiedad de la traslación horizontal para desplazar una función a la izquierda o al derecha (Stewart et. al., 2004). Para hacer estas traslaciones suponemos que existe un h > 0. De tal manera que f (x - h) desplaza la gráfica de la función h unidades a la derecha y que f(x+h) desplaza la gráfica de la función h unidades a la izquierda. En consecuencia, en (2) reemplazamos el signo negativo por el positivo, y desplazamos h unidades a la izquierda o la derecha
La Figura 3 muestra el desplazamiento horizontal de (3) para valores de h = -2, -1,0,1,2.
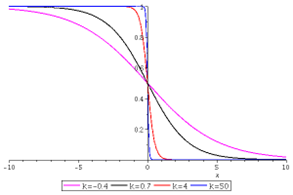
En segundo lugar, en (3) agregamos una constante
En la Figura 4 se observa como la curva de la función tiende a cambiar de forma de una manera más abrupta cuando k = 50. Entre más grande sea el valor de
El principio de esta metodología se encuentra basada en el diseño de filtros analógicos y digitales utilizando las ventanas de Hamming, Blackman, Hanning, entre otras (Proakis, Manolakis, 2004). Por lo tanto la diferencia de f a (x) y f b (x) se encuentra dada por
Véase que en (5) se encuentran especificados los intervalos de graficados y la rapidez con que la ventana se activa y desactiva. En la Figura 5 se muestra el caso donde k = 10, a = -2, b = 4.
Se puede observar en la figura que la ventana se encuentra activa para cualquier intervalo a < x < b. Nótese que a la izquierda tenemos la diferencia en las magnitudes de ambas funciones y en la derecha, la ventana cierra cuando x > b debido a que la función tiende a cero. De este modo, utilizando la ventana se procede a multiplicar cualquier función elemental durante el intervalo intervalo a < x < b eliminando el uso de comandos de programación. Por lo tanto, la expresión matemática para graficar una función queda definida en términos de la ventana con los puntos de inicio y fin del intervalo de graficado dado por
Cabe mencionar que cuando se tiene dos o más funciones que se van a graficar, estas se pueden concatenar con los signo (+) y (-).
Discusión
En esta sección se presentan tres casos de estudio donde se implementa el método de la ventana para graficar funciones piecewise.
Casos de estudio
Ejemplo 1
Realice la gráfica para la función
Solución. Sustituyendo la función y los valores del intervalo que definen a (7) se tiene
En este caso únicamente se ha multiplicado por la función en donde finaliza el intervalo de graficado, es decir, para b = 6. En la Figura 6 se presenta la gráfica de (8) donde muestra la validez de las funciones para los intervalos dados por (7).
Ejemplo 2
Obtenga la función definida por
Solución
Procedemos a sustituir en (6) cada una de las funciones que componen con los respectivos puntos de inicio y final para cada intervalo. (7). Por lo tanto tenemos
Es importante observar que en este ejemplo se tienen cuatro funciones definidas en cuatro intervalos. Puede observarse el concatenado para cada una de las funciones, así como el intervalo donde la ventana estará activa para cada una de las funciones. En la Figura 7 se muestra la gráfica de (8) en donde se pueden ver cada una de las funciones que se definieron en (7). Es importante reiterar que en x < -1 y x > 8.5 la función es 0. Esto se debe a que el sistema de ventanas concatenadas inicia y finaliza sin la necesidad de proponer funciones que se encarguen de cancelar en esos extremos.
Ejemplo 3
En los comics que alguna vez hemos leído en nuestra infancia o tiempos libres aparecen una serie de superhéroes disfrazados que buscan hacer justicia atrapando a los villanos que se dedican a delinquir en las ciudades. Según los comics existen diferentes maneras para llamar a estos superhéroes cuando está ocurriendo un desastre o para detener a un villano está haciendo de las suyas.
Nosotros en este ejemplo invocaremos a uno que pertenece la liga de la justica (Superfriends). Cabe mencionar que estos personajes, sus emblemas y sus historias son propiedad de DC Comics (Avery-Natale, 2013). Graficaremos el emblema de Batman que se utilizó en la película dirgida por Tim Burton en el año de 1989.
Solución:
Para el modelado del logo clásico de Batman se utilizó una imagen de 299x168 pixeles la cual se procedió a modelar el perímetro utilizando splines con los procedimientos de interpolación presentados en (Burden y Faires, 2005). Como resultado de las interpolaciones para la parte superior e inferior de la figura, se tiene
Para la elipse que encierra el logo de Batman se propone
Utilizando las funciones (9) y (10) con sus intervalos en (5) tenemos
Véase que en (12) y (13) se ha incluido el valor absoluto con el fin de considerar que las funciones que han de representar la parte superior e inferior de la FRigura son pares. La Figura 8 presenta el emblema de Batman utilizando el método de ventanas para graficado.
Consideraciones en la implementación
En los casos de estudio presentados en este artículo se graficaron funciones del tipo piecewise por lo que esta metodología facilita el graficado de estas funciones cuando se emplea software didáctico. Asimismo, en todos los ejemplos se eligió k = 1000 con el fin de hacer el corte de los dominios para las ventanas más rápidos.
Limitaciones
Para utilizar esta metodología de graficado es recomendable utilizar funciones algebraicas o trigonométricas con coeficientes enteros como los presentados en los ejemplos 1 y 2.
Conforme se agregan más funciones definidas por trozos y se definen los respectivos intervalos de graficación, es necesario incorporar más ventanas. Esto trae como consecuencia la presencia de más funciones exponenciales que activan y desactivan a cada una de las funciones a graficar. En el ejemplo 3 se utilizaron doce funciones exponenciales para graficar la parte superior del emblema, mientras que para la parte inferior se utilizaron seis funciones exponenciales. Esto trae como consecuencia mayor tiempo de cómputo en el graficado de las funciones. En la Figura 9 se presentan los tiempos de cómputo para graficar el emblema de Batman. Véase que los tiempos de cómputo calculados para la mitad superior son mayores que para la mitad inferior debido a que en la parte superior se han utilizado más funciones exponenciales.
Para obtener esta grafica se procedió a dividir todo el intervalo
Es importante destacar que en el ejemplo 3 se debe implementar en Maple o algún otro software matemático similar debido a que (13) posee muchos términos numéricos y exponenciales. Esta es una limitante para usar software educativo ya que no están diseñados para realizar cómputo científico que implique un cálculo numérico considerable.
Conclusiones
En este artículo se propuso el método de ventana para graficado de funciones que consiste en unir funciones utilizando la función logística con el fin de que los maestros puedan contar con metodologías de graficado para funciones piecewise y puedan ser incluidos en los cursos de precálculo. Se pueden unir varias funciones, hasta donde el software lo permita. Sin embargo, del ejemplo 3 concluimos que cuando se tienen varias funciones con números de punto flotante y funciones exponenciales, lo mejor es optar por un software matemático científico ya que estos programas tienen una alta robustez numérica.
Creemos que la estrategia propuesta en este artículo se puede aplicar en los cursos de precálculo siendo una herramienta útil de trazado ya que por lo general en el aula se proponen funciones algebraicas con números enteros y se descarta el graficado de las funciones por trozos.
Futuras líneas de investigación
Para utilizar el método de la ventana de una manera más eficiente es posible reducir los tiempos de cómputo reemplazando las funciones exponenciales por otras funciones. Esto es necesario cuando se quieren unir varias funciones elementales que incluyan números de punto flotante. De manera alterna, se puede utilizar la regla de Horner en expresiones algebraicas para este propósito (Vazquez-Leal, 2019, Fukushima, 2013).
Es posible considerar el método de la ventana para graficar funciones piecewise en futuras reformas de contenidos dentro de los programas de Subsecretaria de Educación Media Superior y en los cursos de formación docente que promueve la Coordinación Sectorial de fortalecimiento Académico en la República Mexicana. En (Sandoval-Hernandez, et. al, 2021b) se propuso una actualización de contenidos en la asignatura de Matemáticas aplicadas del componente propedéutico del bachillerato tecnológico de la Dirección General de Educación Tecnológica Industrial (D.G.E.T.I.) en donde una de las propuestas de actualización es el estudio de desigualdades y funciones. En esa sección es posible incluir esta metodología de graficado para estudiar las funciones piecewise. Para su incorporación deben de diseñarse las estrategias didácticas piloto e instrumentos de evaluación necesarios para implementar esta propuesta y hacer mediciones en los aprendizajes esperados de los alumnos.











 nova página do texto(beta)
nova página do texto(beta)