Introducción
Es importante que los estudiantes puedan transitar por diversos registros matemáticos. Tal y como lo señala Duval (2016), desde el punto de vista cognitivo, hay diferentes representaciones semióticas y nunca debe confundirse el objeto matemático con su representación semiótica. Por ello, el objetivo del presente trabajo de investigación es resignificar las operaciones matemáticas de los productos notables y la factorización con procedimientos geométricos y razonamiento lógico matemático.
Gómez (2015) parte del hecho de que “la factorización es un contenido del curso de matemática, de segundo básico, que presenta dificultades en su aprendizaje, lo que afecta el desarrollo de los estudiantes en la asimilación de temas posteriores” (p. 25). Esto mismo sucede en la Escuela Normal Urbana Federal Profr. Rafael Ramírez de la ciudad de Chilpancingo, Guerrero, México, la cual oferta la licenciatura en Educación Secundaria con especialidad en Telesecundaria.
En México, el programa de estudios diseñado por la Secretaría de Educación Pública [SEP] (2017) establece que el tópico “Productos notables y factorización” (p. 313) sea impartido en tercer grado de educación secundaria. Dicho tema no es de fácil tratamiento didáctico. Normalmente, los alumnos tienen dificultades para asimilarlo. Parte de su complejidad se debe a la estructura organizativa de los programas, falta de actualización de los profesores que imparten dicha asignatura y carencia de trabajo cooperativo entre los docentes. Según Méndez y Cruz (2008):
Uno de los conceptos que en el proceso de enseñanza-aprendizaje no llegan a dominar los alumnos, durante gran parte de la enseñanza media, es el desarrollo de identidades notables y la factorización. Muchos de ellos no tienen éxito al resolver ejercicios, ni ponen en obra los procedimientos correctos cuando se enfrentan a situaciones en las que este concepto es parte de la solución. El estudio de esta problemática evidencia un fenómeno didáctico complejo (p. 59).
En cuanto a la corriente constructivista, Rico (1998) menciona que:
Todo conocimiento es construido. El conocimiento matemático es construido, al menos en parte, a través de un proceso de abstracción reflexiva.
Existen estructuras cognitivas que se activan en los procesos de construcción.
Las estructuras cognitivas están en desarrollo continuo. La actividad con propósito induce la transformación de las estructuras existentes.
Reconocer el constructivismo como una posición cognitiva conduce a adoptar el constructivismo metodológico (pp. 74-75).
El diseño didáctico siempre busca que los alumnos observen, analicen, construyan, comuniquen, argumenten y resuelvan los problemas planteados en los temas ya mencionados. Es importante mencionar que el profesorado puede consultar textos de educación preescolar, primaria, secundaria y nivel medio superior en la página de la Comisión Nacional de Libros de Textos Gratuitos de México (https://www.conaliteg.sep.gob.mx/secundaria.html). Especialmente, para la enseñanza de las matemáticas a nivel secundaria se recomienda consultar a Ángeles, Guerrero y Loyola (2013).
El tema aquí tratado corresponde a una rama en particular de las matemáticas.
El álgebra tiene una gran presencia como contenido matemático en diferentes etapas en el sistema educativo, especialmente desde la secundaria obligatoria hasta la universidad, aunque en los últimos 20 años han surgido propuestas de incorporar ciertas cuestiones del pensamiento algebraico en la educación primaria (Socas, 2011, p. 5).
Generalmente, estos temas se trabajan de manera tradicional en la escuela secundaria y en el bachillerato. En palabras de Navarro (2018), “de profesores que transmiten y de alumnos que reciben información” (p. 195). El docente ofrece las fórmulas de la factorización para que los alumnos sustituyan los valores en estas y obtengan los resultados correspondientes. Esta acción, sin embargo, no les permite construir las reglas de cada binomio, por lo tanto, cada vez que requieren hacer uso de estas, tienen que ver un formulario de productos notables y factorización.
Aquí, por el contrario, se busca que los alumnos sean activos, no pasivos, que ellos sean los que promuevan ideas de resolución y que no tengan que esperar la explicación del profesor sobre el procedimiento que deberán seguir para resolver el problema (del Carmen, Alfonzo y Trejo, 2016). En esa línea, el docente debe cumplir más bien el rol de facilitador del aprendizaje, no de trasmisor del conocimiento.
La factorización se inicia en la educación primaria (Alarcón, 2005): cuando se calcula el mínimo común múltiplo en las operaciones de suma y resta de fracciones heterogéneas y también cuando se calcula el máximo común divisor. En la escuela secundaria, este contenido se tiene reservado para el tercer grado (Ángeles, 2013)
La pregunta de investigación de este trabajo es la siguiente: ¿construirán los estudiantes las reglas de los productos notables con las actividades didácticas diseñadas? Y la hipótesis es que los estudiantes pueden construir las reglas de los productos notables si analizan cada una de sus partes como multiplicaciones de las operaciones algebraicas.
Metodología
La investigación es cualitativa, exploratoria y explicativa. Se trata de conocer el comportamiento de los educandos, clarificar los problemas de enseñanza-aprendizaje de los productos notables y la factorización y explorar y explicar las causas de la carencia del dominio integral de los contenidos para que, posteriormente, se tomen las medidas pertinentes.
Para la elaboración de la secuencia didáctica, se siguió el siguiente procedimiento:
Se revisaron los textos de telesecundaria, secundaria general, técnicas y de nivel medio superior (telebachillerato).
A través de Google y Google Académico, se consultaron libros en formato digital que pudieran dar mayor información sobre el tema en cuestión.
Los apuntes de clase y planeaciones para tratar dicho contenido.
Se diseñó un posible índice para dar seguimiento a las actividades.
Fueron seleccionados algunos softwares graficadores para apoyar al diseño de la secuencia didáctica.
Se diseñó y aplicó la secuencia didáctica.
Se valoraron los resultados de la aplicación.
Se informa en el presente documento.
Productos notables
Leyes de los exponentes
Actividad 2. Con la fórmula de multiplicación x m x n = x m+n , realiza las siguientes expresiones algebraicas:
Actividad 3. Con la fórmula
Actividad 4. A través de la fórmula
x -2 , x -5 , x -9 , x -1 , x -6 , x -15 , x -12 , x -8 , x -20 y x -17
Actividad 5. Con la fórmula (x n ) m = x mn , realiza las siguientes operaciones de potencia:
Binomio cuadrado
Actividad 6. Encuentra el área de los siguientes cuadrados por partes coloreadas
Área del cuadrado A: _____ Área del cuadrado B: _____ Área del cuadrado C: ______
Actividad 7. Calcula el área que tiene sus lados en términos algebraicos.
Área: __________________ Área: __________________ Área: __________________
Actividad 8. Revisando patrones de regularidad, tenemos los siguientes productos, paso por paso:
Cuadrado D. (a + b)(a + b) = a 2 + ab + ab + b 2 = a 2 + 2ab + b 2
Cuadrado E. (x + 1)(x +1) = x 2 + x + x + 1 2 = x 2 + 2x + 1
Para analizar, vamos a simplificar los binomios de la siguiente manera:
(a + b)(a + b) = (a + b) 2 , (x + 1)(x + 1) = (x + 1) 2 y (x+3)(x + 3) = (x + 3) 2
Ahora tenemos lo siguiente con respecto al cuadrado D: el producto de los lados se representa como (a + b)2, cuyo producto es a 2 + 2ab + b 2
¿Cómo se obtienen los siguientes términos algebraicos?
Ahora tenemos lo siguiente con respecto al cuadrado E: el producto de los lados se representa como (x + 1)2, cuyo producto es x 2 + 2x + 1
¿Cómo se obtienen los siguientes términos algebraicos?
Ahora tenemos lo siguiente con respecto al cuadrado F: el producto de los lados se representa como (x + 3) 2 , cuyo producto es x 2 + 6x + 9
¿Cómo se obtienen los siguientes términos algebraicos?
Escribe una regla para obtener el producto de un binomio al cuadrado: “Es el cuadrado del__________________________________”.
Actividad 9. Con la regla obtenida, resuelve los siguientes binomios cuadrados:
(x + 5) 2 , (x - 2) 2 , (x + 9) 2 , (2x + 4) 2 , (3x - 2) 2 , (3x + 7) 2 , (5x + 10) 2 , (5x + 10) 2
Binomios conjugados
Actividad 10. Contesta las siguientes preguntas:
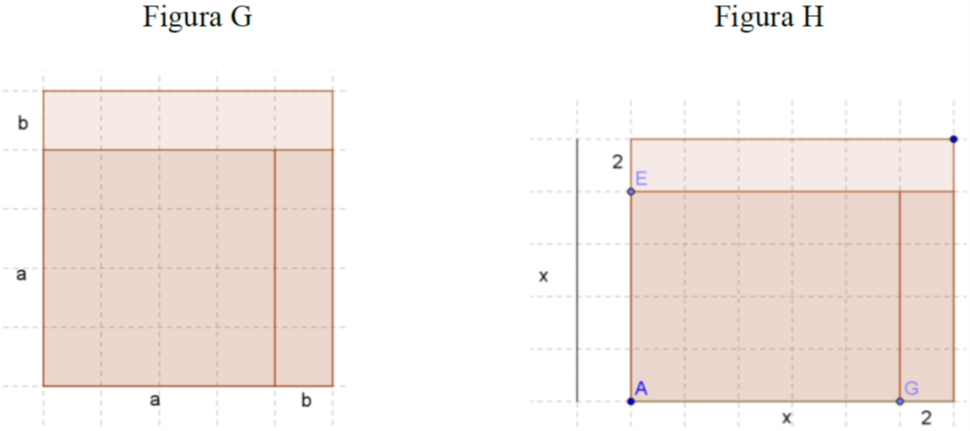
Actividad 11. Determina el área sombreada del color más fuerte de las siguientes figuras geométricas.
¿Qué expresión algebraica le corresponde a la base de la figura G?
¿Qué expresión algebraica le corresponde a la altura de la figura G?
¿Cuál es la expresión algebraica en términos de área de la figura G?
¿Qué expresión algebraica le corresponde a la base de la figura H?
¿Qué expresión algebraica le corresponde a la altura de la figura H?
¿Cuál es la expresión algebraica en términos de área de la figura H?
Actividad 12. Revisando patrones de regularidad, tenemos los siguientes productos, paso por paso:
Cuadrado D. (a + b)(a - b) = a 2 -ab +ab - b 2 = a 2 - b 2
Cuadrado E. (x + 2)(x - 2) = x 2 - 2x + 2x - 4 = x 2 - 4
De la figura G tenemos las siguientes observaciones: sus lados miden (a + b)(a - b), tienen un término común (a), tiene dos términos simétricos (b y - b), su producto se compone de una diferencia de dos términos cuadráticos, uno de ellos es el término común (a 2 ) y el otro es el término simétrico (b 2 ).
¿Cómo se obtienen los dos primeros términos algebraicos?
De la figura H tenemos las siguientes observaciones: sus lados miden (x + 2)(x - 2) tienen un término común (x), tiene dos términos simétricos (2 y -2), su producto se compone de una diferencia de dos términos cuadráticos, uno de ellos es el término común (x 2 ) y el otro es el término simétrico (4).
¿Cómo se obtienen los dos primeros términos algebraicos?
Escribe una regla para obtener el producto de los binomios conjugados: “Es el cuadrado del_______________________________________________________”
Actividad 13. Grafica en tu cuaderno los siguientes binomios conjugados y encuentra el área de cada uno de ellos, aplicando solamente la regla obtenida. Estos son:
(x + 1)(x - 1), (x + 3)(x - 3), (x + 5)(x - 5), (x -8)(x - 8), (x + 10)(x - 10)
Binomios con un término común
Actividad 14. Determina los lados y el área de cada una de las partes que conforman las siguientes figuras geométricas.
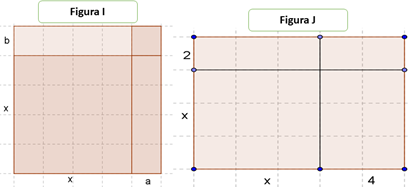
Fuente: Elaboración propia con base en Steven (2013)
Figura 5 Cuadrados que conforman binomios con un término común
¿Qué expresión algebraica le corresponde a la base de la figura I?
¿Qué expresión algebraica le corresponde a la altura de la figura I?
¿Cuál es la expresión algebraica en términos de área de la figura I?
¿Qué expresión algebraica le corresponde a la base de la figura J?
¿Qué expresión algebraica le corresponde a la altura de la figura J?
¿Cuál es la expresión algebraica en términos de área de la figura J?
De acuerdo con lo observado, podemos concluir que el producto de dos binomios con un término común se obtiene de la siguiente manera:
Escribe una regla para obtener el producto de los binomios con un término común: “Es el cuadrado del____________________________________________________”.
Actividad 15. Grafica en tu cuaderno los siguientes binomios con un término común y encuentra el área de cada uno de ellos, aplicando solamente la regla obtenida. Los binomios son los siguientes:
(x + 2)(x + 1), (x + 3)(x + 5), (x + 5)(x + 4), (2x + 8)(2x + 1), (3x + 10)(3x - 4)
La factorización de las expresiones algebraicas
El trinomio cuadrado perfecto
Actividad 16. Contesta las siguientes interrogantes:
Ahora sabemos que a un trinomio cuadrado perfecto factorizado le corresponde un binomio cuadrado. Un ejemplo:
a) a 2 + 2ab + b 2 = (a + b) 2
¿Cómo se obtiene el primer término del binomio cuadrado?
¿Cómo se obtiene el segundo término del binomio cuadrado?
¿Cómo se obtiene el signo que separa a las raíces obtenidas?
Resumen del procedimiento: dado el trinomio cuadrado perfecto, se procede de la siguiente manera:
a2 + 2ab + b2
Paso 1. Se extrae raíz cuadrada a los términos cuadráticos.
Paso 2. Ambas raíces son separadas por el signo del segundo término del trinomio.
Paso 3. Se encierra en un paréntesis las dos raíces separadas con el signo del segundo término del trinomio cuadrado perfecto y se eleva al cuadrado.
Paso 4. La expresión queda de la siguiente manera:
(a + b) 2
Actividad 17. Factoriza los siguientes trinomios (identifica cuáles son):
4x 2 + 24x + 36,25x 2 - 20x + 4, 9x 2 + 24x + 16, 49x 2 + 29x + 4
La diferencia de cuadrados
Actividad 18. Contesta las siguientes interrogantes:
Fíjate en las siguientes igualdades:
(a + b)(a - b) = a2 - b2
¿Cómo crees que se obtiene el término común (a)?
¿Cómo crees que se obtiene el término simétrico (b y -b)?
De acuerdo con lo que mencionaste, escribe una regla para pasar de una diferencia de cuadrados a dos binomios conjugados: “La raíz cuadrada del ____________________________________________________________________”.
Actividad 19. Utilizando la regla antes descrita, factoriza las diferencias de cuadrados de las siguientes expresiones algebraicas:
x 2 - z 2 , 9x 2 - 16y 2 , 49x 2 - 64, 4x 2 - 81, 25x 2 - 36
Binomios con un término común
Actividad 20. Contesta las siguientes interrogantes:
¿Recuerda cómo se obtiene un trinomio de segundo grado?
(x + 3)(x + 4) = x 2 + 7x + 12
El primer término se le llama término cuadrático (x2), el segundo se llama término lineal (7x) y el tercero término independiente o constante (12); mientras que los elementos de los binomios son: término común (x) y términos no comunes (3 y 4)
Contesta las siguientes interrogantes
Con los elementos del trinomio de segundo grado, ¿cómo se obtiene el término común?
Con los elementos del trinomio de segundo grado, ¿cómo se obtiene el término lineal?
Con los elementos del trinomio de segundo grado, ¿cómo se obtiene la constante?
Con el razonamiento anterior, se establece una regla para factorizar los trinomios de segundo grado:
x 2 + 7x + 12
Paso 1. Se abren dos paréntesis:
x 2 + 7x + 12 = ( )( )
Paso 2. Se extrae raíz cuadrada al término cuadrático y esta se coloca al principio de cada paréntesis.
Paso 3. Se buscan dos números que sumados den el término lineal y los mismos multiplicados entre sí sea igual a la constante.
( 3 ) + ( 4 ) = 7
( 3 ) ( 4 ) = 12
Paso 4. Estos números de color rojo se colocan en los paréntesis, y quedan de la siguiente forma:
x 2 + 7x + 12 = (x + 3) (x + 4)
Con el procedimiento anterior, factoriza los trinomios de segundo que se indican a continuación:
Resultados de la intervención
Se pueden considerar de buenos a excelentes, puesto que los estudiantes normalistas comprendieron los dos temas, productos notables y factorización, que se estudian en el primer bloque del tercer grado en telesecundaria. Si se toman en cuenta las competencias matemáticas en la educación secundaria:
Resolver problemas de manera autónoma.
Comunicar información matemática.
Validar procedimientos y resultados.
Manejar técnicas eficientemente.
Las cuatro competencias matemáticas se lograron con los alumnos normalistas.
Tabla 1 Rúbrica de productos notables y factorización
| Criterios de evaluación | Niveles de desempeño | |||
| Excelente | Bueno | Suficiente | Insuficiente | |
| Resolver problemas de manera autónoma |
|
|
|
|
| Criterios de evaluación | Niveles de desempeño | |||
| Excelente | Bueno | Suficiente | Insuficiente | |
| Comunicar información matemática |
|
|
|
|
| Criterios de evaluación | Niveles de desempeño | |||
| Excelente | Bueno | Suficiente | Insuficiente | |
| Validar información matemática |
|
|
|
|
| Criterios de evaluación | Niveles de desempeño | |||
| Excelente | Bueno | Suficiente | Insuficiente | |
| Manejar técnicas eficientemente |
|
|
|
|
Fuente: Elaboración propia
Discusión
El objetivo del trabajo de Osorio (2008), a saber, “encontrar significado a las relaciones de equivalencia entre las expresiones que refiere a la medida de las figuras (congruencias entre longitudes, equivalencia entre magnitudes) y comprender esos significados” (p. 3), lo llevó al diseño de materiales manipulables para que sus estudiantes modelaran las figuras geométricas. Mientras que en este trabajo el procedimiento fue vincular la parte geométrica con la algebraica, después obtener el producto de varias parejas de binomios, para llegar a construir la regla que regirá y así obtener el producto.
Gómez (2015), por su parte, afirma que el estudiante aprende a factorizar cuando se implementa el texto paralelo y la resolución de problemas, puesto que “expresa por escrito lo comprendido en su lectura, soluciona y resuelve problemas de factorización” (p. 5).
En cuanto a los productos notables, Barreto (2009) se ocupa de figuras geométricas como cuadrados y rectángulos para representar a los binomios que se multiplicarán para calcular el área.
Hay trabajos cuyo enfoque es análogo al aquí aplicado pero puesto en práctica en otros contextos. Por ejemplo, para Graciano y Aké (2017):
El interés es la búsqueda de aportaciones para la formación de profesores y la mejora de la práctica en el aula. Al respecto, los resultados que se obtuvieron a través de un cuestionario de respuesta abierta rescatan inconsistencias principalmente en el conocimiento especializado del contenido de productos notables, pero también se reconocen áreas de oportunidad para su fortalecimiento (p. 1320).
Asimismo, el diseño de las secuencias didácticas de Tobón (2017) son asertivas para el logro del objetivo del presente trabajo de investigación, puesto que se tomaron en cuenta las tres fases: en la primera fase, se manejaron contenidos aritméticos o algebraicos que se utilizaron en una segunda fase, donde se abordaron los contenidos matemáticos. Así pues, se trata de dar las bases cognitivas para realizar las multiplicaciones, las cuales se llevaron a cabo en los tres primeros temas.
Además, el aprendizaje colaborativo, según Maldonado (2007), es “un proceso social que se construye en la interacción no solo con el profesor, sino también con los compañeros, con el contexto y con el significado que se le asigna a lo que se aprende” (p. 265).
Por eso, se fomentó durante toda la secuencia didáctica, lo cual resultó favorable al aprendizaje, debido a que algunos alumnos destacaron más que otros, como suele suceder en la mayoría de las clases, y esto se aprovechó para que fungieran como monitores de grupo y dieran apoyo a sus compañeros, puesto que hablan el mismo lenguaje “técnico”.
Se considera importante mencionar que las limitaciones del estudio se refieren a la aplicación de problemas contextuales, puesto que el tratamiento didáctico se dio dentro de la matemática formal, la cual permite sentar las bases para la resolución de problemas; en cuanto a las áreas de debilidades, se puede mencionar al tiempo destinado en la malla curricular para la enseñanza de la matemática, ya que solo se cuentan con dos cursos del total de materias de la licenciatura.
Conclusiones
En donde se presentaron más dudas cognitivas fue en la representación geométrica de los binomios conjugados, puesto que ahí se manejaban términos negativos. De los 20 alumnos con quienes se trabajó, solamente tres de ellos tuvieron algunas dificultades cognitivas, esto se debe a sus antecedentes aritméticos débiles, por lo que durante su carrera profesional deben fortalecer estos puntos débiles para llevar a cabo sus prácticas profesionales y ser excelentes profesionistas.
Con esta aplicación de actividades secuenciadas, los alumnos en formación se dieron cuenta de que los conocimientos estudiados en otros niveles educativos realmente pueden analizarse de ida y vuelta. En este caso, cuando desarrollaban un binomio cuadrado lo que obtenían era el trinomio cuadrado perfecto, del cual, al factorizarse (expresar una suma en un producto), se obtiene el binomio cuadrado; lo mismo sucede con los demás binomios: al obtener su producto y después factorizarse, se regresa a la primera expresión algebraica.
No solo comprendieron a los productos notables desde el punto de vista algebraico, sino también geométrico y en su forma verbal; esto significa que se lograron las competencias matemáticas, tal y como se mencionan en el programa de estudios.
Por otra parte, fue interesante que contestaran al principio de cada binomio lo que ellos sabían del tema y después contrastaran esto con lo aprendían al final de la secuencia. Uno de los contenidos que les resultó de mayor facilidad en la obtención de la regla fue el de los binomios conjugados, puesto que solo multiplicaban los términos comunes y simétricos para llegar al resultado, el cual también tiene su nombre específico, diferencia de cuadrados.
Los binomios con los que tuvieron mayor dificultad fueron los que poseen un término común, estos producen un trinomio de segundo grado con características diferentes a los anteriores.
Desde el punto de vista personal, es importante que se continúen haciendo este tipo de trabajos para beneficio de los alumnos. La función que se realizó de parte de quien diseñó esta secuencia fue la de facilitador del aprendizaje: los estudiantes normalistas fueron constructores de su saber, de tal manera que al final de cada caso, concluyeron con la regla que ayuda a resolver los productos o la factorización.
Lo importante de esta secuencia es el razonamiento que se genera al trabajar con los estudiantes de manera grupal, por equipos y de manera individual; se genera un ambiente de aprendizaje favorable para que los estudiantes pregunten con la confianza debida, porque se sabe que ellos serán los futuros profesores.
Por último, las futuras líneas de investigación se pueden dar en el planteamiento de problemas que impliquen el uso de los productos notables y la factorización, con la finalidad de resolver problemas profesionales desde el punto de vista de la economía.











 nueva página del texto (beta)
nueva página del texto (beta)