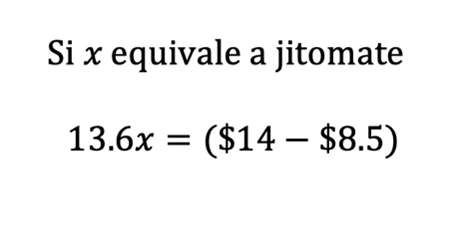Introducción
Debido a los problemas ocasionados por la covid-19, actualmente nos encontramos en una etapa de reconstrucción de la enseñanza y del aprendizaje, la cual ha tenido que sustentarse en estrategias de enseñanza remota de emergencia para atender las necesidades educativas de la población. Como lo cometan Hodges, Moore, Lockee, Trust y Bond (2020), el objetivo principal ha sido proporcionar acceso a la instrucción, así como apoyos pedagógicos que permitan dar continuidad a las actividades educativas y capacitación a los profesores para impulsar el trabajo colaborativo y la enseñanza en entornos virtuales.
Sin embargo, según datos de la Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura (Unesco, 2020), la actual emergencia sanitaria ha provocado que casi 85 % de los alumnos a nivel mundial no pueda desarrollar normalmente sus actividades académicas debido, principalmente, a problemas relacionados el escaso acceso a las tecnologías de la comunicación. En México, por ejemplo, según la Encuesta Nacional sobre la Disponibilidad y Uso de Tecnologías de la Información en los Hogares (Endutih) (Instituto Nacional de Estadística Geografía e Informática [Inegi], 2018), solo 47 % de los habitantes tiene conexión a internet, 52.4 millones de personas viven en situación de pobreza y 9.3 millones en pobreza extrema. Además, 21.1 millones de personas sufren rezago educativo (Consejo Nacional de Evaluación [Coneval], 2018).
Esta realidad es preocupante porque suele afectar con más crudeza a las poblaciones vulnerables (Rojas Maldonado, 2020a), las cuales suelen quedar a la expectativa de las iniciativas humanitarias llevadas a cabo por el Estado. En el caso de México, las estrategias políticas del gobierno en materia educativa para encarar la emergencia sanitaria se han enfocado en procurar que las actividades escolares se mantengan de forma virtual. Sin embargo, la cotidianidad ha demostrado que tanto para profesores y como para estudiantes el proceso de enseñanza y aprendizaje se ha visto entorpecido de manera considerable.
Por este motivo, el objetivo del presente trabajo fue diseñar un instrumento que permitiera determinar, en el marco de la actual emergencia sanitaria generada por el virus SARS-CoV-2, los conocimientos matemáticos previos en torno al concepto límite de alumnos del bachillerato de Ingeniería y Arquitectura (sección 1) del Colegio Primitivo y Nacional de San Nicolás de Hidalgo.
El concepto de límite resulta esencial para la construcción del cálculo diferencial, para encarar con éxito los estudios universitarios relacionados con la matemática y para impulsar la comprensión y el desarrollo tecnológico en la que se basa actualmente nuestra civilización (Cottrill et al., 1996), y ha sido abordado por algunos autores (Artigue, 1998; Cornu, 1991), quienes han demostrado las incorrectas apreciaciones de los alumnos sobre dicho concepto. Para mejorar su comprensión se han aplicado diversas estrategias que se han apoyado en herramientas tecnológicas, las cuales han permitido conseguir resultados ligeramente superiores a los alcanzados con la enseñanza tradicional (Rojas Maldonado, 2015, 2016, 2019).
Marco teórico y antecedentes
De forma general, se puede afirmar que si bien existen investigaciones que se pudieran vincular con el objetivo principal del presente trabajo, en realidad son pocas las que se enfocan en el estudio de los conocimientos previos de los estudiantes en torno al concepto límite en medio de una situación tan particular como la generada por la actual pandemia. Aun así, se pueden rescatar indagaciones como las de Mota Villegas y Valles Pereira (2015), quienes no solo explican la importancia del estudio estructurado de los conocimientos matemáticos previos de alumnos que comienzan en la universidad, sino que también demuestran lo incompleto que pueden ser los instrumentos usados hoy en día para medir tales conocimientos.
Por su parte, Urbina (2009) afirma que la evaluación de los conocimientos iniciales ayuda al docente a determinar el grado de profundidad con que se debe tratar un tema, así como las estrategias que puede emplear para que el alumno asimile los nuevos significados del objeto de aprendizaje ofrecido. Al respecto, el referido autor afirma lo siguiente:
Durante los últimos 20 años, las investigaciones en educación matemática han estado marcadas por el paradigma constructivista. Las ideas claves de este paradigma provienen o tienen sus raíces en investigaciones de muchos autores, entre los cuales se destacan: Piaget, Wallon, Vygotsky, Bruner, Dewey, Gagné, Ausubel, Novak y Henesian, entre otros. Todos ellos han coincidido en que aprender cualquier contenido escolar supone desde la concepción constructivista, atribuir un sentido y construir los significados implicados en dicho contenido, y que esta construcción no se lleva a cabo partiendo de cero (Urbina, 2009, p. 2).
En este sentido, Pino-Fan, Godino y Vincenç (2013) diseñan y aplican un instrumento para explorar la faceta epistémica del conocimiento didáctico-matemático de futuros profesores sobre la derivada. Estos autores demuestran que los objetos matemáticos, sus significados y los procesos identificados en las soluciones plausibles de las tareas se adaptan a los objetos matemáticos, sus significados y los procesos involucrados en las configuraciones cognitivas (análisis ontosemiótico cognitivo) asociadas a las respuestas de los profesores de formación inicial.
Asimismo, Ndjatchi (2019) diseña un instrumento para determinar los conocimientos matemáticos previos y las debilidades de un alumno de la carrera de sistemas computacionales antes de tomar el curso de números complejos. De igual manera, Morantes Moncada, Dugarte Peña y Herrera Díaz (2019) -a partir de la revisión de las habilidades de planificación, control y revisión de las actividades de aprendizaje-caracterizan el perfil de un estudiante estratégico para el análisis del cálculo diferencial en el tema funciones y sus gráficas.
Sin embargo, en numerosas investigaciones (Artigue, 1988; Rojas Maldonado, 2018, 2019, 2020b; Tall, 1995) se indica escasa capacidad para establecer una simbiosis entre la representatividad geométrica y simbólica por parte de los alumnos, habilidad esencial para la abstracción de la matemática (Ndjatchi, 2019). Peña, Murillo, Rodríguez, Cedillo y Green Arrechavala (2014) lo explican de este modo:
Los errores de los estudiantes no son casuales, se basan en conocimientos y experiencias previas, y son motivados por diferentes causas didácticas, epistemológicas, cognitivas o actitudinales. Observamos de esta forma que los errores aparecen en el trabajo de los alumnos principalmente cuando se enfrentan a conocimientos novedosos que los obligan a hacer una revisión o reestructuración de lo que ya saben (p. 48).
Durante la enseñanza y el aprendizaje, como lo menciona Ndjatchi (2019), “pueden surgir dificultades relacionadas a su propia naturaleza, otras por las circunstancias de enseñanza, otra de los profesores y su metodología didáctica” (p. 309), lo cual es congruente con lo señalado por autores como Artigue (1988), Cottrill et al. (1996), Rojas Maldonado (2018, 2019) y Tall (1995). Por ello, antes de elegir una metodología didáctica para desarrollar el quehacer educativo se debe conocer en detalle las dificultades que los alumnos enfrentan.
Resulta apropiado tener en cuenta los conocimientos iniciales de los estudiantes y establecer una relación coherente entre lo que los alumnos saben y los nuevos conocimientos. En caso contrario, se generarían dificultades innecesarias y falta de confianza de los alumnos para afrontar el nuevo conocimiento (Urbina, 2009).
Al respecto, se debe tener en cuenta que el aprendizaje significativo surge cuando el anclaje relacional entre un contenido existente y uno nuevo se halla claro y disponible en la estructura cognitiva del estudiante (Ausubel, 1983), por lo que puede establecer similitudes y diferencias de forma no arbitraria. Por ello, Ausubel (1983) precisa lo siguiente:
La adquisición de información nueva depende en alto grado de las ideas pertinentes que ya existen en la estructura cognitiva y el aprendizaje significativo de los seres humanos ocurre a través de una interacción de la nueva información con las ideas pertinentes que ya existen en la estructura cognitiva (p. 7).
Estos conocimientos previos, como explica López Recacha (2009), son construidos de manera personal por cada individuo mientras interactúa con personas u objetos, y deben ser aprovechados para evitar el aprendizaje memorístico, el cual dista mucho del aprendizaje significativo de Ausubel. Es cierto que en muchos casos los conocimientos previos pueden ser olvidados de manera temporal, pero con un rápido recordatorio los alumnos son capaces de recobrar el significado y las implicaciones.
Ahora bien, en cuanto a los instrumentos usados para determinar los conocimientos previos de los estudiantes, primero se debe tener clara la conceptualización del constructo que se quiere evaluar, así como sus estándares de ejecución y sus respectivos indicadores de evaluación (García, 2018). Como lo comenta Soriano Rodríguez (2015), todo proceso de medición en una investigación debe trascender de la confiabilidad a la validez. Para ello, el instrumento deberá ser producto de una articulación entre paradigma, epistemología, perspectiva teórica, metodología y técnicas para la recolección y análisis de datos. En tal sentido, un instrumento es válido si mide lo que dice medir, mientras que la confiabilidad se enfoca en la probabilidad de obtener los mismos resultados.
Finalmente, un aspecto que procuran quienes realizan una investigación es la necesidad de que el instrumento seleccionado sea óptimo para recabar los datos y tenga un alto nivel de fiabilidad, en especial cuando estos basan su validez en la información verbal de percepciones, sentimientos, actitudes o conductas ( Tuapanta Dacto, Duque Vaca, A. y Mena Reinoso, 2017), de ahí que Jiménez Alfaro y Montero Rojas (2013) consideren que su diseño debe apoyarse en un proceso de perfección continua.
Objetivo
Diseñar un instrumento para determinar, en el marco de la actual emergencia sanitaria generada por el virus SARS-CoV-2, los conocimientos matemáticos previos en torno al concepto límite de alumnos del bachillerato de Ingeniería y Arquitectura (sección 1) del Colegio Primitivo y Nacional de San Nicolás de Hidalgo.
Metodología
Para el diseño del instrumento se siguieron las cuatro fases de construcción que establece Soriano Rodríguez (2015), es decir, 1) objetivos, teoría y constructo, 2) validación juicio de expertos, 3) prueba piloto y 4) validación psicométrica, las cuales se detallan a continuación:
Desarrollo
Fase 1. Objetivos, teoría y constructo
Como parte del proceso del diseño, se efectuó el análisis del programa académico de la materia Cálculo Diferencial con el fin de identificar las necesidades académicas mínimas de la unidad temática límite. Posteriormente, se creó un banco de problemas que han sido estudiados en diversas investigaciones enfocadas a la didáctica del cálculo y que han sido considerados en exámenes de admisión a nivel profesional. Luego, se seleccionaron los reactivos que satisficieran los criterios de la faceta epistémica: 1) conocimiento común 2) conocimiento especializado y 3) conocimiento ampliado (Loewenberg Ball, Hoover Thames y Geoffrey, 2008; Loewenberg Ball, Theule Lubienski y Spangler Mewborn, 2001).
El instrumento fue estructurado para reflejar los saberes académicos previos, como la habilidad aritmética y la habilidad algebraica, con el fin de identificar la resolución de problemas y la construcción de conocimiento matemático.
El diseño del instrumento estuvo enfocado en considerar distintos niveles de algebrización y aritmetización (Godino et al., 2015), pues se buscó la conciencia de la progresión del aprendizaje, así como alertar al docente de las dificultades pertinentes (conceptuales, proposicionales, procedimentales y argumentativas). Para ello, se procedió del siguiente modo (Godino et al., 2015):
Clasificamos el contenido que se ha de evaluar según dos variables: contenido algebraico y contenido didáctico. Para la variable contenido algebraico consideramos tres valores o categorías, en las cuales a su vez se pueden distinguir diversas subcategorías:
- Estructuras: Relación de equivalencia; propiedades de las operaciones, ecuaciones, etc.
- Funciones: Patrones aritméticos, patrones geométricos; función lineal, afín, cuadrática, etc.
- Modelización: Problemas de contexto resueltos mediante el planteamiento de ecuaciones o relaciones funcionales.
Debido a la pandemia, el instrumento fue aplicado a través de Google Forms, herramienta que permitió que los ítems se ordenaran de forma aleatoria y fueran respondidos en un tiempo limitado. En la Figura 1 se estructura el conocimiento matemático común, enfocado en la faceta epistémica, es decir, reconocimiento de procesos algebraicos y aritméticos (conceptos, procedimientos, propiedades, generalización, etc.).
En el anterior nivel los alumnos no requerían una capacidad de análisis o reflexión, sino seguir un mecanismo procedimental.
Por otra parte, en cuanto a las subcategorías de clasificación de contenido, estructuras y funciones de la faceta epistémica conocimiento especializado, en la Figura 2 se evidencia que si bien existe un procedimiento para la resolución del problema, en realidad exige una capacidad de análisis y razonamiento, así como la identificación de distintas variables que involucran propiedades, argumentos y procedimientos.
Dicha noción favorece no solo la identificación sistemática de diferentes procedimientos de resolución, modalidades de expresión, conceptos y propiedades que se ponen en juego en su formulación, sino también la identificación de argumentaciones o justificaciones de los procedimientos y las propiedades (Pino-Fan, Godino, Castro y Font, 2012).
Realizando un análisis epistémico de la Figura 2, se puede señalar lo siguiente:
Proceso de representación
Se pueden identificar elementos a través de la diferenciación, los cuales el alumno debe de ser capaz de distinguir. Asimismo, debe conocer el proceso al que debe de recurrir para establecer una conexión biunívoca que le permita ubicar y seleccionar las variables en una expresión matemática; por ejemplo, la variable X representará a los jitomates, Z a las zanahorias, etc., lo que concierne a una representatividad simbólica o notacional, señalando la correlación entre los dos ítems en sus respectivos momentos. Esto proporciona información que pudiera servir tanto al docente para ajustar su método de enseñanza como al alumno para identificar una debilidad matemática o lógica.
El proceso de representación es parte fundamental para la resolución de problemas, pues su desarticulación lleva a la síntesis, lo cual se representa a través de una gráfica o simbología (reestructura del fenómeno) que para el caso que nos atañe es el límite.
Proceso de composición-descomposición
Identificadas las variables del proceso anterior, se pueden discernir los elementos que respondan a similitudes.
Como lo indican Pino-Fan et al. (2012), “análisis similares pueden realizarse con otras resoluciones de la tarea, que pongan en juego otros procedimientos y justificaciones que involucren distintos elementos lingüísticos, conceptos y proposiciones. En este sentido los procesos de significación no tienen configuraciones únicas” (p. 431). Más adelante, en la Figura 4, se muestra también claramente este proceso, el cual requiere de una mayor capacidad de síntesis, análisis y reflexión.
Proceso de particularización-generalización
En la Figura 3 se partía de un hecho particular que bien puede generalizarse para cada uno de los elementos citados en la Figura 2, es decir, se generaliza para cebollas, chiles, etc. Es de percatarse que está estrechamente vinculado a la transición del conocimiento común y avanzado.
Proceso de materialización-idealización
En este proceso se exploran los conocimientos específicos sobre alguna área de las matemáticas que requieren mayor capacidad de análisis y reflexión por parte del discente, como se muestra en la Figura 4, donde muchas veces se pueden contraponer ideas o conocimientos que ocasionan una disonancia.
Como lo sugiere Godino et al. (2015), en cada ítem incluimos la solución esperada, así como tres respuestas distractoras incorrectas: los objetos y los procesos que se manifiestan para la resolución, el nivel de dificultad correspondiente a la actividad académica y las categorías del conocimiento didáctico-matemático implicadas según la Tabla 1.
Tabla 1 Categorías de conocimiento didáctico-matemático
| Contenido didáctico | Contenido algebraico | |||||
| Estructuras (E) | Funciones (F) | Modelización (M) | ||||
| Primaria | Avanzado | Primaria | Avanzado | Primaria | Avanzado | |
| Epistémico (niveles de algebrización) | EPI-E1 | EPI-E2 | EPI-F1 | EPI-F2 | EPI-M1 | EPI-M2 |
| Cognitivo (significados personales) | COG-E1 | COG-E2 | COG-F1 | COG-F2 | COG-M1 | COG-M2 |
| Instruccional (situaciones y recursos) | INS-E1 | INS-E2 | INS-F1 | INS-F2 | INS-M1 | INS-M2 |
| Contenido algebraico | ALG-E1 | ALG-E2 | ALG-F1 | ALG-F2 | ALG-M1 | ALG-M2 |
Fuente: Godino et al. (2015)
Fase 2. Validación juicio de expertos
Elaborados y depurados los ítems, se solicitó apoyo a tres profesores con experiencia en la materia que se encargaron de evaluar tanto la viabilidad de los reactivos como su redacción.
Fase 3. Prueba piloto
En la Tabla 2 se muestra el índice de dificultad en la prueba piloto, la cual fue aplicada a 14 participantes. El índice [0.100] con 100 representa a un ítem muy fácil, donde todos los alumnos respondieron acertadamente; asimismo, se representa el error típico de los estudiantes que permite construir intervalos de confianza de las estimaciones.
Tabla 2 Índice de dificultad
| Momento 1: Aritmética | Momento 2: Algebra | ||||
| Ítem | Índice de dificultad | Error típico | Ítem | Índice de dificultad | Error típico |
| 1 | 79.5 | 13.6 | 1 | 68.1 | 27.7 |
| 2 | 93.2 | 6.8 | 2 | 45.7 | 30.4 |
| 3 | 61.9 | 14.3 | 3 | 44.7 | 23.4 |
| 4 | 86 | 9.3 | 4 | 78.7 | 14.9 |
| 5 | 61.4 | 36.4 | 5 | 65.2 | 19.6 |
| 6 | 86.4 | 11.4 | 6 | 58.7 | 28.3 |
| 7 | 97.7 | 2.3 | 7 | 41.3 | 28.3 |
| 8 | 75.6 | 19.5 | 8 | 29.3 | 39 |
| 9 | 47.6 | 40.5 | 9 | 67.4 | 17.4 |
| 10 | 63.6 | 36.4 | |||
| 11 | 56.1 | 17.1 | |||
| 12 | 93.2 | 4.5 | |||
| 13 | 60.5 | 23.3 | |||
| 14 | 6.8 | 65.9 | |||
Fuente: Elaboración propia
Fase 4. Validación psicométrica
En esta fase se aseguró el funcionamiento de cada uno de los ítems, así como su descarte (como se muestra en la Tabla 2). Luego se procedió al cálculo del coeficiente de fiabilidad de consistencia interna (alfa de Cronbach) a través del software SPSS (versión 25). Como se muestra en la Tabla 3, se consiguió un coeficiente de 0.807 (muy buena confiabilidad), lo que indica que estos resultados se pueden reproducir en diferentes muestras sin que constituyan un gran sesgo por parte de los participantes. Además, los puntajes de cada pregunta fueron consistentes con el puntaje total del instrumento.
Tabla 3 Estadística de fiabilidad
| Alfa de Cronbach | N.° de elementos |
| .807 | 14 |
Fuente: Elaboración propia
En la Figura 5 se observa cómo el instrumento fue sometido a la prueba de unidimensionalidad del constructo a través del estudio del gráfico de sedimentación en el programa SPSS.
Finalmente, en la Tabla 4 se muestra el porcentaje de varianza del primer componente, que fue mayor a 20, así como el resto menores a 10 (excepto el 2 y 3), por lo que no puede ser considerado como un instrumento multidimensional.
Tabla 4 Análisis de varianza de prueba piloto
| Varianza total explicada | |||||||||
| Autovalores iniciales | Sumas de cargas al cuadrado de la extracción | Sumas de cargas al cuadrado de la rotación | |||||||
| Componente | Total | % de varianza | % acumulado | Total | % de varianza | % acumulado | Total | % de varianza | % acumulado |
| 1 | 3.278 | 23.412 | 23.412 | 3.278 | 23.412 | 23.412 | 2.454 | 17.526 | 17.526 |
| 2 | 2.257 | 16.118 | 39.530 | 2.257 | 16.118 | 39.530 | 2.257 | 16.121 | 33.647 |
| 3 | 1.644 | 11.742 | 51.272 | 1.644 | 11.742 | 51.272 | 1.677 | 11.981 | 45.627 |
| 4 | 1.290 | 9.216 | 60.488 | 1.290 | 9.216 | 60.488 | 1.609 | 11.495 | 57.122 |
| 5 | 1.245 | 8.895 | 69.383 | 1.245 | 8.895 | 69.383 | 1.373 | 9.807 | 66.928 |
| 6 | 1.007 | 7.195 | 76.578 | 1.007 | 7.195 | 76.578 | 1.351 | 9.650 | 76.578 |
| 7 | .816 | 5.829 | 82.407 | ||||||
| 8 | .610 | 4.356 | 86.763 | ||||||
| 9 | .560 | 3.998 | 90.762 | ||||||
| 10 | .462 | 3.299 | 94.061 | ||||||
| 11 | .379 | 2.704 | 96.765 | ||||||
| 12 | .259 | 1.848 | 98.614 | ||||||
| 13 | .120 | .855 | 99.468 | ||||||
| 14 | .074 | .532 | 100.000 | ||||||
| Método de extracción: análisis de componentes principales. | |||||||||
Fuente: Elaboración propia
Conclusiones
La elaboración del instrumento analizado en este trabajo puede ser una herramienta muy útil no solo para detectar los conocimientos previos que los alumnos tienen en cuanto al cálculo diferencial, sino principalmente para crear estrategias didácticas que permitan atender esas debilidades a partir de los estilos de aprendizaje de los estudiantes. Además, se debe prever que, debido a la pandemia, estamos viviendo una época en donde las clases presenciales han sido sustituidas por encuentros virtuales, los cuales exigen métodos de enseñanza y aprendizaje diferentes a los tradicionales.
Para el alumno, por tanto, este instrumento también puede representar una oportunidad no solo para conocer sus debilidades en la materia, sino para emprender acciones que permitan cambiar esa realidad. Al respecto, los estudiantes deben ser conscientes de la responsabilidad que tienen en sus procesos de aprendizaje, lo cual se ha convertido en una necesidad para encarar los retos que han surgido en estos tiempos de covid-19. En efecto, la pandemia evidenció que no basta solo con aprobar las asignaturas, pues el aprendizaje es una labor diaria que demanda mucho esfuerzo independiente, así como, lógicamente, la aplicación de estrategias idóneas que se ajusten a esta nueva realidad.
Futuras líneas de investigación
En primer lugar, se considera prioritaria la creación de diversos instrumentos que permitan al docente diagnosticar el nivel de conocimientos que sus alumnos tienen en determinada materia, pues de ese modo se podrán implementar estrategias que atiendan esas necesidades (Rojas Maldonado, 2015). Sin embargo, después de desarrollar esas actividades propuestas también será indispensable que se efectúen investigaciones para determinar si con ellas se consiguieron los resultados esperados.











 text new page (beta)
text new page (beta)