Introducción
Los modelos de ecuaciones estructurales (SEM) como hoy se conocen tienen su origen en el año de 1918, cuando el genetista Sewall Wright esbozó por primera vez un modelo de trayectorias para describir la contribución genética entre compañeros de camada1. Sin embargo, no fue hasta fines de los años 70 cuando otros investigadores reconocieron la importancia de estas primeras contribuciones y comenzaron a trabajar el modelo de trayectorias. Nombres como Lawley (1940), Boudon (1965), Duncan (1969), Wiley (1969), Blalock (1970), Keesling (1972), Jöreskog (1978), Sörbom (1978) y Satorra (1985) son clave para el desarrollo de esta metodología.
El estadístico sueco Jöreskog y Sörbom desarrollaron en los años 70 el primer programa estadístico, conocido como Linear Structural Relations (LISREL) 2, que permitió estimar y probar los modelos de ecuaciones estructurales. Por otro lado, Jöreskog extendió el análisis factorial exploratorio concebido por Lawley3 en un modelo factorial confirmatorio4. Otros paquetes estadísticos que se desarrollaron fueron EQS (Bentler, 1985) y AMOS (Arbuckle, 2003). En la actualidad, es posible utilizar también STATA5 y R6 para estimar estos modelos.
El SEM es considerado una herramienta estadística multivariada, también conocida como análisis de estructura de covarianzas. Estos modelos permiten probar la relación (no causalidad) que hay entre variables observadas y latentes7. Una variable observada es aquella que es posible medir de manera directa, como la edad o la estatura, y una latente no se puede medir directamente (la inteligencia, la motivación, la depresión o el estrés), por lo tanto, se utilizan otras variables observadas para medirlas8.
Cuando el modelo de ecuaciones estructurales se compone únicamente de variables observadas (path analysis)9, puede tener similitud con el análisis de regresión lineal clásico; sin embargo, una cualidad que lo hace atractivo sobre la regresión es que es posible estimar el efecto (o relación) indirecto y total que tiene una variable sobre otra10.
Tipo de modelos y representación gráfica
Hay 2 tipos de modelos: los que involucran solo variables observadas (path analysis) y los que mezclan variables observadas y latentes: análisis factorial confirmatorio y modelo estructural11,12. Su diferencia radica en que, en el primer caso, se busca estimar la correlación entre las variables latentes, mientras que en el segundo se pretende estimar además su asociación13.
Para plantear las ecuaciones asociadas al modelo, es necesario que en primer lugar se represente gráficamente. Una variable observada se simboliza por medio de un cuadrado, una latente por un círculo o elipse, una asociación con una flecha unidireccional y una correlación con una flecha bidireccional. En la Figura 1 se muestra un modelo estructural que contiene 3 variables latentes ξ1, η2 y η2. La primera corresponde a una variable latente independiente (ξ1) ya que a ella no llega ninguna flecha y, por el contrario, las otras 2 (η2 y η2) son dependientes ya que les llega al menos una flecha. Cada una de estas 3 variables latentes está medida a través de 3 variables observadas. Nótese que se destacan las observadas asociadas a la latente independiente como X, mientras que para las latentes dependientes con Y.

Figura 1 Ejemplo de un modelo de ecuaciones estructurales con 3 variables latentes, cada una de ellas medida a través de 3 variables observadas.
Se define el efecto directo como la relación inmediata que hay entre una variable y otra, el efecto indirecto como la relación entre 2 variables, mediada al menos por otra diferente de estas. y el efecto total como la suma del efecto directo e indirecto14 . En el caso de la Figura 1, los efectos directos entre latentes son las trayectorias que van de ξ1 a η2 (coeficiente γ12), de η2 a η3 (coeficiente β32) y de ξ1 a η3 (coeficiente γ31). El único efecto indirecto es el que va de ξ1 a η2 pasando por η2 (coeficientes γ21 y β32) y, por lo tanto, el efecto total de ξ1 a η3 estaría dado por la suma de los coeficientes de las trayectorias ξ1 η2 +ξ1 η2 η3, esto es, γ31 +(γ21*β32). Las letras representadas como δ, ε y ζ corresponden a los errores asociados a las variables observadas y a las latentes dependientes.
Parámetros del modelo
En los SEM se pueden estimar los siguientes parámetros: todos los coeficientes que conectan a variables latentes con sus respectivas variables observadas, los que conectan a latentes con latentes, los que conectan observadas con observadas, las varianzas de variables independientes y las covarianzas entre ellas, las varianzas de los errores asociados a variables dependientes y las covarianzas entre ellas. A estos parámetros se los denomina libres. En el caso de que el investigador tenga una hipótesis acerca del valor que debería tomar un parámetro podrá establecerlo y, por lo tanto, ya no será libre, sino fijo. Un requisito fundamental es que se tiene que fijar la escala de cada una de las variables latentes del modelo. Para hacer esto, hay 2 caminos:
Identificabilidad del modelo
Se dice que un modelo es identificable si es posible encontrar un valor único para cada uno de los parámetros del modelo. Un modelo no puede ser identificable si se establece como parámetro libre a uno que por definición no es parámetro estimable, por ejemplo, una correlación entre variables dependientes. Cuando el modelo tiene más parámetros fijos que ecuaciones, entonces al menos un parámetro se expresará en términos de otro y, por lo tanto, no tiene un valor único (solución única) o cuando encontramos valores poco plausibles como, por ejemplo, varianzas negativas. Existen reglas que permiten determinar si el modelo planteado es identificable; estas varían dependiendo del tipo de modelo. La regla más sencilla y que aplica a todos los modelos es la regla t. En ella se establece que el número de parámetros libres (t) tiene que ser menor o igual al número de variables observadas del modelo (p) entre 2.t ≤
Sin embargo, además de esta regla se deben utilizar otras en conjunto para asegurar la identificabilidad15. Aunque en este trabajo no se profundiza en este tema, se deja al lector el nombre de estas reglas para que pueda revisarlas con detenimiento. Para los modelos de análisis de trayectoria: regla de la B nula, regla recursiva, regla de condición de rango y orden; para el modelo confirmatorio: regla de 2 variables observadas y de 3 variables observadas, y para el modelo estructural: regla de los 2 pasos y regla MIMIC16 .
Estimación del modelo
La principal hipótesis que se contrasta es que la matriz de varianzas y covarianzas poblacional (Σ) es igual a la matriz de varianzas y covarianzas asociada al modelo teórico (
La diferencia entre estas 2 matrices S −
Los métodos de estimación que se utilizan con mayor frecuencia son máxima verosimilitud (ML), mínimos cuadrados ordinarios (OLS), mínimos cuadrados generalizados (GLS) y mínimos cuadrados no ponderados o de distribución asintóticamente libre (ULS o ADF). Todos estos métodos trabajan iterativamente con el objetivo de minimizar una función de ajuste que se escribe en términos de las matrices antes descritas. Esta función de ajuste dependerá del método de estimación que se utilice.
El método de ML es el que se utiliza con mayor frecuencia y requiere que se cumpla el supuesto de normalidad de los datos, aunque se ha demostrado que bajo pequeñas desviaciones de normalidad el método sigue siendo consistente18 . Los OLS y los GLS también trabajan bajo el supuesto de normalidad de los datos; sin embargo, estos métodos arrojan estimaciones más exactas aun a pesar de violar el supuesto de normalidad y, a diferencia de ML, se comportan mejor aunque el tamaño de muestra sea pequeño (n < 200) 19 . Cuando definitivamente la distribución de los datos no es normal, se puede utilizar el método de ADF20. Este método es empleado particularmente cuando las variables del modelo son categóricas (se emplean correlaciones policóricas, tetracóricas y poliseriales) 21. Una desventaja de este método es que requiere que el tamaño de muestra sea grande (n > 250).
Bondad de ajuste del modelo
Una vez que se estimaron los parámetros del modelo, se tiene que hacer la evaluación del ajuste. Una de las pruebas más conocidas es la prueba de x2, la cual se utiliza para contrastar la hipótesis principal:
esto es, que la matriz de varianzas y covarianzas muestral es igual a la matriz de varianzas y covarianzas descrita en términos de los parámetros del modelo. En el caso en que el ajuste del modelo sea bueno, este estadístico t se distribuye como una ji al cuadrado con
Otros índices de ajuste que se usan son Goodnes of Fit Index (GFI) (este índice se puede interpretar como la proporción de varianza que se explica por medio del modelo), Adjusted Goodnes of Fit Index (AGFI), Root Mean Square Error of Aproximation (RMSEA), Standardized Root Mean Square Residual (SRMR), Comparative Fit Index (CFI), Akaike Information Criterion (AIC), Non Normed Fit Index (TLI o NNFI), Incremental Fit Index (IFI o BL89) y Expected Cross Validation Index (ECVI). La mayoría de los cuales toman valores entre 0 y 1, excepto RMSEA y SRMR. En el caso de RMSEA y SRMR se puede determinar que el ajuste es bueno si se observan valores iguales o inferiores a 0.0523 . Para el resto de los índices, lo deseable es obtener valores cercanos a 1 o al menos superiores a 0.9024 . Cabe mencionar que CFI, AIC, TLI, BL89 y ECVI también son conocidos como índices de incremento, ya que comparan el modelo propuesto con el modelo de independencia, esto es, el modelo en el que se asume que no existe asociación alguna entre las variables. En el caso de AIC y ECVI, también se comparan con el modelo saturado y si se plantean varias versiones del modelo se pueden comparar entre sí. Otra medida que se puede utilizar para evaluar el modelo es el tamano˜ de los residuos estandarizados, ya que por medio de ellos se determina la diferencia que hay entre lo observado por medio de los datos y lo que se obtiene de la estimación del modelo. Lo deseable es obtener residuos muy cercanos a cero, aunque un rango aceptable es entre -2 y 2.
Cuando el ajuste del modelo no resulta aceptable, puede ser viable replantear el modelo (con sustento teórico), verificar su identificabilidad, estimarlo y nuevamente evaluar el ajuste.
Ejemplo de un modelo de ecuaciones estructurales
Atendiendo a que la población a la que va dirigido este artículo metodológico es eminentemente del área médica, se buscó un artículo que pudiera ejemplificar el uso de las ecuaciones estructurales en dicha área. Este apartado no pretende tocar a profundidad los conceptos que se abordan en este modelo, más bien tiene como fin mostrar como a través de varias hipótesis se puede plantear un modelo y analizarlo con esta metodología.
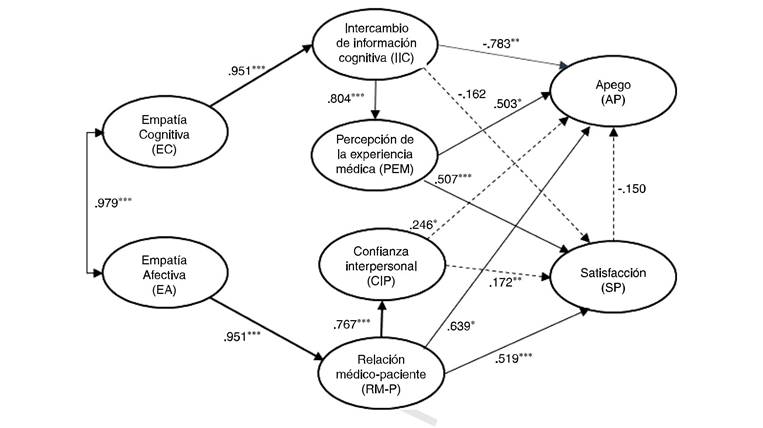
Kim et al. 25 querían explorar el efecto que tiene la empatía médica con la satisfacción y el apego que muestran los pacientes. El estudio se llevó a cabo con 550 pacientes de un hospital universitario en Corea, a los cuales se les aplicó un cuestionario. Midieron 2 tipos de empatía: afectiva (capacidad que tiene el médico para responder con un sentimiento adecuado ante el paciente) y cognitiva (capacidad que tiene el médico para ponerse en el lugar del paciente). Entre las hipótesis que plantearon, mencionan que las 2 empatías tienen un efecto positivo en la satisfacción y el apego; sin embargo, este efecto no es directo, sino que está mediado por otros factores. En el caso de la empatía cognitiva (EC), el efecto que tiene sobre la satisfacción del paciente (SP) está mediada por el intercambio de información cognitiva (IIC) (capacidad que tiene el médico de informar al paciente con precisión y claridad todo lo relacionado con el padecimiento) y la percepción de la experiencia médica (PEM), mientras que la empatía afectiva (EA) lo hace por medio de la confianza interpersonal (CIP) y la relación médico-paciente (RM-P). Otras hipótesis que establecieron son: entre más empático sea el médico mayor serán la satisfacción (SP) y el apego del paciente (AP). Indican, además, que el IIC y la PEM tienen un efecto más fuerte en el factor de apego que en el de satisfacción, mientras que la CIP y la RM-P tienen un efecto mayor sobre la satisfacción que con el apego26-28 . La Figura 2 muestra el modelo hipotético.
Las pruebas que hicieron para evaluar la confiabilidad de las variables latentes no se abordarán en este trabajo, por lo que sugerimos que para mayor detalle se consulte el artículo. Para estimar y evaluar el modelo se utilizó el paquete EQS 5.7. Se ajustaron 2 modelos: un confirmatorio y uno de ecuaciones estructurales, aunque solo discutiremos el segundo (Figura 2). Cabe mencionar que ambos modelos tuvieron un ajuste muy bueno. Para el segundo modelo se reportó una x2 (467) = 1,066.992 con p < 0.001, CFI = 0.931 y RMSEA = 0.049. Considerando el valor de estos 3 índices se puede concluir que el modelo tiene buen ajuste, aunque hubiese sido importante que se mostraran otros índices de incremento. En la Figura 2, los autores destacan con una flecha sólida aquellos coeficientes que resultaron muy significativos (p < 0.001) y con flechas punteadas los que fueron poco o nada significativos. El modelo mostró que la correlación entre la EC cognitiva y afectiva es positiva y muy significativa (p < 0.001). Se confirmó que el médico que tiene mayor EC tiene mayor IIC (0.951, p < 0.001) y que a mayor IIC, mayor PEM (0.804, p < 0.001). A mayor EA, es la RM-P (0.951, p < 0.001), y a mayor RM-P se incrementa la CIP (0.767, p < 0.001). El efecto directo que tiene la IIC en la SP y el AP fue negativo en ambos casos, pero significativo solo con el AP, conclusión que es contraria a lo que se habían planteado. En el caso de PEM, tiene un efecto similar en SP (0.507, p < 0.001) y en AP (0.503, p < 0.05). Tanto RM-P como CIP tienen un efecto directo positivo en SP y AP, aunque la magnitud de los coeficientes es mayor en RM-P con SP y AP (0.519 y 0.639) que en CIP con SP y AP (0.172 y 0.246).
Presentan además los valores del efecto total que tiene cada una de las variables predictoras del modelo en la satisfacción (SP) y el AP (Tabla 1), aunque no mencionan si estos efectos fueron estadísticamente significativos, lo cual resulta importante. La RM-P y la EA mostraron el mayor efecto total sobre la SP y el AP. IIC y EC tienen el efecto total más bajo y negativo sobre el AP. La EC y la CIP los más bajos sobre SP.
Tabla 1 Efecto total que tienen las variables predictoras del modelo en la satisfacción y apego del paciente
| Variable latente predictora | Apego del paciente | Satisfacción del paciente |
| Relación médico-paciente | 0.730 | 0.651 |
| Empatía afectiva | 0.695 | 0.620 |
| Percepción de la experiencia médica | 0.427 | 0.507 |
| Intercambio de información cognitiva | -0.415 | 0.244 |
| Empatía cognitiva | -0.394 | 0.232 |
| Confianza interpersonal | 0.221 | 0.172 |
A modo de ejemplificar brevemente cómo se obtiene el efecto total, haremos el cálculo entre la variable RM-P y el AP. Mencionaremos las trayectorias que se utilizaron para el cálculo, para lo cual el lector puede usar la Figura 2 como apoyo.
RM-P + SP + AP + RM-P + CIP + AP + RM-P + CIP + SP + AP + RM-P + AP
Esto es,
(0.519) (---0.150) + (0.767) (0.246) + (0.767)(0.172) (-0.150) + 0.639 = 0.730.
Algunas conclusiones: los factores emocionales EA y RM-P asociados al médico desempeñaron el papel más importante para aumentar la satisfacción y el apego de los pacientes del estudio, seguido de PEM, que inesperadamente también fue un buen predictor. La relación negativa entre IIC y AP no era esperada, indicando que posiblemente existen otros factores intermedios que no fueron contemplados, como, por ejemplo, problemas en el manejo de la enfermedad, entre otras explicaciones que mencionan.
Ventajas y desventajas de utilizar los Modelos de Ecuaciones Estructurales
Entre las ventajas que supone el uso de esta metodología se encuentra probar simultáneamente la relación directa, la relación indirecta y total entre las variables, la inclusión de más de una variable dependiente y sus respectivos errores de medición, la correlación entre variables y también entre los errores de medición29. También es posible usar los SEM en diseños longitudinales, como series de tiempo30 y modelos de crecimiento16.
Entre las limitaciones que tiene el SEM es que requiere de muestras grandes (n > 200), lo que podría ser difícil de obtener. Algunos autores indican que por cada parámetro libre o por cada variable observada, debe haber al menos 10 casos19. Plantear un modelo supone un reto importante, ya que lo ideal es que el investigador cuente con un amplio conocimiento teórico sobre el fenómeno que quiere estudiar, de lo contrario, se puede tener un modelo con buen ajuste pero sin sustento teórico. Esta metodología no está excluida de fallar si se utilizan variables latentes con baja confiabilidad. Finalmente, emplear esta metodología puede implicar un reto considerable si no se tiene cierto bagaje estadístico.
Financiamiento. Ningún tipo de financiamiento.
Conflicto de intereses. Declaro no tener ningún conflicto de interés.











 nueva página del texto (beta)
nueva página del texto (beta)