En el área de investigación sobre las habilidades numéricas, el conteo es el fenómeno más estudiado en etapas tempranas del desarrollo, dado que representa una habilidad predictora del razonamiento aritmético en edades posteriores. Generalmente el conteo se define como la asignación sucesiva de símbolos y/o etiquetas verbales a las entidades de un conjunto (Brannon & Roitman, 2003; Whyte & Bull, 2008), noción que es compatible con los principios de conteo propuestos por Gelman y Gallistel (1978), que remiten a los siguientes principios:
Orden estable. La secuencia de los elementos debe producirse siempre en el mismo orden.
Correspondencia biunívoca o uno a uno. Debe asignarse un numeral a cada objeto del conjunto sin omisión o repetición de los elementos.
Cardinalidad. La etiqueta asignada al último elemento representa la cantidad del conjunto.
Abstracción. Cualquier colección de elementos discretos puede ser contada, pudiendo establecer así su valor cardinal.
Irrelevancia del orden. Alude a que saber contar también implica comprender que los objetos se pueden contar en cualquier orden, sin que cambie el valor cardinal.
Los primeros tres principios son propiedades que reflejan un conocimiento procedimental necesario para la habilidad de conteo, mientras que los dos últimos remiten a un conocimiento conceptual propio de habilidades aritméticas (LeFevre et al., 2006; McGuire, Kinkie, & Berch, 2012).
Durante la edad preescolar los niños suelen obtener ejecuciones correctas en tareas de conteo según los principios procedimentales, desarrollando, después de los cuatro años, un grado elevado en el dominio del conteo, base para las habilidades aritméticas posteriores -adición, sustracción, multiplicación y división- (LeFevre et al., 2006; Marcos, Marcos, Montero, & Crespo, 2012; McGuire et al., 2012).
Las investigaciones que han dado cuenta sobre las propiedades fundamentales del conteo, se han centrado básicamente en el principio de cardinalidad por ser distintivo de esta habilidad, es decir, aun cuando los tres principios son fundamentales, orden estable, correspondencia uno a uno y cardinalidad, este último define la habilidad numérica. Además, tal evidencia permite señalar que los infantes desarrollan la habilidad del conteo desde muy temprana edad, antes incluso de la instrucción formal (Skwarchuk, Sowinski, & LeFevre, 2014) en la medida en la que los adultos responsables de su cuidado, proporcionan condiciones que permiten la familiaridad del niño con el conteo (Peterson & McNeil, 2013; Shaki, Fischer, & Göbel, 2012; Skwarchuk et al., 2014; Whyte & Bull, 2008), desarrollando progresivamente el conocimiento procedimental de los principios involucrados en el conteo de acuerdo con la calidad y cantidad de experiencias con los números (Cancaya, LeFevre, & Dunbar, 2014; Gelman & Brenneman, 2002; Gelman & Kalish, 2006; Gelman & Meck, 1983; Gelman, 1993; Stock, Desoete, & Roeyers, 2009; Zur & Gelman 2004). A pesar de que se ha observado que los niños identifican los números con una cantidad o tamaño, no es evidencia de la abstracción que implica la propiedad de conteo, sobre todo en niños pequeños la ejecución puede ser resultado de un artilugio de la tarea misma.
Comúnmente se emplea la tarea de “¿Cuántos hay?”, que consiste en presentar al niño una serie de objetos (p.ej. tarjetas con calcomanías de animales, juguetes), acciones (ejecutadas por otro individuo en video), sonidos (sonidos de animales), se pide que cuenten el conjunto y en seguida se le pregunta cuántos hay. A partir de este procedimiento, se encuentra que los niños a muy temprana edad, comienzan a desarrollar una representación abstracta y generalizable de conteo. Sin embargo, cuando se les pregunta “cuántos”, solo los niños mayores de 36 meses pueden dar el número preciso de la secuencia contada lo que sugiere que el principio de cardinalidad se domina a partir de esa edad (Wyyn, 1990). Aun así, se mantiene la idea del posible sesgo propio del procedimiento, pues los niños pueden responder a la pregunta cuántos con un numeral, al margen de la comprensión del concepto de número, lo que cuestiona la idea del desarrollo del sentido de número a partir de los 36 meses.
Para minimizar esta dificultad, Wynn (1990), realizó un estudio con niños de 30 a 40 meses de edad a los que expuso a la misma tarea de “¿Cuántos hay?” además de una tarea adicional denominada “Dame N”. En esta última, los niños debían dar conjuntos de 2, 3, 5 y 6 (se omite el 4 dado que se considera el punto de cambio entre la repetición rápida del número y el conteo, ver p. ej. Formoso, Injoque-Ricle, Jacubovich, & Berreyro, 2014), y se les pedía además que se aseguraran de haber dado la cantidad requerida, con el fin de que el niño volviera a contar los objetos. Los resultados mostraron una fuerte consistencia en la ejecución de ambas tareas, pero sólo en el caso de los niños mayores a 36 meses.
La autora señaló en su discusión que es probable que los niños utilicen una “regla simple de cardinalidad” para contestar la tarea “¿Cuántos hay?”, es decir, en la medida en la que la tarea implica el conteo de un conjunto de objetos señalando cada uno con un número, una rutina de contar, en el momento de preguntar cuántos, el niño recita el último número, de tal suerte que los aciertos se deben al uso de esta regla más que el principio de cardinalidad que implica la abstracción del número. En contraste, ante la tarea “Dame N” no es suficiente usar esta regla simple, lo que permite señalar que es un procedimiento adecuado para valorar la maestría en el conteo. Esta tarea puede indicar diferentes niveles de dominio cardinal: los niños subconjunto-conocedores, que se caracterizan por el hecho de poder contar y entregar solamente conjuntos de uno, dos o tres elementos (un subconjunto de la lista de números que podían recitar rápidamente, sin que se demande la comprensión del conteo); y los cardinal-conocedores, quienes podían contar conjuntos cuyo total correspondiera a cualquiera de los números incluidos en una lista de conteo, reflejando así los números que el niño conoce y el orden que les otorga. En otras palabras, la diferencia en la cantidad de elementos que puede contar eficientemente el niño es evidencia de su nivel de dominio de los diferentes principios de conteo.
Otros estudios también han señalado a la tarea de “Dame N” como más plausible en la valoración de principio de cardinalidad en niños en edad pre-escolar, identificando a través de dicha tarea el nivel de maestría en el conteo (Condry & Spelke, 2008; Le Corre & Carey, 2007; Le Corre, Van de Walle, Brannon, & Carey, 2006), sin embargo, sólo en el estudio de Wynn, se realizó una valoración con ambas tareas, encontrando resultados consistentes en los niños de mayor edad, razón que parece cuestionar el argumento sobre| el uso de reglas de diferente nivel en cada tipo de tarea y sobre la mayor confianza en el uso de la tarea “Dame N”.
Otro aspecto importante a señalar es que en los estudios citados la evaluación del principio de cardinalidad es el aspecto medular de la investigación sobre la habilidad de conteo, pero la relación de este principio con los de orden estable y correspondencia uno a uno, contemplados en el modelo de Gelman y Gallistel, ha sido muy poco estudiada.
Se sabe que desde muy temprana edad, los niños muestran habilidades en la propiedad de correspondencia y orden estable, pero no se ha indicado de manera explícita si éstas son requisito para que se presente la propiedad de cardinalidad; el modelo plantea una visión de desarrollo progresivo de dichas habilidades, pero la evidencia no es del todo clara al respecto. Por ejemplo, en el estudio de Sarnecka y Carey (2008), se expuso a grupos de niños de entre 2 y 4 años a una serie de dos tareas diseñadas para medir la comprensión del principio de correspondencia uno a uno y de orden estable, así como dos tareas de cardinalidad: “¿Cuántos hay?” y “Dame N”. La tarea “¿Cuántos hay?” fue modificada de manera que el experimentador realizara el conteo y después le planteara la pregunta al niño con el fin de evitar el sesgo atribuido a la pregunta y a la regla simple de repetición del numeral (ver Gelman 1993).
En general sus resultados muestran, una ejecución correcta en las tareas de correspondencia uno a uno y orden estable para todos los grupos de edad, además se observa que en general los infantes respondieron correctamente el 83% de los ensayos de la tarea “¿Cuántos hay?”, sin embargo, al describir los datos encontrados en “Dame N” se logró clasificar a los infantes según su nivel de pericia al responder la tarea que, además, se asocia con la edad. Según la ejecución en Dame N los niños “conocedores” de la regla de cardinalidad, son aquellos que manejan conjuntos de más de cinco elementos y en este caso, solo se observa esta ejecución en los niños mayores (rango de variación de edad: 2 años 11 meses a 4 años 3 meses). Varias son las implicaciones de estudio de acuerdo con Sarnecka y Carey (2008), en primer instancia la habilidad mostrada por todos los niños observados según lo prescrito por los dos primeros principios, no es suficiente para la ejecución en tareas de cardinalidad, en segundo término, con la pregunta “cuántos” se otorga como respuesta la última palabra usada para contar (en este caso dada por el experimentador), a pesar de no entender cómo funciona la cuenta, y tercero, solo los niños que han dominado el principio cardinal, o que están cercanos a hacerlo, entienden que agregar objetos a un conjunto significa avanzar (agregar exactamente 1 objeto a un conjunto significa avanzar exactamente 1 en la lista), mientras que restar objetos significa retroceder.
Por otro lado, Peterson y McNeil (2013) señalan que, si bien se puede observar en los niños menores de tres años de edad, cierto dominio del principio de correspondencia, no muestran un nivel adecuado del uso del principio de cardinalidad, esto coincide con consideraciones previas que indican que los principios de correspondencia uno a uno, orden estable y cardinalidad, no se presentan con el mismo nivel de dominio sino hasta la edad pre-escolar (Stock et al., 2009). A pesar de la evidencia mostrada por los estudios citados, no es claro si se presenta una transición gradual de los principios de orden estable, correspondencia y cardinalidad, si se desarrollan de manera independiente o si alguno es requisito de la presencia de otro. Más aún es probable que el desarrollo de estas propiedades esté íntimamente ligado con el nivel de maduración propio de la edad y que el dominio de los niveles previos sea necesario pero no suficiente para el desarrollo de niveles más complejos en el conteo.
En suma podemos indicar que, si bien ya se ha investigado sobre los principios de conteo, sigue siendo tema de discusión lo relativo a su transición gradual. Más aún, las distintas propiedades de contar no han sido medidas de manera apropiada para dar cuenta de su naturaleza como parte de la acción de contar y del nivel de dominio según la edad de los infantes. La evidencia en favor de la tarea de Dame N es escasa. Resulta importante generar información que nos permita conocer si el dominio en las tareas de correspondencia uno a uno y orden estable es suficiente para el desarrollo de la propiedad de cardinalidad, si la maestría en tal habilidad es una función de la edad al margen de la habilidad en correspondencia uno a uno y orden estable y, si la ejecución en la tarea de Dame N permite una mejor medición del principio de cardinalidad. Así, el propósito general de esta investigación es evaluar el desempeño de infantes en las distintas tareas de conteo como una función de la edad, así como comparar la ejecución en las tareas de cardinalidad en niños que satisfacen el requisito de niveles más simples de conteo. Los resultados amplían la evidencia en términos de las ventajas metodológica de una tarea libre de sesgo al contrastarla directamente con el procedimiento tradicional, así como también, contribuyen en la comprensión de las propiedades del conteo y su evolución en niños de edad prescolar.
Método
Participante
48 niños de 30 a 54 meses de edad, seleccionados de una muestra de 247 niños, de nivel socioeconómico medio, reclutados de cinco Centros de Desarrollo Infantil de la Delegación Tlalpan y cinco escuelas particulares de la Delegación Cuauhtémoc, en la Ciudad de México, previo consentimiento informado de los padres o tutores. Los participantes fueron aquellos que cumplieron satisfactoriamente los requisitos de las tareas de orden estable y correspondencia (Gelman & Gallistel, 1978) de la fase de inclusión, mismas que se describen en las siguientes secciones.
Materiales
Una mesa rectangular de 50 cm x 50 cm x 100 cm
Tres sillas infantiles
Dos contenedores de plástico de 30 cm x 20 cm
Quince patos de plástico de 5 cm cada uno
Quince vacas de plástico de 7 cm cada una
Quince gallinas de plástico de 4 cm cada una
Quince borregos de plástico de 5 cm cada uno
Quince cerdos de plástico de 5 cm cada uno
Una serie de 5 tubos de plástico transparentes de 6.7 cm de diámetro, colocados a intervalos regulares de 2 cm en una base de madera de 11 x 47 cm
Una serie de 8 tubos de plástico transparentes de 6.7 cm de diámetro, colocados a intervalos regulares de 2 cm en una base de madera de 11 x 74 cm
Una serie de 10 tubos de plástico transparentes de 6.7 cm de diámetro, colocados a intervalos regulares de 2 cm en una base de madera de 11 x 92 cm
Seis pelotas de plástico de 6 cm de diámetro de color azul
Seis pelotas de plástico de 6 cm de diámetro de color verde
Seis pelotas de plástico de 6 cm de diámetro de color rojo
Seis pelotas de plástico de 6 cm de diámetro de color amarillo
Una marioneta del personaje “Elmo” de 60 cm de longitud
Cinco hojas bond tamaño carta enmicadas que mostraban 3 conejos, 5 perros, 7 gatos, 8 elefantes y 10 patos en blanco y negro
Procedimiento
El experimento constó de dos fases. La fase de inclusión con tres tareas, cuyo cumplimiento satisfactorio implicaba avanzar a la siguiente fase de prueba, que consistió en la manipulación de objetos para medir el desempeño de los niños en dos tareas de cardinalidad.
Las tareas empleadas fueron “Algunos cerditos” y “Dame N” (Wynn, 1990), así como las tareas de correspondencia uno a uno y de orden estable (Le Corre et. al. 2006) y una variante de la tarea “¿Cuántos hay?” empleada por Sarnecka y Carey (2008). Estas tareas se describen a continuación:
Fase de inclusión
Tarea: “Algunos cerditos”
Esta tarea se incluyó con el fin de asegurar que los niños comprendían la instrucción “dame” y que podían conformar conjuntos de una sola especie de animales. Se presentó al niño un recipiente que contenía animales de plástico (cerdos, vacas, patos, borregos, gallinas), a continuación, con apoyo de una marioneta de Elmo, el investigador pregunta al niño: “¿podrías darle algunos “cerditos” a Elmo?”; en caso de que el niño preguntara la cantidad se le contestaba “los que tú quieras” o “unos pocos”, si solamente proporcionaba uno se le decía: “dale más, muchos” y cuando proporcionaba alrededor de 4 a 7 animales se le decía que así eran suficientes; después se le pedía alguna otra especie de animal con la instrucción “ahora vamos a jugar con (mencionando el nombre del animal)”. Se permitió que el niño sacara los juguetes del recipiente y los separara para hacer los conjuntos. El criterio de correcta ejecución fue que el niño conformara conjuntos de una sola especie en los tres ensayos programados, se permitió que el participante regresara al contenedor los animales que no coincidían con los requeridos si él mismo se daba cuenta de su error.
Tarea: Correspondencia término a término
Se le presentaban al niño series de tubos de plástico. La tarea consistía en introducir una pelota en cada uno de los tubos de plástico de la serie presentada; cuando el niño ponía dos o más pelotas en un mismo tubo se señalaba las pelotas de encima y se le decía: “mira, estas están aplastando a la pelotita, mejor la(s) sacamos, ¿no?”. Se inició con la serie de 8 tubos, si el niño la completaba correctamente se seguía con la de 10 tubos; si fallaba se le proporcionaba la serie de 5 tubos, de completarla correctamente se le daba nuevamente la de 8 tubos. El criterio de esta tarea consistió en que se ejecutaran de manera correcta las dos series de tubos proporcionadas, dando dos oportunidades para cada serie de tubos: como ensayo correcto se consideraba aquel en el que el participante colocaba una pelota en cada tubo, no dejara tubos vacíos ni con más de una pelota. Se permitió un error en la serie inicial si el sujeto se daba cuenta y lo corregía, si había un error y no se percataba de él o no lo corregía se consideraba como ensayo fallido, al acumularse dos ensayos fallidos, el participante quedaba fuera del estudio.
Tarea: Orden estable
La tarea consistió en que el niño recitara la lista de números al menos hasta el 10 en el orden convencional dos veces seguidas. Para que recitaran la lista se les decía: “Oye ¿qué crees?, Elmo no se sabe los números ¿se los puedes enseñar?”, en algunos casos los niños se mostraban confundidos o empezaban a recitar el abecedario, entonces el investigador decía “los números, esos que empiezan con el uno ¿sabes cuál sigue?”. Si con esta nueva pregunta el niño no respondía se daba por finalizada la prueba, si respondían se les dejaba seguir hasta el número 10 y después se les pedía que los repitieran para que Elmo los dijera junto con ellos. Se consideró satisfactoria la respuesta del niño si en ambos ensayos se utilizaba la misma secuencia, si ésta correspondía al orden convencional y si se mencionaba al menos hasta el número 10.
Fase de prueba
Tarea: “¿Cuántos hay?”
Para esta tarea se colocaron boca abajo 5 tarjetas con diferentes cantidades de animales 3, 5, 7, 8, y 10 elementos, colocados en orden descendente de izquierda a derecha y se le decía al niño “fíjate bien cómo se juega esto, yo voy a contar los animalitos y tú me vas a decir cuántos hay” siempre se iniciaba con la tarjeta de los conejos (3 elementos) y se le preguntaba al niño “¿que hay aquí?” cuando el niño contestaba con el nombre de los animales se le decía “muy bien, acuérdate que yo los cuento y tú me dices cuántos hay” entonces la investigadora contaba los animales señalándolos con el dedo conforme los enumeraba y al final le preguntaba al niño “¿Cuántos conejos hay?”, en caso de que el niño contara los animales se ponía la tarjeta boca abajo y se repetía la instrucción, después se volteaba nuevamente y el investigador reiniciaba el conteo. Dado que esta tarea formaba parte de la fase de prueba, no había criterio de exclusión por lo que se continuaban con todos los ensayos programados (uno por cada tarjeta) independientemente de lo acertado de la respuesta de los participantes a fin de sondear el uso del principio de cardinalidad.
Tarea: “Dame N”
Se proporcionaba al niño la caja de animales. Esta tarea se iniciaba preguntando al niño: “¿Qué te parece si jugamos otra vez con los animalitos?, ahora tienes que darle a Elmo los que él te pida”, entonces con la voz de la marioneta se decía, por ejemplo: “dame 3 gallinas por favor”, cuando el niño conformaba el conjunto el investigador preguntaba “¿así son tres?” si el niño decía que sí pero no los contaba, se le decía “a ver cuéntalos”. Cuando el conteo llevaba al niño a una cantidad diferente de la que se le había pedido el investigador decía “pero Elmo quiere tres ¿Cómo podemos hacerle?”, una vez que el niño corregía su conjunto el investigador decía “muy bien”. Después se seguía con los ensayos programados (1 para cada cantidad requerida: 3, 4, 5, 6, 7, 8, 9 y 10 elementos).
Las pruebas se llevaron a cabo en el espacio asignado por los directivos de cada escuela. Estos espacios eran familiares a los niños y durante la sesión se utilizaron únicamente para la aplicación de las pruebas; en el transcurso de éstas sólo se encontraban presentes el investigador y el participante. La silla del participante se colocó de espaldas a la puerta y los materiales debajo de la mesa con el fin de evitar que el niño se distrajera.
Las tareas se realizaron de manera individual y las instrucciones fueron las mismas para todos los participantes. En la fase de inclusión las tareas se presentaban a todos los niños en la misma secuencia: algunos cerditos, correspondencia término a término y orden estable. En la fase de prueba, se aplicó a los niños las tareas “¿Cuántos hay?” y “Dame N” de manera contrabalanceada. Se incluyeron ensayos para los conjuntos de 9 y 10 elementos en la tarea Dame N, puesto que estas cantidades no habían sido exploradas en estudios anteriores.
Análisis de datos
Para comparar los resultados en la fase de prueba se tomaron los valores de las medianas y su rango intercuartil (RIQ). Para dar cuenta del efecto de la edad sobre el desempeño de los niños en las tareas de cardinalidad, los datos se analizaron mediante una regresión lineal usando la edad en meses como predictor del nivel numérico obtenido en las tareas de cardinalidad.
El nivel numérico para ambas tareas se asignó considerando el mayor número de elementos dados/contados por el participante, sin tener errores en cantidades menores, por ejemplo, si un niño proporcionaba correctamente los conjuntos de 3, 4, 5 y 7 elementos no se consideraba el 7 como su nivel numérico puesto que no fue capaz de proporcionar la cantidad inmediata anterior (6 elementos) por lo que se le asignaba un nivel numérico de 5.
Debido a la diferencia de las cantidades manejadas en cada tarea de cardinalidad (3, 5, 7, 8, y 10 en ¿Cuántos hay? en contraste, 3, 4, 5, 6, 7, 8, 9 y 10 en Dame N) fue necesario realizar un ajuste en el que los niños clasificados como 4, 6 y 9 según la tarea de Dame N, se colocaron en el nivel numérico inmediato inferior (3, 5 y 8, respectivamente) sólo como una forma de ajuste para poder compararlos con el nivel numérico en la tarea de ¿Cuántos hay?, que no genera ningún sesgo en la clasificación del nivel de dominio, puesto que los niños que calificaron 4 en Dame N dominan el número 3, pero no el 5, y así respectivamente.
La obtención de datos, así como el uso y descripción de los mismos en el presente estudio se ajustan a las recomendaciones del Código ético del psicólogo de la Sociedad Mexicana de Psicología (2007) relativas al apartado IV inciso A y B, sobre el respeto a los derechos y dignidad de las personas y el cuidado responsable, así como a el artículo 8 del segundo capítulo respecto a la responsabilidad de la conducción ética de la investigación.
Resultados
Los valores de mediana y Rango intercuartil del nivel numérico obtenido en cada tipo de tarea, incluyendo el ajuste a los valores en la tarea Dame N para hacerlos comparables con la tarea ¿Cuántos hay? se presentan en la Tabla 1, incluyendo todos los infantes agrupados en tres rangos de edad (menores de 36 meses, entre 37 y 48 meses, mayores de 48 meses). Para la tarea de Dame N, en el grupo de niños menores de 36 meses, se observan puntuaciones bajas y alto grado de dispersión de los datos (ver RIQ). En el grupo de edad de 37 a 48 meses, se observan valores intermedios de nivel numérico y se mantiene un alto grado de dispersión en la distribución. En los niños mayores, el valor de la mediana incrementa, pero a niveles moderados de ejecución y la dispersión es menor en este grupo.
Tabla 1 Medidas descriptivas de los infantes por rango de edad para cada tarea en la fase de prueba.
| Edad en meses | |||||||
| 36 o menos | Entre 37 y 48 | Mayor 48 | |||||
| Mediana | RIQ | Mediana | RIQ | Mediana | RIQ | ||
| “Dame N” | 4 | 5 | 5 | 4 | 7 | 4 | |
| “Dame N” Ajustada | 3 | 5 | 5 | 5.75 | 6v | 4 | |
| “¿Cuántos hay?” | 4 | 5 | 9 | 5.5 | 10 | 0 | |
En contraste en la tarea ¿Cuántos hay? El nivel numérico es alto para los niños mayores de 36 meses (los dos grupos de edad) e incluso se observa un efecto de techo en la ejecución de los niños mayores de 48 meses.
Los datos de acuerdo con el análisis de regresión para las variables en cada una de las tareas de cardinalidad, indican que, para el nivel numérico obtenido en “Dame N” se observó que la edad en meses explica de manera significativa el desempeño en la tarea (b = 0.196; r2 = 0.257; t(47) = 3.99, p < .001). Asimismo, existe una correlación positiva entre ambas variables (r=0.507, ver Figura 1)
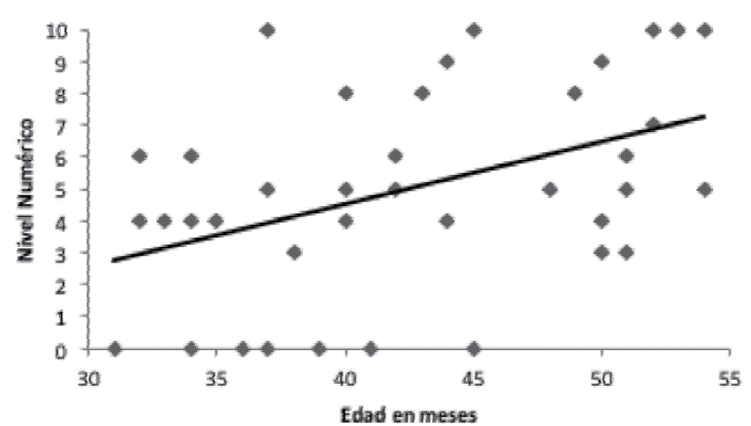
Figura 1 Diagrama de dispersión que representa el nivel numérico en la tarea “Dame N” en función de la edad de los participantes, así como la línea de mejor ajuste (Y´= -3.3594 + 0.1961edad)
Para el segundo análisis se utilizó la edad en meses como predictor del nivel numérico obtenido en “Dame N” una vez realizada la reclasificación que permite la comparación del nivel número en ambas tareas de la fase de prueba. Así, los niños originalmente clasificados como 4, 6 ó 9-conocedores se reasignaron en la categoría inmediata anterior, dado que para ser clasificados en un nivel numérico específico fue necesario que otorgaran correctamente los conjuntos de cantidades menores. Nuevamente el nivel numérico es predecible a partir de la edad en meses de los participantes (b = 0.247; r2 = 0.302; t(47) = 4.46, p < .001), igualmente ambas variables se correlacionan de manera positiva (r=0.550, ver Figura 2).
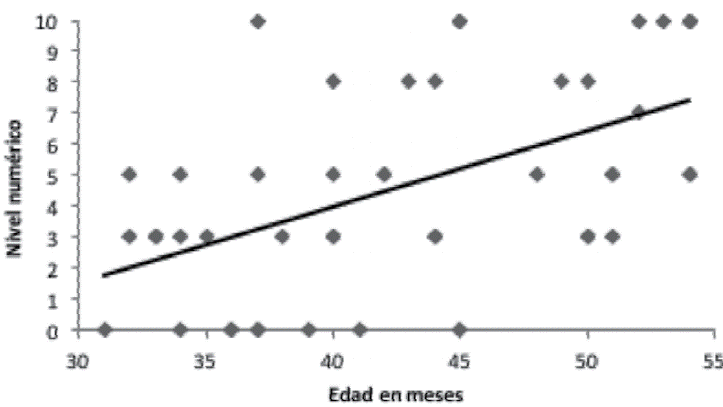
Figura 2 Nivel numérico obtenido en “Dame N” en función de la edad y línea de mejor ajuste (Y´= -5.8846 + 0.2471edad), con la reclasificación de los datos de acuerdo con el nivel de pericia.
En un tercer análisis, se utilizó la edad en meses como predictor del nivel numérico obtenido en “¿Cuántos hay?”. Los resultados muestran que la variable independiente explica de manera significativa el nivel numérico obtenido en esta tarea (b= 0.226; r2 = 0.234; t(47) = 3.75, p < .001), también se observa una correlación positiva entre ambas variables (r=0.484 ver Figura 3), sin embargo esta correlación es ligeramente menor respecto a la existente entre la edad y el nivel numérico obtenido en “Dame N” en ambos análisis antes descritos, además hay un importante efecto de techo de nivel numérico muy evidente en los niños de más de 48 meses lo que cuestiona la confianza del nivel de ajuste del modelo lineal.
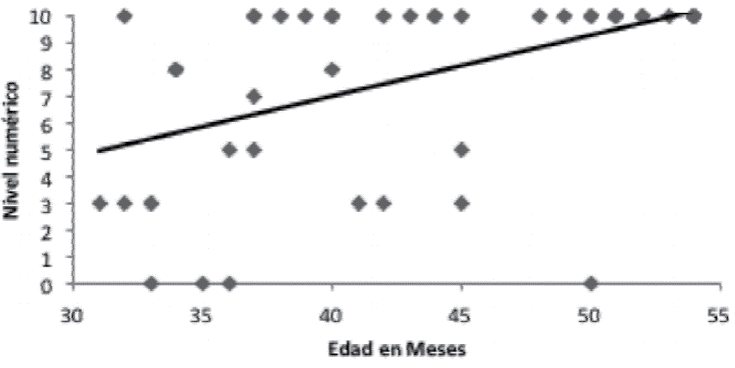
Figura 3 Representa el mayor número reconocido en la tarea “¿Cuántos hay?” en función de la edad en meses de los participantes, así como la línea de mejor ajuste (Y´= -2.0608 + 0.2263edad).
Por último, se realizó una regresión lineal con la edad en meses como predictor de la diferencia de los niveles numéricos obtenidos en ambas tareas. Para esto se restó el nivel numérico obtenido en “Dame N” al obtenido en “¿Cuántos hay?” una vez reclasificados los casos de los 4, 6 y 9-concedores. Este análisis no arrojó datos significativos (, p=0.759).
Discusión
Este estudio se diseñó con el propósito de generar evidencia para responder tres cuestiones: si el dominio en las tareas de correspondencia uno a uno y orden estable es suficiente para el desarrollo de la propiedad de cardinalidad, si la maestría en tal habilidad es una función de la edad al margen de la habilidad en correspondencia uno a uno y orden estable y, si la ejecución en la tarea de Dame N permite una mejor medición del principio de cardinalidad.
De manera general los niños ejecutaron las tareas de diferente nivel de dominio de conteo, de manera satisfactoria, más del cincuenta por ciento de los casos de los niños entre los 36 y los 48 meses, mostraron un nivel de dominio en las tareas de cardinalidad, que permite considerarlos como medianamente conocedores de las reglas de conteo (particularmente siguiendo los criterios de la tarea Dame N) y los niños mayores de 48 meses, tienen un nivel alto de dominio en estas reglas. Estos datos son evidencia de la habilidad de conteo desde temprana edad, resultados que coinciden con lo reportado por otros autores (LeFevre et al., 2006; Marcos et al., 2012; McGuire et al., 2012; Sarnecka y Carey, 2008; Skwarchuck et al., 2014; Wynn, 1990).
Respecto a la primera interrogante del estudio, el diseño metodológico implicó que, como requisito para la fase de prueba, los niños ejecutarán satisfactoriamente las tareas de correspondencia y orden estable de la primera fase. En otras palabras, todos los niños dominaron estas habilidades. Los datos observados en las tareas de cardinalidad, indican que los niños muestran un nivel diferencial de desempeño -sólo los niños cercanos o mayores a los 48 meses son los que se pueden clasificar como conocedores de acuerdo con la tarea de Dame N (Sarnecka y Carey, 2008; Wynn, 1990). En otras palabras, el nivel de maestría en el conteo difiere en la muestra de infantes, a pesar de que en todos los casos se cumple con el dominio de las habilidades de correspondencia y orden estable, estos datos apoyan la noción de que los tres principios se desarrollan de manera secuencial (Peterson & McNeil, 2013).
Se puede considerar que estos datos son evidencia acerca de que el dominio de las habilidades señaladas por los primeros principios del modelo de Gelman y Gallistel (1978), no representan una condición suficiente para el desarrollo de la cardinalidad. A pesar de lo anterior, es importante no confundir el argumento. Los niños mostraron un nivel diferencial de dominio en tareas de conteo propiamente dicho, teniendo un dominio alto en las habilidades más simples, pero no resulta claro si las dos propiedades de conteo, correspondencia y orden estable, deben desarrollarse previas a la propiedad de cardinalidad y si son requisito para el desarrollo de ésta. Se requieren datos más contundentes al respecto, para cuestionar la prescripción del modelo de Gelman y Gallistel en el sentido del desarrollo progresivo de las habilidades de conteo que en éste se plantean.
Sólo podemos sugerir, a partir de la evidencia, que la habilidad de cardinalidad parece que se desarrolla de manera independiente de los otros dos principios, sin embargo se requiere mayor cantidad de arreglos metodológicos para que se pueda tener evidencia sistemática al respecto de la forma en la que evolucionan las propiedades de conteo según el modelo citado, y si efectivamente el desarrollo de una habilidad más compleja es del todo independiente de las habilidades más simples. Por ejemplo, habrá que diseñar un estudio para evaluar si el hecho de empezar a enseñar la lista, o incluso las reglas de conteo a una edad temprana, facilitaría que los niños apliquen este conocimiento cuando se les presentan tareas de conteo que requieran la manipulación de objetos, al margen de su dominio en las propiedades previas.
En relación con el segundo planteamiento de si la maestría en tal habilidad es una función de la edad al margen de la habilidad en correspondencia uno a uno y orden estable, los resultados analizados mediante herramientas de regresión lineal, indican una proporción de varianza explicada baja, pero significativa de la edad de los infantes sobre el desempeño en las tareas de cardinalidad. Conforme aumenta la edad de los participantes, aumenta el nivel numérico obtenido en ambas tareas de la fase de prueba, dato que puede parecer obvio en primera instancia, pero coincide con los argumentos en párrafos previos respecto de la relación entre los tres primeros principios del modelo. Es decir, los niños más pequeños tienen mayor dificultad para las tareas de cardinalidad, a pesar de su nivel adecuado de ejecución en las de correspondencia y orden estable. Se apoya la consideración de que la adquisición y dominio del conteo, al menos en lo que respecta al principio de cardinalidad, es gradual (Briars & Siegler, 1984; Fuson, 1988; Fluck & Henderson, 1996; Gelman & Gallistel, 1978).
Asimismo la evidencia a partir de estos análisis, coincide con la consideración de que los principios de cardinalidad se adquieren conforme el niño se enfrenta a tareas que requieren la aplicación de los mismos y probablemente, como resultado de la familiaridad que va adquiriendo el niño con las reglas de números a partir de las actividades reguladas por los adultos (Fluck & Henderson, 1996; Gelman & Gallistel, 1978). Sus experiencias van a moldear gradualmente la habilidad de conteo como se ha señalado en otros estudios (Cancaya et al., 2014; Gelman & Brenneman, 2002; Gelman & Kalish, 2006; Gelman & Meck, 1983; Gelman, 1993; Stock et al., 2009; Zur & Gelman 2004; Skwarchuk et al., 2014).
Respecto del tercer planteamiento del estudio, la comparación de las tareas utilizadas en la fase de prueba permitió generar evidencia con respecto a la adecuación de las tareas de “¿Cuántos hay?” y “Dame N” para evaluar la misma dimensión de conteo: cardinalidad. Es importante iniciar mencionando que, por su forma en el procedimiento de la tarea “Dame N” se puede sondear tanto las habilidades procedimentales del niño, como la comprensión y aplicación del principio de cardinalidad. Además, considerando que esta tarea ha sido validada mediante la comparación con otras pruebas (Le Corre et. al. 2006), y que en el presente estudio se controló la variabilidad debida a las habilidades procedimentales mediante la fase de inclusión, se puede apuntar a la idea de que los resultados obtenidos en la tarea “Dame N” dependen de si el niño comprende/utiliza o no las reglas para aumentar o disminuir elementos.
En cuanto a la tarea “¿Cuántos hay?” cabe mencionar que ha sido desestimada para medir la propiedad de conteo porque se considera que la pregunta ocasiona un sesgo: después de realizar el conteo los niños tiende a repetir el último número escuchado de la lista. Así mismo, se puede suponer que cuando se cumplen los requerimientos procedimentales propios de la tarea, se desvía la atención del niño hacia los números repetidos, haciendo que pierda la cuenta de los elementos presentes en la tarjeta y que conteste erróneamente aun sabiendo contar, particularmente en los niños más pequeños.
Además, también se ha indicado que la tarea “¿Cuántos hay?” no mide con precisión el principio de cardinalidad, puesto que los niños emplean una regla que implica que utilizan la palabra “cuántos” como un indicador para contestar con un numeral (Sarnecka & Carey, 2008). Así, una respuesta correcta se debe al efecto de recencia, que provoca que los niños respondan con el último numeral mencionado sin que esto signifique que comprendan el principio de cardinalidad. De hecho, los niños de mayor edad, responden sin error cuando se presentan tarjetas de 10 elementos en la tarea de ¿Cuántos hay?, mientras que en la tarea de Dame N, se muestran errores cuando la lista de conteo es mayor de 7 elementos. Esta tendencia en la respuesta fue reportada previamente en el estudio de Sarnecka y Carey (2008), siendo evidencia de que la tarea de ¿Cuántos hay? sólo parece demostrar un desempeño más simple que no refleja la comprensión de esta propiedad del conteo, siendo la tarea de Dame N una forma de mejor control en la medición de cardinalidad. Además, el efecto de techo en la tarea se convierte en un sesgo en la interpretación correcta del resultado del análisis de regresión, que evidencia aún más la validez de la tarea de ¿Cuántos hay?
A manera de conclusión, podemos decir que los datos del presente estudio son un indicio de que las propiedades de conteo, al menos las más simples del modelo de Gelman y Gallistel (1978), se desarrollan de forma gradual e independiente, siendo la tarea de Dame N una estrategia de mayor precisión metodológica en el estudio de la habilidad cardinal, que permite detectar mejor sus propiedades y evolución a partir de la edad. La comprensión de dichas características, es fundamental si se considera que estas habilidades son básicas para el desarrollo de conocimiento matemático posterior. Dada la muestra con que se trabajó, los resultados de esta investigación podrían resultar de interés para la formación de los niños en edad preescolar, en la medida en que demuestran que la repetición de una lista de números no es evidencia de que el infante desarrolla el concepto de número.
Además, con la exploración del desarrollo de la habilidad de conteo, mediante una tarea más adecuada, se pueden obtener otros resultados que contribuyan a dar sugerencias de situaciones didácticas que ayuden a los niños a comprender la utilidad del conteo.
Bajo esta línea de pensamiento, podría implementarse un estudio longitudinal en el que se apliquen tareas que evalúen los tres principios de conteo antes y después de la implementación de diversas actividades que requieran que el niño emplee estos conocimientos. Esto con el fin de averiguar, si la familiarización con este tipo de actividades facilita la comprensión y aplicación de los principios de conteo.
Una vez estudiada la forma en que los niños adquieren los principios de conteo, podría entonces iniciarse un trabajo cuyo objetivo fuese facilitar dicha adquisición mediante la implementación de tareas que ayuden al niño a familiarizarse con los principios, de tal manera que logre su comprensión y utilización. Dicho trabajo tendría que partir indagando si la comprensión de los principios de conteo puede acelerarse y mediante qué tareas o situaciones didácticas. De existir tareas que propicien la comprensión, debería averiguarse también si cambiando el orden o la frecuencia de presentación se obtienen mejores resultados para ampliar de manera sistemática los conocimientos sobre esta línea de investigación y sus aportaciones en la promoción del desarrollo académico o en la corrección de dificultades en el aprendizaje a nivel básico.











 nueva página del texto (beta)
nueva página del texto (beta)


