Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Chapingo serie ciencias forestales y del ambiente
versión On-line ISSN 2007-4018versión impresa ISSN 2007-3828
Rev. Chapingo ser. cienc. for. ambient vol.17 no.spe Chapingo ene. 2011
https://doi.org/10.5154/r.rchscfa.2010.09.071
La variación de las temperaturas extremas en la 'Comarca Lagunera' y cercanías
Extreme temperature variation in the 'Comarca Lagunera' and nearby areas
Jairo Omar Inzunza-López1; Bernardo López-Ariza1; Ricardo David Valdez-Cepeda1,2¶; Blanca Mendoza3; Ignacio Sánchez-Cohen4; Gabriel García-Herrera1
1 Maestría en Ciencias en Recursos Naturales y Medio Ambiente en Zonas Áridas, Unidad Regional Universitaria de Zonas Áridas, Universidad Autónoma Chapingo. Bermejillo, Dgo., MÉXICO. Correo-e: vacrida@hotmail.com (¶Autor para correspondencia).
2 Centro Regional Universitario Centro Norte, Universidad Autónoma Chapingo. Unidad Académica de Matemáticas, Universidad Autónoma de Zacatecas. Zacatecas, Zac., MÉXICO.
3 Instituto de Geofísica, Universidad Nacional Autónoma de México. Ciudad Universitaria, México, D.F.
4 CENID-RASPA, Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias. Gómez Palacio, Dgo., MÉXICO.
Recibido: 07 septiembre, 2010
Aceptado: 17, marzo, 2011
RESUMEN
Las series de temperaturas máxima y mínima diarias, con registros de al menos 30 años, de 23 estaciones meteorológicas de la Comarca Lagunera y lugares cercanos, fueron analizadas con las técnicas de regresión lineal simple y densidad de espectro potencial para obtener las tendencias y frecuencias significativas. Las series de 15 de las 23 estaciones presentaron tendencias significativas (P≤0.05) para ambas temperaturas. El promedio de las tendencias de temperatura máxima fue de -0.22 °C por decenio; pues 15 de las 23 series presentaron decrementos, 13 de forma significativa. El promedio de las tendencias de temperatura mínima fue de -0.085 °C por decenio; ya que 13 de 23 series presentaron tendencias negativas, 11 de forma significativa. La variación a largo plazo fue la predominante ya que los promedios de dimensión fractal fueron 1.46 y de 1.47 para temperatura máxima y mínima, respectivamente. La mayoría de las series presentaron frecuencias cuasi-bianuales, cuasi-trianuales y cuasi-tetra-anuales. En cinco estaciones se apreciaron frecuencias de 10 a 11 años para ambos tipos de temperatura; una estación presentó la frecuencia de 20 años en las dos temperaturas.
Palabras clave: Temperatura máxima, temperatura mínima, regresión lineal, densidad de espectro potencial.
ABSTRACT
Time series of daily maximum and minimum temperatures, of at least 30 years long, from 23 weather stations in the 'Comarca Lagunera' (Lagoon region) and nearby areas were analyzed using simple linear regression and power-spectrum density techniques for significant trends and frequencies. Time series from 15 of the 23 stations showed significant (P≤0.05) trends for both temperatures. The trend average for maximum temperature was -0.22 0C per decade, as 15 of 23 series showed downward trends, 13 significantly. The trend average for minimum temperature was -0.085 0C per decade, since 13 of 23 series showed negative trends, 11 significantly. Long-term variation was predominant because the fractal dimension averages were 1.46 and 1.47 for maximum and minimum temperature, respectively. Most series showed quasi-biennial, quasi-three-year and quasi-four-year frequencies. Five stations showed 10- to 11-year frequencies for both minimum and maximum extreme temperatures; one station showed the 20-year frequency for both temperatures.
Key words: Maximum temperature, minimum temperature, linear regression, power-spectrum density.
INTRODUCCIÓN
El clima depende de un gran número de factores que interactúan de manera compleja. A diferencia del concepto tradicional de clima, como el promedio de alguna variable, hoy en día se piensa en éste como un estado cambiante de la atmósfera, mediante sus interacciones con el mar y el continente, en diversas escalas de tiempo y espacio. Cuando un elemento meteorológico, como la precipitación o la temperatura, diverge de su valor medio de muchos años, se denomina anomalía climática ocasionada por forzamientos internos, como inestabilidades en la atmósfera y el océano, o por fuerzas externas. Por ejemplo, algún cambio en la intensidad de la radiación solar recibida e incluso cambios en las características del planeta (e. g. concentración de gases de efecto invernadero, cambios en el uso de suelo) resultado de la actividad humana (Magaña, 2004).
El cambio climático es una desviación estadística del clima o la variabilidad que persiste durante un período prolongado (normalmente decenios e incluso más tiempo). Dicho cambio se puede deber a procesos naturales internos, a cambios del forzamiento externo, variaciones en la composición de la atmósfera o en el uso de las tierras (IPCC, 2007); es decir, a cambios asociados a actividades antropogénicas. El interés sobre el cambio climático se ha incrementado en los últimos 30 años debido, principalmente, a las predicciones globales asociadas con el efecto de invernadero, el cual parece indicar un incremento sustancial en la temperatura de la atmósfera terrestre (Valdez-Cepeda et al., 2003ab). Tal incremento ha sido de 0.084 ± 0.021 °C por decenio de 1901 a 2005 y de 0.268 ± 0.069 °C por decenio entre 1979 y 2005 (Brohan et al., 2006; Trenberth et al., 2007) y se ha asociado a causas antropogénicas (IPCC, 2001) o a causas astronómicas (Landscheidt, 2000; Soon et al., 2000a; Soon et al., 2000b). Se prevé que el incremento continuo de gases con efecto de invernadero originará un incremento sustancial en la temperatura del aire, un incremento en el nivel del mar, descongelamiento de los polos y glaciares, y sequías en el interior de los continentes (Houghton et al., 1996; 2001).
Las implicaciones de esos resultados han llevado a muchos científicos a examinar los registros climáticos de diferentes regiones del mundo a fin de comprender la variación de la temperatura (Valdez-Cepeda et al., 2003ab) y otros elementos climáticos. Un gran número de esos estudios se han llevado a cabo usando datos de estaciones europeas con registros de más de dos siglos (Valdez-Ce-peda et al., 2003ab). Desafortunadamente, se carece de registros de largo plazo de elementos climáticos de más de un siglo o siglo y medio para muchas estaciones a través del continente americano, en particular para Latinoamérica (Valdez-Cepeda et al., 2003ab).
Varios métodos se han usado para caracterizar cuantitativamente la variación de la temperatura. Con el fin de evidenciar tendencias de incremento o decremento, lo más común es evidenciar la tendencia a largo plazo a través del análisis de regresión lineal simple (Montgomery et al., 2007). La densidad de espectro potencial se ha usado en forma rutinaria (Király y Jánosi, 2002) con el fin de evidenciar periodicidades y sus posibles causas, es decir, fenómenos exógenos (e.g. fenómenos asociados a la actividad solar). Otros métodos usados son: análisis de entropía de difusión (Scaffeta y West, 2003); análisis de desviación estándar (Scaffeta y West, 2003) y análisis de fluctuación sin tendencia (Király y Jánosi, 2002; Király y Jánosi, 2005).
También se han analizado series de temperatura sin tendencia mediante técnicas espectrales. Por ejemplo, Yano et al. (2004) reportaron que para el caso de la temperatura del aire superficial en Kexue (3.9 °S, 155.9 °E), el exponente β cambia de -1 a -1.4 en un período de 50 horas para el caso; el exponente /3 adquirió un valor de -1.6 para un rango de tiempo de 0.5 - 50 horas para la temperatura registrada en Vickers (2.9 °N, 156.7 °E). Estos investigadores señalaron que la variación es descrita por una ley potencial que se conserva aún después de la extracción de eventos pico con la duración de la escala intra-estacional.
Varios investigadores (Jánosi y Vattay, 1992; Eichner et al., 2003; Monetti et al., 2003; Yano et al., 2004; Koscielny-Bunde et al., 2006) han analizado la fluctuación de temperaturas diarias. Jánosi y Vattay (1992) encontraron que la fluctuación de la temperatura diaria registrada en Szombathely, Hungría se describe mediante un exponente β = 0 en la parte baja de la frecuencia (f<~0.002día-1) del espectro potencial; mientras que el rango de frecuencia alta (f >0.1día-1, aproximadamente medio decenio) puede ajustarse a una ley potencial con un exponente β = -2.
Valdez-Cepeda et al. (2003a) analizaron el espectro de la señal de la serie de temperaturas mínimas extrema, de enero de 1921 a abril de 1963, registrada en Guanajuato, México (21° 01'N, 101° 14'O, 2037 m) y encontraron que β = -2.028 para escalas de tiempo de dos a 254 meses; además, cuando se eliminaron las tendencias lineal y la periodicidad anual, β = -2.09; es decir, la ley potencial se mantuvo después de que se eliminaron dichos componentes.
Para la Comarca Lagunera no se conoce este tipo de información; por ello, el presente estudio tiene como objetivos identificar las tendencias y frecuencias significativas de las variables temperaturas máximas y mínimas registradas en 23 estaciones meteorológicas mediante el análisis de regresión lineal y la técnica de espectro-potencial. La Comarca Lagunera es una zona que se caracteriza por sus limitados recursos hídricos y por su clima seco templado. En el contexto productivo, esta región mantiene a más de 100 mil cabezas de ganado vacuno productor de leche que se alimentan con más de 1,750.000 t de forraje verde y se considera la cuenca lechera más importante de México.
MATERIALES Y MÉTODOS
Área de estudio
Las estaciones meteorológicas consideradas en el presente estudio están dentro o en las cercanías de la Comarca Lagunera. El área considerada con las estaciones cubre desde los 102.173° hasta los 106.324° O y desde los 23.183° hasta los 26.75° N; cubre gran parte de Durango, norte de Zacatecas, oriente de Coahuila y sur de Chihuahua (Figura 1).

Recopilación de datos
El Extractor Rápido de Información Climatológica, ERIC III, versión 1.0 fue la fuente de datos (IMTA, 2007). Este programa contiene información del banco de datos histórico nacional del Servicio Meteorológico Nacional (SMN) de la Comisión Nacional del Agua (CONAGUA). Las estaciones de la Comarca Lagunera y cercanías se seleccionaron para lograr los objetivos planteados.
Tratamiento de la información
De manera inicial, las series de 54 estaciones fueron seleccionadas; sin embargo, se realizó una depuración. El primer filtro fue la continuidad de los datos, es decir, aquellas series con registros cuyos periodos sin datos fueron mayores a un año se descartaron. El segundo filtro consistió en revisar que la disponibilidad de datos continuos fuera de al menos 30 años. Así, las series que cumplieron los requisitos corresponden a 23 estaciones (Cuadro 1), ocho corresponden a la Comarca Lagunera y 13 a las cercanías. Cabe mencionar que los datos faltantes en las series seleccionadas fueron estimados al aplicar el método de interpolación Kriging puntual. Kriging puntual es una técnica de estimación (de valores faltantes) precisa e insesgada que se basa en la estructura de la variación y la definición de una vecindad cercana óptima (Valdez-Cepeda, 1991).
En la siguiente fase, los gráficos de dispersión de cada una de las series se obtuvieron con la finalidad de identificar datos atípicos. Luego, los estimadores intercepto (ordenada asociada al origen) y la pendiente se estimaron a través de análisis de regresión lineal usando Excel (Microsoft, 2007) y Statistica (StatSoft, 2000). También, los niveles de significancia del intercepto (β0) y la pendiente de la recta (β1) fueron estimados. Después de haber obtenido las tendencias (pendientes), el análisis del espectro potencial se realizó por medio del software Benoit (TruSoft, 1999).
Regresión lineal simple
La dependencia de una variable Y de una variable independiente X se define mediante el análisis de regresión (Snedecor y Cochran, 1984). Un modelo de regresión lineal simple usa un solo regresor x que tiene una relación con una respuesta y, donde la relación es:

La y se conoce como variable dependiente y la x es conocida como variable independiente (Steel et al., 1997); β0 es la ordenada al origen y β1 la pendiente, ambas son constantes desconocidas; e es un componente aleatorio de error. El supuesto básico es que los errores tienen promedio cero y varianza (σ2) desconocida pero mínima (Montgomery et al., 2007). Además, se supone que los errores no están correlacionados. Esto quiere decir que el valor de un error no depende del valor de otro error (Hair et al., 1999).
A los estimadores β0 y β1 se les llama coeficientes de regresión. Éstos tienen una interpretación simple y útil. La pendiente β1 es el cambio de la media de la distribución de y producido por un cambio unitario en x. Si el intervalo de los datos incluye x = 0, entonces la ordenada al origen β0, es la media de la distribución de la respuesta y cuando x = 0. Si no incluye al cero, β0 no tiene interpretación práctica (Montgomery et al., 2007).
Técnica de espectro potencial
Las series fractales auto-afines, por lo general, son tratadas cuantitativamente al usar técnicas espectrales (Turcotte, 1992). La variación del espectro potencial P(f) con frecuencia f parece seguir una ley potencial (Turcotte, 1992):

El espectro potencial P(f) se define como el cuadrado de la magnitud de la transformada de Fourier de la variable, al denotarla como una función del tiempo mediante Z(t); así se tiene:

donde t0 y t1 son los límites del tiempo sobre el que se distribuyen las observaciones que conforman cada serie. En el caso del registro de temperatura se muestrea a intervalos de tiempo discretos, por ello se debe utilizar una versión discreta de la Ecuación (3):
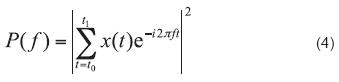
Después, una relación entre el exponente -β y la dimensión fractal Ds se obtiene; luego se considera a dos series de tiempo Z1(tt) y Z2(t) relacionadas mediante:

Se puede observar que Z1(t) tiene las mismas propiedades estadísticas que Z2(t), y dado que Z2 es una versión re-escalada de Z1, sus densidades de espectro potencial también deben ser re-escaladas apropiadamente. Por lo tanto, se puede escribir:

donde Ds denota la dimensión fractal estimada a partir del espectro potencial y H es el exponente de Hurst.
En la práctica, para obtener una estimación de la dimensión fractal Ds, se calcula el espectro potencial P(f) (donde f = 2p/ es el número de onda y l es la longitud de onda), y se grafica el logaritmo de P(f) contra el logaritmo de f (Valdez-Cepeda et al., 2003ab). Si el perfil es auto-afín (i.e. los ejes, ordenadas y abscisas, consideran diferentes unidades y escalas), ésta gráfica debe seguir una línea recta con una pendiente negativa -p (Valdez-Cepeda et al., 2003ab).
RESULTADOS Y DISCUSIÓN
Tendencias
Las pendientes (tendencias) estimadas y sus niveles de significancia para las variables temperatura máxima y mínima se aprecian en los Cuadros 2 y 3, respectivamente, como resultado de los análisis de regresión lineal. La pendiente (positiva o negativa) se cuantificó por decenio, es decir β1*365*10; la razón es que se requiere un valor de referencia y comparación debido a que los períodos de las series difieren en tamaño (n).
Para la temperatura máxima se tiene un promedio de tendencia de -0.22 °C por decenio, en tanto que para la temperatura mínima se estimó un promedio de tendencia de -0.085 °C por decenio. Con este primer resultado se puede aseverar que las temperaturas extremas del área de estudio, en general, tienden a disminuir.
Un análisis más exhaustivo indica que la temperatura máxima tiende a disminuir en 15 de 23 series; en 13 series el decremento es significativo (P<0.05). Por su parte, la temperatura mínima tiende a decrecer en 13 de 23 series; en 11 series la tendencia negativa es significativa (P<0.05).
El promedio de todas las tendencias negativas, para la temperatura máxima, fue de -0.414°C por decenio; en tanto que para la temperatura mínima fue de -0.358 °C por decenio. El promedio de todas las tendencias positivas fue de 0.142 °C por decenio para la temperatura máxima; mientras que para la temperatura mínima fue de 0.269 °C por decenio. Los valores absolutos de esas tendencias sugieren que en el área de estudio predomina la tendencia negativa en ambos tipos de temperatura extrema.
Los valores absolutos mayores de tendencias deceniales positivas y negativas para la temperatura máxima fueron de 0.308 °C (Cuencamé) y -1.397 °C (Canatlán). En cuanto a la temperatura mínima, los valores absolutos mayores fueron 0.547 °C (San Pedro) y -1.441 °C (El Pueblito).
En general, nuestros resultados sugieren que predomina la tendencia negativa en ambos tipos de temperaturas extremas (máxima y mínima) registrada a nivel diario en la región de estudio; pero ello no sugiere que se contrapone a lo reportado como incremento a nivel global de 0.084 ± 0.021 °C por decenio de 1901 a 2005 y de 0.268 ± 0.069 °C por decenio de 1979 a 2005 (Brohan et al., 2006; Trenberth et al., 2007), ya que el calentamiento del planeta tierra ha sido evidenciado sobre la base de temperaturas medias a los niveles mensual y anual. Debe remarcarse, sin embargo, que los resultados presentados en esta contribución coinciden con lo reportado por otros investigadores para otras localidades y regiones en el sentido de presentar tendencias de decremento e incremento en ambos tipos de temperaturas. Ello implica, entonces, que nuestros resultados son una evidencia de que puede haber tendencias locales y regionales sin representatividad a nivel global, como previamente fue señalado por Valdez-Cepeda et al. (2003a).
En un análisis acucioso, las series fueron separadas de acuerdo a las tendencias de las temperaturas máxima y mínima en conjunto para formar nueve situaciones distintas (Figura 2).

Con dicha clasificación de escenarios, ninguna de las estaciones presentó el escenario uno; es decir, aquél en el que la oscilación térmica se mantuviera a consecuencia de que ambas series (temperatura máxima y mínima) presentaran tendencias nulas ( =0). Sin embargo, la oscilación térmica se ha mantenido en 1° estaciones a pesar de las tendencias significativas: Ocho (Ciénega de Escobar, El Pueblito, El Tarahumar, El Escalón, Juan Aldama, Nazas, Rodeo y Sardinas) de las 23 estaciones corresponden al escenario seis, pues las series de ambas temperaturas, máxima y mínima, presentaron tendencias negativas; en solo dos (Cuencamé y Palmito II) de las 23 estaciones se evidenciaron tendencias positivas en ambas temperaturas (escenario siete). Sin embargo, merece ser resaltado que las temperaturas extremas han cambiado significativamente en esas 1° localidades.
=0). Sin embargo, la oscilación térmica se ha mantenido en 1° estaciones a pesar de las tendencias significativas: Ocho (Ciénega de Escobar, El Pueblito, El Tarahumar, El Escalón, Juan Aldama, Nazas, Rodeo y Sardinas) de las 23 estaciones corresponden al escenario seis, pues las series de ambas temperaturas, máxima y mínima, presentaron tendencias negativas; en solo dos (Cuencamé y Palmito II) de las 23 estaciones se evidenciaron tendencias positivas en ambas temperaturas (escenario siete). Sin embargo, merece ser resaltado que las temperaturas extremas han cambiado significativamente en esas 1° localidades.
La oscilación térmica se ha incrementado en seis estaciones: En dos estaciones (Parras y Peña del Águila), la tendencia de la temperatura máxima fue nula, mientras que la de la temperatura mínima decreció de manera significativa (escenario dos); en tres estaciones (Cañón de Fernández, Guanaceví y Santiago Papasquiaro), la tendencia de la temperatura máxima disminuyó de manera significativa y la de la temperatura mínima fue nula (escenario cinco); y en una estación (El Sauz), la tendencia de la temperatura máxima fue positiva y la de la temperatura mínima fue negativa, ambas de forma significativa (escenario nueve). Es notorio que en cinco de esas seis localidades, una de las dos temperaturas extremas ha cambiado significativamente.
Por el contrario, la oscilación térmica se ha reducido en las siete estaciones restantes: En dos estaciones (Ciudad Lerdo y Narciso Mendoza), la tendencia de la temperatura máxima fue nula y la de la temperatura mínima creció de manera significativa (escenario tres); en una estación (Tlahualilo), la tendencia de la temperatura máxima disminuyó de manera significativa y la de la temperatura mínima fue nula (escenario cuatro); en cuatro estaciones (5 de Mayo, Canatlán, San Pedro y Santa Clara), la tendencia de la temperatura máxima fue negativa y la de la temperatura mínima fue positiva, ambas de manera significativa (escenario ocho). Es preciso resaltar que las dos temperaturas extremas han cambiado de forma significativa en cuatro de esas ocho localidades.
Fractalidad y frecuencias
Como ejemplo de los resultados del análisis correspondiente, la densidad del espectro potencial en función de la frecuencia de la estación de Ciudad Lerdo se presenta en las Figuras 3 y 4 para las series de temperatura máxima y mínima a nivel diario, respectivamente. En cada gráfica, la línea recta fue ajustada por medio de la Ecuación 2.
Además, en esos gráficos, los picos más importantes se marcaron y asociaron a las frecuencias correspondientes con el fin de identificar a las posibles fuerzas externas que afectan la variación de la temperatura. En el Cuadro 4 se presentan las frecuencias estimadas para temperatura máxima y mínima, respectivamente; así como los estimadores beta (β), dimensión fractal (Ds) y coeficiente de Hurst (H) para cada serie.
Los datos de las series de las 23 estaciones se ajustaron a líneas rectas en las gráficas log-log con pendiente β, cuyos valores variaron de -1.613 a -2.507 (para la temperatura máxima) y de -1.695 a -2.532 (para la temperatura mínima) lo cual sugiere que:
P (f) μ f -β
Por consiguiente, el espectro es singular y puede ser representado por una curva en el plano complejo en todos los casos. Los valores de H variaron de 0.307 a 0.753 (para la temperatura máxima) y de 0.348 a 0.766 (para la temperatura mínima).
En el caso de la temperatura máxima, las series presentaron valores de dimensión fractal (Ds) desde 1.247 (Palmito II) hasta 1.693 (Guanaceví) con un valor promedio de 1.459 (±0.08). Esto indica que, en general, predomina la variación a largo plazo; es decir, las temperaturas futuras se ven influidas por las del pasado (De la Fuente et al., 1999). Las excepciones son las series cuyo valor de Ds es mayor a 1.5.
En el caso de la temperatura mínima, las series presentaron valores de Ds desde 1.234 (El Escalón) hasta 1.652 (Guanaceví) con un valor promedio de 1.469 (±0.09). Entonces, en general, en las series de temperatura mínima casi predomina también la variación a largo plazo.
Es notable que en el caso de temperatura máxima, las series de 19 de las 23 estaciones presentaron valores de Ds menores a 1.5; mientras que para la temperatura mínima en sólo 12 de 23 series se presentó tal situación. Se confirma, entonces, que predomina la variación a largo plazo en los casos de temperatura máxima; mientras que ambos tipos de variación (a largo plazo, 12 a corto plazo, 11 casos) tienen casi igual importancia en lo concerniente a temperatura mínima.
Las frecuencias importantes identificadas se aprecian en las Figuras 5 y 6 para temperatura máxima y mínima, respectivamente. En casi todas las series se identificó una frecuencia asociada posiblemente a la oscilación semestral (0.5 años), relacionada al movimiento de traslación de la Tierra, que claramente puede influir sobre la variación de la temperatura. También, es posible que esté presente la oscilación cuasi-bianual, relacionada con la temperatura de la estratósfera del polo norte y la actividad solar (Labitzke y Van Loon, 1989; Mendoza et al., 2001).
La mayoría de las series presentan frecuencias de entre tres y siete años, las cuales se pueden relacionar con la actividad del fenómeno Oscilación del Sur El Niño que presenta periodicidades de tres a cinco años (Weber y Talkner, 2001) o de tres a seis años (Monetti et al., 2003).
En las series de las estaciones Cañón de Fernández, El Saúz, Guanaceví, Palmito II, Rodeo (Laguna) y Santiago Papasquiaro se observaron frecuencias de 10 años, lo cual sugiere que pueden estar afectadas por el ciclo de manchas solares (Mendoza et al., 2001). En las series de ambas temperaturas, registradas en Guanaceví, se apreció la frecuencia de 20 años, lo cual indica que posiblemente están influidas por el ciclo magnético del Sol (Mendoza et al., 2001; Valdez-Cepeda et al., 2003a).
Las series de temperatura máxima que sólo presentaron frecuencias de 10 años son las de las estaciones Canatlán, El Escalón y Santa Clara; mientras que para la temperatura mínima esas frecuencias se presentaron en las series de las estaciones 5 de Mayo, Cuencamé, El Pueblito, Narciso Mendoza y Nazas. Entonces, todas esas series pueden estar influidas por el ciclo de manchas solares (Mendoza et al., 2001; Valdez-Cepeda et al., 2003a).
Es importante señalar que los resultados permiten sugerir que es necesario abordar con mayor profundidad, en futuros trabajos de investigación, la asociación entre cada una de las series de temperatura extrema (máxima y mínima) con las series de tiempo de los fenómenos con periodicidades de magnitud similar a las identificadas (e.g. ciclo cuasi-bianual, Oscilación del Sur El Niño y los ciclos de manchas y magnético del sol). El propósito de esta sugerencia es generar conocimiento básico para entender mejor las relaciones entre el cambio de las temperaturas extremas y los fenómenos con influencia global y la actividad solar.
CONCLUSIONES
Poco más de la mitad (24) de las series analizadas (46) presentaron tendencia significativa de disminución de temperatura máxima (13 de 23 estaciones) y temperatura mínima (11 de 23 estaciones). Sólo 14 de las series mostraron tendencia significativa de incremento de temperatura máxima (8 de 23 estaciones) y temperatura mínima (seis de 23 estaciones).
La temperatura máxima presentó un promedio de decremento de -0.22 °C por decenio; en tanto que a la temperatura mínima se asocia un promedio de -0.085 °C por decenio. Sin embargo, cuando se consideraron solo los valores negativos de tendencia, los promedios absolutos se incrementaron llegando a -0.414 °C y -0.358 °C para temperatura máxima y mínima, respectivamente.
Los valores extremos de las tendencias fueron: 0.308 °C (Cuencamé) y de -1.397 °C (Canatlán) para la temperatura máxima; mientras que para la temperatura mínima fueron 0.547 °C (San Pedro) y -1.441 °C (El Pueblito).
De nueve escenarios posibles de combinación de las tendencias de ambas temperaturas, ocho de 23 estaciones presentaron el escenario en el que ambas temperaturas tienden a disminuir de manera significativa.
Los valores de dimensión fractal espectral presentaron promedios de 1.459 ± 0.08 y 1.469 ± 0.09 para temperatura máxima y mínima, respectivamente. Ello indica que predomina la variación de largo plazo y que ambas temperaturas son predecibles.
Las frecuencias cuasi-anual y cuasi-bianual fueron evidenciadas en la mayoría de las series. Sólo en las series de las estaciones Cañón de Fernández, El Sauz, Guanaceví, Palmito II, Rodeo y Santiago Papasquiaro se evidenciaron frecuencias de 1° y en Guanaceví la de 20 años, para ambas temperaturas (máxima y mínima).
AGRADECIMIENTOS
Al Fondo Mixto del Estado de Durango y al Consejo de Ciencia y Tecnología del Estado de Durango por el soporte financiero otorgado mediante el proyecto 'Comportamiento de Temperaturas, Evaporación y Precipitación en el Contexto del Cambio Climático en la Comarca Lagunera', Clave DGO-2008-C01-88130.
LITERATURA CITADA
BROHAN, P.; KENNEDY, J. J.; HARRIS, I.; TETT, S. F. B.; JONES, P. D. 2006. Uncertainty estimates in regional and global observed temperature changes: A new data set from 1850. J. Geophys. Res., 111, D12106. DOI: 10.1029/2005JD006548. [ Links ]
DE LA FUENTE, I. M.; MARTÍNEZ, L.; AGUIRREGABIRIA, J. M.; VEGUILLAS J.; IRIARTE, M. 1999. Long-range correlations in the phase-shifts of numerical simulations of biochemical oscillations and in experimental cardiac rhythms. J. Biol. Systems 7: 113-130. [ Links ]
EICHNER, J. F.; KOSCIELNY-BUNDE, E.; BUNDE, A.; HA-VLIN, S.; SCHELLNHUBER, H.-J. 2003. Power-law persistence and trends in the atmosphere: A detailed study of long temperature records. Phys. Rev. E. 68: 046133-046137. [ Links ]
HAIR, J. F. JR.; ANDERSON, R. E.; TATHAM, R. L.; BLACK, W. C. 1999. Análisis Multivariante. Quinta Edición. Prentice Hall. 79-81 pp. [ Links ]
HOUGHTON, J. T.; MEIRA FILHO, L. G.; CALLANDER, B. A.; HARRIS, N.; KATTENBERG, A.; MASKELL, K. (Eds.). 1996. Climate Change 1995: The Science of Climate Change. Cambridge University Press. Cambridge. [ Links ]
HOUGHTON, J. T.; DING, Y.; GRIGGS, D. J.; NOGUER, M.; VAN DER LINDEN, P. J.; DAI, X.; MASKELL, K.; JOHNSON, C. A. (Eds.). 2001. Climate Change 2001: The Scientific Basis. Cambridge University Press. Cambridge. [ Links ]
INSTITUTO MEXICANO DE TECNOLOGÍA DEL AGUA (IMTA). 2007. Extractor Rápido de Información Climatológica v.1.0. Software. http://www.csva.gob.mx/sih/info/pag_ficha_datos.php?xficha=905#mas_info [ Links ]
INTERGOVERNMENTAL PANEL ON CLIMATE CHANGE (IPCC). 2001. Climatic Change 2001: Synthesis Report. Contribution of Working Group I and III to the Third Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press. Cambridge. [ Links ]
INTERGOVERNMENTAL PANEL ON CLIMATE CHANGE (IPCC). 2007. Climatic Change 2007. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press. Cambridge. [ Links ]
JÁNOSI, I. M.; VATTAY, G. 1992. Soft turbulent state of the atmospheric boundary layer. Phys. Rev. A 46: 6386-6389. [ Links ]
KIRÁLY, A.; JÁNOSI, M. 2002. Stochastic modeling of daily temperature fluctuations. Phys. Rev. E. 65: 51-102. [ Links ]
KIRÁLY, A.; JÁNOSI, I. M. 2005. Detrended fluctuation analysis of daily temperature records: Geographic dependence over Australia. Meteorol. Atmos. Phys. 88: 119-128. [ Links ]
KOSCIELNY-BUNDE, E.; KANTELHARDT, J. W.; BRAUN, P.; BUNDE, A.; HAVLIN, S. 2006. Long-term persistence and multifractality of river runoff records: Detrended fluctuation studies. J. Hydrol. 322: 120-137. [ Links ]
LABITZKE, K.; VAN LOON, H. 1989. Associations between the 11-year solar cycle, the QBO and the atmosphere. Part I: the troposphere and stratosphere in the Northern Hemisphere in winter. J. Atmosph. and Solar-Terr. Phys. 50: 197. [ Links ]
LANDSCHEIDT, T. 2000. Solar wind near Earth: Indicator of variations in global temperature. In: Proceedings of the 1st Solar and Space Weather Euro-Conference on the Solar Cycle and Terrestrial Climate. Santa Cruz de Tenerife, España. September 25-30, 2000. 497-500 pp. [ Links ]
MAGAÑA R., V. O. 2004. El cambio climático global: comprender el problema, In: Cambio climático: una visión desde México, Instituto Nacional de Ecología, Secretaría del Medio Ambiente y Recursos Naturales, ISBN 968-817704-0. México, D.F. 525 p. [ Links ]
MENDOZA, B.; LARA, A.; MARAVILLA, D.; JÁUREGUI, E. 2001. Temperature variability in central Mexico and its possible association to solar activity. J. Atmosph. and Solar-Terr. Phys. 63: 1891-1900. [ Links ]
MICROSOFT CORPORATION. 2008. Microsoft Office Excel 2007 (Computer program). Part of Microsoft Office Enterprise. One Microsoft Way, Redmond, WA 980526399, Web Site http://office.microsoft.com/en-us/excel/default.aspx [ Links ]
MONETTI, R. A.; HAVLIN, S.; BUNDE, A. 2003. Long-term persistence in sea-surface temperature fluctuations. Physi-ca A 320: 581-589. [ Links ]
MONTGOMERY, D. C.; PECK, E. A.; VINING, G. G. 2007. Introducción al Análisis de Regresión Lineal. 3ra Edición, 4ta Reimpresión, Grupo Editorial Patria. México, D.F. 588 p. [ Links ]
SCAFETTA, N.; WEST, B. J. 2003. Solar flare intermittency and the Earth's temperature anomalies. Phys. Rev. Letters 90: 248701, 4 p. [ Links ]
SNEDECOR, W. G.; COCHRAN W. G. 1984. Métodos Estadísticos- Editorial CECSA, Décima Impresión, México, D.F. 703 p. [ Links ]
SOON, W.; BALIUNAS, S.; POSMENTIER, E. S.; OKEKE, P. 2000a. Variations of solar coronal whole area and terrestrial tropospheric air temperature from 1979- to mid-1998: Astronomical forcings of change in earth's climate? New Astron. 4: 563-579. [ Links ]
SOON, W.; SOON, W.; BALIUNAS, S. 2000b. Climate hypersensitivity to solar forcing? Ann. Geophysic.-Atm. Hydr. 18: 583-588. [ Links ]
STATSOFT, INC. 2000. STATISTICA for Windows (Computer Program Manual). Tulsa, OK: StatSoft, Inc., 2300 East 14th Street, Tulsa, OK 74104, phone: (918) 749-1119, fax: (918) 749-2217, email: info@statsoft.com, Web Site: http://www.statsoft.com [ Links ]
STEEL, R. G. D.; TORRIE, J. H.; DICKEY, D. A. 1997. Principles and Procedures of Statistics: A Biometrical Approach. 3rd Edition. McGraw-Hill. USA. 972 p. [ Links ]
TRENBERTH, K. E.; JONES, P. D.; AMBENJE, P.; BOJARIU, R.; EASTERLING, D.; KLEIN TANK, A.; PARKER, D.; RAHIMZADEH, F.; RENWICK, J. A.; RUSTICUCCI, M.; SODEN, B.; ZHAI, P. 2007. Observations: Surface and Atmospheric Climate Change. In: Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change [SOLOMON, S.; QIN D.; MANNING, M.; CHEN, Z.; MARQUIS, M.; AVERYT, K.B.; TIGNOR, M.; MILLER, H.L. (Eds.)]. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA. [ Links ]
TRUSOFT, INTERNATIONAL INC. 1999. Benoit-your door into the world of Fractal Analysis, Version 1.31. 204 37th Ave. N #133 St. Petersburg, FL 33704 Tel: (727) 894-7426, Fax: (727) 822-3040, email: -sales@trusoft-international.com, Web Site: http://www.trusoft-international.com [ Links ]
VALDEZ-CEPEDA, R. D. 1991. Estimación del agua en el suelo. Terra 9(2): 114-121. [ Links ]
VALDEZ-CEPEDA, R. D.; HERNÁNDEZ-RAMÍREZ, D.; MENDOZA, B.; VALDÉS-GALICIA, J.; MARAVILLA, D. 2003a. Fractality of monthly extreme minimum temperature. Fractals 11: 137-144. [ Links ]
VALDEZ-CEPEDA, R. D.; MENDOZA, B.; DÍAZ-SANDOVAL, R.; VALDÉS-GALICIA, J.; LÓPEZ-MARTÍNEZ, J. D.; MARTÍNEZ-RUBÍN DE CELIS, E. 2003b. Power-spectrum behaviour of yearly mean grain yields. Fractals 11(3): 295-301. [ Links ]
WEBER, R. O.; TALKNER, P. 2001. Spectra and correlations of climate data from days to decades. J. Geophys. Res. D 106: 20131-20144. [ Links ]
YANO. J.-I.; BLENDER R.; ZHANG, C.; FRAEDRICH, K. 2004. 1/f noise and pulse-like events in the tropical atmospheric surface variabilities. Q. J. R. Meteorol. Soc. 130: 1697-1721. [ Links ]














