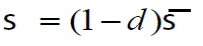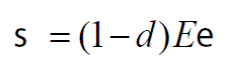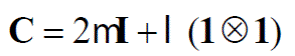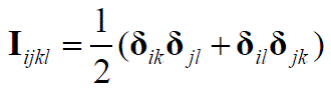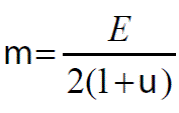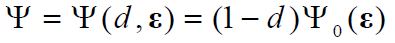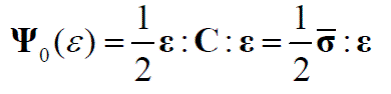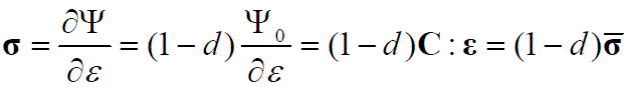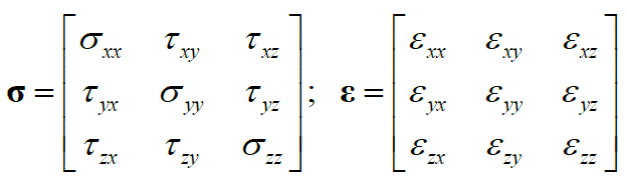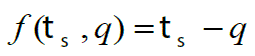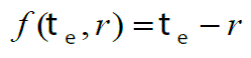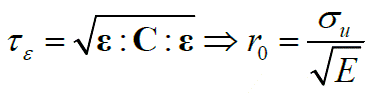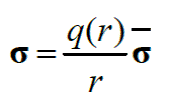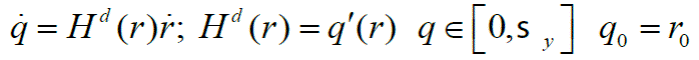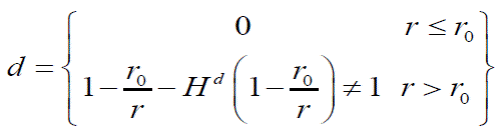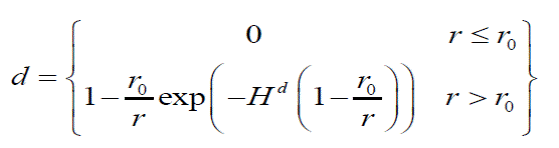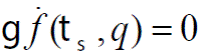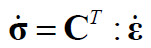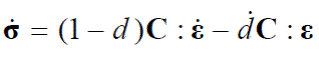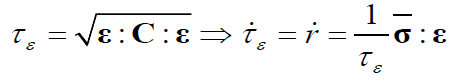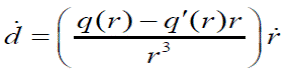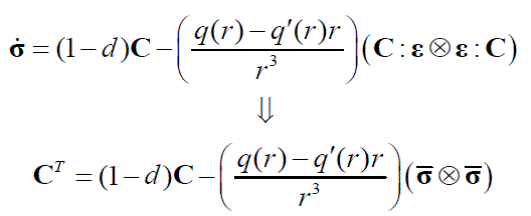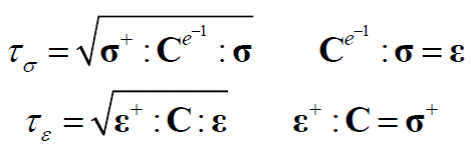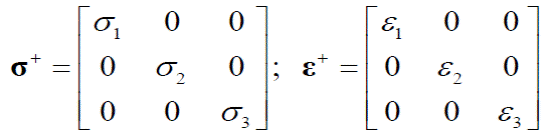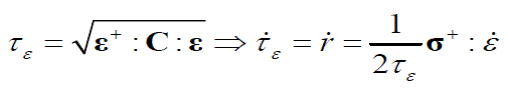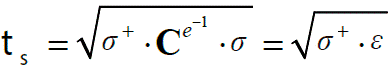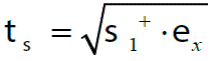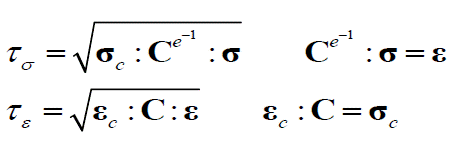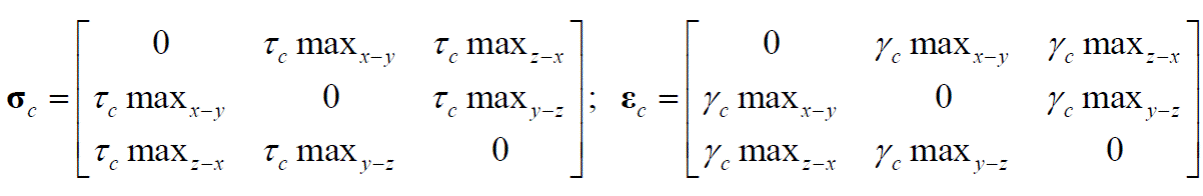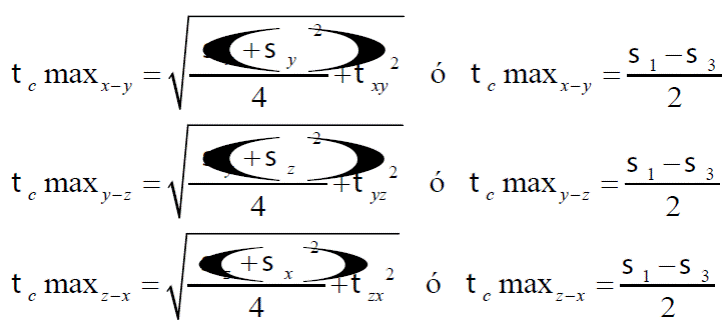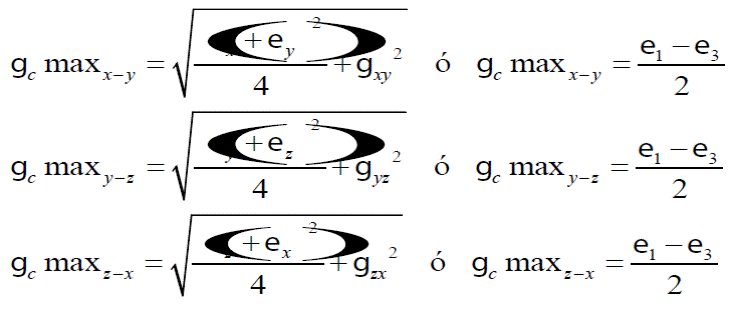1. Introducción
La mecánica de daño proporciona las bases para desarrollar modelos constitutivos que describen el deterioro progresivo de las propiedades mecánicas de los materiales. El daño es un proceso por el cual los materiales se rompen, debido a la degradación progresiva de sus propiedades mecánicas, i.e., el módulo de Young y el esfuerzo último del material (Luccioni 2003). Además, puede ocurrir plasticidad caracterizada por deformación permanente después de la descarga completa.
Existen otras aproximaciones para simular la degradación en materiales como el modelo de agrietamiento distribuido, el cual representa la pérdida de rigidez del material como un conjunto de grietas paralelas entre sí, distribuidas sobre el volumen de un elemento finito; sin embargo, el modelo de agrietamiento distribuido presenta problemas de atoramiento de esfuerzos y modos cinemáticos falsos que pueden proporcionar soluciones incorrectas (Rots 1985). Otro modelo para estudiar la falla en materiales es la mecánica de fractura, utilizado principalmente en materiales frágiles; este modelo tiene la limitante de necesitar grietas iniciales y técnicas de remallado que lo hacen computacionalmente costoso. El modelo de discontinuidades embebidas permite introducir discontinuidades (grietas) dentro de los elementos finitos durante el análisis, sin necesidad de modificar la malla ni de tener grietas iniciales (Juárez y Ayala 2009, Retama-Velazco y Ayala 2010); sin embargo, este modelo requiere de algoritmos tediosos para realizar la propagación de discontinuidades. Por lo anterior, en este trabajo se utiliza la mecánica de daño para estudiar el deterioro del material, que distribuye el daño en cada punto de integración de Gauss dentro del elemento; además de no requerir de grietas iniciales, ni necesitar algoritmos tediosos para propagar el daño.
La introducción del concepto de daño fue realizada por Kachanov (1958); posteriormente, Lemaitre (1971) desarrolló la teoría basada en la mecánica de medios continuos, dándole el sentido de daño con el enfoque clásico de la mecánica de fractura, utilizando bases rigurosas de termodinámica y micromecánica. Los efectos de la plasticidad también se consideran mediante modelos acoplados de daño-plasticidad como: Simo y Ju (1987 a, b), Ju (1989), Lubliner et al. (1989) y Luccioni et al. (1996), entre otros.
Juárez y Ayala (2010a, b) modelaron la falla de sólidos con elementos finitos mixtos, en los que utilizan un modelo de daño igual tensión-compresión; sin embargo, este modelo presenta problemas de traslape de volúmenes cuando se tienen elementos en compresión con una resistencia mayor a la de tensión, como es el caso del comportamiento constitutivo del concreto. Para superar el problema de traslape, Méndez-Martínez y Juárez-Luna (2012) desarrollaron e implantaron un modelo de daño con diferente umbral en tensión y compresión, el cual se validó con el modelado y comparación de elementos de concreto simple y reforzado, reportados en la literatura, sujetos a cargas hasta llevarlos al colapso. Dentro del desarrollo de modelos constitutivos dentro de la mecánica de daño, Oliver et al. (1990) proponen tres normas: (1) con igual degradación en tensión-compresión, 2) sólo en tensión y 3) diferente tensión-compresión, implantando sólo la segunda la cual se validó con un espécimen sujeto a tensión en el que la falla se propaga en dirección vertical; sin embargo, como se mostrará en este artículo, el modelo sólo tensión es válido únicamente cuando el daño ocurre en dirección vertical, perpendicular al esfuerzo horizontal σx, puesto que cuando el daño se propaga en otra dirección, el sólido permanece elástico debido a que el producto de la norma propuesta es pequeña. Posteriormente, Vieira (2003) propuso dos normas de daño: sólo tensión y diferentes umbrales en tensión-compresión; ambas normas se basan en una superficie con umbrales de igual tensión-compresión.
En un elemento estructural, el estado de esfuerzos depende de la carga actuante; cuando las cargas son a tensión se presentan fallas por apertura, pero cuando las cargas son a compresión, como cilindros de concreto o pruebas de arcillas, los elementos fallan por la formación de una línea de cortante. Por lo anterior, el objetivo de este artículo es la formulación, implantación y validación de normas de falla igual tensión-compresión, sólo cortante y diferente tensión-compresión para estudiar elementos estructurales sometidos a distintas acciones de carga hasta llegar al colapso. Estos modelos se implantaron en lenguaje Fortran dentro de subrutinas del programa FEAP (Taylor 2008), acrónimo de su nombre en idioma Inglés, Finite Element Analysis Program. Se presentan ejemplos numéricos que muestran la validez de las superficies de falla formuladas para predecir elementos al colapso. Los modelos implantados no presentan el problema de atoramiento de esfuerzos, como sucede con el modelo de agrietamiento distribuido, lo que garantiza una adecuada liberación de energía cuando el material falla.
2. Formulación de modelos de daño
2.1. Modelo de daño isotrópico igual tensión-compresión (MDITC)
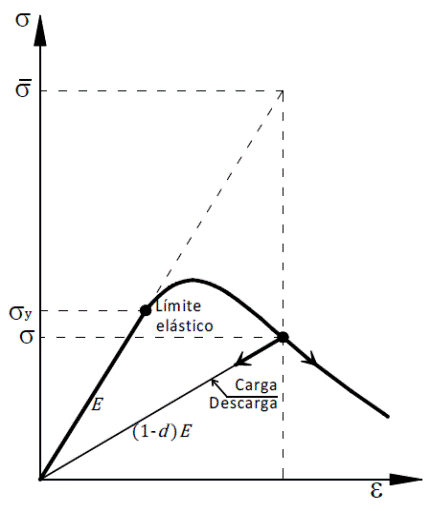
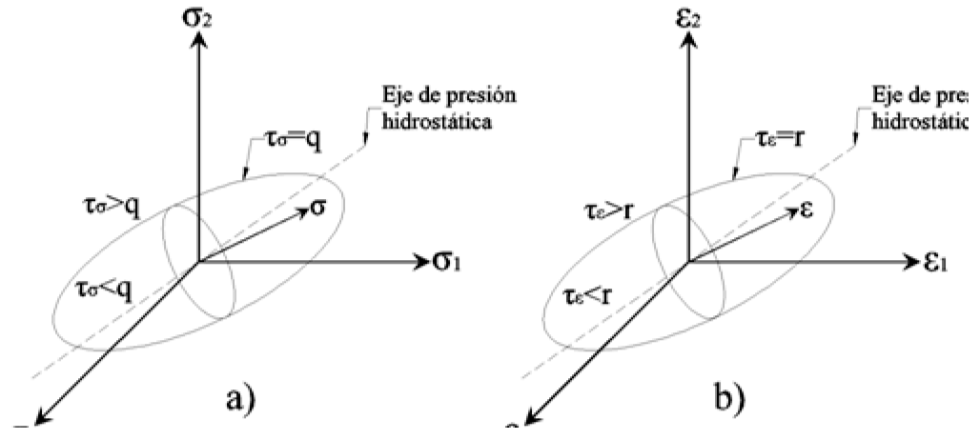
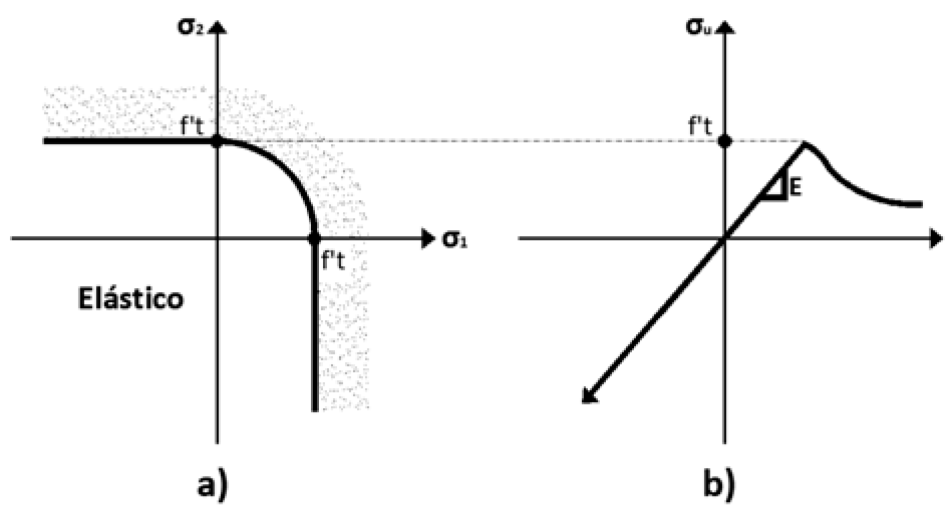
La variable de daño, que puede ser un escalar d, caracteriza el deterioro del material relacionando el esfuerzo σ con el esfuerzo efectivo, como se muestra en la Figura 1, caracterizándose mediante la siguiente ecuación:
Relacionando el esfuerzo efectivo y la deformación del material mediante la ley de Hooke se obtiene:
donde E es el módulo de Young del material. Sustituyendo la ec. (2) en la ec. (1), se tiene:
La notación de los esfuerzos, las deformaciones y la relación constitutiva para el caso unidimensional son tensores de orden cero, pero para sólidos en tres dimensiones (3D), se utilizan tensores de cuarto orden, manteniendo sólo con magnitud escalar la variable de daño d, tal que:
En la ec. (4), C es el tensor constitutivo elástico de cuarto orden y Cd es el tensor constitutivo elástico degradado. El tensor C queda en función de μ y λ, que son las llamadas constantes de Lamé, definidas como:
En la ec. (5), el 1 representa un tensor unitario de segundo orden, I un tensor unitario de cuarto orden. En las ec. (7) y (8), υ es la relación de Poisson.
2.2. Ecuación constitutiva
El propósito de las ecuaciones constitutivas es representar el comportamiento idealizado de un material, estableciendo relaciones entre los campos cinemáticos, térmicos y mecánicos; donde existe una variedad de ecuaciones obtenidas de las leyes fundamentales de la mecánica del medio continuo (Vieira 2003). Le densidad de energía libre de Helmholtz por unidad de volumen Ψ, para el caso de un modelo de daño isotrópico, se define como:
Donde Ψ 0 (ε) es la densidad de energía libre de Helmholtz de un material elástico no dañado en función del campo de las deformaciones ε. Esta energía puede escribirse como:
Sustituyendo la ec. (10) en la ec. (9) se obtiene:
Los esfuerzos se obtienen derivando la ec. (9) respecto a ε, tal que:
La cual corresponde a la ecuación constitutiva secante del modelo de daño.
2.3. Criterio de daño
Para delimitar el comportamiento elástico y el de degradación que sufren las propiedades del material, se utiliza el criterio de daño, que requiere de una norma en el espacio de los esfuerzos como:
Donde los tensores de esfuerzos y deformaciones son:
Análogo a la función de daño definida en la ec. (13) se puede definir la norma en el espacio de las deformaciones como:
Las normas, definidas en las ecs. (13) y (15), se pueden relacionar mediante:
Las funciones que delimitan la superficie de daño, en el espacio de esfuerzos y deformaciones correspondientes, mostradas en la Figura 2, que definen el límite elástico del comportamiento del material son respectivamente:
Donde q es una función que define el ablandamiento/endurecimiento, y r es la variable interna cuyo valor define el límite elástico. En el caso unidimensional de la ec. (18), se obtiene el valor r0 que representa el valor umbral inicial:
Donde σu es la magnitud del esfuerzo último. La variable de ablandamiento/endurecimiento q se define como:
De las ecs. (4) y (20) se obtiene la siguiente relación de esfuerzos:
2.4. Regla de ablandamiento/ endurecimiento
La regla de ablandamiento/endurecimiento se define por la siguiente ecuación:
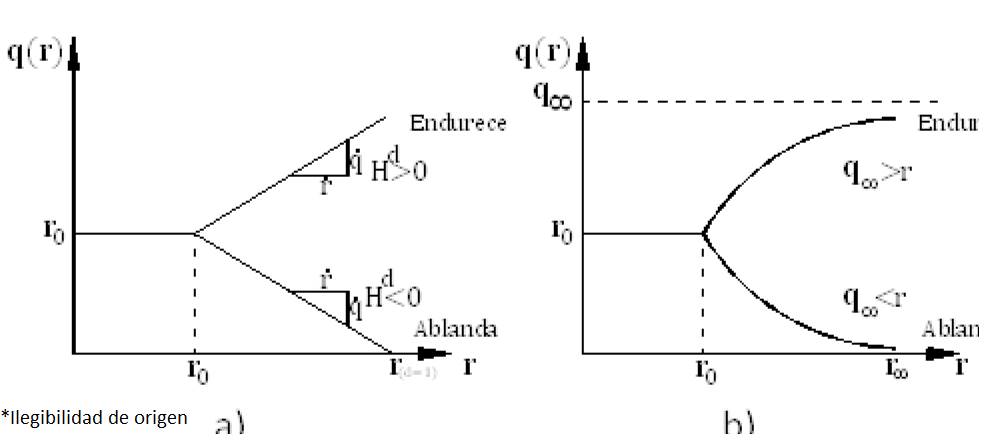
Donde Hd es el módulo de ablandamiento/endurecimiento continuo. En la Figura 3a, se muestra la función de endurecimiento lineal, la cual se define como:
Y en la Figura 3b, para la regla exponencial:
Para el caso lineal, la variable de daño se expresa de la siguiente forma:
Y en el caso exponencial:
Las leyes de evolución de la variable interna y de la variable de daño son:
Donde γ es un valor escalar no negativo denominado parámetro de consistencia de daño. El intervalo de la variable interna es [0, ∞). Si la variable de daño es cero, la variable interna r tiene el valor de r0, y cuando el daño es igual a uno, la variable es r = r∞.
2.5. Condición de carga y descarga
Para obtener el multiplicador de daño γ, se utilizan las condiciones de carga y descarga, conocidas como las condiciones de Kuhn-Tucker:
Y la condición de consistencia:
Las ecuaciones (29) y (30) determinan la condición de carga o descarga que presente el material:
Si se cumple que f (t s , q) < 0 el material se encuentra en la condición elástica, por lo tanto ts - q < 0 en un tiempo t , de lo que se sabe que ts = q , con lo cual se determina que g = r = 0 y que g f (ts , q) = 0.
Si por el contrario, se cumple que f (ts , q) } = 0 el material se encuentra en su intervalo inelástico, por lo tanto ts q = 0 en un tiempo t ; de lo anterior se puede saber que ts = q lo que determina que g = r ≥ 0 requiriendo que g f (ts , q) = 0 .
2.6. Módulo tangente
El operador que relaciona la evolución de los esfuerzos y deformaciones se denomina módulo tangente CT , tal que:
Derivando la ec. (4), se obtiene:
Diferenciando te, definido en la ec. (15) y considerando la ec. (23), se obtiene:
De la ec. (25) se obtiene la derivada de la variable de daño:
Finalmente se obtiene el tensor constitutivo tangente sustituyendo la ec. (34) en la ec. (32):
En la Figura 4 se muestra la superficie de daño que contiene el estado de esfuerzos elásticos del MDITC, el cual se resume con las ecuaciones de la Tabla 1.
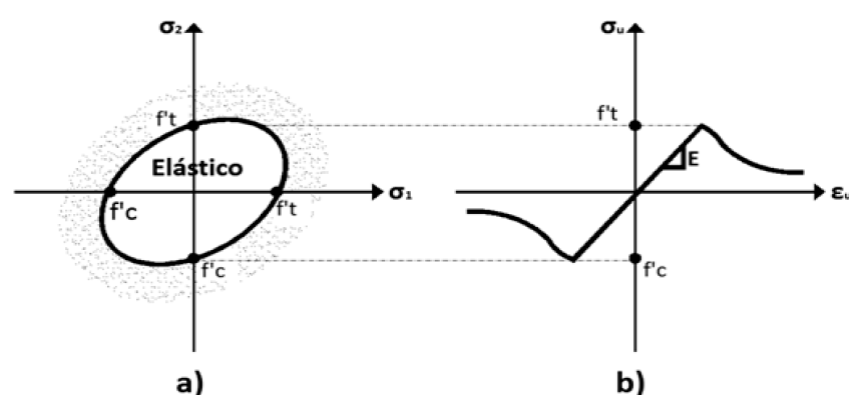
Figura 4: Modelo de daño igual tensión-compresión: a) superficie de daño en 2D y b) curva esfuerzo-deformación unidimensional.
2.7. Modelo de daño isotrópico sólo tensión (MDST)
La formulación del modelo de daño sólo tensión (MDST) se basa en el MDITC, la diferencia principal entre ambos modelos de daño es la definición de la norma, para lo cual se revisaron las propuestas siguientes, realizadas por otros autores:
Oliver et al. (1990) proponen para un modelo en sólo tensión la norma siguiente:
Donde s+ es el tensor de esfuerzos principales sólo positivos (s n ≥ 0) ; sin embargo, al implantar esta norma por Hernández-García (2012) se demostró que no se modela apropiadamente la degradación del material, por lo que se concluyó que esta norma no es adecuada para esta superficie de falla.
Vieira (2003) usa el tensor de esfuerzos principales y el de deformaciones cartesianas para proponer la norma siguiente:
siendo:
Donde ε+ es el tensor de deformaciones principales sólo positivas (e n ≥ 0) , y los tensores σ y ε son los tensores de esfuerzos y deformaciones cartesianas, respectivamente, definidas en la ec. (14). Es de interés mencionar que las normas propuestas en la ec. (36) por Oliver et al. (1990) y en la ec. (37) por Vieira (2003) no fueron implantadas ni validadas en los trabajos reportados por estos autores; Hernández-García (2012) implantó y realizó simulaciones de elementos a la falla utilizando estas normas, encontrando que la primera no presenta apropiadamente la degradación de los materiales, mientras que con la propuesta dada por Vieira (2003) se obtuvo una degradación adecuada, por lo que se validó el uso de esta norma para el modelo de daño, misma que se presenta en este artículo.
2.8. Módulo tangente
Diferenciando la norma te, definida en la ec. (37), con respecto al tiempo y considerando la ec. (18) se obtiene:
Sustituyendo la ec. (39) en las ecs. (32) y (34) se obtiene el módulo tensor tangente:
El MDST con la superficie mostrada en la Figura 5 se resume en las ecuaciones dadas en la Tabla 2. La norma propuesta por Vieira (2003) sólo es válida para algunos estados de deformación, pues sólo se alcanza la superficie de falla cuando las deformaciones máximas ocurren en dirección horizontal X (ex > ey , ex > ez ) , lo cual se confirma revisando la norma propuesta
donde se utiliza un tensor de esfuerzos principales sólo positivos (s n ≥ 0) y un tensor de deformaciones cartesianas ε; sin embargo, un tensor de esfuerzos principales se ordena de 1 a 3 siendo de mayor a menor en magnitudes. Puesto que el esfuerzo principal uno siempre es el mayor (s1 > s2 > s3 ) , considerando un problema donde la deformación máxima sea e x , la norma seria
con la cual se obtienen resultados congruentes comparados con resultados experimentales. Contrario a esto, si la deformación máxima es e y ó e z los resultados ya no son consistentes, pues las normas serían
, esto se debe a que e x < e y ó e z , y el esfuerzo σ 1 siempre es mayor, al calcular la norma donde se realiza el producto de s1·e x , los valores serían muy pequeños por lo que no se alcanza la superficie de daño. En consecuencia, se requiere de una carga mayor para alcanzar la superficie de falla, obteniéndose resultados incongruentes con pruebas experimentales o numéricas.
En la ec. (41)a se muestra el producto de vectores consistentes y en la (41)b los casos en que se obtienen resultados inadecuados, por lo que este modelo sólo es válido cuando las deformaciones que ocurren en el material sean mayores en la dirección horizontal X.
2.9. Modelo de daño isotrópico sólo cortante (MDSC)
Para la formulación del modelo de daño sólo cortante (MDSC) se partió del MDITC, en el que se propone una norma que considere principalmente los esfuerzos a cortante, análoga al criterio de Tresca, la norma propuesta para este modelo de daño es:
Tal que:
Donde t c max n-m y gc max n-m son los esfuerzos y deformaciones por cortante máximos respectivamente, calculados como:
La magnitud de r0 se obtiene análoga al de la falla a tensión como en la ec. (19):
2.10. Módulo tangente
Diferenciando la norma t e, definida en la ec. (42) y considerando la ec. (18):
El módulo tensor tangente se obtiene sustituyendo la ec. (47) en las ec. (34) y (32):
El MDSC se resume con las ecuaciones de la Tabla 3 con el umbral de daño mostrado en la Figura 6. Cabe mencionar que este modelo de daño sólo es válido para elementos sujetos a cortante puro, donde las deformaciones por cortante y esfuerzos cortantes son mayores una vez que se inicia el incremento de carga, esto quiere decir g nm > e nn y t nm > s nn . Por ejemplo, para un cilindro de concreto ensayado a compresión, en el que se espera alcanzar un esfuerzo a compresión último σcu, la falla que se presenta no es precisamente en compresión, sino que ocurre a cortante. Aunque el MDSC se puede emplear en elementos donde la concentración de esfuerzos es de cortante, no puede emplearse para sólidos en los que el esfuerzo inicial es a compresión y las deformaciones por cortante son casi nulas, impidiendo al modelo de daño alcanzar la superficie de falla, como se muestra en la Figura 7. Para este tipo de problemas se utilizó el MDITC, donde los esfuerzos analizados son a tensión y compresión simulando esta prueba con resultados consistentes como se mostrará en los ejemplos de aplicación.
2.11. Ejemplos de aplicación
En esta sección se muestran algunos ejemplos de aplicación, en los que se validan los MDST, MDSC y MDITC, los cuales se comparan con otras formulaciones numéricas y/o resultados experimentales reportados en la literatura. Todos los ejemplos realizados se someten a cargas de falla las cuales se indujeron mediante desplazamientos prescritos, para evitar problemas numéricos asociados al ablandamiento del material.
2.12. Espécimen de concreto de sección variable con dos ranuras
Un espécimen con sección variable en su eje transversal y dos ranuras en la parte media del eje longitudinal (superior e inferior), se somete a un estado de esfuerzos de tensión pura uniaxial, las propiedades del material son: módulo de Young E=16,900 MPa (172,332.040 kgf/cm2 ), relación de Poisson ν=0.2, esfuerzo máximo de tensión σu=2.400 MPa (24.473 kgf/cm2) y densidad de energía de fractura Gf=0.3 J/m2 (3.059x10-4 kgf-cm/cm2).
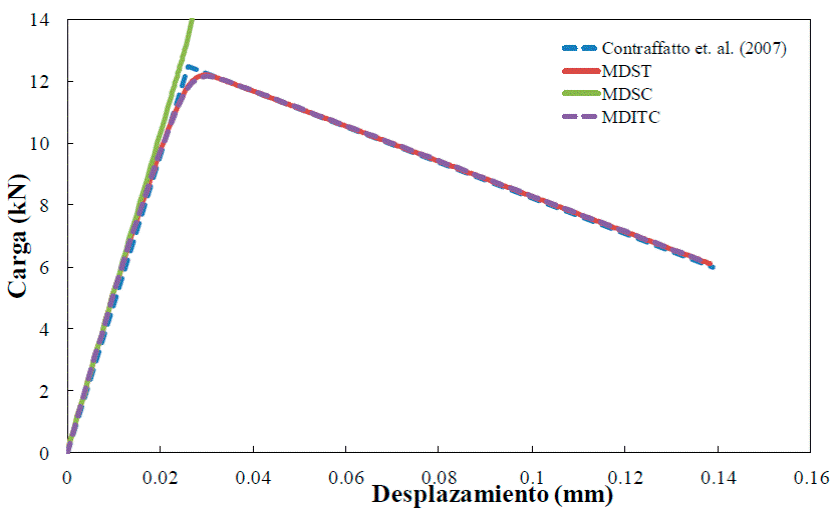
Este ejemplo se eligió para validar el modelo con la solución de un problema numérico realizado por Contraffatto et al. (2007), quienes utilizaron elementos finitos con discontinuidad de interiores; la geometría y condiciones de frontera de la sección variable se muestran en la Figura 8, donde se observa que se restringió el desplazamiento horizontal en el área transversal más pequeña, mientras que en la sección opuesta se ejerce una fuerza que provoca esfuerzos de tensión en el sólido, con la cual se espera una falla de modo I, por apertura, en la zona próxima a las dos ranuras. En la Figura 9 se muestra una malla estructurada de hexaedros para la simulación en 3D, que consta de 1240 elementos finitos; como se esperaba, la concentración de esfuerzos se presenta en la parte ranurada de la sección y se presenta la falla tipo I. En la Figura 10 se muestra que las curvas de carga contra desplazamiento obtenidos con el MDST, MDITC y los reportados por Contraffatto et al. (2007) son consistentes; sin embargo, la curva obtenida con el MDSC permanece en su intervalo elástico puesto que no se presentan deformaciones por cortante en el material, por lo que la norma no alcanza la superficie de falla.
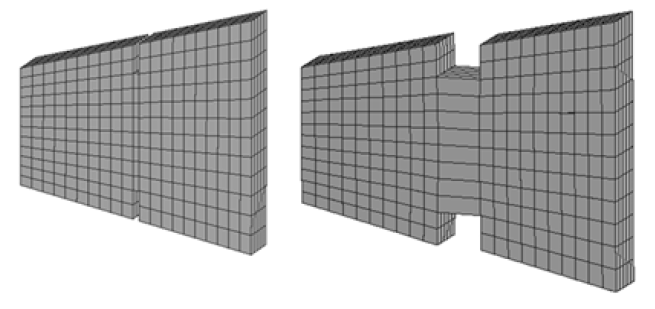
Figura 9: Mallas de elementos finitos antes y después del daño, utilizada en el análisis 3D con el MDST.
2. Cilindro de concreto simple en tensión pura
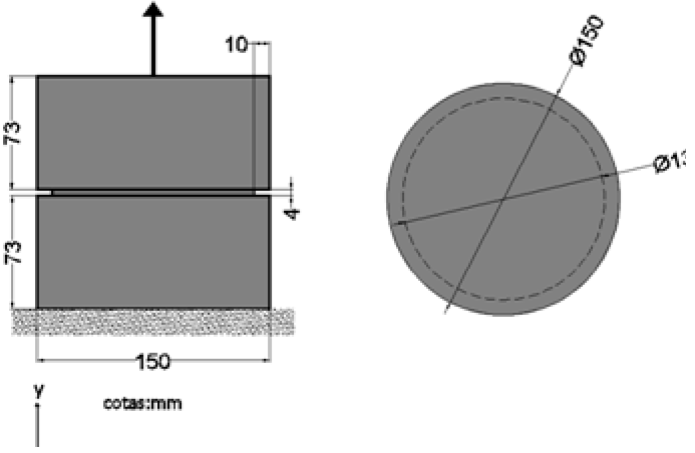
En este ejemplo se estudia un cilindro de concreto simple que tiene una ranura perimetral en el centro del eje longitudinal, sometido a carga de tensión pura uniaxial con la geometría y condiciones de frontera mostradas en la Figura 11, el cual se tomó de los especímenes ensayados a tensión por Barragán (2002). Las propiedades del material son: módulo de Young E=30.500 GPa (3,109.072 kgf/cm2) , relación de Poisson ν=0.2, esfuerzo máximo de tensión σu=1.790 MPa (18.253 kgf/cm2) y densidad de energía de fractura Gf=100 N/m (0.102 kgf/cm).
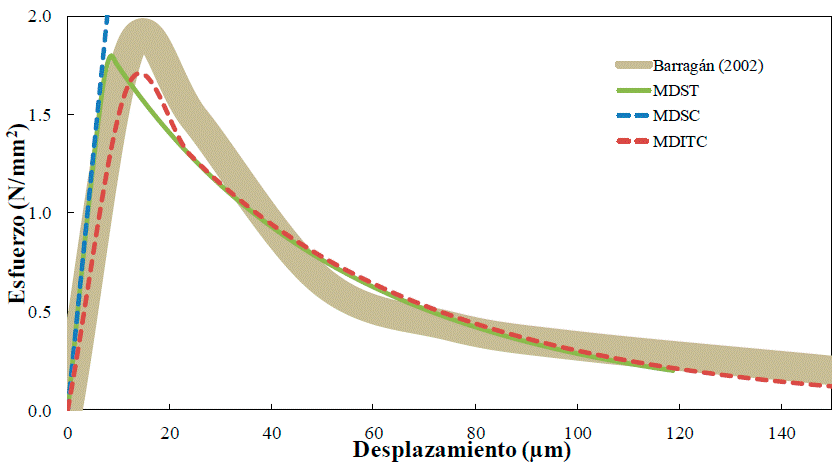
Para el modelado en 3D se estructuró una malla de hexaedros de 848 elementos finitos mostrados en la Figura 12, donde se observa la malla antes y después de generarse el daño. En la Figura 13 se muestran las curvas esfuerzo contra desplazamiento, donde se observa que los resultados numéricos obtenidos con los MDST y MDITC son congruentes con los resultados experimentales reportados por Barragán (2002); sin embargo, al igual que el ejemplo anterior, la curva calculada con el MDSC permanece en su intervalo elástico al no existir deformaciones por cortante en el material, por lo que no se alcanza la superficie de falla.
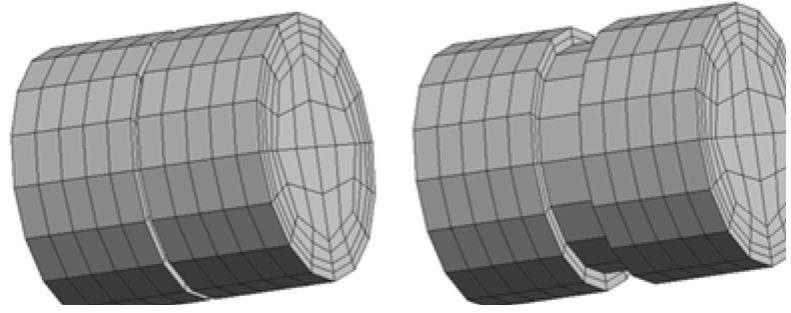
Figura 12: Malla de elementos finitos antes y después del daño, utilizada en el análisis 3D en el MDST.
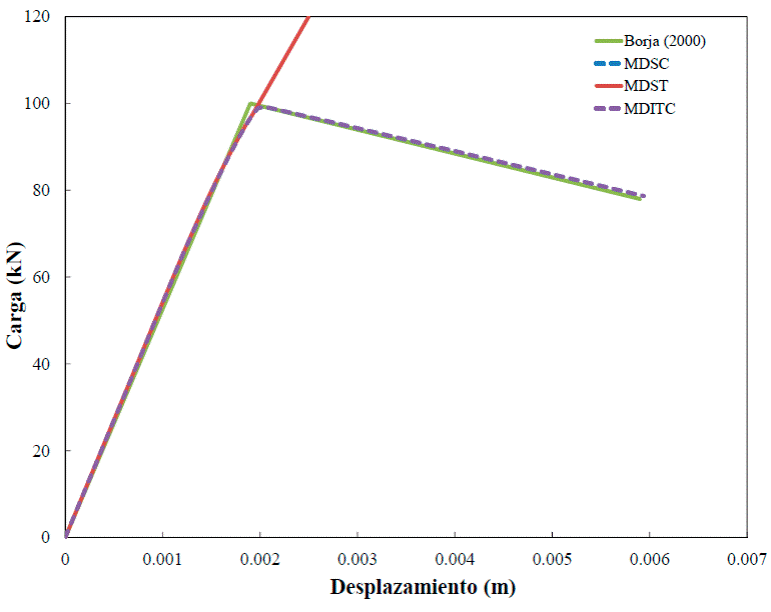
3. Espécimen en cortante puro
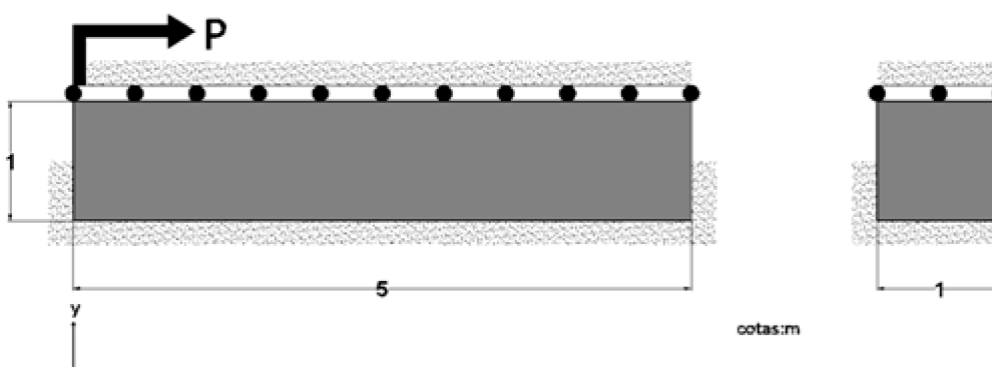
Un espécimen rectangular, con geometría y condiciones de frontera mostradas en la Figura 14, se some te a una carga horizontal aplicada en la parte superior. Debido a que el espécimen está restringido a la mitad de su altura, esfuerzos de cortante puro se concentran a lo largo de su eje longitudinal. Las propiedades del material son: módulo de Young E=26,500 kPa (265.036 kgf/cm2) , relación de Poisson ν=0.3, esfuerzo máximo de tensión σu=40 kPa (0.408 kgf/cm2) , esfuerzo máximo a cortante τu=20 kPa (0.204 kgf/cm2), módulo de rigidez a cortante G=10,000 kPa (101.972 kgf-cm/ cm2) y módulo de ablandamiento discreto Hs =-0.100.
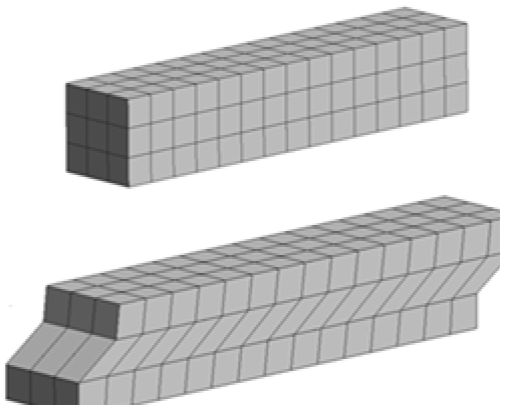
Para la simulación de este espécimen se utilizó una malla de hexaedros en 3D que se muestra en la Figuras 15. Las curvas de carga contra desplazamiento obtenidas con los tres modelos y los resultados numéricos de un modelo de discontinuidades interiores, reportada por Borja (2000), se muestran en la Figura 16, donde se observa que las curvas obtenidas con los MDITC y MDSC son congruentes. Es de interés mencionar que Borja (2000) utilizó una superficie de plasticidad con ablandamiento, por lo que en el MDSC se tomó el esfuerzo de fluencia como el esfuerzo último. El MDST no alcanza la superficie de falla porque las deformaciones por cortante son mayores en magnitud a las deformaciones cartesianas, es decir g m >> e m . En consecuencia se necesitaría una fuerza mayor a la que fallaría el material para alcanzar la superficie de falla por tensión, lo cual no es congruente.
4. Cilindro de concreto en compresión simple (cortante indirecto)
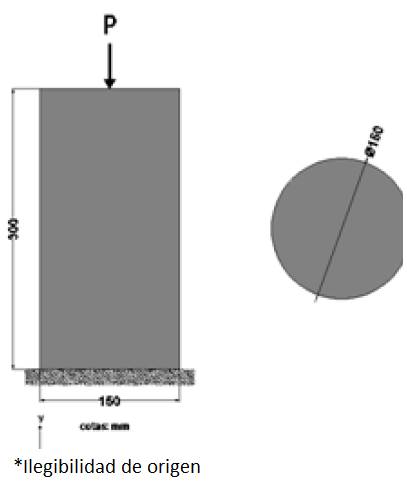
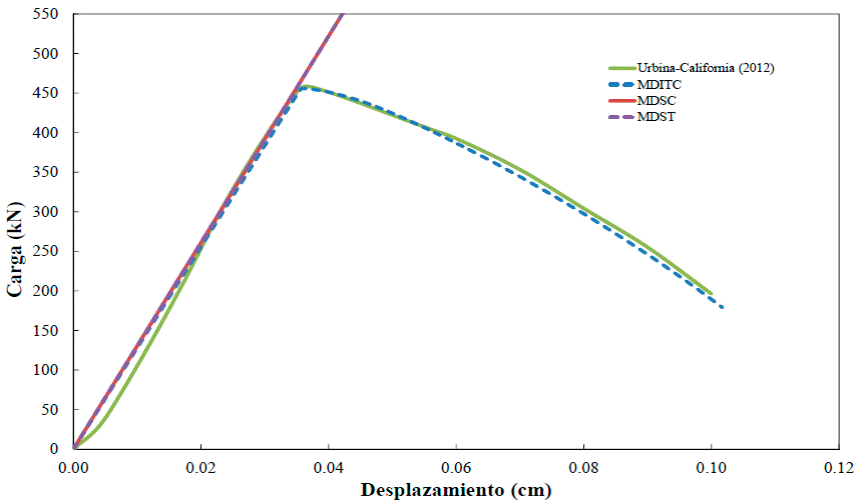
Este ejemplo consiste en una prueba a compresión simple realizada a un cilindro de concreto, como parte de pruebas de calidad del concreto utilizado para la construcción de trabes acarteladas de Urbina-Californias (2013). La geometría y condiciones de frontera del espécimen de concreto se muestran en la Figura 17.
El concreto tiene un módulo de Young Ec=22,145.400 MPa ( 225,820.234 kgf/cm2) , resistencia última a la compresión σcu=25,506 kPa (260.089 kgf/cm2) , resistencia última a la tensión σtu=2,550.600 kPa (26.008 kgf/cm2) , resistencia última a cortante τu=12,753 kPa (130.044 kgf/cm2), relación de Poisson ν=0.2 y módulo de ablandamiento discreto Hs/E=-0.01.
Se utilizó una malla estructurada de hexaedros como se muestra en la Figura 18a, con un mallado más fino en la parte media del cilindro, donde se supone que se presenta la concentración de esfuerzos; se modeló solamente la mitad del cilindro considerando la simetría del modelo para reducir el tiempo de cómputo. En la Figura 20 se muestran las curvas de carga contra desplazamiento, donde se observa que sólo el MDITC presenta resultados congruentes con los experimentales reportados por Urbina-Californias (2013); mientras que los MDSC y MDST presentan un comportamiento elástico, debido a que en el material no se presentan deformaciones por cortante o en tensión que activen las respectivas superficies de falla de estas normas. Al aplicar la carga en el espécimen se tiene el mismo estado de esfuerzos en todos los puntos de integración de la malla, por lo que se disminuyó al 95% la magnitud del esfuerzo último en un elemento de la malla, como se muestra en la Figura 19, induciendo así el inicio de la falla en el modelado.
Conclusiones
En esta investigación se realizó la formulación, implantación y validación de modelos de daño para la modelación de elementos estructurales, los cuales se validaron con modelos en 3D llegando a las siguientes conclusiones:
Los resultados obtenidos con los modelos desarrollados en esta investigación son congruentes con los resultados reportados experimental y numéricamente, concluyendo que se obtiene una adecuada simulación del ablandamiento del material localizando sus zonas de degradación;
Es posible asignar la energía de fractura en los modelos implantados en este trabajo, obtenida por experimentos o reportada en la literatura, siendo dependiente de los resultados numéricos;
Los modelos de daño implantados no presentan atoramientos numéricos, lo cual garantiza una adecuada simulación de estructuras evolucionando al colapso; y
En los cuatro ejemplos presentados en este artículo, el MDITC fue el que mostró resultados congruentes con los experimentales o numéricos reportados en la literatura. Aunque en el cilindro de concreto en compresión se presentó un aplastamiento prematuro; éste se debe a que el material tiene diferentes umbrales a tensión y compresión, lo cual puede superarse con un una superficie de falla con diferentes umbrales como la desarrollada por Juárez-Luna et al. (2014).
Las limitantes encontradas en este trabajo son:
El MDST no modela adecuadamente la falla cuando las deformaciones máximas ocurren en dirección vertical, lo cual no ocurre en la dirección perpendicular, con lo que se concluye que este modelo de daño sólo es válido para problemas que presenten deformaciones máximas en dirección horizontal;
El MDSC también presentó problemas para modelar la falla cuando no existen deformaciones por cortante, necesarias para que la norma alcance la superficie de falla, con lo cual se concluye que sólo es válido para problemas donde las fuerzas externas produzcan cortante puro en los sólidos; y
-
En general, no son recomendables los MDST y MDSC para el análisis del colapso en elementos estructurales, pues sus normas son dependientes de la dirección en la que se presenten las deformaciones máximas, por lo que no se alcanza la superficie de falla o se obtiene una carga última mayor
El modelado numérico en la práctica es una herramienta que permite conocer las zonas donde se presentan concentraciones de deformaciones en elementos estructurales, donde debe reforzarse una estructura para evitar la presencia de daño. Otra de las aplicaciones es conocer la capacidad residual de las estructuras, una vez que existe daño en los elementos. En pruebas de laboratorio, el modelado numérico permite determinar las magnitudes de carga del primer agrietamiento, propagación y cargas de colapso, lo que permite un mejor diseño del espécimen. Por lo que en la aplicación de los modelos de daño para modelar estructuras en su evolución al colapso de deben considerar las recomendaciones siguientes:
El tiempo de cómputo de un modelado numérico en 2D es menor en comparación con un modelo en 3D, obteniendo resultados congruentes; sin embargo, en 3D se obtiene una mejor aproximación de la estructura en su evolución al colapso;
Verificar la magnitud de las cargas a las que estará sometida la estructura, para la elección del modelo de daño que se adecue a las solicitaciones;
Seleccionar un tamaño óptimo de la malla de elementos finitos, la cual debe ser estructurada y refinada en la zona de concentración de deformaciones; y
Cuando sea posible, considerar la simetría del modelo, lo cual reducirá el tiempo de cómputo.











 nueva página del texto (beta)
nueva página del texto (beta)