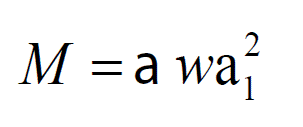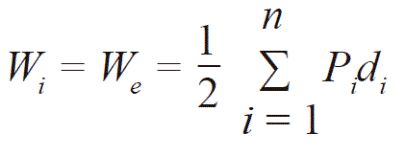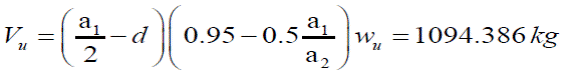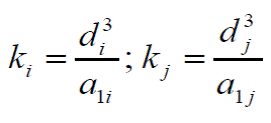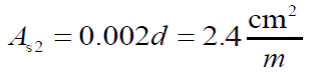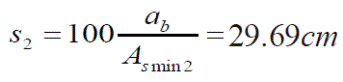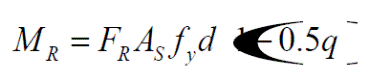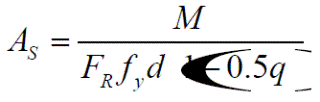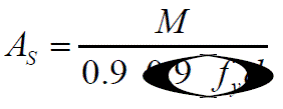1. Introducción
Las losas son elementos utilizados en la construcción de sistemas estructurales que cumplen funciones arquitectónicas y estructurales. Las losas son elementos planos sin curvatura aparente que proporcionan una superficie horizontal para el desarrollo de actividades diversas, las cuales transfieren las cargas producidas hacia su perímetro de apoyo, evitando desplazamientos verticales (flechas) para asegurar su funcionalidad, por lo que lo que estos elementos requiere de métodos de análisis y diseño que garanticen su seguridad estructural. Los trabajos pioneros en el análisis y diseño de losas fueron los realizados por Westergaard y Slater (1921) y Westergaard (1926), quienes determinaron los momentos máximos desarrollados en las secciones críticas de losas cuadradas para diferentes condiciones de apoyo en los bordes. Obtuvieron coeficientes de distribución de momentos con base en la teoría de la elasticidad, los cuales se compararon con coeficientes experimentales obtenidos en pruebas realizadas en losas apoyadas perimetralmente por Bach y Graf (1915). Además, Westergaard y Slater (1921) demostraron la existencia del fenómeno de redistribución de esfuerzos dependiente de las rigideces relativas.
Marcus (1929) desarrolló un procedimiento aproximado, mediante el cual los momentos máximos elásticos en una placa apoyada sobre vigas rígidas se determinan con base en el análisis de una franja de losa y obteniendo factores de reducción para corregir los momentos obtenidos. Marcus consideró los efectos producidos por la presencia de un muro colocado en medio del claro de la losa, construyendo cuatro tablas de coeficientes de momentos, las cuales proporcionan valores para la distribución del panel de carga en dos direcciones, la evaluación de momentos negativos en bordes continuos y positivos para la mitad del centro del claro.
Di Stasio y Van Buren (1936) realizaron una propuesta para el comité del ACI (Método I), la cual se basa en el uso de factores de distribución de carga para la obtención de los momentos en la losa. Posteriormente, el comité del ACI realizó modificaciones en 1947 a las propuestas realizadas por Westergaard (Método II), para cubrir todas las posibles combinaciones de losas en un sistema de piso. Para la primera modificación se analizó cada panel por separado, considerando sólo sus condiciones de continuidad en los bordes, la condición de losa monolítica con las vigas de apoyo o muros y cierta rigidez torsional para las condiciones de apoyo; la segunda modificación consistió en limitar de manera práctica la relación de los bordes de los paneles. Con estas consideraciones, el comité propuso una tabla de coeficientes para el momento positivo en el centro del claro y para el momento negativo en los bordes.
Newmark y Siess (1950) realizaron estudios analíticos basados en un proceso de redistribución de momentos, análogo al método de Cross, para determinar el valor de los momentos en placas continuas apoyadas en vigas rígidas. Además estudiaron diversos parámetros que influyen en dichos valores de momento, entre los que pueden citarse la relación entre lados, la localización relativa de la losa respecto a uno de los bordes de la placa, la rigidez torsional de las vigas de apoyo, el tipo de carga, las variaciones en tamaño y forma para losas adyacentes. Recientemente, Hassan et al. (2011) determinaron coeficientes para los momentos de diseño de losas planas interiores utilizando el método avanzado de Hillerborg y el método de los elementos finitos.
En México, Covarrubias (1960) proporcionó coeficientes para el diseño de losas perimetrales sujetas a cargas lineales con base en la teoría de líneas de fluencia. Díaz de Cossio (1962) estudió experimentalmente el efecto del tamaño y de la forma de vigas y losas de concreto sobre su resistencia a fallas por cortante. Basila-Hajj (1962) determinó experimentalmente características de resistencia de bloques huecos utilizados en la construcción de losas encasetonadas. Esteva (1963) obtuvo coeficientes de diseño de losas con bordes libres aplicando la teoría de líneas de fluencia. Guzmán y Díaz de Cossio (1968) proporcionan recomendaciones de diseño de losas con claros pequeños. Díaz y Robles (1971) estudiaron la respuesta humana ante el agrietamiento en losas de concreto. Mendoza (1976) determinó experimentalmente recomendaciones para diseñar y construir losas reforzadas con mallas de alambre estiradas en frío. Contreras (1977) propone recomendaciones de espesor mínimo de losas para evitar problemas de vibraciones. Tapia y Rosenblueth (1977) estudiaron el efecto de correlación entre resistencia y carga vertical en diseño de losas de concreto. Loera y Ávila (2000) proporcionan recomendaciones para el análisis de losas planas con capiteles sujetas a carga vertical. Loera y Ávila (2001) proponen un ancho equivalente de losas planas con capiteles y ábacos ante fuerzas laterales. Juárez-Luna y Caballero-Garatachea (2014) proporcionan coeficientes de diseño para losas aisladas circulares, elípticas y triangulares.
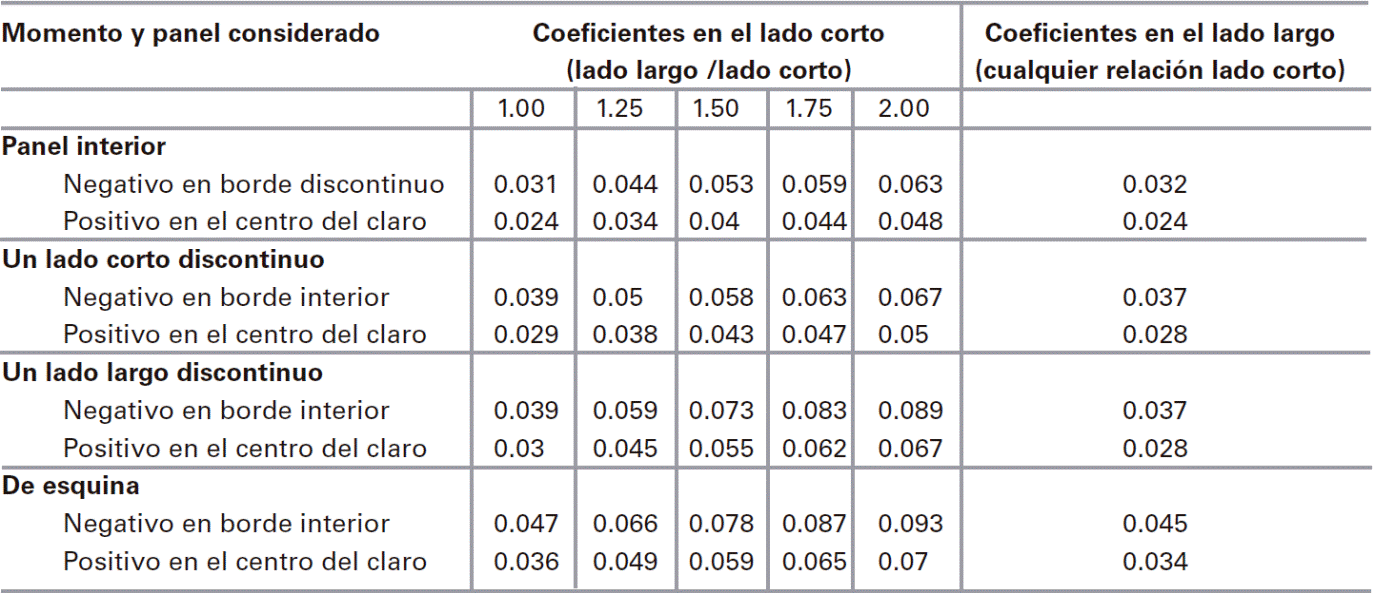
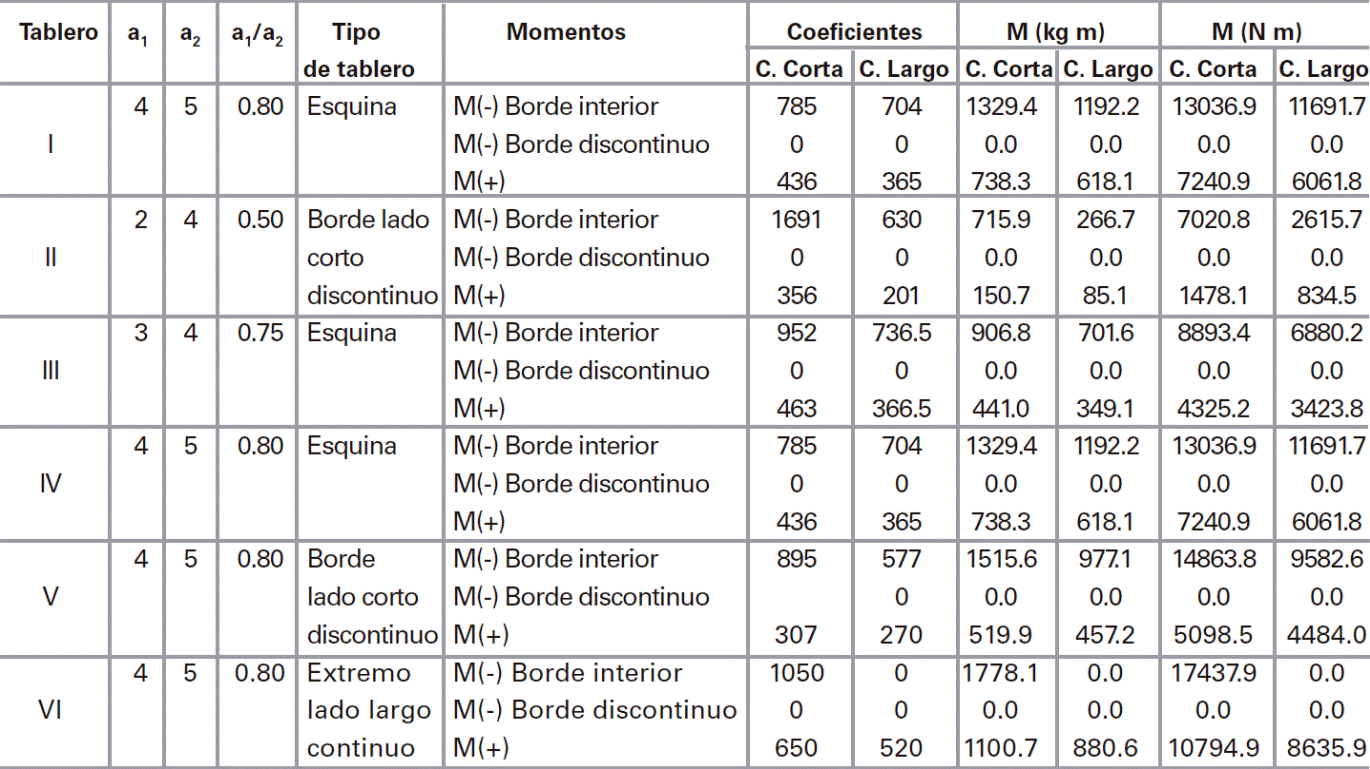
Para el análisis de losas el ACI-318-14 recomienda el método directo, el método del marco equivalenteo cualquier otro procedimiento que satisfaga las condiciones de equilibrio y compatibilidad geométrica, así como los requisitos de resistencia y de servicio. Mientras que el Eurocódigo-2 (EC-2) recomienda utilizar el método del marco equivalente o algún otro método válido para el diseño de losas perimetralmente apoyadas. Es importante mencionar que el manual de diseño de estructuras de concreto para el Eurocódigo-2 (IStructE-06), del Instituto de Ingenieros Estructurales de Europa proporciona como una opción el uso de coeficientes para determinar los momentos de diseño, los cuales se enlistan en la Tabla 1.
El Reglamento de Construcciones del Distrito Federal (RCDF-04) y sus Normas Técnicas Complementarias para Diseño y Construcción de Estructuras de Concreto del 2004 (NTCC-04) proporcionan recomendaciones de diseño para losas macizas de concreto reforzado apoyadas perimetralmente en dos direcciones. En estas recomendaciones, los momentos de diseño se calculan utilizando una tabla de coeficientes, los cuales fueron adaptados de la edición del ACI-318-63 (González-Cuevas 2011), que a su vez se derivaron del trabajo de Newmark y Siess (1950). Las NTCC-04 proporcionan 476 coeficientes, α, para el diseño de losas coladas y no coladas monolíticamente con sus vigas de apoyo para relaciones de lados m=a1/a2, donde a1 es la longitud del lado corto y a2 la longitud del lado largo. El IStruct E-06 sólo presenta coeficientes para losas coladas monolíticamente con vigas de apoyo como se muestran en la Tabla 1. Ambos códigos determinan los momentos de diseño por unidad de ancho con la ec.(1):
Donde M es el momento de diseño y w es la carga uniformemente distribuida sobre el panel.
Flores-Eslava (2012) muestra algunos casos donde los coeficientes obtenidos con modelos numéricos son mayores a los presentados en las tablas de diseño de las NTCC-04. Por lo anterior, este artículo tiene por objetivo actualizar la magnitud de los coeficientes de diseño que actualmente proporcionan las NTCC-04 mediante la mecánica computacional, los cuales se calculan de la distribución de momentos flexionantes de modelos de losas con relaciones de lados m de 0.5, a 1, en incrementos de 0.1. Se modelan paneles apoyados sobre vigas y sobre muros confinados de los que se tomaron las magnitudes de los coeficientes más desfavorables; además se estudiaron paneles colados y no colados monolíticamente con sus apoyos, los cuales se modelaron con el acoplamiento de los grados de libertad. Los modelos se realizaron en el programa SAP2000 (CSI 2009), considerando un material elástico-lineal, homogéneo e isotrópico. Es de importancia enfatizar que es válido utilizar los coeficientes propuestos en este trabajo para calcular los momentos de diseño cuando los paneles estén apoyados: 1) sobre vigas principales, que a su vez estén apoyadas en sus cuatro esquinas, 2) en muros y 3) paneles con algunos de sus bordes sobre vigas y el resto sobre muros. No es válido utilizar los coeficientes para el diseño de paneles apoyados sobre vigas secundarias.
El contenido de este artículo se describe a continuación. En la sección 2 se determina el tamaño del elemento que se utilizará para el modelado, así como su validación con resultados de soluciones analíticas. Adicionalmente, esta sección proporciona una descripción de los modelos de los paneles que se analizaron. La sección 3 presenta el análisis de los coeficientes calculados en los modelos numéricos. La sección 4 muestra la comparación entre los coeficientes obtenidos numéricamente y los propuestos actualmente por la NTCC-04. Finalmente, las conclusiones derivadas de este trabajo y sugerencias se proporcionan en la sección 5.
2. Determinación de coeficientes
2.1. Calibración del tamaño de la malla
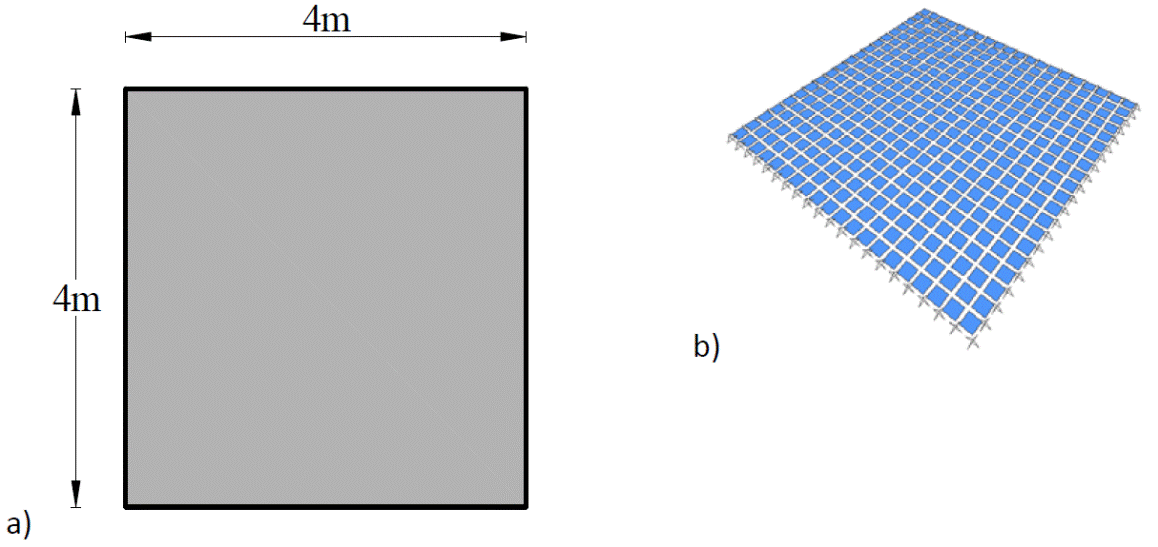
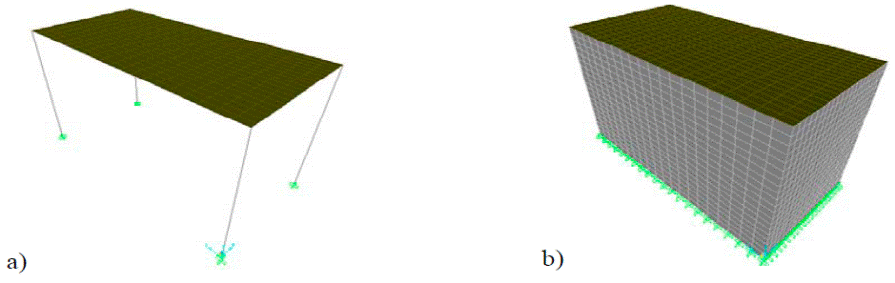
En este trabajo se utilizó la energía de deformación para establecer un criterio del tamaño de malla de los modelos de elementos finitos. Se estudió una losa cuadrada de 4 m por lado mostrada en la Fig. 1a, la cual se discretizó con 5, 10, 20 y 40 elementos por borde; en la Fig. 1b se muestra la discretización con 20 elementos por borde. Para la discretización del modelo se utilizaron elementos tipo placa delgada con cuatro nodos. La losa se restringió simplemente apoyada en todos sus bordes, aplicándole una presión vertical uniformemente distribuida de 9.81kN/m2. El material de la losa es de concreto con las propiedades mecánicas siguientes: módulo de Young E= 2.171x104MPa (2.214x105 kg/cm2), relación de Poisson, v=0.2, y esfuerzo último a compresión, 24.517MPa (250 kg/cm2).
Considerando que la energía de deformación interna, Wi, es igual al trabajo externo, We, inducido a un medio continuo, ésta se calcula como:
Donde Pi son las cargas por sus acciones externas que se concentran en los nodos, di son los desplazamientos de los nodos y n es número de nodos del modelo. En este modelo las cargas y los desplazamientos sólo se presentan en la dirección en la que se aplica la carga.
La energía Wi calculada para cada uno de los modelos discretizados con 5, 10, 20 y 40 elementos por borde se muestra en la Fig. 2, donde se observa que Wi se estabiliza a partir de un mallado con 20 elementos por borde, por lo que se utilizó este número en los modelos estudiados en este artículo, pues el tener una malla más fina sólo incrementaría el tiempo de cómputo, pero no mejoraría los resultados. Es importante mencionar que en los modelos estudiados se consideró un espesor de 0.1 m, que satisface los requisitos de resistencia por cortante.
2.2. Calibración con soluciones analíticas
Una vez determinado el tamaño de la malla, el modelo numérico de la losa aislada de 4 m, mostrado en la Fig. 1a, se calibró con soluciones analíticas reportadas por Timoshenko y Woinosky-Krieger (1959). La distribución de momentos en la losa se muestra en la Fig. 3, donde se tienen sólo momentos positivos debido a la condición de apoyo simple, los cuales son mayores en el centro del claro. Debido a que se trata del modelo de una losa cuadrada, la magnitud de los momentos es la misma en ambas direcciones del modelo.
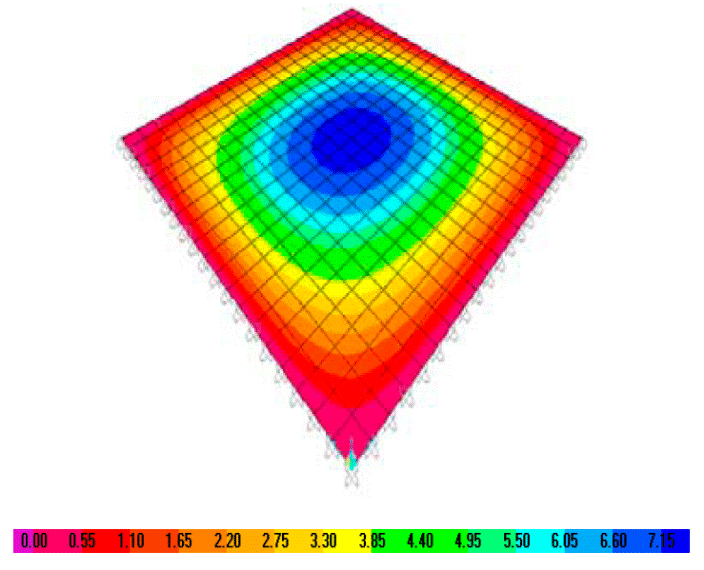
Fig. 3: Distribución de momentos (kNm) del modelo: se tiene la misma magnitud en ambas direcciones por ser una losa cuadrada
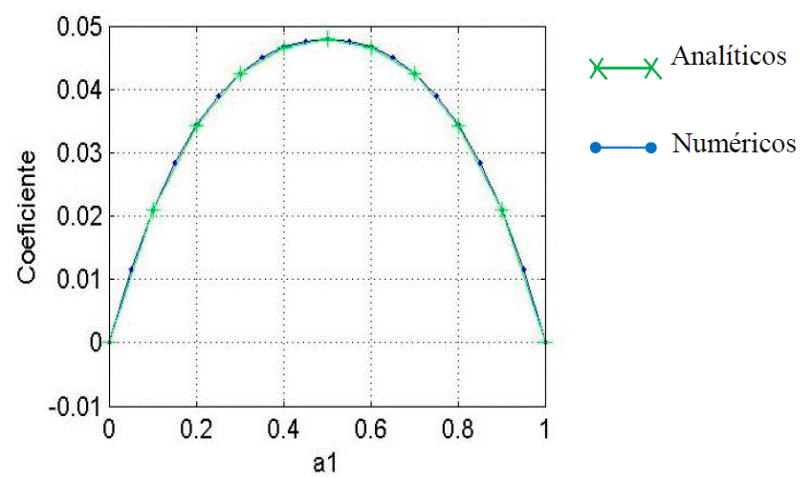
Los resultados analíticos reportados por Timoshenko y Woinosky-Krieger (1959) están en función del coeficiente αa, por lo que de la ec. (1) se despejó el coeficiente αn para determinar sus magnitudes en la franja central con los momentos de los modelos numéricos. En la Fig. 4 se muestran las curvas con los coeficientes αn y αa, observándose que ambas son prácticamente iguales. Por lo tanto, el número de elementos por borde y el elemento placa utilizado se validó para estudiar las losas con distintas relaciones m.
2.3. Determinación de coeficientes
2.3.1. Tipos de continuidad
Los modelos de las losas estudiadas están apoyados sobre vigas o sobre muros confinados, con ambos tipos de continuidad que consideran las NTCC-4: 1) tipo I, cuando la losa está colada monolíticamente con sus vigas de apoyo, como se muestra en la Fig. 5a, y 2) tipo II, cuando la losa no está colada monolíticamente con sus apoyos, i.e., cuando la losa se apoya sobre vigas de acero, bloques de concreto, como se muestra en la Fig. 5b, o existe una junta fría entre la losa y los apoyos que permitiera rotar los bordes de la losa; es importante mencionar que el IStruct E-06 sólo proporciona coeficientes para losas tipo I.
Las vigas y columnas se modelaron con elementos tipo viga-columna (frame) y las losas y muros con elementos tipo lámina (Shell). Ambos elementos, viga-columna y lámina, tienen seis grados de libertad (dx, dy, dz,θx, θy, θz) en cada nodo, como se muestra en la Fig. 6. Para modelar las losas tipo I o muros perimetrales, se discretizaron las láminas y las vigas-columnas del mismo tamaño, conectándose ambos elementos en los mismos nodos, tal que se acoplan los seis grados de libertad; mientras que para una losa con apoyo tipo II se utilizaron dos nodos en el mismo punto donde se apoyan las láminas sobre las vigas: tal que un nodo conecta las láminas, el otro conecta las vigas y en ambos nodos se acoplan los tres grados de libertad dx, dy, dz, lo que permite que la losa pueda rotartal como lo idealiza un apoyo simple. Al igual que las losas, los muros se discretizaron con mallas de 20 elementos por borde y las vigas con 20 elementos para tener continuidad con la malla de los bordes de las losas y los muros. Para la discretización de las losas se utilizó el elemento lámina delgada en el programa SAP2000, que excluye las deformaciones por cortante, pues la relación del espesor t entre la longitud del lado corto a1 fue menor a 0.2, i.e., t/a1<0.2.
2.4. Descripción geométrica de los modelos
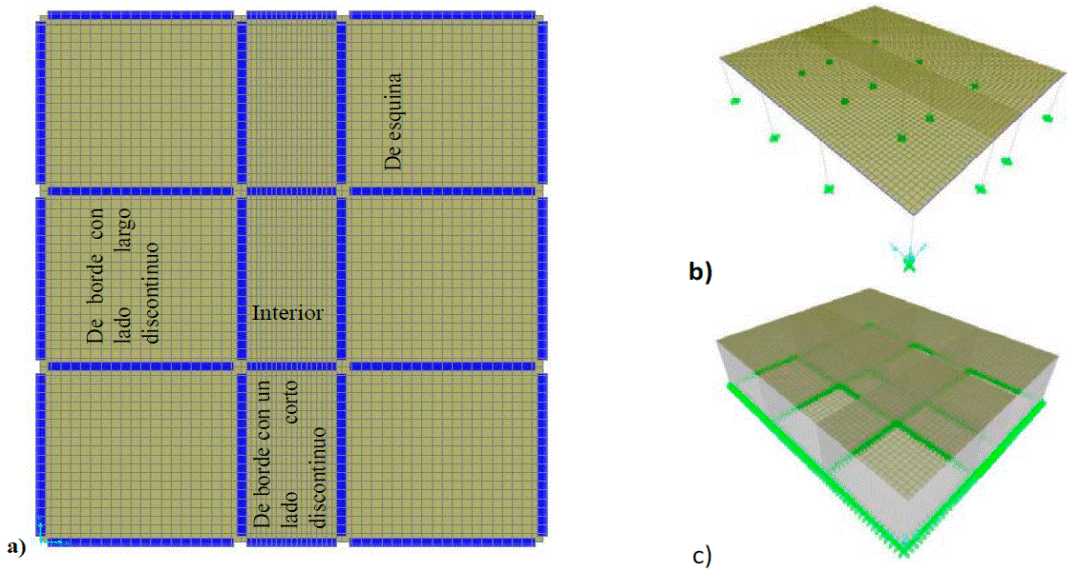
Las NTCC-04 proporcionan los coeficientes de diseño para relaciones m de 0, 0.5, 0.6, 0.7, 0.8, 0.9 y 1.0, considerando losas con sus vigas de apoyo tipo I y tipo II; sin embargo, el IStructE-06 proporciona coeficientes para relaciones inversas, a2/a1, de 1.0, 1.25, 1.5, 1.75 y 2.0. En los modelos realizados en este trabajo, los paneles que se estudiaron fueron aquellos que consideran la NTCC-04: interior, de borde con un lado corto discontinuo, de borde con un lado largo discontinuo, de esquina, de extremo con un lado largo continuo, de extremo con un lado corto continuo y aislado, los cuales se muestran en la Fig. 7. En estos modelos, el lado largo se mantuvo constante en 4 m y el lado corto se varió de 2 a 4 m, la altura de las columnas y muros fue de 2.5 m.
2.4.1. Modelos tipo A
Los paneles aislados se estudiaron con modelos como los que se muestran respectivamente en la Fig. 8 sobre vigas y sobre muros confinados, en el que la relación m es 0.5, tal que a1=2 m y a2=4 m. En el resto de los modelos, a1 se incrementó para tener el resto de las relaciones m.
2.4.2. Modelos tipo B
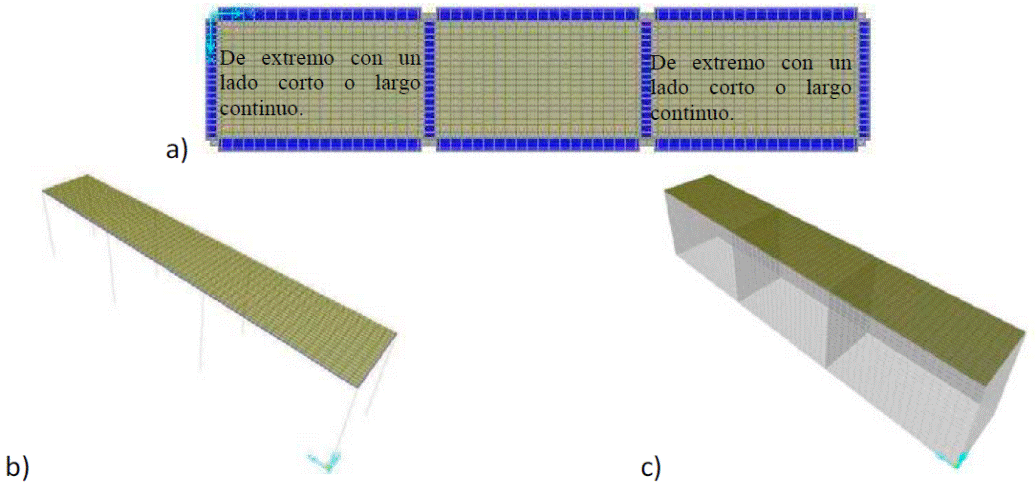
Los paneles de extremo con un lado corto o largo discontinuo se estudiaron incluyendo dos paneles adyacentes, como se muestra en la Fig. 9, pues el tener más paneles adyacentes como los de la Fig. 7 no es relevante en la distribución de momentos de los paneles de extremo, incrementando innecesariamente el costo computacional.
2.4.3. Modelos tipo C
Para decidir el número de paneles del modelo donde se estudió el panel interior, de borde con un lado corto discontinuo, de borde con un lado largo discontinuo y de esquina, se analizaron dos modelos de losas cuadradas con 3 y 5 paneles por borde, respectivamente, como se muestran en la Fig. 10. Los coeficientes calculados en las franjas centrales de los paneles interior, de borde y de esquina en los modelos con 3 y 5 paneles por borde se muestran respectivamente en la Fig. 11, donde se puede observar que se obtuvieron resultados similares, por lo que en el estudio de los tableros con otras relaciones de lados se utilizó el modelo con 3 paneles por borde, los cuales tienen menor número de elementos, que consecuentemente reducen el costo computacional.
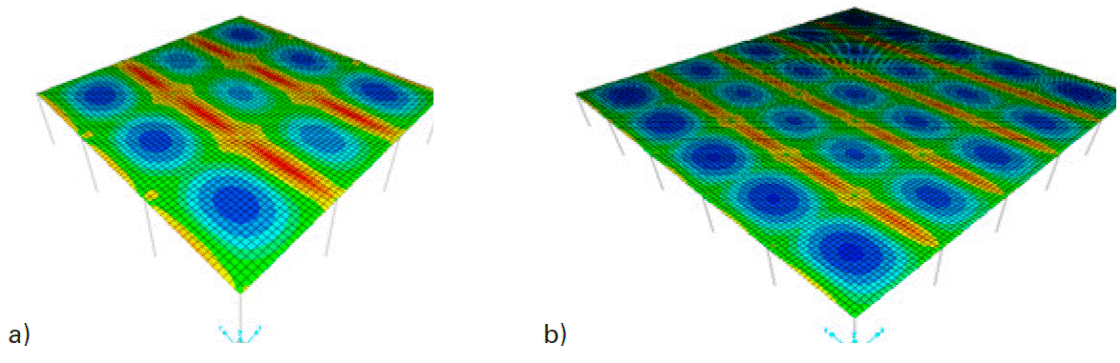
a) 3 y b) 5
Fig. 10: Distribución de momentos (kN m) en franjas horizontales de losa con paneles por borde.
Como ejemplo de los modelos estudiados del tipo A, en la Fig. 12 se muestra el modelado de una losa donde se analizaron los paneles de borde con un lado corto discontinuo e interior, donde la relación m para los paneles de esquina y de borde con un lado largo discontinuo se mantuvo constante en 1, mientras que las relaciones de lados de los paneles interiores y de borde con un lado corto discontinuo se varió de 0.5 a 1.0 con incrementos de 0.1.
3. Distribución de coeficientes
Del modelo realizado a los paneles mostrados en la Fig. 8, se obtuvo la distribución de momentos actuando paralelamente al lado corto, en la cual los modelos con continuidad tipo I presentan momentos negativos en los bordes, debido a la restricción parcial al giro que produce la rigidez a torsión de las vigas en la losa, como se muestra en la Fig. 13a. En losas con continuidad tipo II, sólo se tienen momentos positivos, como se muestra en la Fig. 13b, pues las losas están simplemente apoyadas sobre las vigas.
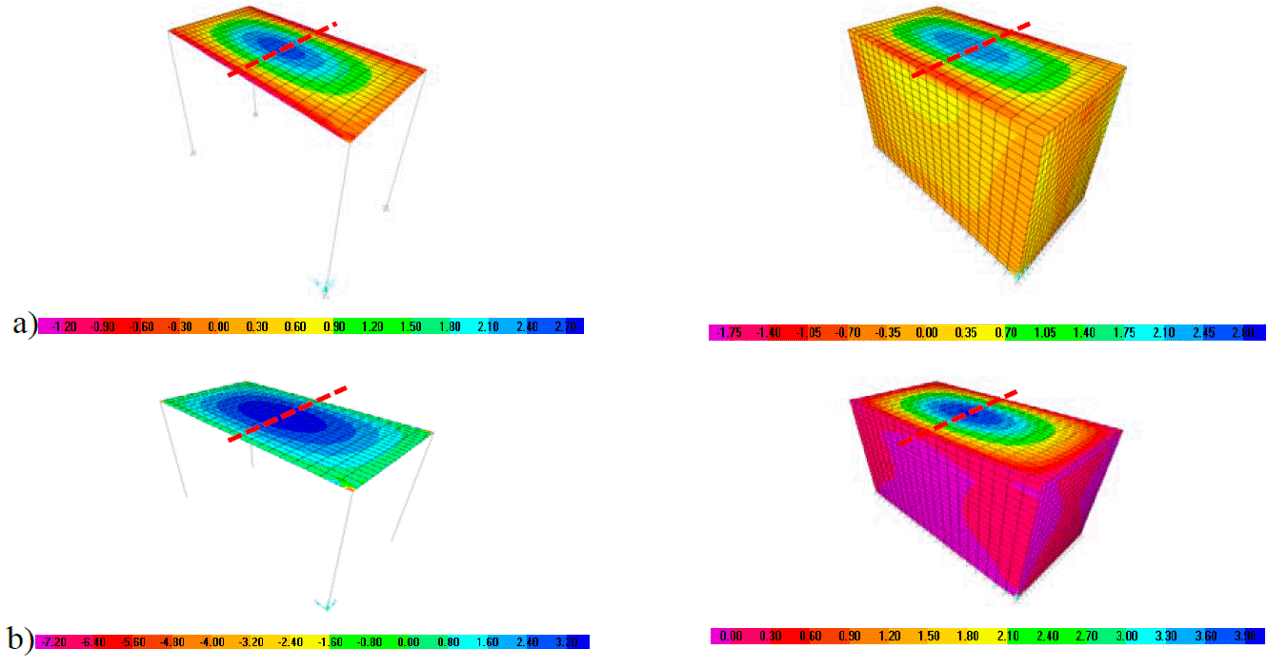
a) I y b) II
Fig. 13: Distribución de momentos (kN m) en franjas del lado corto del panel aislado tipo.
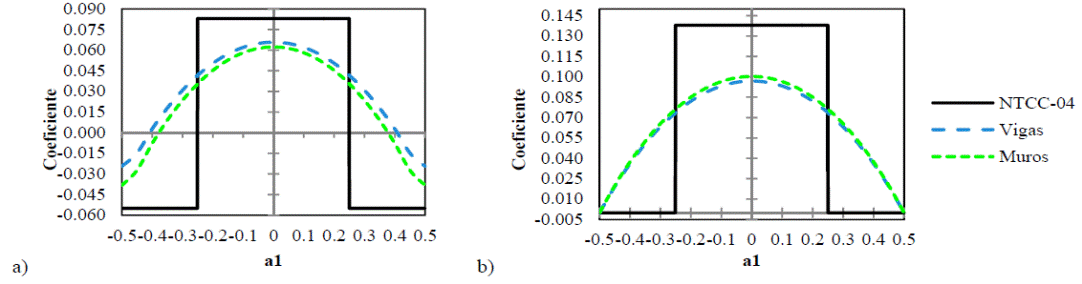
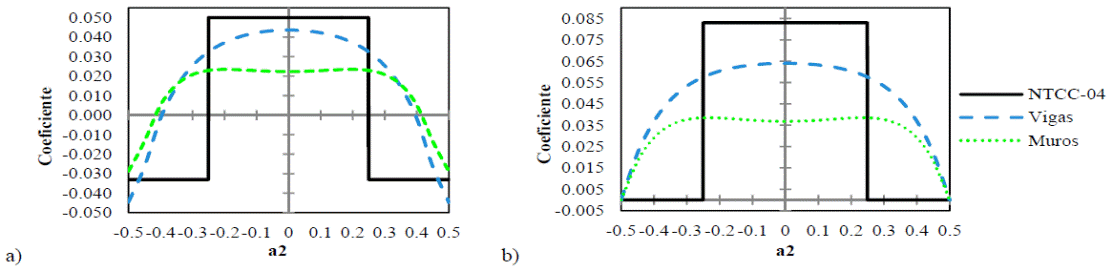
Aunque se tienen los coeficientes numéricos en todo el panel, se analizan sólo los de la franja central, donde los proporcionan las NTCC-04 y el IStructE-06, que es donde generalmente se encuentran los momentos máximos. En las Figuras 14 y 15 se muestran los coeficientes de las franjas centrales del lado corto y del lado largo, respectivamente, del panel aislado; siendo la curva denominada "Vigas", la distribución de coeficientes en la línea central del panel soportado por vigas perimetrales, la curva denominada "Muros", corresponde a la distribución de coeficientes del mismo panel, pero soportado por muros en su perímetro, y las líneas rectas, muestran la distribución de coeficientes proporcionados actualmente por las NTCC-04.
Las NTCC-04 proporcionan coeficientes para la franja central, donde generalmente se presentan los momentos positivos y negativos con mayor magnitud en los paneles, en las franjas de borde se permite diseñar con el 60% de los coeficientes, puesto que la magnitud del momento disminuye hacia los bordes del panel, como se muestran en las distribuciones de momentos. Sobre la línea que se encuentra a un cuarto del borde, la magnitud de los coeficientes numéricos son entre el 60 y 70% de los coeficientes que se encuentran en la franja central.
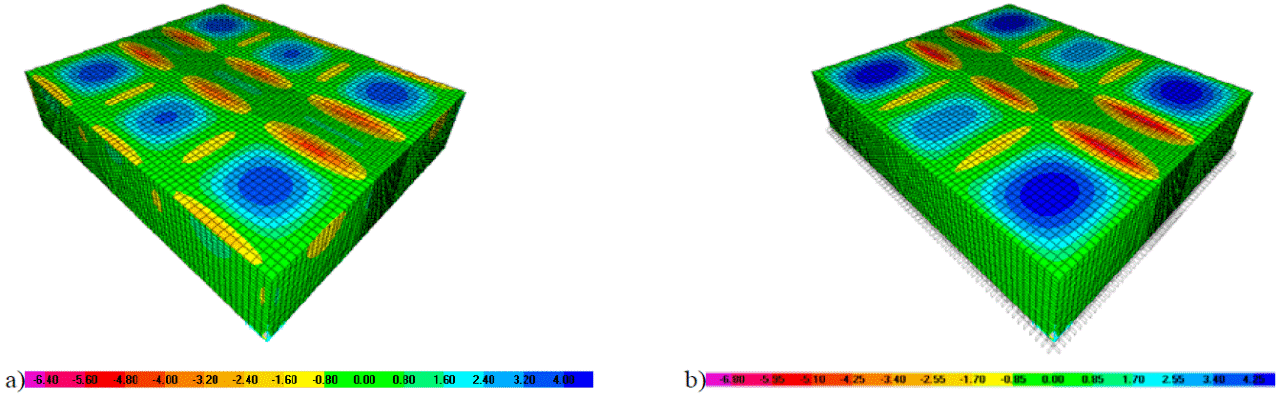
En las Figuras 14b y 15b los coeficientes sólo tienen valores positivos, ya que se trata de la distribución de coeficientes de un panel aislado tipo II. Para este panel, los coeficientes positivos propuestos por las NTCC-04 son mayores a los calculados numéricamente; sin embargo, en la Fig. 15 a los coeficientes negativos son menores. De la distribución de momentos en la franja corta y larga de la losa apoyada sobre vigas y muros de las Figs.16 a 17, sólo se considera la distribución de momentos del panel interior y de un panel de borde con un lado corto discontinuo para determinar los coeficientes numéricos. En la losa tipo I, los momentos negativos en los bordes interiores son mayores a los momentos en bordes perimetrales, tal como se esperaba, pues los paneles adyacentes causan que la rigidez a torsión sea mayor que en un borde extremo. Por la misma razón, los momentos negativos sólo se presentan en bordes interiores en la losa tipo II, como la que se muestra en la Fig. 17.
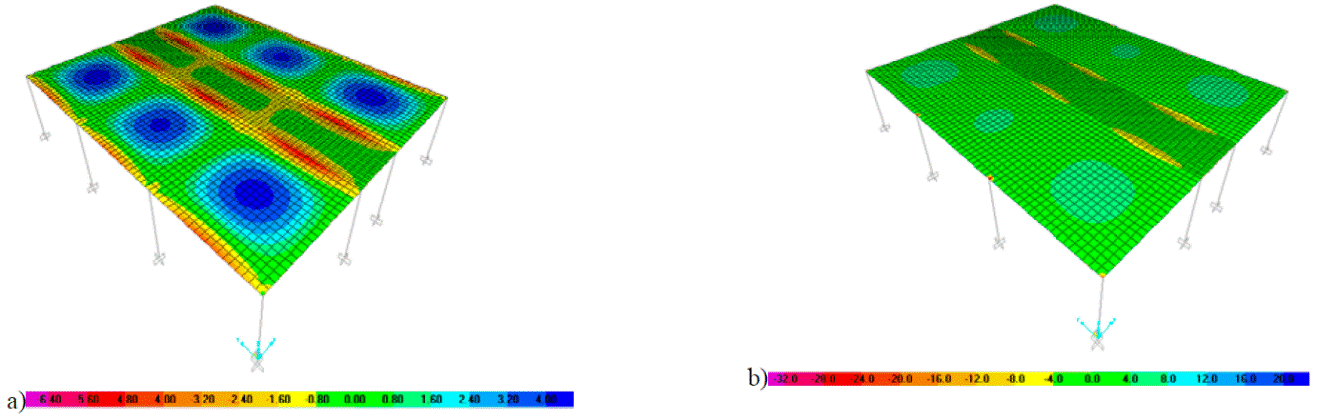
a) I y b) II
Fig. 16: Distribución de momentos (kN m) en franjas del lado corto en losa sobre vigas tipo.
a) I y b) II
Fig. 17: Distribución de momentos (kNm) en franjas del lado corto en losa sobre muros tipo.
La Fig. 18 muestra el efecto en la distribución de los momentos de algunos paneles que causan los muros y que las losas vecinas sean más grandes, en la que se observa que en el centro del panel se producen momentos negativos, de modo que la losa se desplaza como se muestra en la Fig. 19, lo cual no está considerado en las NTCC-04, ya que en el centro siempre se supone acero para momento positivo en el lecho inferior. Este efecto también se presenta en otros paneles, como el interior y desaparece gradualmente al incrementarse la relación m, es decir, este efecto ya no se presenta para la relaciones m=1.
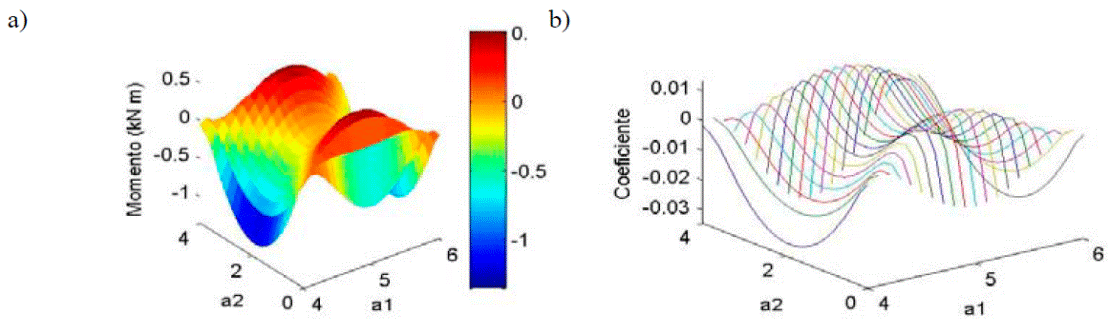
Tipo I de: a) momentos y b) coeficientes
Fig. 18: Distribución en franja larga de panel de borde con un lado corto discontinuo apoyado sobre muros.
En el panel interior, los coeficientes positivos propuestos por las NTCC-04 son mayores a los numéricos en la franja corta, como se muestra en la Fig. 20; sin embargo, los coeficientes numéricos son mayores a los propuestos por las NTCC-04 en los extremos. En la franja larga, los coeficientes positivos numéricos de losas apoyadas sobre muros y los propuestos por las NTCC-04 tienen aproximadamente la misma magnitud, pero los primeros no se localizan en el centro del claro, sino en los extremos, como se muestra en la Fig. 21, donde también se observa que los coeficientes negativos de losas sobre muros son menores a los de las losas sobre vigas e incluso menores a los propuestos por las NTCC-04.
En los paneles de borde, los coeficientes numéricos son mayores a los de las NTCC-04 en los bordes de la franja paralela al borde discontinuo mostrando magnitudes simétricas al centro, como se muestra en la Fig. 22, pero en la franja perpendicular al borde discontinuo, la magnitud de los coeficientes es asimétrica como se muestra en la Fig. 23, ya que la rigidez en el borde extremo es menor que en el borde interior. En paneles apoyados sobre vigas, este efecto produce que el momento máximo positivo no se encuentre en el centro del panel, sino cerca del borde con menor rigidez como se muestra en la Fig. 23. Los muros producen en los paneles tipo I, que los momentos positivos máximos se produzcan a un cuarto de los extremos, no obstante, en losas tipo II, los muros producen momentos negativos en el centro del panel y momentos máximos positivos a una distancia menor a un cuarto del claro respecto al borde interior.
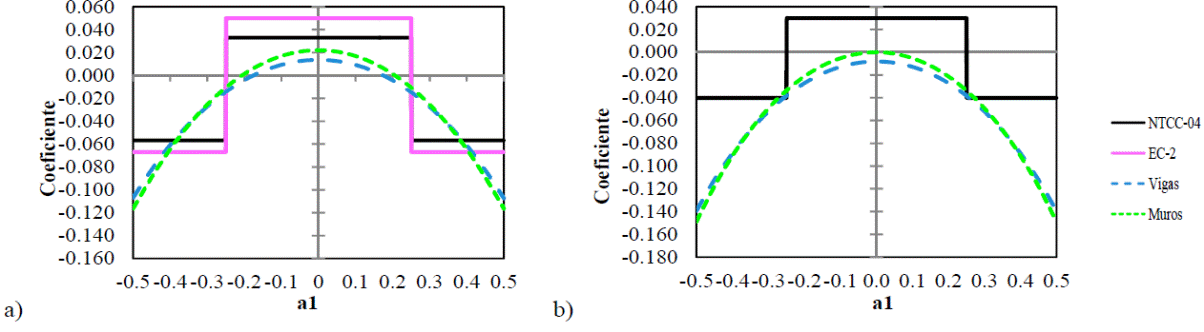
Tipo: a) I y b) II
Fig. 22: Coeficientes en la franja paralela al borde discontinuo del panel de borde con un lado corto discontinuo.
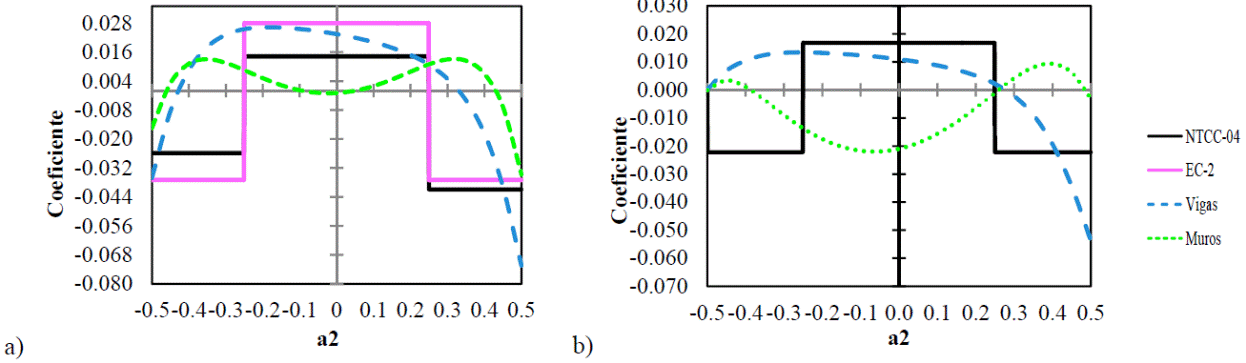
Tipo: a) I y b) II
Fig. 23: Coeficientes en la franja perpendicular al borde discontinuo del panel de borde con un lado corto discontinuo.
Los coeficientes de momento positivo propuestos por el IStructE-06 son mayores a los de las NTCC-04 en todos los casos; sin embargo, en algunos casos los coeficientes en los bordes interiores, son iguales o presentan una pequeña diferencia. De los resultados obtenidos se destaca que los coeficientes que presenta el IStructE-06 para determinar el momento positivo son iguales o mayores a los coeficientes numéricos. En bordes discontinuos, los coeficientes de momento negativo del IStructE-06 son, en todos los casos, mayores a los calculados numéricamente; sin embargo, en los bordes interiores son ligeramente menores. Note en la Tabla 1 que el IStructE-06 utiliza un sólo coeficiente para calcular el momento negativo en cada panel, el cual se emplea, tanto en los bordes interiores como extremos y en todas las relaciones de lados.
4. Comparación de los coeficientes propuestos por las NTCC-04
Las NTCC-04 actualmente presentan un total de 408 coeficientes para determinar los momentos en distintos paneles, los cuales se compararon con los coeficientes numéricos obtenidos en este trabajo. En la Tabla 2 se muestran los resultados obtenidos, donde los coeficientes sombreados son los coeficientes calculados numéricamente que resultaron ser mayores a los propuestos por las NTCC-04, mientras que los valores que no están sombreados son los que actualmente proponen las NTCC-04 y que resultaron mayores a los coeficientes calculados numéricamente.
Tabla 2: Coeficientes máximos en franjas centrales1
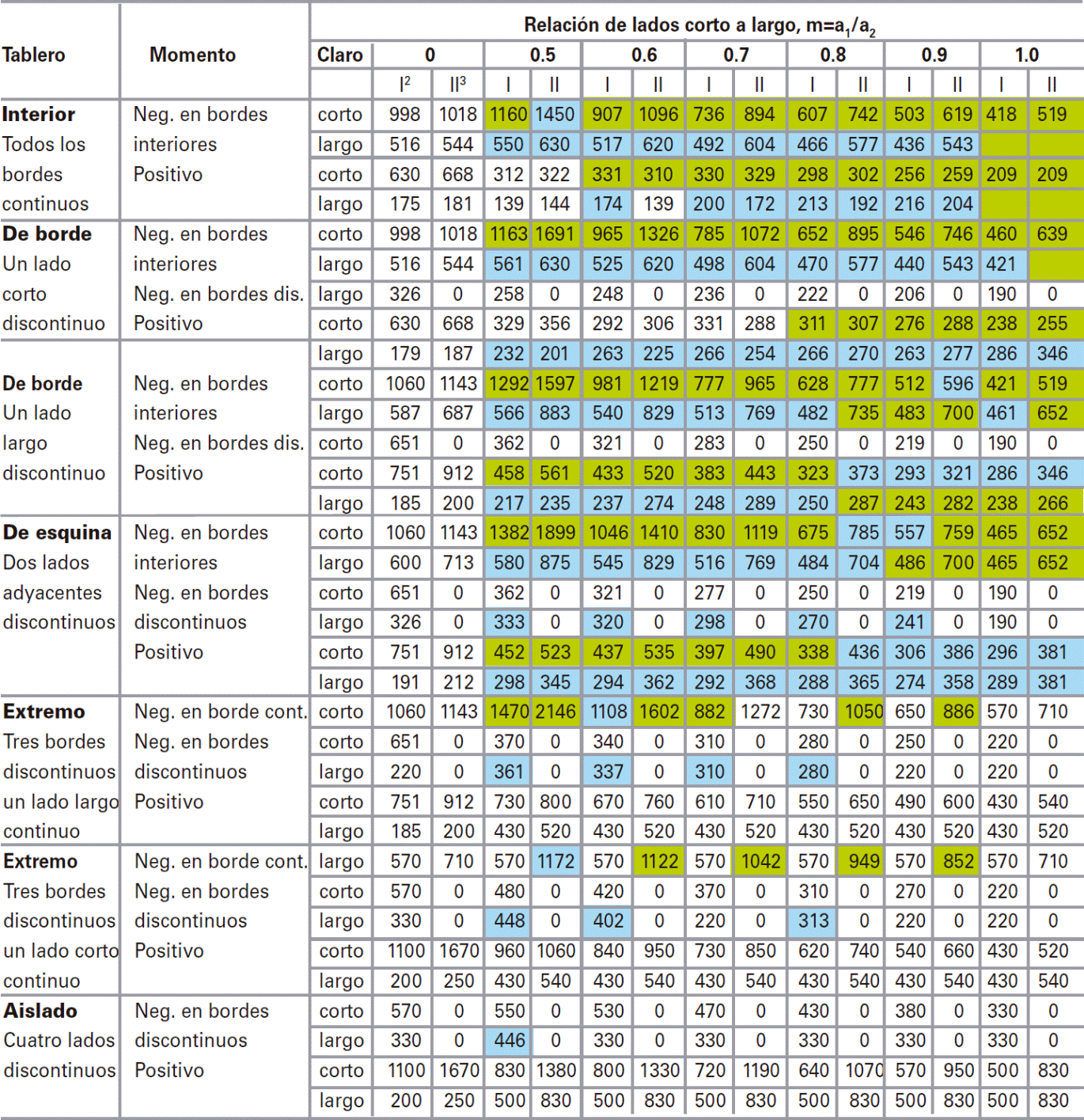
1 Para las franjas extremas multiplíquese los coeficientes por 0.60
2 Caso I. Losa colada monolíticamente con sus apoyos.
3 Caso II. Losa no colada monolíticamente con sus apoyos
Los coeficientes multiplicados por 10-4wa 2, dan momentos flexionantes por unidad de ancho; si w esta en kN/m2 (en kg/m2) y a, en m, el momento da en kN-m/m (en kg-m/m)
Para el caso I, a1 y a2 pueden tomarse como los claros libres entre paños de vigas, para el caso II se tomarán como los claros entre ejes, pero sin exceder del claro libre más dos veces el espesor de la losa
Es válido utilizar estos coeficientes para calcular los momentos de diseño cuando los paneles estén apoyados sobre: 1) vigas principales, que a su vez estén apoyadas en sus esquinas, 2) en muros y 3) algunos de sus bordes en vigas y el resto en muros.
No es válido utilizar los coeficientes en tableros apoyados sobre vigas secundarias, pues los momentos obtenidos tienen otra distribución. Por lo que en este caso se recomienda realizar el modelado numérico del sistema de losa.
Normalizando los valores de los coeficientes máximos obtenidos numéricamente de la Tabla 2 respecto a los valores propuestos por las NTCC-04, se obtienen los valores presentados en la Tabla 3, donde se observan casos en los que la magnitud de los coeficientes numéricos es el doble o mayor que la magnitud de los coeficientes actualmente recomendados por las NTCC-04. Los coeficientes numéricos positivos de los paneles interiores de ambos tipos (I y II) son menores a los propuestos por las NTCC-04, sólo para la relación m=0.5, mientras que para las otras relaciones, son mayores. Los coeficientes positivos máximos en el lado corto se presentan cuando se tienen muros, mientras que en la otra dirección, los momentos positivos máximos se obtiene de los paneles apoyados sobre las vigas. Los muros producen que la distribución de los momentos en paneles interiores con relación m<0.7 presenten dos máximos positivos cerca de los bordes, como se muestra en la Fig. 18a, y en el centro un coeficiente que puede ser negativo como el que se muestra en la Fig. 18b.
Tabla 3: Relación entre los coeficientes numéricos máximos y los propuestos por las NTCC-04 en franjas centrales
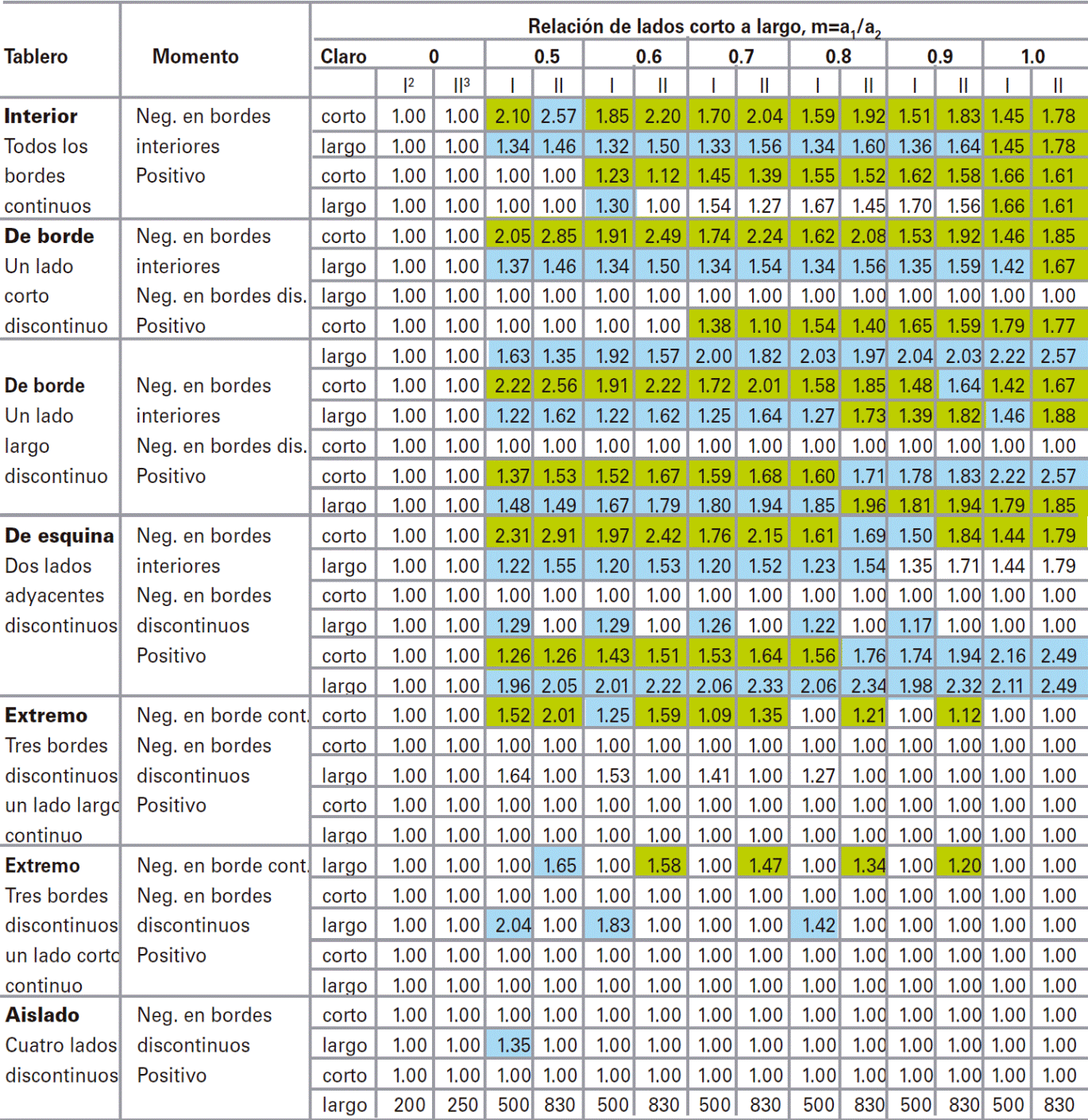
1 Para las franjas extremas multiplíquese los coeficientes por 0.60
2 Caso I. Losa colada monolíticamente con sus apoyos.
3 Caso II. Losa no colada monolíticamente con sus apoyos
Los coeficientes multiplicados por 10-4wa 2, dan momentos flexionantes por unidad de ancho; si w esta en kN/m2 (en kg/m2) y a en m, el momento da en kN-m/m (en kg-m/m)
Para el caso I, a1 y a2 pueden tomarse como los claros libres entre paños de vigas, para el caso II se tomarán como los claros entre ejes, pero sin exceder del claro libre más dos veces el espesor de la losa
Es válido utilizar estos coeficientes para calcular los momentos de diseño cuando los paneles estén apoyados sobre: 1) vigas principales, que a su vez estén apoyadas en sus esquinas, 2) en muros y 3) algunos de sus bordes en vigas y el resto en muros.
No es válido utilizar los coeficientes en tableros apoyados sobre vigas secundarias, pues los momentos obtenidos tienen otra distribución. Por lo que en este caso se recomienda realizar el modelado numérico del sistema de losa.
Los coeficientes negativos numéricos de mayor magnitud se presentan en los extremos de la franja corta, los cuales pueden ser mayores al 200% que los actualmente propuestos por las NTCC-04. Las diferencias de coeficientes en la franja larga son del 20% para paneles tipo I y entre el 30% y 40% en los paneles tipo II. Los paneles de borde con un lado corto discontinuo tienen menor rigidez a flexión en el borde discontinuo, por lo que los coeficientes negativos en este borde son menores a los coeficientes negativos de los bordes interiores. En la dirección corta, la distribución de coeficientes es simétrica; sin embargo, en la otra dirección no lo es, debido a la diferencia de rigideces en los bordes.
La diferencia entre los coeficientes numéricos negativos y de las NTCC-04 es del 200% en paneles de borde con un lado corto discontinuo tipo II, en la dirección corta y en paneles tipo I, esta diferencia de coeficientes es máxima en el panel con relación m=0.5 y decrece hasta ser el 20% en el panel con relación m=1. En los bordes interiores de los paneles tipo I en la dirección larga, la diferencia de coeficientes es del 20%, mientras que en paneles tipo II la diferencia es del 20 a 30%. En los bordes extremos los coeficientes numéricos son menores o iguales a los de las NTCC-04. Los momentos positivos en estos paneles son 200% más grandes que los de las NTCC-04, mientras que en los otros casos es menor.
El comportamiento descrito en los paneles de borde con un lado corto discontinuo se repite en los paneles de borde con un lado largo discontinuo, con la diferencia de que la distribución de coeficientes es asimétrica en la dirección corta de los paneles y simétrica en la dirección larga. Las diferencias entre coeficientes en paneles de borde con un lado largo discontinuo tipo I, en la franja larga es del 20% en los bordes interiores y en los coeficientes positivos del 200%. En paneles tipo II, la diferencia en los coeficientes positivos y negativos es mayor. En la dirección corta de paneles de borde con un lado largo discontinuo tipo I, los coeficientes numéricos en el borde discontinuo son menores a los de las NTCC-04, mientras que en el borde interior la diferencia máxima es de 150% y disminuye hasta el 20% a medida que se incrementa la relación m. En paneles de borde con un lado largo discontinuo tipo II, la diferencia de la magnitud de coeficientes es del 300% en la dirección corta en bordes interiores y la cual decrece, igualmente hasta una diferencia del 150% al incrementar la relación m.
Los paneles de esquina tienen en todos los casos distribuciones de coeficientes asimétricas, debido a los bordes discontinuos. Los coeficientes positivos de las NTCC-04, son menores a los numéricos y la diferencia entre ellos aumenta con la relación m y en algunos casos es del 250% o mayor. En los bordes extremos los coeficientes numéricos son iguales o menores a los de las NTCC-04, mientras que en los bordes interiores la diferencia es variable en ambos tipos de paneles y en ambas direcciones.
En los paneles de extremo con un lado corto discontinuo y de extremo con un lado largo discontinuo, los coeficientes de momentos propuestos por las NTCC-04 son mayores a los coeficientes numéricos positivos en todos los casos y en la mayoría de los coeficientes negativos de los bordes. En los casos donde los coeficientes numéricos son mayores a los de las NTCC-04, la mayor diferencia entre estos se encentra en los paneles con relación m=0.5 que al igual que en otros tipos de paneles, esta disminuye a medida que aumenta la relación m.
En los paneles aislados los coeficientes de momento positivo que presentan las NTCC-04 son mayores a los coeficientes numéricos y sólo hay diferencia en los coeficientes de momento negativo en los bordes de los paneles tipo II, en franja larga, los cuales disminuyen a medida que incrementa la relación m.
5. Ejemplo de aplicación
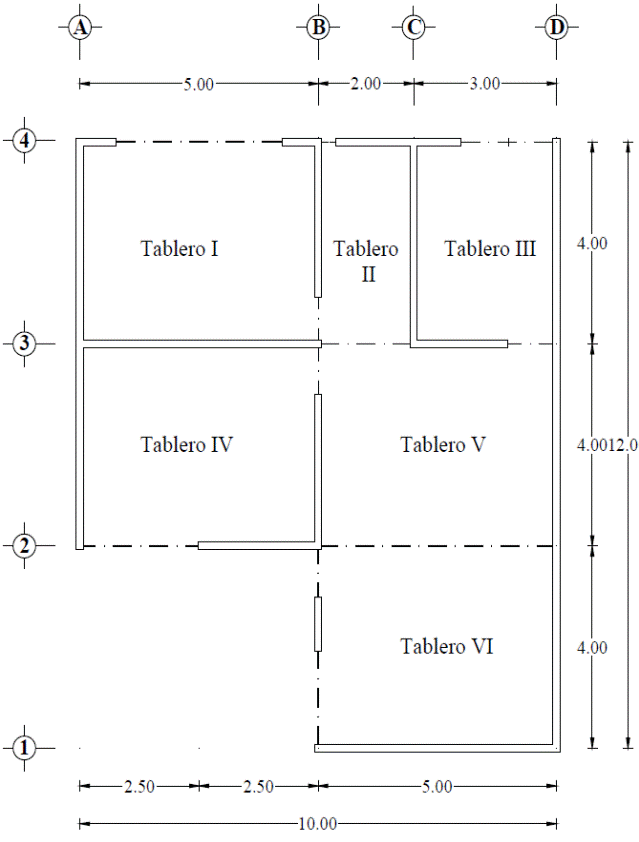
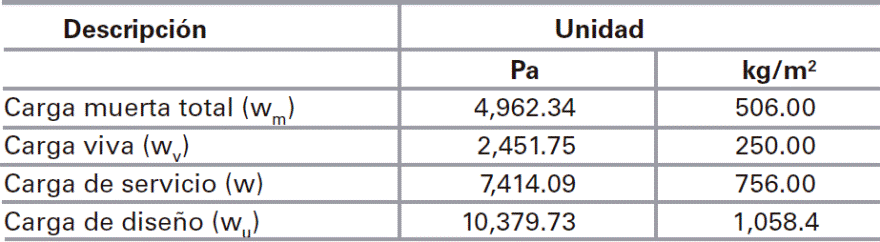
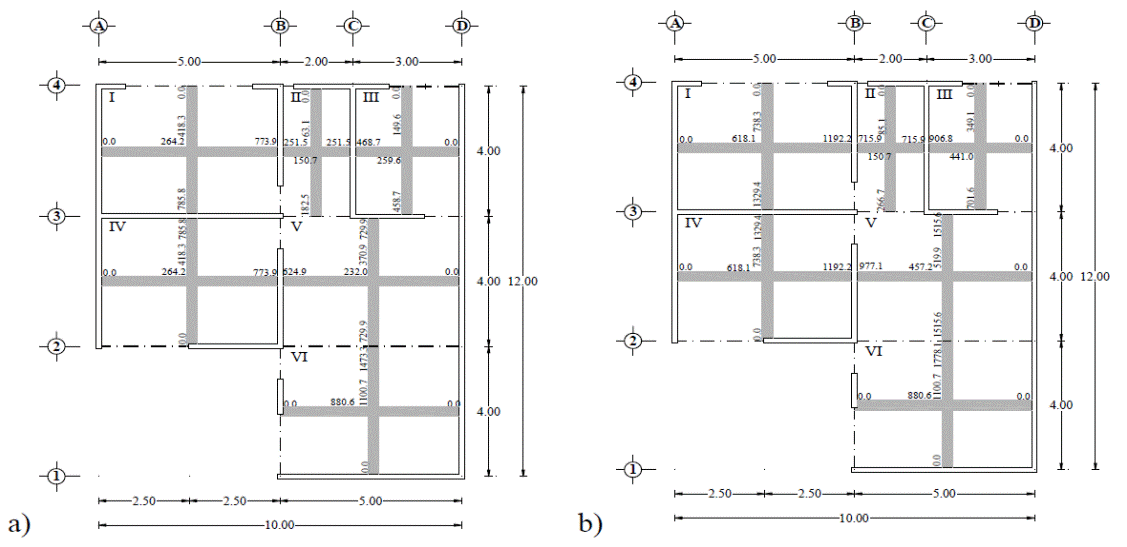
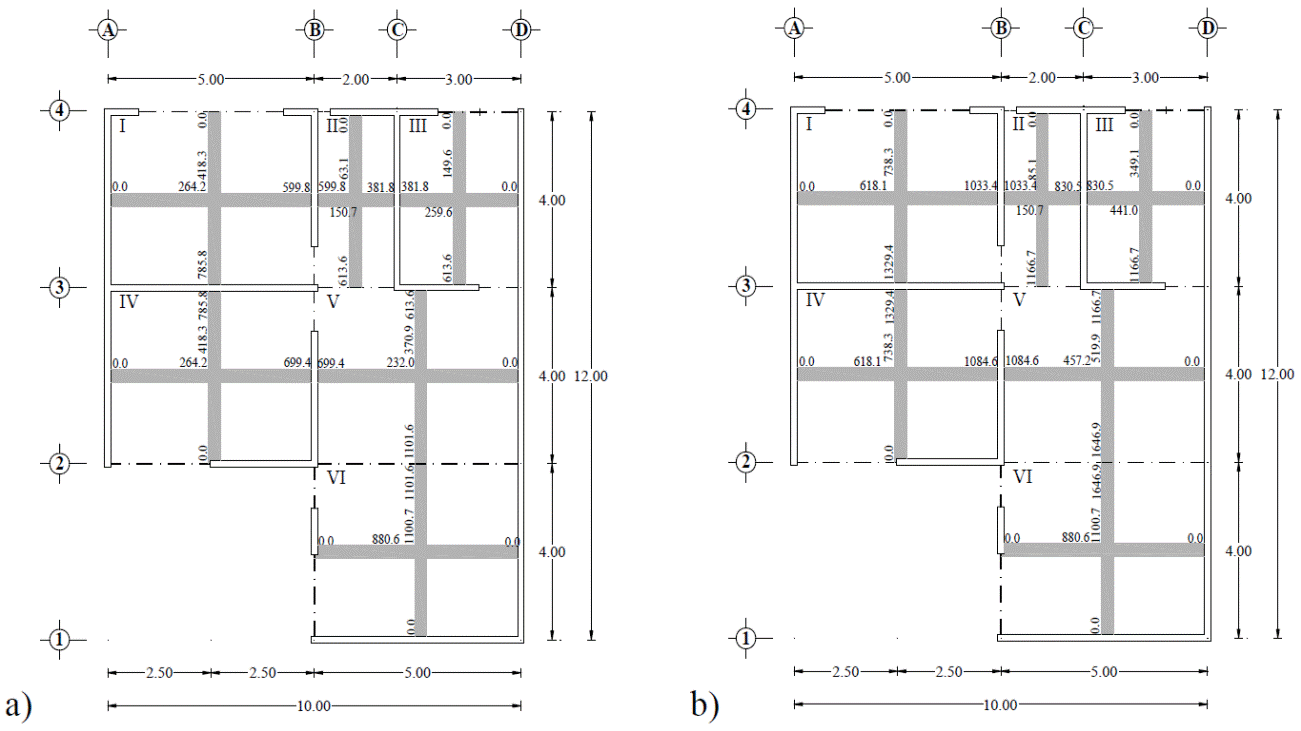
Se presenta el diseño de una la losa de entrepiso de un inmueble que funciona como oficinas, cuyas dimensiones e identificación de tableros se muestran en la Fig. 24. Para el sistema de piso se propone una losa maciza de concreto con un espesor h=12 cm, considerando un peralte d=10 cm y un recubrimiento de 2 cm con el que la carga muerta de la losa es de wm= 4,491.446 Pa (458 kg/m2), como se describe en la Tabla 4. La carga viva es de wv=2,451.662 Pa (250 kg/m2), con la que se determinó la carga de servicio w y la carga de diseño wu, utilizando un factor de carga de 1.4 como se muestra en la Tabla 5. El material de la losa es concreto con las propiedades mecánicas siguientes: módulo de Young E =2.171x104 MPa (2.214x105 kg/cm2), relación de Poisson, v=0.2, y esfuerzo último a compresión, 24.517 MPa (250 kg/cm2). Se consideró una continuidad tipo II, pues la losa se construirá no monolíticamente con sus vigas de apoyo.
5.1. Revisión del peralte mínimo
El peralte mínimo de la losa se revisó considerando el tablero VI, pues aunque los tableros I, IV y V tiene el mismo perímetro, es el tablero VI que se considera más desfavorable por tener tres bordes discontinuos. El peralte mínimo para omitir el cálculo de deflexiones se determina como:
En la ec. (3), los tres bordes discontinuos del tablero VI se incrementaron el 50%, pues la losa está colada no monolíticamente con sus vigas de apoyo, pues en el caso de estar monolíticamente se incrementa solo el 25%. El peralte propuesto es menor al mínimo, 10 cm <11.46 cm, por lo que se propone modificar el peralte y espesor tal que d=12 cm y h=14 cm, incluyendo 2 cm de recubrimiento, por lo que las cargas de análisis se modifican como se muestran en la Tabla 6.
El peralte mínimo modificado para omitir el cálculo de deflexiones se determina con la carga de servicio modificada como:
por lo que se valida el peralte d=12 cm.
5.2. Revisión por fuerza cortante del peralte propuesto
Considerando a1= 4 m y a2=5 m en el tablero VI, la fuerza cortante máxima que ocurre es:
Mientras que la resistencia de la losa a fuerza cortante es:
Puesto que Vu<Vr, se acepta el peralte d =12 cm para el diseño del armado de la losa.
5.3. Cálculo de los momentos de diseño
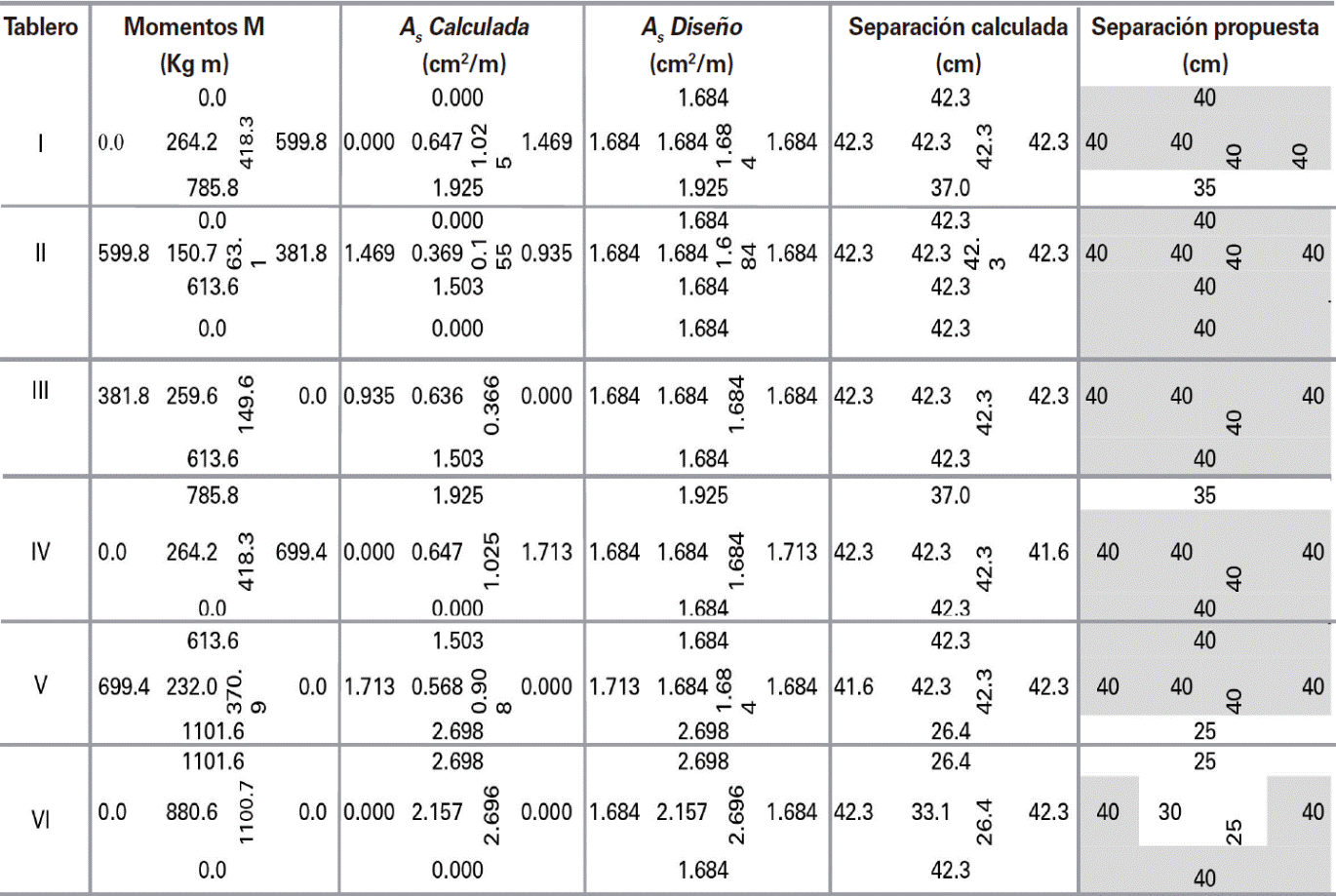
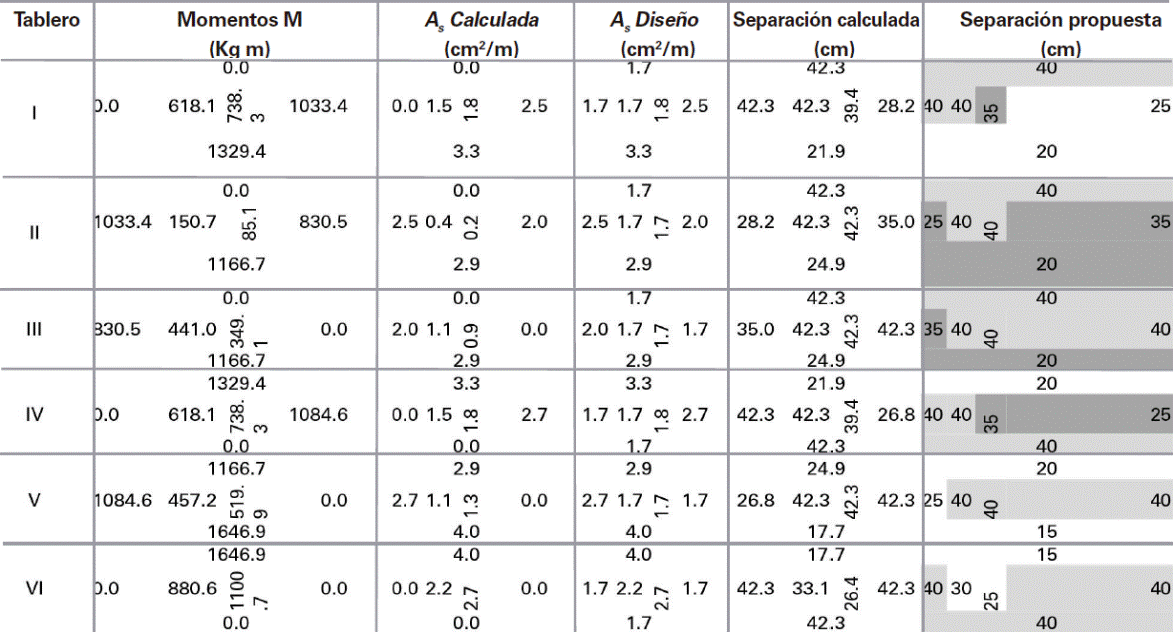
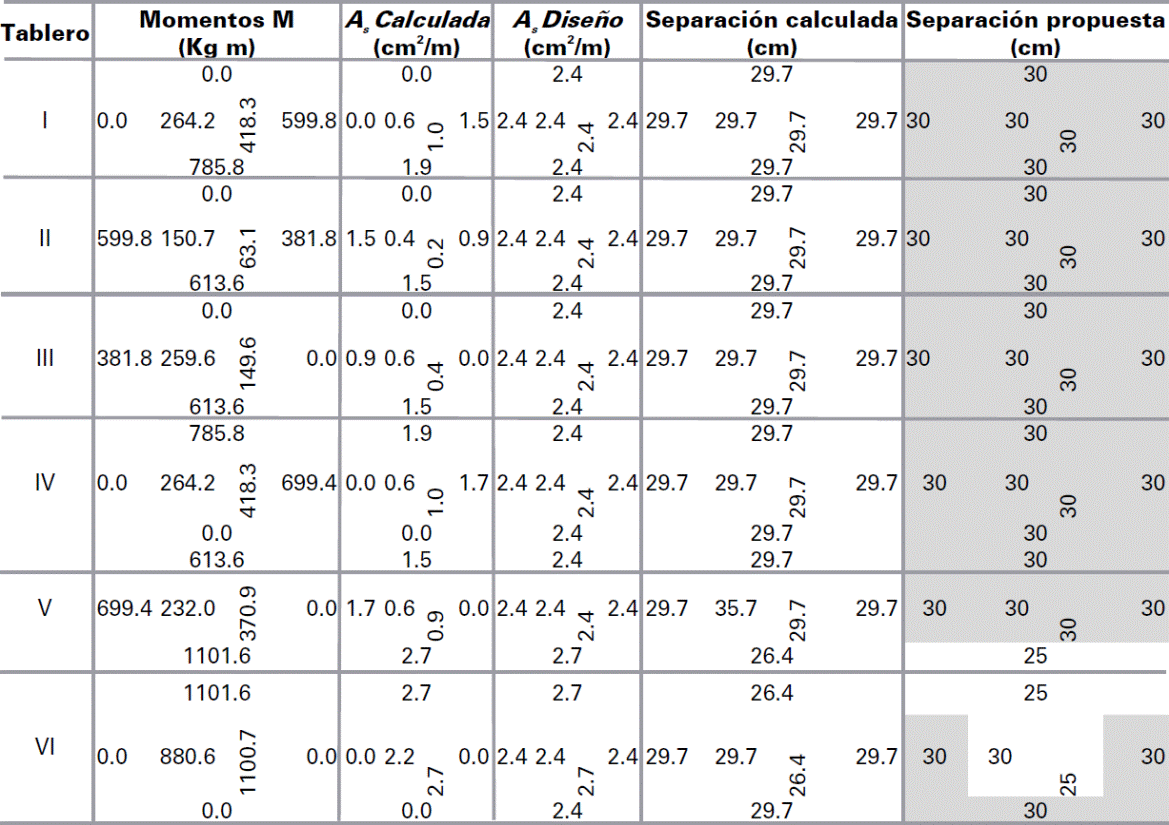
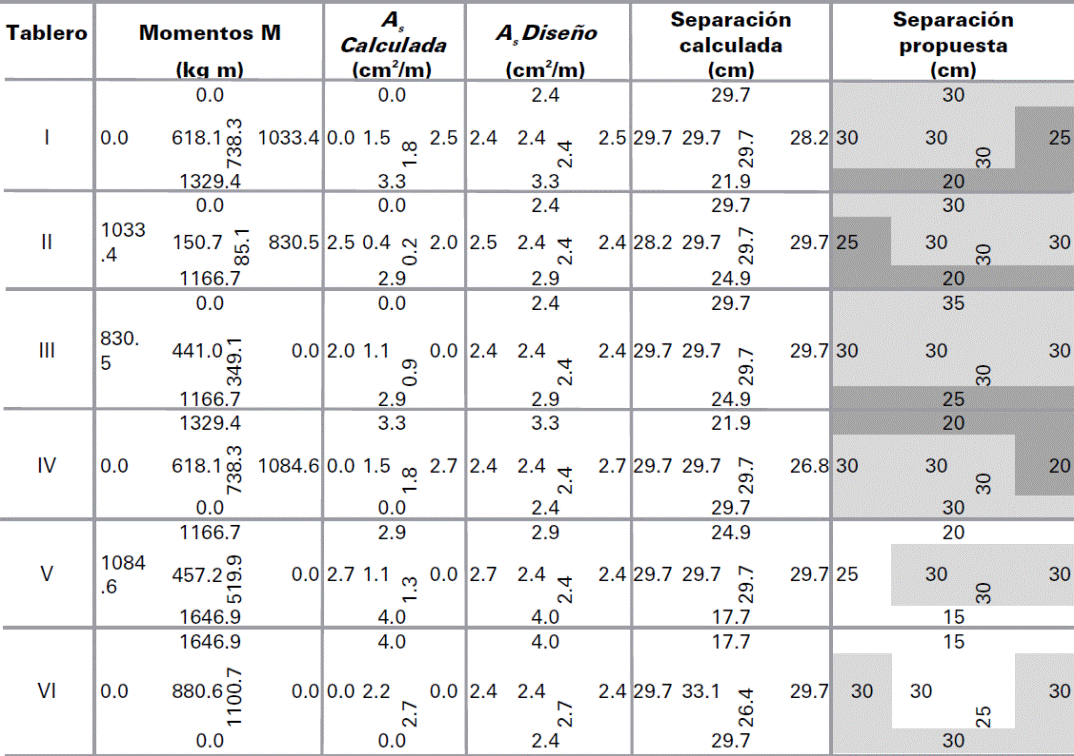
Para determinar los momentos de diseño, se identificaron los seis tableros mostrados en la Fig. 24, a los que se les asignó los coeficientes de diseño proporcionados por las NTCC-04, así como los que se proponen en este artículo en la Tabla 2. Los valores de los coeficientes en cada tablero, para continuidad tipo II, se muestran respectivamente en las Figs. 25 a y b Sólo a los coeficientes del tablero III, que tiene una relación de lados m=0.75, se les realizó una interpolación lineal entre los valores inmediatos superior e inferior, i.e., m = 0.70 y m= 0.80.
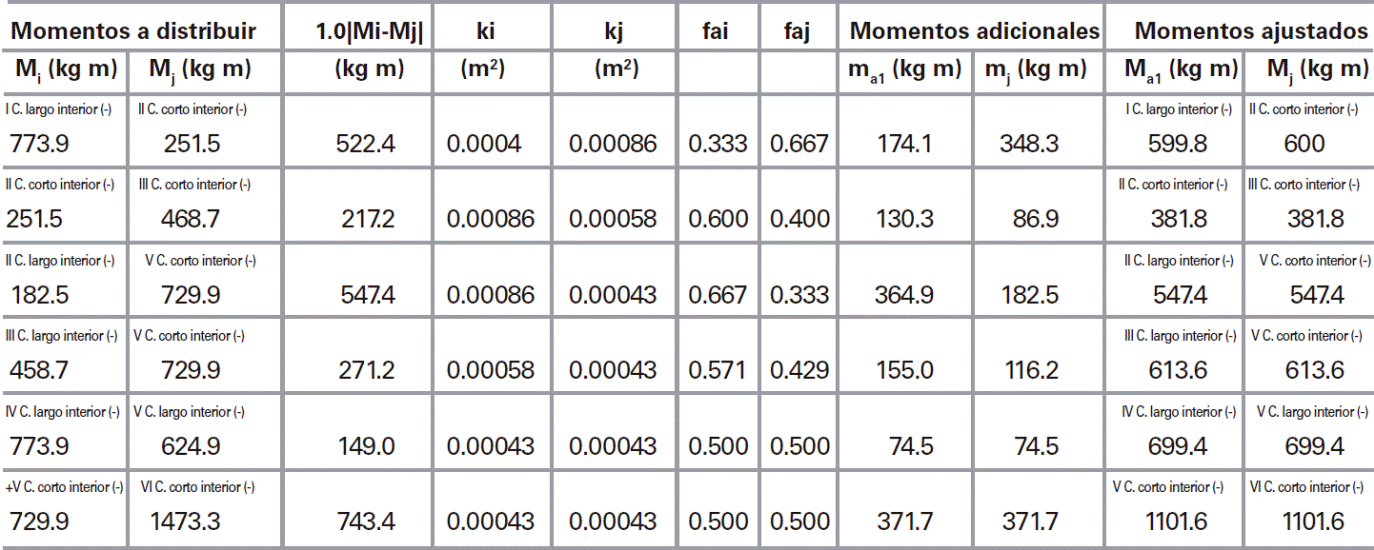
Los momentos de diseño se determinaron con la ec. (1), donde la carga distribuida corresponde a la de diseño de wu= 10,379.73 Pa (1,058.4kg/m2) en todos los tableros. El cálculo detallado de los momentos de diseño para cada uno de los tableros, utilizando los coeficientes de las NTCC-04 y los propuestos en la Tabla 2, se muestran respectivamente en las Tablas 7 y 8, donde se observa que la mayoría de los momentos calculados con los coeficientes propuestos tienen mayor magnitud que los calculados con los propuestas con las NTCC-04, con una relación de hasta 2.8 como se muestra en la Tabla 9, la cual corresponde al Tablero II, borde interior, claro corto. Los momentos de diseño en las franjas centrales de cada tablero se muestran respectivamente en la Fig. 26.
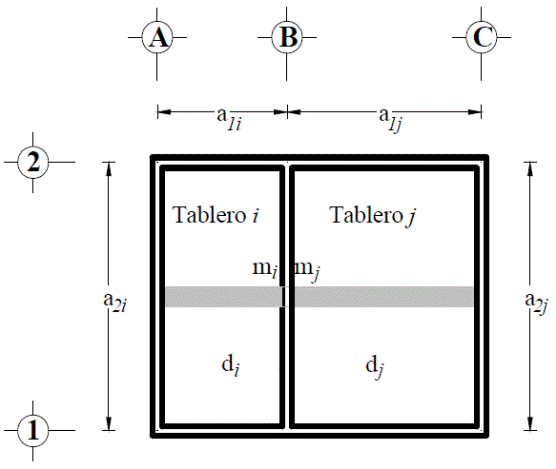
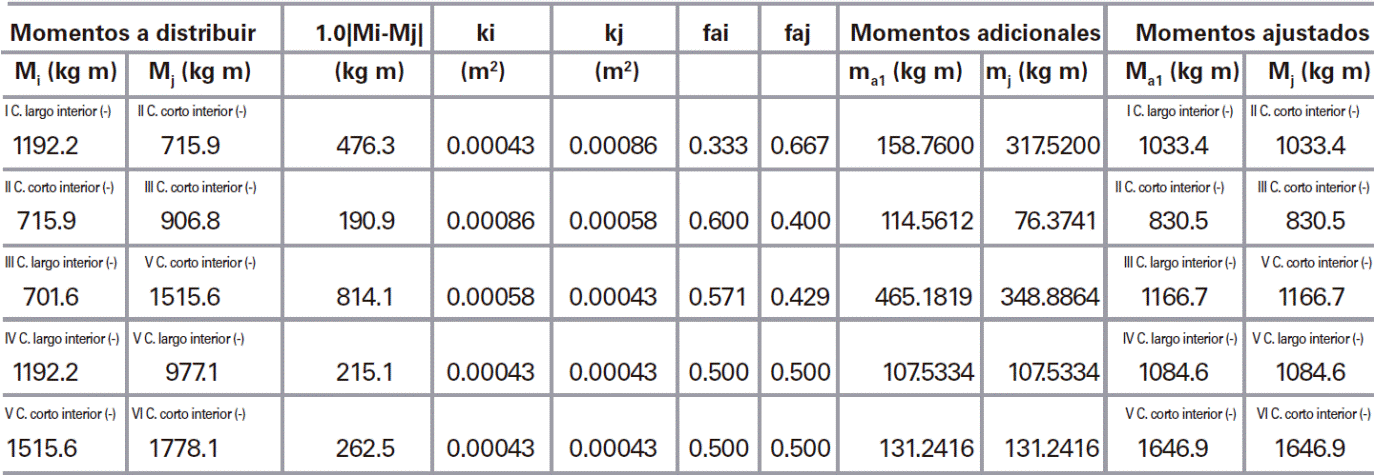
Se realizó una redistribución de momentos, mi y mj, entre los borde de dos tableros, i y j, como se muestra en la Fig. 27. Para la redistribución de momentos, se calcula el momento de desequilibrio como:
El momento por distribuir es:
Donde la constante de distribución es kd = 1 cuando las losas coladas no monolíticamente con sus apoyos y de kd = 2/3 para cuando las losas están coladas monolíticamente con sus apoyos. Los factores de ajuste se determina para cada tablero como:
Donde las rigideces de ambos tablero se determinan como:
Con los factores de ajuste que se determinan los momentos adicionales:
Finalmente, los momentos ajustados se determinan como:
La redistribución de momentos se realizó en seis bordes de tableros utilizando las ecs. (7) a (12). El cálculo detallado se muestra en las tablas 7 y 8, donde se observa que el tablero V tiene un borde contiguo con los tableros II y III, por lo que se realizó el ajuste con ambos, pero se asignó el valor mayor al tablero V, i.e., 613.6 kg-m y 1166.7 kg-m para los momentos respectivamente calculados con las NTCC-04 y los coeficientes propuestos. Las magnitudes de los momentos redistribuidos se muestran en la Fig. 28, donde se observa que se tiene la misma magnitud de momentos en los bordes los tableros contiguos, debido a que se asume que no influye la torsión de los apoyos en los bordes de las losas al estar coladas no monolíticamente con sus vigas de apoyo.
a) NTCC-04 y b) propuestos
Fig. 28: Redistribución de momentos de diseño calculados con los coeficientes.
5.4. Refuerzo mínimo
El refuerzo mínimo por cambios volumétricos se puede determinar de la sección 5.7 de las NTCC-04 como:
En un ancho de 100 cm se tiene un área de acero mínima:
Con barras de acero del #3, la separación corresponde a:
Puesto que la separación entre barras no debe exceder 50cm ni 3.5 h, 42 cm, se propone una separación mínima s1= 40 cm.
Otra opción proporcionada por la NTCC-04 es utilizar la una cuantía de r = 0.002 para elementos protegidos de la intemperie, con la que se obtiene el área de acero mínimo siguiente:
Con barras de acero del #3, la separación s2 corresponde a:
Con lo que se propone una separación mínima de s2=30 cm. Note que con esta opción, la separación es más conservadora, pues s2 es 10 cm menor que la separación s1.
5.5. Cálculo del acero de refuerzo
El área del acero de refuerzo se determina a partir de la relación del momento resistente, MR, de la ecuación siguiente:
Donde q está dada por:
Despejando el área deacero, Az, de la ec. (17) e igualando el momento resistente al momento de diseño se tiene:
Donde el factor de resistencia tiene un valor de FR=0.9 y asumiendo que (1-0.5q) =0.9 (Gallo et al. 2007), entonces la ec. (19) es:
El cálculo del área de acero con la ec. (20) se muestra en las tablas 12 a 15, donde las zonas que sólo requieren acero mínimoestán en sombreado claro, aquellas que con los coeficientes propuestos requieren una mayor cantidad de acero de refuerzo en sombreado obscuro y las zonas que requieren un área de acero mayor al mínimo con ambas opciones de coeficientes no están sombreadas. El área de acero mínima As1 se asignó cuando As< As1 como se muestra en las tablas 12 y 13, pero el área de aceró mínima As2 se asignó cuando As< As2como se muestra en las tablas 14 y 15. La distribución del acero de refuerzo para resistir los momentos calculados con los coeficientes actualmente propuestos por las NTCC-04 se muestra en las Figs. 29a y 30a, más la distribución de acero de refuerzo para los momentos calculados con los coeficientes propuestos se muestran en las Figs. 29b y 30b, para las áreas de acero mínima As1 y As2, respectivamente.
En general, en este ejemplo de diseño se observó en la Tabla 9 que 19 de los 23 momentos calculados con los coeficientes numéricos son mayores hasta 2.8 veces a los calculados con los de las NTCC-04, sin incluir los que tienen un valor de cero. Al considerar el área de acero mínima As1, 6 de los momentos calculados con las NTCC-04 requieren un área mayor acero como se muestra en la Tabla 12; sin embargo, 17 de los momentos calculados con los coeficientes numéricos requieren un área mayor acero como se muestra en la Tabla 13. Por otra parte, al considerar el área de acero mínima As2, 4 de los momentos calculados con las NTCC-04 requieren un área mayor acero como se muestra en la Tabla 14; sin embargo, 13 de los momentos calculados con los coeficientes numéricos requieren un área mayor acero como se muestra en la Tabla 15.
Respecto a la colocación del acero de refuerzo de las Figs. 29 y 30, en el tablero II se deberá colocar sólo acero superior en la dirección horizontal debido a que la dimensión del claro corto es pequeña respectolos tableros vecinos, por lo que éste tendría un comportamiento similar al del elemento intermedio de la Fig. 19. Por otra parte, la separación del acero de refuerzo en la dirección vertical de los tableros II, III y IV deberá homologarse con la separación del tablero VI, pues para su construcción deben tener separaciones congruentes.
6. Conclusiones
El modelado numérico de losas permite conocer la distribución de momentos, de los que se determinan los coeficientes de diseño, con lo que se pueden eliminar incertidumbres en el diseño y así evitar problemas de agrietamiento incipiente, flechas y vibración en las losas.
Los coeficientes positivos y negativos en los bordes discontinuos que presenta el IStructE-06 son, en general, mayores a los calculados numéricamente; sin embargo, en bordes interiores son menores a los coeficientes numéricos, los cuales se encuentran aproximadamente entre el 70% y 80% de los coeficientes numéricos que se obtuvieron en los modelos con vigas perimetrales. Por el contrario, los coeficientes presentados por las NTCC-04 son, en general, menores en bordes interiores. En bordes discontinuos los coeficientes presentados por las NTCC-04 son aproximadamente el 80% del valor de los coeficientes numéricos máximos.
La diferencia entre los coeficientes numéricos propuestos en este trabajo y los proporcionados actualmente en las NTCC-04 se debe a que estos últimos fueron adaptados del ACI-318-63 (González-Cuevas 2011), los cuales se calcularon considerando distribuciones de momentos en tableros sobre apoyos rígidos.
En el ejemplo de diseño, el área de acero de refuerzo en algunos bordes es mayor cuando se utilizan los coeficientes propuestos en este trabajo que cuando se utilizó los actualmente recomendados por las NTC-04; esta diferencia es de hasta el 2.8 veces, al igual que los momentos de la Tabla 9, puesto que el área de acero de refuerzo depende de los momentos como se muestra en la ec. (20). Los coeficientes calculados numéricamente proporcionan el acero de refuerzo necesario para garantizar un diseño seguro, pues algunos de los coeficientes actualmente recomendados por las NTCC-04 pueden proporcionar secciones con menor acero de refuerzo que no proporcionen la resistencia adecuada.
Es válido utilizar los coeficientes propuestos en este trabajo para calcular los momentos de diseño cuando los paneles estén apoyados sobre: 1) vigas principales, que a su vez estén apoyadas en sus esquinas, 2) en muros y 3) algunos de sus bordes en vigas y el resto en muros. No es válido utilizar los coeficientes en tableros apoyados sobre vigas secundarias, pues los momentos obtenidos no son congruentes por lo que en este caso se recomienda realizar el modelado numérico del sistema de losa.











 nueva página del texto (beta)
nueva página del texto (beta)