Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Concreto y cemento. Investigación y desarrollo
versão impressa ISSN 2007-3011
Concr. cem. investig. desarro vol.5 no.2 Ciudad de México Jan./Jun. 2014
Modelado numérico del daño en estructuras de concreto reforzado
Jaime Retama Velasco1, A. Gustavo Ayala Milián1 y J. Jesús Gutiérrez Trejo1
1 Instituto de Ingeniería, Universidad Nacional Autónoma de México, Mecánica Aplicada, Circuito Escolar S/N, Ciudad Universitaria, C.P. 04510, Del. Coyoacán, México D.F. E-mail: jretamav@iingen.unam.mx, gayalam@iingen.unam.mx, jgutierrezt@iingen.unam.mx
Resumen
Este artículo se presenta la formulación variational e implantación numérica de un problema de interés en el estudio del comportamiento mecánico de elementos de concreto reforzado, basada en una aproximación de desplazamientos del método de los elementos finitos, en dos dimensiones, en la que el acero de refuerzo se modela utilizando elementos barra localizados dentro del dominio de los elementos finitos de concreto. Para simular el efecto del endurecimiento por deformación en el acero de refuerzo, se utiliza un modelo constitutivo elasto—plástico y el daño en el concreto se introduce mediante una aproximación de discontinuidades interiores. La formulación desarrollada, se implanta en un programa de computadora y se aplica a un problema de tensión de un elemento estructural, donde se considera que la falla inicia predominantemente en modo-I; para posteriormente evolucionar hacia el colapso en un modo mixto de falla. En este ejemplo se utiliza una sección de concreto con y sin refuerzo.
Palabras clave: Concreto reforzado, elemento finito, mecánica del daño, discontinuidades interiores, análisis inelástico.
Abstract
This paper presents a variational formulation and numerical implementation of a problem of interest in the study of the mechanical behavior of reinforced concrete elements based on a two dimensional displacement approximation of the finite element method in which the steel reinforcement is introduced using bar elements located within the concrete finite elements. To simulate the strain hardening effect of the reinforcement steel an elastic—plastic constitutive model is used. The damage undergone by the concrete material is modeled by an embedded discontinuity approach. The developed formulation is implemented in a finite element computer program and applied to a structural element subjected to tension; considering that the failure process initiates in mode—I, to continue in a mixed mode on its evolution to collapse. This example considers a cross section with and without two different reinforcements.
Keywords: Reinforced concrete, finite element, damage mechanics, embedded discontinuities, inelastic analysis.
Resumo
Este artigo apresenta a formulação variational e implementação numérica de um problema de interesse para o estudo do comportamento mecânico dos elementos de betão armado, com base numa aproximação do método de deslocamento de elementos finitos em duas dimensões, em que o reforço de aço é modelado utilizando elementos de barras localizadas no domínio finito elemento concreto. Para simular o efeito de encruamento no reforço de aço, modelo p constitutivo elasto-plástico é usado. O dano em concreto é introduzido através da aproximação descontinuidades internas. A formulação desenvolvida é implementado num programa de computador e é aplicado a um problema de tensão de um elemento estrutural, onde se considera -que o modo de falha iniciar-I predominantemente; depois 39 evoluir para o colapso de um modo de falha mista. Neste exemplo, uma secção de betão foi utilizado sem e com dois braços diferentes.
Palavras chaves: Betão armado, elemento finito, danos mecánicos, descontinuidade interna, análise inelástica.
Introducción
El concreto reforzado ha llegado a ser uno de los materiales de construcción más ampliamente utilizados en la ingeniería estructural. Su costo, eficiencia, rigidez y resistencia, hacen al concreto reforzado un material viable para la construcción de una gran variedad de sistemas estructurales (Retama y Ayala, 2013). Desafortunadamente, la complejidad del comportamiento mecánico no lineal de este material, particularmente el experimentado en su evolución al colapso, no ha sido suficientemente estudiado y por tanto no plenamente entendido. Debido a la complejidad de este problema, existen diversos esfuerzos de investigación en los que se continúa estudiándolo tanto a nivel experimental (Katz, 1999) como mediante simulaciones numéricas (Retama, 2010a; Retama y Ayala, 2010b; Retama y Ayala, 2011; Juárez, 2006) que consideran la no-linealidad inherente en el comportamiento mecánico de estructuras construidas con este material ante escenarios que las lleven a mecanismos inelásticos que pueden conducir a su colapso total o parcial. Algunas de las complejidades relacionadas con el modelado del comportamiento del concreto reforzado son:
1. El concreto reforzado es un material compuesto formado por dos materiales diferentes, concreto y acero, ambos con comportamiento no lineal complejo.
2. El comportamiento mecánico de los componentes de este material compuesto a niveles elevados de deformación es altamente no lineal aun ante demandas monótonamente crecientes. Este comportamiento da origen a propiedades cambiantes en el concreto debidas a la aparición y propagación de grietas, y en el acero de refuerzo a su plastificación.
3. La adherencia entre el concreto y el acero de refuerzo es un problema unilateral, difícil de incorporar dentro de modelos de análisis convencionales.
4. El comportamiento esfuerzo—deformación del concreto es no—lineal, función de diferentes variables de estado no suficientemente investigadas.
5. Las deformaciones del concreto están influenciadas por el flujo plástico y la contracción; ambas problemas dependientes del tiempo.
Dentro del contexto del desarrollo de nuevos y mejores modelos analíticos, para simular el comportamiento de elementos de concreto reforzado (Ngo y Scordelis, 1967; Oliver et al., 2008; Neto et al., 2004; Katz, 1999; Kumar y Barai, 2010) la experimentación en laboratorio sigue siendo una parte fundamental mediante la cual se investigan los modelos constitutivos de este material y se obtienen las propiedades necesarias para su uso en formulaciones numéricas y herramientas de análisis estructural como las basadas en el método de los elementos finitos.
Para eliminar las limitaciones de las formulaciones numéricas y herramientas de análisis existentes, en este artículo se presenta una formulación variational y su implantación numérica basada en el método de los elementos finitos que considera:
1) La adherencia entre el concreto y el acero.
2) El comportamiento no-lineal de las varillas de refuerzo considerando el endurecimiento por deformación.
2 3) El agrietamiento experimentado por el concreto utilizando una formulación discreta de discontinuidades interiores.
1. Modelado numérico del concreto reforzado
Las formulaciones numéricas actualmente usadas en el modelado del comportamiento de elementos de concreto reforzado son diversas, cada una con ventajas y desventajas; atribuibles generalmente a los modelos constitutivos utilizados, y a la formulación e implementación numérica en un programa de computadora de elementos finitos no lineales (Retama y Ayala, 2013).
Al ser el concreto reforzado un material compuesto, no es válido caracterizarlo como un material de una sola fase. 40 Por ello, diferentes investigadores han estudiado el problema como uno de interacción a nivel macroscópico entre dos materiales, el concreto y el acero. A este respecto, a continuación se describen brevemente algunos de los modelos I numéricos desarrollados para este fin que utilizan el método de los elementos finitos:
1. El modelo numérico más comúnmente utilizado en la práctica de la ingeniería estructural, considera al concreto reforzado como un material homogéneo con propiedades equivalentes en el que, por lo general, el material acero se transforma en uno equivalente de concreto (Katz, 1999).
2. Otro tipo de formulación numérica es en el que un elemento estructural de concreto reforzado se discretiza mediante elementos sólidos en dos (2D) o tres dimensiones (3D). El concreto se modela mediante elementos continuos y el efecto del acero de refuerzo, se incluye mediante elementos barra unidimensional con un único grado de libertad por nodo, (Fig. 1). Para lograr esto, es necesario que los nodos de los elementos barra coincidan con los nodos de los elementos sólidos; lo que obliga a utilizar mallas estructuradas para localizar correctamente las barras de acero (Retama y Ayala, 2011; Ngo y Scordelis, 1967; Oliver et al., 2008; Kwak y Filippou, 1990).

3. Otro modelo, que permite una aproximación más general del comportamiento de este material, mejor que la del modelo anterior, considera al acero de refuerzo con elementos barra embebidos dentro de elementos sólidos de concreto, (Fig. 2). En esta aproximación no es necesario utilizar mallas estructuradas de elementos finitos para introducir, dentro del concreto las varillas de refuerzo (Retama y Ayala, 2013).

2. Modelo de daño cohesivo
Para modelar la evolución del daño en un material debido a la aparición y propagación de una discontinuidad, caracterizado por un fenómeno no lineal asociado la localización de deformaciones, se han desarrollado relaciones constitutivas cohesivas tracción—salto (Retama, 2010a; Hillerborg et al., 1976; Bazant y Planas, 1998) que consideran los diferentes modos posibles de falla en el material.
En este modelo constitutivo, se considera que la respuesta inelástica del material está caracterizada, básicamente, por dos propiedades: el esfuerzo de fluencia σto y la energía de fractura GF. En este modelo, en el momento en que el esfuerzo principal máximo alcanza el esfuerzo σto, similar al criterio de Rankine en teoría de plasticidad clásica, se introduce una discontinuidad dentro del elemento, mediante la cual se simula el daño que éste experimenta.
Para definir el nivel de daño en una grieta se utiliza una función f de carga/descarga, definida como:

donde 〈un〉 corresponde a los valores positivos de la componente normal del vector salto de desplazamientos en la discontinuidad, definidos por los corchetes de McAuley, 〈 〉, y k es una variable de estado que toma en cuenta el daño acumulado en el material, definida como:
〉, y k es una variable de estado que toma en cuenta el daño acumulado en el material, definida como:

El considerar solo los valores positivos de un en la ecuación 1, garantiza un proceso de falla monótonamente creciente.
Las tracciones normales a la discontinuidad se relacionan con el salto de los desplazamientos mediante:
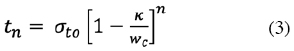
donde wc es el salto normal máximo permitido en la grieta y n es una constante que define la forma de la curva de ablandamiento, (Fig. 3).

Para obtener una disipación de energía consistente con la energía de fractura del material, las tracciones en la discontinuidad se relacionan con GF mediante:

El tensor constitutivo tangente, T, que define el comportamiento del material en la zona de la discontinuidad, se obtiene de la derivada de las tracciones en la discontinuidad, ecuación 3, con respecto a la variable de estado k, esto es

En el momento en que inicia el proceso de daño, y se introduce la discontinuidad, se tienen las siguientes condiciones iniciales:

donde ko es la apertura inicial de la grieta, σI es el esfuerzo principal máximo y ts es la tracción normal a la discontinuidad. El resto de los términos se definieron en secciones anteriores.
3. Formulación variacional
La formulación variacional del problema descrito en los párrafos anteriores, se deriva de la desarrollada por Retama (Retama, 2010a), en la que se aborda el problema de un sólido en que aparece una discontinuidad dentro de su dominio. Para esto, sea un sólido, inicialmente continuo, con volumen Ω, frontera Γ y fuerzas de cuerpo bv aplicadas en Ω y en el que se encuentra localizado el acero de refuerzo, como se muestra en la Fig. 4. Las condiciones esenciales de frontera, ū, están definidas en Γu mientras que, las tracciones,  , correspondientes a las condiciones naturales de frontera, se aplican en Γt; de tal forma que Γ= Γu U Γt y ∅ = Γu ∩ Γt. En esta figura v es el vector normal a la frontera Γt.
, correspondientes a las condiciones naturales de frontera, se aplican en Γt; de tal forma que Γ= Γu U Γt y ∅ = Γu ∩ Γt. En esta figura v es el vector normal a la frontera Γt.

El funcional de energía para este sólido se define como:

donde Πint corresponde a la energía de deformación interna del concreto, Πdises la energía consumida en el proceso de daño en la zona de la grieta, Πref es la energía de deformación interna del acero, Πitz es la energía de deformación en la zona de adherencia entre el concreto y el acero; generalmente representada mediante elementos de interfaz, y Πext corresponde al trabajo desarrollado por las cargas externas que actúan en el sólido.
4. Aproximación mediante elemento finito
Para aproximar el campo de desplazamientos del problema descrito en el parrado anterior, se utiliza una formulación de elementos finitos que considera elementos sólidos 2D en los que el acero de refuerzo se encuentra dentro de su dominio; como se muestra en la Fig. 5.

En la Fig. 5, los nudos 2 y 4 corresponden a los extremos del elemento barra y los 1 y 3 son los correspondientes nudos dentro del elemento de concreto. Esta definición de nudos permite incluir de manera explícita el corrimiento de una barra de refuerzo dentro de la masa de concreto.
A diferencia de otras formulaciones numéricas, utilizadas para simular el comportamiento del concreto reforzado, en esta se permite que las varillas de acero puedan cruzar el elemento. La ventaja de esta formulación, es que no es necesario utilizar mallas estructuradas de elementos finitos para localizar apropiadamente las varillas de acero dentro del sólido continuo.
Al minimizar el funcional de energía dado por la ecuación 7, con respecto al campo de desplazamientos e interpolados mediante una aproximación de elemento finito, se obtiene, para el elemento sólido triangular, de deformación constante mostrado en la Fig. 5, la siguiente ecuación matricial de equilibrio del elemento,

donde K es la matriz de rigidez del elemento enriquecido, definida como:

La matriz k1 es la matriz de rigidez del elemento que considera la existencia de daño en el concreto, definido como una discontinuidad dentro de su dominio, k2 es la matriz correspondiente al acero de refuerzo que cruza al elemento y k3 la correspondiente a la adherencia entre el concreto y las varillas de refuerzo. La forma condensada de esta matriz es:
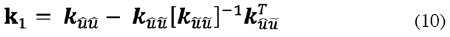
donde:

es la matriz de rigidez del elemento barra. La matriz de transformación Rα rota la matriz de rigidez elemental, del elemento barra, al sistema global y Rn es una matriz de transformación que transmite el efecto de las varillas de refuerzo a los nodos del elemento sólido 2D. Los términos ni1, ni2, ni3 y "s son las funciones de forma para el elemento sólido 2D evaluadas en el nodo i del elemento barra, (Fig. 5); mientras que nj1, nj2, nj3son las mismas funciones evaluadas en el nodo j. En el trabajo de Retama y Ayala (2011) se da una descripción detallada de esta formulación.
La matriz correspondiente a la adherencia entre el concreto y las varillas de refuerzo está dada como:

donde:

con β como una constante que caracteriza la adherencia entre el concreto y el acero, y el resto de los términos como ya se han definido. Finalmente, los vectores u y Fext dados en la ecuación 8, son el de desplazamientos y fuerzas nodales del elemento, respectivamente.
5. Ejemplo de aplicación
Para ilustrar la aplicación de la formulación descrita en los párrafos anteriores, a continuación se presenta un ejemplo correspondiente a un elemento estructural de concreto reforzado, sometido a tensión. La geometría del elemento, condiciones de apoyo y localización de las varillas de acero longitudinal se muestran en la Fig. 6. En este ejemplo se ignora el acero transversal.
Las propiedades mecánicas del concreto son:
• Resistencia a la compresión f'c = 19.6 Mpa
• Módulo de elasticidad Ec = 19.6 Mpa
• Relación de Poisson v =0.20
• Esfuerzo de fluencia σt0 = 1.94 Mpa
• Energía de fractura
y las del acero de refuerzo:
• Módulo de elasticidad Es = 2x105 Mpa
• Esfuerzo de fluencia fy = 196,140 Mpa
El experimento numérico se realiza para tres cuantías de acero de refuerzo. En el primer caso se analiza un concreto simple, sin acero de refuerzo; posteriormente se incluyen cuatro varillas del número tres (9.5 mm de diámetro), distribuidas como se indica en la Fig. 6, y en el último caso, se consideran cuatro varillas de refuerzo del número cuatro (12.7 mm de diámetro), con la misma distribución del caso anterior.
6. Resultados
Para el modelado mediante el método de los elementos finitos, se utilizan elementos sólidos 2D, triangulares de deformación constante, conjuntamente con elementos barra 1D, (Fig. 7). Es importante mencionar que debido a la naturaleza del experimento numérico en el que se pretende llevar al espécimen hasta la falla, el análisis se realiza mediante un control de desplazamientos.

En la Fig. 8 se muestran las curvas desplazamiento contra reacción para los tres tipos de armado que se estudian.
Al observar las curvas de respuesta en la Fig. 8, reacción en el apoyo contra desplazamiento, se aprecia que la pendiente de la rama ascendente se incrementa ligeramente a medida que se utiliza más acero de refuerzo, esto significa que, como era de esperarse, la estructura se vuelve más rígida. Con respecto a la rama descendente, donde la estructura ha sufrido daño y comienza a degradarse hasta llegar al colapso total, se observa que las pendientes para las tres curvas, es muy diferente. Cuando no se utiliza acero de refuerzo, se observa que el comportamiento de la estructura es frágil; mientras que a mayores porcentajes de acero, el comportamiento es más dúctil.
7. Conclusiones
El comportamiento mecánico del concreto reforzado, visto como un material compuesto, es un problema complejo cuyo modelado numérico aún no está plenamente estudiado. A partir de los diferentes modelos numéricos utilizados por diferentes autores, se puede observar que existen varios factores que influyen en el desarrollo de una formulación numérica, consistente con el problema físico real.
Una aproximación que se ha considerado aquí como razonable es que, en estructuras bien diseñadas, antes de que se pierda la adherencia entre el acero y el concreto, este último material falla; permitiendo el desarrollo de macro—grietas que evolucionan hasta que la estructura llega al colapso total. Esta suposición implica el considerar una adherencia perfecta entre ambos materiales, pudiendo no ser totalmente representativo del problema general. A pesar de esta limi-tante, es de interés mencionar que la formulación presentada da resultados satisfactorios; permitiendo una disipación de energía consistente con el comportamiento real de este tipo de estructuras, a base de concreto reforzado.
Futuros desarrollos de esta formulación en los que se simule la pérdida de adherencia entre el concreto y el acero requieren un modelo de ablandamiento escalar que relacione el corrimiento del refuerzo con los esfuerzos en la zona de adherencia; similar al utilizado para elementos finitos de interfaz.
Agradecimientos
Se agradece a la Dirección General de Asuntos para el Personal Académico de la UNAM el patrocinio del proyecto PAPIIT IN108512, "Simulación numérica del proceso de falla en elementos de concreto reforzado considerando el efecto del calor de hidratación del cemento en los concretos jóvenes".
Referencias
Bazant Z.P. y Planas J. (1998), "Fracture and size effect in concrete and other quasibrittle materials", CRC Press, Boca Raton, FL, EUA. [ Links ]
Hillerborg A., Modeer M. y Petersson P.E. (1976), "Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements", Cement and Concrete Research, Vol. 6, pp. 776—782. [ Links ]
Juárez G. (2006), "Modelado numérico de problemas de fractura en sólidos mediante discontinuidades interiores", Tesis de Doctorado, Universidad Nacional Autónoma de México, México. [ Links ]
Katz A. (1999), "Bond mechanics of FRP rebars to concrete", Materials and Structures, Technical Report, Vol. 32, pp. 761—768. [ Links ]
Kumar S. y Barai S.V. (2011), "Concrete fracture models and applications", Springer—Verlag, Berlín Heidelberg, Alemania. [ Links ]
Kwak H. G. y Filippou F.C (1990) "Finite Element Analysis of Reinforced Concrete Structures Under Monotonic Loads", Structural Engineering Mechanics and Materials Reporte, No. UCB/SEMM-90/14, Department of Civil Engineering University of California, Berkeley, CA, EUA. [ Links ]
Neto P., Alfaiate J. Almeida J.R., y Pires E.B. (2004), "The influence of mode II fracture on concrete strengthened with CFRP", Computer & Structures, Vol. 82, pp. 1495—1502. [ Links ]
Ngo B., y Scordelis C. (1967), "Finite element analysis of reinforced concrete beams", ACI Journal, Vol. 64, Núm. 3, pp. 152—163. [ Links ]
Oliver J., Linero D.L. Huespe A.E. y Manzoli O.L. (2008), 'Two—dimensional modeling of material failure in reinforced concrete by means of a continuum strong discontinuity approach", Computer Methods in Applied Mechanics and Engineering, Vol. 197, pp. 332—348. [ Links ]
Retama V.J. (2010a), "Formulation and approximation to problems in solids by embedded discontinuity models", Tesis de Doctorado, Universidad Nacional Autónoma de México, México. [ Links ]
Retama V.J. y Ayala M.G. (2010b), "Modelado del daño en sólidos mediante formulaciones variacionales de discontinuidades interiores", Revista Internacional de Métodos Numéricos para Cálculo en Ingeniería, Vol. 26, Núm. 3, pp. 171 — 177. [ Links ]
Retama V.J. y Ayala M.G. (2011), "Simulación de la pérdida de rigidez en estructuras de concreto armado, mediante el modelo de discontinuidades interiores", CMNE 2011, Congreso de Métodos Numéricos en Ingeniería, Coimbra, 48 Portugal. [ Links ]
Retama V.J. y Ayala M.G. (2013), "Reinforced concrete modelling using enriched finite elements", CFRAC 2013, The third international conference on computational modelling of fracture and failure of materials and structures, Praga, República Checa. [ Links ]
Zhang C., Jin F. y Xu Y. (2013),"Seismic safety evaluation of concrete dams", Department of Hydraulic Engineering, Tsinghua University, Beijing, China. [ Links ]















