Introducción

El Capítulo IV de Diferencia y repetición -“Síntesis ideal de la diferencia”- contiene el primer y más completo desarrollo del célebre concepto deleuziano de lo virtual -el cual será determinante en prácticamente toda su producción ulterior-. Allí, lo virtual se identifica con la noción de “Idea”, en una singular apropiación de la tradición “platónica, leibniziana y kantiana” (^{Deleuze, 1968: 222}) que busca depurarla de su impronta representativa y pensarla desde la diferencia en sí misma. Para ello, la Idea o lo virtual se presenta como un universal concreto, pre-individual y problemático, que subyace y orienta la producción de los dominios e individuos actuales que pueblan el plano de la ciencia y la experiencia efectivas. La estructura de esa Idea es mapeada, en el comienzo del mencionado Capítulo IV, mediante el cálculo diferencial: “dx es la Idea”, escribe ^{Deleuze (1968: 222)}. Sin embargo, las páginas inmediatamente siguientes a esa presentación se enfrentan al problema de sostener a la vez la centralidad del cálculo para esta propuesta y su independencia relativa con respecto de aquél. ¿En qué sentido el discurso de la filosofía de la diferencia deleuziana queda atado al discurso matemático, hasta qué punto le es necesario, y en qué medida es independiente de él? Esta pregunta anima el presente trabajo.

De hecho, Deleuze afirma la independencia relativa de la Idea respecto a la matemática, poniendo al cálculo diferencial como un momento -entre otros- de un movimiento ontológico más fundamental, caracterizado como una dialéctica ideal (^{Deleuze, 1968: 231-232}). A partir de este movimiento, la estructura de la Idea, tal como fue modulada a partir del cálculo, es extendida hacia otros dominios de lo real (físico, biológico, psíquico, lingüístico, sociológico) (Ver ^{Deleuze, 1968: 238 y ss.}). Pero el desarrollo de esta dialéctica no implica el fin de la injerencia del discurso matemático; lejos de ello, el recurso al cual Deleuze apela para determinarla es la filosofía de la matemática de Albert Lautman (Francia, 1908-1944). Es decir que, al igual que en su singular apropiación de la noción de “Idea”, la recuperación deleuziana de la dialéctica no remite tanto a las fuentes canónicas -Platón, Kant, Hegel- sino a un filósofo relativamente marginal en la tradición del pensamiento matemático. Se trata de un movimiento paradójico, en tanto busca elucidar la naturaleza estructural-genética de la dialéctica ideal apelando a la matemática y a la vez afirmando su exceso respecto a ella.

En efecto, el doble e indisoluble aspecto estructural y genético de la dialéctica lautmaniana, junto con su impronta problemática y su carácter simultáneamente inmanente y trascendente a los dominios de soluciones que ella produce, son algunas notas persistentes en las recurrentes referencias deleuzianas. En lo que sigue, nos proponemos: 1) presentar los lineamientos generales de dialéctica ideal de Lautman; 2) mostrar su aspecto estructural y genético, que Deleuze recupera especialmente, y 3) detenernos en el tratamiento lautmaniano de la teoría de las singularidades de Poincaré (fundamental para comprender la distinción deleuziana entre lo actual y lo virtual, y el carácter de doble del uno con respecto al otro). Finalmente, 4) reflexionaremos acerca del movimiento de extensión de esta dialéctica, desde la filosofía matemática hacia el todo de lo real, que marca la originalidad de la apropiación deleuziana. Buscamos con ello contribuir al debate -actual en los estudios deleuzianos- acerca del lugar y el rol de lo virtual en Deleuze, como así también de sus relaciones con la filosofía de las matemáticas.

1. Lautman y su dialéctica

Junto a Cavaillès, Lautman es uno de los introductores, en Francia, del formalismo alemán, lo que lo convierte en una influencia mayor para el célebre grupo Bourbaki, con varios de cuyos miembros fundadores trabó amistad. En el contexto del debate sobre los fundamentos de las matemáticas que tiñe la primera mitad del siglo XX, Lautman abraza una postura que puede llamarse “formalismo estructuralista” (^{Duffy, 2013: 211-215}), la cual se distancia de las corrientes preponderantes. Rechaza a la vez los planteos logicistas representados por Frege y Rusell (pues Lautman niega la posibilidad de reducir analíticamente la diversidad y riqueza de las matemáticas a un vocabulario lógico); rechaza también los intuicionismos representados por Poincaré y Brouwer (pues afirma la existencia en acto del infinito matemático y de toda entidad matemática formalmente definible por una teoría axiomatizada, y acepta el principio de tercero excluido como válido para la demostración); rechaza, finalmente, los planteos aprioristas de corte neo-kantiano (afirmando que los hechos matemáticos son derivados de las teorías que los hacen posibles, y estas a su vez surgen de problemas dialécticos, y no del análisis de conceptos ni de construcciones en la intuición).

Su lealtad filosófica yace con el formalismo de Hilbert (^{Zalamea, 2010: 26}), quien funda la realidad matemática en la formulación axiomática de las teorías. Ahora bien, Lautman afirma que esta formulación es motivada dinámicamente por la existencia de problemas que obligan permanentemente a reestructurar esas teorías o a crear nuevas, en un movimiento sintético que, veremos, excede la realidad propiamente matemática, y supone una metamatemática de corte metafísico que va más allá de los planteos hilbertianos. A su vez, Lautman recupera al célebre filósofo de las matemáticas francés Léon ^{Brunschvicg (1912)}, siguiendo su tendencia espiritualista, pero rechazando su psicologismo. Lautman conjuga así una visión formalista, estructuralista, sintética, antipsicologista, anti-logicista y anti-reduccionista, con una metafísica que rescata y enarbola estandartes platónicos.

En efecto, en la obra de Lautman “es posible hablar de un platonismo inmanentista, en la medida en que las Ideas no tienen una existencia separada, sino que se descubren en las teorías como su fundamento y origen” (^{Kretschel, 2014: 30}). Un movimiento ontológico original subyace, orienta y regula la producción de diferentes teorías matemáticas: una dialéctica Ideal asociada a una teoría de los problemas. Escribe ^{Deleuze (1968: 212)}: “Nadie mejor que Albert Lautman, en su obra admirable, ha mostrado que los problemas eran ante todo Ideas platónicas, ligazones ideales entre nociones dialécticas, relativas a ‘situaciones eventuales de lo existente’; pero también que ellas se actualizaban en las relaciones reales constitutivas de la solución buscada en un campo matemático, o físico, etc.” La matemática representa para Lautman un sitio de expresión de Ideas de una naturaleza extra- o metamatemática (en ese sentido, trascendentes), pero que solo cobran cuerpo y sentido gracias a dicha expresión en su dominio científico determinado (en ese sentido, inmanentes al mismo). Debe distinguirse entonces entre “Idea”, relativa a la dialéctica problemática, y “teoría”, “noción”, o “concepto”:

Mientras que las relaciones matemáticas describen ciertos enlaces existentes de hecho entre seres matemáticos distintos, las Ideas de relaciones dialécticas no afirman ningún enlace existente de hecho entre nociones cualesquiera. Como “preguntas planteadas”, no constituyen sino una problemática, relativa a ciertas situaciones eventuales de lo existente. Resulta entonces de nuevo, exactamente como en los análisis de Heidegger, que las Ideas que constituyen esa problemática están caracterizadas por una insuficiencia esencial, y en ese esfuerzo por culminar la comprensión de la Idea es donde, una vez más, se ven emerger las nociones más concretas relativas a lo existente, es decir, las verdaderas teorías matemáticas (^{Lautman, 2011: 341}).

Las diversas teorías matemáticas, con sus relaciones y conexiones mutuas, son entonces el producto del esfuerzo intelectual por proveer una comprensión acabada de problemas ideales. Si la tarea de la matemática es encarnar, a través de teorías, relaciones dialécticas relativas a una situación puramente problemática, la tarea de la filosofía de la matemática es reconocer y describir esa realidad problemática que se sobrepasa hacia su encarnación matemática (^{Cfr. Lautman, 1938: 7}). Esta realidad, en tanto “situación eventual de lo existente”, es sin embargo aquello que motoriza la creación de teorías y nociones “relativas a lo existente”; ella no es, entonces, originalmente planteada en los términos de una teoría lógico-deductiva, sino admitida “por una incomprensible necesidad de hecho” (^{Lautman, 1938: 9}).

Incomprensibles desde el punto de vista de la formulación matemática, las Ideas se realizan en ella a partir de “la intuición extra-matemática de la urgencia de un problema lógico” (^{Lautman, 1938: 149}), que solo puede ser formulado matemáticamente, aunque en sí mismo no es matemático. Esa intuición tampoco ha de buscarse en la subjetividad de un matemático particular (Lautman rechaza, contra Brunschvicg, la “psicología de la creatividad científica”), sino que refiere a una instancia objetiva ligada al a los medios de expresión dados por una teoría determinada en un momento puntual del devenir histórico de la matemática efectiva. Las teorías matemáticas existentes son fruto de una materia problemática viva, o mejor, una materia vivificada en la génesis de nuevas soluciones: “más allá de las condiciones temporales de la actividad matemática, pero en el seno mismo de esta actividad, aparecen los contornos de una realidad ideal que es dominatriz en relación a una materia matemática que ella anima, y, sin embargo, sin esta materia no podría revelar toda la riqueza de su poder formador” (^{Lautman, 1938: 150}).

Las Ideas no son entonces susceptibles de un estudio matemático directo, pero no podemos aprehenderlas sino a través de la materia que ellas vivifican y sin la cual no existen realmente (de ahí el platonismo inmanentista). Esa materia no se identifica con lo sensible inmediato, sino con la simbología, las operaciones, las teorías, objetos y diagramas propiamente matemáticos. El problema de la filosofía matemática, como el problema del platonismo clásico, es entonces el problema de la participación: ¿de qué modo las Ideas dialécticas se encarnan en las teorías matemáticas concretas? En su Ensayo sobre las nociones de estructura y existencia en matemáticas (principal obra referida por Deleuze), Lautman recurre al término kantiano “esquema” para referir a este fenómeno de participación de lo ideal en lo material: “creemos que el movimiento propio de una teoría matemática dibuja el esquema de los enlaces que sostienen entre ellas ciertas ideas abstractas, dominantes con respecto a las matemáticas” (2011: 126). A continuación, nos detendremos en el modo en que las teorías matemáticas concretas sirven de “esquema” para esas ligazones ideales abstractas pero dominantes.

2. Esquemas de estructura y esquemas de génesis

En su tesis doctoral, Ensayo sobre las nociones de estructura y existencia en matemática, ^{Lautman (2011)} estudia dos tipos de esquemas, “de estructura” y “de génesis”, a través de un análisis descriptivo que pretende capturar, valiéndose de la exposición de ciertas teorías matemáticas, la naturaleza de estos esquemas que “median” entre la Idea y su expresión en esos dominios matemáticos. Pasaremos revista a algunos de los ejemplos lautmanianos sin entrar en el detalle técnico de las teorías matemáticas -lo que excede los objetivos del presente trabajo- sino centrándonos en su sentido filosófico.

Los esquemas de estructura corresponden al estudio de tensiones dialécticas manifestadas en dualidades del tipo “punto de vista local y punto de vista global”, “propiedades intrínsecas y propiedades inducidas”, “lo imperfecto y lo perfecto”. Lautman pasa revista a diferentes problemas y nociones que dan cuenta de cómo estas dualidades se presentan y en las relaciones entre diferentes teorías, motivando síntesis que dan pie a nuevas teorías y, de ahí, a nuevos modos de presentación de esas tensiones.

De acuerdo a la primera de estas dualidades, el estudio desde un punto de vista local, a partir de algunos elementos de un conjunto o estructura y sus conexiones recíprocas, se contrapone al estudio desde un punto de vista global sobre las propiedades generales de ese conjunto o estructura. Dicha contraposición se presenta a los matemáticos en diversos campos, como dos modos de abordaje en tensión, irreductibles el uno al otro. ^{Lautman (1938: 22-25)} desarrolla el conflicto en geometría entre el punto de vista local, representado por Riemann y el punto de vista global, representado por Klein. Mientras que la geometría de tipo kleiniano estudia globalmente las propiedades de un espacio que atraviesa en su conjunto transformaciones lineales idénticas para todos los puntos, la geometría riemanniana parte de las propiedades locales del espacio mediante el análisis de sus vecindades o entornos infinitesimales, donde la relación de cada punto con cualquier otro que no pertenezca a su vecindad puede hacerse de una infinidad de maneras. Klein define un espacio global homogéneo mientras que Riemann define uno local y heterogéneo. ^{Lautman (2011: 25)} sigue aquí al matemático francés Henri Cartan en la conclusión de que no puede decirse que uno de estos puntos de vista geométricos preceda o sea preponderante sobre el otro; en tanto esquemas de una tensión entre polos dialécticos, ambos reenvían necesariamente uno al otro sin perder su diferencia de naturaleza.

“La constatación de esta dualidad sugiere naturalmente a los matemáticos la búsqueda de una síntesis. […] En uno y otro caso se busca establecer una ligazón entre la estructura del todo y las propiedades de las partes para que se manifieste en las partes la influencia organizativa del todo al cual ellas pertenecen” (^{Lautman, 1938: 28-29}). Esta síntesis de lo local y lo global encuentra su esquema, según ^{Lautman (1938: 30 y ss.)}, en las relaciones de la geometría diferencial con la topología, en la teoría de grupos, y en la teoría de la prolongación analítica de funciones de Weierstrass. Del análisis de estas teorías, ^{Lautman (1938: 38)} extrae elementos para afirmar que “es imposible considerar un ‘todo’ matemático como resultando de la yuxtaposición de elementos definidos independientemente de toda consideración de conjunto relativa a la estructura del todo en el cual estos elementos se integran. Existe así un descenso del todo hacia la parte, y un ascenso de la parte hacia el todo”. La relación de co-implicación entre el todo y las partes se manifiesta entonces en estas teorías como la instanciación de una relación dialéctica (todo-parte) que encuentra ecos en la biología o la sociología, pero que solo podría expresarse de un modo completamente acabado y riguroso desde el punto de vista matemático: “el ser matemático, tal cual lo concebimos, es análogo a un ser viviente; creemos, sin embargo, que la idea de la acción organizativa de una estructura sobre los elementos de un conjunto es plenamente inteligible en matemáticas, aunque al transportarse a otros dominios pierda su limpidez racional” (^{Lautman, 1938: 29}).

Otra tensión dialéctica se manifiesta en la diferencia entre propiedades intrínsecas e inducidas (relativas, respectivamente, ya a la estructura interna o propiedades intrínsecas de un objeto matemático, ya a sus relaciones de exterioridad con otros elementos de un medio exterior, que “inducen” propiedades al objeto en cuestión). Este problema replica el célebre contrapunto entre Kant y Leibniz acerca de la naturaleza del espacio. La pregunta es si puede reducirse el punto de vista euclidiano, que funciona por inmersión de un objeto en un espacio pre-determinado (y que remite a la posición kantiana), al punto del análisis situs (propio de Leibniz) que supone el tratamiento topológico inmanente a la figura. Lautman analiza aquí tres casos de esquemas: el paralelismo de vectores en una superficie de Riemann, las propiedades de los espacios definidos por la topología algebraica, y los teoremas de dualidad en topología (Cfr. ^{Lautman, 1938: 45-60}). Si bien en principio los métodos reductivos desarrollados por la topología parecen ser concluyentes, volviendo aparentemente la estética kantiana reductible a una analítica, lo cierto es que ellos encuentran limitaciones que reenvían a la necesidad de un estudio por “inmersión” de la figura. ^{Lautman (1938: 60)} ve estas limitaciones ilustradas en los análisis de Louis Antoine sobre homeomorfismos en curvas cerradas en espacios euclidianos: “Ocurre en esto como si la topología no pudiera desarrollarse sino dando la razón a Leibniz, pero constantemente ella encuentra hechos que dan la razón a Kant y la obligan a buscar nuevos métodos”.

Los esquemas de estructura suponen entonces una tensión dialéctica como problemática que motoriza la producción de nuevas teorías. Ellas no anulan el problema, sino que lo traducen, lo desplazan, lo reformulan según nuevos términos en los cuales la misma (u otra) tensión dialéctica se presentará de otro modo, en otros términos u objetos, definibles por la nueva teoría. Para resolver las problemáticas planteadas por Ideas dialécticas, las teorías matemáticas sientan las condiciones para la creación de nuevos seres matemáticos, los cuales presentan a su vez desequilibrios estructurales que conducen a nuevas creaciones. De acuerdo con esto, los esquemas de estructura están ligados indisolublemente a esquemas de génesis, por los cuales se pasa necesariamente de la indagación de un dominio o teoría dados a la existencia de nuevos seres u objetos matemáticos (funciones, transformaciones, tipos numéricos) que pueden considerarse como preformados en la estructura del dominio o teoría (Cfr. ^{Lautman, 2011: 128}).

Así, la dialéctica motiva una serie indefinida de producciones de seres matemáticos cualitativamente diferentes, pero mutuamente enlazados por problemas:

[L]os seres abstractos que nacen de la estructura de un dominio más concreto pueden servir a su vez como dominio de base para la génesis de otros seres. Por lo tanto, es sólo en el seno de un problema determinado que pueden asignarse funciones distintas a géneros de seres diferentes; el hecho esencial es la génesis de los géneros del ser, unos a partir de otros, y es en un sentido puramente relativo (para dar cuenta de esas relaciones mutuas) que emplearemos siempre el término de “dominio” para la estructura dada y aquel de “ser creado” para el objeto final de la génesis descrita (^{Lautman, 1938: 94}).

Esta ligazón indisoluble entre estructura y génesis, dada en la producción y división de dominios y objetos teóricos motivada por problemas dialécticos, será fundamental para Deleuze. Se trata de un movimiento que puede asociarse, en Diferencia y repetición, al modo en que la Idea, en tanto relación diferencial, designa un medio problemático de determinación recíproca que motiva la génesis, desde una función de partida (primitiva), de nuevas funciones (derivadas) cualitativamente distintas, funcionando como elemento puro de la cualitabilidad, que abre una red indefinida de tipo: Idea de la Idea… (ver ^{Deleuze, 1968: 224}; ^{Santaya, 2017: 175-193}).

Hasta aquí hemos seguido algunas de las tesis de Lautman para presentar una caracterización acerca de esos problemas, y el modo en que ellos se encarnan en teorías. Analizamos separadamente a continuación un caso de esquema de génesis, dada su fundamental relevancia en la teoría deleuziana de lo virtual.

3. La doble naturaleza de las singularidades

En el último capítulo de su tesis, ^{Lautman (1938: 125)} aborda un ejemplo de esquemas de génesis ligado al “carácter excepcional de la existencia”. Con esto se refiere no ya al pasaje de un dominio estructural a la existencia de otro dominio -ya por realización, ya por descomposición-, sino a “un nuevo modo de ligazón entre la estructura y la existencia, donde el ser buscado resulta de la selección, en el seno de un dominio, de un elemento distinguido de todos los otros por sus características excepcionales”. Esto ocurre por ejemplo en el cálculo de variaciones, que tiene por objeto la determinación de máximos y mínimos para una relación dada. Esas cantidades máximas y mínimas juegan el papel de elementos destacados dentro del dominio de los elementos que efectúan dicha relación. En esta determinación de existencia de un ser matemático por sus condiciones de extremo se realiza, según Lautman, un nuevo esquema lógico de las relaciones entre esencia y existencia: la “esencia” de la relación determina la existencia de un (y solo un) elemento de su dominio cuyo valor es el mínimo (o máximo) posible. Este es solo un ejemplo de los esquemas de selección que operan en el seno de estructuras diversas, de las cuales Lautman presenta una serie de ejemplos relativos a los espacios de Hilbert y a las singularidades de Poincaré. Son estos últimos los que nos interesan a continuación, pues Deleuze los recupera explícitamente.

^{Lautman (1938: 130 y ss.)} recurre a un artículo de ^{Poincaré (1881)} que sostiene la importancia del punto de vista cualitativo como estudio topológico de las curvas basado en la clasificación que permiten establecer ciertos tipos de singularidades (cuellos, nudos, focos y centros). Hay un interés especial de Lautman por estos puntos, pues en ellos convergen muchos de los elementos analizados previamente:

Los puntos singulares, en tanto que puntos, pertenecen al dominio de base como todos los otros puntos de este dominio, pero ellos tienen un rol cada vez más dominante y excepcional en las teorías modernas; […] en ellos vienen a confundirse un gran número de perspectivas lógicas que hemos caracterizado separadamente en el curso de este trabajo (^{Lautman, 1938: 135}).

Deleuze recuperará de este fragmento la idea del doble modo de existencia de los puntos singulares. Ellos forman parte del domino de base (en el caso de una ecuación diferencial, este dominio corresponde al rango de valores recorridos por las variables) y en ese sentido no se destacan (son un valor entre otros); ahora bien, en virtud de los requisitos de una ecuación específica, la determinación local de dichos puntos puede volverse relevante para estudiar la estructura global de su representación geométrica. ^{Lautman (1938: 136-138)} complementa aquí el tratamiento de las singularidades de Poincaré con la teoría de la prolongación analítica de Weierstrass, para mostrar cómo ambos puntos de vista locales se dirigen a la determinación global de un espacio (sobre la complementariedad Poincaré-Weierstrass en la interpretación deleuziana de los puntos singulares ver ^{Duffy, 2013: 39-44}).

Este movimiento reenvía así del esquema de génesis por selección al esquema de estructura local-global, que fue la primera de las manifestaciones dialécticas abordadas por Lautman. La importancia de la teoría de los puntos singulares proviene de que permite enlazar los distintos niveles de lo real matemático: los hechos matemáticos, los seres definidos a partir de estos hechos, las teorías matemáticas en las cuales se organizan estos seres, las Ideas dialécticas que estas teorías encarnan mediante diversos esquemas. En efecto, los puntos singulares:

1° permiten la determinación de un sistema fundamental de soluciones, prolongables analíticamente a lo largo de todo camino que no encuentre singularidades […]; 2° […] su rol es descomponer un dominio, de manera que la función que asegura la representación sea definible sobre este dominio; 3° permiten el pasaje de la integración local de las ecuaciones diferenciales a la caracterización global de las funciones analíticas que son soluciones de estas ecuaciones. […] Este encuentro de puntos de vista lógicos distintos en el seno de un mismo problema […] [muestra] la unión íntima y la independencia completa de la lógica dialéctica […] y de las matemáticas. Las teorías matemáticas se desarrollan por su propia fuerza, en una estrecha solidaridad recíproca y sin referencia alguna a las Ideas que su movimiento aproxima (^{Lautman, 1938: 138-139}; las cursivas son mías).

Estas conclusiones hacen resonar esa “doble existencia” de los puntos singulares, que mencionábamos unas líneas más arriba, con el carácter doble que las Ideas dialécticas poseen para Deleuze: inmanentes y trascendentes, la paradójica relación de “unión íntima e independencia completa”, o de “estrecha solidaridad recíproca” y ausencia de referencia, que el filósofo de las matemáticas menciona entre Idea dialéctica y teoría matemática. Este será un punto central de lo virtual deleuziano.

En su póstumo El problema del tiempo, ^{Lautman (1946: 41 y ss.)} vuelve sobre este análisis de Poincaré a partir de la noción de campo vectorial, relativa a la existencia y distribución de singularidades para una función que describe un determinado espacio y las transformaciones posibles del conjunto de sus puntos. En las ecuaciones diferenciales trabajadas por Poincaré, compuestas de polinomios Q y P bajo la forma, las variables x e y son diferenciadas en función de un nuevo parámetro t, obteniendo el sistema:

Este sistema define no solo una dirección (tangente) para cada punto de la curva, sino también un sentido, con lo cual se constituye un campo de vectores (en el sentido más intuitivo posible, esto significa que lo que se asigna a cada punto de la curva no es una mera recta, sino una flecha). La información que proveen estas derivadas se complejiza (un vector, al asignar un sentido a una línea, añade un rasgo a la mera dirección o ángulo de dicha línea). El campo de vectores indica la dirección y el sentido seguido por cada punto del espacio en una transformación lineal definida por el sistema de ecuaciones. Al respecto, Lautman señala:

Los puntos de indeterminación donde P = Q = 0 constituyen las singularidades del campo de vectores. […] La existencia y la repartición de singularidades son nociones relativas al campo de vectores definido por la ecuación diferencial; la forma de las curvas integrales es relativa a las soluciones de esta ecuación. Los dos problemas son complementarios porque la naturaleza de las singularidades del campo es definida por la naturaleza de las curvas en su vecindad; no es menos cierto que el campo de vectores, por un lado, las curvas integrales por el otro, son realidades matemáticas esencialmente distintas (^{Lautman, 1946: 42}).

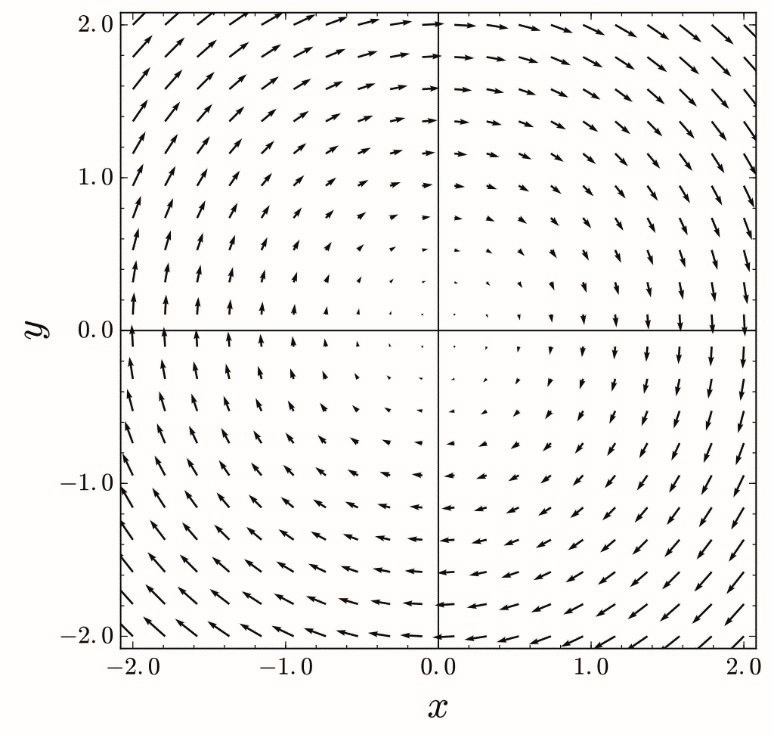
Imagen de Eviatar Bach, compartida bajo licencia CC 4.0, disponible en: https://commons.wikimedia.org/w/index.php?curid=69406827; último acceso: 19 de agosto de 2020.

Figura 1: diagrama de un campo vectorial con una singularidad tipo “centro” en el punto (0, 0). 

Nuevamente, esto muestra la existencia paradójica, doble, de las singularidades que pueblan un espacio matemático y en torno a las cuales algo pasa en el comportamiento del mismo: las direcciones y sentidos de los vectores que configuran dicho espacio adquieren un comportamiento ordenado, una tendencia. Este comportamiento del espacio matemático estructurado en torno de los puntos singulares es lo que les da su carácter de elementos excepcionales del dominio, por el cual a la vez existen en él e insisten más allá de él, estructurándolo en su conjunto.

¿Qué significa este doble carácter de “inmanencia y trascendencia” en la teoría de la Idea? La pregunta es relevante sobre todo considerando que la apuesta ontológica deleuziana en su conjunto es por una filosofía de la inmanencia. El término “trascendencia” nos acercaría a una concepción trascendente de la Idea, si nos precipitamos en leer en este término la reivindicación de un platonismo ingenuo. Sin embargo, como vimos, la filosofía de la matemática de Lautman defendía un platonismo caracterizado como “inmanentista”, dado que era solo en el seno de las teorías matemáticas efectivamente existentes que las Ideas cobran consistencia y realidad. En ese sentido, las Ideas no gozan de una realidad separada con respecto a algo que las manifiesta inadecuadamente en otro plano de la existencia; no se trata de la “participación” de una “copia” en un “modelo”, sino de una expresión -en términos de ^{Deleuze (1968: 334)}- donde “lo expresado no existe por fuera del expresante”. Las teorías matemáticas solo se determinan en la medida en que expresan Ideas, a través de los esquemas lógicos determinados por ellas en tanto problemas dialécticos, que solicitan la creación de teorías siempre nuevas. La relación que Lautman afirma una y otra vez entre las Ideas y sus encarnaciones es ante todo de “dominación”, entendida como generación y organización.

Deleuze no retoma el término “dominación” para la actividad de las Ideas, pero habla del “rol director” de los problemas con respecto a “la determinación de las soluciones mismas” (1968: 230). Este rol director es el que constituye el aspecto de trascendencia de las Ideas, y es caracterizado como la existencia y repartición de puntos singulares. El aspecto de inmanencia, por su parte, es definido por la especificación de esas singularidades, su cualificación, dada por el comportamiento de los puntos regulares en su vecindad. No se trata, entonces, de una Idea trascendente “en sí misma”, absolutamente separada e independiente, sino simultáneamente trascendente e inmanente con respecto a su solución, determinada por las singularidades de la Idea que ella expresa. Trascendente, porque ninguna teoría ni ser matemático agotan la potencia problemática de la Idea que encarnan, y hay siempre un exceso por el cual ella supera su expresión teórica.¹ Inmanente, porque es solo en teorías efectivamente existentes que la Idea se especifica, se encarna, en resumen: existe, en tanto expresado que solo existe en y por su expresión, que a su vez determina.

La Idea, entonces, dirige u organiza desde adentro la génesis de un dominio de soluciones a la vez que lo abre a su afuera, desde el cual motoriza la génesis de nuevos dominios.² Ambos aspectos son relativos, complementarios, pero heterogéneos. La especificación hace a la singularidad inmanente al trazado de las curvas correspondientes a una ecuación, mientras que la existencia y distribución de singularidades las hace trascendentes con respecto a la curva. En resumen, el carácter estructural-genético de la Idea va de la mano con su carácter inmanente-trascendente, y este estrecho vínculo encuentra su máxima expresión en la teoría de los puntos singulares.

4. Deleuze y la extensión de la dialéctica lautmaniana

Volviendo a nuestro tema inicial, la introducción de Lautman en el Capítulo IV de Diferencia y repetición es entonces fundamental, porque es a través de su dialéctica ideal que puede determinarse en su dimensión metafísica el carácter sub-representativo, extraproposicional y metamatemático del cálculo diferencial, en tanto herramienta matemática que describe el régimen de lo virtual-problemático. Ahora bien, lo virtual es presentado allí como principio estructural-genético e inmanente-trascendente de la realidad efectiva, no solo de la matemática. En efecto, Deleuze pretende realizar una extensión de la dialéctica de Lautman a todos los dominios de lo real.³

Las distintas teorías matemáticas mencionadas aquí, en consecuencia, son tan solo un momento de esa dialéctica, momento relativo a un cierto estadio de desarrollo de un cierto campo disciplinar que goza de realidad en la medida en que encarna esa dialéctica. Por dialéctica se entiende, precisamente, “el elemento de lo problemático, en la medida en que se distingue del elemento propiamente matemático de las soluciones” (^{Deleuze, 1968: 231}). Así como las singularidades, en tanto puntos del dominio de base, gozaban a su vez de una realidad que sobrepasaba la expresión matemática de las curvas que ellas modulaban, todas las teorías matemáticas poseen elementos o significaciones que sobrepasan su expresión, y que son el índice de problemas no ya matemáticos, sino dialécticos. Más allá de la matemática, la extensión deleuziana de esta dialéctica apunta a señalar la realidad de lo problemático como instancia ontológica que subyace a toda la realidad efectiva, habiendo singularidades físicas, lingüísticas, psíquicas, sociales, etc., en aquellos puntos, instantes, o momentos inherentes a esos distintos tipos de sistemas, puntos en sí mismos inasignables o no localizables por fuera de la estructuración y metamorfosis que introducen en los estados de cosas definidos por dichos sistemas.⁴

Así como las ecuaciones diferenciales, en tanto herramienta estrictamente matemática, sirven de mecanismo de extracción y determinación de singularidades en un campo vectorial, hay un “cálculo diferencial” para cada campo problemático manifestándose en la realidad efectiva (y a la inversa, toda manifestación realefectiva es la expresión de un problema virtual y sub-representativo). La extensión deleuziana de la dialéctica generaliza para todo dominio científico o discursivo (y en el límite, para todo aquello que pueda caer como objeto de la representación), el proceso de lo indeterminado-determinable-determinación, la estructura de la Idea (^{Santaya, 2017}). Esta extensión debe asignar a cada dominio sus propios elementos diferenciales, sus propias relaciones diferenciales o ligazones dialécticas, sus propias singularidades. Esto no implica una matematización del ser, una reducción de los fenómenos y las ciencias al análisis matemático; implica, por el contrario, la captación de elementos irreductibles pertenecientes a cada dominio específico, y cuyo comportamiento permite descubrir la doble naturaleza de los elementos que componen los problemas relativos a un campo en las soluciones que dicho campo -estructurado u organizado según las condiciones del problema- revela.

No son solo las matemáticas las que, en sus distintas teorías, encarnan problemas dialécticos de una realidad metamatemática, sino que todo campo discursivo o proposicional es dirigido u organizado por problemas extra-proposicionales. En ese sentido, se hace preciso, en el desarrollo del Capítulo IV de Diferencia y repetición, hablar no ya de la Idea sino de las Ideas. La modulación de la teoría de las Ideas mediante las herramientas matemáticas del cálculo y la dialéctica metamatemática de Lautman conduce a afirmar la necesaria coexistencia de distintos órdenes ideales o dialécticos, diferentes órdenes problemáticos.

Los problemas son siempre dialécticos, la dialéctica no tiene otro sentido, los problemas tampoco tienen otro sentido. Lo que es matemático (o físico, o biológico, o psíquico, o sociológico) son las soluciones. Pero es cierto, por un lado, que la naturaleza de las soluciones envía a órdenes dialécticos diferentes de problemas en la dialéctica misma; y por otro lado, que los problemas, en virtud de su inmanencia no menos esencial que la trascendencia, se expresan ellos mismos técnicamente en el dominio de soluciones que ellos engendran en función de su orden dialéctico. Como la recta y el círculo son duplicados por la regla y el compás, cada problema dialéctico es duplicado por un campo simbólico en el que se expresa (^{Deleuze, 1968: 232}).

Este pasaje tiene un alcance importante con respecto a la teoría de lo virtual. Por un lado, permite entender en qué sentido la Idea se “fragmenta”, en el curso del Capítulo IV, en una teoría de las Ideas, por la cual vemos aparecer una lista abierta de órdenes de Ideas (biológica, lingüística, psíquica, social, etc.), cada una de las cuales es actualizada en los diversos sistemas que, en Diferencia y repetición, ^Deleuze asocia al concepto de simulacros (1968: 165 y ss.). Por otro lado, muestra cómo el carácter de duplicación, de doble, que lo virtual posee con respecto a lo actual, está asociado al concepto fundamental de expresión. Los diferentes órdenes ideales son dominios técnicos, cualitativamente diferentes, en los cuales distintos problemas hallan modos de resolución. La separación de Ideas solo tiene sentido de acuerdo con el carácter de inmanencia de un problema, por el cual este se especifica expresándose en dominios cualitativamente diversos que lo “resuelven” de diversos modos. Desde el punto de vista de la trascendencia del problema, estas diversas Ideas son en realidad soluciones -campos científicos o dominios discursivos- solo en cuyo seno los problemas existen y, sobre todo, “insisten y persisten”.

Palabras finales: una mathesis supra-matemática

Escribe ^{Deleuze (1968: 235}): “A la universalidad de la dialéctica corresponde en este sentido una mathesis universalis. Si la Idea es la diferencial del pensamiento, hay un cálculo diferencial correspondiente a cada Idea, alfabeto de lo que significa pensar.”⁵ Si bien no son las matemáticas las que se aplican o extienden a otros ámbitos, sino la dialéctica la que se expresa en esos ámbitos asignando a cada uno un “cálculo” propio, lo cierto es que el lenguaje matemático es preponderante en la descripción de lo virtual -más allá de la intervención de Lautman, el capítulo IV de Diferencia y repetición continúa en una ulterior determinación del plano virtual a través de nociones tomadas del álgebra de Abel y Galois y la geometría de Riemann (Ver ^{Deleuze, 1968: 233 y 236})-. La matemática, de la mano de la dialéctica, conduce a una mathesis universalis, cuando vamos más allá de la actividad de resolución de problemas para concentrarnos en la naturaleza de los problemas mismos.

Sin duda, para Deleuze, el modo en que las teorías matemáticas encarnan sus problemas dialécticos provee un ejemplo privilegiado para acceder a esa universalidad de la dialéctica. Volvemos entonces a nuestra pregunta del comienzo: ¿sostiene esta filosofía un privilegio de las matemáticas a la hora de elaborar su esquema de inteligibilidad de lo real? Y, ¿en qué sentido? La dialéctica no es en última instancia matemática, sino que la matemática “surge con los campos de solución en los cuales se encarnan las Ideas dialécticas de último orden, y con la expresión de los problemas relativa a esos campos” (^{Deleuze, 1968: 235}). Los problemas virtuales existen como dobles de las instancias actuales que los encarnan, abriéndolos a nuevos problemas y consecuentemente a nuevas actualizaciones posibles. Si la diferenciación entre órdenes dialécticos remitía, como vimos, a la expresión de los problemas en las soluciones que ellos engendraban, en las matemáticas esta expresión alcanza una suerte de límite: ellas encarnan, según el pasaje que venimos de citar, “Ideas de último orden”. Siguiendo esta enigmática afirmación, no habría ningún dominio de racionalidad que vaya más allá en la expresión de Ideas dialécticas.

Este privilegio que Deleuze otorga a las matemáticas para expresar la ontología tiene que ver no con una naturaleza ontológica que resida únicamente en las matemáticas (pues la dialéctica se expresa por igual en todos los dominios, los duplica por igual a todos), sino por el modo en que la matemática expresa esa naturaleza. Como señala ^{Duffy (2013: 214)}: “La matemática es peculiar porque todos sus objetos son de hecho construidos por el discurso mismo”. Existe, en este sentido, una interesante resonancia con el modo en que , un año después de la aparición de Diferencia y repetición, caracteriza el lugar singular de las matemáticas en La arqueología del saber, y que permitiría echar luz sobre este “privilegio” matemático. En relación a los sucesivos umbrales que el punto de vista arqueológico permitiría distinguir en la constitución histórica de un discurso científico, la matemática ocupa un lugar, por así decir, extra-histórico, porque franquea de un solo golpe todos los umbrales a la vez: “Hay una ciencia para la que no pueden distinguirse estos diferentes umbrales ni describirse entre ellos un tal conjunto de desajustes: las matemáticas, única práctica discursiva que ha franqueado de una vez el umbral de la positividad, de la epistemologización, de la cientificidad y de la formalización” (^{Foucault, 2016: 255}). Así, por el mismo motivo, las matemáticas escaparían al punto de vista historicista que sigue el arqueólogo, pero servirían a la vez como modelo excepcional al dialéctico que explora las condiciones de esa supra-historicidad propia de los problemas virtuales. Ni Deleuze ni Foucault, sin embargo, desarrollan ulteriormente esta intuición epistemológica a partir de un estudio pormenorizado de las matemáticas, cuyo despliegue efectivo puede encontrarse realizado ejemplarmente en la obra de Lautman.

En definitiva, al igual que los problemas dialécticos, según Lautman, habitan y fuerzan la transformación de una enunciación o dominio matemático concreto, lo virtual deleuziano aparecerá como ámbito puramente potencial que simultáneamente habita y rodea una situación u objeto actual, “como neblina” (^{Deleuze y Parnet, 1996: 179}) o como doble.⁶ Esta dimensión de lo real será su causa inmanente de auto-despliegue y auto-diferenciación, guiada en cada caso por las singularidades variables que, emitidas en el plano virtual, componen los diferentes procesos de individuación y comprometen todas sus composiciones, transformaciones y disoluciones, poniendo en movimiento una ontología de las multiplicidades. La doble naturaleza, inmanente y trascendente, de las singularidades virtuales, conduce a esa dialéctica del adentro y el afuera, la lógica del pliegue que signará toda la topología del pensamiento deleuziano. “El afuera no es un límite fijo, sino una materia moviente animada por movimientos peristálticos, pliegues y arrugas que constituyen un adentro: no otra cosa que el afuera, sino exactamente el adentro del afuera” (^{Deleuze, 1986: 103}). Esta potencialidad o virtualidad del Ser, que anima una dinámica incesante de interiorización nunca acabada y fuga siempre retomada, fuente genética de todo ente actual, se da incluso (como Lautman demuestra) en la pureza escritural de la más abstracta de las ciencias.