Technique based on PA

^{Pandey and Ramasastri (2001}; ²⁰⁰²) established that when a PA is less than 75% of the annual average (PMA) in one year, an SM has occurred. The number of droughts (NS) per year, that is, the times when PA is less than 0.75 per PMA, divided by the size (n) of the series or sample of PA and expressed as a percentage, is actually its probability of occurrence (% O), since it meets the basic definition of probability: quotient between the number of cases favorable to the number of possible cases. These authors prefer to use the reciprocal (n/NS) and designate it average return period (PRP) in years of the SM. The drought severity indicator is its average intensity (IM), defined as the average relative deficit, whose expression is ((^{Ponce et al., 2000}; ^{Pandey & Ramasastri, 2001}; ^{Pandey & Ramasastri, 2002}):

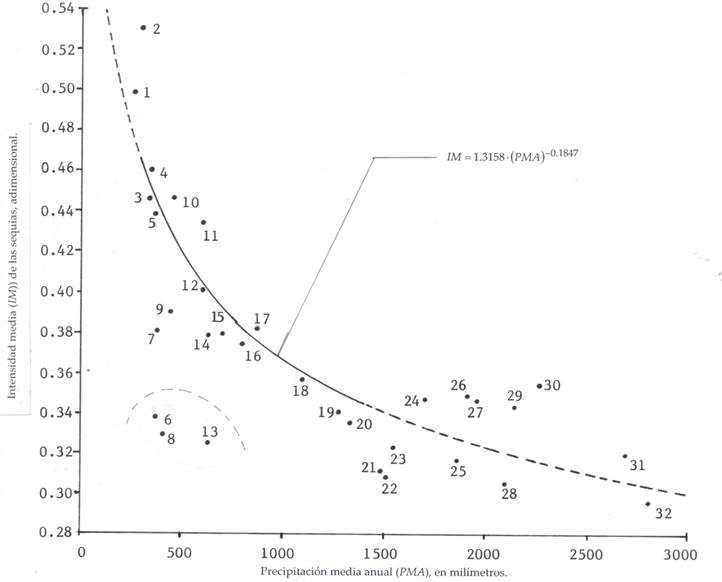
A graph with PMA on the abscissa and the IM in the ordinates usually shows an exponential decline or a hyperbolic curve. This graph constructed for a certain geographical region, allows the estimation in any locality of such area, of its IM of SMs, with only having the value of its PMA.

^{Campos-Aranda (2018c)} processed 32 PA records of the state of San Luis Potosí, Mexico, with amplitudes ranging from 45 to 65 data and defined the graph shown in Figure 1. This method is the simplest procedure for characterizing the annual SMs.

Figure 1 Evolution of the IM of the SM with the PMA, in 32 rain-gauge stations of the state of San Luis Potosí, Mexico. 

Pedj Drought Index (ISP)

^{Elagib and Elhag (2011)} indicate that the annual variability of the PA record or series can be detected and analyzed by means of its standardized anomaly index (IAE), defined by the following two expressions:

being PA the annual precipitation in millimeters, PMA its average value and DEP its standard deviation not biased, with n equal to the number of years of the record processed:

IAE of the annual average temperature (TM) series is calculated with two similar equations. D. A. Pedj proposed in Russia in 1975 an index to detect annual droughts that is defined by the difference between the IAE of the average temperature minus that of precipitation. The Pedj Drought Index (ISP) whose annual value classifies the climate as wet (ISP<0) or drought (ISP>0), was verified empirically, finding that it has a negative correlation with the anomaly of precipitation and varies directly with the anomaly of the average temperature, but the most important thing is that it captures both directions or trends. The annual slight, moderate, severe and extreme SMs are held as the ISP varies between 0 and 1, 1 and 2, 2 and 3 and more than 3, respectively (^{Elagib & Elhag, 2011}).

^{Campos-Aranda (2018a)} applied the ISP in the state of Zacatecas, Mexico, integrating 16 annual series with 65 values in the common period of 1950-2014; based on their statistical analysis, he establishes the local and regional behavior of the annual SMs. He concludes that the ISP is a simple and accurate technique to characterize the annual SMs; which incorporates at the average temperature.

Aridity Index (IA)

The United Nations Environmental Programme (UNEP) proposed at the beginning of the 1990s the PMA/ETP ratio to characterize the desert areas and called it the Dryness Index. Starting from this century, such quotient is called the Aridity Index (IA) and it defines the arid climates when IA varies between 0.200 and 0.050 and when the hyper-arid climates with IA is less than 0.050 (^{Elagib, 2009}). The annual aridity index (IA = PA/ETP) has been used in studies of SM, due to the fact that it is conceptually correct to relate the supply and demand of the atmosphere. Due to its simplicity of calculation the IA has been used in regional studies and large territories (^{Elagib, 2009}). Commonly, ETP estimation is made by means of empirical methods, such as those of Thornthwaite and Hargreaves-Samani, which use air temperature data (^{Vangelis, Tigkas, & Tsakiris, 2013}; ^{Campos-Aranda, 2016}; ^{Campos-Aranda, 2018b}; ^{Campos-Aranda, 2018d}).

The chronological series of annual values of IA is ordered from highest to lowest, keeping the respective year and obtaining the median to define, with the values lower than it, the years with drought. Then, such data are used to assign percentages of types of SM (slight, moderate, severe and extreme) and find their respective years.

^{Campos-Aranda (2016)} describes the statistical analyses made based on the IA in 16 rain-gauge stations of the state of Zacatecas, Mexico, in a common period of 65 years, to monitor the annual SM, in a timely and regional manner. IA represented a conceptual breakthrough when incorporating ETP; however, it has been replaced by the RDI_st of the following subsection, which is applied in monthly periods.

Reconnaissance Drought Index (RDI)

^{Tsakiris and Vangelis (2005)} present a generalization of the IA in the following two aspects: (1) it is applied in k periods of months and (2) is standardized. This led to a new ratio called RDI. Its calculation starts by evaluating the quotient (a _i ) between the accumulated monthly precipitation and the respective potential evapotranspiration (ETP), in the k months considered as duration of the SM of each year i of the processed record. ^{Tsakiris and Vangelis (2005)}, and ^{Tsakiris, Tigkas, Vangelis and Pangalou (2007)} find that the values of a _i follow a Log-Normal distribution and then the Standardized RDI values are obtained with the following equation:

in which, y _i is the natural logarithm of a _i , y- and S _y are the arithmetic mean and the standard deviation of y _i . The positive values of the RDI_st indicate wet years and the negative annual SMs, with the following severity: slight up to -1.00, moderate ranging from -1.00 to -1.50, severe ranging from -1.50 to -2.00 and finally, extreme lower than -2.00. ^{Vangelis et al. (2013)} find that the empirical method of estimating ETP has no influence on the results of the RDI_st.

^{Campos-Aranda (2018a)} contrasts the RDI_st index with the ISP, in 16 rain-gauge stations in the state of Zacatecas, Mexico. The contrast was based on the percentages of each type of droughts and its total number. He suggests the systematic application of both indexes, to improve the estimation of the drought chronological series, oriented the latter to his forecast (^{Mishra & Singh, 2011}).

Palmer Drought Severity Index (PDSI)

Proposed in the mid-sixties (^{Palmer, 1965}), the Palmer PDSI makes a monthly balance of precipitation and ETP in the soil that considers it composed of two layers; whereby it is perhaps the first multivariate index (^{Hao & Singh, 2015}). The PDSI has been criticized for not having a simple calculation, applying several empirical rules, not allowing to consider the duration in months of the SM and not being sufficiently sensitive to the changes induced in precipitation and temperature, when attempting to characterize future SMs according to the likely climate change of a locality or region ((^{Alley, 1984}; ^{Karl, 1986}; ^{Wells, Goddard, & Hayes, 2004}; ^{Ma et al., 2014}).

China-Z Index (IZC)

IZC was introduced by the National Meteorological Center of China in the early 1990s, it assumes that monthly precipitation comes from a Pearson type III distribution and therefore uses the Wilson-Hilferty approach (^{Zelen & Severo, 1972}) to relate to the statistical Z-Index (IEZ) with this index, according to the following expression (^{Wu, Hayes, Weiss, & Hu, 2001}; ^{Morid, Smakhtin, & Moghaddasi, 2006}; ^{Dogan, Berktay, & Singh, 2012}):

being Cs _k the coefficient of asymmetry, whose equation is:

in which x _k,j is the precipitation of the mobile sequence j and of a duration k, in months. The mean and standard deviation of Equation 6 are:

The IEZ comes from the variable Normal standardized (Z) and is defined as:

Defined the duration of the SM in months (k) which can be 1, 3, 6, 9, 12, 18, 24, 30, 36, 48, 60 and 72, we start by obtaining all the possible sequences of such duration in the record, which are obtained as mobile sums. For example, for a seasonal drought with k = 4 the first sequence will be the sum of the month one to the fourth, the second sequence will be the sum of the month two to the fifth and so on. The number of sequences or data (NS) to process will be:

being NA the number of years of the complete record available (NA > 30), which usually starts in January and ends in December.

^{Campos-Aranda (2017)} contrasts the results of the China-Z index (IZC) and the standardized precipitation index (SPI), in three dissimilar climatic locations in the state of San Luis Potosí, Mexico; he finds that their values are quite similar and it can be said that the first is a numerical simplification of the second. IZC is simpler to apply, but sometimes its calculation fails, when IEZ is negative and the Cs large, the parenthesis of the Equation 5 turns out negative.

Standardized Precipitation Index (SPI)

This index called SPI based on a probabilistic approach of monthly precipitation proposed by ^{McKee, Doesken and Kleist (1993)} has shown an efficient use of the available information; its main criticism lies in using only such data, ignoring other indicators of drought, such as temperature and ETP.

Calculated the mobile sums of duration k, the Mixed Gamma probability distribution function of two parameters is fitted to the series of NS (Equation 10) calculated, since such sample may contain zeros. ^{Guttman (1999)} proposes to use the Pearson type III distribution. ^{Stagge, Tallaksen, Gudmundsson, Van Loon and Stahl (2015)} ratify the use of the Mixed Gamma distribution. Then, a rational numerical approximation is used to convert the estimated cumulative probability with Mixed Gamma distribution, in the standardized Normal variable Z of zero mean and unit variance, which defines the SPI index. Definition of slight, moderate, severe and extreme SMs is made based on the numerical values cited for the RDI_st; as in the IZC exposed and in the following SPEI and SPDI indices.

^{Cacciamani, Morgillo, Marchesi and Pavan (2007)}, and ^{Campos-Aranda (2017)} have exposed the mathematical formulation necessary for the calculation of the SPI. In contrast, ^{Wu, Hayes, Wilhite and Svoboda (2005)}, and ^{Wu, Svoboda, Hayes, Wilhite and Wen (2007)} discussed with two important aspects of the SPI application: the amplitude of the record and its use in arid climates. ^{Cheval (2015)} has presented a thorough evolution of the SPI in its theoretical, practical and perspectives aspects. ^{Campos-Aranda (2017)} presents the evolution graph of the SPI, with duration of 6, 12 and 24 months, in the rain-gauge stations Villa de Arriaga, Rio Verde and Xilitla of the state of San Luis Potosí, Mexico, of dissimilar climates.

SPEI Index

The current trend seeks the characterization of SM through indexes based on multiple variables (^{Hao & Singh, 2015}), whose main approaches of construction of these new multivariate indices are the use of soil moisture balance and the hidden variables. A hidden or latent variable is formed with a difference or quotient of variables that have great physical significance in the SMs; for example, precipitation and ETP and thus the RDI was proposed with the quotient of such variables and the SPEI (Standardized Precipitation Evapotranspiration Index) with its difference, which implies a condition of deficit or excess of water (^{Vicente-Serrano et al., 2010}).

The SPEI is similar to SPI calculation and also sensitive to the alterations induced in the historical records of precipitation and temperature, according to the expectations presented by the climate change in such an area or region, for the study of future SMs. Like the SPI, the evolution graphs of their calculated values for certain duration (k), allow the exact definition of the beginning and end of the periods of drought and the date of occurrence of their extreme values, when using Equation 10. Figure 2 shows the evolution chart of the SPEI, at the Fresnillo rain-gauge station in the state of Zacatecas, Mexico, whose record covers 66 years in the span of 1949 to 2014; therefore, when k = 12 months the number of sequences processed is 781.

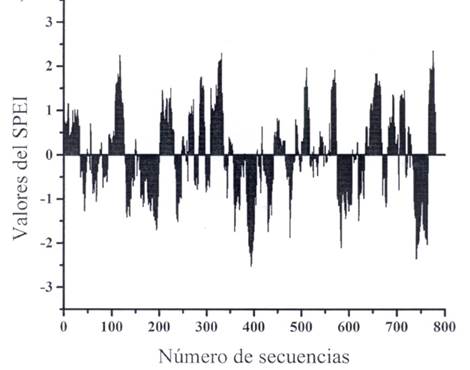
Figure 2 Evolution of the SPEI of 12-month duration at the Fresnillo rain-gauge station, Zacatecas, Mexico. 

The fundamental change of the SPEI with the SPI is to use as starting data the differences (d) of the precipitation minus the ETP, both accumulated in one or several consecutive months. Since most of these differences are negative, many mobile sums (Equation 10) less than zero are obtained and then the distribution of probabilities that must be fitted to the formed sequences must be of three fitting parameters, with the location (u) lower than the minimum sequence (^{Beguería, Vicente-Serrano, Reig, & Latorre, 2014}; ^{Stagge et al., 2015}).

^{Campos-Aranda (2018c)} details the operating procedure of the SPEI and applies it to the Zacatecas rain-gauge station, Mexico, with 86 years of registration in the period from 1930 to 2015. Based on the SPEI it estimates the historical and future droughts, according to probable climate change (see Appendix), with nine durations ranging from 3 to 48 months. The SPEI is a drought index with greater potential than the SPI, by using a more realistic measure of water availability, the difference between precipitation and ETP; in addition, it is sensitive to probable climate change.

Standardized Palmer Drought Index (SPDI)

A comparative study conducted by ^{Ma et al. (2014)} of the PDSI, SPI and SPEI indices found deficiencies and limitations in the difference d used by the SPEI, as an equation of the monthly climate balance and propose to use the calculated one within the operating procedure of the Palmer index (PDSI), called humidity deviation (dh), which is the difference between the observed precipitation and one estimated for the normal climate conditions of the region, which is calculated based on the results of the water balance of the soil. When processing the dh differences with the SPI probabilistic approach, a new index has been developed, the Standardized Palmer Drought Index or SPDI, which includes the theoretical part that can be recovered from the Palmer Index, the computational efficiency of the SPI and reproduces the sensitivity of the SPEI to consider the probable climatic changes (^{Ma et al., 2014}).

^{Campos-Aranda (2018d)} exposes contrasts, in durations of drought of 6, 12 and 24 months, of the SPDI against the SPI and the SPEI, in the rain-gauge stations: Villa de Arriaga, Rio Verde and Xilitla from the state of San Luis Potosí, Mexico, which have different climates.

In Figure 3, the graph b) corresponds to the SPDI with historical record (769 sequences processed) altered with 20% reduction in annual precipitation. The graph c) shows the differences between SPDI altered and the original, that is, b) minus a).

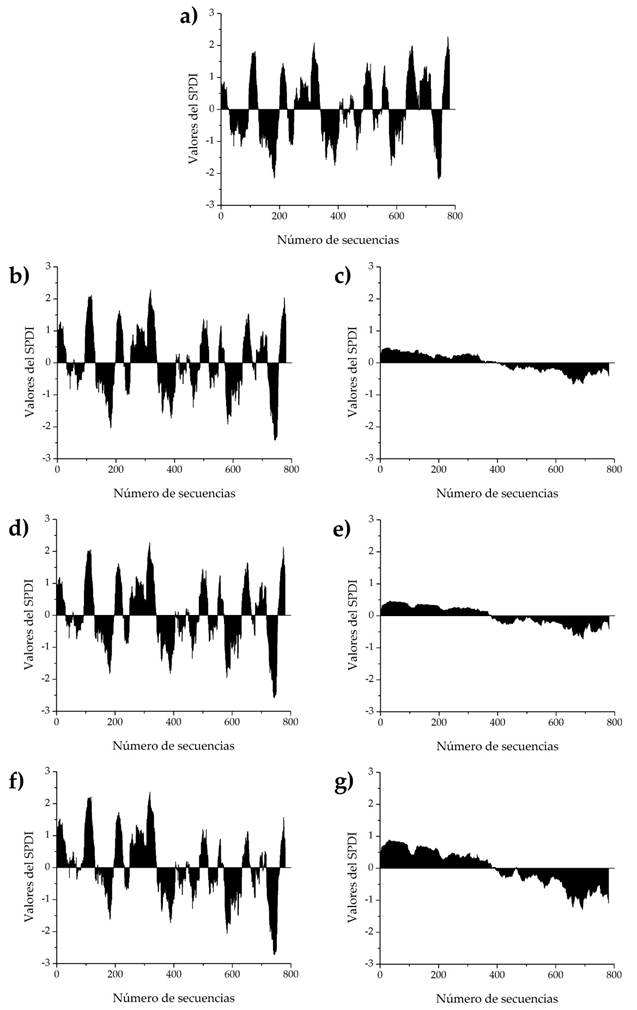
Figure 3 Evolution of the SPDI of 24-month duration at the Fresnillo rain-gauge station of the state of Zacatecas, Mexico (Graph a) historical record; other descriptions in the text). 

Graph d) corresponds to the SPDI with altered historical record with an increase of 4°C in the average annual temperature. Graph e) shows the differences between the altered SPDI and the original, that is, d) minus a).

Graph f) corresponds to the SPDI with an altered historical record with a 20% reduction in annual precipitation and an increase of 4°C in average annual temperature. Graph g) shows the differences between the altered SPDI and the original, that is, f) less a).