Introducción
Generalidades
El diseño hidrológico en las etapas de planeación, construcción, operación y revisión de las obras hidráulicas está basado en las llamadas crecientes de diseño (CD), ya sea que se trate de embalses, diques de protección, canalizaciones, puentes y/o estructuras de drenaje urbano. Las CD son gastos máximos del río asociados con bajas probabilidades de excedencia, cuya estimación más confiable se realiza por medio del análisis de frecuencias de crecientes (AFC) cuando se dispone de datos hidrométricos de gastos máximos anuales.
El AFC es un procedimiento probabilístico que consta de los cinco pasos siguientes: (1) verificación de la calidad estadística de los datos o muestra disponible; (2) selección de una función de distribución de probabilidades (FDP) o modelo probabilístico del cual es probable que procedan los datos; (3) estimación de los parámetros de ajuste de la FDP; (4) cálculo de las predicciones o valores asociados con cierta probabilidad de no excedencia y que se realiza con base en la FDP probaba, y (5) selección de resultados, donde se busca de manera objetiva el mejor ajuste logrado con cada FDP y método de estimación de sus parámetros (Kite, 1977; Stedinger, Vogel, & Foufoula-Georgiou, 1993; Rao & Hamed, 2000; Meylan, Favre & Musy, 2012; Salas, Obeysekera & Vogel, 2018).
Cuando no existen datos hidrométricos, la estimación de las CD se aborda a través de los llamados métodos hidrológicos, los cuales transforman hietogramas de diseño en los hidrogramas o gasto pico buscados (Majumdar & Kumar, 2012). La estimación de las tormentas de diseño se basa en las curvas intensidad-duración-frecuencia, pero debido a la escasez de registros pluviográficos, por lo general se realiza por medio del análisis probabilístico de los registros pluviométricos de precipitación máxima diaria (PMD). Estos registros por lo común tienen mayor amplitud y mucho mayor cobertura espacial (Teegavarapu, 2012; Johnson & Sharma, 2017).
El AFC es idéntico a los análisis probabilísticos de los registros de PMD y, por ello, el primer paso de ambos procedimientos consiste en verificar que las muestras de datos anuales de gastos máximos o de PMD hayan sido generados por un proceso aleatorio estacionario, es decir, que no ha cambiado en el tiempo. Lo anterior significa que el registro por procesar no debe tener componentes determinísticas, como tendencia, persistencia o cambios bruscos en la media.
Desafortunadamente, los efectos de cambio climático global o regional, y las alteraciones físicas que sufren las cuencas de drenaje o el entorno de las estaciones pluviométricas dan origen a registros de crecientes y de PMD que son no estacionarios por mostrar tendencias. En general, las tendencias ascendentes en las muestras de crecientes son consecuencia de la urbanización o de la deforestación, y las descendentes de la construcción de embalses de aprovechamiento y/o control. En las series de PMD anual, las tendencias están asociadas comúnmente a los efectos del cambio climático regional (Nguyen, El Outayek, Lim & Nguyen, 2017; Serago & Vogel, 2018; Salas et al., 2018).
Khaliq, Ouarda, Ondo, Gachon y Bobée (2006) describen de manera concisa los diversos enfoques existentes para realizar el procesamiento de registros que no son estacionarios. En cambio, El Adlouni, Ouarda, Zhang, Roy y Bobée (2007) exponen un procedimiento específico basado en el ajuste de la distribución General de Valores Extremos (GVE), mediante la técnica de máxima verosimilitud generalizada y comparan el modelo estacionario (GVE0) con el no estacionario que acepta dependencia lineal en su parámetro de ubicación (u) con una covariable o modelo GVE1. Cuando la dependencia es cuadrática o curva se define el modelo GVE2, y cuando se tiene dependencia lineal también en el parámetro de escala (α) se establece el modelo GVE11. El Adlouni y Ouarda (2008) presentan la generalización del método de los momentos L al ajuste de las distribuciones GVE1 y GVE2 no estacionarias.
Los enfoques anteriores, así como el de Aissaoui-Fqayeh, El Adlouni, Ouarda y St. Hilaire (2009), permiten el uso de una covariable diferente al tiempo, por ejemplo, las asociadas con el comportamiento climático global. Campos-Aranda (2018) expone ejemplos de la aplicación de los modelos GVE1 y GVE2, usando la generalización del método de momentos L, y como covariables el tiempo y el índice de la oscilación del sur (SOI).
Serago y Vogel (2018) sugieren realizar el análisis probabilístico de los registros no estacionarios mediante una regresión bivariada, la cual describe la relación entre los datos (x) y la variable exógena o covariable. Después obtienen la media, varianza y asimetría condicionales de x y de y = ln(x), para aplicarlas a las FDP de tres parámetros de ajuste: Log-Normal (LN3), Log-Pearson tipo III (LP3) y GVE estacionarias, y obtener su respectivos modelos no estacionarios. La distribución Log-Normal fue la primera que alcanzó una aplicación generalizada en los AFC, en la década de 1960. Las funciones LP3 y GVE fueron las primeras cuya aplicación fue establecida bajo precepto en EUA e Inglaterra. El modelo GVE se convirtió en la distribución clásica de los análisis de frecuencias de valores extremos hidrológicos y la función LP3 es el modelo básico de los AFC, por ello su versión no estacionaria (LP31); ahora, desarrollada por Serago y Vogel (2018), seguramente tendrá gran trascendencia en la estimación de las CD a través de registros con tendencia.
Salas et al. (2018) indican que Serenaldi y Kilsby (2015), entre otros autores, han recomendado que la estacionariedad permanezca siempre como una opción por aplicar en los AFC. Lo anterior se justifica por el hecho de que la condición de no estacionario detectada pudiera no ser causada por causas físicas de acciones antrópicas o del cambio climático, sino haber sido originada por componentes de baja frecuencia del sistema océano-atmósfera (López-de-la-Cruz & Francés, 2014; Álvarez-Olguín & Escalante-Sandoval, 2016) o por los efectos de la persistencia (Khaliq et al., 2006).
Objetivo
En este trabajo se describe con detalle el procedimiento operativo de Serago y Vogel (2018) para aplicar las distribuciones estacionarias LN3, LP3 y GVE, y las no estacionarias LN31, LP31 y GVE1 a registros de crecientes y de PMD anual que muestran tendencia lineal. Se presentan dos aplicaciones numéricas: la primera a un registro de 77 gastos máximos anuales y la segunda a una serie de PMD anual con 58 datos; ambas exhiben tendencia ascendente. La selección entre las tres FDP se realiza con base en el error estándar de ajuste. La contribución fundamental de este estudio consiste en describir y aplicar la versión no estacionaria de la distribución LP3, aplicable a registros con tendencia, con un método bastante simple que corrige su función de cuantiles.
Teoría operativa y datos por procesar
Modelo de regresión lineal
El modelo general de regresión, cuya estructura y propiedades teóricas serán analizadas y aplicadas es (Serago & Vogel, 2018; Salas et al., 2018):
en el cual x son los datos de la serie de valores hidrológicos extremos anuales (crecientes, vientos, niveles, precipitaciones, temperaturas, etc.); f(·), una transformación de x para volverla lineal; w 1 y w 2, las covariables del clima o del uso del terreno; β1 y β2, los coeficientes del modelo, y ε es el error del modelo, el cual se considera independiente, con varianza uniforme y distribución Normal.
Vogel, Yaindl y Walter (2011), así como Prosdocimi, Kjeldsen y Svensson (2014), han encontrado que el modelo anterior, cuando y = ln(x) y w 1, se considera el tiempo (t) en años, es útil para analizar crecientes con tendencia en ríos de EUA y del Reino Unido, sin importar si la tendencia era o no significativa. Serago y Vogel (2018) destacan que tal modelo simple no implica ninguna hipótesis respecto a la FDP de la variable y. Además, modifican la regresión lineal para introducir los valores medios (μ) de las variables, y entonces se tiene:
ahora, la variable y está condicionada por la variable explicativa w; β es el coeficiente de la regresión, y ε es nuevamente el error del modelo con media cero y varianza constante e igual a:
en donde ρ es el coeficiente de correlación lineal entre y y w. Considerando que no existen valores faltantes en la serie anual de valores hidrológicos extremos y que su tamaño es n, entonces las estimaciones de la Ecuación (2) son (Prosdocimi et al., 2014; Serago & Vogel, 2018):
Por lo cual:
Aplicando las Ecuaciones (6) y (7) a los datos originales x, se definen su media (
Momentos no condicionales
De acuerdo con Serago y Vogel (2018), cuando se realiza un análisis de frecuencias estacionario los momentos de x y de y = ln(x) no dependen de la variable explicativa w, por ello son momentos no condicionales y están definidos por sus medias (μ x , μ y ), desviaciones estándar (σ x , σ y ) y coeficientes de asimetría (γ x , γ y ).
Momentos condicionales de y
Serago y Vogel (2018) usan la Ecuación (2) para obtener los momentos condicionales que se emplearán en el análisis de frecuencias no estacionario, sin hacer ninguna consideración sobre la FDP de la variable y. La media de la Ecuación (2) conduce a la expresión del valor esperado de y condicionado por w, ésta es:
De manera similar, la varianza condicional de y se obtiene usando las Ecuaciones (3) y (10), para obtener:
La ecuación anterior demuestra que la varianza condicional de y decrece conforme se incrementa el poder explicativo de la tendencia, tendiendo a cero cuando ρ se aproxima a la unidad. Por el contrario, cuando ρ tiende a cero, la varianza condicional tiende a la original. En general, en los análisis de frecuencias no estacionarios, la varianza condicional de y es menor que la varianza no condicional. Serago y Vogel (2018) encuentran que la asimetría condicional de y es:
La expresión anterior indica que la asimetría condicional de y es igual a la asimetría no condicional, cuando la asimetría de la variable explicativa (γ w ) es cero, caso de w igual al tiempo (t).
Momentos condicionales de x
Serago y Vogel (2018) aplican la función exponencial a la Ecuación (2) y obtienen la expresión:
en la cual x w y y w son los valores condicionados por la variable explicativa w. Notar que no se han establecido hipótesis respecto a las FDP de x w y de y w , pero de acuerdo con la Ecuación (15) es probable que x w provenga de una distribución Normal y que y w lo haga de una función Log-Normal. Lo anterior es válido debido a que la única variable del lado derecho de la Ecuación (15) es el error del modelo ε y exp(ε), las cuales son aproximadamente Normal y Log-Normal, respectivamente.
Para obtener las expresiones de los momentos condicionales de x se aceptará que x w se aproxima a una distribución Log-Normal, y entonces se usan las ecuaciones que relacionan la media, varianza y asimetría de x y de y = ln(x) en la distribución Log-Normal, que son (Serago & Vogel, 2018):
Por último, se amplían las Ecuaciones (16) a (18) aplicando las expresiones (12) y (13), para obtener:
Distribución LN3 estacionaria
Si una serie de valores hidrológicos extremos anuales (y) definidos como
en donde:
siendo:
y
En la expresión anterior, γ x se calcula con la Ecuación (11). Por último, Z en la Ecuación (23) es la variable normal estandarizada; se estima con base en el algoritmo siguiente (Zelen & Severo, 1972) para una probabilidad de no excedencia (p):
con:
c 0 = 2.515517c 1 = 0.802853c 2 = 0.010328
d 1 = 1.432788d 2 = 0.189269d 3 = 0.001308
lo anterior cuando 0 < p < 0.50, hacer Z = -Z; en caso de que 0.50 < p < 1.0 emplear: p = 1 - p en la Ecuación (29), sin cambiar Z.
Distribución LN3 no estacionaria
La función de cuantiles de la distribución Log-Normal de tres parámetros de ajuste no estacionaria (LN31) es similar a la Ecuación (23), pero emplea momentos y variables condicionales (Serago & Vogel, 2018):
Para cuantificar
Distribución LP3 estacionaria
Si una serie de valores hidrológicos extremos anuales (y), definidos como y = ln(x), sigue una distribución Pearson tipo III, también conocida como Gamma de tres parámetros, entonces la variable x tiene distribución Log-Pearson tipo III (LP3). Las predicciones asociadas a un cierto periodo de retorno (Tr), que es el recíproco de la probabilidad de excedencia, se estiman con las expresiones (WRC, 1977; Kite, 1977; Bobée & Ashkar, 1991):
en la Ecuación (32), K p es el llamado factor de frecuencia, es una variable estandarizada Pearson tipo III, cuya aproximación se logra con base en la variable normal estandarizada Z (Ecuaciones (29) y (30)) y el coeficiente de asimetría corregido (γ c ), con las ecuaciones siguientes (Kite, 1977):
siendo:
y
Distribución LP3 no estacionaria
La Ecuación (33) es en realidad la función de cuantiles de la distribución LP3, cuya versión no estacionaria (LP31) se obtiene sustituyendo los momentos condicionales de y (Ecuaciones (12) y (13)), esto es (Serago & Vogel, 2018):
Los valores constantes de la expresión anterior, de izquierda a derecha, están definidos en las Ecuaciones (6), (9), (4), (34), (7), (9) y (5); estos tres últimos, al cuadrado. Para el cálculo de K p con la Ecuación (34), Serago y Vogel (2018) establecen una expresión diferente a la Ecuación (35) para el coeficiente de asimetría y lo definen así:
Distribución GVE estacionaria
La distribución General de Valores Extremos (GVE) incluye tres familias de funciones: la Gumbel, que son rectas en el papel de probabilidad Gumbel-Powell (Chow, 1964); la Fréchet, que son curvas con concavidad hacia arriba y límite inferior, y la Weibull, que tienen concavidad hacia abajo y límite superior. Su función de cuantiles es la siguiente:
en la cual, u, α y k son los parámetros de ubicación, escala y forma y p es la probabilidad de no excedencia. Bhunya, Jain, Ojha y Agarwal (2007) han propuesto expresiones para estimar los parámetros de ajuste de la GVE, con base en la media (
y cuando γ x ≥ 1.15
Para -0.50 ≤ k ≤ 0.50 se tiene:
cuando 0.010 ≤ k ≤ 0.50
y cuando -0.50 ≤ k ≤ 0.010, se aplica la Ecuación (44), siguiente:
Los valores de
Distribución GVE no estacionaria
Cuando se aplican las ecuaciones de los momentos condicionales de x, definidos por las Ecuaciones (20), (21), (22) y (19), en las Ecuaciones (40) a (44), se obtienen los parámetros de ajuste de la distribución GVE no estacionaria (GVE1), denominados
Error estándar de ajuste
El error estándar de ajuste (EEA) se ha establecido como un indicador objetivo cuantitativo debido a que evalúa la desviación estándar de las diferencias entre los valores observados y los estimados con la FDP que se prueba; en este estudio, los modelos LN3, LP3, GVE, LN31, LP31 y GVE1. Su expresión es la siguiente (Kite, 1977):
en la cual, n y np son el número de datos y de parámetros de ajuste, en este caso tres, para las FDP estacionarias y cuatro para las no estacionarias; X
i
son los datos ordenados de menor a mayor, y
donde m es el número de orden del dato, con 1 para el menor y n para el mayor.
Planteamiento de los análisis probabilísticos
El EEA ayuda a seleccionar, entre diversas distribuciones aplicadas a los datos o muestra disponible, la de mejor ajuste. Lógicamente, tales modelos deben ser del mismo tipo, estacionarios o no estacionarios. Entonces, en cada registro por procesar, primero se aplican las distribuciones LN3 y LN31, después las LP3 y LP31, y por último, las GVE y GVE1; se analizan sus valores del EEA y se adoptan las predicciones buscadas. En este proceso, cuando los EEA son similares, se puede adoptar una distribución con base en juicios de seguridad hidrológica, es decir, la que reporta las predicciones más desfavorables o críticas.
Por medio de Ecuaciones (31), (37) y (45) se calculan predicciones con periodos de retorno (Tr) de 2, 25, 50 y 100 años, a través del periodo de registro, aplicando la variable w i en el intervalo de 1 a n. La primera predicción es la mediana, ya que su probabilidad de no excedencia (F) es de 50% y las tres siguientes se calculan para probabilidades complementarias, para definir su valor superior e inferior (Park, Kang, Lee, & Kim, 2011), es decir, para los valores siguientes: F = 0.96 y F = 0.04 para el Tr de 25 años; F = 0.98 y F = 0.02 para el Tr de 50 años, y F = 0.99 y F = 0.01 para el Tr de 100 años.
Las predicciones que emplean la variable w i igual al tamaño del registro (n) corresponden al final de registro histórico. Las predicciones a futuro son posibles utilizando como magnitud de la variable w i la suma del tamaño del registro (n) más el lapso en años hacia el futuro. Se realizaron extrapolaciones de las predicciones en tres fechas a futuro, a 10, 25 y 50 años de concluido el registro disponible.
Mudersbach y Jensen (2010) establecen que el diseño hidrológico de las obras hidráulicas debe ser confiable o seguro hasta el final de su vida útil o fecha futura. Si el registro de crecientes o de PMD anual disponible para estimar las CD muestra tendencia ascendente, entonces sus predicciones deben ser estimadas en tal fecha futura para que su dimensionamiento hidrológico esté correcto y no sea inseguro.
En tal contexto, Salas et al. (2018) han sugerido acortar los valores de la vida útil a 25 o 50 años, y al mismo tiempo hacer más versátil el diseño y la construcción de las obras hidráulicas, de manera que permitan ampliaciones y/o modificaciones a costos menores para la sociedad.
Registros por procesar
La primera serie de datos hidrológicos extremos corresponde a los gastos máximos anuales del río Neponset en Norwood, Massachusetts, EUA, en el periodo de 1939 a 2015 (n = 77). Esta cuenca de drenaje tiene 89.8 km2, con un 16% de su extensión de área impermeable, lo cual ha incrementado sus gastos máximos, pero también es un río con embalses pequeños para abastecimientos municipales en industriales (Serago & Vogel, 2018). Los valores aproximados leídos de una figura logarítmica de dichos autores se tienen en la Tabla 1 y en la Figura 1; se observa que tal registro muestra tendencia ascendente ligera.
Tabla 1 Gastos máximos anuales (Q, m3/s) del río Neponset, EUA (Serago & Vogel, 2018).
| Núm. | Q | Núm. | Q | Núm. | Q | Núm. | Q |
|---|---|---|---|---|---|---|---|
| 1 | 12.4 | 21 | 9.0 | 41 | 23.9 | 61 | 13.3 |
| 2 | 6.4 | 22 | 6.9 | 42 | 12.6 | 62 | 9.3 |
| 3 | 6.7 | 23 | 8.9 | 43 | 8.7 | 63 | 20.8 |
| 4 | 8.5 | 24 | 10.4 | 44 | 18.5 | 64 | 7.3 |
| 5 | 6.5 | 25 | 13.5 | 45 | 12.9 | 65 | 9.6 |
| 6 | 5.7 | 26 | 11.0 | 46 | 26.7 | 66 | 12.4 |
| 7 | 7.2 | 27 | 8.6 | 47 | 8.7 | 67 | 14.1 |
| 8 | 11.7 | 28 | 5.5 | 48 | 11.2 | 68 | 24.2 |
| 9 | 6.0 | 29 | 11.0 | 49 | 19.6 | 69 | 14.4 |
| 10 | 11.2 | 30 | 31.7 | 50 | 10.9 | 70 | 16.2 |
| 11 | 4.7 | 31 | 17.9 | 51 | 8.9 | 71 | 16.9 |
| 12 | 5.0 | 32 | 19.2 | 52 | 17.6 | 72 | 33.0 |
| 13 | 7.1 | 33 | 8.4 | 53 | 9.0 | 73 | 12.9 |
| 14 | 9.4 | 34 | 12.1 | 54 | 7.0 | 74 | 11.0 |
| 15 | 11.1 | 35 | 12.3 | 55 | 11.1 | 75 | 13.3 |
| 16 | 12.3 | 36 | 11.4 | 56 | 10.3 | 76 | 14.1 |
| 17 | 41.1 | 37 | 8.5 | 57 | 7.1 | 77 | 14.2 |
| 18 | 13.7 | 38 | 19.4 | 58 | 10.4 | - | - |
| 19 | 7.0 | 39 | 11.1 | 59 | 21.7 | - | - |
| 20 | 10.8 | 40 | 15.0 | 60 | 30.7 | - | - |

Figura 1 Serie cronológica de datos y curvas de predicciones estimadas con la distribución LP31 en una estación hidrométrica del río Neponset, EUA.
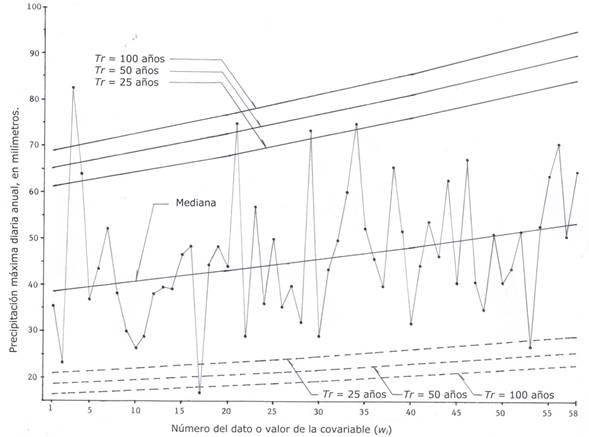
La segunda serie de datos hidrológicos extremos que fue analizada procede de Campos-Aranda (2016) y corresponde a las precipitaciones máximas diarias (PMD) anuales de la estación climatológica Zacatecas, en la ciudad del mismo nombre en México, con un registro de 58 años en el lapso de 1953 a 2010. La serie tiene tendencia ascendente, como se observa en la Figura 2.
Resultados y discusión
Predicciones en el río Neponset
En la Tabla 2 se muestra una selección de las predicciones obtenidas durante el registro histórico con la distribución LN31. Los parámetros básicos de este ajuste no estacionario fueron ρ = 0.414, β = 0.0085, a
x
[ w = 3.807 ], u
x
[ w = 2.4830 ], γ
c
= 1.83614 y σ
y
= 0.5182. En la Tabla 3 se exponen los EEA y las predicciones del modelo LN3 estacionario con a = 0.5879 y μ
y
= 2.3842
Tabla 2 Predicciones (m3/s) en el registro histórico obtenidas con la distribución LN31 en el río Neponset, EUA.
| Núm. | Dato | Mediana | Tr = 25 años | Tr = 50 años | Tr = 100 años | |||
|---|---|---|---|---|---|---|---|---|
| Sup. | Inf. | Sup. | Inf. | Sup. | Inf. | |||
| 1 | 12.4 | 8.3 | 17.6 | 4.5 | 20.3 | 4.2 | 23.0 | 3.9 |
| 10 | 11.2 | 9.0 | 19.0 | 4.9 | 21.9 | 4.5 | 24.9 | 4.2 |
| 20 | 10.8 | 9.7 | 20.7 | 5.3 | 23.8 | 4.9 | 27.0 | 4.6 |
| 30 | 31.7 | 10.6 | 22.5 | 5.8 | 25.9 | 5.3 | 29.4 | 5.0 |
| 40 | 15.0 | 11.5 | 24.5 | 6.3 | 28.2 | 5.8 | 32.0 | 5.4 |
| 50 | 10.9 | 12.6 | 26.6 | 6.9 | 30.7 | 6.3 | 34.9 | 5.9 |
| 60 | 30.7 | 13.7 | 29.0 | 7.5 | 33.4 | 6.9 | 37.9 | 6.4 |
| 70 | 16.2 | 14.9 | 31.6 | 8.1 | 36.3 | 7.5 | 41.3 | 7.0 |
| 77 | 14.2 | 15.8 | 33.5 | 8.6 | 38.5 | 7.9 | 43.8 | 7.4 |
Tabla 3 Predicciones (m3/s) de la distribución LN3 estacionaria y no estacionaria LN31 en el río Neponset, EUA.
| Distribución aplicada | EEA (m3/s) | Periodos de retorno en años | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 25 | 50 | 100 | 500 | 1 000 | ||
| LN3 | 1.00 | 17.4 | 21.7 | 27.5 | 32.0 | 36.8 | 48.8 | 54.4 |
| LN31 (n) | 4.67 | 22.3 | 27.1 | 33.5 | 38.5 | 43.8 | 57.0 | 63.2 |
| LN31 (n+10) | 4.67 | 24.3 | 29.5 | 36.4 | 41.9 | 47.7 | 62.1 | 68.8 |
| LN31 (n+25) | 4.67 | 27.6 | 33.4 | 41.4 | 47.6 | 54.1 | 70.5 | 78.1 |
| LN31 (n+50) | 4.67 | 34.1 | 41.3 | 51.1 | 58.8 | 66.8 | 87.1 | 96.5 |
En la Tabla 4 se muestra una porción de las predicciones obtenidas durante el registro histórico con la distribución LP31. Los parámetros básicos de este ajuste no estacionario fueron
Tabla 4 Predicciones (m3/s) en el registro histórico obtenidas con la distribución LP31 en el río Neponset, EUA.
| Núm. | Dato | Mediana | Tr = 25 años | Tr = 50 años | Tr = 100 años | |||
|---|---|---|---|---|---|---|---|---|
| Sup. | Inf. | Sup. | Inf. | Sup. | Inf. | |||
| 1 | 12.4 | 8.1 | 18.8 | 4.4 | 22.2 | 4.1 | 26.1 | 3.8 |
| 10 | 11.2 | 8.8 | 20.2 | 4.8 | 24.0 | 4.4 | 28.1 | 4.1 |
| 20 | 10.8 | 9.6 | 22.0 | 5.2 | 26.1 | 4.8 | 30.6 | 4.4 |
| 30 | 31.7 | 10.4 | 24.0 | 5.6 | 28.4 | 5.2 | 33.3 | 4.8 |
| 40 | 15.0 | 11.3 | 26.1 | 6.1 | 30.9 | 5.6 | 36.3 | 5.3 |
| 50 | 10.9 | 12.3 | 28.4 | 6.7 | 33.6 | 6.1 | 39.5 | 5.7 |
| 60 | 30.7 | 13.4 | 30.9 | 7.3 | 36.6 | 6.7 | 42.9 | 6.2 |
| 70 | 16.2 | 14.6 | 33.6 | 7.9 | 39.8 | 7.3 | 46.7 | 6.8 |
| 77 | 14.2 | 15.5 | 35.7 | 8.4 | 42.3 | 7.7 | 49.6 | 7.2 |
Tabla 5 Predicciones (m3/s) de la distribución LP3 estacionaria y no estacionaria LP31 en el río Neponset, EUA.
| Distribución aplicada | EEA (m3/s) | Periodos de retorno en años | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 25 | 50 | 100 | 500 | 1 000 | ||
| LP3 | 0.75 | 16.8 | 21.3 | 28.0 | 33.8 | 40.3 | 58.8 | 68.6 |
| LP31 (n) | 2.71 | 22.4 | 27.8 | 35.7 | 42.3 | 49.6 | 69.9 | 80.4 |
| LP31 (n+10) | 2.71 | 24.4 | 30.3 | 38.8 | 46.0 | 54.0 | 76.1 | 87.5 |
| LP31 (n+25) | 2.71 | 27.7 | 34.4 | 44.1 | 52.2 | 61.3 | 86.4 | 99.3 |
| LP31 (n+50) | 2.71 | 34.2 | 42.5 | 54.4 | 64.5 | 75.7 | 106.7 | 122.7 |
En la Tabla 6 se expone una parte de las predicciones durante el registro histórico, estimadas con la distribución GVE1, con γ x [ w = 2.2731 ], y parámetros de ajuste μ x [ w = 14.015 ], a x [ w = 4.742 ] y k x [ w = -0.139 ]. En cambio, en la Tabla 7 se tienen los EEA y las predicciones del modelo GVE estacionario con γ x = 1.8361, u = 9.817, α = 4.607 y k = -0.101, así como del no estacionario al final de registro y a futuro en las tres fechas planteadas.
Tabla 6 Predicciones (m3/s) en el registro histórico obtenidas con la distribución GVE1 en el río Neponset, EUA.
| Núm. | Dato | Mediana | Tr = 25 años | Tr = 50 años | Tr = 100 años | |||
|---|---|---|---|---|---|---|---|---|
| Sup. | Inf. | Sup. | Inf. | Sup. | Inf. | |||
| 1 | 12.4 | 8.3 | 17.4 | 4.7 | 20.3 | 4.3 | 23.4 | 3.9 |
| 10 | 11.2 | 9.0 | 18.8 | 5.1 | 21.9 | 4.6 | 25.3 | 4.3 |
| 20 | 10.8 | 9.8 | 20.5 | 5.5 | 23.8 | 5.0 | 27.5 | 4.6 |
| 30 | 31.7 | 10.6 | 22.3 | 6.0 | 25.9 | 5.5 | 30.0 | 5.0 |
| 40 | 15.0 | 11.6 | 24.2 | 6.5 | 28.2 | 5.9 | 32.6 | 5.5 |
| 50 | 10.9 | 12.6 | 26.4 | 7.1 | 30.7 | 6.5 | 35.5 | 6.0 |
| 60 | 30.7 | 13.7 | 28.7 | 7.7 | 33.4 | 7.0 | 38.6 | 6.5 |
| 70 | 16.2 | 14.9 | 31.2 | 8.4 | 36.4 | 7.7 | 42.0 | 7.1 |
| 77 | 14.2 | 15.8 | 33.1 | 8.9 | 38.6 | 8.1 | 44.6 | 7.5 |
Tabla 7 Predicciones (m3/s) de la distribución GVE estacionaria y no estacionaria GVE1 en el río Neponset, EUA.
| Distribución aplicada | EEA (m3/s) | Periodos de retorno en años | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 25 | 50 | 100 | 500 | 1 000 | ||
| GVE | 1.01 | 17.3 | 21.5 | 27.2 | 31.9 | 36.8 | 49.7 | 55.9 |
| GVE1 (n) | 4.65 | 21.9 | 26.5 | 33.1 | 38.6 | 44.6 | 60.9 | 69.1 |
| GVE1 (n+10) | 4.65 | 23.9 | 28.9 | 36.0 | 42.0 | 48.5 | 66.3 | 75.2 |
| GVE1 (n+25) | 4.65 | 27.1 | 32.8 | 40.9 | 47.7 | 55.1 | 75.2 | 85.4 |
| GVE1 (n+50) | 4.65 | 33.5 | 40.5 | 50.6 | 58.9 | 68.1 | 92.9 | 105.5 |
Con base en los valores del EEA mostrados en la Tabla 3, Tabla 5 y Tabla 7, se adoptan las predicciones o resultados de las distribuciones LP3 y LP31 contra las de los modelos LN3 y LN31, GVE y GVE1, por conducir a sus magnitudes más bajas, indicando con ello un mejor ajuste a los datos disponibles. Las predicciones de la distribución no estacionaria LP31 resultaron ser las más severas o críticas, brindando con ello mayor seguridad en el diseño hidrológico al término de la vida útil de 10, 25 o 50 años.
En la Figura 1 se muestra la serie cronológica de las crecientes de río Neponset, EUA, y sus curvas de predicciones estimadas con la distribución no estacionaria LP31.
Predicciones en la estación Zacatecas
En la Tabla 8 se muestra una parte de las predicciones obtenidas durante el registro histórico con la distribución LN31. Los parámetros básicos de este ajuste no estacionario fueron ρ = 0.298, β = 0.0057, a x [ w = -66.8647 ], μ x [ w = 4.7920 ], γ c = 0.42827 y σ y = 0.1411. En la Tabla 9 se exponen los EEA y las predicciones del modelo LN3 estacionario con a = -54.6459 y μ y = 4.6091 y del no estacionario, lógicamente al final del registro histórico (n) y en los tres escenarios futuros planteados.
Tabla 8 Predicciones (mm) en el registro histórico obtenidas con la distribución LN31 en la estación Zacatecas, México.
| Núm. | Dato | Mediana | Tr = 25 años | Tr = 50 años | Tr = 100 años | |||
|---|---|---|---|---|---|---|---|---|
| Sup. | Inf. | Sup. | Inf. | Sup. | Inf. | |||
| 1 | 35.1 | 38.8 | 63.3 | 19.7 | 68.2 | 16.9 | 72.7 | 14.4 |
| 10 | 26.4 | 40.9 | 66.6 | 20.8 | 71.7 | 17.8 | 76.5 | 15.2 |
| 20 | 44.0 | 43.3 | 70.5 | 22.0 | 75.9 | 18.8 | 81.0 | 16.1 |
| 30 | 29.2 | 45.8 | 74.6 | 23.3 | 80.4 | 19.9 | 85.7 | 17.0 |
| 40 | 32.0 | 48.5 | 79.0 | 24.6 | 85.1 | 21.1 | 90.8 | 18.0 |
| 50 | 41.0 | 51.3 | 83.6 | 26.1 | 90.0 | 22.3 | 96.1 | 19.1 |
| 58 | 65.0 | 53.7 | 87.5 | 27.3 | 94.2 | 23.3 | 100.5 | 19.9 |
Tabla 9 Predicciones (mm) de la distribución LN3 estacionaria y no estacionaria LN31 en la estación Zacatecas, México.
| Distribución aplicada: | EEA (mm) | Periodos de retorno en años | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 25 | 50 | 100 | 500 | 1 000 | ||
| LN3 | 1.52 | 58.4 | 65.6 | 73.9 | 79.5 | 84.8 | 96.0 | 100.6 |
| LN31 (n) | 8.93 | 68.9 | 77.6 | 87.5 | 94.2 | 100.5 | 114.1 | 119.6 |
| LN31 (n+10) | 8.93 | 72.9 | 82.1 | 92.6 | 99.7 | 106.4 | 120.7 | 126.6 |
| LN31 (n+25) | 8.93 | 79.4 | 89.4 | 100.8 | 108.6 | 115.9 | 131.5 | 137.8 |
| LN31 (n+50) | 8.93 | 91.5 | 103.0 | 116.2 | 125.1 | 133.5 | 151.5 | 158.8 |
En la Tabla 10 se expone una porción de las predicciones estimadas durante el registro histórico con la distribución LP31. Los parámetros básicos de este ajuste no estacionario fueron:
Tabla 10 Predicciones (mm) en el registro histórico obtenidas con la distribución LP31 en la estación Zacatecas, México.
| Núm. | Dato | Mediana | Tr = 25 años | Tr = 50 años | Tr = 100 años | |||
|---|---|---|---|---|---|---|---|---|
| Sup. | Inf. | Sup. | Inf. | Sup. | Inf. | |||
| 1 | 35.1 | 38.9 | 61.3 | 21.0 | 65.3 | 18.6 | 69.0 | 16.6 |
| 10 | 26.4 | 40.9 | 64.5 | 22.2 | 68.8 | 19.6 | 72.6 | 17.4 |
| 20 | 44.0 | 43.3 | 68.2 | 23.4 | 72.8 | 20.7 | 76.9 | 18.4 |
| 30 | 29.2 | 45.8 | 72.2 | 24.8 | 77.0 | 21.9 | 81.3 | 19.5 |
| 40 | 32.0 | 48.5 | 76.4 | 26.3 | 81.5 | 23.2 | 86.1 | 20.7 |
| 50 | 41.0 | 51.3 | 80.9 | 27.8 | 86.3 | 24.6 | 91.1 | 21.9 |
| 58 | 65.0 | 53.7 | 84.7 | 29.1 | 90.3 | 25.7 | 95.4 | 22.9 |
Tabla 11 Predicciones (mm) de la distribución LP3 estacionaria y no estacionaria LP31 en la estación Zacatecas, México.
| Distribución aplicada | EEA (mm) | Periodos de retorno en años | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 25 | 50 | 100 | 500 | 1 000 | ||
| LP3 | 1.51 | 58.6 | 65.8 | 73.6 | 78.7 | 83.3 | 92.6 | 96.1 |
| LP31 (n) | 4.46 | 68.1 | 76.0 | 84.7 | 90.3 | 95.4 | 105.5 | 109.3 |
| LP31 (n+10) | 4.46 | 72.1 | 80.5 | 89.6 | 95.6 | 100.9 | 111.7 | 115.7 |
| LP31 (n+25) | 4.46 | 78.5 | 87.6 | 97.6 | 104.1 | 109.9 | 121.6 | 126.0 |
| LP31 (n+50) | 4.46 | 90.4 | 101.0 | 112.5 | 120.0 | 126.7 | 140.1 | 145.2 |
En la Tabla 12 se muestra una parte de las predicciones durante el registro histórico, estimadas con la distribución GVE1, con γ x(w = 2.1646 y parámetros de ajuste u x [ w = 46.955 ], a x [ w = 10.950 ] y k x [ w = -0.131 ]. En cambio, en la Tabla 13 se tienen los EEA y las predicciones del modelo GVE estacionario con γ x = 0.4283, u = 40.896, α = 13.166 y k = 0.152, así como del no estacionario, término de registro y en las tres fechas futuras planteadas.
Tabla 12 Predicciones (mm) en el registro histórico estimadas con la distribución GVE1 en la estación Zacatecas, México.
| Núm. | Dato | Mediana | Tr = 25 años | Tr = 50 años | Tr = 100 años | |||
|---|---|---|---|---|---|---|---|---|
| Sup. | Inf. | Sup. | Inf. | Sup. | Inf. | |||
| 1 | 35.1 | 36.9 | 65.4 | 25.4 | 74.3 | 24.1 | 83.9 | 23.0 |
| 10 | 26.4 | 38.9 | 68.9 | 26.7 | 78.2 | 25.3 | 88.3 | 24.2 |
| 20 | 44.0 | 41.2 | 72.9 | 28.3 | 82.8 | 26.8 | 93.5 | 25.6 |
| 30 | 29.2 | 43.6 | 77.1 | 29.9 | 87.6 | 28.4 | 99.0 | 27.1 |
| 40 | 32.0 | 46.1 | 81.6 | 31.7 | 92.7 | 30.0 | 104.7 | 28.7 |
| 50 | 41.0 | 48.8 | 86.4 | 33.5 | 98.1 | 31.8 | 110.9 | 30.4 |
| 58 | 65.0 | 51.1 | 90.4 | 35.1 | 102.7 | 33.3 | 116.0 | 31.8 |
Tabla 13 Predicciones (mm) de la distribución GVE estacionaria y no estacionaria GVE1 en la estación Zacatecas, México.
| Distribución aplicada | EEA (m3/s) | Periodos de retorno en años | ||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 25 | 50 | 100 | 500 | 1 000 | ||
| GVE | 1.44 | 58.6 | 66.0 | 74.2 | 79.6 | 84.5 | 93.8 | 97.2 |
| GVE1 (n) | 9.45 | 65.1 | 75.6 | 90.4 | 102.7 | 116.0 | 151.9 | 169.8 |
| GVE1(n+10) | 9.45 | 68.9 | 80.0 | 95.7 | 108.7 | 122.8 | 160.8 | 179.7 |
| GVE1(n+25) | 9.45 | 75.0 | 87.1 | 104.2 | 118.4 | 133.7 | 175.1 | 195.7 |
| GVE1(n+50) | 9.45 | 86.5 | 100.4 | 120.1 | 136.4 | 154.1 | 201.8 | 225.5 |
Con base en los valores del EEA expuestos en la Tabla 9, Tabla 11 y Tabla 13, se adoptan las predicciones o resultados de los modelos GVE y LP31, por conducir a sus magnitudes más bajas, indicando con ello un mejor ajuste a los datos disponibles. Las predicciones de los tres modelos estacionarios son casi idénticas. La función GVE1 reporta predicciones más extremas o críticas, pero su EEA es mayor del doble del obtenido con la distribución LP31, por ello no fueron seleccionadas.
En la Figura 2 se muestra la serie cronológica de la PMD anual de la estación climatológica Zacateas, México, y sus casi rectas de predicciones estimadas con la distribución no estacionaria LP31.
Conclusiones
Los análisis frecuencias (AF) de registros de datos hidrológicos extremos anuales que no son homogéneos al presentar tendencia serán bastante frecuentes en el futuro inmediato debido a los efectos del cambio climático global o regional, y a los impactos físicos de las alteraciones en las cuencas de drenaje, como son la urbanización y deforestación, así como la construcción de embalses.
Otro aspecto que favorecerá tales AF no estacionarios consiste en brindar protección hidrológica al término de la vida útil de una obra hidráulica. Lo anterior obliga a tomar en cuenta la tendencia observada en el registro por procesar, para obtener predicciones más confiables en una fecha futura, cuando concluya la vida útil de la obra hidráulica que se dimensiona. Lo anterior es importante cuando el registro muestra tendencia ascendente.
En método descrito, desarrollado por Serago y Vogel (2018), y también expuesto por Salas et al. (2018), basado en los momentos condicionales de y = ln(x) y de x, que son los datos disponibles, permite obtener de manera simple las funciones de cuantiles no estacionarias de tres de las distribuciones de probabilidad más utilizadas y de mayor universalidad en los AF de crecientes y otros datos hidrológicos extremos anuales, que son la Log-Normal (LN3), la Log-Pearson tipo III (LP3) y la General de Valores Extremos (GVE).
El método usa como covariable el tiempo, con una tendencia lineal, y por ello se ajustan los modelos no estacionarios LN31, LP31 y GVE1. Las funciones de cuantiles, que permiten obtener sus predicciones buscadas, son sólo levemente más complicadas que sus versiones estacionarias, lo cual vuelve bastante práctico este enfoque para obtener predicciones en registros con tendencia, dentro de ellos, en su final y en fechas futuras. Lo anterior se demostró en las dos aplicaciones numéricas descritas, cuya selección del mejor ajuste logrado se basó en el error estándar de ajuste, técnica de uso generalizado en los análisis frecuencias.











 texto en
texto en