Introducción
Generalidades
Las lluvias de diseño son precipitaciones máximas de cierta duración asociadas con bajas probabilidades de excedencia con las cuales se estiman, por medio de métodos hidrológicos, las crecientes de diseño cuando no se dispone de registros hidrométricos. Detalles de lo anterior se pueden consultar en Teegavarapu (2012), Mujumdar y Nagesh-Kumar (2012). Las crecientes de diseño permiten el dimensionamiento de las obras hidráulicas durante su planeación o cuando se revisan por seguridad. La estimación más confiable de las lluvias de diseño se basa en el análisis probabilístico (AP) de los datos máximos anuales, el cual asume que el proceso aleatorio que generan las precipitaciones observadas es estacionario y, por ello, sus propiedades estadísticas no cambian con el tiempo. En el AP se ajusta una función de distribución de probabilidad (FDP) conocida al registro de precipitaciones y con base en ella se realizan las predicciones buscadas o lluvias de diseño. Debido a la escasez de estaciones pluviográficas y la abundancia relativa de estaciones pluviométricas, los registros de valores extremos más comúnmente procesados de lluvias son los de precipitación máxima diaria (PMD) anual.
Actualmente, todas las estaciones pluviométricas están sometidas a los efectos del cambio climático global, o bien su entorno geográfico sufre modificaciones físicas generadas por las actividades del hombre. Entre las más impactantes están la urbanización, deforestación, desecación de lagunas y construcción de embalses, que alteran los procesos atmosféricos locales, dando origen a series o registros de PMD anual no estacionarios (Strupczewski & Kaczmarek, 2001; Khaliq, Ouarda, Ondo, Gachon, & Bobée, 2006; El Adlouni, Ouarda, Zhang, Roy, & Bobée, 2007; El Adlouni & Ouarda, 2008).
Para realizar el AP de registros no estacionarios, la teoría estadística de valores extremos ha sido extendida para ajustar el modelo clásico que siguen asintóticamente las series de datos hidrológicos máximos, es decir, la FDP General de Valores Extremos estacionaria (GVE0) con tres parámetros de ajuste (u, α, k); lo anterior, con base en la introducción de las llamadas covariables. Una de las más utilizadas es el tiempo (t) en años, a través de la cual se puede tomar en cuenta la tendencia observada en la serie de datos, adoptando como variable el parámetro de ubicación (u t ). Cuando la tendencia es lineal (u t = μ0 + μ1·t) se ajusta el modelo GVE1 de cuatro parámetros de ajuste (μ0, μ1, α, k). Si la tendencia es curva (u t = μ0 + μ1·t + μ2·t 2), se aplica el modelo GVE2 de cinco parámetros de ajuste (μ0, μ1, μ2, α, k); en este modelo se pueden usar dos covariables (u t = μ0 + μ1·t + μ2·h) (Khaliq et al., 2006; Prosdocimi, Kjeldsen, & Miller, 2015).
Respecto a otras distribuciones no estacionarias, se tienen varias, por ejemplo la Log-normal (Vogel, Yaindl, & Walter, 2011; Aissaoui-Fqayeh, El Adlouni, Ouarda, & St. Hilaire, 2009) y los modelos Logística Generalizada (Kim, Nam, Ahn, Kim, & Heo, 2015) y Pareto Generalizada (Rao & Hamed, 2000), susceptibles de un tratamiento idéntico al que será expuesto para la distribución GVE. También se pueden usar otras covariables en lugar del tiempo (t), como algunos índices climáticos globales o regionales (Prosdocimi, Kjeldsen, & Svensson, 2014; López-de-la-Cruz & Francés, 2014; Álvarez-Olguín & Escalante-Sandoval, 2016; Campos-Aranda, 2018).
Objetivo
El objetivo de este trabajo consistió en exponer la teoría del ajuste de las distribuciones no estacionarias GVE1 y GVE2, por medio de la generalización del método de los momentos L, planteada inicialmente por El Adlouni y Ouarda (2008), y aplicada después por Gado y Nguyen (2016). Además, se exponen y procesan cuatro series de PMD anual, todas con tendencia, y se describen los resultados del ajuste del modelo GVE1 o GVE2, destacando la sencillez y utilidad de la extensión del método de los momentos L para obtener las predicciones dentro del registro histórico y a futuro.
Métodos y materiales
Distribución General de Valores Extremos
Los valores máximos anuales son eventos que ocurren en la cola derecha de la FDP, la cual define el comportamiento de la variable aleatoria hidrológica. Por lo anterior, las lluvias de diseño se pueden predecir con base en la FDP, como el valor máximo que corresponde a un cierto intervalo promedio de recurrencia o periodo de retorno (Tr), cuya probabilidad de excedencia es p = 1/Tr. La teoría de valores extremos estableció que los datos extremos siguen de manera asintótica a la FDP General de Valores Extremos (GVE), cuya aplicación ha sido recomendada (Stedinger, Vogel, & Foufoula-Georgiou, 1993; Hosking & Wallis, 1997; Coles, 2001; Khaliq et al., 2006; Papalexiou & Koutsoyiannis, 2013; Gado & Nguyen, 2016) para modelar datos hidrológicos extremos (dh) con una probabilidad de no excedencia (F(dh)), que es:
En la expresión anterior, u, α y k son los parámetros de ubicación, escala y forma de la GVE0. Cuando k = 0, se obtiene la distribución Gumbel, que es una línea recta en el papel de probabilidad Gumbel-Powell, por lo cual el intervalo de la variable es -∞ < dh < ∞. Cuando k > 0, la distribución es Weibull, que es una curva con concavidad hacia abajo y límite superior, por lo cual -∞ < dh ≤ u + α/k. Finalmente, si k < 0, la distribución es Fréchet, que también es una curva, pero con concavidad hacia arriba y frontera inferior, por lo que u + α/k ≤ dh < ∞. Las predicciones buscadas (DH Tr ) se obtienen con la solución inversa de la Ecuación (1):
Momentos L de la muestra de datos
El método de los momentos L es quizás el más simple de los procedimientos confiables para estimar los parámetros de ajuste de las FDP utilizadas en hidrología. Lo anterior debido a que los momentos L, que son combinaciones lineales (Hosking & Wallis, 1997) de los momentos de probabilidad ponderada (β r ), no son afectados de manera significativa por los valores dispersos (outliers) de la muestra. Los primeros tres momentos L de una muestra (l 1, l 2, l 3) y el cociente L de asimetría (t 3) se estiman a través del estimador insesgado (b r ) de los β r , como sigue:
El estimador insesgado de los β r es (Hosking & Wallis, 1997):
donde r = 0, 1, 2,…. y dh
i
son los datos de la muestra o serie disponible de datos hidrológicos de tamaño n, ordenados de menor a mayor
Parámetros de ajuste de la distribución GVE estacionaria
Para el modelo GVE0 con el método de los momentos L, sus tres parámetros de ajuste se calculan con las ecuaciones (Stedinger et al., 1993; Hosking & Wallis, 1997; Rao & Hamed, 2000; Campos-Aranda, 2018):
siendo:
Para la estimación de la función Gamma Γ(ω) se utilizó la fórmula de Stirling (Davis, 1972), mostrada en la Ecuación (12):
AP no estacionario con GVE1 y GVE2
Según Strupczewski y Kaczmarek (2001), el ajuste de las distribuciones no estacionarias GVE1 y GVE2 implica dos supuestos: (1) se acepta que la no estacionariedad de las series de PMD anual es causada por cambios graduales del entorno geográfico y/o por el cambio climático global, generando una alteración ligera de sus parámetros estadísticos; y (2) se acepta que la FDP es independiente del tiempo, entonces la distribución GVE, con parámetros de ajuste variables con el tiempo, es aceptable para modelar datos extremos no estacionarios. Por lo anterior, se debe considerar variable en el tiempo la media (μ t ) de la distribución GVE, cuya expresión es (Rao & Hamed, 2000):
Ajuste de la distribución GVE1
La inspección de la serie cronológica de PMD i permitirá definir si se adopta una tendencia de la media (μ t ) lineal o curva. Cuando la tendencia en la media es lineal y se introduce en la Ecuación (13), se puede despejar el parámetro de ubicación (u), que ahora será variable con respecto al tiempo t, que varía de 1 a n. Su expresión es (El Adlouni & Ouarda, 2008; Gado & Nguyen, 2016):
Las magnitudes μ0 y μ1 de la recta que representa la tendencia lineal de la muestra o serie de datos PMD
i
se obtienen con base en las ecuaciones del Apéndice 1. Para probar que la pendiente μ1 es estadísticamente diferente de cero se aplican las ecuaciones del Apéndice 2. Para estimar los valores de los parámetros de escala (α) y forma (k) de la expresión anterior que corresponden a la FDP estacionaria (GVE0), se retira la tendencia de la serie PMD
i
para obtener una serie estacionaria
Enseguida se aplican las Ecuaciones (8) a (10) para obtener los valores buscados de α y k. Por último, se aplica la Ecuación (2), empleando la Expresión (14) para tomar en cuenta el parámetro de ubicación variable (u t ) con el tiempo y realizar predicciones dentro del registro histórico (t < n) al final de éste (t = n), así como varios años después (t > n), por ejemplo, en el futuro al término de la vida útil de la obra hidráulica analizada, con lo cual se toma en cuenta la tendencia observada en la serie de datos hidrológicos (Mudersbach & Jensen, 2010).
Ajuste de la distribución GVE2
Cuando la tendencia de la media (μ t ) es curva y se introduce en la Ecuación (13), el parámetro de ubicación variable (u t ) con respecto al tiempo es igual a (El Adlouni & Ouarda, 2008; Gado & Nguyen, 2016):
Las magnitudes μ0, μ1 y μ2 de la ecuación de la curva que representa la tendencia de la muestra o serie de datos PMD
i
se obtienen con base en las ecuaciones del Apéndice 3. Para estimar los valores de los parámetros de escala (α) y forma (k) de la expresión anterior que corresponden a la FDP estacionaria (GVE0) se retira la tendencia de la serie PMD
i
para obtener una serie estacionaria
Enseguida se aplican las Ecuaciones (8) a (10), para obtener los valores buscados de α y k. Por último, se aplica la Ecuación (2), empleando la Expresión (16), para tomar en cuenta el parámetro de ubicación variable (u t ) con el tiempo y realizar predicciones dentro del registro histórico (t < n) al final de éste (t = n) y en un tiempo futuro, como se indicó para el modelo GVE1.
La distribución no estacionaria GVE2 también se puede aplicar con dos covariables (t y h), quedando el parámetro de ubicación variable (u t ) igual a (Prosdocimi et al., 2014; Prosdocimi et al., 2015):
Las magnitudes μ0, μ1 y μ2 de la ecuación de la regresión lineal múltiple que representa la tendencia de la muestra o serie de datos PMD
i
se obtienen con base en las ecuaciones del Apéndice 4. Para estimar los valores de los parámetros de escala (α) y forma (k) de la expresión anterior que corresponden a la FDP estacionaria (GVE0), se retira la tendencia de la serie PMD
i
para obtener una serie estacionaria
Enseguida se aplican las Ecuaciones (8) a (10), para obtener los valores buscados de α y k. Después se aplica la Ecuación (2), empleando la Expresión (18), para tomar en cuenta el parámetro de ubicación variable (u t ) con el tiempo y realizar predicciones dentro del registro histórico (t < n) al final de éste (t = n) y en un tiempo futuro (t > n), como se indicó para el modelo GVE1.
Error estándar de ajuste
Desde mediados de la década de 1970 se formuló al error estándar de ajuste (EEA) como una medida cuantitativa que estima la habilidad descriptiva del modelo probabilístico ajustado (Meylan, Favre, & Musy, 2012), y que además permite la comparación objetiva entre las diversas FDP que se prueban o ajustan a una serie o muestra de datos, pues tiene las unidades de los datos (PMD i ). Su expresión es la siguiente (Kite, 1977):
donde n es el número de datos de la serie disponible; npa, el número de parámetros de ajuste de la FDP que se prueba, con cuatro para el modelo GVE1 y cinco para los dos modelos GVE2;
donde m es el número de orden del dato, con 1 para el menor y n para el mayor. El cálculo del EEA con la Ecuación (20) permite la comparación de otros modelos probabilísticos no estacionarios en la serie que se procesa. Cuando los valores del EEA son similares, se puede adoptar un modelo no estacionario de manera subjetiva, por ejemplo, el que conduce a las predicciones más desfavorables.
Planteamiento de los análisis probabilísticos
Con base en la Ecuación (2) se estiman las predicciones con periodos de retorno (Tr) de 2, 10, 25, 50 y 100 años, a través del periodo de registro, aplicando variable el parámetro de ubicación (u t ). La primera predicción corresponde a la mediana, ya que su probabilidad de no excedencia (1-p) es de 50% y las cuatro siguientes se calculan para los valores siguientes: 0.90, 0.96, 0.98 y 0.99, respectivamente. Además, en las series procesadas se hacen predicciones a futuro, para los años 2025 y 2050. Se considera que extrapolar más de 30 años el comportamiento observado de la tendencia histórica es bastante arriesgado. También se muestran en los gráficos de datos y predicciones las estimaciones de los periodos de retorno extremos (2 y 100 años) con el modelo estacionario GVE0, las cuales son líneas rectas horizontales que se indican punteadas.
AP no estacionario con LOG y PAG
Las FDP Logística Generalizada (LOG) y Pareto Generalizada (PAG) son dos modelos probabilísticos utilizados por lo regular en los análisis de frecuencias de datos hidrológicos extremos y que resultan aplicables en sus versiones no estacionarias con parámetro de ubicación variable (u t ) por medio de la generalización del método de los momentos L, como se ha expuesto a partir de la Ecuación (13). Esta ecuación clave del método tiene las expresiones siguientes en las distribuciones LOG y PAG (Rao & Hamed, 2000):
Respecto a las Ecuaciones (1) y (2), correspondientes a las distribuciones LOG y PAG, se pueden consultar en Hosking y Wallis (1997), y Campos-Aranda (2018).
Criterio de severidad de la tendencia lineal
Las ecuaciones del Apéndice 2 conducen a dos estadísticos asociados con la pendiente de la regresión lineal: el DS calculado y su correspondiente valor crítico
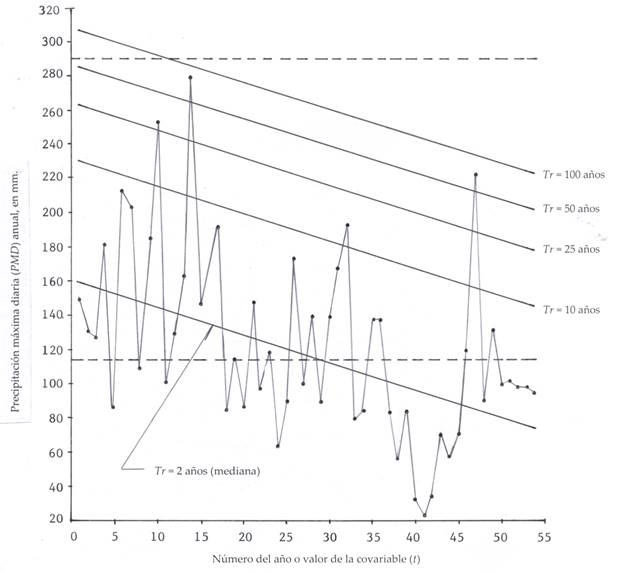
Serie 1 con tendencia lineal descendente severa
Este registro de PMD anual pertenece a la estación pluviométrica Abritas, ubicada en el municipio de Ciudad del Maíz en la zona norte de la región huasteca del estado de San Luis Potosí, México. Abarca 54 años, en el periodo de 1961 a 2015, ya que tiene incompleto el año de 1998. Con excepción de la serie 2, la información de este registro y de los demás fue proporcionada por la Dirección Local San Luis Potosí de la Comisión Nacional del Agua. Sus valores se citan en la Tabla 1.
Tabla 1 Datos máximos anuales de PMD en milímetros, en tres estaciones del estado de San Luis Potosí, México.
| Núm. dato | Abri-tas | Las Adjun-tas | Los Fil-tros | Núm. dato | Abri-tas | Las Adjun-tas | Los Fil-tros | Núm. dato | Los Fil-tros |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 150.0 | 57.4 | 15.9 | 28 | 140.0 | 38.0 | 58.0 | 55 | 40.2 |
| 2 | 131.5 | 75.0 | 20.6 | 29 | 90.0 | 182.5 | 42.9 | 56 | 111. |
| 3 | 127.5 | 42.0 | 50.9 | 30 | 140.0 | 134.7 | 26.4 | 57 | 43.3 |
| 4 | 183.0 | 65.5 | 40.5 | 31 | 168.0 | 69.4 | 65.5 | 58 | 76.9 |
| 5 | 87.0 | 72.2 | 63.6 | 32 | 194.0 | 118.2 | 22.0 | 59 | 42.8 |
| 6 | 215.5 | 63.2 | 41.9 | 33 | 80.0 | 111.4 | 51.2 | 60 | 46.1 |
| 7 | 203.5 | 131.5 | 60.0 | 34 | 85.0 | 92.3 | 66.5 | 61 | 42.5 |
| 8 | 110.0 | 70.9 | 35.9 | 35 | 138.0 | 86.0 | 26.0 | 62 | 45.3 |
| 9 | 187.5 | 100.3 | 48.6 | 36 | 138.0 | 108.7 | 31.5 | 63 | 44.5 |
| 10 | 254.0 | 141.5 | 63.0 | 37 | 84.0 | 67.5 | 46.5 | 64 | 26.0 |
| 11 | 102.0 | 58.1 | 35.5 | 38 | 56.0 | 72.0 | 44.0 | 65 | 59.1 |
| 12 | 130.0 | 74.7 | 40.0 | 39 | 85.0 | 76.8 | 41.0 | 66 | 44.1 |
| 13 | 164.0 | 87.0 | 63.2 | 40 | 33.0 | 58.0 | 55.0 | 67 | 63.0 |
| 14 | 280.0 | 134.0 | 39.4 | 41 | 23.1 | 83.0 | 21.5 | 68 | 51.6 |
| 15 | 147.0 | 78.4 | 27.2 | 42 | 35.0 | 58.9 | 29.8 | - | - |
| 16 | 170.0 | 237.5 | 59.0 | 43 | 70.4 | 116.8 | 41.5 | - | - |
| 17 | 193.0 | 80.0 | 32.0 | 44 | 57.0 | 141.0 | 24.9 | - | - |
| 18 | 85.0 | 59.2 | 30.0 | 45 | 71.0 | 119.3 | 59.0 | - | - |
| 19 | 116.5 | 93.0 | 40.2 | 46 | 120.0 | 86.3 | 33.5 | - | - |
| 20 | 87.0 | 72.2 | 31.5 | 47 | 223.2 | 146.1 | 46.5 | - | - |
| 21 | 150.0 | 85.0 | 31.5 | 48 | 90.9 | 115.5 | 51.0 | - | - |
| 22 | 97.0 | 68.0 | 52.0 | 49 | 133.0 | 132.7 | 40.0 | - | - |
| 23 | 120.0 | 86.4 | 52.3 | 50 | 100.0 | 303.8 | 35.5 | - | - |
| 24 | 64.0 | 66.7 | 31.3 | 51 | 102.0 | 75.3 | 45.5 | - | - |
| 25 | 90.0 | 80.5 | 35.0 | 52 | 98.0 | 70.0 | 25.9 | - | - |
| 26 | 175.0 | 100.0 | 28.5 | 53 | 98.0 | 151.5 | 20.7 | - | - |
| 27 | 100.0 | 133.5 | 57.2 | 54 | 95.0 | 125.1 | 37.5 | - | - |
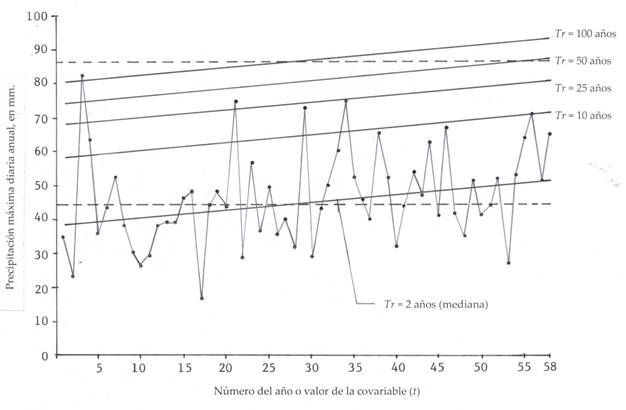
Serie 2 con tendencia lineal ascendente leve
Campos-Aranda (2016) expuso el registro de PMD anual de la estación pluviométrica Zacatecas de la capital del estado del mismo nombre en México, con 58 datos en el lapso de 1953 al 2010, el cual mostró tendencia lineal ascendente logarítmica; debido a ello fue procesado en tal referencia, con base en la FDP Log-normal no estacionaria de dos parámetros de ajuste sugerida por Vogel et al. (2011).
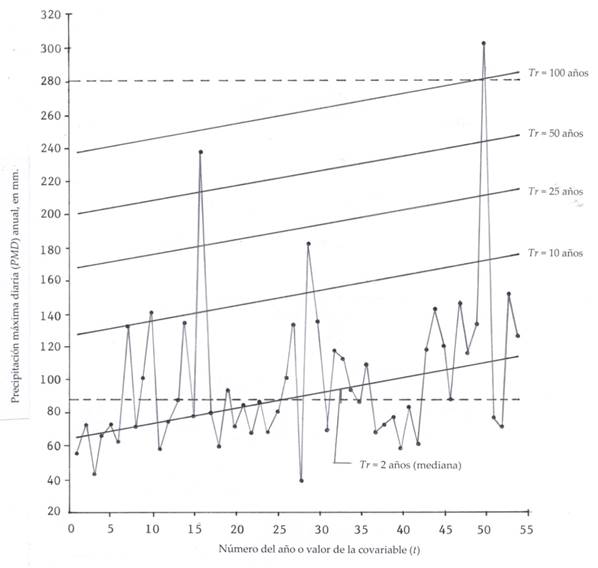
Serie 3 con tendencia lineal ascendente moderada
Este registro de PMD anual pertenece a la estación pluviométrica Las Adjuntas, ubicada donde se unen los ríos Tampaón y Moctezuma para formar el río Pánuco, en la zona oriente de la región huasteca del estado de San Luis Potosí, México. Comprende 54 años del intervalo de 1961 a 2015, debido a que falta el año de 1986; sus valores se exponen en la Tabla 1.
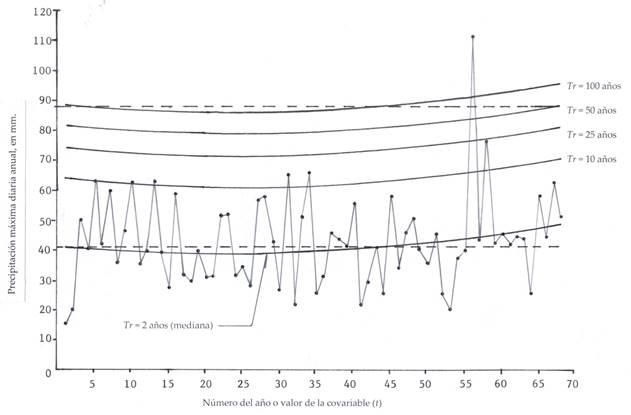
Serie 4 con tendencia curva convexa
Este registro de PMD anual pertenece a la estación pluviométrica Los Filtros, ubicada dentro de la ciudad de San Luis Potosí, capital del estado del mismo nombre en México. Abarca 68 años del intervalo de 1949 a 2016. Sus valores se tienen en la Tabla 1.
Descripción de los resultados
Predicciones en la estación Abritas, S.L.P.
Primero se aplicaron las ecuaciones del Apéndice 1, y se obtuvo μ0 = 167.6315, μ1 = -1.6057 y r xy = -0.4619. Después se probó la tendencia lineal con las ecuaciones del Apéndice 2 y se obtuvo un DS = -3.7558 y un DS c = 2.0066, por lo cual resultó altamente significativa.
La serie estacionaria (
En la Tabla 2 se expone una parte de las predicciones dentro de registro histórico y una extrapolación a una década (año 2025), pues a futuro son menores debido a la pendiente descendente. Las predicciones con el modelo estacionario GVE0 de periodos de retorno 2 y 100 años son: 114.9 y 290.8 mm, con un EEA = 6.0 mm.
Tabla 2 Predicciones en milímetros en el periodo histórico y a futuro en la estación Abritas, San Luis Potosí, México, con base en la distribución no estacionaria GVE1.
| t | Año | Periodos de retorno (años) | ||||
|---|---|---|---|---|---|---|
| 2 | 10 | 25 | 50 | 100 | ||
| 1 | 1961 | 159.6 | 230.9 | 263.5 | 286.3 | 307.8 |
| 10 | 1970 | 145.1 | 216.5 | 249.0 | 271.8 | 293.4 |
| 20 | 1980 | 129.0 | 200.4 | 233.0 | 255.8 | 277.3 |
| 30 | 1990 | 113.0 | 184.3 | 216.9 | 239.7 | 261.3 |
| 40 | 2001 | 96.9 | 168.3 | 200.8 | 223.6 | 245.2 |
| 50 | 2011 | 80.9 | 152.2 | 184.8 | 207.6 | 229.2 |
| 54 | 2015 | 74.5 | 145.8 | 178.4 | 201.2 | 222.7 |
| 64 | 2025 | 58.4 | 129.8 | 162.3 | 185.1 | 206.7 |
En la Figura 1 se expone la serie cronológica de los datos y las rectas de las predicciones, las cuales se dibujan, con base en las predicciones de la Tabla 2, dentro del registro histórico con los valores de la covariable t, que varían de 1 a n.
Predicciones en la estación Zacatecas, Zac.
Al aplicar las ecuaciones del Apéndice 1 se obtuvo μ0 = 40.1247, μ1 = 0.2246 y r xy = 0.2638. Enseguida se probó la tendencia lineal con las ecuaciones del Apéndice 2; se obtuvo un DS = 2.0463 y un DS c = 2.0032, por lo cual resultó escasamente significativa.
La serie estacionaria (
En la Tabla 3 se expone una parte de las predicciones dentro de registro histórico y a futuro de los años 2025, 2050 y 2100. Como este registro de 58 datos concluye en 2010, entonces el valor del tiempo t en 2025 es 73, en 2050 es 98 y en 2100 es 148. Las predicciones con el modelo estacionario GVE0 de periodos de retorno 2 y 100 años son 45.2 y 86.7 mm, respectivamente, con un EEA = 1.5 mm. En la Figura 2 se expone la serie cronológica de los datos y las rectas de las predicciones trazadas según resultados de la Tabla 3.
Tabla 3 Predicciones (mm) en el periodo histórico y a futuro en la estación Zacatecas, Zacatecas, México, con base en la distribución no estacionaria GVE1.
| t | Año | Periodos de retorno (años) | ||||
|---|---|---|---|---|---|---|
| 2 | 10 | 25 | 50 | 100 | ||
| 1 | 1953 | 38.5 | 58.9 | 68.1 | 74.6 | 80.7 |
| 10 | 1962 | 40.5 | 60.9 | 70.1 | 76.6 | 82.7 |
| 20 | 1972 | 42.8 | 63.1 | 72.4 | 78.9 | 85.0 |
| 30 | 1982 | 45.0 | 65.4 | 74.6 | 81.1 | 87.2 |
| 40 | 1992 | 47.3 | 67.6 | 76.9 | 83.3 | 89.5 |
| 50 | 2002 | 49.5 | 69.9 | 79.1 | 85.6 | 91.7 |
| 58 | 2010 | 51.3 | 71.7 | 80.9 | 87.4 | 93.5 |
| 73 | 2025 | 54.7 | 75.0 | 84.3 | 90.8 | 96.9 |
| 98 | 2050 | 60.3 | 80.6 | 89.9 | 96.4 | 102.5 |
| 148 | 2100 | 71.5 | 91.9 | 101.1 | 107.6 | 113.7 |
Predicciones en la estación Las Adjuntas, S.L.P.
Al aplicar las ecuaciones del Apéndice 1 se obtuvo μ0 = 74.9213, μ1 = 0.8813 y r xy = 0.2981. Enseguida se probó la tendencia lineal con las ecuaciones del Apéndice 2; se obtuvo un DS = 2.2520 y un DS c = 2.0066, por lo cual resultó moderadamente significativa.
La serie estacionaria (
En la Tabla 4 se expone una parte de las predicciones dentro de registro histórico y a futuro en los años 2025, 2050 y 2100. Como este registro de 54 datos concluye en 2015, entonces el valor del tiempo t en 2025 es 64, en 2050 es 89 y 2100 es 139. Las predicciones con el modelo estacionario GVE0 de periodos de retorno 2 y 100 años son 87.4 y 280.9 mm, con un EEA = 11.3 mm. En la Figura 3 se expone la serie cronológica de los datos y las rectas de las predicciones dibujadas a partir de los resultados de la Tabla 4.
Tabla 4 Predicciones (mm) en el periodo histórico y a futuro en la estación Las Adjuntas, San Luis Potosí, con base en la distribución no estacionaria GVE1.
| t | Año | Periodos de retorno (años) | ||||
|---|---|---|---|---|---|---|
| 2 | 10 | 25 | 50 | 100 | ||
| 1 | 1961 | 65.7 | 127.8 | 167.0 | 200.2 | 237.2 |
| 10 | 1970 | 73.6 | 135.7 | 174.9 | 208.2 | 245.1 |
| 20 | 1980 | 82.4 | 144.5 | 183.7 | 217.0 | 253.9 |
| 30 | 1991 | 91.2 | 153.4 | 192.6 | 225.8 | 262.7 |
| 40 | 2001 | 100.0 | 162.2 | 201.4 | 234.6 | 271.5 |
| 50 | 2011 | 108.9 | 171.0 | 210.2 | 243.4 | 280.3 |
| 54 | 2015 | 112.4 | 174.5 | 213.7 | 246.9 | 283.9 |
| 64 | 2025 | 121.2 | 183.3 | 222.5 | 255.8 | 292.7 |
| 89 | 2050 | 143.2 | 205.4 | 244.6 | 277.8 | 314.7 |
| 139 | 2100 | 187.3 | 249.4 | 288.6 | 321.8 | 358.8 |
Predicciones en la estación Los Filtros, S.L.P.
Las ecuaciones del Apéndice 3 conducen a los valores siguientes: μ0 = 43.7097, μ1 = -0.2339 y μ2 = 0.0049 como coeficientes de la regresión polinomial (Ecuación (A3.1)).
La serie estacionaria
En la Tabla 5 se muestra una parte de las predicciones dentro de registro histórico y a futuro en los años 2025 y 2050. Como este registro de 66 datos concluye en 2016, entonces, el valor del tiempo t en 2025 es 77 y en 2050 es 102. Las predicciones con el modelo estacionario GVE0 de periodos de retorno 2 y 100 años son 41.5 y 87.5 mm, respectivamente, con un EEA = 3.7 mm. En la Figura 4 se muestra la serie cronológica de los datos y las curvas de predicciones trazadas con base en los resultados de la Tabla 5.
Tabla 5 Predicciones (mm) en el periodo histórico y a futuro en la estación Los Filtros, S.L.P., con base en la distribución no estacionaria GVE2.
| t | Año | Periodos de retorno (años) | ||||
|---|---|---|---|---|---|---|
| 2 | 10 | 25 | 50 | 100 | ||
| 1 | 1949 | 41.3 | 63.6 | 74.0 | 81.4 | 88.6 |
| 10 | 1958 | 39.7 | 62.0 | 72.4 | 79.8 | 86.9 |
| 20 | 1968 | 38.8 | 61.1 | 71.5 | 79.0 | 86.1 |
| 30 | 1978 | 38.9 | 61.2 | 71.7 | 79.1 | 86.2 |
| 40 | 1988 | 40.1 | 62.3 | 72.8 | 80.2 | 87.3 |
| 50 | 1998 | 42.2 | 64.5 | 74.9 | 82.3 | 89.4 |
| 60 | 2008 | 45.3 | 67.5 | 78.0 | 85.4 | 92.5 |
| 68 | 2016 | 48.4 | 70.7 | 81.2 | 88.6 | 95.7 |
| 77 | 2025 | 52.8 | 75.1 | 85.5 | 92.9 | 100.0 |
| 102 | 2050 | 69.0 | 91.3 | 101.8 | 109.2 | 116.3 |
Predicciones
Las cuatro aplicaciones numéricas descritas cubren los casos más comunes que se tienen de registros de PMD i no estacionarios, los cuales corresponden a series con tendencia lineal descendente (severa) y ascendente (leve y moderada), y con tendencia curva ascendente (leve en un contexto apreciativo) hacia el futuro. Las tendencias ascendentes, por lo general ocurren en estaciones pluviométricas ubicadas en ciudades, o en las que se ha construido un gran embalse cercano. En el primer caso existe un aumento de la temperatura por efectos de la isla de calor y, en el segundo, puede acontecer un incremento en la humedad relativa por la evaporación. Las tendencias descendentes pueden estar asociadas con el cambio climático regional.
Como es lógico, las predicciones asociadas con bajas probabilidades de excedencia tienen menor importancia en los registros con tendencia descendente, al ser menores en el futuro. Lo contrario ocurre en series con tendencia ascendente, en las cuales es necesario explicar o justificar el origen físico probable de tal tendencia para aceptar las extrapolaciones de las predicciones a futuro e intentar discernir sobre el alcance real de ellas, ya que resulta extremadamente riesgoso adoptar el comportamiento de tendencia en aumento, cuando, por ejemplo, no se sabe si continuará el desarrollo urbano.
Conclusiones
Los análisis probabilísticos de registros de PMD i no estacionarios que muestran tendencia serán, en el futuro inmediato, cada vez más comunes debido a los impactos del cambio climático y del desarrollo urbano. Un enfoque simple y sin dificultades computacionales para procesar tales registros se basa en la extensión de la teoría de valores extremos a través del ajuste con momentos L, de las distribuciones no estacionarias GVE1 y GVE2 con parámetro de ubicación (u) variable con el tiempo (t), u otras covariables.
A través de la descripción de las cuatro aplicaciones numéricas en registros no estacionarios de PMD i se observa la simplicidad del método expuesto, además de la facilidad para obtener las predicciones asociadas con probabilidades de no excedencia. La selección entre los modelos expuestos (GVE1 y GVE2) depende de la tendencia observada, por ello su contraste gráfico es básico para validar la habilidad descriptiva de las predicciones dentro del registro histórico y en el futuro cercano (años 2025 y 2050). Los resultados numéricos del error estándar de ajuste permitirán el contraste y la aceptación de otros modelos probabilísticos no estacionarios.











 texto en
texto en