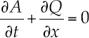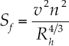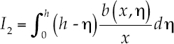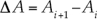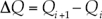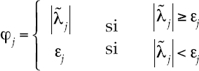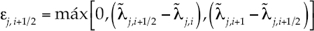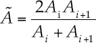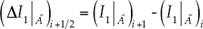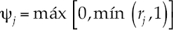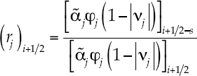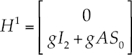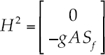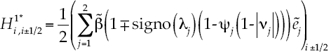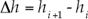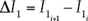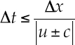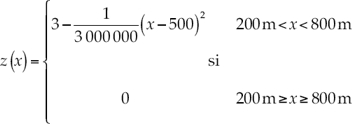Introducción
La ocurrencia simultánea de flujo en lámina libre y flujo en presión en un conducto cerrado se conoce comúnmente como flujo mixto. Este fenómeno se puede encontrar de manera frecuente en colectores pluviales, túneles, tuberías de obras de toma de instalaciones hidroeléctricas, llenado/vaciado de tuberías, colectores de almacenamiento, etcétera. El proceso de transición de flujo en lámina libre a flujo en presión puede ser inducido, entre otras causas, por la variación de caudales de entrada, bloqueo o reducción de la capacidad de la tubería, sumersión de la salida de la tubería, operación de elementos de control (vertedores, compuertas, etc.), fallo de estaciones de bombeo y presencia de pozos de caída (Bourdarias & Gerbi, 2007; Li & McCorquodale, 1999).
En el ámbito urbano, el rol tradicional de una red de alcantarillado ha sido principalmente la conducción de aguas pluviales y aguas residuales. La gran mayoría de los colectores pluviales de una red de drenaje se diseñan para operar en condiciones normales con flujo en lámina libre y régimen lento, considerando caudales de diseño para eventos de precipitación bajos. Cuando la capacidad de uno o más colectores es excedida por un evento de precipitación, lo que no es raro, o por cambios bruscos en las condiciones de contorno, el tipo de flujo puede cambiar de lámina libre a flujo en presión.
Durante la transición de flujo en lámina libre a flujo en presión pueden ocurrir fuertes transitorios de presión y provocar daños a los colectores, levantamiento de tapas de los pozos de visita, expulsión de agua e inundación de la superficie urbana (Li & McCorquodale, 1999). Los frentes de onda generados en la transición de flujo en lámina libre a flujo en presión pueden ser de dos tipos: gradual, que consiste de un frente de onda en lámina libre con condiciones de flujo en lámina libre en ambos lados del frente, y brusco, que es un frente de onda a conducto lleno con condiciones de flujo en lámina libre adelante y de flujo en presión atrás del frente (Wright, Vasconcelos, Creech, & Lewis, 2008).
Para modelar el flujo mixto existen diferentes aproximaciones, como el método de la columna rígida (Li & McCorquodale, 1999) y las incluidas dentro de los modelos dinámicos. Los modelos dinámicos se pueden clasificar en aquellos que utilizan uno o dos sistemas de ecuaciones. Los métodos que utilizan un sistema de ecuaciones requieren de una aproximación adicional para considerar flujo en presión. Entre estas aproximaciones se encuentran el método TPA (Two-Component Pressure Approach) (Vasconcelos, Wright, & Roe, 2006) y el método de la ranura de Preissmann, uno de los más conocidos y utilizados.
Preissmann (1961) fue quien reconoció la similitud de la forma entre canales abiertos y conductos cerrados; además, propuso que una ranura hipotética se agregara a la clave de los conductos cerrados, tal que tanto el flujo en lámina libre como el flujo en presión pudieran ser analizados mediante las ecuaciones de Saint Venant en una dimensión (Li & McCorquodale, 1999). El método de la ranura de Preissmann fue implementado por primera vez por Cunge y Wegner (1964), al estudiar flujo en presión, posteriormente varios autores (Capart, Sillen, & Zech, 1997; García-Navarro, Priestley, & Alcrudo, 1994; Ji, 1998; Kerger, Archambeau, Erpicum, Dewals, & Pirotton, 2011; León, Ghidaoui, Schmidt, & García, 2009; Song, Cardle, & Leung, 1983; Trajkovic, Ivetic, Calomino, & D’Ippolito, 1999) han desarrollado modelos numéricos basados en este método para simular flujo mixto.
Cuando se usa esta aproximación pueden aparecer cuatro limitaciones principales asociadas con la aproximación misma y con el esquema numérico empleado para resolver las ecuaciones del flujo. La primera es que asume flujo a superficie libre en todo el sistema; por consiguiente, si la carga piezométrica cae por debajo de la clave del colector se desarrolla flujo en lámina libre y por tanto es incapaz de simular flujo en presión subatmosférica (León et al., 2009, León, Ghidaoui, Schmidt, & García, 2010; Li & McCorquodale, 1999; Politano, Odgaard, & Klecan, 2007; Vasconcelos et al., 2006); la segunda, inestabilidades asociadas con el pobre desempeño del esquema numérico cuando el flujo cambia rápidamente de flujo en lámina libre a flujo en presión; la tercera, inconsistencias en el balance de masa y momento asociados con el ancho de la ranura; la cuarta, inexactitudes en la propagación de transitorios hidráulicos relacionados con el ancho de la ranura (León et al., 2009).
Para superar la primera limitación, recientemente Kerger et al. (2011) ampliaron el concepto de la ranura de Preissmann, desarrollando la ranura de Preissmann negativa, que consiste en extender la ranura por debajo de la clave de la tubería para modelar flujos con presiones subatmosféricas o negativas, y aire atrapado, acoplando un modelo matemático de equilibrio homogéneo. Con respecto a la segunda, León et al. (2009) propusieron una modificación al método, introduciendo una transición geométrica gradual entre la tubería y la ranura, desde 0.95 hasta 1.5 veces el diámetro de la tubería. Esta modificación permite que exista continuidad en la velocidad de la onda en lámina libre y en presión, en función del ancho de la ranura; mientras que Barnett (2010) sugiere una transición geométrica exponencial del tipo w = T s e kz ; w es el ancho de la ranura al nivel z, medida hacia abajo desde el punto donde w = T s y T s es el ancho de la ranura de Preissmann en función de la celeridad de la onda de presión a. La forma de la ranura depende esencialmente del parámetro k; valores más pequeños corresponden a transiciones más elongadas. Con este tipo de transiciones existe un aumento del área de la sección tanto en el colector como en la ranura, que conlleva un almacenamiento extra no real en dicha transición, por lo que pueden aumentar los problemas relacionados con la tercera y cuarta limitación.
El método de la ranura de Preissmann ha sido usado para la modelación de transición gradual (suave) de flujo mixto con éxito, y transición brusca (rápida) con poco éxito o sin éxito. El poco éxito en la modelación es principalmente consecuencia de los problemas de inestabilidad si la onda de presurización es demasiado brusca, lo cual puede causar que la simulación aborte incluso para anchos de la ranura 0.1 veces el diámetro (León et al., 2009).
Por otra parte, para la solución de sistemas de ecuaciones hiperbólicas, como las ecuaciones de Saint Venant, actualmente existen diferentes esquemas, entre ellos los métodos directos (Shock Capturing Methods), que son muy atractivos, pues permiten describir o capturar discontinuidades del flujo (p. ej., frentes de onda, resaltos hidráulicos) de forma automática (Toro, 1999). Estos métodos inicialmente fueron desarrollados en el campo de la dinámica de gases y después extendidos a la hidráulica de ríos y canales (Bladé, Gómez-Valentín, Sánchez-Juny, & Dolz, 2008; Toro & García-Navarro, 2008). En los últimos años, estos esquemas han sido utilizados para el cálculo de flujo mixto (Aragón-Hernández, Concha, Bladé, & Gómez, 2009; Capart et al., 1997; León et al., 2009; Sanders & Bradford, 2011; Vasconcelos et al., 2006).
El objetivo de este trabajo es presentar el desarrollo de un modelo numérico estable y robusto, incluso para transiciones bruscas, para reproducir flujo mixto en conductos cerrados. El modelo emplea las ecuaciones completas de Saint Venant en una dimensión para el flujo en lámina libre y el método de la ranura de Preissmann para considerar flujo en presión. La resolución numérica de dichas ecuaciones se realiza con el método de los volúmenes finitos con un esquema conservativo y descentrado de primer orden más unas correcciones de segundo orden, para finalmente obtener un esquema con una precisión de alta resolución. En específico, este esquema numérico ampliamente utilizado en ríos será evaluado por primera vez al modelar flujo mixto en conductos cerrados y de entrada permitirá superar la segunda limitación mencionada.
Este modelo forma parte de una investigación más amplia relacionada con la modelación numérica de la dinámica del agua en zonas urbanas. El modelo se integra dentro de un modelo más general que se utiliza para simular el comportamiento hidráulico del flujo de agua en el sistema de drenaje superficial o sistema de drenaje mayor (canales, tejados, calles, aceras) y en el sistema de drenaje subsuperficial o sistema de drenaje menor (colectores, unión de colectores), integrado completamente a través del intercambio de flujo en los puntos físicos correspondientes (rejas, pozos de visita) en ambas direcciones, conocido como drenaje urbano dual (Aragón-Hernández, 2013).
Para validar el modelo numérico desarrollado, se emplea un caso de referencia y dos ensayos de laboratorio existentes en la literatura técnica. En dichos casos de validación se incluye la mayoría de los tipos de flujo que de forma general se pueden presentar en conductos cerrados y, sobre todo, en colectores pluviales, como flujo en lámina libre en régimen lento, rápido y transcrítico, y flujo mixto.
Así, el trabajo se estructura en cinco apartados. En el primero se describen las ecuaciones para flujo en lámina libre; en el segundo, la aproximación para considerar flujo en presión; en el tercero se plantea el esquema numérico; en el cuarto se hace la validación numérica, y finalmente, en el quinto se presentan las conclusiones.
Flujo en lámina libre
Para modelar flujo en lámina libre se utilizan las ecuaciones completas de Saint Venant en una dimensión. La deducción de estas ecuaciones se realiza de manera directa aplicando las leyes de conservación de la masa y cantidad de movimiento a un volumen de control, considerando una sección arbitraria y canal no prismático, resultando un sistema de ecuaciones en forma conservativa (Chaudhry, 1993):
Utilizando notación vectorial resulta:
Donde el vector de variables conservativas U, el vector de flujo F y el término fuente H responden a las expresiones:
En las expresiones anteriores, A es el área de la sección mojada; Q, el caudal circulante; g, la aceleración de la fuerza de gravedad; x, la coordenada longitudinal en dirección del flujo; t, el tiempo; S 0, la pendiente del terreno; S f , la pendiente de fricción o motriz; I 1, la fuerza debida a la presión del agua en una sección o momento de primer orden de la sección respecto a la superficie libre del agua, e I 2 es la contribución de las fuerzas de presión del contorno; las tres últimas se expresan, respectivamente, como:
Donde n es el coeficiente de fricción de Manning; R h , el radio hidráulico; h, el calado; v, la velocidad del flujo; b, el ancho de la superficie libre del agua, y η es la profundidad del centro de gravedad de la sección. Para canales prismáticos, aunque tengan una sección cualquiera, el término I 2 es idénticamente igual a cero. Tal es el caso de la mayoría de los conductos cerrados.
Flujo mixto
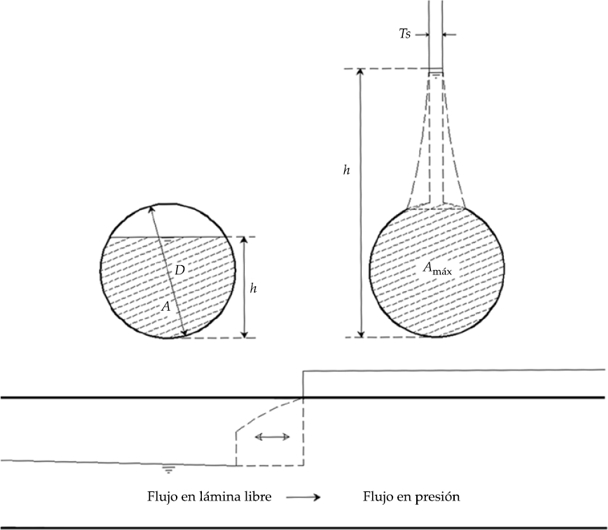
Como se definió antes, el flujo mixto es la ocurrencia al mismo tiempo de flujo en lámina libre y flujo en presión en un conducto cerrado. Cuando se usa un modelo dinámico de un solo sistema de ecuaciones es necesaria una aproximación adicional; en este trabajo se utiliza el método de la ranura de Preissmann. El método consiste en implementar una ranura hipotética de ancho T s en la clave de los conductos cerrados (figura 1), proporcionando la presión hidrostática extra, mientras que se permite el uso de las ecuaciones de flujo en lámina libre para ambos tipos de flujo (flujo en lámina libre y flujo en presión) (Capart, Bogaerts, & Kevers-Leclercq, 1999; García-Navarro et al., 1994; León et al., 2009; Politano et al., 2007; Preissmann, 1961).
En esencia, esta aproximación explota la similitud de la ecuación de onda del flujo en lámina libre y flujo en presión. Así, a partir de la ecuación (8), que define la celeridad de la onda de gravedad, y para evitar caer en el tercer y cuarto problema asociados con el ancho de la ranura, ésta se calcula bajo la consideración de que la celeridad de la onda de presión a es igual a la celeridad de la onda de gravedad c y el área a tubo lleno A máx.
De esta forma, el ancho de la ranura de Preissmann T S queda definido como:
Cuando en un colector ocurre flujo en presión, el calado calculado es la carga de presión. Cuando se usa un ancho de ranura pequeño para poder representar grandes niveles de agua o una velocidad de onda grande, el método es numéricamente inestable (Politano et al., 2007; Yen, 1978); tales inestabilidades pueden ser removidas haciendo ranuras más anchas. Sin embargo, cambiar el ancho de la ranura destruye la equivalencia con la celeridad de la onda mencionada anteriormente. El ancho de la ranura es un parámetro significativo y una elección óptima del mismo determinará la calidad de los resultados. Es importante destacar que al implementar este método, la ranura no debería aumentar el área de la sección transversal ni el radio hidráulico del conducto en presión (Chaudhry, 1987), pero en la práctica se permite utilizar ranuras con un ancho de hasta 0.1D, donde D es el diámetro de la tubería (Trajkovic et al., 1999).
Debido a que se utiliza un único sistema de ecuaciones, no hay necesidad de rastrear la propagación del movimiento de la interfase entre el flujo en lámina libre y flujo en presión (Li & McCorquodale, 1999; Vasconcelos et al., 2006), el cual puede ser capturado como ondas de choque o frentes de onda con los métodos directos (Toro, 1999).
Esquema numérico
Para la resolución de las ecuaciones de Saint Venant en una dimensión se utiliza el método de los volúmenes finitos. El método de volúmenes finitos se basa en las ecuaciones de gobierno escritas en forma integral sobre una celda o volumen finito. El dominio de estudio o malla de cálculo se discretiza en un dominio espacial x en celdas de longitud Δx y un dominio temporal t, en intervalos de tiempo Δt. Las variables hidráulicas utilizadas (A, Q) representan el valor medio de las variables dependientes en cada celda i, centradas en el nodo x i y se extienden de i - ½ a i + ½. De esta forma, el esquema numérico para la solución de la ecuación (3) viene dado por:
Donde 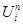 y
y  son los valores medios del vector U en la celda i en el instante de tiempo t
n
y t
n+1
, respectivamente; F*1±1/2 es el flujo numérico en las interceldas, y H*
i
es un valor representativo del promedio del término fuente H en la celda i en el instante de tiempo t
n
y t
n+1
. F*1±1/2 y H*
i
en general dependen de las celdas contiguas a la celda i en los instantes de tiempo t
n
y t
n+1
.
son los valores medios del vector U en la celda i en el instante de tiempo t
n
y t
n+1
, respectivamente; F*1±1/2 es el flujo numérico en las interceldas, y H*
i
es un valor representativo del promedio del término fuente H en la celda i en el instante de tiempo t
n
y t
n+1
. F*1±1/2 y H*
i
en general dependen de las celdas contiguas a la celda i en los instantes de tiempo t
n
y t
n+1
.
El método de Godunov es un esquema conservativo que utiliza una discretización descentrada en volúmenes finitos, cuya particularidad es que el flujo numérico F*1±1/2 entre dos celdas i, e i + 1 se obtiene de la solución de un problema de Riemann local entre dos estados constantes 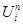 y
y  . El problema de Riemann tiene una estructura compleja y encontrar su solución es costoso, por lo cual diversos autores (Harten, Lax, & Van Leer, 1983; Osher & Solomon, 1982; Roe, 1981) desarrollaron métodos para encontrar una respuesta aproximada del problema de Riemann, conocidos como aproximate Riemann solvers (Toro, 1999). Uno de ellos es el Riemann solver de Roe, empleado en este trabajo, el cual lleva a un esquema conservativo denominado método de Godunov con el Riemann solver de Roe; este esquema es de primer orden de precisión.
. El problema de Riemann tiene una estructura compleja y encontrar su solución es costoso, por lo cual diversos autores (Harten, Lax, & Van Leer, 1983; Osher & Solomon, 1982; Roe, 1981) desarrollaron métodos para encontrar una respuesta aproximada del problema de Riemann, conocidos como aproximate Riemann solvers (Toro, 1999). Uno de ellos es el Riemann solver de Roe, empleado en este trabajo, el cual lleva a un esquema conservativo denominado método de Godunov con el Riemann solver de Roe; este esquema es de primer orden de precisión.
En zonas cercanas a fuertes gradientes o donde se presentan discontinuidades de la solución, los esquemas de primer orden son disipativos (amplitud de la onda menor a la de la solución exacta), mientras que los esquemas de segundo orden son dispersivos (producen oscilaciones en la solución). Por esta razón, se necesitan esquemas de segundo orden o mayor, que no presenten dispersión en las discontinuidades, como los esquemas TVD (Total Variation Dimishing). Un esquema así se puede obtener a partir de un esquema de primer orden más un esquema de segundo orden. Para evitar la dispersión del esquema de segundo orden se debe limitar el flujo numérico del mismo; en este trabajo se utiliza el esquema WAF (Weight Averaged Flux). Así, el esquema numérico WAF-TVD resultante se puede escribir como un esquema de primer orden más unas correcciones de segundo orden, para conseguir que la precisión sea de alta resolución (Bladé, 2005):
Donde:
Los coeficientes constantes o las llamadas fuerzas de cada onda 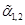 , los valores y vectores propios
, los valores y vectores propios 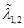 y
y  de la matriz jacobiana definida como
de la matriz jacobiana definida como 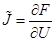 se escriben, respectivamente, como:
se escriben, respectivamente, como:
La velocidad  , los incrementos de área hidráulica ΔA y del caudal circulante ΔQ se definen como:
, los incrementos de área hidráulica ΔA y del caudal circulante ΔQ se definen como:
De la descomposición de los vectores propios resulta 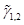 , definida como:
, definida como:
La corrección de entropía de Harten e Hyman  , según Toro (1999), es:
, según Toro (1999), es:
Donde:
Algunas formulaciones utilizadas para la celeridad promedio c no reproducen el salto de las fuerzas de presión, por lo que en este trabajo se utiliza una expresión que mantiene el significado físico de la celeridad, entendido como la variación de las fuerzas de presión respecto a la variación del área de flujo en cada sección transversal (Bladé et al., 2008):
El área hidráulica  y el ancho de la superficie libre del agua
y el ancho de la superficie libre del agua  son:
son:
La variación de las fuerzas de presión  para un área constante
para un área constante  es:
es:
Donde 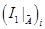 y
y  son las fuerzas de presión en el volumen finito i e i + 1 para un valor del área
son las fuerzas de presión en el volumen finito i e i + 1 para un valor del área  .
.
Una de las funciones de limitación ψj más utilizadas y también la empleada en este trabajo es la función la de Minmod, definida como:
Donde r j es un indicador del salto que sufre la solución a través de una onda en el contorno aguas arriba del elemento de volumen respecto del mismo salto en el otro contorno. Una posible expresión es el cociente entre contribuciones de la onda j y el término que hace que el esquema sea de segundo orden, ya que éstas son precisamente las que provocan las oscilaciones espurias, es:
Por otra parte, para el tratamiento del término independiente H, es conveniente la descomposición del mismo en función de los términos de fricción y de los términos de la pendiente del fondo, como:
En la ecuación (10), H i * es la expresión numérica del término independiente H y representa el término independiente integrado en todo el volumen finito; por lo tanto, considerando (28), se tiene:
El término H i *2, que incluye los términos de fricción, se puede considerar en una discretización centrada simple como:
Mientras que según Vázquez-Cendón (1999), H
i
*1, los términos de la pendiente del fondo deben discretizarse de acuerdo con el esquema numérico utilizado; para satisfacer la propiedad de conservación exacta puede ser dividido en dos contribuciones en las fronteras del volumen finito y descompuesto sobre los vectores propios de la matriz jacobiana 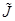 de la siguiente manera:
de la siguiente manera:
Donde:
Los coeficientes  , los incrementos de calado o carga de presión Δh, de las fuerzas de presión ΔI1 y de la elevación del fondo del colector Δz quedan definidos como:
, los incrementos de calado o carga de presión Δh, de las fuerzas de presión ΔI1 y de la elevación del fondo del colector Δz quedan definidos como:
Los esquemas numéricos como los anteriores son esquemas explícitos que tienen un coste computacional pequeño en cada paso de tiempo, pero para ser estables necesitan trabajar con incrementos de tiempo también pequeños y deben cumplir con la condición de estabilidad de Courant-Friedrichs-Lewy (Chaudhry, 1993). La condición significa que ninguna onda presente en el dominio viaja más de una distancia Δx en un tiempo Δt. Así, para el esquema numérico se tiene:
Lo cual también se pueden escribir según el llamado número de Courant-Friedrichs-Lewy (CFL), como:
Validación numérica
Para validar el modelo numérico desarrollado, en esta sección se presentan un caso de referencia y dos ensayos de laboratorio existentes en la literatura técnica. En los casos de validación se presentan flujos que son muy comunes que ocurran en colectores pluviales y otros conductos cerrados. Los tipos de flujo involucrados son flujo en lámina libre y flujo mixto. En el caso de flujo en lámina libre, puede existir flujo con régimen lento, rápido y transcrítico (de lento a rápido y de rápido a lento).
Así, el flujo en régimen lento aparece en los tres casos de validación numérica, mientras que el flujo en régimen rápido se exhibe en el primer y tercer caso de validación numérica; por otro lado, el flujo en régimen transcrítico de lento a rápido ocurre en el primer caso de validación; mientras que, de rápido a lento a través de un resalto hidráulico, se manifiesta en el tercer ensayo y, en este mismo, se presenta flujo mixto. Dichos casos se exponen a continuación.
Flujo en régimen transcrítico
Para demostrar la habilidad del modelo para reproducir régimen transcrítico, éste es aplicado a un caso de referencia sencillo; este caso sirve para validar el desempeño del esquema numérico al discretizar los términos convectivos, que por lo general causan las inestabilidades numéricas; es decir, no se consideran la influencia de la pendiente del fondo y la pendiente de fricción.
Para ello, se toma en cuenta un canal prismático horizontal con una sobreelevación suave del fondo de forma parabólica. Utilizando las condiciones de contorno adecuadas se consigue que el flujo sobre el obstáculo sea en régimen lento, rápido o transcrítico (de rápido a lento o de lento a rápido). En esta oportunidad se considera flujo en régimen transcrítico de lento a rápido. El canal de sección rectangular tiene 1 000 m de largo, 10 m de ancho y sin rugosidad. Las condiciones de contorno son las siguientes: aguas arriba, un caudal constante de 300 m3/s; aguas abajo se considera flujo supercrítico (cuando aguas abajo de la sobreelevación se presenta flujo subcrítico, se utiliza la condición de calado crítico; es decir, existe una caída libre). La condición inicial es un caudal nulo y la superficie libre del agua correspondiente al calado crítico impuesto aguas abajo. La cota del fondo del canal viene dada por:
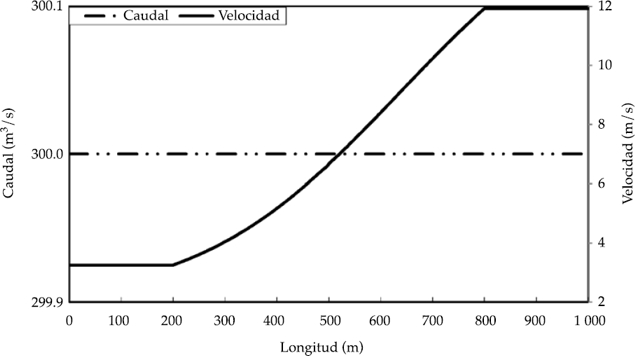
El dominio de cálculo se discretizó en celdas de 4 m. De esta forma, la cota de la lámina de agua resultado de la aplicación del modelo se observa en la figura 2. El flujo crítico se presenta cuando el número de Froude es igual a uno; esto se produce en el punto localizado en x = 500 m. En este punto, el calado corresponde al calado crítico con un valor de 4.51 m. Además, en este mismo punto se produce el cambio de régimen; aguas arriba del mismo existe régimen lento y aguas abajo régimen rápido.
También, en la figura 3 se pueden ver los valores de la velocidad a lo largo del canal; dichos valores son suaves y continuos. Además, y para mostrar la bondad del método implementado, se utilizó el método paso a paso (Chaudhry, 1993) para calcular la curva de remanso correspondiente. Los resultados obtenidos con el modelo numérico y el calculado con el método paso a paso son muy similares, por lo que los obtenidos con este último no se graficaron debido a que las diferencias son imperceptibles, siendo siempre menores a 1 mm. Tanto los valores del calado como los de las velocidades, en conjunto con la comparación mencionada, dejan evidencia de la capacidad del esquema numérico para simular flujo en régimen permanente.
Propagación hidráulica en un colector
Los experimentos de Ackers & Harrison (1964) sobre la propagación de flujo a superficie libre se realizaron en un colector circular con diámetro de 0.0762 m. Los datos originales del experimento no están disponibles, pero sí los valores correspondientes a una escala 1:4, bajo semejanza de Froude (White, 2004). Siguiendo a León, Ghidaoui, Schmidt y García (2006), al igual que a Sanders y Bradford (2011), los datos escalados de laboratorio son una tubería con una longitud de 304.8 m, diámetro de 0.3048 m, pendiente de 0.001, coeficiente de fricción de Manning de 0.0115 s/m1/3 para el caudal base y 0.0116 s/m1/3 para el caudal punta. La prueba se inicia en flujo permanente, con un caudal base de 0.004984 m3/s y un calado normal en el extremo aguas abajo de 0.0768 m; después se impone un hidrograma trapecial simétrico. El hidrograma es caracterizado por un caudal punta de 0.018689 m3/s durante 12 s, y 60 s en las ramas ascendente y descendente. Aguas abajo se consideró caída libre para forzar la existencia de flujo crítico. Los calados fueron medidos en dos puntos localizados en x = 8.66 m y x = 77.94 m desde el extremo aguas arriba.
El modelo numérico de flujo en lámina libre se aplicó utilizando 348 volúmenes finitos. En la figura 4 se observan los calados medidos y calculados en x = 8.66 m y x = 77.94 m.
La figura 4 muestra que el modelo predice adecuadamente el hidrograma en el punto localizado en x = 77.94 m, la rama ascendente y el calado en la punta del hidrograma del punto correspondiente a x = 8.66 m; sin embargo, en la rama descendente existen algunas diferencias. Las diferencias mostradas fueron reportadas también por otros autores (León et al., 2006; Sanders & Bradford, 2011), quienes reprodujeron numéricamente este experimento. Según León et al. (2006), con base en otros autores, las diferencias son consecuencia de posibles problemas de escala y al hecho de que el experimento incluye caudales en la región de transición entre flujo laminar y flujo completamente turbulento. Lo anterior causa que el coeficiente de fricción de Manning sea una función del número de Reynolds.
Entrada en carga desde aguas abajo
En la literatura técnica, el flujo mixto se ha estudiado de forma experimental y numérica, en especial con la entrada en carga desde aguas abajo; pero el flujo mixto con entrada en carga desde aguas arriba y por ambos extremos de forma simultánea también es posible. En este trabajo se modela numéricamente el experimento de flujo mixto de Trajkovic et al. (1999), correspondiente a la entrada en carga desde aguas abajo.
El dispositivo experimental utilizado consiste de una tubería de metacrilato de sección circular de 10 m de longitud, un diámetro interno de 0.10 m y un coeficiente de rugosidad de Manning de 0.008 s/m1/3. Se colocaron dos compuertas automáticas en los extremos aguas arriba y aguas abajo de la tubería, respectivamente. Con la operación de estas compuertas, las condiciones del flujo se pueden cambiar de forma rápida. Se colocaron tubos de ventilación en la clave de la tubería para evitar la posible interferencia de la fase de aire. Se llevaron a cabo diferentes tipos de ensayos, variando la pendiente de la tubería, condiciones iniciales y condiciones de contorno a través de la operación de las compuertas (Trajkovic et al., 1999).
En los experimentos tipo A, los autores utilizaron una pendiente de la tubería del 2.7%. Las condiciones del experimento fueron un caudal de entrada constante de 0.0013 m3/s, correspondiente a una apertura de la compuerta en el extremo aguas arriba de e 1 = 0.014 m, y en el extremo aguas abajo, la compuerta totalmente abierta con un calado normal de 0.1 veces el diámetro. Debido a ello, el tipo de flujo es permanente y supercrítico. En un instante de tiempo dado del experimento, la compuerta del extremo aguas abajo fue cerrada rápidamente (cierre no instantáneo), generando un transitorio en forma de frente de onda positivo moviéndose hacia aguas arriba. Después de 30 s del cierre, la compuerta fue reabierta de forma parcial, produciendo otro fenómeno transitorio. Se probaron diferentes valores para la reapertura de la compuerta; el correspondiente a una apertura de e 2 = 0.008 m es el considerado para la validación. Con esta apertura se registró una pequeña disminución de la carga de presión en el instante de tiempo 30 s, pero debido a que el caudal de salida en la tubería es menor al de entrada, la carga de presión continuó incrementándose. Se midieron valores de la carga de presión en lo puntos P5 y P7, localizados en x = 7.2 m y x = 9.2 m desde el extremo aguas arriba, respectivamente.
Para la modelación numérica de este experimento se utilizaron volúmenes finitos de 0.10 m, una celeridad de la onda de 6 m/s, correspondiente a una ranura de Preissmann de 0.021 veces el diámetro; el valor de la celeridad se utilizó como una variable de calibración, por lo que corresponde a la que tiene un error relativo menor. La carga de presión medida y calculada se muestra en la figura 5.

Figura 5 Carga de presión medida y calculada en las secciones P5 y P7 para la reapertura de compuerta e 2 = 0.008 m.
En la figura 5 se puede observar que la carga de presión calculada coincide con la medida, incluso cuando se presenta la reapertura de la compuerta; el error relativo es de 3.7 y 3.1% para el punto P5 y P7, respectivamente. Por otra parte, la velocidad del frente de onda fue reproducida con buena aproximación (diferencia menor a 1 s en el punto P7 e inexistente en el punto P5); en cambio, la forma del frente de onda calculado es más pronunciada que el medido (diferencias máximas de 2.3 y 2.7 cm en los puntos P5 y P7, respectivamente). Algunos autores (León et al., 2009; Trajkovic et al., 1999) que han reproducido este experimento asumen que esta diferencia se debe a que en los cálculos el cierre de la compuerta aguas abajo se considera de manera instantánea, mientras que en los ensayos hay un periodo de tiempo para realizar tal acción. En este trabajo se simuló el tiempo de cierre de la compuerta con distintas duraciones (0-2 s); los resultados no mejoraron la forma del frente de onda, por lo que dicha diferencia podría tener otro origen, probablemente relacionada con la discontinuidad del flujo. Para los esquemas numéricos empleados, el salto hidráulico es una discontinuidad en la solución y se modela como tal (las variables hidráulicas de la celda dependen de las celdas vecinas solamente), y la discontinuidad se produce en una distancia corta, mientras que la longitud del resalto hidráulico que se produce en el ensayo es mayor. Lo anterior podría mejorarse empleando volúmenes finitos de menor tamaño (acción no realizada).
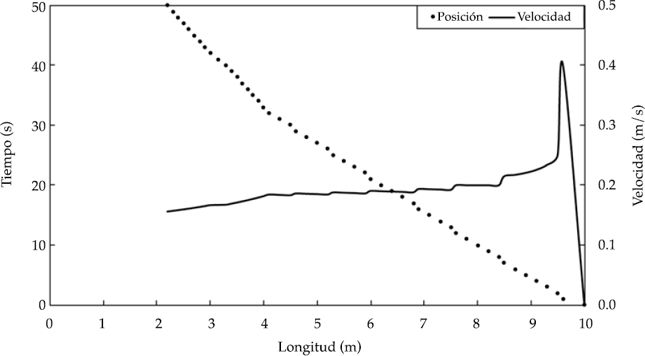
En la figura 6 se muestra la posición con respecto al tiempo y la velocidad del frente de onda a lo largo de la tubería. En ésta se observa que instantes posteriores a la apertura de la compuerta, la velocidad alcanza valores de hasta de 0.4 m/s; después, a medida que el resalto hidráulico se propaga hacia aguas arriba, el valor de la velocidad comienza a descender hasta llegar a un valor de 0.16 m/s al final de la simulación. Tanto la velocidad como la posición tienen un cambio en su comportamiento al momento de la reapertura parcial de la compuerta, lo que provoca una disminución de la velocidad del frente de onda y, por tanto, un cambio de pendiente en la línea que representa la posición del mismo.
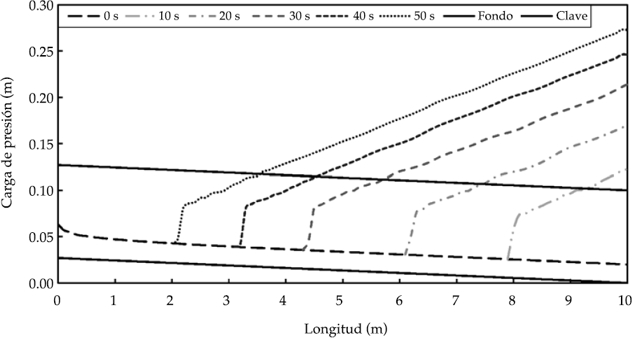
Finalmente, en la figura 7 se muestran las condiciones del flujo antes del cierre de la compuerta en el extremo aguas abajo del colector; el flujo es en lámina libre con régimen permanente y supercrítico. En el momento en que se realiza el cierre rápido de la compuerta se genera un frente de onda que propicia un cambio de régimen (de rápido a lento), lo cual obliga a la formación de un resalto hidráulico que de inmediato provoca la entrada en carga del colector y éste se propaga hacia aguas arriba. De la misma manera, en la reapertura parcial de la compuerta se aprecia la disminución de la velocidad del frente de onda, la cual se manifiesta como una disminución en la separación entre las líneas punteadas que representan la carga de presión a lo largo del colector en distintos instantes de tiempo, con una separación temporal constante (cada 10 s).
Conclusiones
En este trabajo se desarrolló un modelo numérico para reproducir flujo en lámina libre y flujo en presión de forma simultánea (flujo mixto) en conductos cerrados. El modelo es capaz de reproducir flujo en lámina libre en régimen lento, rápido y transcrítico, con presencia de discontinuidades sin necesidad de cálculos adicionales. La capacidad del modelo para simular flujo en régimen lento y rápido de forma automática es gracias a que el esquema numérico utilizado es un esquema conservativo y descentrado en volúmenes finitos. El flujo en presión se modela con la ayuda del método de la ranura de Preissmann.
En el primer caso de la validación numérica, los resultados obtenidos permiten deducir que el modelo, en primer lugar, es capaz de reproducir flujo en régimen transcrítico de lento a rápido de forma precisa, tal como lo muestra la comparación con el método paso a paso. La localización y el valor del calado crítico son correctos, además de obtenerse diferencias en lámina de agua menores a 0.001 m, consideradas despreciables. En segundo lugar, el modelo es capaz de simular flujo permanente, que algunos modelos numéricos son incapaces de preservar.
En el segundo caso, el modelo se utilizó para la propagación hidráulica de un hidrograma en un colector circular en régimen lento. Se trata de una actividad muy común en la ingeniería práctica para determinar la atenuación y traslación del hidrograma a su paso por un conducto. Los resultados muestran que, de forma general, el modelo reproduce muy bien el experimento, salvo la rama descendente del punto de medida más próximo al extremo aguas arriba, x = 8.66 m. Resultados similares fueron obtenidos por otros autores, indicando que las diferencias son debidas, entre otras causas, al problema del escalado de los datos.
Finalmente, el tercer caso es muy especial, pues se presenta flujo en régimen supercrítico cuando el colector trabaja con la compuerta aguas abajo totalmente abierta; flujo en régimen transcrítico de rápido a lento a través de un resalto hidráulico al cerrarse la compuerta aguas abajo, el cual se conserva durante el tiempo que dura el experimento; flujo en presión provocado también por el cierre de la compuerta aguas abajo, al alcanzar la lámina de agua la clave del colector. La variedad de flujos y fenómenos hidráulicos que se presentan en un espacio tan pequeño y un tiempo tan corto son un reto para los modelos numéricos; en este caso, el modelo numérico desarrollado fue capaz de reproducir el ensayo de forma más que aceptable y robusta.











 nueva página del texto (beta)
nueva página del texto (beta)