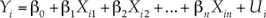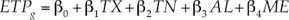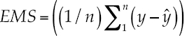Introducción
La evapotranspiración (ET) es la transmisión de agua de la tierra a la atmósfera por procesos de evaporación de la superficie del suelo y transpiración de las plantas (Wang & Dickinson, 2012). La ET es un fenómeno complejo que controla el intercambio de masa y energía en el sistema atmosférico global y se considera como una herramienta útil para el monitoreo del cambio de energía y transferencia de humedad del suelo a la atmósfera, pues es gobernado por diversas variables climáticas, como radiación, temperatura, velocidad del viento, humedad atmosférica y su efecto en la humedad del suelo, y el albedo (Chen, Liu, & Thomas, 2006; Kousari & Ahani, 2012). Dos conceptos relacionados con la ET son la evapotranspiración real o de referencia (ET 0), y la evapotranspiración potencial (ETP). La ET 0 es definida como la cantidad de agua perdida por el complejo suelo-planta en las condiciones meteorológicas, edáficas y biológicas existentes; mientras que la ETP es la máxima cantidad de agua capaz de ser perdida por una capa continua de vegetación que cubre todo el terreno, cuando la cantidad de agua suministrada al suelo es ilimitada (Ortiz-Solorio, 2011). Aun cuando se reconoce que estos conceptos son diferentes, ambos indican cantidades máximas de agua perdida en favor de la atmósfera; por ello, en algunos estudios, han sido considerados como equivalentes (McKenney & Rosenberg, 1993; Henríquez-Dole & Miner-Vega, 2014). La estimación precisa de la ETP es importante para asegurar el uso del agua con aplicaciones agrícolas y ecológicas, manejo de recursos naturales y otras actividades de planeación (Villa-Nova, Pereira, & Shock, 2007; Bates, Kundzewics, Wu, & Palutikof, 2008; Suleiman & Hoogenboom, 2009). Existen diferentes ecuaciones empíricas y teóricas para estimar el valor de la ETP bajo ciertas condiciones climáticas (El-Nashar & Hussein, 2013), por ejemplo, los métodos de Penman (PN) (Penman, 1948), Penman-Monteith (PM) (Allen, Pereira, Raes, & Smith, 1998), y Hargreaves y Samani (HS) (1985), entre otros. No obstante, la selección de la ecuación a emplear depende de la disponibilidad de datos climáticos en una región determinada y la precisión requerida (El-Nashar & Hussein, 2013). En este sentido, las ecuaciones de PN y PM se basan en un balance de energía, siendo PM la más utilizada y considerada como método estándar; sin embargo, tienen la desventaja de requerir parámetros específicos (radiación solar, temperatura del aire, humedad, presión de vapor y velocidad del viento), que en muchas ocasiones no se encuentran en estaciones meteorológicas (EM) comunes, problema que se incrementa en países en vías de desarrollo (Droogers & Allen, 2002). Al respecto, la ecuación HS es una alternativa cuando los datos son escasos, ya que sus resultados se ajustan a los de PM (Trezza, 2008; Vásquez-Méndez, Ventura-Ramos, & Acosta-Gallegos, 2011; De Melo & Fernandes, 2012; Moeletsi, Walker, & Hamandawana, 2013; Chen et al., 2014). Para México, el método de HS se recomienda para estimaciones de ETP cuando el método de PN no es aplicable por falta de datos meteorológicos (Campos-Aranda, 2005). El método de HS utiliza la temperatura media y la amplitud estacional a partir de datos de temperaturas máximas (TX) y mínimas (TN), además de datos geográficos, como la latitud de las EM o del sitio de estudio, para la estimación de la radiación extraterrestre (Hargreaves & Samani, 1985). Aunque, para la obtención de la radiación, también pueden utilizarse mapas de radiación solar incidente (Campos-Aranda, 2005), poco comunes en México. Las TX y TN son trascendentes en el modelo de HS, mientras que en el modelo de PN son útiles en el cálculo del déficit de vapor a saturación (Allen et al., 1998; Ortiz-Solorio, 2011), lo cual resalta la importancia de la temperatura en el comportamiento de la ETP. Asimismo, diferentes investigadores han planteado que la altitud (AL) influye en la ETP, pues ésta tiende a disminuir cuando la AL aumenta (Jaramillo-Robledo, 2006; Vega & Jara, 2009; Henríquez-Dole & Miner-Vega, 2014), a consecuencia del gradiente alto-térmico (Velázquez-Ruiz, Martínez, & Carrillo-González, 2012), lo que afecta la distribución y comportamiento de la vegetación, organismos e incluso de los cultivos (Romo-Benito, 2008; Robertson, Edlinb, & Edwards, 2010; Yu et al., 2013). Por tal motivo, la influencia de la AL en la temperatura puede considerarse relativamente similar a la influencia de la latitud (Ortiz-Solorio, 2011), lo que permite deducir que la AL es otra variable en el cálculo de la ETP. Un factor más que afecta el comportamiento de la temperatura y, por consiguiente, de la ETP es el tiempo que transcurre durante el año o los meses (ME), al provocar una variación estacional de tales elementos climáticos (Ruiz-Álvarez, 2014). Sin embargo, modelos multivariados que involucren la TX, TN, AL y ME como variables independientes son escasos. México cuenta con 4 027 estaciones climáticas con 60 años de datos, que ofrecen información para la aplicación de modelos empíricos tradicionales que se basen en datos de temperatura y latitud, principalmente; no obstante, en muchas ocasiones, la falta de datos provoca la búsqueda de alternativas para la obtención de datos climáticos (Ortiz-Solorio, 2011) o la generación de nuevos modelos que puedan utilizarse en lugares donde no existan estaciones climáticas e incluso que puedan emplearse en invernaderos. Al respecto, Martí y Zarzo (2012) mencionaron que los procesos estadísticos multivariados son efectivos en el análisis de datos climáticos cuando se conocen valores previos de la variable a estimar. Si se considera lo anterior, es probable que al relacionar la TX, TN, AL y los ME, con los resultados de ETP del método de HS (ETP HS ) como método estándar, mediante regresiones lineales múltiples, se obtengan modelos sencillos y con aplicabilidad para México, sin el uso de la latitud ni la radiación. Por tal motivo, los objetivos del presente trabajo fueron los siguientes: 1) relacionar las variables TX, TN, AL y ME con resultados de ETP HS en México, mediante regresiones lineales para obtener modelos multivariados (general y para cada mes) que estimen ETP mensual, y 2) evaluar la precisión de los modelos obtenidos respecto a la ETP de HS y PN, con el fin de determinar su utilización.
Materiales y métodos
Zona de estudio
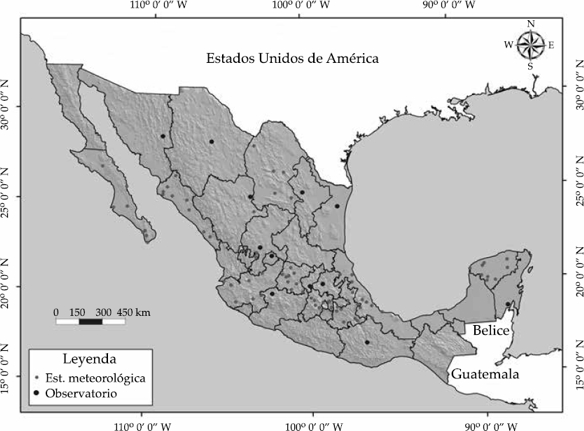
El estudio se realizó en México (figura 1), que se localiza entre los 14° 32’ y 32° 43’ latitud norte y 86° 42’ y 118° 27’ longitud oeste; ocupa un área de 1 964 375 km2. Este país tiene una geología que, por su origen, presenta rocas sedimentarias (64%), ígneas (32%) y metamórficas (4%) de distintas eras geológicas; 6% Precámbrica; 3% Paleozoica; 62% Mesozoica, y 29% Cenozoica (Ortiz-Villanueva & Ortiz-Solorio, 1990). Asimismo, tiene diferentes tipos de fisiografía debido a los procesos de orogenia y vulcanismo, el intemperismo y otros factores modeladores del paisaje (González-Medrano, 2003). Cuenta con diversos climas, siendo los principales el cálido húmedo (4.7%), cálido subhúmedo (23.0%), templado húmedo (2.7%), templado subhúmedo (20.6%), seco (24.3%) y muy seco (24.7%) (García, 2004). La vegetación natural domina en México con una extensión de 61%, donde abundan bosques (templado y tropical), que cubren una superficie de 29%, y los matorrales con 26% (Rzedowski, 2006). El uso del suelo es dominantemente agrícola y pecuario (25% de la superficie total del país), mientras las zonas urbanas cubren tan sólo 0.23% (INEGI, 1999).
Métodos
Un total de 81 EM pertenecientes al Servicio Meteorológico Nacional (SMN, 2015) fueron seleccionadas dentro del territorio de México (figura 1). El número de EM se obtuvo mediante el cálculo del tamaño de muestra (n) proporcional finita (Pérez-López, 2005), con un universo (N) de 4 027 (total de EM en México); nivel de confianza de 95% (Z = 1.96); margen de error máximo (e) de 4.7%, y una proporción (p) que se esperaba encontrar de 50%. El número de estados que se utilizaron para distribuir las EM también se estimó con n, donde N = 31, pues no se consideró la Ciudad de México, Z = 1.96, e = 12.1% y p = 50%, dando un total de nueve.
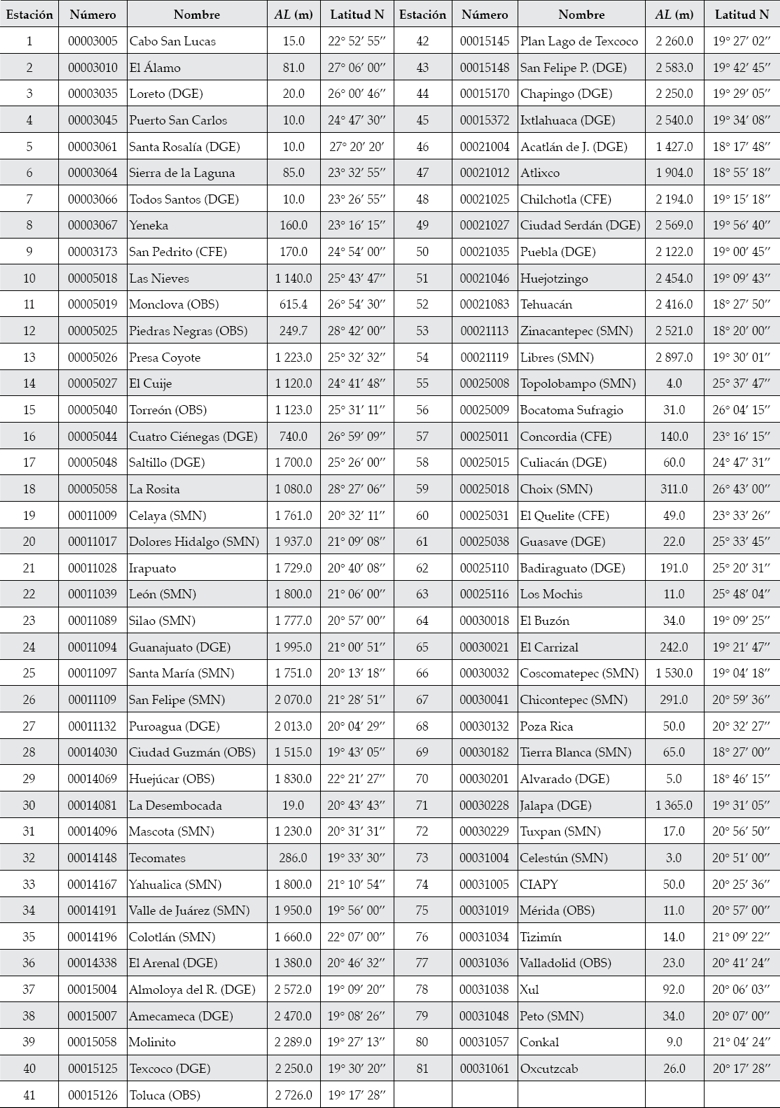
Las EM se distribuyeron en los estados siguiendo el método de muestreo aleatorio estratificado, por lo cual, en cada entidad se ubicaron nueve estaciones al azar, con el fin de tenerlas en diferentes AL y latitudes (cuadro 1), para captar las variaciones de los elementos climáticos que se utilizaron en el estudio. Así se obtuvieron las TX y TN de cada mes, y la AL de cada estación. Es importante resaltar que estos datos son promedios de registros de 60 años (1951-2010).
Los datos de las estaciones se usaron para calcular la ETP HS (ecuación (1)) con el método de Hargreaves y Samani (1985):
donde ETP HS es la evapotranspiración potencial dada en mm/día, que para este estudio se estimó para el día 15 de cada mes; después se multiplicó por los días que corresponden a cada mes para obtener la ETP mensual; Ra es la radiación extraterrestre para el día 15 de cada mes; T m , la temperatura media mensual; TX, la temperatura máxima, y TN es la temperatura mínima para el día 15 de cada mes.
Un grupo de 81 datos de AL correspondientes al total de las estaciones meteorológicas y 972 grupos de datos de TX, TN y ETP HS , que se obtuvieron de los doce meses del año por el total de las estaciones, se usaron para proponer funciones multivariadas, donde se tuvieron variables dependientes e independientes (Martínez-Rodríguez, 2005).
Modelación de la ETP, en función de TX, TN, AL y ME
Se generaron dos modelos de regresión lineal múltiple (MRLM) para establecer la relación de un conjunto de variables independientes X 1, X 2,… X n , y una variable dependiente Y, que se representan en la siguiente expresión general (Salinas & Silva, 2007):
donde Y i es la variable dependiente, X i1 , X i2 ,… X in son variables independientes; mientras que los parámetros o coeficientes son β0 intercepto, β1, β2, β3, y β3 pendientes, respectivamente; finalmente, U i es el error.
El primer MRLM fue general e involucró a los 972 grupos de datos, con ETP HS como variable dependiente y TX, TN como variables independientes, así como los 81 datos de AL, que correspondieron a la altitud de las estaciones meteorológicas seleccionadas y 81 grupos de ME que concernieron a los meses del año para cada estación; es importante mencionar que los meses se codificaron del 01 al 12, donde el 01 correspondió, por ejemplo, a enero y el 12 a diciembre. El modelo quedó definido como:
El segundo modelo fue para cada mes e involucró las variables independientes TX, TN y AL agrupadas por mes, pues en este caso ME fue considerada como una variable independiente categórica, con la ETP HS como variable dependiente, por lo que los modelos se definieron para cada mes como:
La selección de las variables que aparecieron en los modelos finales para cada mes dependió de la significancia estadística (Fc, P ≤ 0.05) de las variables independientes y la baja multicolinialidad, de tal manera que en la ecuación de los modelos para cada mes sólo aparecieran dos variables independientes, con el fin de obtener modelos sencillos. En este sentido, tanto el modelo general como los mensuales fueron de tipo predictivo (Martínez-Rodríguez, 2005).
Validación de los modelos
Un total de 12 estaciones meteorológicas (cuadro 2) y 10 observatorios (cuadro 3) diferentes a los que se utilizaron para la obtención de los modelos (ETP g y ETP m ) fueron seleccionados de manera aleatoria para registrar los datos de AL, latitud, TX y TN; es importante aclarar que los datos de las estaciones correspondieron al periodo de 1951 a 2010; mientras que los datos promedio de los observatorios fueron de 1951 a 1980, ya que sólo se contó con ese periodo. Los datos de las estaciones fueron útiles para el cálculo de la ETP mensual con los modelos ETP g , ETP m y ETP HS , donde el último se consideró como de referencia (Moeletsi et al., 2013), mismos que fueron divididos entre el número de días correspondientes a cada mes para obtener la ETP en mm/día y después se compararon entre sí. Aparte, con los datos TX, TN, AL y ME de los observatorios, la ETP mensual se calculó de nuevo con los modelos ETP g y ETP m y los resultados se dividieron entre el número de días del mes correspondiente, para obtener ETP promedio por día, para compararlos con los de ETP PN de los mismos observatorios (cuadro 3), que se obtuvieron de la publicación de Datos Agroclimáticos para América Latina y el Caribe (FAO, 1985), que al estar reportados como promedio mensuales, se dividieron entre el número de días de cada mes, lo que sirvió para la verificación del desempeño de los modelos obtenidos con respecto a PN.
Análisis estadístico
Los coeficientes de determinación (R 2), valor de Fc (P ≤ 0.05) de las variables independientes y el factor de inflación de la varianza (FIV) que se obtuvieron del análisis de varianza de las regresiones (Cuadras, 2014) se emplearon para comparar los modelos ETP g y ETP m . Por otra parte, el desempeño de estos modelos se obtuvo mediante índices estadísticos, como la raíz cuadrada de la media del error (RCME) y el error medio del sesgo (EMS), con las siguientes ecuaciones (Douglas, Jacobs, Sumne, & Ray, 2009):
donde RCME es la raíz cuadrada de la media del error en mm/día; y, la ET calculada con los modelos obtenidos (ETP g o ETP m , en mm/día), y ŷ es la ET de referencia (en su caso, HS o PN, en mm/día):
donde EMS es el error medio del sesgo en mm/ día; el resto de los símbolos indica lo mismo que en la ecuación (4).
El RCME es un indicador del desempeño de un modelo en un periodo de tiempo dado (Douglas et al., 2009) y su valor es siempre positivo (Yapo, Gupta, & Sorooshian, 1998); mientras que el EMS proporciona información del comportamiento a largo plazo de las correlaciones, lo que permite una comparación de la desviación real entre los valores pronosticados y medidos, término a término (Gunhan, Demir, Hancioglu, & Hepbasli, 2005); en ambos casos, el cero es ideal.
Finalmente, se llevaron a cabo dos regresiones ortogonales. Los valores de ETP g y ETP m se consideraron como variables independientes y ETP HS como variable dependiente. Este tipo de regresión se utilizó para determinar si los modelos (ETP g y ETP m ) son equivalentes o estiman lo mismo que el modelo de referencia (ETP HS ), lo cual se definió con los parámetros de cada regresión, donde las condiciones que debían cumplir fueron las siguientes: “el intervalo de confianza (IC) de la pendiente debe contener el número 1 y el IC de la intersección debe contener el 0” (Martínez-Arnaiz, 1994), considerando un IC al 95% en ambos casos, y asumiendo que las variables dependientes e independientes tienen la misma varianza (Carrol & Ruppert, 1996; Frez, 2002). El procesamiento de datos se realizó en el softwareMinitab17 (2014).
Resultados y discusión
Durante el periodo de 1951 a 2010, las variables TX, TN y ETP HS de las estaciones que se utilizaron tuvieron variaciones que se pueden ver en el cuadro 4. El comportamiento de los valores de TX y TN fue similar a ETP HS . Lo anterior no es raro, puesto que la variación durante el año de la TX y TN es normal; además, en la estimación de la ETP HS se utilizaron las temperaturas máximas y mínimas (Hargreaves & Samani, 1985; Moeletsi et al., 2013).
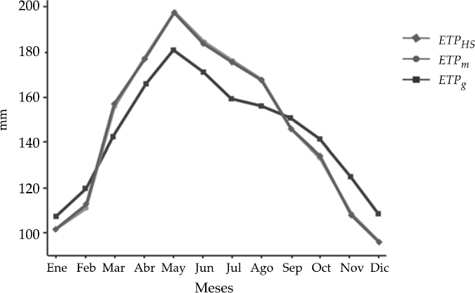
Asimismo, dichas variables respondieron a la ubicación de las estaciones meteorológicas tanto por altitud como por latitud. En este sentido, se sabe que el incremento de 305 m en la elevación produce un descenso aproximado de 1.66 °C, mientras que la variación de latitud genera cambios en la temperatura (Körner, 2007; Ortiz-Solorio, 2011). Por otra parte, los promedios de las variables climáticas en el lapso del año tuvieron una distribución normal, de tal manera que la TX y la ETP HS presentaron los valores máximos en mayo (32.2 °C y 197.54 mm, respectivamente); en tanto que la TN promedio tuvo su máximo (17.1 °C) en junio (figura 2), similar a lo reportado por Ortiz-Solorio (2011).
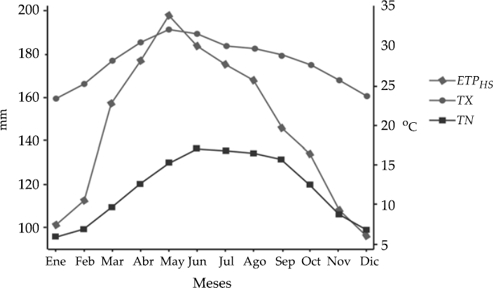
Figura 2 Distribución de las variables TX, TN y ETP. Promedios mensuales de 1981 a 2010 durante el año.
Modelación de la ETP general y mensual
El análisis de varianza de la regresión lineal múltiple para obtener el modelo general, utilizando todas las variables, mostró que la variable TN tuvo una probabilidad de rechazo de 0.074, mayor que la propuesta (P ≤ 0.05) y una Fc de 3.21 (P ≤ 0.05) más baja respecto al resto de las variables, lo que sugiere que un modelo con las variables TX, AL y ME podría ser más adecuado. En cambio, en los modelos para cada mes, la significancia de las variables TN y AL varió en función de los meses o temporada del año. La AL tuvo probabilidades de rechazo menor que 0.05 y Fc mayores que los de TN en los meses de noviembre a febrero, lo que sugiere que en estos meses considerar a TX, AL y ME (variable categórica) en los modelos es más apropiado; mientras que TN tuvo más significancia que AL en el resto de los meses. Una vez que se generaron nuevamente los modelos correspondientes, se tuvieron los siguientes resultados:
Los modelos ETP g y ETP m fueron estadísticamente significativos (P ≤ 0.05) y se ajustaron con precisión a los datos (cuadros 5 y 6, respectivamente). Además, sus variables independientes tuvieron una moderada correlación; es decir, baja multicolinealidad, ya que su FIV se encontró en el rango 1-5, lo que eliminó la redundancia de las variables independientes en la explicación del comportamiento de la variable dependiente (Katz, 2011).
El modelo general tuvo un R 2 ajustado igual a 0.7911 y un R 2 predicho de 0.7896; es decir, tiene una capacidad predictiva de 78.96%. Este resultado sugiere que ETP g es adecuado para la estimación de la evapotranspiración en cualquier época del año, ya que las variables TX, AL y ME explican un 79.18% del comportamiento de la ETP, donde el aumento de un grado Celsius en TX incrementa 8.140 mm la ETP, con la adición de 1.82 mm cada vez que se incrementan 100 metros en la altitud, a la que se sustrae 1.757 mm por el efecto del mes y finalmente la resta de 95.10 mm de la constante.
Por otra parte, el modelo mensual está integrado por 12 MRLM; cada uno corresponde a un mes del año (cuadro 6). Las ecuaciones de regresión tienen un R 2 ajustado que va de 0.7649 a 0.9942, siendo menor en el mes de noviembre y mayor en agosto, con una capacidad predictiva de 75.01 a 99.37%, respectivamente.
Los coeficientes de determinación de las regresiones para cada mes son adecuados, siendo estos una primera medida de evaluación (Martínez-Rodríguez, 2005); así como el valor de Fc (P ≤ 0.05) varió de 131.89 hasta 6920.96, lo que indica su significancia estadística y fortalece su validez. Por otra parte, las variables independientes de estas ecuaciones fueron significativas (P ≤ 0.05) y diferentes en cada una de ellas; además, tienen baja multicolinealidad. La TX tuvo mayor efecto sobre el comportamiento de la ETP y apareció en todos los modelos; las variables TN y AL tuvieron efectos en función de la temporada del año, de tal manera que AL influyó principalmente en invierno (de noviembre a febrero), y TN en el resto del año. Wong-González (2010) señala que la magnitud de los coeficientes de las variables independientes influye en el comportamiento de la variable dependiente. Los valores de los coeficientes de esta investigación se muestran en un orden de mayor a menor como TX > TN > AL, con tendencia positiva, negativa y positiva, respectivamente. Este comportamiento no es extraño para TX y TN, pues el aumento de la temperatura hasta un máximo (TX) incrementará la ETP, y la disminución de la temperatura hasta un mínimo (TN) provoca un decrecimiento de ETP, pues estas temperaturas influyen en la presión de saturación de vapor y por lo tanto afectan la estimación de ET (Allen et al., 1998; Hargreaves & Samani, 1985; Ortiz-Solorio, 2011). No obstante, llama la atención el signo positivo del coeficiente de AL en el modelo general y en algunos mensuales, pues difiere de la tendencia negativa en la relación ETP-altitud, que reportaron Jaramillo-Robledo (2006), Vega y Jara (2009), y Goulden et al. (2012). La tendencia que se encontró en este estudio tiene sentido válido desde un punto de vista físico, pues la discrepancia podría deberse a la relación inversa que existe entre la altitud y la presión atmosférica (Pereira, Valero, Picornell-Buendía, & Martín-Benito, 2010), lo que provoca, a su vez, un aumento en la evaporación, independientemente de la temperatura (Castellan, 1987; Maderey & Jiménez, 2001; Armstrong, Pomeroy, & Martz, 2015) y que para México se hace evidente en invierno. De acuerdo con Allen et al. (1998), la presión atmosférica es otro de los parámetros atmosféricos que determinan la ET.
En este contexto, Bautista, Bautista y Delgado (2009) mencionaron que los modelos tradicionales generalmente utilizan una o más variables atmosféricas o algunas mediciones relacionadas, como la evaporación. Aunque asumen un estado ideal donde no interviene la elevación; pero, como se observa en este estudio, la altitud sí tiene influencia. Al respecto, Hagreaves y Samani (1985), en su ecuación, hicieron una modificación en función de la correlación que encontraron entre las temperaturas máximas y mínimas con la altitud para El Salvador; sin embargo, es escasa más información relacionada con este aspecto.
Aplicación de los modelos ETPg y ETPm
Los resultados de la aplicación de los modelos ETP g y ETP m (cuadro 7) por estación y por mes muestran que en ocasiones se subestiman o sobreestiman los valores de ETP respecto a ETP HS mensual; es importante resaltar que al seleccionar de manera aleatoria EM y observatorios diferentes a las que se utilizaron para generar los modelos, se corrió el riesgo de seleccionar alguna que estuviera fuera del rango que se utilizó, situación no deseada cuando se generan modelos (Salinas & Silva, 2007). En este sentido, tres EM y un observatorio presentaron datos que no se encontraron en el rango de valores con los que se generaron los modelos (EM: 1. Pabellón de Arteaga [enero TN = -3.0 °C; febrero TN = -2.2 °C]; 9. Bacalar [AL = 2.0 m], y 10. Arivechi [mayo TX = 40.2 °C; junio TX = 42.6]; Observatorio Durango [enero TN = -3.9 °C; febrero TN = -2.6]). No obstante, estos datos no influyeron en los resultados, pues cuando fueron utilizados en los modelos ETP g y ETP m no se observaron diferencias grandes respecto a ETP HS , ya que la varianza de los resultados de los modelos obtenidos se encuentra dentro del índice de confianza (95%) de la varianza de ETP HS (cuadro 8), lo que sugiere que los resultados de ETP con HS y de las dos ecuaciones de este estudio son similares. Estos resultados pudieron ocurrir porque en Pabellón de Arteaga y en el observatorio de Durango los datos correspondieron a TN, que no se utilizaron en el cálculo; en Bacalar, la variación en la altitud es de un metro menor que el límite del rango, así como en Arivechi, con temperatura superiores al límite mayor por 0.1 y 1.5 °C, lo que provocó variaciones mínimas en los resultados.
Cuadro 7 Evapotranspiración potencial de las estaciones de prueba por los modelos HS, ETP g y ETP m .

Cuadro 8 Resultados de ETP mensual de los modelos HS, general y para cada mes.
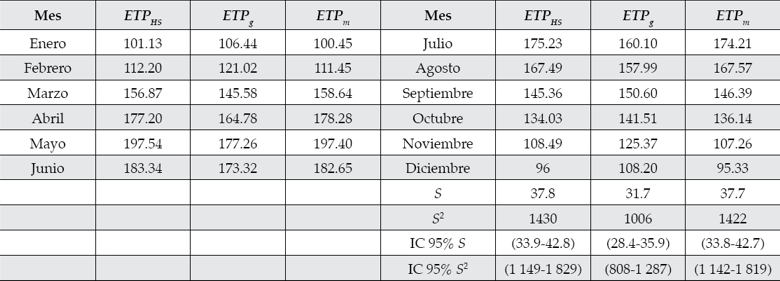
S: desviación estándar; S 2: varianza; IC: intervalo de confianza.
De tal manera que la ETP mensual con los tres modelos tiene una distribución parecida (figura 3); resultados de distribución de ETP semejantes a los reportados por Campos-Aranda (2005) y Ruíz-Álvarez et al. (2014).
Análisis estadísticos de ETPg y ETPm
Al analizar el resultado de los modelos ETP g y ETP m con el total de las estaciones de prueba respecto a ETP HS , los estadísticos RCME y EMS del ETP g (0.42 y 0.09 mm/día, respectivamente) fueron mayores que los de ETP m (RCME = 0.16 mm/día y un EMS = 0.07 mm/día); en cambio, cuando el desempeño de los modelos se evaluó por mes, el RCME del ETP g varió de 0.24 a 0.76 mm/día, resultados mayores que los obtenidos con ETP m (cuadro 9), con excepción del mes de octubre (0.24 mm/día). El EMS en el modelo general tuvo valores de -0.05 a 0.68 mm/día, con marzo en la condición ideal (más cercano a cero); mientras que en los modelos para cada mes se tuvo un EMS de 0.01 a 0.16 mm/día, donde los valores más cercanos a cero y menores a 0.01 se encontraron en marzo, abril, mayo, junio, julio, agosto, septiembre y diciembre. Comportamiento parecido a lo reportado por Vásquez-Méndez et al. (2011), quienes concluyeron que el método de HS tuvo un mejor desempeño con datos a nivel mensual.
Cuadro 9 Evaluación del desempeño estadístico de los modelos ETP g y ETP m con los métodos de referencia.
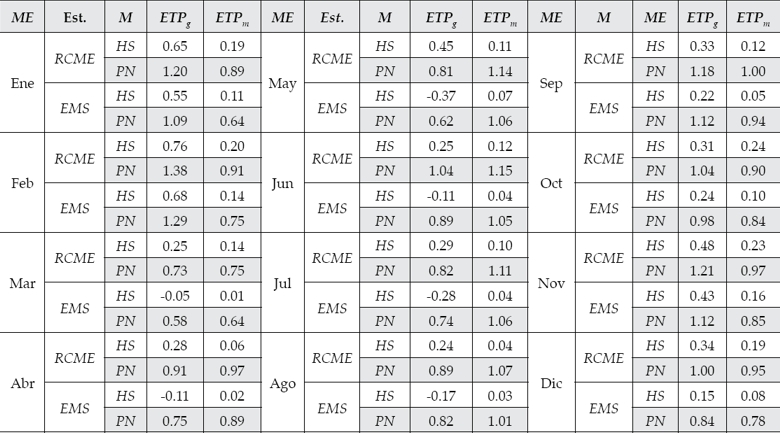
ME: mes; M: modelo.
El valor promedio de la RCME significa que los dos modelos generados en este estudio estiman la ETP con bajo error, aunque en el ETP g tiene un error mayor que en ETP m (0.38 y 0.14 mm/día, respectivamente), lo cual sugiere que el modelo para cada mes (ETP m ) tuvo el mejor desempeño. Por su parte, el EMS del modelo general tuvo valores positivos y negativos, lo que revela subestimaciones y sobreestimaciones, en tanto que el modelo para cada mes tiende a una ligera sobreestimación.
Cuando los resultados de ETP g y ETP m en los observatorios fueron comparados con los de PN (FAO, 1985), el RCME de la ETP g del mes de marzo fue el más bajo (0.73 mm/día), en tanto que febrero fue más grande (1.38 mm/día), mayores que ETP m (cuadro 9). Por otra parte, el EMS detecta ligeras sobreestimaciones de los modelos obtenidos en todos los meses. No obstante, el desempeño de los modelos de este estudio a nivel mensual respecto a PN es satisfactorio, ya que se encuentran en los grupos 1 y 2 (RCME-EMS < 1 mm/día y RCME-EMS entre 1-2 mm/día, respectivamente), propuestos por Vásquez-Méndez et al. (2011). En este sentido, los modelos obtenidos tienen un comportamiento semejante a HS cuando se compararon con PN. Al respecto, Gavilán, Lorite, Tornero y Berengena (2006) reportaron un resultado similar al comparar datos de ETP calculados con PM y HS. Asimismo, Campos-Aranda (2005) y Ortiz-Solorio (2011) indicaron que el método de PM con datos de observatorios de México produce valores de ETP mayores que HS. Sin embargo, diversos autores han concluido que el HS es un método alternativo cuando no existen datos para aplicar PM (Maeda, Wiberg, & Pellikka, 2011; Moeletsi et al., 2013; Raziei & Pereira, 2013).
Al analizar lo anterior, el desempeño del modelo general y para cada mes con respecto a HS sugiere que el uso de cualquiera de ellos para la estimación de la ETP es factible. Sin embargo, la regresión ortogonal reveló que los coeficientes de la regresión ETP g no cumplen con la condición que en el IC (95%) de la intersección se encuentre el “0” y en el IC (95%) de la pendiente se encuentre el “1” (figura 4a); por lo tanto, existe evidencia de que el modelo ETP g y el modelo HS estiman evapotranspiraciones potenciales diferentes. En cambio, el modelo ETP m estimó valores similares a los de HS, ya que el “0” se encontró en el IC (95%) de la intersección y el “1” dentro del IC (95%) de la pendiente (figura 4b); así, se deduce que no existe evidencia de que las dos ecuaciones estimen datos de ETP distintos.
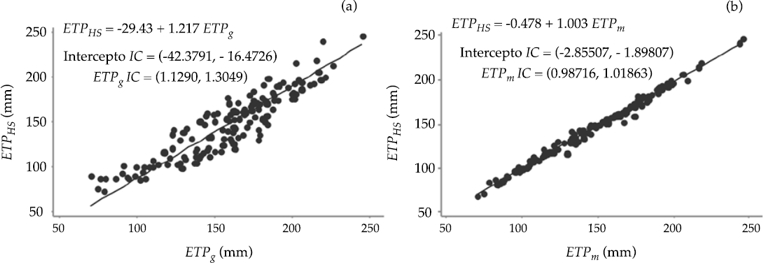
Figura 4 Regresiones ortogonales: a) relación entre ETP HS y ETP g ; b) relación entre ETP HS y ETP m .
El resultado anterior podría deberse a que la regresión ortogonal considera el error en las variables dependiente (datos de modelos propuestos) e independiente (datos del modelo de referencia), cuando generalmente en los análisis de regresión se considera sólo el error de la variable independiente, de tal manera que este procedimiento es recomendable para estudios de Ciencias de la Tierra (Carroll & Rupert, 1996; Frez, 2002), donde podría existir error en la medición de las variables dependientes e independientes, como en el caso de la combinación de elementos climáticos, geográficos y de tiempo, como en este estudio.
Conclusiones
La metodología propuesta en el presente estudio demostró que las variables TX, TN, AL y ME pueden emplearse en sencillos modelos lineales múltiples para estimar ETP mensual. En este sentido, la TX es la variable que mayor efecto tiene en el comportamiento de la ETP. Asimismo, la TN y la AL influyen en la ETP de forma distinta en los meses, de tal manera que estas variables compensan el efecto de TX en diferente magnitud en el transcurso del año. Durante los meses de primavera, verano y otoño, la TN con tendencias negativas en las ecuaciones es más significativa que la AL; en cambio, en invierno, la AL tiene más significancia y con tendencias positivas. Por otra parte, la regresión ortogonal resultó ser una herramienta estadística útil en la comparación de modelos que estiman datos climáticos, como ETP. Asimismo, con base en el RCME, EMS y la regresión ortogonal, el modelo para estimar ETP para cada mes (ETP m ) es el más apropiado para México. Los resultados de este modelo son similares a los que se obtienen con Hargreaves y Samani (1985), con la ventaja de requerir únicamente valores de TX y TN o AL de manera directa, como se demostró en este estudio. Por lo tanto, el modelo ETP m que estima valores de ETP para cada mes es un modelo sencillo aplicable para México, sin considerar la latitud ni la radiación. Aun cuando el modelo para cada mes de esta investigación puede emplearse en la estimación de la ETP mensual en México, es necesario verificar la validez del uso de las variables TX, TN y AL en otras regiones del mundo, considerando HS o PM como métodos de referencia, bajo la metodología planteada en este trabajo. Asimismo, al no considerarse la radiación en los modelos de ETP m , significa que podría utilizarse a nivel de invernadero o casa sombra, pero se requiere de la evaluación y validación en los mismos.











 nueva página del texto (beta)
nueva página del texto (beta)