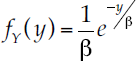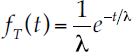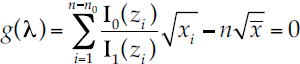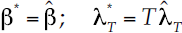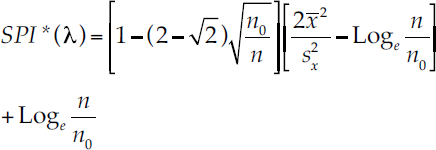Introducción

En la hidrología moderna es común observar series de eventos hidrometeorológicos que ocurren de manera aleatoria en el tiempo (^{Govindaraju, 2013}). Los procesos de Poisson proporcionan modelos probabilísticos apropiados para explicar el número de eventos que ocurren o se producen a partir de cierto fenómeno (^{López-Segovia, Villaseñor-Alva, & Vaquera-Huerta, 2002}). En hidrología es frecuente relacionar la distribución de Poisson con la ocurrencia de los eventos de precipitación, para explicar, por ejemplo, el intervalo de ocurrencia de tormentas como variables discretas, en donde se evalúa la ocurrencia o no de un evento de lluvia; intensidad y duración se presentan como dos variables aleatorias independientes y discretas (^{Tapsoba, 1997}; ^{Bacchi, Becciu, & Kottegoda, 1994}; ^{Le Barbé, Lebel, & Tapsoba, 2002}; ^{Gutiérrez-López, Descroix, & Lebel, 2002a}). Incluso estudios tan precisos, como cuantificar el número de gotas, se basan en esta distribución. ^{Calder (1986)} propone un modelo estocástico de modelación de precipitación, el cual relaciona, mediante la distribución de Poisson, el número promedio de gotas de lluvia retenidas en una superficie dada con el número promedio de gotas de lluvia caídas. Lo anterior fundamenta la afirmación de que el proceso de Poisson es una herramienta adecuada para representar el comportamiento de fenómenos hidrometeorológicos (^{Ribstein, 1983}; ^{Wong, Lambert, Leonard, & Metcalfe, 2010}; ^{Sol'áková De Michele, & Vezzoli, 2014}; ^{Sohrabi, Ryu, Abatzoglou, & Tracy, 2015}). Cuando se utiliza el modelo mezclado Poisson-exponencial es posible evaluar también el riesgo hidrológico asociado con inundaciones y sequías de forma simultánea (^{Gutiérrez-López, Lebel, & Descroix, 2002b}) de forma similar a un proceso jerarquizado de Neyman-Scott (^{Rodríguez-Iturbe, 1986}). En esta distribución mezclada se demuestra que los parámetros de las dos distribuciones están relacionados a través de un factor de reducción de varianza, el cual es función de la estructura de correlación espacial de la precipitación (^{Cammalleri, Micale, & Vogt, 2016}). Suponiendo que la lámina media por evento de precipitación sigue una distribución exponencial, el parámetro de escala ajustado a partir de la serie de lluvia diaria adquiere el mismo valor del parámetro de escala de la distribución de valores extremos tipo Gumbel, ajustando los valores máximos de lluvia mensual (^{Sivapalan & Blóschl, 1998}; ^{Gutiérrez-López, Lebel, & Mejía, 2005}). Trabajos similares reemplazando la distribución exponencial por la distribución gamma han sido desarrollados en cuencas con registros de precipitación horaria en el centro del Reino Unido y Estados Unidos (^{Eagleson, 1978}; ^{Onof & Wheater, 1994}; ^{Wilks, 1998}). Asimismo, la distribución de Poisson suele emplearse para modelar periodos de sequía (^{Sharma, 1996}; ^{Cameron, Beven, & Tawn, 2000}). Por lo general, los periodos de sequía y de humedad durante una temporada de lluvias tienden a conservarse y pueden ser modelados utilizando un proceso de Markov de orden uno. Una forma tradicional para el análisis de estos fenómenos mínimos consiste en mezclar más de dos distribuciones. Así, una función de probabilidad de Poisson delimita la ocurrencia de periodos de sequía; la distribución geométrica se utiliza para obtener las probabilidades asociadas con el número de periodos, y la distribución Weibull modela la precipitación total dentro de un periodo húmedo (^{Mirakbari, Ganji, & Fallah, 2010}). El análisis completo, que requiere la estimación conjunta de los parámetros de estas distribuciones, arroja resultados relacionados con la probabilidad de que en un día cualquiera se presente sequía; la probabilidad de que un día seco sea consecutivo a otro día seco, o la probabilidad de que un día húmedo sea consecutivo a otro día húmedo. Si bien este tipo de resultados describen de forma adecuada el intervalo de tiempo entre periodos de sequía, es deseable correlacionar los parámetros de una distribución de probabilidad, por ejemplo, con algún índice de aridez. Éste es precisamente el tercer objetivo de este trabajo. Para el caso de caudales en un río, un esquema similar de detección del déficit o exceso de corrientes en un intervalo de tiempo puede ser modelado por una distribución de Poisson (^{Coles, Pericchi, & Sisson, 2003}; ^{Hughes, 2003}). Debido a que en la mayoría de los países los ingenieros civiles evalúan las crecientes de diseño utilizando la extrapolación de valores extremos para el diseño de estructuras hidráulicas, el pronóstico hidrológico se realiza a partir de una interpretación de las frecuencias de probabilidades de ocurrencia de los eventos máximos (^{Pandey & Nguyen, 1999}). En virtud de que el nombre de valores extremos es asignado a estas distribuciones debido a que éstas pueden ser obtenidas como distribuciones límite de los valores grandes o pequeños entre variables aleatorias independientes, cada una teniendo una distribución continua (^{Pandey & Nguyen, 1999}; ^{Escalante & Reyes, 2002}), puede entonces hacerse la hipótesis de que el proceso compuesto Poisson-exponencial representa fenómenos extremos de sequía o de inundación debido a que contiene una distribución de extremos. Esto permitiría asociar la distribución mezclada Poisson-exponencial con una ley de valores extremos; es decir, eventos definidos por un proceso de Poisson, que dan lugar a lluvias puntuales distribuidas de forma exponencial.

Proceso compuesto Poisson-exponencial (Ley Fuga)

Esta distribución mezclada de probabilidad tiene su origen en el estudio de series cronológicas de eventos separados por duraciones aleatorias. Las dos hipótesis de base son la estacionariedad, que significa que las propiedades estadísticas de la serie cronológica no cambian con el tiempo, y la independencia, que se refiere a que cada uno de dichos eventos ocurre de manera independiente de los demás. El nombre de "Ley Fuga" (Loi de Fuites) proviene del estudio que realizó M. Morlat (^{Babusiaux, 1969}) en la distribución de los gastos que se fugaban de una red de distribución de gas en Francia. Consiste en utilizar simultáneamente una distribución de Poisson, para representar la probabilidad de ocurrencia de un evento y una distribución exponencial para expresar la magnitud media de dicho evento.

Si se considera una variable aleatoria y > 0, que sigue una distribución exponencial simple, con parámetro de escala β, su función de densidad puede expresarse como:

1

Sea ℓ un número entero aleatorio que sigue una Ley de Poisson, de parámetro de forma λ > 0, el valor de su probabilidad será:

2

Así, una variable aleatoria X = Y₁ + Y₂ +...+ Y puede representarse como la suma de ℓ> 0 variables aleatorias independientes que siguen un proceso compuesto Poisson-exponencial con parámetro de forma λ, que denota la tasa de llegadas de un evento por unidad de tiempo, y un parámetro de escala β. Respecto a la duración, es equivalente decir que un número de eventos n(t) seguirá una Ley de Possion para una duración t, o bien que el intervalo T entre dos eventos consecutivos sigue una ley exponencial sobre el mismo tiempo t.

3

donde:

Cabe recordar que la distribución exponencial es un caso particular de la llamada familia de distribuciones Gamma (^{Saporta, 1990}). Sea t = T₁ + T₂ +...+ T la suma de r variables que siguen una distribución exponencial (ecuación (3)). Es sabido que la función de densidad de la suma de r variables aleatorias independientes es el producto de convolución de las densidades de cada una de ellas (^{Tapsoba, 1997}), lo cual permite considerar T como una variable que define las probabilidades de tener 1, 2, o más eventos desde cero hasta T.

Así, la función de densidad de probabilidad de la llamada Ley Fuga (proceso compuesto Poisson-exponencial) para la variable reducida U = X/β estará dada por la expresión:

4

Donde:

Es importante mencionar que este proceso compuesto Poisson-exponencial tiene una discontinuidad para el valor cero (excepto cuando λ = 1); es decir, la ordenada al origen tiene un valor de λe^-λ . La Figura 1 muestra las funciones de distribución y probabilidad de dicho proceso.

Figura 1 Funciones de densidad y acumulada para diferentes valores de λ. 

Estimación de parámetros

Considerando las hipótesis de esta distribución de probabilidad y el significado de los parámetros, se infiere que un procedimiento simple es el número de eventos nulos n₀ que existan en la muestra; esto es, el número de días secos, en la serie histórica de datos. Si n₀ ≠ 0, el procedimiento de estimación requiere, para una correcta solución, tomar en cuenta el tamaño n de la muestra (^{Tapsoba, 1997}). El logaritmo de la función de verosimilitud, de la cual se busca obtener el máximo, es la siguiente:

5

La anulación de las derivadas parciales de L respecto a λ y β conducen a un sistema de ecuaciones:

6

7

en donde:

8

I₁(z) es la primera derivada de I₁(z). Resolviendo el sistema de ecuaciones miembro a miembro de las ecuaciones (6) y (7) se obtiene:

9

Las propiedades de la función de Bessel permiten escribir la derivada de I₁ como:

I₀ es la función de Bessel de orden cero. Empleando esta expresión en la ecuación (5) y sustituyendo x- en la expresión (9) zi2λ=xix- se obtiene:

cuya solución es un valor único y positivo de λ^. La función g(λ) es monótona y decreciente, su solución se encuentra en el intervalo [10-4,5λ^mom], en donde λ^mom, corresponde al valor del parámetro estimado por el método de momentos. El valor de p se obtiene de la expresión (8). ^{Le Barbé y Lebel (1997)} proponen un procedimiento alternativo para la estimación de los parámetros del proceso compuesto Poisson-exponencial. Este método propone emplear el número promedio de días secos n₀ dentro del periodo T del total de n días. Tal procedimiento tiene una singular importancia, pues la información de los días secos no se emplea de manera directa en la estimación de parámetros de los métodos de momentos. De esta forma se tiene que los parámetros estará dados por:

10

Aplicación de la Ley Fuga

Para ejemplificar la aplicación de esta distribución en la modelación y análisis de la variabilidad espacial de la precipitación se seleccionaron ocho estados del norte de México, empleando series de lluvia diaria en registros promedio de 50 años de extensión dentro de un periodo que comprende los años de 1960 a 2013. El número de estaciones es variable, sin sg embargo se considera bien representado para cada uno de los estados seleccionados: Aguascalientes (49 estaciones); Estado de México (38); Guanajuato (21); Jalisco (85); Michoacán (20); Querétaro (31); San Luis Potosí (28), y Zacatecas (29). Para la validación del modelo se seleccionó la Región Hidrológica 10, situada al noroeste de la república mexicana. Las lluvias en esta zona se presentan en una época bien definida, pues el periodo más abundante se registra entre los meses de junio y octubre (^{Conagua, 2014}). Sin embargo, es también una región sensible y expuesta a los cambios climáticos y a las sequías. Se han registrado largos periodos de sequía y también inundaciones provocadas principalmente por fenómenos meteorológicos extremos.

Validación del modelo

Se utilizaron las series históricas de las 93 estaciones climatológicas dentro de la región hidrológica 10 y se estimaron los parámetros del proceso compuesto Poisson-exponencial, empleando los tres procedimientos ya descritos. Con base en el estadístico X² se seleccionaron los mejores ajustes y el método de momentos demostró, en la mayoría de los casos, dar el mejor ajuste a las muestras de datos (^{Gutiérrez-López et al., 2002b}). Como se mencionó antes, el parámetro p ofrece una ventaja adicional, ya que con éste puede deducirse la distribución de la lluvia considerando diferentes intervalos de tiempo. Así, los parámetros λ* y β* deducidos en forma simplificada pueden estimarse de forma directa multiplicando por el intervalo de tiempo deseado. Es decir, los parámetros tienen un significado físico específico y pueden ser usados para diferentes valores de T. De esta forma, se tiene que el parámetro β permanece constante a lo largo del tiempo y el parámetro de forma λ puede calcularse para cualquier duración T, esto es:

11

Se aceptará que existe no estacionaridad en el caso de que el valor de λ tenga una variación mayor a 20% entre el valor máximo y mínimo dentro del periodo considerado. Esto quiere decir que se considerará como un proceso estacionario mientras se mantenga constante durante 80% del periodo; en caso contrario, el parámetro de escala debe estimarse como (^{Gutiérrez-López et al., 2002b}):

12

Cuando se dispone de datos de lluvia diaria es recomendable elegir T igual a un día (^{Lebel & Le Barbé, 1997}; ^{Lebel, Taupin, & D'Amato, 1997}). El Cuadro 1 muestra la validación del modelo para la estación Tamazula para el periodo 1947-2005. Los parámetros estimados del análisis de la lluvia diaria por el método de momentos fueron λ^ = 0.654 y β^ = 12.214 . De ellos se pueden deducir los parámetros, por ejemplo, para un intervalo de 10 días, empleando la ecuación (4). Esto es: λ* = 0.654 x 10 = 6.54 y β* = 12.214. Mientras que los valores reales de los parámetros, estimados de la serie de datos original, para el intervalo de 10 días son λ^ = 7.071; β^ = 11.465. De la misma forma se pueden estimar los parámetros para la cualquier otra duración T deseada.

Cuadro 1 Validación de los valores de los parámetros de escala y forma del proceso compuesto Poisson-exponencial. 

Una ventaja de utilizar este proceso compuesto Poisson-exponencial radica en la posibilidad de asociar sus parámetros con un significado físico, los cuales pueden ser relacionados con conceptos de la gestión del riesgo hidrológico, ya que el parámetro y β^ puede asociarse con una medida de la probabilidad de lluvia extrema y λ^ puede relacionarse con la probabilidad de ocurrencia de lluvia (sequía), tal y como se desarrollará a continuación.

El parámetro λ de la Ley Fuga como índice de sequía

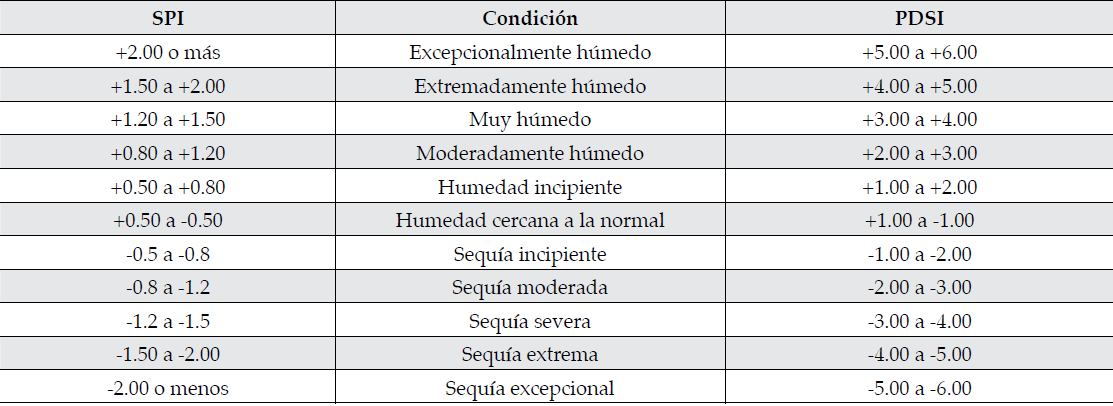
El índice de precipitación estandarizado SPI (Standardized Precipitation Index) es uno de los índices utilizados en el mundo para evaluar y monitorear las sequías (^{Palmer, 1965}; ^{McKee, Doesken, & Kleist, 1993}; ^{Edwards & McKee, 1997}). En general, este índice se calcula para intervalos de tiempo entre 3 (valor de SPI mínimo) y 48 meses (valor de SPI máximo), y permite identificar y clasificar posibles zonas susceptibles a presentar algún tipo de daño por sequía. La metodología para el cálculo del SPI se fundamenta en el ajuste de una serie de registros históricos de precipitación total mensual a una función de distribución Gamma incompleta, y en la transformación de los datos resultantes a la función de distribución normal estándar. Cabe recordar que la deducción del proceso compuesto Poisson-exponencial empleando una distribución exponencial es un caso particular de la llamada familia de distribuciones Gamma. De esta forma, el SPI representa el número de desviaciones estándar que cada registro de precipitación se desvía del promedio histórico. Los registros de precipitación superiores al promedio histórico del mes correspondiente tendrán valores positivos del SPI (presencia de humedad), mientras que los registros de precipitación inferiores al promedio histórico arrojarán valores del SPI negativos (déficit de humedad), tal como se muestra en el Cuadro 2. Si bien se han propuesto otros índices de sequía simplificados (^{Pita, 2003}; ^{Karamouz, Rasouli, & Nazif, 2009}), a la fecha ningún trabajo ha incluido de modo explícito el número de días lluviosos (intuitivamente incluido en la precipitación mensual) para estimar un índice de sequía. La aplicación del proceso compuesto Poisson-exponencial ofrece una ventaja, pues establece una relación del parámetro de posición de dicha distribución de probabilidad con el índice SPI (^{Kim, Valdés, & Yoo, 2006}; ^{Liu et al., 2013}). Basados en el hecho de que un evento de sequía puede caracterizarse definiendo su régimen, es decir, su magnitud y frecuencia, parece apropiado introducir la variable correspondiente al número de días con lluvia.

Cuadro 2 Valores convencionales de los índices SPI y PDSI (^{NDMC, 2003}; ^{Hayes, 2000}). 

De esta forma, se propone relacionar el índice tradicional de sequía SPI con el parámetro 1 del proceso compuesto Poisson-exponencial. A partir de la estimación de parámetros propuesta por ^{Babusiaux (1969)}, empleando la ecuación (10) y poniendo todo en función del índice SPI, se obtiene una relación SPI-1, que permite estimar un índice modificado SPI*. Esta relación es de la forma:

13

Donde:

La Figura 2 muestra la relación que existe entre el índice SPI y el valor del parámetro 1 de la distribución de probabilidad Poisson-exponencial, representado con la letra L, para el mes de enero en el estado de Querétaro. De la misma forma, se obtuvieron las correlaciones para el resto de los estados analizados. En todos los casos se observa que existe una correlación promedio de 0.90, lo que garantiza una estimación confiable de la relación que existe entre el número de días con lluvia (1) y el índice SPI. Las ecuaciones que predominan son los ajustes a rectas con valores agrupados en el valor de λ < 0.40 y después valores dispersos para valores superiores. A continuación se evalúan todos los meses del año para los estados en estudio. Los resultados de este procedimiento se muestran en la ilustración 3. En este caso y por razones de espacio, sólo se muestran algunos de los ajustes más representativos en los estados, en los meses de mayor sequía histórica.

Figura 2 Correlación del índice de sequía SPI y el valor del parámetro λ del proceso compuesto Poisson-exponencial, para el mes de enero en el estado de Querétaro. 

Discusión

Una vez que se verifica la correlación del índice de sequía SPI y el valor del parámetro λ de la distribución de probabilidad Poisson-exponencial para todos los meses más representativos de los estados analizados, se procede a calcular el valor de SPI* como un estimado del valor real de SPI. Es importante mencionar que en algunos de los estados de nuestro país, la condición del SPI medio es muy cercana a la condición del SPI mínimo, como puede observarse en las Figuras 3b, 3d y 3e.

Figura 3 Correlación del índice de sequía SPI y el valor del parámetro 1 del proceso compuesto Poisson-exponencial, para algunos de los meses más representativos de los estados analizados 

En estas condiciones ocurre en los meses de invierno (diciembre, enero y febrero) lo que caracteriza el régimen de precipitaciones típico de la zona central de nuestro país, con escasa precipitación en dicho periodo. Para un mes históricamente seco, como abril, la Figura 3f muestra las condiciones mínima y máxima también muy próximas. Sin embargo, para los meses considerados dentro de la temporada extendida de lluvia (mayo y noviembre), inicio y final de la temporada, respectivamente (Figuras 3a y 3c), los patrones en el ajuste de los valores de SPI y el valor del parámetro 1 se observan bien definidos, y separadas las condiciones mínima y media. A continuación se estiman los valores del índice SPI* para cada uno de los estados seleccionados, en cada una de sus estaciones climatológicas. Estos resultados se muestran en los Cuadros 3 y 4, en forma comparativa con el valor del SPI tradicionalmente calculado según ^{McKee et al. (1993)}, y ^{Edwards y McKee (1997)}. Se puede observar cómo en todos los casos, excepto uno, la condición de sequía es la misma. Cabe mencionar que si bien el valor calculado no es el mismo, una vez que se compara la condición de sequía resulta la misma (Cuadro 2). Los resultados muestran que el cálculo del parámetro SPI* preserva la condición de sequía de un evento, tal que éste se inicia cuando se observa a través del tiempo, una tendencia marcada de valores negativos continuos del SPI. De esta manera, el evento de sequía termina cuando el valor del SPI alcanza valores positivos. Sin embargo, como puede intuirse, para una estimación exhaustiva de una condición de sequía o aridez se deben estimar otros índices empleando distintas variables, como precipitación, evapotranspiración, caudales en cauces naturales, niveles de lagos y embalses, niveles de acuíferos, etc. (^{Maity, Sharma, Nagesh-Kumar, & Chanda, 2013}).

Cuadro 3 Condición de sequía para el estado de Querétaro, según la formulación tradicional del índice SPI y la comparación con el índice SPI* basado en el número de días de lluvia del mes de enero. 

Cuadro 4 Condición de sequía para el estado de Querétaro, según la formulación tradicional del índice SPI y la comparación con el índice SPI* basado en el número de días de lluvia del mes de mayo. 

Conclusiones

La lluvia en el norte de la república mexicana es sin duda un fenómeno complejo de estudiar. Sin embargo, los resultados de la aplicación del proceso compuesto Poisson-exponencial en esta zona del país han permitido un conocimiento simple del fenómeno, a partir de sólo contar el número de días de lluvia. La Ley Fuga, como se le conoce, muestra ventajas. En un principio facilitó conocer la distribución espacial y temporal de la lluvia, a través de la obtención de los dos parámetros de la distribución, tal como lo demostraron ^{Chulsang, Daeha, Tae-Woong y Kyu-Nam (2008)}. La sencillez de dichos parámetros permitió encontrar relaciones simples con su entorno geográfico y físico.

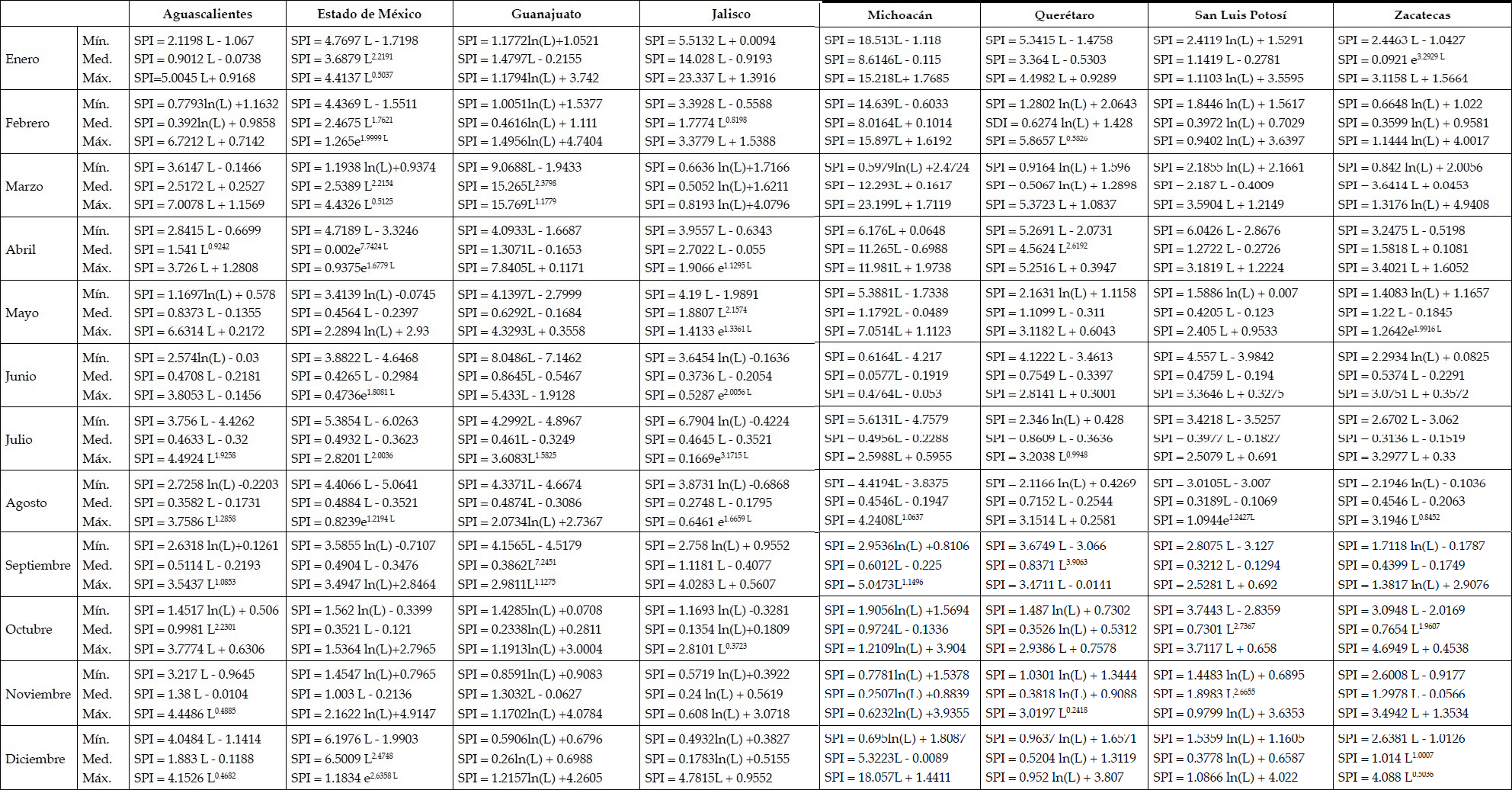
Se demuestra que el modelo propuesto es significativamente consistente con la descripción de los cambios asociados con los fenómenos extremos, pues permite identificar en una forma confiable la condición de sequía de una zona a través de la evolución del parámetro 1. Para la mejor aplicación del procedimiento propuesto se presenta el Anexo A, en donde se muestran el total de ecuaciones para los ocho estados analizados a lo largo del año. Las ecuaciones son muy sencillas y representan la variabilidad del fenómeno de sequía de 1960 a 2013. Es suficiente tener acceso a datos diarios de precipitación y realizar un análisis de frecuencia con la ecuación (4), estimando sus parámetros con las ecuaciones (5) a (10). A continuación se debe verificar la propiedad aditiva de los parámetros, según se propone en las ecuaciones (11) y (12). Por último, se cuenta el número de días con lluvia para el mes analizado; por ejemplo, seis días de lluvia promedio para el mes de enero en Amealco, Querétaro, esto es, λ = 6/31 = 0.1936, que sustituyendo este valor en la ecuación de SPI"* media presentada en el Anexo A, se obtiene SPI* = 0.121, condición de sequía equivalente a "humedad cercana a la normal"; misma condición obtenida de la aplicación del cálculo tradicional del índice SPI. Es así como se considera que la metodología propuesta y el empleo del proceso compuesto Poisson-exponencial se adaptan a las necesidades de estimación del riesgo hidrológico y permiten profundizar en el conocimiento de la climatología regional del norte de la república mexicana.

Respecto a la comparación entre el índice SPI y el número de días con lluvia, se puede observar que el parámetro 1 por sí solo representa de forma aceptable un riesgo de sequía y que permite obtener a través de una relación sencilla el índice tradicional de sequía SPI. El proceso compuesto Poisson-exponencial permite estimar de manera rápida y confiable un índice de sequía que en lo general es difícil estimar y sobre todo de interpretar. Cabe mencionar que estos índices de aridez suelen apreciarse también a través de diversas características fisiográficas o climatológicas de la región, como el potencial de evaporación (^{Arora, 2002}).