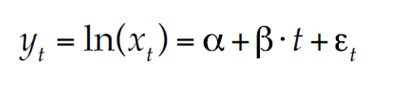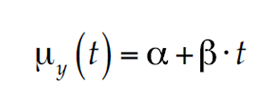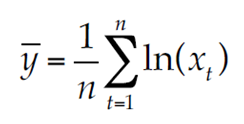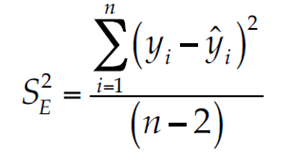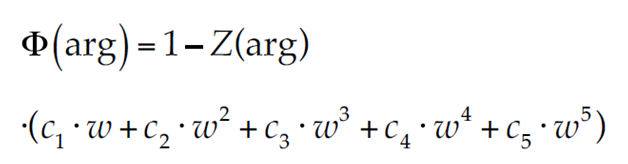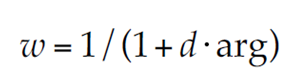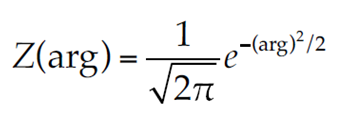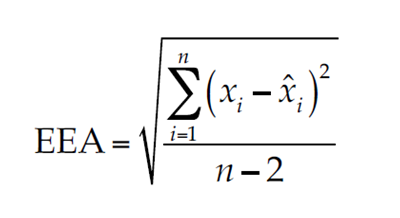Introducción y objetivo
Cuando se dispone de un registro de datos hidrológicos extremos, como gastos, niveles, lluvias de cierta duración y vientos, todos ellos máximos anuales, se puede realizar un análisis de frecuencias para estimar predicciones de tales variables aleatorias, asociadas con determinadas probabilidades de excedencia, cuyo recíproco es el llamado periodo de retorno o intervalo promedio en años entre la ocurrencia de un evento igual o mayor. En resumen, el análisis de frecuencias permite estimar eventos de diseño y consta de cuatro pasos: (1) selección de un modelo probabilístico o función de distribución de probabilidades acumuladas (FDP); (2) aplicación de uno o varios métodos de estimación de los parámetros de ajuste de la FDP; (3) adopción de la FDP que mejor representa al registro disponible, lo anterior, de acuerdo con un criterio de calidad estadística del ajuste, y (4) con base en la FDP seleccionada, estimación de las predicciones buscadas (Khaliq, Ouarda, Ondo, Gachon, & Bobée, 2006).
Cuando no existe el registro de crecientes requerido en el sitio de interés o es inadecuado por amplitud escasa, se recurre al análisis regional de frecuencias, el cual se desarrolla en dos etapas: a) se busca y selecciona un grupo de cuencas aforadas, relativamente cercanas, con un régimen hidrológico similar al de la cuenca bajo estudio; b) se estiman las predicciones buscadas en el sitio sin datos, a través de diversos métodos de transferencia de información hidrológica de los sitios o registros identificados en la etapa A (Leclerc & Ouarda, 2007). La técnica también es aplicable a estaciones pluviográficas o pluviométricas.
La validez de los resultados del análisis de frecuencias local o regional está basado, de manera especial, en dos suposiciones clásicas del registro: que sus datos sean independientes y que sus propiedades estadísticas no cambien en el tiempo o condición de estacionario. En la práctica, la independencia se pierde cuando el muestreo de los datos es próximo o cercano, y entonces un valor puede estar ligado con el anterior. En registros anuales, tal problema no ocurre. Lo no estacionario se origina por el cambio climático o por los efectos de las actividades humanas en la cuenca, principalmente los aprovechamientos hidráulicos, o bien los cambios de uso del suelo, sobre todo la urbanización (Khaliq et al., 2006; Vogel, Yaindl, & Walter, 2011).
Por lo general, y con base en la zona geográfica, el cambio climático puede generar tendencias sutiles ascendentes o descendentes en los registros de datos hidrológicos extremos. Sin embargo, las tendencias fuertes ascendentes observadas en los registros de crecientes anuales y de precipitación máxima diaria anual se originan por la urbanización ocurrida en la cuenca o en las inmediaciones de la estación pluviométrica, y la tendencia severa descendente se asocia en los registros de crecientes con los aprovechamientos hidráulicos, y en las series de lluvias máximas con las deforestaciones o desecación de lagos, ambas cercanas (Vogel et al., 2011).
El objetivo de este trabajo consistió en exponer con detalle el método probabilístico más simple que se puede establecer para el análisis de frecuencias en registros de datos hidrológicos extremos que presentan tendencia importante. Este modelo utiliza la FDP log-normal de dos parámetros de ajuste, en la cual su media varía linealmente con el tiempo (Vogel et al., 2011). Se aplica tal modelo al análisis de frecuencias de dos registros de crecientes anuales de la Región Hidrológica núm. 10, Sinaloa; el de la estación Badiraguato con tendencia ascendente y el de la estación Puente Subpacífico con tendencia descendente. También se realiza el análisis de frecuencias del registro de precipitación máxima diaria anual de la estación climatológica Zacatecas de la Región Hidrológica núm. 37, El Salado, que presenta tendencia ascendente.
Descripción del modelo probabilístico no estacionario
FDP adoptada
Como el objetivo del estudio consiste en identificar la tendencia en los registros de datos hidrológicos extremos anuales y estimar sus consecuencias en el análisis de frecuencias, es necesario utilizar una función de distribución de probabilidades (FDP) que describa la relación entre magnitudes de los datos y predicciones asociadas con determinadas probabilidades de no excedencia. En este caso, y de acuerdo con Vogel et al. (2011), se adopta la distribución lognormal de dos parámetros (LN2), que fue uno de los primeros modelos probabilísticos utilizados en los análisis de frecuencias de crecientes y que aún sigue vigente con su versión de dos (Ashkar & Aucoin, 2012) y tres parámetros de ajuste (Hosking & Wallis, 1997). Sin embargo, la razón principal de tal selección radica en que la función LN2, cuando se combina con un modelo de tendencia logarítmico lineal, origina una FDP no estacionaria bastante simple, la cual permite estimar el impacto de la tendencia en la magnitud y el periodo de retorno de las predicciones, en un lapso a futuro seleccionado.
Un registro de datos hidrológicos extremos anuales es una serie anual de máximos xt, en donde t varía de 1 a n su número de datos. Si tal serie es estacionaria, puede seguir una distribución LN2, cuya función de cuantiles que permite estimar las predicciones con probabilidad de excedencia p o de periodos de retorno T = 1/p es (Vogel et al., 2011):
en la cual, μy y σy son la media y la desviación estándar de los logaritmos naturales de xt, es decir, que yt = ln(xt) y zp es el valor de la variable aleatoria normal estándar con probabilidad de excedencia p.
FDP no estacionaria
El modelo más simple que se puede establecer para describir la tendencia de la serie anual de máximos es el logarítmico lineal con pendiente β estadísticamente diferente de cero. Este enfoque es adecuado en series de valores hidrológicos extremos, pues al emplear logaritmos de sus datos se puede aceptar que la muestra procede de una población normal. El modelo es (Vogel et al., 2011):
siendo α la ordenada al origen y εt los errores del modelo, los cuales proceden de las variaciones de las observaciones respecto a la recta de regresión; esta línea, por sí misma, proporciona la forma en que μy varía a través del tiempo, es decir:
Como la solución de mínimos cuadrados de los residuos para la ordenada al origen es (Ryan, 1998):
Entonces, sustituyendo la ecuación (4) en la (3) se obtiene el modelo de tendencia de la media:
en donde β es la estimación de mínimos cuadrados de los residuos, cuya expresión es (Ryan, 1998):
además, las medias son:
Como ya se indicó, la ecuación (1) es un modelo probabilístico estacionario, pues asume que los momentos de y, dados por μy y σy no varían con el tiempo. Entonces, la sustitución del modelo de tendencia de la media o ecuación (5) en la ecuación (1) conduce al modelo probabilístico no estacionario desarrollado y propuesto por Vogel et al. (2011):
en el cual Sy es la estimación de la desviación estándar de los logaritmos naturales de los datos hidrológicos extremos anuales y t es el contador de años, variando de 1 a n. En realidad, éste es el modelo más simple que se puede establecer para la tendencia, teniendo al tiempo como única covariable explicativa (López-De-La-Cruz & Francés, 2014). Sy se calcula con la expresión:
Factor de aumento de la predicción
Como el propósito de los análisis es estimar el impacto en las predicciones de la tendencia observada en el registro hidrológico de extremos anuales, primero se evaluará el denominado factor de aumento de la predicción (FAP), definido como el cociente entre la predicción estimada en un lapso futuro y la del presente; en relación con la ecuación (9), se obtiene como (Vogel et al., 2011):
La expresión anterior indica que el incremento o decremento en una predicción en un tiempo Δt del futuro sólo depende de la tendencia β estimada en el registro, sea ésta positiva o negativa. Vogel et al. (2011) encuentran en cuencas localizadas en las áreas periféricas de las grandes ciudades de Estados Unidos, como son Los Ángeles, Chicago y Boston, que los FAP en una década a futuro y para registros de crecientes con tendencias ascendentes varían de 2 a 5; es decir, que detectaron pendientes severas fluctuando de 0.070 a 0.160. En cambio, para registros de crecientes con tendencia descendente, los factores de disminución de la predicción (FDP) de un decenio a futuro oscilaron de 0.94 a 0.68.
Reducción del periodo de retorno
La reducción de la recurrencia será el tiempo promedio entre dos predicciones: la del futuro con periodo de retorno Tf ligado con el tiempo tf', y la actual con valores correspondientes T0 y t0. Cada predicción está vinculada con estas probabilidades de excedencia pf = 1/Tf y p0 = 1/T0. Igualando las predicciones, estimadas con la ecuación (9), se podrá obtener el Tf buscado, esto es (Vogel et al., 2011):
Despejando, se obtiene:
en donde Φ(·) es función de densidad de probabilidad de una variable normal estandarizada y representa la probabilidad de no excedencia de que tal variable sea menor que el valor del paréntesis. En el análisis de registros con tendencia descendente, el Tf aumentará.
Prueba de la pendiente del modelo logarítmico lineal
En relación con la ecuación (2), su establecimiento implica procesar registros preferentemente sin datos anuales faltantes, pues es una regresión lineal; además, se debe probar que su pendiente β es estadísticamente diferente de cero (Kund-zewicz & Robson, 2004; Machiwal & Jha, 2008). Para ello se aplicó la prueba sugerida por Ostle y Mensing (1975) basada en el estadístico de la t de Student, que utiliza las varianzas de los errores y de la pendiente de la recta de regresión (
siendo:
y:
En la expresión anterior, y es el valor estimado con la recta de regresión, es decir, con la ecuación (2). Para el cálculo del estadístico Etc se utilizó el algoritmo computacional propuesto por Zelen y Severo (1972), cuyas expresiones son:
siendo zp la variable normal estandarizada, cuyos valores para niveles de significancia (α) de 10, 5 y 1%, en una prueba de dos colas son 1.64485, 1.95996 y 2.57583; ν son los grados de libertad.
Aproximaciones para la distribución normal
En las ecuaciones (1) y (9) se requiere la evaluación de la variable normal estandarizada zp', la cual se estimó con la aproximación racional expuesta por Zelen y Severo (1972). Cuando la probabilidad de excedencia p varía de 0 a 0.50, sus expresiones son:
siendo:
a0 = 2.515517 a1 = 0.802853 a2 = 0.010328
b1 = 1.432788 b2 = 0.189269 b3 = 0.001308
Cuando p > 0.50, se usa 1 p en la ecuación (19) y se le cambia el signo al valor calculado de zp con la ecuación (18).
Para estimar la probabilidad normal Φ(·) de no excedencia en la ecuación (13) se utilizó una aproximación polinomial también sugerida por Zelen y Severo (1972), cuya expresión es:
en la cual:
d = 0.2316419 c1 = 0.31938153
c2 = -0.356563782 c3 = 1.781477937
c4 = -1.821255978 c5 = 1.330274429
En la ecuación (20), Z(arg) es la ordenada de la curva normal calculada con la ecuación:
Error estándar de ajuste
Desde mediados de la década de los años setenta se formuló el error estándar de ajuste (EEA) como una medida cuantitativa que estima la calidad estadística del modelo probabilístico ajustado y que además permite la comparación objetiva entre los diversos modelos que se prueban o ajustan a una muestra, al tener las unidades de los datos. Su expresión es la siguiente (Kite, 1977):
en donde n es el número de datos de la muestra; xi', los datos ordenados de menor a mayor; ^xi', los valores estimados con la ecuación (9), en la cual t varía de 1 a n y le va correspondiendo una probabilidad de no excedencia P(X < x), estimada con la fórmula de Weibull (Benson, 1962):
en la cual m es el número de orden del dato, con 1 para el menor y n para el mayor.
Datos y resultados de las aplicaciones numéricas
Estimaciones del análisis de frecuencias
La descripción detallada del modelo probabilístico no estacionario de los incisos anteriores se puede resumir en las seis estimaciones siguientes: 1) se calculan los parámetros β y α del modelo logarítmico lineal con las ecuaciones (6) y (4), y se prueba si el primero es estadísticamente diferente de cero por medio de las ecuaciones (14) a (17); 2) en seguida se calculan dos factores de aumento de las predicciones (FAP), uno para la primera década y otro para un lapso de 20 años con base en la ecuación (11); 3) después se calculan dos reducciones del periodo de retorno de 100 años de una predicción a través de la ecuación (13), utilizando Δt de 10 y 20 años, este cálculo y los dos siguientes utilizan las ecuaciones auxiliares (18) y (20); 4) haciendo uso de la ecuación (9), primero se calcula el error estándar de ajuste, según la ecuación (23); 5) después se evalúan las curvas de cuantiles con periodos de retorno (Tr) de 2, 10, 50 y 100 años, esto es, utilizando zp = 0, 1.28155, 2.05375 y 2.32635, respectivamente; 6) por último, se estiman las predicciones asociadas con los periodos de retorno de diseño empleados por lo común en los análisis de frecuencia de datos hidrológicos extremos, por medio de la ecuación (9) utilizando t = n.
Cuando la tendencia del registro procesado en ascendente, se estiman FAP y reducciones de la recurrencia de la predicción de Tr = 100 años, así como predicciones mayores que las obtenidas con una FDP estacionaria. Cuando la tendencia es descendente, se estimarán FDP y aumentos en la recurrencia del evento de Tr = 100 años, además de predicciones menores que las obtenidas con una FDP estacionaria. Lo anterior se ilustra en las tres aplicaciones numéricas siguientes.
Estación hidrométrica Badiraguato
Crecientes anuales y su tendencia ascendente
Esta estación de aforos pertenece a la Región Hidrológica núm. 10, Sinaloa, y se ubica en el río del mismo nombre. Su registro actualizado de gastos máximos anuales procede de la GASIR de la Comisión Nacional del Agua (Conagua), con clave 10079, abarca 40 años en el periodo de 1960 a 1999, y se expone en la segunda columna del cuadro 1. Su análisis de homogeneidad detecta tendencia ascendente con las pruebas de Kendall y de Spearman (WMO, 1971; Kottegoda, 1980; Kundzewicz & Robson, 2004; Machiwal & Jha, 2008; Campos-Aranda, 2015). La aplicación de las ecuaciones (4) y (6) aporta α = 5.8595 y β = 0.023393. La pendiente estimada es importante y, sin embargo, resulta estadísticamente igual a cero, ya que Et = 1.7697 < Etc = 2.0244; lo anterior debido a que la varianza de los errores ( 𝑆 𝐸 2 ) resultó muy grande, en parte debido a la enorme dispersión que muestran los datos al variar de 64 a 9 245 m3/s (ver columna 3 del cuadro 1). Al tomar en cuenta que el registro no presenta persistencia, pues su coeficiente de correlación serial de orden 1 (r1) es de sólo 0.054, se decidió continuar con el ajuste del modelo probabilístico no estacionario; es decir, considerar que el registro de crecientes anuales de la estación de aforos Badiraguato presenta tendencia ascendente.
Impacto de la tendencia ascendente en las predicciones
Con base en la ecuación (11) y para dos lapsos a futuro, la primera y segunda décadas, se estimó el factor de aumento de las predicciones en 1.264 y 1.597, lo cual significa que cualquier predicción estimada al final del registro en los siguientes 10 años aumentará un 26.4%, y en los subsiguientes 10 años llegará a casi un 60%. Por otra parte, y de acuerdo con la ecuación (13), la creciente de periodo de retorno de 100 años estimada al final del registro (zp0 = 2.32635) reducirá su recurrencia en la primera década a 54.3 años y al término del segundo decenio a 31.0 años. Las cantidades anteriores ponen de manifiesto la importancia del impacto de la tendencia ascendente observada en las crecientes de la estación Badiraguato en las predicciones.
Error estándar de ajuste y curvas de cuantiles
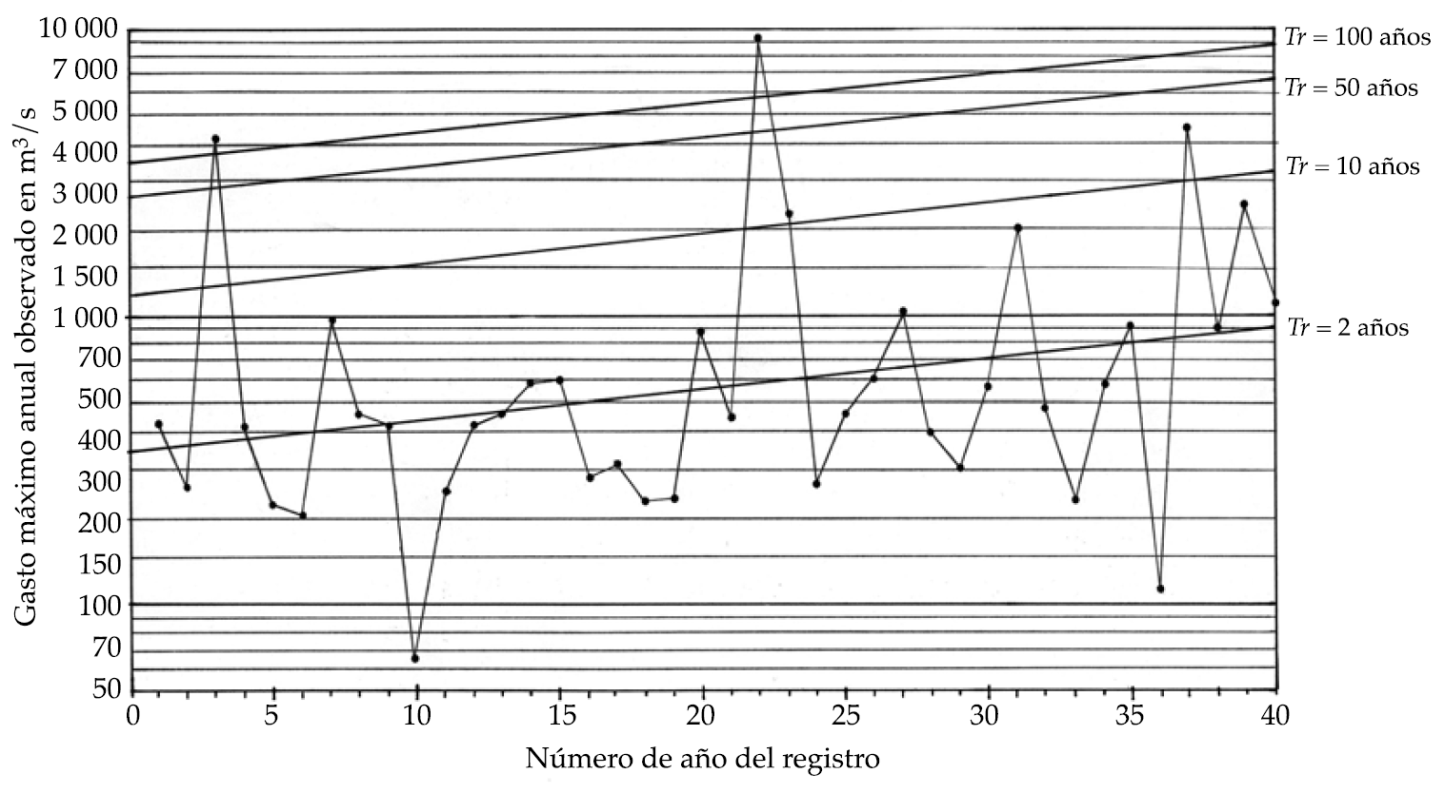
En la columna 4 del cuadro 1 se tienen las estimaciones realizadas con la ecuación (9) para t, variando de 1 a n; zp asociada con la probabilidad definida con la fórmula de Weibull o ecuación (24), y Sy = 0.978602. La aplicación de la ecuación (23) con los valores de las columnas 3 y 4 del cuadro 1 conduce al error estándar de ajuste de 585 m3/s. De nuevo, la aplicación de la ecuación (9) permite estimar las curvas de cuantiles con periodos de retorno de 2, 10, 50 y 100 años, cuyos valores se muestran en las columnas 5 a 8 del cuadro 1. La curva de cuantiles de Tr = 2 años corresponde a la recta de regresión logarítmica, la cual se muestra en la figura 1 con los datos del registro de crecientes. Se observa en la figura 1 que arriba de la curva de cuantiles de Tr = 10 años quedan cuatro datos, lo cual es correcto, pues n = 40; también se detecta que las crecientes de los años 1962 y 1981 tienen un Tr superior a los 100 años.
Predicciones con periodos de retorno de diseño
La aplicación de la ecuación (9) con t = n permite estimar las predicciones asociadas con los ocho periodos de retorno mostrados en el cuadro 2. Con objeto de verificar que las predicciones estimadas con el modelo probabilístico no estacionario tienen magnitud mayor, se ajustaron a los datos las cuatro FDP más comunes en los análisis de frecuencias de crecientes, destacando que su aplicación no es válida, pues el registro de la estación Badiraguato mostró tendencia ascendente. Estas FDP se ajustaron con sus métodos más comunes, los cuales se pueden consultar en Stedinger, Vogel y Foufoula-Georgiou (1993); Hosking y Wallis (1997); Rao y Hamed (2000) y Campos-Aranda (2006). Las predicciones de las FDP aplicadas corresponden a su método de ajuste que condujo al menor EEA y se muestran en el cuadro 2.
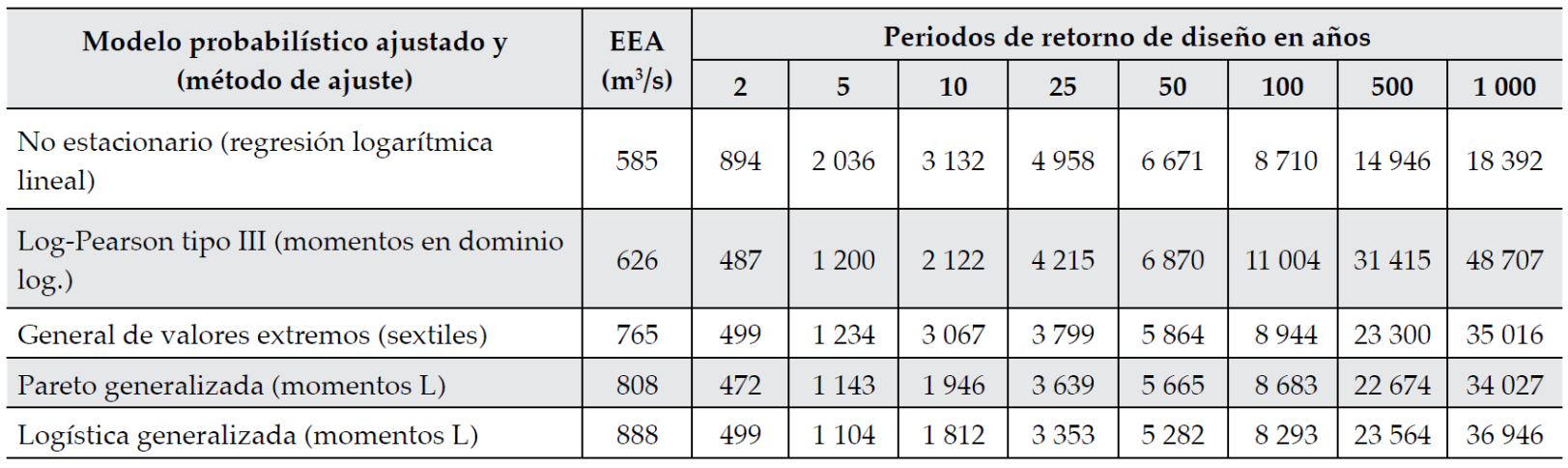
Cuadro 2 Predicciones de diseño (m3/s) en la estación hidrométrica Badiraguato estimadas con el modelo probabilístico no estacionario y su contraste con las obtenidas ajustando cuatro FDP comunes en el análisis de frecuencias de crecientes.
Se observa que el EEA obtenido con el modelo no estacionario es el menor y sus predicciones son superiores en los periodos de retorno bajos, y ello se cumple hasta el Tr de 100 años. Las FDP aplicadas conducen a predicciones muy grandes en los periodos de retorno elevados (Tr > 100 años) debido a presencia de los valores extremos de los años 1981, 1996 y 1962 (ver cuadro 1).
Estación hidrométrica Puente Subpacífico
Crecientes anuales y su tendencia descendente
Esta estación de aforos también pertenece a la Región Hidrológica núm. 10, Sinaloa. Mide las descargas del río Culiacán después de su paso por la ciudad del mismo nombre, capital del estado, y su área drenada es de 15 731 km2. Al río Culiacán lo forman dos grandes colectores: el río Humaya y el río Tamazula; en el segundo se localiza la presa Sanalona, construida durante los años 1940 a 1948, con un área de cuenca de 3 250 km2. En el río Humaya se ubica la presa Adolfo López Mateos, construida durante los años 1957 a 1964, con un área de cuenca de 10 972 km2 (Aldama, Ramírez, Aparicio, MejíaZermeño, & Ortega-Gil, 2006). De acuerdo con los datos anteriores, la estación hidrométrica Puente Subpacífico tiene una cuenca libre de sólo 1 509 km2, por lo cual su régimen hidrológico estará sumamente afectado por los dos aprovechamientos descritos.
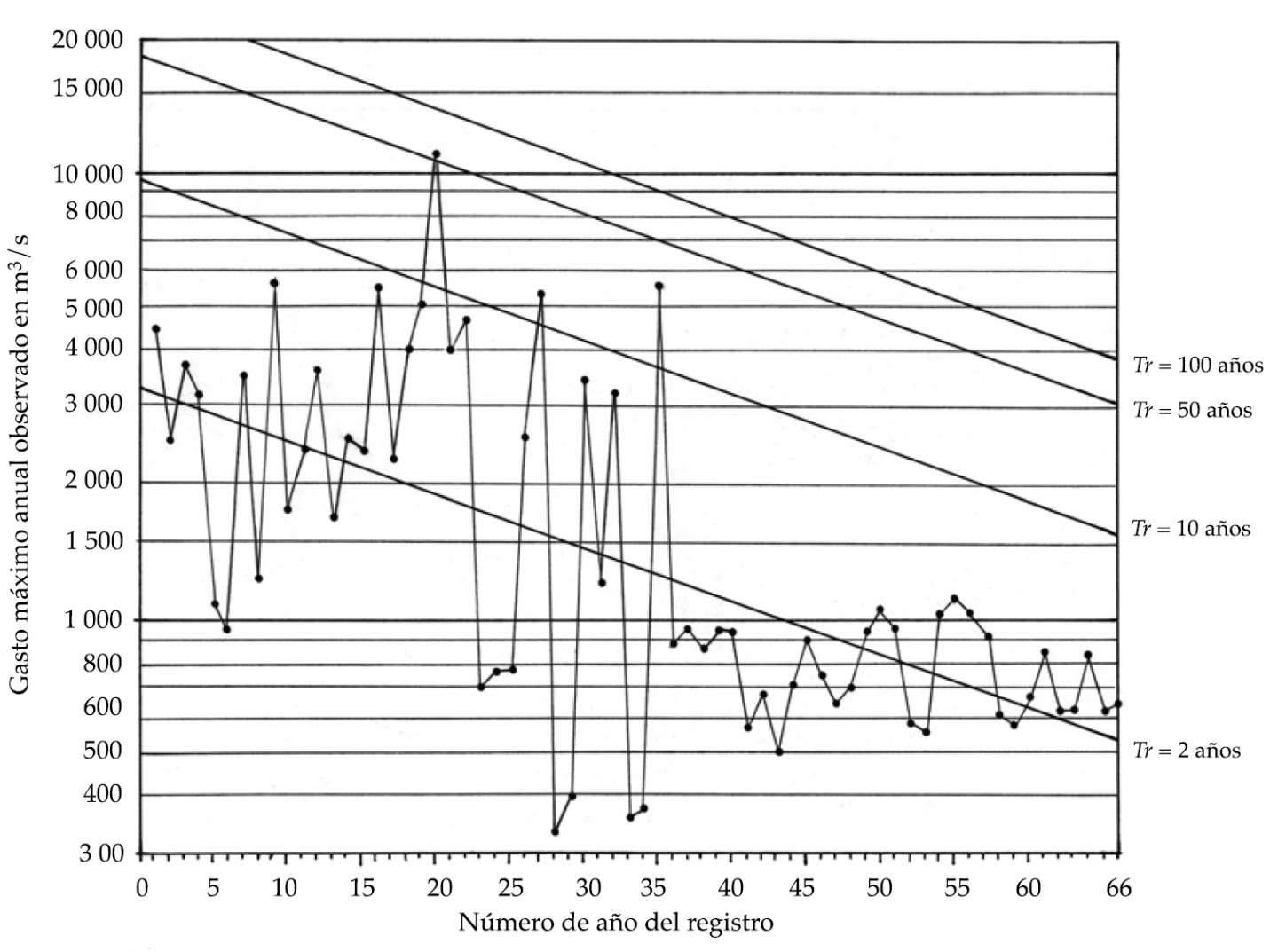
Su registro de crecientes anuales procede del sistema BANDAS (IMTA, 2003) y abarca del año 1924 a 1992, contando con 66 datos, pues el lapso de 1959 a 1961 está faltante. De modo sorpresivo, la creciente máxima registrada de 11 000 m3/s ocurrió en 1943, durante el periodo de construcción de la presa Sanalona, y la última creciente importante aconteció en 1958, con 5 715 m3/s, ya iniciado el proceso constructivo de la presa Adolfo López Mateos, cuyo impacto cambia de forma notable el régimen hidrológico como se observa en la figura 2, a partir del dato número 36. Para este registro, en el cuadro 3, similar al cuadro 1, se citan en exclusiva sus valores y estimaciones por quinquenios. El análisis de homogeneidad del registro citado detecta persistencia (r1 = 0.366), y tendencia descendente con las pruebas de Kendall y de Spearman (WMO, 1971; Kottegoda, 1980; Kundzewicz & Robson, 2004; Machiwal & Jha, 2008; Campos-Aranda, 2015). La aplicación de las ecuaciones (4) y (6) aporta α = 8.1150 y β = -0.027661. La pendiente estimada es importante y por ello resulta estadísticamente diferente de cero, ya que Et = 6.4115 > Etc = 1.9977. Un valor de 0.842596 resultó para Sy.
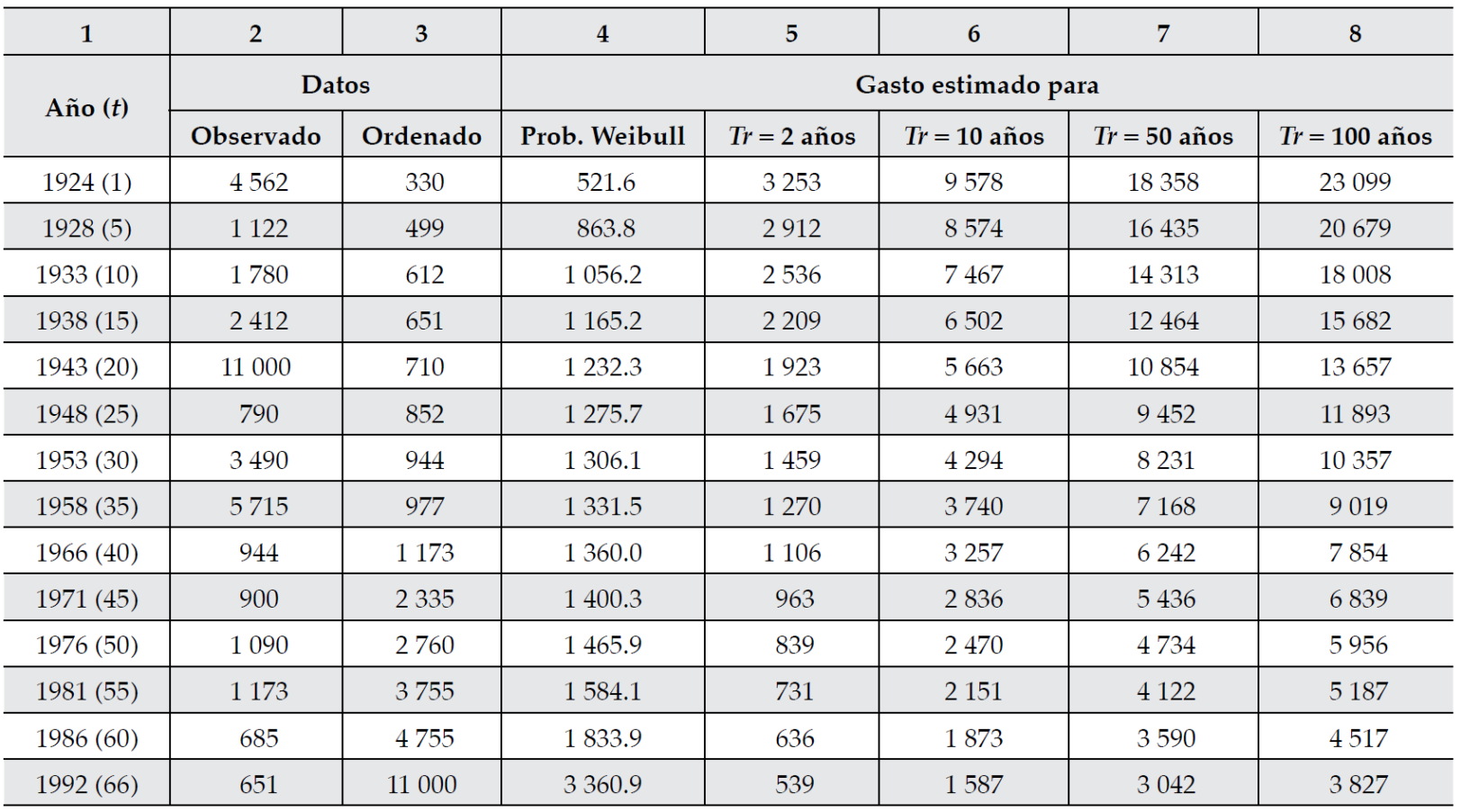
Cuadro 3 Gastos máximos anuales (m3/s) en la estación hidrométrica Puente Subpacífico y cálculos asociados con el error estándar de ajuste y con sus curvas de cuantiles expuestos por quinquenios.
Impacto de la tendencia en las predicciones
Con base en la ecuación (11) se estimó el factor de disminución de las predicciones (FDP) en 0.758 y en 0.575, para la primera y segunda décadas a futuro; son reducciones importantes debido a que la pendiente negativa estimada es fuerte. En relación con la creciente de periodo de retorno 100 años calculada al final del registro, de acuerdo con la ecuación (13), aumentará su recurrencia en la primera década a 252.2 años y en la segunda década a 701.4 años.
Error estándar de ajuste y curvas de cuantiles
Siguiendo un procedimiento idéntico al descrito para este mismo inciso, se obtuvo un error estándar de ajuste de 1 652 m3/s, así como las curvas de cuantiles con periodos de retorno de 2, 10, 50 y 100 años, cuyos valores por quinquenios se muestran en las columnas 5 a 8 del cuadro 3 y en la figura 2, con los datos del registro de crecientes. La curva de cuantiles de Tr = 2 años corresponde a la recta de regresión logarítmica.
Predicciones con periodos de retorno de diseño
La aplicación de la ecuación (9) con t = n permite estimar las predicciones asociadas con los ocho periodos de retorno mostrados en el cuadro 4. La verificación de la magnitud menor de estas predicciones se realizó aplicando las cuatro FDP más utilizadas en los análisis de frecuencias de crecientes, ajustada cada una con sus métodos más comunes (Stedinger et al., 1993; Hosking & Wallis, 1997; Rao & Hamed, 2000, Campos-Aranda, 2006); los resultados se exponen en el cuadro 4 para los EEA menores. Se observa que las FDP reportan EEA mucho más bajos, debido principalmente a que las FDP empleadas son bastante flexibles y se ajustan mejor a los datos dispersos o extremos del registro; pero se aclara que su aplicación no es válida, pues el registro de crecientes anuales de la estación de aforos Puente Subpacífico es no estacionario.
Estación pluviométrica Zacatecas
PMD anual y su tendencia ascendente
El registro de precipitación máxima diaria (PMD) anual de la estación climatológica Zacatecas fue proporcionado y verificado en sus valores extremos por la Dirección Local Zacatecas de la Conagua y consta de 58 datos en el lapso de 1953 a 2010; sus valores se exponen en la columna 2 del cuadro 5. Su estudio de homogeneidad detecta tendencia ascendente con las pruebas de Kendall y de Spearman (WMO, 1971; Kottegoda, 1980; Kundzewicz & Robson, 2004; Machiwal & Jha, 2008; Campos-Aranda, 2015) y no tiene persistencia (r1 = 0.002). Los parámetros del modelo logarítmico lineal, según las ecuaciones (6) y (4) resultaron ser α = 3.6287 y β = 0.005679. Con base en las ecuaciones (14) a (17), se obtuvo un Et = 2.3361 > Etc = 2.0032, de manera que esta prueba indica que la pendiente ascendente β es estadísticamente diferente de cero. Además, Sy = 0.319011.
Impacto de la tendencia en las predicciones
Con base en la ecuación (11) se estimó el factor de aumento de las predicciones (FAP) en un 5.8% y en un 12%, para la primera y segunda décadas a futuro; son incrementos reducidos debido a que la pendiente β estimada es realmente baja. En relación con la creciente de periodo de retorno 100 años estimada al final del registro, de acuerdo con la ecuación (13) reducirá su recurrencia en la primera década a 63.2 años y en la segunda década a 41.0 años.
Error estándar de ajuste y curvas de cuantiles
A partir de un procedimiento idéntico al descrito para este mismo inciso, se obtuvo un error estándar de ajuste de 5.7 milímetros, así como las curvas de cuantiles con periodos de retorno de 2, 10, 50 y 100 años, cuyos valores se muestran en las columnas 5 a 8 del cuadro 3, y en la figura 3 con los datos del registro. Se insiste en que la curva de cuantiles de Tr = 2 años corresponde a la recta de regresión logarítmica. Se observa en la figura 3 que arriba de la curva de cuantiles de Tr = 10 años quedan cinco datos, lo cual es correcto, pues n = 58; también detecta que la PMD máxima del año 1955 tiene un Tr del orden de 100 años.
Predicciones con periodos de retorno de diseño
Por último, la aplicación de la ecuación (9) con t = n permite estimar las predicciones asociadas con los ocho periodos de retorno mostrados en el cuadro 6. La verificación de la magnitud mayor de estas predicciones se realizó aplicando las cuatro FDP más utilizadas en los análisis de frecuencias de crecientes, ajustada cada una con sus métodos más comunes (Stedinger et al., 1993; Hosking & Wallis, 1997; Rao & Hamed, 2000, Campos-Aranda, 2006); los resultados se exponen en el cuadro 6 para los EEA menores. Se observa que las FDP reportan EEA más bajos, debido en parte a que este registro no presenta valores dispersos e incluso las FDP ajustadas muestran límite superior; pero se insiste que su aplicación no es válida, pues el registro de PMD anual de la estación pluviométrica Zacatecas es no estacionario.
Conclusiones
El modelo probabilístico no estacionario desarrollado y propuesto por Vogel et al. (2011), para los análisis de frecuencias, descrito con detalle en este trabajo, es quizás el enfoque más simple y práctico que toma en cuenta la tendencia (ascendente o descendente) encontrada en ciertos registros de datos hidrológicos extremos, pues considera como única covariable explicativa al tiempo, con respecto al cual varía la media del modelo ajustado, que es la distribución lognormal de dos parámetros.
Dos aspectos prácticos importantes del modelo son las estimaciones de los factores de aumento de las predicciones (ecuación 11) y de la reducción de la recurrencia de una cierta predicción (ecuación 13), pues permiten estimar numéricamente el impacto real de la tendencia ascendente observada en las predicciones, como al final de una década o al término de 20 años hacia el futuro.
Cuando un registro de datos hidrológicos extremos muestre tendencia (ascendente o descendente) y ésta resulte estadísticamente diferente de cero, un primer modelo probabilístico que se recomienda probar para abordar el análisis de frecuencias no estacionario es el descrito por la ecuación (9), en particular debido a su extraordinaria sencillez de uso e interpretación de sus diferentes resultados, como se mostró en las tres aplicaciones numéricas descritas con detalle.











 nueva página del texto (beta)
nueva página del texto (beta)