Nota técnica

 

Ajuste de las distribuciones GVE, LOG y PAG con momentos L depurados (1, 0)

 

Fitting of GPA, GLO and GEV Distributions with Trimmed L-moments (1, 0)

 

Daniel Francisco Campos-Aranda
Profesor Jubilado de la Universidad Autónoma de San Luis Potosí, México
*Autor de correspondencia

 

Dirección institucional del autor

Dr. Daniel Francisco Campos Aranda

Profesor jubilado de la Universidad Autónoma de San Luis Potosí
Genaro Codina 240, Colonia Jardines del Estadio
78280 San Luis Potosí, San Luis Potosí, México
campos_aranda@hotmail.com

 

Resumen

Los momentos estadísticos han sido utilizados para caracterizar las distribuciones de probabilidad, así como las muestras de datos observados. En este trabajo se describe someramente la teoría de los momentos L y de los llamados momentos L depurados (1, 0), que son capaces de reducir la influencia del valor más bajo de la muestra, para mejorar el ajuste y obtener predicciones extremas más confiables. Se citan las ecuaciones, recientemente expuestas en la literatura estadística, que permiten estimar los parámetros de ubicación (u), escala (α) y forma (k) de las tres funciones de distribución de probabilidades más utilizadas en los análisis de frecuencias de datos hidrológicos extremos, que son la General de Valores Extremos (GVE), la Logística Generalizada (LOG) y la Pareto Generalizada (PAG). Estas tres distribuciones se ajustaron con los métodos de momentos L y momentos L depurados (1, 0), a los 21 registros de gasto máximo anual disponibles en la Región Hidrológica núm. 10 (Sinaloa). Se evaluó la calidad de cada ajuste a través del error estándar. El análisis de los resultados indica que la distribución PAG conduce a los menores errores de ajuste en trece registros con el método de los momentos L depurados (1, 0) y en el resto con el de momentos L. Las conclusiones sugieren la aplicación sistemática de los tres modelos probabilísticos utilizados y del método de los momentos L depurados (1, 0), como una versión avanzada del procedimiento de los momentos L, actualmente de uso universal.

Palabras clave: momentos L, momentos L depurados (1, 0), distribuciones de probabilidad GVE, LOG y PAG, error estándar de ajuste, Región Hidrológica núm. 10 (Sinaloa).

 

Abstract

Statistical moments have been used to characterize probability distributions and samples of observed data. This work briefly describes the theory of L-moments and trimmed L-moments (1,0), which can reduce the influence of the lowest value in a sample, in order to improve the fit and obtain more reliable extreme predictions. Recent equations found in the statistical literature that estimate the location, scale and shape of the probability distribution functions are cited, which are often used to analyze the frequencies of extreme hydrological data. These include the General Extreme Values (GEV), Generalized Logistic (GLO) and Generalized Pareto (GPA) equations. These three distributions were fitted with the methods of L-moments and trimmed L-moments (1,0) to 21 annual maximum flow registries from Hydrological Region No. 10 (Sinaloa). The quality of each fit was evaluated based on the standard error. The analysis of the results indicate that the GPA distribution provides the smallest fitting errors for 13 registries using the trimmed L-moments (1,0) and for the rest of the registries using L-moments. The conclusions suggest that the three probabilistic models studied can be applied with the trimmed L-moments (1,0) as an advanced version of the L-moments procedure which is universally used.

Keywords: L-moments, trimmed L-moments (1, 0), probability distributions GEV, GLO and GPA, standard error of fit, Hydrological Region No. 10 (Sinaloa).

 

Introducción

Los momentos estadísticos han sido usados de modo tradicional para caracterizar las funciones de distribución de probabilidades (FDP), o bien las series de datos observados. Los momentos L, de creación más reciente, son combinaciones lineales de los valores esperados de los estadísticos de orden (Asquith, 2011), comparables a los momentos convencionales, pero tienen menores varianzas muestrales y son más robustos a la influencia de los valores dispersos o extremos (outliers). De manera análoga a los momentos estadísticos, los momentos L de orden uno a cuatro, también caracterizan, respectivamente, localización, escala, asimetría y curtosis.

De acuerdo con Karvanen (2006), el concepto de los momentos L se originó hacia finales de los años sesenta, con varios resultados desvinculados sobre combinaciones lineales de los estadísticos de orden, que culminan con el trabajo de Greenwood, Landwehr, Matalas y Wallis (1979). Hosking (1990) unifica la teoría de los momentos L y proporciona guías para sus aplicaciones prácticas, las cuales se han realizado en las disciplinas de la hidrología, meteorología, control de calidad e ingeniería civil. Karvanen (2006) también cita avances recientes en los aspectos teóricos, por ejemplo: (1) Mudholkar y Hutson (1998) remplazan los valores esperados de los estadísticos de orden por funcionales que inducen estimadores rápidos como la mediana, el estimador Gastwirth y la media truncada; estos análogos, llamados momentos LQ, siempre existen y son simples de evaluar; (2) Elamir y Seheult (2003) introducen una extensión natural de los momentos L, llamados momentos depurados; se designan momentos TL de Trimmed, que significa depurado, truncado o cortado; (3) también Elamir y Seheult (2004) derivan la estructura exacta de la varianza de muestreo de los momentos L.

Por otra parte, el análisis de frecuencias de datos hidrológicos, crecientes, lluvias máximas y sequías, busca principalmente valores de éstos, asociados con bajas probabilidades de excedencia. Tales magnitudes, llamadas predicciones, se obtienen con base en el ajuste de una FDP a la muestra de datos disponible. Entre las FDP que más se han utilizado en estos estudios y que incluso su aplicación ha sido establecida bajo precepto, se tienen los modelos probabilísticos: General de Valores Extremos (GVE), Logística Generalizada (LOG) y Pareto Generalizada (PAG). Estas FDP han sido adoptadas en los análisis de frecuencias debido a su extremo derecho grueso o denso (heavy tail), que es la porción donde se estiman las predicciones (El Adlouni, Bobée, & Ouarda, 2008).

El objetivo de este trabajo consiste en exponer con detalle los aspectos teóricos asociados con los llamados momentos L depurados, en especial de aquellos que eliminan el valor más bajo de la serie o muestra de datos, y su aplicación en el ajuste de las distribuciones GVE, LOG y PAG. Lo anterior se complementa con un contraste numérico en los 21 registros disponibles de crecientes anuales de la Región Hidrológica núm. 10 (Sinaloa), que no tienen régimen de escurrimientos afectado por embalses y que cuentan con más de 20 datos, según la información actualizada hasta el año 2011, proporcionada por la Comisión Nacional del Agua (Conagua).

 

Resumen de la teoría operativa

Definición poblacional de los momentos L

Sea X una variable aleatoria y sea X_j:n uno de sus estadísticos de orden, es decir, una variable aleatoria distribuida como el j-ésimo elemento más pequeño de una muestra aleatoria de tamaño n, tomada de la distribución de X, entonces, los momentos L de X son las cantidades siguientes (Hosking, 1990):

cuya expresión general es:

En la ecuación (5), el segundo paréntesis es un cociente de factoriales que define el número de combinaciones posibles de los m términos, tomando q en cada arreglo; su expresión general es (Bhattarai, 2004; Asquith, 2011):

Por convención 0! = 1. Recordar que la función factorial Gamma es Γ (m + 1) = m!, la cual se puede estimar con la fórmula de Stirling (Davis, 1965), que será expuesta posteriormente. Por otra parte, los valores esperados de los estadísticos de orden de la ecuación (5) se estimarán con la expresión (Hosking & Wallis, 1997; Kottegoda & Rosso, 2008; Asquith, 2011):

siendo x(F) la función de cuantiles o solución inversa de la función de distribución de probabilidades acumuladas F(x) = F.

 

Momentos L depurados poblacionales y de la muestra

Como ya se indicó brevemente, los momentos L tienen usos similares a los momentos convencionales, además existen siempre que la media de la distribución exista, aunque algunos momentos de orden superior puedan no existir y son relativamente robustos a los efectos de los valores extremos. Hosking (2007) indica que estas dos ventajas son insuficientes en el manejo de ciertos datos con muchos valores extremos y de FDP que involucran colas muy gruesas (very heavy tails), ya que el primer momento puede no existir. Los momentos L depurados son generalizaciones que no requieren que exista la media de la FDP de soporte. Se definen de manera general como (Elamir & Seheult, 2003; Hosking, 2007):

siendo s y t enteros positivos. El término depurado (trimmed), que también puede ser truncado o cortado, es apropiado debido a que la definición de λ_r^(s,t) no involucra los valores esperados de los estadísticos de orden de los s datos o valores más pequeños ni de los t mayores de la muestra de tamaño r + s + t; es decir, les asigna peso cero. Los cocientes de momentos L depurados τ_r^(s,t) = λ_r ^(s,t) / λ₂^(s,t) son medidas adimensionales de la forma de la distribución. Hosking (2007) señala que una cuestión para decidir es el grado de depuración o de corte apropiado y al respecto indica que la inspección de los datos de la muestra puede ayudar en tal selección. De manera reciente, Elamir (2010) encontró que la cantidad de depuración conduce a diferentes varianzas de los estimados; entonces, una selección óptima será la suma mínima de los errores absolutos entre los datos y los estimados, con la FDP ajustada con tales momentos L depurados.

A partir de una muestra ordenada (x ₁ ≤ x₂ ≤ ⋅⋅⋅≤x_n) los momentos L depurados λ_r ^(s,t) pueden ser estimados de manera no sesgada con la expresión siguiente (Elamir & Seheult, 2003; Hosking, 2007):

 

Momentos L depurados (1, 0) poblacionales y de la muestra

Ahmad, Shabri y Zakaria (2011b) indican que los momentos L depurados fueron introducidos por Elamir y Seheult (2003) como una opción para tomar en cuenta los valores extremos; son fáciles de calcular y más robustos que los momentos L a la presencia de tales datos atípicos o dispersos (outliers). También señalan que la mayoría de los trabajos de aplicación de los momentos L depurados se han centrado en casos simétricos de truncado, por lo general suprimiendo el valor más bajo y el más grande de la muestra conceptual (s = t = 1); por ejemplo, Abdul-Moniem y Selim (2009), y Bílková (2014), proponen emplear los momentos L depurados (1, 0), en los cuales sólo el valor más bajo de la muestra es eliminado, buscando con ello un mejor ajuste de la FDP a los valores extremos superiores. De acuerdo con la ecuación (8) y considerando s = 1 y t = 0, se definen los siguientes cuatro primeros momentos L depurados (1, 0), según Ahmad et al. (2011b):

Los cocientes poblacionales de momentos L depurados de asimetría y curtosis son, respectivamente:

Las estimaciones no sesgadas de los momentos depurados (1, 0) se basan en una muestra (x_i) de datos ordenados en forma progresiva y se obtienen a partir de la ecuación (8) modificada:

Abdul-Moniem y Selim (2009) aplican los métodos de los momentos L y de los depurados simétricamente (s = t = 1) al ajuste de la distribución Pareto Generalizada; manteniendo conocido el parámetro de forma (k), estiman los parámetros de ubicación (u) y de escala (α) en muestras sintéticas de tamaños 10(10)40, con diez mil replicaciones cada una, en las cuales u = 2 y α = 0.20(0.20)1.40. Encontraron que el error cuadrático medio (ECM) entre los parámetros estimados y los reales o asignados decrece conforme n se incrementa, además creció conforme aumentó el parámetro de escala, pero tal error es siempre menor en las estimaciones realizadas con los momentos L depurados.

Ahmad et al. (2011b) también utilizan la distribución Pareto Generalizada y a través de simulación aleatoria encuentran que los momentos L depurados (1, 0) reducen la influencia probable del dato más pequeño de la muestra en la estimación de los eventos de alto periodo de retorno. Sus resultados con datos reales muestran que, en algunos casos, los momentos L depurados (1, 0) son una mejor opción que los momentos L, en especial en la estimación de predicciones de baja probabilidad de excedencia.

Ahmad, Shabri y Zakaria (2013) contrastan las distribuciones GVE, LOG y PAG ajustadas por momentos L y momentos depurados (1, 0) y (1,1), en 12 registros de gastos máximos anuales de la porción noreste de Malasia; encuentran que los momentos depurados (1, 0) conducen a mejores ajustes en la mayoría de los registros procesados.

 

Ajuste con momentos L de las distribuciones GVE, LOG y PAG

De acuerdo con Hosking y Wallis (1997), según su tabla 5.1, estas tres funciones de distribución de probabilidad (FDP), cuando su parámetro de forma k < 0, tienen sus colas derechas más gruesas o densas de entre todas las que son utilizadas de manera regular en los análisis de frecuencias de datos hidrológicos; además, ellas tienen una frontera superior cuando k > 0 y cuando k = 0 definen distribuciones de dos parámetros: la Gumbel, la logística y la exponencial, respectivamente.

El método de obtención de sus parámetros de ubicación, escala y forma (u, α y k) de las distribuciones GVE, LOG y PAG con base en los momentos L se puede consultar, respectivamente, en Stedinger, Vogel y Foufoula-Georgiou (1993), Hosking y Wallis (1997), y Rao y Hamed (2000). A continuación se citan para cada una de estas tres FDP su fórmula matemática o F(x), su solución inversa o función de cuantiles x(F) y las ecuaciones de cálculo necesarias para estimar sus tres parámetros de ajuste.

 

Distribución General de Valores Extremos

Intervalo de x: u + α/k ≤ x ∞ si k < 0; - ∞ < x < ∞ si k = 0 y - ∞ x ≤ u + α/k si k > 0.

siendo y la variable reducida:

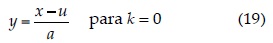
La función factorial Gamma fue estimada con la fórmula de Stirling (Davis, 1965), que para valores grandes del argumento e es bastante aproximada con un error cercano a cero, y está dada por:

 

Distribución Logística Generalizada

Intervalo de x, idéntico al de la GVE:

siendo y igual a la ecuación (18):

 

Distribución Pareto Generalizada

Intervalo de x: u ≤ x < ∞ si k ≤ 0; u ≤ x ≤ u + α/k si k > 0.

siendo y igual a la ecuación (18):

 

Ajuste con momentos L depurados (1, 0) de las distribuciones GVE, LOG y PAG

Ahmad, Shabri y Zakaria (2011a), y Ahmad et al. (2013) obtienen las expresiones para estimar los tres parámetros de ajuste de estas distribuciones, basados en los momentos L depurados (1, 0), éstas son:

 

Distribución General de Valores Extremos

 

La ecuación (39) fue obtenida con base en la expresión de t₃, en función k expuesta por Ahmad et al. (2013), y es válida en el intervalo para k de -0.70 a 0.50. El recíproco de la función Gamma fue estimado con la siguiente fórmula del producto infinito de Euler (Davis, 1965), la cual fue evaluada para np = 50; con ello, ya no cambian sus cinco cifras decimales:

siendo γ = 0.5772156649 la constante de Euler con el valor aproximado indicado. La función 1/ Γ (z) es continua y pasa por cero en los puntos z = 0, -1, -2, -3, ...

 

Distribución Logística Generalizada

 

Distribución Pareto Generalizada

 

 

Indicador cuantitativo del ajuste

Coles (2001) indica que la motivación para ajustar una FDP a los datos es poder obtener conclusiones respecto a la población de la cual probablemente proceden los valores disponibles. Como la confiabilidad de tales conclusiones depende de la exactitud de la FDP ajustada, entonces es necesario verificar que tal modelo probabilístico es capaz de reproducir los datos que se emplearon para estimarlo (Flowers-Cano, Flowers, & Rivera-Trejo, 2014).

Desde mediados de la década de los años setenta se estableció el error estándar de ajuste (EEA) como una medida cuantitativa que estima la calidad estadística del ajuste y que además permite la comparación objetiva entre las diversas distribuciones de probabilidad que se prueban o ajustan a una muestra, ya que tiene las unidades de los datos. Su expresión es la siguiente (Kite, 1977):

en donde n es el número de datos de la muestra; x_i, los datos ordenados de menor a mayor; _i, los valores estimados con la función de cuantiles o solución inversa, utilizando las ternas de parámetros de ajuste (u, α, k) que se prueban para una probabilidad de no excedencia P(X < x), estimada con la fórmula de Weibull (Benson, 1962):

en la cual m es el número de orden del dato, con 1 para el menor y n para el mayor. Por último, np es el número de parámetros de ajuste; para las distribuciones GVE, LOG y PAG es tres.

 

Indicadores cualitativos del ajuste

Recientemente se han popularizado dos gráficos de diagnóstico: el de Probabilidades y el de Cantidades (Coles, 2001; Wilks, 2011); el primero emplea en el eje de las abscisas la probabilidad empírica estimada con la ecuación (50) y en las ordenadas la probabilidad que define el modelo para cada dato disponible ordenados en forma progresiva de magnitud (x ₁ ≤ x₂ ≤ ⋅⋅⋅≤x_n), la cual se estima con las ecuaciones (17), (27) y (33) para las distribuciones GVE, LOG y PAG, respectivamente. En el gráfico de Cantidades se indican en las abscisas el valor del dato observado (x ₁ ≤ x₂ ≤ ⋅⋅⋅≤x_n) y en las ordenadas el valor estimado con la solución inversa del modelo; es decir, con las ecuaciones (20), (28) y (34) para las funciones GVE, LOG y PAG, para la probabilidad empírica estimada con la ecuación (50). En resumen, las coordenadas x y y de cada gráfico son (Coles, 2001):

Probabilidades

Cantidades

 

Descripción de la aplicación numérica

Registros hidrométricos procesados

La aplicación numérica que se describe utilizó los 21 registros de crecientes máximas anuales disponibles en la Región Hidrológica núm. 10 (Sinaloa) en estaciones hidrométricas cuyo régimen de escurrimiento no está afectado por embalses y cuentan con más de 20 años de datos en el sistema BANDAS (IMTA, 2002). Los registros de las estaciones hidrométricas Huites y Guamúchil abarcan hasta el año en que la construcción del embalse respectivo afectó su régimen; los datos de la estación San Francisco proceden del Boletín Hidrológico 36 (SRH, 1975). Esta información hidrométrica se actualizó en las oficinas de la Comisión Nacional del Agua (Conagua) y entonces 12 registros fueron ampliados con datos que abarcan, como máximo, hasta el año 2011, los cuales fueron Santa Cruz, Jaina, Palo Dulce, Ixpalino, Chinipas, Tamazula, Acatitán, Choix, Badiraguato, Zopilote, Chico Ruiz y El Bledal. En las primeras cinco columnas del cuadro 1 se exponen las características generales de los registros que serán procesados, expuestos en orden decreciente de tamaño de cuenca; el registro más corto tiene 23 años y los más amplios 60 años, con un valor mediano de 33 años. Campos-Aranda (2014a) presenta un mapa con la localización de las 21 estaciones hidrométricas procesadas y sus respectivas cuencas de drenaje.

 

Pruebas estadísticas aplicadas a los registros

Para verificar la calidad estadística de los registros hidrométricos que serán procesados, se aplicó una prueba general y seis tests específicos que buscan persistencia (Anderson y Sneyers), tendencia (Kendall y Spearman), exceso o déficit de variabilidad (Bartlett) y cambio en la media (Cramer). La prueba general fue la de Von Neumann, que detecta aleatoriedad contra componentes determinísticas no especificadas. Todas estas pruebas se pueden consultar en WMO (1971), y Machiwal y Jha (2008, 2012).

La prueba de Von Neumann encontró sólo dos registros no homogéneos: Choix y Pericos, ambos con persistencia detectada por los tests de Anderson y de Sneyers. Tres registros (Santa Cruz, Jaina y Acatitán) mostraron tendencia descendente y uno (Badiraguato) ascendente ligera, de acuerdo con los tests de Kendall y Spearman. Al tomar en cuenta que los registros que mostraron tendencia descendente tienen años faltantes, principalmente en su lapso final de 1995 al 2011, se consideraron susceptibles de procesamiento probabilístico, ya que tal componente determinística puede estar siendo inducida por la falta de continuidad.

 

Momentos L depurados (1, 0)

Con base en la ecuación (16) se calcularon estos momentos, los cuales se han concentrado en las columnas 6, 7 y 8 del cuadro 1; en su columna final se tiene el cociente de asimetría, evaluado según la ecuación (14).

 

Errores estándar de ajuste

Con base en los momentos L y sus cocientes (Hosking & Wallis, 1997; Campos-Aranda, 2014a), se obtuvieron los tres parámetros de ajuste de las distribuciones GVE, LOG y PAG, por medio de las ecuaciones (22) a (26), (30) a (32) y (36) a (38), respectivamente. Después, haciendo uso de sus soluciones inversas, ecuaciones (20), (28) y (34), se realizaron las estimaciones _i o predicciones necesarias para aplicar la ecuación (49) del error estándar de ajuste (EEA). Los resultados se han concentrado en el cuadro 2, en las columnas indicadas con "moL".

De manera similar, pero utilizando los valores de los momentos L depurados (1, 0) del cuadro 1, se estimaron los tres parámetros de ajuste de las funciones GVE, LOG y PAG, a través de las ecuaciones (39) a (42), (43) a (45) y (46) a (48). En seguida, a partir de sus soluciones inversas, expresiones (20), (28) y (34), se obtuvieron los valores de _i para obtener los errores estándar de ajuste, los cuales se tienen en el cuadro 2, en las columnas con designación "moLD".

 

Gráficos de diagnóstico

En las figuras 1 y 2 se presentan los gráficos de probabilidad del registro de la estación hidrométrica San Francisco, con n = 33, para las distribuciones GVE y PAG. Se observa, en general, un mejor ajuste del modelo PAG con todos los datos de la muestra, sobre todo para los valores bajos, en los que la función GVE presenta la mayor dispersión.

Respecto a los gráficos de cantidades, se exponen los de las distribuciones LOG y PAG en las figuras 3 y 4, para el mismo registro en la estación de aforos San Francisco, destacando el ajuste excelente que tiene la función PAG en los valores bajos y cómo ambas funciones no pueden reproducir los valores altos del registro a partir del dato 28.

 

Análisis de los resultados y predicciones de diseño

En el cuadro 2 se han indicado entre paréntesis circular los valores mínimos del error estándar de ajuste; se observa que en todos los registros, la distribución PAG condujo a los valores menores, por ello es la seleccionada para exponer sus predicciones, las cuales se han concentrado en el cuadro 3. Campos-Aranda (2014b) expone varios métodos simples para el ajuste de la función PAG.

En tres registros, los de las estaciones Chinipas, El Quelite y Chico Ruiz, ocurren valores iguales del EEA y para tales casos se decidió adoptar las predicciones más altas del método de momentos L o de los momentos L depurados (1, 0), lo cual se indica con paréntesis rectangular en el cuadro 2. Conviene destacar que en dos primeros registros citados, el ajuste de la distribución PAG con momentos L depurados (1, 0), condujo a predicciones más altas en los periodos de retorno elevados.

También se debe destacar que el ajuste por momentos L depurados (1, 0) de la función PAG llevó a un valor menor del EEA en más de la mitad (catorce) de los 21 registros procesados. Lo anterior demuestra que tal método en efecto otorga mayor ponderación a los datos de mayor magnitud a través de un mejor ajuste de la FDP, lo que conduce a predicciones más confiables.

Con el método de momentos L depurados (1, 0), se obtienen menores EEA apreciables en el ajuste de la distribución GVE en ciertos registros, como Huites, San Francisco, Naranjo, Badiraguato y Bamícori. En relación con la función LOG, lo anterior ocurre en los mismos registros y en Jaina y Guamúchil.

Un contraste individual entre las predicciones mostradas en el cuadro 3 y las adoptadas por Campos-Aranda (2014a), procedentes de las distribuciones GVE, LOG y Log-Pearson tipo III, demostró una similitud alta en todas las estaciones hidrométricas hasta los periodos de retorno de 100 años, pero también mostró que la función PAG aporta, en algunos registros, predicciones menores en los periodos de retorno elevados (>100 años). En la última columna del cuadro 2 se tiene el llamado error relativo del máximo EEA, calculado con la expresión siguiente:

en la cual EEA_M y EEA_m son los errores estándar de ajuste máximo y mínimo de los seis valores calculados. Destacan los ER de las estaciones de aforos La Huerta, Zopilote y Chico Ruiz, cuyos registros carecen de valores extremos, ya que el parámetro de forma (k), estimado con momentos L de la distribución PAG, resultó positivo en las tres, y en la función GVE también es positivo en la primera y cercano a cero en las restantes. En estos tres registros, el ajuste de las distribuciones GVE y LOG a través del método de los momentos L depurados (1, 0) conduce a EEA mayores que los del método de momentos L, lo cual indica que no es conveniente eliminar su dato más bajo.

 

Conclusiones

Los resultados numéricos de este trabajo establecen a la distribución Pareto Generalizada como un modelo probabilístico que conviene probar en los análisis de frecuencias de crecientes y de otros datos hidrológicos extremos, ya que conduce a errores estándar de ajuste (EEA) bajos.

En diez de los 21 registros procesados en la aplicación numérica descrita, los EEA obtenidos con las distribuciones GVE y LOG están dentro del 10% del error relativo (ecuación (47)), como se observa en la columna final del cuadro 2; por lo anterior, su aplicación debe seguir siendo una norma o precepto.

Los resultados concentrados en el cuadro 2 relativos al EEA demuestran que en determinados registros de crecientes anuales, más de la mitad de los 21 procesados, el método de los momentos L depurados (1, 0) es una buena opción para abatirlo y lograr mejores ajustes con cada una de las tres funciones de probabilidad aplicadas (GVE, LOG y PAG); por ello se sugiere utilizarlo sistemáticamente, como una versión avanzada del procedimiento de los momentos L, el cual ya es de uso universal en los análisis de frecuencias hidrológicos.

 

Agradecimientos

Se agradece a los ingenieros de la Conagua, José Luis Juárez Rubio de la Dirección Local San Luis Potosí y Alejandro García Ruiz de la GASIR, el haber proporcionado al autor la información hidrométrica actualizada de crecientes anuales en 19 estaciones de aforos de la Región Hidrológica núm. 10 (Sinaloa).

 

Referencias

Abdul-Moniem, I. B., & Selim, Y. M. (2009). TL-Moments and L-Moments Estimation for the Generalized Pareto Distribution. Applied Mathematical Sciences, 3(1), 43-52.         [ Links ]

Ahmad, U. N., Shabri, A., & Zakaria, Z. A. (2011a). Flood Frequency Analysis of Annual Maximum Stream Flows Using L-Moments and TL-Moments Approach. Applied Mathematical Sciences, 5(5), 243-253.         [ Links ]

Ahmad, U. N., Shabri, A., & Zakaria, Z. A. (2011b). Trimmed L-Moments (1, 0) for the Generalized Pareto Distribution. Hydrological Sciences Journal, 56(6), 1053-1060.         [ Links ]

Ahmad, U. N., Shabri, A., & Zakaria, Z. A. (2013). An Analysis of Annual Maximum Stream Flows in Terengganu, Malaysia using TL-Moments Approach. Theoretical and Applied Climatology, 111(3-4), 649-663.         [ Links ]

Asquith, W. H. (2011). Distributional Analysis with L-moment Statistics using the R Environment for Statistical Computing. Chapter 3: Order Statistics (pp. 47-59) and Chapter 6: L-Moments (pp. 87-122). Texas, USA: Author Edition (ISBN-13: 978-1463508418).         [ Links ]

Benson, M. A. (1962). Plotting Positions and Economics of Engineering Planning. Journal of Hydraulics Division, 88(6), 57-71.         [ Links ]

Bhattarai, K. P. (2004). Partial L-Moments for the Analysis of Censored Flood Samples. Hydrological Sciences Journal, 49(5), 855-868.         [ Links ]

Bílková, D. (2014). Trimmed L-Moments: Analogy of Classical L-Moments. American Journal of Mathematics and Statistics, 4(2), 80-106.         [ Links ]

Campos-Aranda, D. F. (2014a). Análisis regional de frecuencia de crecientes en la Región Hidrológica núm. 10 (Sinaloa), México. 2: contraste de predicciones locales y regionales. Agrociencia, 48(3), 255-270.         [ Links ]

Campos-Aranda, D. F. (octubre-diciembre, 2014b). Predicción de crecientes usando la distribución Pareto Generalizada ajustada con tres métodos simples. Revista digital Tláloc, 65.         [ Links ]

Coles, S. (2001). Theme 2.6.7: Model Diagnostics (pp. 36-44). In An Introduction to Statistical Modeling of Extreme Values. London: Springer-Verlag.         [ Links ]

Davis, P. J. (1965). Gamma Function and Related Functions. Chapter 6 (pp. 253-296). In M. Abramowitz & I. A. Stegun (Eds.). Handbook of Mathematical Functions. New York: Dover Publications.         [ Links ]

El Adlouni, S., Bobée, B., & Ouarda, T. B. M. J. (2008). On the Tails of Extreme Event Distributions in hydrology. Journal of Hydrology, 355(1-4), 16-33.         [ Links ]

Elamir, E. A. H. (2010). Optimal Choices for Trimming in Trimmed L-Moment Method. Applied Mathematical Sciences, 4(58), 2881-2890.         [ Links ]

Elamir, E. A. H., & Seheult, A. H. (2003). Trimmed L-Moments. Computational Statistics & Data Analysis, 43(3), 299-314.         [ Links ]

Elamir, E. A. H., & Seheult, A. H. (2004). Exact Variance Structure of Sample L-Moments. Journal of Statistical Planning and Inference, 124(2), 337-359.         [ Links ]

Flowers-Cano, R. S., Flowers, R. F., & Rivera-Trejo, F. (2014). Evaluación de criterios de selección de modelos probabilísticos: validación con series de valores máximos simulados. Tecnología y Ciencias del Agua, 5(5), 189-197.         [ Links ]

Greenwood, J. A., Landwehr, J. M., Matalas, N. C., & Wallis, J. R. (1979). Probability Weighted Moments: Definition and Relation to Parameters of Several Distributions Expressible in Inverse Form. Water Resources Research, 15(5), 1049-1054.         [ Links ]

Hosking, J. R. M. (1990). L-moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. Journal of the Royal Statistical Society, B, 52(1), 105-124.         [ Links ]

Hosking, J. R. M. (2007). Some Theory and Practical Uses of Trimmed L-Moments. Journal of Statistical Planning and Inference, 137(9), 3024-3039.         [ Links ]

Hosking, J. R. M., & Wallis, J. R. (1997). Chapter 2: L-Moments (pp. 14-43); Chapter 5: Choice Of A Frequency Distribution (pp. 73-86); Appendix: L-Moments For Some Specific Distributions (pp. 191-209). In Regional Frequency Analysis. An Approach Based on L-moments. Cambridge, England: Cambridge University Press.         [ Links ]

IMTA (2002). Banco Nacional de Datos de Aguas Superficiales (BANDAS). 8 CD. Jiutepec, México: Comisión Nacional del Agua, Secretaría de Medio Ambiente y Recursos Naturales, Instituto Mexicano de Tecnología del Agua.         [ Links ]

Karvanen, J. (2006). Estimation of Quantile Mixtures Via L-Moments and Trimmed L-Moments. Computational Statistics & Data Analysis, 51(2), 947-959.         [ Links ]

Kite, G. W. (1977). Chapter 12: Comparison of Frequency Distributions (pp. 156-168). In Frequency and Risk Analyses in Hydrology. Colorado, USA: Water Resources Publications.         [ Links ]

Kottegoda, N. T., & Rosso, R. (2008). Chapter 3: Random Variables and their Properties (pp. 83-164). In Applied Statistics for Civil and Environmental Engineers. Chichester, United Kingdom: Blackwell Publishing.         [ Links ]

Machiwal, D., & Jha, M. K. (2008). Comparative Evaluation of Statistical Tests for Time Series Analysis: Application to Hydrological Time Series. Hydrological Sciences Journal, 53(2), 353-366.         [ Links ]

Machiwal, D., & Jha, M. K. (2012). Chapter 4: Methods for Time Series Analysis (pp. 51-84). In Hydrologic Time Series Analysis: Theory and Practice. Dordrecht, The Netherlands: Springer.         [ Links ]

Mudholkar, G. S., & Hutson, A. D. (1998). LQ-Moments: Analogs of L-Moments. Journal of Statistical Planning and Inference, 71(1-9), 191-208.         [ Links ]

Rao, A. R., & Hamed, K. H. (2000). Chapter 9: The Logistic Distribution (pp. 291-321). In Flood Frequency Analysis. Boca Raton, USA: CRC Press.         [ Links ]

SRH (1975). Boletín Hidrológico núm. 36. Región Hidrológica núm. 10 (Sinaloa). Tomos I y VI. México, DF: Secretaría de Recursos Hidráulicos, Dirección de Hidrología.         [ Links ]

Stedinger, J. R., Vogel, R. M., & Foufoula-Georgiou, E. (1993). Chapter 18: Frequency Analysis of Extreme Events (pp. 18.1-18.66). In D. R. Maidment (Ed.). Handbook of Hydrology. New York: McGraw-Hill.         [ Links ]

Wilks, D. S. (2011). Theme 4.5: Qualitative Assessments of the Goodness Fit (pp. 112-116). In Statistical Methods in the Atmospheric Sciences (3rd edition). San Diego, USA: Academic Press (Elsevier).         [ Links ]

WMO (1971). Annexed III: Standard Tests of Significance to Be Recommended in Routine Analysis of Climatic Fluctuations (pp. 58-71). Technical Note No. 79. In Climatic Change. Geneva: World Meteorological Organization.         [ Links ]