Artículos técnicos

 

Fórmulas para el coeficiente de arrastre y la ecuación Navier-Stokes fraccional

 

Formulas for Drag Coefficient and the Navier-Stokes Fractional Equation

 

José Roberto Mercado*, Pedro Guido, Jorge Sánchez-Sesma, Mauro Íñiguez
Instituto Mexicano de Tecnología del Agua,
*Autor de correspondencia.

 

Dirección institucional de los autores

Dr. José Roberto Mercado
Dr. Pedro Guido
Dr. Jorge Sánchez-Sesma
Dr. Mauro Íñiguez

Instituto Mexicano de Tecnología del Agua (IMTA)
Paseo Cuauhnáhuac 8532, Colonia Progreso
62550 Jiutepec, Morelos, México
Teléfono: +52 (777) 3293 600
rmercado@tlaloc.imta.mx
pedroguido@tlaloc.imta.mx
jsanchez@tlaloc.imta.mx
mic@tlaloc.imta.mx

 

Recibido: 31/05/2012
Aceptado: 03/07/2013

 

Resumen

Se quiere encontrar la relación entre la ecuación de Navier-Stokes fraccional y las fórmulas para el coeficiente de arrastre, como las de Kármán-Schoenherr, Prandtl-Kármán, y Nikuradse. Los cambios de escala producen una renormalización para las ecuaciones de la capa límite, que contiene la hipótesis esencial de la delgadez de dicha capa, y da lugar a una descripción multifractal. Se obtiene una generalización del resultado experimental de Blasius para el factor de fricción. Si se reajustan las relaciones del número de rasgos del multifractal, se infieren las fórmulas, objeto de este estudio, y se las representa como un bi-multifractal, lo que permite un camino analítico para el número de Reynolds crítico y señala a la de Kármán-Schoenherr como la fórmula apropiada para el límite a la derecha de la subcapa viscosa. Los reajustes se traducen en matizar las aproximaciones de la relación entre los números de Euler y Reynolds, o bien en los decaimientos relativos del coeficiente de arrastre. Se aplican los resultados a la descripción de la capa límite turbulenta y a las interacciones entre corrientes y fondos (en ríos, desiertos y huracanes).

Palabras clave: ecuación Navier-Stokes, coeficiente de arrastre, multifractal, capa límite.

 

Abstract

The aim of this paper is to find the relationship between the Navier-Stokes fractional equation and formulas for the drag coefficient, such as the Kármán-Schoenherr, Prandtl-Kármán, and Nikuradse. Scale changes produce a renormalization of boundary layer equations, which contains the key hypothesis about the thinness of this layer and leads to a multifractal description. A generalization is obtained from the Blasius experimental result for friction. By adjusting the relation of the number of features of the multifractal, the formulas that are the objective of this study can be inferred and represented as a bi-multifractal. This allows for an analysis with the critical Reynolds number and indicates that the Kármán-Schoenherr is the most suitable formula for the right boundary of the viscous sublayer. The adjustments resulted in refining the relation between Euler and Reynolds numbers, or obtaining the decays related to the drag coefficient. The results are applied to the description of the turbulent boundary layer and the interactions between flows and bottoms (for rivers, deserts and hurricanes).

Keywords: Navier-Stokes fractional equation, drag coefficient, multifractal, boundary layer.

 

Introducción

El propósito principal del presente artículo es encontrar la relación entre las fórmulas de Kármán-Schoenherr, de Prandlt-Kármán y de Nikuradse para el coeficiente de arrastre o el factor de fricción, y la ecuación Navier-Stokes fraccional.

En las referencias Mercado et al. (2013 y 2012) se presenta la ecuación Navier-Stokes fraccional. El planteamiento esencial se basa en afirmar que los esfuerzos viscosos producen un flujo dispersivo de momentum, que se describe a través de una ley de Darcy fraccional, y que la divergencia del flujo dispersivo coincide con el cambio temporal de momentum de acuerdo con la ley de Newton.

Como en el caso clásico, la simplificación importante de la ecuación Navier-Stokes fraccional, que conduce a las ecuaciones de la capa límite, estriba en su espesor relativamente delgado, lo que a su vez implica que la velocidad principal es en la dirección longitudinal, con un gran gradiente de velocidad vertical, comparado con el longitudinal, mismo que lleva a la velocidad a cumplir la condición de no deslizamiento en el fondo del canal; y por el contrario, con los gradientes de presión leves en la dirección transversal vertical, comparados con los fuertes en la longitudinal (Landau y Lifshitz, 1987).

Los cambios de escala se obtienen a partir de reconocer la longitud y velocidad características horizontales y macroscópicas, y buscar sus complementos verticales, que preserven la forma para la conservación de la masa y el momentum.

Se introduce el potencial de la velocidad, por lo que tanto la componente de la velocidad aguas abajo como también la componente transversal vertical se dan por medio del mismo. Entonces, la ecuación de momentum se expresa en términos del potencial de velocidad aguas abajo.

El esfuerzo friccional se halla calculando la derivada fraccional de la función potencial y se obtiene que el esfuerzo presenta la forma de una potencia del inverso del número de Reynolds indexado, y depende del índice de ocupación espacial; además, decrece con la distancia horizontal a una potencia también dependiente del grado de ocupación espacial. La constante de proporcionalidad contiene una potencia de la viscosidad y del valor de la curvatura de la función subpotencial en el origen. Se observa, además, que cuando el índice de ocupación espacial tiende a la unidad, se recupera la expresión clásica del esfuerzo friccional para la capa límite laminar.

En la aproximación Falkner-Skan se establece el equilibrio por medio de un triángulo dinámico conformado por las fuerzas viscosa, inercial y la del gradiente longitudinal de la presión, a través de la velocidad libre o exterior dependiente de una potencia de la coordenada longitudinal. En contraste, en la aproximación de Blasius, el gradiente de presión está ausente debido a la anulación de la potencia de la velocidad exterior.

Se obtiene la fuerza de fricción en las dos aproximaciones mencionadas, para ello se integra el esfuerzo de fricción; se le expresa en forma adimensional, introduciendo el coeficiente de arrastre o drag. Resulta que este coeficiente también se representa como una potencia del número de Reynolds indexado, potencia determinada en forma acoplada tanto por el índice de ocupación espacial como por la potencia de la velocidad exterior. La potencia está conformada por el producto de dos factores; el primero es una función creciente, de manera que entre mayor sea el índice de ocupación espacial mayor será el exponente del número de Reynolds indexado, lo que se consigue con el movimiento viscoso; por el contrario, entre mayor sea la turbulencia menor será el índice de ocupación espacial y menor será el exponente del número de Reynolds indexado. El segundo factor es creciente para el exponente negativo, lo que trasluce un gradiente longitudinal adverso y es también creciente para el exponente mayor que la unidad que refleja un gradiente de presión favorable.

Además, se observa que la fuerza de fricción puede describirse como una derivada fraccional de un multifractal, donde el orden de la derivada depende del índice de ocupación espacial, en tanto el espectro de dimensiones del multifractal depende, en forma acoplada, tanto de la potencia de la velocidad exterior como del índice de ocupación espacial.

Pueden hallarse también el coeficiente de Chézy como una magnitud alternativa y la velocidad adimensional como razón entre la velocidad media y la velocidad de corte.

La ecuación de Navier-Stokes clásica adolece de un parámetro que refleje el carácter fractal del movimiento del fluido. En tanto, su versión fraccional lo expresa en el orden de la derivada que aporta la fuerza de fricción viscosa. Si se quiere ver a qué corresponde ese orden, se puede estudiar la fuerza de fricción sobre un fondo plano extenso, a través de las ecuaciones de la capa límite. El resultado engloba una expresión experimental de Blasius, que se interpreta como un multifractal. Si se mantiene esa interpretación multifractal para las otras fórmulas, como la de Prandtl-Kármán, se obtiene que las dimensiones fractales no superan el valor 1, y es más pequeño en la medida que el movimiento sea más turbulento.

Por tanto, la afirmación es la siguiente: la ecuación Navier-Stokes fraccional aplicada a la capa límite, con un escalamiento que refleja la delgadez de dicha capa, y que se interpreta como un multifractal, produce las fórmulas de Blasius, Kármán-Schoenherr, Prandtl-Kármán y Nikuradse, como formas que establecen vínculos de dependencia de distintos grados entre el número de Euler y el número de Reynolds. Cada una de ellas puede describirse con una dimensión similar a la de Blasius, dimensión que se hace cada vez más pequeña a medida que sea mayor el número de Reynolds.

En la sección "Ecuación Navier-Stokes fraccional", se describe la ecuación Navier-Stokes fraccional, ya considerada en Mercado et al. (2012). Se toman en cuenta las simplificaciones que introduce la capa límite. Se hallan el esfuerzo, la fuerza de fricción y el coeficiente de arrastre. Se obtiene una generalización del resultado experimental de Blasius. Se analiza su estructura multifractal. Luego se consideran las fórmulas de Kármán-Schoenherr, Prandtl-Kármán y Nikuradse. Se encuentra una expresión para el número de Reynolds crítico. Por último, se aplican a las interacciones entre fluidos y superficie como entre ríos y sus lechos, entre los vientos y la arena, y entre vientos y océano, como en los huracanes.

 

Métodos

Ecuación Navier-Stokes fraccional

El movimiento del fluido se describe desde el punto de vista Euleriano, considerando un volumen de fluido limitado por una superficie de frontera, con su momentum por unidad de volumen dado por ρv. Por su importancia, se considera primero la interacción por fricción interna. El gradiente fraccional se expresa por ∇^β_Mρv, donde ρ es la densidad de masa; v, la velocidad; β, el índice de ocupación espacial, y M es la medida de mezcla de las distintas direcciones espaciales. La difusividad del momentum es la α-viscosidad cinemática v_α, así que el flujo de Darcy del momentum es q_D. La razón de cambio del momentum por unidad de tiempo es la divergencia negativa, o convergencia, del flujo de Darcy; o bien, se escoge M, tal que el flujo sea proporcional al negativo del laplaciano fraccional (Mercado et al., 2013), lo que se muestra en (1), con α = 1 + β:

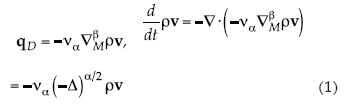
En seguida se toma en consideración la contribución de las variaciones de presión al cambio del momentum del fluido a través de la fuerza que aporta el gradiente de presión, de tal manera que la suma del esfuerzo de fricción viscoso y la presión hidrostática conforma el tensor T = v_α∇^β_Mρv–pI y da lugar a la ley de deformación. A continuación se incorpora una fuerza potencial externa, por unidad de volumen, del tipo –∇ρɸ. Después se introduce la hipótesis de la incompresibilidad del fluido. Se hace explícita la derivada material que componga la variación local con la advectiva. Pero la exigencia de objetividad requiere la invarianza bajo los cambios de coordenadas, por lo que se debe modificar el aporte advectivo y surge el término de la vorticidad. Por último, la contribución a la fuerza inercial de la vorticidad se escribe al lado derecho de la ecuación como v × rotv, y puede imaginarse como originado en una fuerza externa que dinamiza la evolución del campo de velocidades a través de su vorticidad, entrando en contradicción con la fuerza viscosa; en tanto, el otro término se interpreta como una restricción que a lo largo de las líneas de corriente contiene la ecuación de D. Bernoulli. El coeficiente v_α puede compararse con la viscosidad turbulenta de Boussinesq:

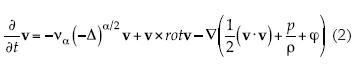
Como ya se comentó, las ecuaciones de la capa límite se obtienen de la ecuación Navier-Stokes fraccional por las simplificaciones que se inducen a partir de la premisa de un espesor relativamente delgado. Ahora la ecuación de la capa límite bidimensional se le considera en su versión estacionaria o permanente, junto con la conservación de la masa en su forma de divergencia nula, tal como se muestra en la ecuación (3):

Donde el gradiente de presión se da por .

A la velocidad principal, aguas abajo, se le da la forma potencial, representándola a través del potencial de la velocidad ψ(u,v) como u = δ_yψ, v = –δ_xψ. En la aproximación Blasius se establece un equilibrio entre dos: entre la fuerza viscosa y la fuerza inercial, al asumir como nulo el aporte del gradiente de presión. En la aproximación Falkner-Skan está presente el gradiente longitudinal de la presión como la tercera contribución al equilibrio, permitiendo que la velocidad libre o exterior dependa de la coordenada longitudinal. Surge entonces la función subpotencial g(ξ) como solución de la ecuación diferencial de la ecuación Blasius fraccional o Falkner-Skan fraccional (Landau y Lifshitz, 1987; White, 2006).

Se calcula el esfuerzo por τ_xy = µ_αδ^β_yδ_yψ(u,v), siendo µ_α = ρv_α. Con el coeficiente de Blasius fraccional 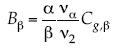, donde 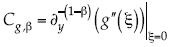, y el número de Reynolds indexado R_lβ = ul^β/v_α, el esfuerzo puede escribirse como en (4):

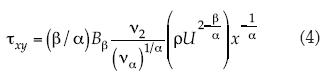
Se calcula la fuerza de fricción por unidad de longitud binormal, o transversal-horizontal, como 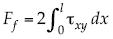, y con el esfuerzo representado como en (4), puede escribirse 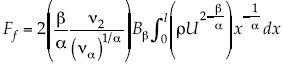(Mercado, 2010). En la aproximación Falkner-Skan se considera U = Kx^m, con m ≠ 0; se denota el coeficiente por 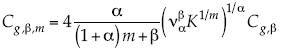; después de integrar se obtiene:

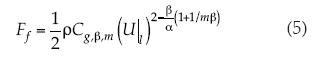
Se adimensionaliza la fuerza de fricción por unidad de área de la superficie tangencial, por lo que surge el coeficiente de arrastre (6):

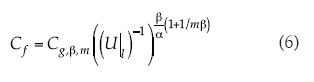
Al exponente del coeficiente de arrastre se le llamará el exponente Blasius (7):

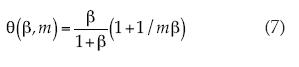
Además, en la aproximación Blasius se considera m = 0; se integra y se obtiene el exponente Blasius:

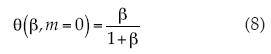
Se pueden reunir las dos en una sola expresión (9):

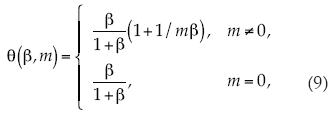
El exponente Blasius, en tanto dimensión, debe ser θ ≥ 0, por lo que se requiere o bien que m > 0, lo que significa un gradiente de presión favorable, o bien m ≤ –1/β, que se traduce en un gradiente de presión adverso.

En particular, el estado dado por β → 0 es equivalente al estado m = –1/β, y podría llamársele turbulento.

Se observa también que es posible la representación θ = β(σ + 1/(1 + β)), porque para σ > 0 existe un m > 0, dado por , que permite tal representación, misma que puede considerarse una generalización del resultado experimental de Blasius. Para m = 0 existe la representación como β/(1 + β), el cual contiene, entre otros, el resultado experimental de Blasius para β = 1/3, y también el resultado para el régimen laminar θ = 1/2, para β = 1 (Mercado et al., 2013). Se aprecia que el valor de σ > 0 puede llegar a ser bastante grande, a condición de tomar a m > 0 suficientemente cercano a cero.

En la aproximación Falkner-Skan, para poder definir la variable de similaridad, se presenta la disyuntiva: o m = 1, o β = 1, porque son las dos opciones bajo las cuales los coeficientes de la ecuación, para la función subpotencial, se hacen independientes de x.

En la primera opción, m = 1, se tiene θ(β,1) = 1, por lo que resulta que la variación de la presión con la velocidad es lineal como en el modelo de Hagen-Poiseuille para flujo laminar.

Para la segunda opción, el exponente de Blasius es , y el valor m es arbitrario, aunque, por supuesto, está excluido el valor m = 0; y además se requiere m > 0 o bien m ≤ –1/β, que en este caso se reduciría a m ≤ –1. La primera forma parte de los flujos inviscosos contra una elevación o cuña de ángulo 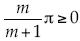; la segunda, de los flujos inviscosos, a través de una depresión de ángulo 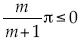, en sentido horario (White, 2006). Además, se destaca que este exponente contiene el resultado experimental de Blasius con m = –2. Ahora la ley de variación de la presión con la velocidad es turbulenta, cercana a la fórmula de Chézy, la que se asume exactamente cuando se toma el valor m = –1.

Es posible representar el factor de fricción por la relación que se muestra en (10) y describirlo como una transformación, por medio de derivadas fraccionales de orden γ = β²/(1 + β) de un multifractal de dimensiones en otro análogo de dimensiones θ:

 

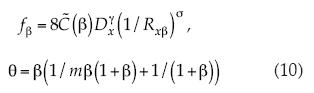
Blasius y un multifractal

El término multifractal se usaba en general antes de 1980 y fue acuñado en turbulencia por Frisch (1995). Las propiedades multifractales son destacables cuando una distribución se muestra en conjuntos que exhiben la característica de ser irregulares y esparcidos. Se trata de una medida que da la probabilidad de que un punto caiga en un conjunto determinado, pero con una distribución singular, de tal manera que no existe una densidad para describirla, y es entonces cuando el formalismo multifractal toma relevancia. Las propiedades multifractales constituyen el contexto apropiado para describir las cualidades de una ley de escalamiento determinada.

Se conforma una malla como una colección de cubos (C_k)_k de lado 1/R_e, con 0 < 1/R_e < 1, denominando a 1/R_e como la resolución. En el nivel microscópico, se considera una medida m, con la capacidad de estimar la probabilidad de que un punto determinado caiga en el cubo C_k por µ(C_k) ≈ (1/R_e)^β bajo la condición natural de que la malla de cubos intersecte el soporte de la medida. Ahora se consideran todos los cubos en donde la medida sea del orden β, así que (1/R_e)^β+ε ≤ µ(C_k) < (1/R_e)^β, siendo 1/R_e, pequeño, y ε arbitrario, positivo y pequeño. Se le llaman rasgos al número de cubos en donde la medida es del orden de β (Falconer, 1990; Riedi y Scheuring, 1997; Meneveau y Sreenivasan, 1991):

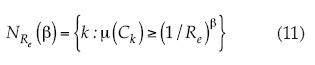
La ley de escalamiento queda definida por la particularidad de que los rasgos son del orden de θ(β) y, por tanto, obedecen a una ley de potencia, cuando la resolución se acerca a cero:

Afirmación 1. El exponente de Blasius presenta una estructura multifractal.

Las propiedades de un multifractal se pueden analizar en el estimado que surge de la aproximación de Blasisus 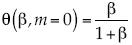. Se debe recordar que el orden de la singularidad o dimensión local es β, que representa el índice de ocupación espacial o razón de la dimensión fractal a la dimensión topológica y el espectro multifractal de singularidades, como θ(β). La medida micro se escala como µ ≈ R_e^(–β), siendo la resolución 1/R_e y R_e el número de Reynolds, y los rasgos como . Se comprueba que θ(β) goza de la propiedad de la concavidad respecto de β, lo que debido a su diferenciabilidad se puede inspeccionar a través de la segunda derivada, porque 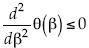. La función de estructura es la transformada de Legendre del espectro que cambia por optimización la variable de la dimensión local β a la del orden de reiteración s u orden del momento. Siempre se tiene que τ(s) es la transformada de Legendre del espectro aquí denotado por θ(β) o sea 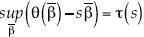. En tanto que cuando el espectro es diferenciable y se alcanza el supremo, la condición de optimalidad produce . 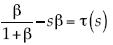Se escribe θ(β)– sβ = τ(s) o , y la condición de optimalidad arroja 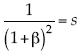, así que invirtiendo se tiene 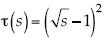; y entonces la condición de optimalidad pasa a ser 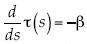, que tiene la propiedad de la convexidad 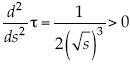con la condición de normalización τ(1) = 0.

¿Qué magnitud física representa la función de partición? , , 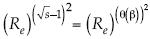luego 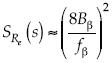. Por tanto, la función de partición representa al cuadrado del inverso del factor de fricción.

Así que tomando como guía los fractales, se representa al factor de fricción por o bien , donde se ve a 1/R_e como la resolución, bajo la condición 0 < 1/R_e < 1, y a la cantidad 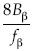como al número de rasgos, por lo que se obtiene un multifractal de dimensión θ, que varía con β. Análogamente, el coeficiente de arrastre corresponde al número de rasgos de un multifractal de dimensión θ(β). También el coeficiente de Chézy satisface , donde corresponde al número de rasgos de un multifractal de dimensión θ/2, y con resolución 1/R_e:

 

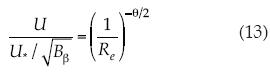
Kármán-Schoenherr

Los resultados experimentales del coeficiente de arrastre sobre una superficie plana presentan una primera fase con exponente 1/2, para bajos números de Reynolds, resolución gruesa o alta; luego una región de transición con crecimiento ligero del coeficiente de arrastre, una meseta; luego un descenso que se aproxima por un exponente tipo 1/5, para resolución media, y después la representación de Kármán-Schoenherr (Rouse, 1946).

La ley de Blasius se generaliza e interpreta como un multifractal, tomando al inverso del número de Reynolds como la resolución, y al espectro de singularidades por el exponente de Blasius. Esta ley puede explicar las fases de exponentes 1/2 y 1/5, descritas en el párrafo anterior, e incluso la meseta en el límite cuando el exponente tiende a cero θ → 0, lo que puede interpretarse como turbulencia totalmente desarrollada, en donde se elimina la participación de la viscosidad a través de anular el exponente.

Se puede reconstruir el resultado de Kármán-Schoenherr por medio de debilitar los rasgos desde B/C_f hasta con dos constantes A y K. En congruencia con el método para el resultado de Blasius, se considera ahora la dimensión 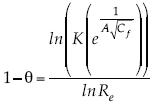, siendo ; si además es A = 4.13loge y KB = 1, se reconstruye la fórmula Kármán-Schoenherr o KS en (14):

Por tanto, la fórmula KS corresponde también a una aproximación que establece una dependencia débil entre el número de Euler y el de Reynolds, dado por 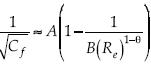, con la particularidad de que entre más intensa sea la turbulencia mayor será el valor del exponente en el número de Reynolds 1 – θ. Este exponente depende tanto de β como de m, con la restricción m ≥ 1 requerida para que θ ≤ 1.

Se inspecciona ahora su decaimiento y se le compara con la misma para la ley de Blasius. Se aprecia que al disminuir la dimensión θ, el decaimiento de C_f, relativo a sí mismo, es cada vez menor, porque si θ₂ ≤ θ₁, entonces 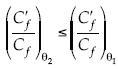; por tanto, si se disminuye la dimensión θ, disminuye también la velocidad de decaimiento. Por otra parte, en el caso de Kármán-Schoenherr, se encuentra que 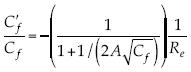; así se está cambiando la dimensión 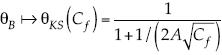, la cual quedaría definida de manera implícita. Se observa que como 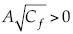, se tiene que θ_KS < 1, y que es cada vez más pequeño entre menor sea C_f, lo que se presenta cuando el número de Reynolds es suficientemente alto, y por tanto se obtiene una menor inclinación o pendiente. Se podría introducir un entero n_KS como el mayor entero mayor o igual a 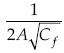, lo que da 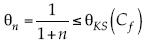. Así, eventualmente, con el crecimiento del número de Reynolds se produce una caída más leve con Kármán-Schoenherr que con la ley de Blasius. Por ejemplo, en un intervalo de cambio del coeficiente de arrastre disminuyendo de 0.010 a 0.001, el número n_KS cambia de 3 a 9, y θ_KS disminuye también de 1/4 a 1/10.

 

Fórmula Prandtl-Kármán

Por otra parte, y en congruencia con el desarrollo anterior, para la fórmula Prandtl-Kármán o PK se asume un multifractal con resolución 1/R_e, con rasgos proporcionales a 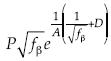y de dimensión 1 – θ. Entonces, con A = 2 loge, D = 0.8 y PB = 1, se recupera la fórmula Prandtl-Kármán:

En el caso de Prandtl-Kármán, se encuentra el decaimiento relativo del coeficiente de arrastre 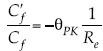, siendo la dimensión 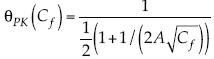. También se observa que como 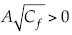, se tiene que θ_PK < 1, siempre que 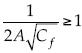. Así, θ_PK se hace cada vez más pequeño entre menor sea C_f, lo que se presenta cuando el número de Reynolds es suficientemente alto; por tanto, también se obtiene una menor inclinación o pendiente. Se introduce un entero n_PK como el mayor entero mayor o igual a 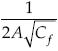, lo que da 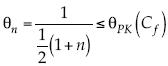. Por tanto, eventualmente, con el crecimiento del número de Reynolds, se produce una caída más leve con Prandtl-Kármán que con la ley de Blasius. Por ejemplo, en un intervalo de cambio del coeficiente de arrastre, disminuyendo de 0.010 a 0.001 el número n_PK, cambia de 6 a 8, y θ_PK disminuye también de 2/7 a 1/10.

 

Fórmula de Nikuradse

Ahora, en vez de los rasgos de la ley de Blasius B/C_f, se les debilita por 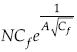; la idea es que si C_f disminuye, con el incremento del número de Reynolds la cantidad NC_f baja, pero lo hace con mayor intensidad la cantidad 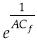; así, 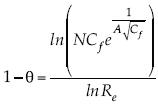y nuevamente bajo la hipótesis y NB = 1, se obtiene:

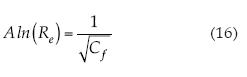
Su decaimiento relativo se da por 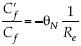con 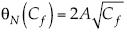; en este caso, se aprecia que θ_N puede ser mayor que la unidad cuando 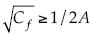; sin embargo, en caso contrario también será menor que la unidad como en las tres fórmulas anteriores, pero permanece la propiedad de decaimiento de θ_N con el crecimiento del número de Reynolds. Por ejemplo, en el rango para el coeficiente de arrastre entre 0.01 y 0.001, θ_N cambia, disminuyendo desde 0.358 hasta 0.113.

Por tanto, las distintas fórmulas pueden verse como consecuencias de la ecuación Navier-Stokes fraccional, su reducción a la capa límite, su interpretación multifractal, y el reajuste de sus rasgos o de sus decaimientos relativos, lo que permite disminuir sus dimensiones con el crecimiento del número de Reynolds. Se puede entonces destacar al menos un bimultifractal tal, que para relativamente altos números de Reynolds los rasgos son proporcionales a 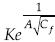, la resolución 1/R_e y las dimensiones 1 – θ; en tanto que para bajos números de Reynolds, los rasgos son inversamente proporcionales al factor de fricción: , la resolución también 1/R_e y las dimensiones θ:

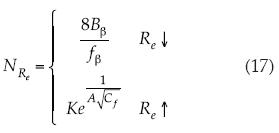
En especial, el cambio en la representación permite obtener un camino analítico para encontrar un número de Reynolds crítico que señale el cambio de régimen de laminar a turbulento, o más específicamente, de la subcapa viscosa a la subcapa de mezcla o transición.

Si el cambio de régimen se define a su vez por el cambio en la ley de la variación de la presión con la velocidad, se traduce en el cambio de la dimensión desde θ = 1 a un valor inferior θ < 1 (Sommerfeld, 1950). Así, para números de Reynolds considerados relativamente bajos se tiene el comportamiento dado por la ley de Blasius, en tanto que para relativamente altos podría tomarse la fórmula de Kármán-Schoenherr, y el número de Reynolds que realiza la transición puede ser considerado como el Reynolds crítico. Así, en la fórmula KS se toma θ = 1, se infiere que 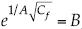; y con f = 4C_f se obtiene f = 4/(A ln B)²; en tanto de la fórmula de Blasius f = 4/(B/R_e), con θ = 1, por lo que el número de Reynolds crítico que señale la transición se puede estimar por R_ec = B(A ln B)², o bien puede expresarse el coeficiente B en términos de A y R_e, haciendo uso de la función de Lambert W y se obtiene 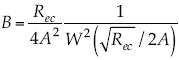. En particular, para B = 64 y A = 4.13 loge = 4.13/ln 10, se obtiene R_ec = 3 561.1, que se valora del mismo orden de magnitud que el valor experimental estimado en 2000, y se recuerda que tanto el valor de B como el de A se determinan de modo experimental (Rouse, 1946).

Por otra parte, en el caso de la fórmula de Nikuradse se combina 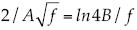con f = 4B/R_e, y se obtiene 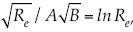, que se traduce en 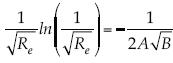, cuya solución se expresa por la función de Lambert W, como 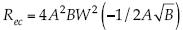; su evaluación numérica con B = 64 y A = 4.13/ln10 produce R_ec = 1.0749, el cual está en otro orden de magnitud, comparado con el valor 2000. Análogamente, para la fórmula KP se obtiene, también a través de la función de Lambert, una estimación que produce 0.86709. En conclusión, se señala a la fórmula KS como la apropiada para el límite inferior de la subcapa de mezcla o transición.

 

Resultados y discusión

Se consideran tres aplicaciones. En la primera se quiere aportar en la descripción de la estructura de la capa límite turbulenta. En la segunda se estudia la interacción entre la rugosidad de la arena y la velocidad del viento. En la tercera se trata de ver la interacción entre velocidad del viento y rugosidad oceánica.

Capa turbulenta

Dentro de las aplicaciones se quiere aportar en la descripción de la estructura de la capa límite turbulenta. Se conocen cuatro zonas de la capa límite: una, la zona de pared, compuesta por dos subcapas: la viscosa y la de transición o mezcla. Luego la capa inercial con la turbulencia totalmente desarrollada y la estela.

Para superficies lisas o regulares, la subcapa viscosa puede extenderse hasta unas cinco unidades de pared o cinco longitudes características. La segunda, la de mezcla, hasta unas 30 longitudes características. La tercera, desde unos 30 hasta 400 unidades de pared. El resto corresponde a la estela. En tanto, para superficies rugosas, la longitud característica decrece, porque debe haber un desplazamiento hacia abajo debido a que la rugosidad incrementa las pérdidas de momentum (Clifford et al., 1993; Landau y Lifshitz, 1987; Levi, 1989).

El multifractal para números de Reynolds relativamente bajos o intermedios se describe por y además la velocidad adimensional es 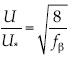, por lo que se propone para la velocidad adimensional la representación 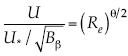. Ahora, la altura y se adimensionaliza con la longitud característica o intrínseca 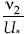, y se obtiene como el número de Reynolds asociado con la velocidad de corte, que se toma para la resolución del multifractal de dimensión β/2; entonces, 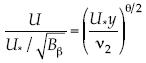, que podría escribirse U₊ = (y₊)^θ/2. Se observa que si θ → 2, se recupera la aproximación de la ley de pared U₊ = y₊. La pendiente es , luego es creciente porque θ ≥ 0. Para la curvatura 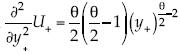, entonces muestra una primera subfase convexa si θ ≥ 2; e incluso para θ = 4 se tiene el comportamiento parabólico.

Una segunda subfase cóncava para θ ≤ 2 puede ser representada como una ley tipo Blasius U = y^1/7, la cual es cóncava. Así que es posible describir la capa de mezcla desde el punto de inflexión hasta la capa totalmente turbulenta, y después también la estela o subcapa intermitente (Barenblatt et al., 1997):

Para la parte totalmente turbulenta se toma la fórmula de Nikuradse, con lo que se tiene 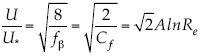; así 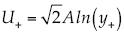, la cual es lineal con el logaritmo, 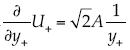creciente y cóncava.

Para superficie rugosa, se toman la rugosidad y la velocidad de corte como magnitudes para adimensionalizar la pendiente hidráulica J, y se garantiza la invarianza de forma de la pendiente citada si se toma 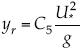, donde U_* es la velocidad de corte y g es la gravedad, que coincide en forma con la rugosidad de Charnock (1955) para la superficie oceánica (Mercado et al., 2012).

Arena y viento

En el transporte de arena por el viento fluctuante, la rugosidad también se describe por 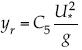con U_*, la velocidad de corte; g la gravedad; y los valores del parámetro C₅, se encuentran en el intervalo [0.02, 0.05] para flujo de arenas en túneles de viento y hasta 0.18 para experimentos de campo (Clifford et al., 1993). Aunque la fórmula es la misma, el parámetro C₅ tiene un rango de distintos valores que en la rugosidad de Charnock.

Los huracanes

Nuevamente 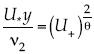, esta rugosidad controla la variación vertical de la velocidad del viento (Powell et al., 2003), que lo equipara con el factor de fricción descrito por Nikuradse, suficientemente justificado para el régimen completamente rugoso, de tal manera que el rizado de la superficie marina producida por el viento clasifica a la superficie marina en el estado rugoso y permite aproximar el factor de fricción por la fórmula de Nikuradse.

En el modelo de Barenblatt et al. (2005) se explica el fenómeno por la disminución de la energía turbulenta en la capa límite del fluido aire sobre la rugosidad oceánica, la cual se basa en la presencia de gotas de agua relativamente grandes o pesadas, lo que se traduce en la disminución del coeficiente de arrastre.

Ríos y lecho

La interacción entre el flujo y el lecho del río da lugar a estructuras coherentes en el lecho mismo, que presentan como una de sus características cuantitativas la altura de la rugosidad, lo que permite tomarla como frontera 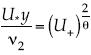, o bien si β → 1 tiene .

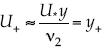El valor de la altura de la rugosidad puede hacerse corresponder con la condición de frontera para el perfil logarítmico de la capa inercial. De acuerdo con los resultados de Nikuradse, para superficie regular o lisa, el espesor de la subcapa viscosa es del orden de 100 veces esa condición de frontera; en tanto, para superficie rugosa, el espesor de la subcapa es algo mayor (Rouse, 1946; Landau y Lifshitz, 1987). Otra vez se adimensionaliza la altura y_r, de la rugosidad con la longitud intrínseca 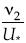, y se obtiene otra vez como número de Reynolds asociado con la velocidad de corte; pero debido a que la velocidad de corte para superficie rugosa es algo mayor que para la lisa, este número de Reynolds se incrementa. La longitud característica es , su valor numérico con los datos citados en Clifford et al. (1993), A. Kirkbride, cap. 7., es 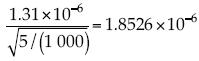. La longitud de la rugosidad de Charnock (1955) es 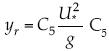∈ [0.015, 0.035]; pero ahora con valores de la constante en el intervalo [0.02, 0.05], e incluso con el valor 0.18. Sus valores se ubican en 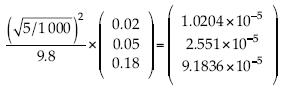. El espesor de la capa viscosa será del orden de .

El valor reportado del espesor de la subcapa viscosa es de 2.1 × 10^-7 m. Sin embargo, el límite inferior conocido para grava es de 2.0 × 10^-3 m. Valor comparable con el segundo de los citados, que señala el coeficiente en C₅ = 0.05. La comparación entre la altura de la rugosidad y el espesor de la capa viscosa 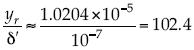está dentro del orden esperado. Sin embargo, para 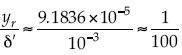, la subcapa viscosa no puede desarrollarse debido a que la longitud de la rugosidad excede, y con mucho, al espesor de esta subcapa.

 

Conclusiones

• Al estudiar la interacción de un fluido con una superficie plana, a través de su capa límite, es posible establecer que la fuerza de fricción y, por tanto, el coeficiente de arrastre, se caracteriza por una potencia del inverso del número de Reynolds indexado, potencia que se ha denominado el exponente de Blasius, el cual presenta la dependencia de dos parámetros en forma de variables acopladas: uno manifiesta la viscosidad y el otro el gradiente de presión.

• De este exponente es posible establecer un estimado que responde a una estructura multifractal, que se reduce al suficientemente conocido para la subcapa viscosa (1/2), cuando el índice de ocupación espacial se acerca a la unidad.

• Se incrementan los rasgos y se mantiene la estructura multifractal, con lo que es posible obtener las fórmulas de Kármán-Schoenherr, Prandtl-Kármán y Nikuradse para el factor de fricción para superficies planas y para tubos tanto lisos como rugosos.

• Combinando la expresión multifractal con la velocidad adimensional, e introduciendo la altura de la rugosidad adimensional pueden describirse las cuatro subcapas de la capa límite turbulenta.

• La descripción bi-multifractal aporta un camino analítico para encontrar el número de Reynolds crítico, y solamente la fórmula de Kármán-Schoenherr produce un estimado acorde con el orden de magnitud de resultados conocidos experimentalmente.

 

Referencias

BARENBLATT, G., CHORIN, A., and PROSTOKISHIN, V. A Note Concerning the Lighthill "Sandwich Model" of Tropical Cyclones. PNAS, 2005, 102 pp.         [ Links ]

BARENBLATT, G.I., CHORIN, A.J., and PROSTOKISHIN, V.M. Scaling Laws for Fully Developed Turbulent Flow in Pipes: Discussion of Experimental Data. Proc. Natl. Acad. Sci. USA. Applied Mathematics. Vol. 94, 1997, pp. 773-776.         [ Links ]

CHARNOCK, H. Wind Stress on a Water Surface. Q.J.R. Meteorol. Soc. Vol. 81, 1955, pp 639-640.         [ Links ]

CLIFFORD, N.J., FRENCH, J.R., and HARDISTY, J. Turbulence, Perspectives on Flow and Sediment Transport. Chichester: Sand Transport Response to Fluctuating Wind Velocity, 1993, pp. 304-334.         [ Links ]

FALCONER, K. Fractal Geometry. Chichester: John Wiley, 1990, 288 pp.         [ Links ]

FRISCH, U. Turbulence. The Legacy of A.N. Kolmogorov. Cambridge: Cambridge University Press. ISBN 0-521-45103-5. MR 1428905, 1995, pp. 294.         [ Links ]

LANDAU, L.D. and LIFSHITZ, E.M. Fluid Mechanics. Oxford: Pergamon Press, 1987, 539 pp.         [ Links ]

LEVI, E. El agua según la ciencia. México, D.F.: Conacyt, Ed. Castell Mexicana, 1989, pp. XXX.         [ Links ]

MENEVEAU, C. and SREENIVASAN, K.R. The Multifractal Nature of Turbulent Energy Dissipation. J. Fluid Mech. Vol. 224, 1991, pp. 429-484.         [ Links ]

MERCADO, J.R., GUIDO P., SÁNCHEZ-SESMA, J., ÍÑIGUEZ, M., and GONZÁLEZ, A. Analysis of the Blasius' Formula and the Navier-Stokes Fractional Equation. In: Klapp, J., Medina, A., Cros, A., and Vargas, C.A. (editors). Fluid Dynamics in Physics, Engineering, and Environmental Applications, Environmental Science and Engineering. Berlin: Springer-Verlag, 2013, pp. 475-480.         [ Links ]

MERCADO, J.R. Ecuación Blasius fraccional. Artículo publicado en las Memorias bajo la referencia 237. Congreso Latinoamericano de Hidráulica, Punta del Este, Uruguay, 2010.         [ Links ]

MERCADO, J.R., GUIDO, P., OJEDA, W., SÁNCHEZ-SESMA, J., and OLVERA, E. Saint-Venant Fractional Equation and Hydraulic Gradient. Journal of Math., and System Science. Vol. 2, No. 8, 2012, pp. 494-503.         [ Links ]

POWELL, M.D., VICKERY, P.J., and REINHOLD, T.A. Reduced Drag Coefficient for High Wind Speeds in Tropical Cyclones. Nature. Vol. 422, No. 20, March, 2003, pp. 279-280.         [ Links ]

RIEDI, R.H. and SCHEURING, I. Conditional and Relative Multifractal Spectra. Fractals. Vol. 5, No. 1, 1997, pp. 153-168.         [ Links ]

ROUSE, H. Elementary Mechanics of Fluids. New York: Dover, Publ., 1946, pp. 376.         [ Links ]

SOMMERFELD, A. Mechanics of Deformable Bodies. New York: Academic Press, 1950, pp. 396.         [ Links ]

WHITE, F.M. Viscous Fluid Flow. New York: McGraw-Hill, 2006, pp. 629.         [ Links ]