Artículos técnicos

 

Generación de mallas curvilíneas compuestas para el cálculo de flujos bidimensionales

 

Generation of Curvilinear Composite Grids for Computing Two-dimensional Flows

 

Alejandro Mendoza-Reséndiz*, Moisés Berezowsky-Verduzco
Universidad Nacional Autónoma de México,
*Autor de correspondencia.

 

Dirección institucional de los autores

M.I. Alejandro Mendoza–Reséndiz
Dr. Moisés Berezowsky–Verduzco

Instituto de Ingeniería
Coordinación de Hidráulica, edificio 5
Universidad Nacional Autónoma de México
Ciudad Universitaria
Delegación Coyoacán
04510 México, D.F., México
Teléfono: +52 (55) 5623 3600, extensiones 8644 y 8629
Fax: +52 (55) 5665 1344
amendozar@iingen.unam.mx
mbv@pumas.iingen.unam.mx

 

Recibido: 12/04/2011
Aceptado: 03/07/2013

 

Resumen

Se presenta un método para generar mallas compuestas con base en sistemas coordenados curvilíneos ajustados a las fronteras. Las mallas curvilíneas tienen la ventaja de describir con exactitud la forma de las orillas del dominio. La idea principal consiste en la transformación de una geometría dada en el espacio cartesiano hacia un sistema coordenado curvilíneo en el que la malla es rectangular. En su forma tradicional, una malla curvilínea requiere la definición de cuatro ejes que delimiten el dominio, lo cual restringe su uso para geometrías con formas que no pueden ser delimitadas por cuatro ejes. Con las mallas compuestas, que son conformadas por múltiples bloques en sistemas curvilíneos, conectados entre ellos, se supera dicha limitación. En la literatura se encuentra que este tipo de mallas es utilizado por algunos autores para la modelación de flujos, sin embargo, no se proporcionan detalles prácticos para su generación. En este trabajo se plantea un método para generar este tipo de mallas. Se discuten también brevemente las implicaciones de su uso en la solución de flujos bidimensionales.

Palabras clave: generación de mallas, coordenadas curvilíneas, mallas compuestas, flujos bidimensionales.

 

Abstract

A method to generate composite grids based on boundary-fitted curvilinear coordinate systems is presented. Curvilinear grids have the advantage of accurately describing the shape of the edge of the domain. The main idea is to transform a geometry given in the Cartesian space into a curvilinear coordinate system in which the grid is rectangular. In its traditional form, curvilinear grids require the definition of four axes that delimit the domain, which restricts its use for geometries that cannot be bounded by four edges. The composite grids that are formed by multiple-connected blocks of curvilinear meshes solves this limitation. While the literature shows that some authors use this type of grid for flow modeling, no practical details are provided about the generation of the mesh. This paper outlines a method to generate this kind of grid. The implications for its use in solving two-dimensional flows are also discussed.

Keywords: grid generation, curvilinear coordinates, composite grids, two-dimensional flow.

 

Introducción

La solución de las ecuaciones de fluidos se ha realizado por tres metodologías: con diferencias finitas, volumen finito o elemento finito (Thompson et al., 1998). Las primeras han estado tradicionalmente ligadas con mallas rectangulares, aunque se tienen también desarrollos basados en mallas curvilíneas ajustadas a las fronteras; ejemplo de esto son los trabajos de Hauser et al. (1986), y Mejía y Berezowsky (1996), que plantean la solución de las ecuaciones de aguas someras, o Shi et al. (2001), que resuelven las ecuaciones de Boussinesq.

Cuando la geometría del dominio tiene formas complicadas, y se busca que la malla haga una representación adecuada de las fronteras, en general se tienen dos opciones: emplear mallas no estructuradas, asociadas principalmente con esquemas de elemento finito, o utilizar sistemas curvilíneos ajustados a las fronteras. La ventaja de las mallas no estructuradas es que pueden adaptarse a cualquier geometría, por compleja que sea. Su desventaja es que los esquemas numéricos son más complicados, y esto se ve reflejado en el tiempo de solución del problema (Mejía y Berezowsky, 1996); además, se requiere mayor información para describir la malla, como una lista de las conexiones de todos sus componentes; esto incrementa la dificultad de programar los esquemas numéricos de solución.

Por otra parte, las mallas curvilíneas tienen la ventaja respecto a las mallas rectangulares de adaptarse a la forma que tengan las orillas; por ello pueden emplearse en geometrías con fronteras que tienen una forma irregular y hacen una representación adecuada de las mismas. Además, conservan la ventaja de tratarse de mallas estructuradas, por tanto pueden utilizarse los esquemas numéricos desarrollados para este tipo de mallas, que son más eficientes que los desarrollados para las no estructuradas (Ahusborde y Glockner, 2011).

En las siguientes secciones se describen las mallas curvilíneas tradicionales, sus limitaciones y cómo las mallas compuestas superan dichas limitaciones, además del procedimiento propuesto para generar este tipo de mallas y de las consideraciones para su uso.

 

Sistemas coordenados curvilíneos

Los sistemas coordenados curvilíneos generales tienen sus ejes coordenados adaptados a una geometría dada; se denominan generales porque los ejes coordenados no son necesariamente perpendiculares entre ellos (Warsi, 1998). El sistema coordenado curvilíneo se adapta de tal forma que los ejes sean coincidentes con las fronteras o contornos de dominio donde se pretenden resolver las ecuaciones del flujo en estudio.

En la figura 1 se ejemplifica una región representada en el plano cartesiano y curvilíneo; es delimitada por cuatro ejes con formas irregulares, con los que se hacen coincidir los ejes coordenados. Cualquier punto 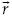en el plano cartesiano tiene una representación en el denominado espacio computacional, donde los ejes curvilíneos ξ, η son líneas rectas, tal como se indica en la figura 1b. Sin perder generalidad, es común aceptar que el espaciamiento de la malla computacional sea unitario, lo cual simplifica los planteamientos de solución.

Las ecuaciones de gobierno se resuelven en el espacio computacional (figura 1b), donde, por tratarse de una malla rectangular uniforme, se obtienen las ventajas asociadas con este tipo de mallas. Ello implica que las ecuaciones de gobierno deben transformarse del sistema coordenado cartesiano, con ejes x, y, al sistema curvilíneo, con ejes ξ, η.

Como puede observarse en la figura 1b, la malla en el espacio computacional es un rectángulo delimitado por cuatro ejes, y dado que cualquier punto 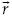tiene una representación única al pasar del plano cartesiano al computacional, los cuatro ejes E's, E'w, E'n y E'e deben estar definidos en el plano cartesiano, es decir, existe un mapeo entre los ejes E's y Es (y lo mismo para los otros tres ejes). Lo anterior marca una limitante para el uso de los sistemas coordenados curvilíneos cuando están conformados por un único bloque, dado que no en todas las geometrías pueden definirse cuatro ejes que delimiten al espacio físico donde se pretende resolver el flujo. Un ejemplo de esto es cuando hay obstáculos interiores, como islas, y consecuentemente se tienen fronteras interiores; en estas condiciones es complicado utilizar cuatro ejes para definir las fronteras interiores y las exteriores. Otro caso ocurre en regiones en las que pueden definirse cuatro ejes que delimiten el área, pero que por su forma producen una malla muy deformada; un ejemplo se indica en la figura 2a. Se ha demostrado (Sankaranarayanan y Spaulding, 2003), que el error de truncamiento en los esquemas de diferencias finitas se incrementa cuando el ángulo entre los ejes coordenados curvilíneos se aleja de los 90° (mallas ortogonales); también influye en dicho error la relación de aspecto de los elementos de la malla; las celdas alargadas, en conjunto con ángulos no ortogonales, contribuyen a amplificar el error de truncamiento.

Para este mismo ejemplo (figura 2a), si de alguna forma se puede ampliar el número de fronteras a más de cuatro, se obtiene una malla con una mejor distribución; tal es el caso de la malla mostrada en la figura 2b, donde los ángulos son próximos a 90° y la relación de aspecto de las celdas es cercana a la unidad.

En la literatura se han propuesto metodologías para resolver la limitante de las mallas curvilíneas conformadas por un único bloque delimitado por cuatro ejes. Una consiste en tomar el bloque y hacerle cortes para ramificarlo (Thompson et al., 1985), un ejemplo de esto es la malla mostrada en la figura 2b, donde se realiza un corte en la parte inferior del bloque y se divide en dos ramas, lo que da origen a una malla menos deformada. Otra técnica es dividir la región donde se va a generar la malla con varios bloques, este último método es el que sigue este trabajo y se detalla más adelante. Antes se describen brevemente los conceptos de los sistemas coordenados curvilíneos generales, dado que algunos elementos se utilizan en las ecuaciones de generación de la malla; además se requieren en el proceso de transformación del sistema coordenado cartesiano al curvilíneo.

 

Elementos del sistema curvilíneo

Existe un conjunto de elementos métricos que se emplean en el sistema coordenado curvilíneo y la transformación de las ecuaciones. Como se indicó antes, un punto 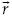tiene representación única entre el sistema coordenado curvilíneo y el cartesiano, ello permite definir la relación siguiente:

Mientras que en el plano curvilíneo los ejes ξ, η se representan como líneas rectas, perpendiculares entre sí, en el plano cartesiano estos mismos ejes son representados como curvas. Esto puede verse en la figura 1b, donde en el plano curvilíneo, el eje E's es una recta con ξ = cte, mientras que su representación en el plano cartesiano, mostrado en la figura 1a, es la curva definida por el eje E's.

Los vectores tangenciales a los ejes coordenados curvilíneos definen la base covariante, cuya representación en el plano cartesiano es:

Los subíndices ()_ξ,η definen la derivación respecto a los ejes curvilíneos. De igual manera, los vectores normales a los ejes curvilíneos definen la base contravariante; su representación en el plano cartesiano es:

Además de las implicaciones de su definición, las bases definidas por las ecuaciones (2) y (3) son importantes, porque se utilizan en los procesos de transformación de las ecuaciones de flujo para ser resueltas en el sistema curvilíneo. Los elementos métricos se definen a través del producto escalar de los vectores de las bases, y el Jacobiano de la transformación se define con el módulo del producto vectorial de la base covariante:

La interpretación física de a₁₁ se obtiene al considerar que es igual al módulo al cuadrado de . Esto quiere decir que un incremento diferencial de 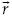en el espacio físico a partir de un incremento diferencial de ξ en el plano curvilíneo está dado por . El tratamiento con a₂₂ y el eje coordenado η es análogo. Los elementos a₁₂ y a₂₁ son idénticos por las propiedades del producto escalar, y como puede observarse fácilmente, son nulos cuando los ejes ξ y η son ortogonales entre ellos. Se observa que el Jacobiano de la transformación dado por la ecuación (6) se define a través del producto vectorial y esto representa el área definida por el paralelogramo que forma los vectores de la base covariante.

 

Transformación de las ecuaciones de gobierno

Como se comentó, cuando se trabaja con las ecuaciones en el plano computacional, se obtienen las ventajas que proporcionan las mallas rectangulares. La transformación de las ecuaciones se realiza en las variables independientes, es decir, los ejes coordenados x y y; de forma alternativa, también pueden transformarse algunas de las variables dependientes. Este proceso de transformación de las ecuaciones produce un mayor número de términos en las mismas (Baghlani et al., 2008).

Para las ecuaciones de flujo que son de naturaleza hiperbólica se tienen tres formas de transformación (Shi et al., 2001). La primera consiste en transformar sólo los ejes coordenados y se dejan sin transformar los componentes de velocidad. Otros tipos de transformación involucran utilizar los componentes covariantes o contravariantes de velocidad, que son, de manera respectiva, tangenciales y normales a los ejes coordenados curvilíneos, y resolver con estas variables transformadas las ecuaciones del flujo.

El enfoque donde sólo se realiza la transformación de los ejes coordenados y emplea los componentes físicos de velocidad ha sido utilizado, por ejemplo, en los trabajos de Hauser et al. (1986), y Soto y Berezowsky (2003). El enfoque donde se utilizan los componentes contravariantes de velocidad es empleado, por ejemplo, por Baghlani et al. (2008) y Shi et al. (2001). El uso de los componentes covariantes se reporta en Ferziger y Peric (2002), y Romanenkov et al. (2001).

Respecto al criterio de cuál de los tres conjuntos de componentes es más adecuado utilizar, en el trabajo de Romanenkov et al. (2001) se hace un análisis de las ventajas y desventajas de cada tipo de transformación; estos autores realizan pruebas numéricas y concluyen que la transformación con componentes contravariantes tiene la ventaja de tener una representación más simple de la ecuación de continuidad y de facilitar la formulación de las condiciones de borde en fronteras tipo pared, que de otra forma se complica cuando se utilizan transformaciones con componentes cartesianos o covariantes. Por otro lado, cuando se emplean los componentes covariantes y contravariantes, el término de advección tiene una representación más complicada, lo que incrementa la dificultad de su solución; mientras que con los componentes cartesianos de velocidad se tiene mayor estabilidad numérica y pueden utilizarse pasos de tiempo más grandes.

 

Mallas compuestas

Si la región en la que se pretende generar la malla tiene una forma irregular, pueden emplearse múltiples bloques interconectados entre ellos. Se entiende por bloques a mallas curvilíneas delimitadas por cuatro ejes, como el caso indicado en la figura 1. Lo anterior se comprende mejor si se usa la analogía de las esponjas (Thompson et al., 1998). Se considera que una esponja originalmente con forma rectangular puede deformarse al estirarla o comprimirla mientras conserva los cuatro ejes que la delimitan; esto es análogo a lo que sucede con los sistemas curvilíneos: mientras en el espacio computacional la malla es rectangular, en el espacio físico la malla ha sido deformada para adaptarse a la forma de las fronteras. Existe cierto tipo de geometrías donde la malla puede generarse mediante varias mallas interconectadas entre sí, esto es como si se emplearan diferentes esponjas para conformar la forma del dominio físico. El enfoque anterior permite emplear sistemas coordenados curvilíneos, donde se elimina la restricción de requerir cuatro ejes que delimiten la región.

Este tipo de metodologías se ha empleado de manera amplia en la literatura. Se tienen dos categorías para este tipo de mallas: uno es donde los bloques que conforman la malla se traslapan entre sí, como se indica, por ejemplo, en Chesshire y Henshaw (1990) y Hu et al. (2006); otro tipo de mallas es donde los bloques se conectan sólo en sus fronteras, como se indica en Hauser et al. (1986) y Thompson et al. (1998).

El enfoque con traslape entre bloques tiene la ventaja de proporcionar una mayor flexibilidad para la generación de las mallas, porque los bloques no se obligan a coincidir en un eje. Pero se requiere, además de transferir información entre bloques, interpolar la información entre los vértices o celdas de las mallas, puesto que en general no son coincidentes. También es necesario plantear esquemas de solución iterativos entre los bloques.

Por otra parte, los esquemas sin traslape no requieren interpolación de un conjunto de vértices de un bloque a otro, puesto que no existen regiones en común, ya que sólo coinciden los puntos en los ejes de las fronteras entre los bloques. Otra ventaja es que al no existir regiones con redundancia en la malla, se simplifica el almacenamiento de la información y, en consecuencia, se incrementa la rapidez de cálculo.

La estructura en el sistema de ecuaciones que se produce al discretizar las ecuaciones diferenciales (ya sea las que gobiernan el flujo o las empleadas para generar la malla) tiene una forma peculiar si se toma en cuenta el esquema de numeración de los vértices, se realiza de forma secuencial —de un bloque a otro—, y al final se numeran los vértices en las fronteras de los mismos bloques. Este proceso se ejemplifica más adelante.

Las ecuaciones diferenciales que se emplean para generar la malla (descritas más adelante) se expresan como ecuaciones en diferencias con una plantilla de cálculo, como la indicada en la figura 3, lo que conduce a obtener un sistema de ecuaciones. Siguiendo el esquema de numeración de los vértices planteado aquí, si se considera una malla conformada por n bloques, el sistema resultante toma la forma:

En el sistema (7), las matrices A_i con i = 1, 2,..., n corresponden a la discretización de cada uno de los bloques que conforman la malla. La matriz A_Γ resulta de los vértices en las fronteras entre los bloques; el subíndice Γ hace referencia a las fronteras entre bloques. Los vectores [u]_i representan la solución en los bloques i, y [b]_i son los vectores de términos independientes en cada uno de los bloques.

Se observa que la expresión (7) es un sistema de ecuaciones que se encuentra expresado en bloques; se emplea el método de Gauss en bloques (Ortega, 1988) para transformarlo a un sistema con una matriz triangular superior:

 

Como puede verificarse con facilidad, las matrices del renglón inferior son:

Se observa que la solución en la frontera entre los bloques se obtiene al resolver el sistema de ecuaciones correspondiente al último renglón del sistema en bloques dado por la ecuación (8), cuya matriz y vector de términos independientes lo conforman las ecuaciones (9) y (10), respectivamente.

La solución en los bloques de la malla se obtiene por sustitución regresiva, pero dada la estructura de la matriz en bloques, se puede obtener la solución en cada bloque de forma independiente, al resolver el sistema de ecuaciones asociado con cada uno, que se obtiene como:

Con el fin de ejemplificar la metodología de numeración de los vértices de la malla, se presenta una región en forma de L, indicada en la figura 4a, que ha sido descompuesta con tres bloques.

La numeración de los vértices se muestra en el esquema de la figura 4b; se numeran de forma secuencial los vértices interiores del primero al último bloque, para terminar numerando los vértices que se encuentran en la frontera entre los mismos, que en la figura 4a se denota como Γ. En el cuadro 1 se indica la numeración global de los vértices, su numeración interna respecto a cada bloque o a la frontera Γ, y cuáles son los vértices que se encuentran en la vecindad, esto último es muy útil para determinar los vértices a ser usados en la plantilla mostrada en la figura 3, que al final conducen a generar un sistema de ecuaciones con una estructura como la indicada por la expresión (7).

Puede decirse que el cuadro 1 es similar a las tablas de incidencias que se tienen en las mallas no estructuradas; sin embargo, los datos contenidos en el cuadro 1 se generan de manera automática. Si los índices i, j indican el renglón y columna de un vértice dentro de un bloque, el identificador local de los vértices se determina como id local = j* nc + i, donde s es el número de nodos en la dirección horizontal, y de esta forma es posible determinar el identificador de cada uno de los nueve vértices vecinos que rodean al punto C indicado en la figura 3, sumando o restando la unidad a los índices i, j, que se tienen en la misma figura.

 

Generación numérica de la malla

Existen básicamente tres metodologías para la generación de la malla: con métodos algebraicos, por medio de ecuaciones diferenciales o con métodos variacionales. En este trabajo se emplean un método basado en ecuaciones diferenciales elípticas. Los generadores elípticos tienen la ventaja de crear una malla con una distribución uniforme de los vértices interiores, incluso cuando la forma de los bordes sea muy irregular (Knupp y Steinberg, 1993). Se trata de un problema de valor de frontera (Mejía y Berezowsky, 1996), ya que se conoce la posición de los bordes, y lo que se busca es determinar la posición de los vértices interiores de la malla.

La ecuación diferencial que se resuelve para generar la malla es (Thompson et al., 1998):

Los subíndices ()_ξ,η denotan derivación respecto a los ejes coordenados curvilíneos; los elementos métricos a_i,j son definidos por la expresión (4). Los coeficientes P^k_ij son funciones de control. Si estos son cero, entonces (12) es una ecuación de tipo Laplaciano. Las funciones de control se especifican de acuerdo con las condiciones que se deseen obtener en la malla; esto es, ortogonalidad en las fronteras y en los vértices interiores, o lograr un tamaño de celdas dado en ciertas regiones. Los valores que toman las funciones de control para estos casos pueden encontrarse, por ejemplo, en Thompson et al. (1998).

La discretización con diferencias finitas de (12) conduce a un sistema de ecuaciones lineal de nueve diagonales, que produce una plantilla de cálculo para las ecuaciones en diferencias, como la indicada en la figura 3. Dado que los elementos métricos a_i,j dependen de la conformación de la malla (ubicación de los vértices interiores ), el proceso de solución es iterativo, partiendo de una malla inicial que se genera, por ejemplo, con interpolación transfinita. Sin embargo, los autores han utilizado para generar la malla inicial un sistema Laplaciano de generación, que consiste en dar solución a:

Para resolver la ecuación (13), sólo se requiere conocer los bordes; con este procedimiento se han obtenido resultados satisfactorios; además, esta técnica para generar la malla inicial es más apropiada para los sistemas de mallas compuestas. El sistema de ecuaciones resultante de las expresiones (12) y (13), con un esquema para numerar los vértices como se explicó antes, puede reducirse a un sistema como el indicado en (8) y resolverse con el esquema propuesto.

Para aplicar este método se requiere, además de conocer la ubicación de los bordes, dividir la región de forma adecuada en bloques, ensamblar el sistema de ecuaciones y resolverlo como fue descrito en los párrafos anteriores.

 

Ejemplos

Con el fin de mostrar las ventajas que proporcionan este tipo de mallas para ser aplicados a geometrías complejas, se muestran tres casos de aplicación, en los que las mallas fueron obtenidas con un generador numérico que utiliza la metodología aquí propuesta. El primer ejemplo corresponde a la unión de dos canales a un ángulo agudo. Para este caso, la región se divide en cuatro bloques, tal como se muestra en la figura 5a. La malla generada se muestra en la figura 5b. En este ejemplo pueden existir otras opciones para definir los bloques, por ejemplo, considerar los bloques 2, 3 y 4 como uno solo, de esta forma se definirían sólo dos bloques: uno para el canal principal y otro para el canal que llega en ángulo agudo (bloque 1); sin embargo, los autores encontraron que es más sencillo estructurar la información si se tiene una conexión completa entre los ejes de los bloques. Esto se ve, por ejemplo, en la figura 5a, donde el eje norte del bloque 1 se conecta con el eje sur del bloque 3; o el eje este del bloque 2 se conecta con el eje oeste del bloque 3.

En este caso, si se emplea una malla cartesiana rectangular, las fronteras correspondientes al canal del bloque 1 quedan representadas de forma escalonada; este problema se reduce al emplear una malla con mayor refinamiento, sin embargo ello implica un aumento en el tiempo de cálculo. Por otra parte, si para este mismo ejemplo se emplea una malla curvilínea conformada por un único bloque, la malla queda con celdas muy distorsionadas.

El segundo caso analizado corresponde a un estuario. La geometría de la frontera del dominio se toma de Shi et al. (2001); la región analizada comprende la confluencia de tres ríos que descargan hacia el mar (bloques 8 al 13), la entrada de estos ríos corresponden a los bloques 1, 2 y 5, indicados en la figura 6a, que confluyen para llegar al canal representado por el bloque 7; la geometría del dominio y la descomposición en bloques realizada para generar la malla se indican en esta misma figura; la malla fue dividida en 13 bloques. En la figura 6b se muestra la malla generada con la metodología propuesta. Se observa que la malla representa de forma adecuada la forma de las fronteras; está conformada por 1 827 vértices internos y 377 vértices en las fronteras; el grado de refinamiento requerido, si se emplea una malla rectangular para una adecuada representación de las fronteras, incrementaría de manera considerable el número de vértices.

El último caso analizado corresponde a la bifurcación del río Mezcalapa en los ríos Samaria y Carrizal, en el estado de Tabasco, México; la conformación del terreno para determinar las posición de las orillas de los ríos se tomó de Jiménez et al. (2007). En la figura 7a puede observarse que la bifurcación tiene además dos islas. La malla se generó con el uso de 18 bloques, que se indican en la misma figura; la malla obtenida con el generador se muestra en la figura 7b.

En los tres ejemplos, las fronteras entre los bloques indicadas como líneas discontinuas en los esquemas mostrados de las figuras 5a, 6a y 7a no corresponden a las fronteras reales entre bloques, sino que esta ubicación es resuelta por el mismo esquema, de tal forma que cumpla con la ecuación (12).

 

Conclusiones

Las mallas curvilíneas resultan útiles cuando se tienen fronteras con formas irregulares, las cuales, si se emplean, por ejemplo, mallas rectangulares, requieren de un mayor refinamiento para representar de forma adecuada las fronteras, lo que impacta en el tiempo de cálculo. Cuando la forma del dominio es compleja, el enfoque tradicional de emplear un único bloque produce una malla con celdas distorsionadas o inclusive no se puede generar la malla. La conformación de la malla compuesta por bloques permite que las celdas tengan una forma más regular; el método propuesto aquí permite generar una malla de este tipo. El sistema de ecuaciones resultante para obtener la malla es estructurado por bloques, lo que permite resolver de manera independiente cada bloque una vez que se obtiene la solución en las interfaces entre ellos. Además, debido a que la ubicación frontera entre los bloques es una incógnita también, se obtiene una transición suave de la malla entre los mismos. La calidad de las mallas obtenidas es satisfactoria, como puede observarse en los tres casos analizados, que fueron calculados con un generador de malla que sigue la metodología planteada en este trabajo.

El uso de mallas curvilíneas implica la transformación de las ecuaciones del flujo, lo cual aumenta el número de términos en las mismas. La complejidad de las ecuaciones transformadas varía de acuerdo con los componentes de velocidad que se utilicen en la transformación. Estos componentes son los covariantes, contravariantes y físicos; cada uno presenta ventajas y desventajas en los aspectos del manejo de las condiciones de frontera, número de términos en las ecuaciones o estabilidad numérica. El criterio para utilizar alguna de ellas dependerá del problema a resolver.

Cabe resaltar que aunque el esquema propuesto aquí tuvo su origen en la generación de mallas para resolución de flujos bidimensionales, el método puede aplicarse para la solución de otro tipo de problemas. El proceso es el mismo, las ecuaciones de gobierno del fenómeno estudiado deben transformarse al sistema coordenado curvilíneo.

 

Agradecimientos

Los autores agradecen las certeras observaciones del revisor anónimo, que ayudaron a mejorar el escrito. También agradecen al Conacyt por el apoyo financiero para realizar esta investigación.

 

Referencias

AHUSBORDE, E. and GLOCKNER, S. A 2D Block-Structured Mesh Partitioner for Accurate Flow Simulations in Non-Rectangular Geometries. Computers & Fluids. Vol. 43, 2011, pp. 2-13.         [ Links ]

BAGHLANI, A., TALEBBEYDOKHTI, N., and ABEDINI, M.J. A Shock Capturing Model Based on Flux-Vector Splitting Method in Boundary-Fitted Curvilinear Coordinates. Applied Mathematical Modeling. Vol. 32, 2008, pp. 249-266.         [ Links ]

CHESSHIRE, G. and HENSHAW, W.D. Composite Overlapping Meshes for the Solution of Partial Differential Equations. Journal of Computational Physics. Vol. 90, No. 1, 1990, pp. 1-64.         [ Links ]

FERZIGER, J.H. and PERIC, M. Computational Methods for Fluid Dynamics. Tercera edición. Berlín: Springer, 2002, 422 pp.         [ Links ]

JIMÉNEZ, A.A., GRACIA, J., BEREZOWSKY, M. y MARTÍNEZ, J. Estudio de la bifurcación de un río con modelación numérica. México, D.F.: Instituto de Ingeniería, CI-29, 2007, 45 pp.         [ Links ]

HAUSER, J., PAAP, H.G., EPPEL, D., and SENGUPTA, S. Boundary Conformed Co-ordinate Systems for Selected Two-Dimensional Fluid Flow Problems. Part I: Generation of BFGs. International Journal for Numerical Methods in Fluids. Vol. 6, 1986, pp. 507-527.         [ Links ]

HU, K., MINGHAM, G., and CAUSTON, D.M. A Mesh Patching Method for Finite Volume Modeling of Shallow Water Flow. International Journal for Numerical Methods in Fluids. Vol. 50, 2006, pp. 1381-1404.         [ Links ]

KNUPP, P. and STEINBERG, S. Fundamentals of Grid Generation. Boca Ratón, USA: CRC Press, 1993, 286 pp.         [ Links ]

MEJÍA, M.A. y BEREZOWSKY, M. Numerical Generation of Grids with Curvilinear Coordinates for Free Surface Flow Calculations. Hydraulic Engineering in Mexico. Vol. IX, No. 3, September-December, 1996, pp. 13-24.         [ Links ]

ORTEGA, J.M. Introduction to Parallel and Vector Solution of Linear Systems. New York: Plenum Press, 1988, 305 pp.         [ Links ]

ROMANENKOV, D.A., ANDROSOV, A.A., and VOLTZINGER, N.E. Comparison of Forms of the Viscous Shallow-Water Equations in the Boundary-Fitted Coordinates. Ocean Modelling. Vol. 3, 2001, pp. 193-216.         [ Links ]

SANKARANARAYANAN, S. and SPAULDING, M.L. A Study of the Effects of Grid Non-Orthogonality on the Solution of Shallow Water Equations in Boundary-Fitted Coordinate Systems. Journal of Computational Physics. Vol. 184, 2003, pp. 299-320.         [ Links ]

SHI, F., DALRYMPLE, R.A., KIRBY, J.T. CHEN, Q., and KENNEDY, A. A Fully Nonlinear Boussinesq Model in Generalized Curvilinear Coordinates. Coastal Engineering. Vol. 42, 2001, pp. 337-358.         [ Links ]

SOTO, C.G. y BEREZOWSKY, V.M. Numerical Simulation of Wetting and Drying in Shallow Waters Using a Curvilinear Adaptive Scheme. Hydraulic Engineering in Mexico. Vol. XVIII, No. 3, July-September, 2003, pp. 29-44.         [ Links ]

THOMPSON, J.F., WARSI, Z.U.A., and WAYNE, C. Numerical Grid Generation, Foundations and Applications. Mississippi: North-Holland, 1985, 483 pp.         [ Links ]

THOMPSON, J.F., SONI, B.K., and WEATHERILL, N.P. Handbook of Grid Generation. Boca Ratón, USA: CRC Press, 1998, 1096 pp.         [ Links ]

WARSI, Z.U.A. Fluid Dynamics, Theoretical and Computational Approaches. Boca Ratón, USA: CRC Press, 1998, 683 pp.         [ Links ]