Nota técnica

 

Resolución de la ecuación de la advección-dispersión en una dimensión, usando funciones splines

 

Solving an one-dimensional advection-dispersion equation with spline functions

 

David Ernesto Marón-Domínguez*, Alberto Gutiérrez-de-la-Rosa

 

Instituto Superior Politécnico "José Antonio Echeverría", Cuba. *Autor de correspondencia.

 

Dirección institucional de los autores:
Dr. David Ernesto Marón Domínguez
Lic. Alberto Gutiérrez de la Rosa
Centro de Estudios de Matemática
Instituto Superior Politécnico José Antonio Echeverría (CUJAE)
Calle 114 # 11901 e/Ciclo-vía y Rotonda
Mariano, La Habana, Cuba
Teléfono: +53 (7) 2663 512
dmaron@cemat.cujae.edu.cu
agutierrez@cemat.cujae.edu.cu.

 

Recibido: 14/02/2012
Aceptado: 21/09/2012

 

Resumen

Se muestra una aplicación de los polinomios splines cúbicos a la resolución numérica de la ecuación diferencial 1D de la dispersión. Para el caso no estacionario, la variación en el tiempo se refleja en los coeficientes del polinomio spline y la discretización en el tiempo se hace aplicando el Método de las Diferencias Finitas. Todos los algoritmos son implementados computacionalmente en el asistente matemático Matlab. Se comparan los resultados obtenidos de las soluciones aproximadas con las mediciones de un caso real de una prueba de trazador y además con la solución del Método de los Elementos Finitos.

Palabras clave: splines cúbicos, interpolación, ecuación diferencial, dispersión.

 

Abstract

The application of cubic spline polynomials to the numeric solution of a one-dimensional differential dispersion equation is presented. For the non-stationary case, the variation in time was reflected by the spline polynomial coefficients and the discretization in time was obtained using the finite difference method. All the algorithms were implemented with the MATLAB mathematical assistant. The results were compared to tracer test measurements from a real case as well as with the finite element method solution.

Keywords: cubic splines, interpolation, differential equation, dispersion.

 

Introducción

Los polinomios splines tienen gran aplicación en la interpolación de funciones. En el problema de la interpolación con los polinomios splines es necesario añadir condiciones adicionales en los extremos del intervalo. Samarski (1986) plantea el problema de la interpolación por tramos 1D a partir de los polinomios splines cúbicos de forma que debe resolver un sistema lineal de ecuaciones con matriz tridiagonal. Para obtener solución única añade dos condiciones adicionales, asociadas con la segunda derivada en los extremos, lo cual se corresponde con el llamado spline natural (Samarski, 1986). Álvarez et al. (2004) plantean la obtención del polinomio cúbico, integrando dos veces un polinomio lineal que interpola los valores de la segunda derivada en un intervalo. Los splines también se aplican en la resolución de ecuaciones diferenciales, con lo cual se obtiene que las funciones solución cumplen condiciones de continuidad de las derivadas en puntos interiores de la región sin necesidad de tener que conocer de forma previa los valores de las derivadas en dichos puntos. Szymkiewicz (1993) descompone la ecuación 1D del transporte en dos ecuaciones, una con la parte advectiva y otra ecuación con la parte difusiva (Szymkiewicz, 1993). Utiliza el método de las características junto con los splines cúbicos para resolver la ecuación de la parte advectiva y utiliza el Método de los Elementos Finitos para resolver la ecuación de la parte difusiva. Tsai et al. (2004) también utilizan los polinomios splines cúbicos para resolver la ecuación 1D no estacionaria del transporte (Tsai et al., 2004) y emplean diferentes tipos de condiciones adicionales en los extremos del intervalo.

El objetivo de este trabajo es mostrar la resolución de la ecuación diferencial 1D de la dispersión, utilizando los splines cúbicos para un caso real de estudio de una prueba de trazador, así como evidenciar las ventajas de aplicar este método que fundamentalmente radica en que la solución obtenida por este método garantiza la suavidad de la misma en cada uno de los puntos de la discretización de la región de estudio, lo cual no ocurre con el Método de los Elementos Finitos.

 

La función spline cúbica

Se tiene una red formada por los subintervalos [x_i, x_i+1], con i = 1,...N_x, de un intervalo [0, L] La función u = u(x) definida en dicho intervalo se puede aproximar por un spline cúbico, expresado en función del extremo izquierdo del intervalo de la forma:

Las condiciones de interpolación que debe cumplir el spline son las siguientes:

Las condiciones de continuidad del spline cúbico y las condiciones de suavidad de su primera y segunda derivadas son las siguientes:

Como puede observarse de (2) y de (3) se tiene N_x + 1 condiciones de interpolación, y de (4) hasta (6) se tiene 3(N_x - 1) condiciones de continuidad; por lo tanto se tienen 4N_x - 2 condiciones en total y hay 4N_x coeficientes incógnitas. Teniendo en cuenta las condiciones de (1) a (6) se obtiene el siguiente sistema de ecuaciones:

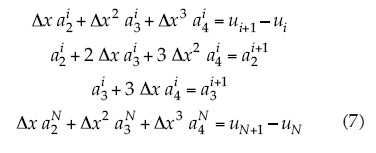
donde i = 1, ..., N_x – 1 y Δx representa la longitud del intervalo.

En el problema de la interpolación se conocen todos los valores u_i con i = 1,..., N_x + 1, de la función a interpolar u = u(x) en los N_x + 1 nodos. Los valores de los coeficientes aⁱ_l, correspondientes a los términos independientes de (1), coinciden con los valores de la función incógnita u_i; por lo tanto, el número de coeficientes incógnitas se reduce a 3N_x y el número total de ecuaciones se reduce a 3N_x - 2. Se le añaden dos condiciones adicionales en los extremos para que el problema tenga solución única. Para cada valor de i, con i = 1,..., N_x - 1, las tres primeras ecuaciones del sistema (7) se pueden escribir en notación matricial en la forma:

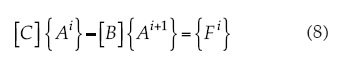
donde C y B son matrices, y A y F son vectores, según se muestran a continuación:

La resolución del sistema de ecuaciones (8), en conjunto con las dos condiciones adicionales en los extremos del intervalo, da la solución del problema de interpolación.

 

Aplicación de los polinomios splines cúbicos a la resolución de la ecuación de la dispersión 1D no estacionaria en un medio poroso

Se considera la ecuación de la dispersión 1D no estacionaria en un medio según la forma (Marón, 2002):

donde θ es la porosidad del medio; R_T, el coeficiente de retardo; C = C (x, t), la función incógnita que representa la concentración; U, la velocidad del agua; D, el coeficiente de dispersión, y λ es el coeficiente de degradación o de decaimiento. A la ecuación anterior hay que añadirle una condición inicial y dos condiciones de frontera:

Como este problema es no estacionario, entonces la variación en el tiempo se propone que sea recogida en los coeficientes del spline cúbico, de forma que el polinomio tiene la forma:

Sustituyendo (10) en (9), para X = X_i se obtiene la expresión:

donde i = 2,..., N_x y k = 2,..., N_t + 1. Para el polinomio del primer tramo del spline correspondiente a i = 1 se obtiene:

la expresión anterior tiene incluida la condición de frontera en el extremo izquierdo. Evaluando el polinomio spline del último tramo en X = X_Nx+1, se obtiene:

Las ecuaciones (11), (12) y (13) expresan que se debe satisfacer la ecuación diferencial (9) en todos los puntos de la red. Para cada tiempo, el sistema final de ecuaciones se obtiene ensamblando el sistema (8), junto con las ecuaciones (11), (12) y (13).

Para el cálculo de la solución en el primer intervalo de tiempo es necesario calcular los valores de los coeficientes de los splines en todos los tramos. Para esto se hace uso de la condición inicial, utilizando la interpolación propuesta por el sistema (8).

 

Comprobación de los algoritmos propuestos utilizando una aplicación práctica

Con el objetivo de comprobar los algoritmos propuestos en este trabajo se hace uso de los mismos datos o mediciones reales de la prueba de trazador detallada en el artículo de Marón (2002). En el citado trabajo, los datos fueron utilizados para la calibración o estimación de los parámetros hidráulicos de un humedal construido en el laboratorio. Marón utilizó, para la discretización en el espacio, el Método de los Elementos Finitos (MEF), con ayuda de los elementos cuadráticos y cúbicos. Esto permite que la comparación del método desarrollado en este trabajo con los splines se haga no sólo con los datos reales observados sino también con los resultados obtenidos por el MEF cúbico, ya que los polinomios utilizados para la construcción del spline fueron cúbicos. Para la discretización en el tiempo se hizo uso del Método de las Diferencias Finitas, al igual que en el artículo citado. El algoritmo de cálculo propuesto fue implementado en el asistente matemático Matlab, el cual se acopló con un algoritmo de optimización, que ayudó a la estimación de los parámetros de dispersión, retardo y degradación (D, R_T y λ).

En el cuadro 1 se muestran los resultados de la calibración de dichos parámetros con el algoritmo de los splines y se comparan con los resultados obtenidos por el MEF cúbico, obtenidos por Marón en su trabajo (Marón, 2002).

En el cuadro 1 se aprecia la no existencia de diferencias sustanciales entre los valores obtenidos por el MEF desarrollado por Marón (Marón, 2002) y el método utilizado por los autores. Se observa que no se detectó retardo en ambos casos, y se aprecia buena aproximación en los resultados de las estimaciones de los coeficientes de dispersión y degradación.

En la figura 1 se muestran las concentraciones observadas en las secciones x = 0.9 m y x = 1.9 m, correspondientes a los puntos de observación, en conjunto con las obtenidas según el algoritmo desarrollado en este trabajo a partir de los splines con polinomios cúbicos y las obtenidas según el MEF con elementos cúbicos, referidas por Marón en su trabajo.

En la figura 1 se observa que se han obtenido buenas aproximaciones entre las concentraciones observadas, (Cobs(*)), y las calculadas, (Ccal(o)), en ambas secciones (gráficas de la derecha). Es bueno señalar, además, que la comparación se puede hacer entre los valores calculados con los splines y los valores obtenidos por el MEF referidos en el trabajo de Marón (Marón, 2002). Para el algoritmo correspondiente a los splines cúbicos, se calculó el número de Peclet, cuyo valor fue 2.5571.

 

Conclusiones

Para el ejemplo real utilizado se evidenció que se obtuvieron resultados satisfactorios para valores del número de Peclet mayor que 1.

El método desarrollado por los splines cúbicos aporta resultados superiores al Método de los Elementos Finitos, ya que la función solución satisface en los nodos interiores de la red condiciones de suavidad hasta la segunda derivada, lo cual no se cumple en el Método de los Elementos Finitos.

Queda esbozado el uso de un método que muestra resultados satisfactorios para que un especialista en el estudio de aguas residuales disponga de una herramienta más.

 

Referencias

ÁLVAREZ, B.M., GUERRA, H.A. y LAU, F.R. Matemática numérica. La Habana: Editorial Félix Varela, 2004.         [ Links ]

MARÓN, D.E. Un modelo de dispersión en el transporte de contaminantes. Ingeniería Hidráulica en México. Vol. XVII, núm.3, julio-septiembre, 2002, pp. 89-101,         [ Links ]

SAMARSKI, A.A. Introducción a los métodos numéricos. Moscú: Editorial Mir, 1986.         [ Links ]

SZYMKIEWICZ, R. Solution of the advection-diffusion equation using the spline function and finite elements. Communications in Numerical Methods in Engineering. Vol. 9, 1993, pp. 197-206.         [ Links ]

TSAI, T-L., YANG, J-C., and HSIUNG, L-H. Characteristics Method Using Cubic-Spline Interpolation for Advection-Diffusion Equation. Journal Hydraulic Engineering. Vol. 130, No. 6, 2004.         [ Links ]